Melting Phenomenon in a Squeezed Rheology of Reactive Rate Type Fluid

Introduction

Recently, scientists and researchers have shown intent to analyze the features of non-Newtonian fluid flow imposed by squeezed surfaces, regarding their wide-spread build up and trade area in many industrial and biological processes, such as in the polymer industry, compression, injection shaping, liquid-metal lubrication, formation of paper sheets and thin fiber, molding of plastic sheets and metal and squeezed film, through which power is transmitted. Many researchers discussed the Jeffrey fluid model corresponding to various physical aspects. But this model is not studied widely with the squeezing phenomenon. At beginning, Stefan [1] depicted work on squeezing flow. Muhammad et al. [2] exposed squeezed nanomaterial flow with modified version of heat and mass fluxes. Adesanya et al. [3] showed the radiative and chemically reactive flow of Powell-Eyring liquid squeezed through infinite parallel walls. MHD-squeezed fluid flow confined between parallel two plates under suction/injection has been constructed by Su and Yin [4]. Naduvinamani and Shankar [5] disclosed the heat transport phenomenon due to radiative MHD-squeezed flow in a Casson fluid. Ullah et al. [6] exhibited squeezed flows through porous medium under aspect of magnetic field strength. Lahmar et al. [7] demonstrated the characteristics of the heat transport phenomenon due to varying thermal conductivity on MHD-squeezed nanoparticle. Khan et al. [8] analyzed entropy generation features in autocatalytic-squeezed flow through parallel sheets analytically.

Characteristics of heat transfer have increased noteworthy interest of recent explorers and engineers because of various technical processes in the area of engineering, physiological and industrial processes, including glass blowing and glass fiber productions, wire coating, paper making, metal spinning, expulsion of plastic sheets by aerodynamic, drawing of plastic films and unceasing casting. However, little attention is paid to disclose the features of heat transport through melting phenomenon. It has widespread applications, such as the making of semiconductors, melting permafrost and hardening of magma flow, heat exchanger coils coated by freeze soil in grounded pump, sewage treatment via freeze process, melting of soil, welding processes, and casting of manufacturing processes. Behavior of double-diffusive convection in stagnant Maxwell liquid flow considering melting phenomenon has been explored by Hayat et al. [9]. Krishnamurthy et al. [10] scrutinized the Williamson nanofluid flow via porous structure. Behavior of Carreau liquid flow caused by stretchable cylinder considering melting phenomenon has been illustrated by Hashim et al. [11]. Soomro et al. [12] explored the melting effects in radiative Sisko fluid flow past a moving sheet. Mabood et al. [13] depicted the aspects of heat transport through melting condition in radiative Sisko nanofluid flowing over stretchable sheet with heat generation/absorption. Javed et al. [14] reported the domination of heat transport phenomenon via melting affects the MHD reactive liquid flow through non-porous stretchable surfaces of varying thickness. Hayat et al. [15] exhibited the features of melting flow phenomenon in the squeezed third grade liquid flow past a plate with modified heat flux phenomenon. Irreversibility and melting heat transport properties in dissipative flow of liquid passed through a stretched sheet has been exhibited by Hayat et al. [16]. Properties of melting flow phenomenon in hydro-magnetic nanomaterial flow are depicted by Dinh et al. [17]. Their investigations motivated a few other researchers to work on heat transport in different conditions [18, 19].

A literature survey indicates that researchers have disclosed the properties of squeezed Newtonian and non-Newtonian fluid flow with different boundary conditions of heat transfer widely. But such analysis of squeezing flow with melting heat transport has not explored as of yet. So, the main strategic concern is to fill this void. Thus, the present attempt is concerned to demonstrate the melting mechanism in squeezed Jeffrey fluid flow through two parallel plates. Behavior of heat with mass transport is modeled and exposed considering thermal radiation, viscous dissipation and chemical reaction. The transformed coupled non-linear differential system is evaluated via a homotopy technique [20–24]. Graphical studied is evaluated for the features of velocity, liquid temperature and fluid concentration via emerging parameters. Moreover, the layout of the current paper is as follows. Mathematical formulation describes the mathematical modeling of governing equations related to the work under consideration. Homotopy analysis solutions illustrates the solution method utilized for the flow analysis. The acquired results are discussed and analyzed in Analysis. Closing remarks is related to key points of present paper.

Mathematical Formulation

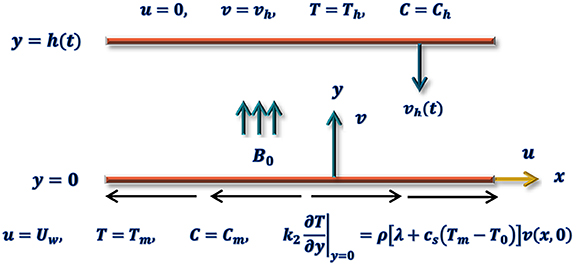
Consider unsteady, incompressible squeezed Jeffrey fluid flow between horizontal two plates. The bottom plate is located at y = 0 while top sheet is placed at $y=h(t)=\sqrt{\nu (1-\gamma t)/a}$, which approaches stretchable bottom plate with squeeze velocity. Fluid is assumed to be electrically conducting so that fluid is influenced by applied magnetic field along vertical direction. The induced magnetic and electric fields are neglected, considering the small Reynolds number (magnetic). Heat transport phenomenon is characterized by a modern and advanced condition at boundary (i.e., melting heat transport). Viscous dissipation and thermal radiation are assumed to elaborate the heat transfer phenomenon. Features of mass transfer are explored via first order chemical reaction. We consider Cartesian co-ordinates (x, y) and physical situation to be exposed in Figure 1. The flow problem under the basic conservative laws takes the form:

$\begin{array}{ll}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,\hfill & (1)\end{array}$

$\begin{array}{l}\rho \left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)=-\frac{\partial p}{\partial x}+\frac{\mu }{1+{\lambda }_1}(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\hfill \\ +{\lambda }_2(\frac{{\partial }^{3}u}{\partial x^2\partial t}+u\frac{{\partial }^{3}u}{\partial x^3}+v\frac{{\partial }^{3}u}{\partial x^2\partial y}+2\frac{\partial u}{\partial x}\frac{{\partial }^{2}u}{\partial x^2}+2\frac{\partial v}{\partial x}\frac{{\partial }^{2}u}{\partial x\partial y}\hfill \\ +\frac{{\partial }^{3}u}{\partial y^2\partial t}+\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial y\partial x}+u\frac{{\partial }^{3}u}{\partial y^2\partial x}+\frac{\partial v}{\partial y}\frac{{\partial }^{2}u}{\partial y^2}+v\frac{{\partial }^{3}u}{\partial y^3}+\frac{\partial u}{\partial y}\frac{{\partial }^{2}v}{\partial x^2}\hfill \\ +\frac{\partial v}{\partial y}\frac{{\partial }^{2}v}{\partial x\partial y}))-\frac{{\sigma }_1{B}_0^2}{1-\gamma t}u,\hfill & (2)\end{array}$

$\begin{array}{l}\rho \left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)=-\frac{\partial p}{\partial y}+\frac{\mu }{1+{\lambda }_1}(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}\hfill \\ +{\lambda }_2(\frac{{\partial }^{3}v}{\partial x^2\partial t}+u\frac{{\partial }^{3}v}{\partial x^3}+v\frac{{\partial }^{3}v}{\partial x^2\partial y}+2\frac{\partial v}{\partial y}\frac{{\partial }^{2}v}{\partial y^2}+2\frac{\partial u}{\partial y}\frac{{\partial }^{2}v}{\partial x\partial y}\hfill \\ +\frac{{\partial }^{3}v}{\partial y^2\partial t}+\frac{\partial u}{\partial x}\frac{{\partial }^{2}u}{\partial y\partial x}+u\frac{{\partial }^{3}v}{\partial y^2\partial x}+\frac{\partial v}{\partial x}\frac{{\partial }^{2}u}{\partial y^2}+v\frac{{\partial }^{3}v}{\partial y^3}+\frac{\partial u}{\partial x}\frac{{\partial }^{2}v}{\partial x^2}\hfill \\ +\frac{\partial v}{\partial x}\frac{{\partial }^{2}v}{\partial x\partial y})),\hfill & (3)\end{array}$

$\begin{array}{l}\rho c_p\left(\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)=k_2\left(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}\right)\hfill \\ +\frac{16{\sigma }^{\ast }{T}_{\infty }^3}{3k_1}\frac{{\partial }^{2}T}{\partial y^2}+\frac{\mu }{1+{\lambda }_1}(2{\left(\frac{\partial u}{\partial x}\right)}^2+2{\left(\frac{\partial v}{\partial y}\right)}^2\hfill \\ +{\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)}^2+{\lambda }_2(2\frac{\partial u}{\partial x}\left(\frac{{\partial }^{2}u}{\partial x\partial t}+u\frac{{\partial }^{2}u}{\partial x^2}+v\frac{{\partial }^{2}u}{\partial x\partial y}\right)\hfill \\ +2\frac{\partial v}{\partial y}\left(\frac{{\partial }^{2}v}{\partial y\partial t}+v\frac{{\partial }^{2}v}{\partial y^2}+u\frac{{\partial }^{2}v}{\partial x\partial y}\right)+\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)(\frac{{\partial }^{2}u}{\partial y\partial t}\hfill \\ +\frac{{\partial }^{2}v}{\partial x\partial t}+u\frac{{\partial }^{2}u}{\partial x\partial y}+v\frac{{\partial }^{2}u}{\partial y^2}+u\frac{{\partial }^{2}v}{\partial x^2}+v\frac{{\partial }^{2}v}{\partial x\partial y}))),\hfill & (4)\end{array}$

$\begin{array}{ll}\left(\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}\right)=D\left(\frac{{\partial }^{2}C}{\partial x^2}+\frac{{\partial }^{2}C}{\partial y^2}\right)-K\left(t\right)C.& (5)\end{array}$

Here, velocity components are u and v along x and y direction, respectively. p represents pressure, μ represents absolute viscosity, γ is the dimensional positive constant, B₀ represents magnetic field, T denotes the fluid temperature, ρ represents the fluid density, σ₁ denotes electric conductivity, C denotes fluid concentration, k₂ is the co-efficient of thermal conductivity, specific heat is c_p, k₁ is absorption coefficient, σ^* denotes the Stefan-Boltzmann constant, D is the diffusion co-efficient, ν is the kinematics viscosity, K(t) = K₀/1 − γt is time-dependent reaction rate with reaction rate K₀, λ₁ is relaxation time and λ₂ is ratio among relaxation and retardation time.

FIGURE 1

Figure 1. Physical situation of the problem.

The boundary conditions are as follow

$\begin{array}{l}u=U_w=\frac{ax}{1-\gamma t},T=T_m,C=C_m,aty=0,\hfill \\ u=0,v=v_h=\frac{dh}{dt}=-\frac{\gamma }{2}\sqrt{\frac{\nu }{a\left(1-\gamma t\right)}},T=T_h,\hfill \\ C=C_{h}aty=h\left(t\right),\hfill \\ {k_2\frac{\partial T}{\partial y}|}_{y=0}=\rho \left[\lambda +c_s\left(T_m-T_0\right)\right]v\left(x,0\right).\hfill & (6)\end{array}$

Transformations are taken as follows

$\begin{array}{l}\eta =\frac{y}{h\left(t\right)},\psi =\sqrt{\frac{a\upsilon }{1-\gamma t}}xf\left(\eta \right),u=U_w{f}^{\prime }\left(\eta \right),\hfill \\ v=-\sqrt{\frac{a\upsilon }{1-\gamma t}}f\left(\eta \right),\hfill \\ \theta \left(\eta \right)=\frac{T-T_m}{T_h-T_m},\varphi \left(\eta \right)=\frac{C-C_m}{C_h-C_m}.\hfill & (7)\end{array}$

Pressure term is eliminated from equations (2) and (3), governing equations in view of equation (7) take the forms:

$\begin{array}{ll}\begin{array}{l}{f}^{(iv)}+\left(1+{\lambda }_1\right)\left(f{f}^{‴}-f^{\prime }{f}^{″}-\frac{S_q}{2}\left(3f^{″}+n{f}^{‴}\right)\right)\hfill \\ +\beta \left(\frac{S_q}{2}\left(5f^{\left(iv\right)}+\eta f^{\left(v\right)}\right)+2f^{″}{f}^{‴}-f^{\prime }{f}^{\left(iv\right)}-f{f}^{\left(v\right)}\right)\hfill \\ -H{a}^2{f}^{″}=0,\hfill \end{array}& (8)\end{array}$

$\begin{array}{ll}\begin{array}{l}\left(1+{\lambda }_1\right)\left(1+N_r\right){\theta }^{″}+Pr\left(1+{\lambda }_1\right)\left(f{\theta }^{\prime }-\frac{S_q}{2}\eta {\theta }^{\prime }\right)\hfill \\ +PrEc({\left(f^{″}\right)}^2+4\delta {\left(f^{\prime }\right)}^2+\beta \left(4{\delta }^2(\frac{S_q}{2}(2{\left(f^{\prime }\right)}^2+\eta f^{\prime }{f}^{″}\right)\hfill \\ -f{f}^{\prime }{f}^{″})+(\frac{S_q}{2}\left(3{\left(f^{″}\right)}^2+\eta f^{″}{f}^{‴}\right)+f^{\prime }{\left(f^{″}\right)}^2\hfill \\ -f{f}^{″}{f}^{‴})))=0,\hfill \end{array}& (9)\end{array}$

$\begin{array}{ll}{\varphi }^{″}-Sc\left(\frac{S_q}{2}\eta {\varphi }^{\prime }-f{\varphi }^{\prime }\right)-Sc\sigma \varphi =0.& (10)\end{array}$

The subjected boundary conditions are

$\begin{array}{l}f\left(1\right)=\frac{S_q}{2},f^{\prime }\left(0\right)=1,f^{\prime }\left(1\right)=0,M{\theta }^{\prime }\left(0\right)+Prf\left(0\right)=0,\hfill \\ \theta \left(0\right)=0,\theta \left(1\right)=1,\varphi \left(0\right)=0,\varphi \left(1\right)=1,\hfill & (11)\end{array}$

where squeezing parameter is S_q, Deborah number is β, magnetic parameter is Ha, Prandtl number is Pr, Schmidt number is Sc, thermal radiation parameter is N_r, Eckert number is Ec, the chemical reaction parameter is σ and the melting parameter is M.

These dimensionless quantities are given by

$\begin{array}{l}{S}_q=\frac{\gamma }{a},\beta =\frac{a{\lambda }_2}{1-\gamma t},H{a}^2=\frac{{\sigma }_1{B}_0^2}{\rho a},N_r=\frac{16{\sigma }^{\ast }{T}_{\infty }^3}{3k_1{k}_2},\hfill \\ Pr=\frac{\mu c_p}{k_2},Sc=\frac{\nu }{D},\hfill \\ Ec=\frac{a^2{x}^2}{c_p{\left(1-\gamma t\right)}^2\left(T_h-T_m\right)},\sigma =\frac{K_o}{a},\hfill \\ M=\frac{c_p\left(T_h-T_m\right)}{\left[\lambda +c_s\left(T_m-T_0\right)\right]},\delta =\sqrt{\frac{\nu \left(1-\gamma t\right)}{a{x}^2}}.\hfill & (12)\end{array}$

Viscous dissipation effect vanishes when Ec = 0. Further, σ > 0 gives destructive and σ < 0 gives generative chemical reactions. When β = 0, λ₁ = 0, Jeffrey fluid converts to viscous fluid. Moreover, the plates illustrate inward movement for S_q > 0, and for S_q < 0, away movement is observed.

Defining skin friction co-efficient, heat and mass transfer rate as follows

$\begin{array}{l}Cf=\frac{\mu {\left({\tau }_{xy}\right)|}_{y=h\left(t\right)}}{\rho U_w^2},Nu=\frac{-x{k}_2\left(1+\frac{16{\sigma }^{\ast }{T}_{\infty }^3}{3k_1{k}_2}\right){\left(\frac{\partial T}{\partial y}\right)|}_{y=h\left(t\right)}}{k_2\left(T_h-T_m\right)},\hfill \\ Sh=\frac{-xD{\left(\frac{\partial C}{\partial y}\right)|}_{y=h\left(t\right)}}{D\left(C_h-C_m\right)}.\hfill & (13)\end{array}$

In view of dimensionless forms, one may write.

$\begin{array}{l}{\left(Re\right)}^{\frac{1}{2}}Cf=\frac{1}{1+{\lambda }_1}\left(f^{″}\left(1\right)+\frac{3}{2}\beta S_q{f}^{″}\left(1\right)\right),\hfill \\ {\left(Re\right)}^{-\frac{1}{2}}Nu=-\left(1+N_r\right){\theta }^{\prime }\left(1\right),{\left(Re\right)}^{-\frac{1}{2}}Sh=-{\varphi }^{\prime }\left(1\right).\hfill & (14)\end{array}$

Homotopy Analysis Solutions

The homotopic procedure was initially purposed by Liao [20], which has been employed to construct the solutions of coupled non-linear problem. For this method, initial guesses (f₀, g₀, j₀) and concerned linear operators ${{L}}_f,{{L}}_{\theta },{{L}}_{\Phi }$ for constitutive equations are defined in the form:

$\begin{array}{l}{f}_0\left(\eta \right)=\frac{1}{2Pr}(-2M+2Pr\eta +6M{\eta }^2\hfill \\ -\text{}4Pr{\eta }^2+3Pr{S}_q{\eta }^2-4M{\eta }^3+2Pr{\eta }^3-2Pr{S}_q{\eta }^3),\hfill & (15)\end{array}$

$\begin{array}{ll}{\theta }_0\left(\eta \right)=\eta ,{\varphi }_0\left(\eta \right)=\eta ,& (16)\end{array}$

$\begin{array}{ll}{ℒ}_f=f^{(iv)},{ℒ}_{\theta }={\theta }^{″},{ℒ}_{\varphi }={\varphi }^{″},& (17)\end{array}$

with

$\begin{array}{l}{ℒ}_f\left(C_1+C_2\eta +C_3{\eta }^2+C_4{\eta }^3\right)=0,{ℒ}_{\theta }\left(C_5+C_6\eta \right)=0,\hfill \\ {ℒ}_{\varphi }\left(C_7+C_8\eta \right)=0.\hfill & (18)\end{array}$

where C_i(i = 1, 2, ……8) are arbitrary constants.

Convergence of Problem

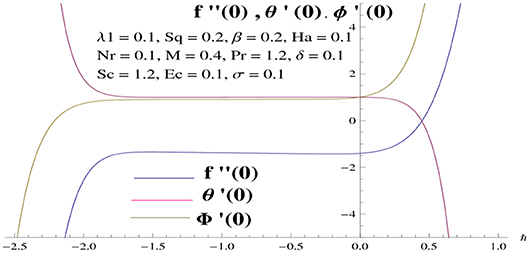
Clearly, convergent homotopic solutions incorporate the auxiliary non-zero parameters ℏ_f, ℏ_θ and ℏ_ϕ. Said parameters significantly provide way to regulate the convergence. In order to prefer the reasonable estimation of ℏ_f, ℏ_θ and ℏ_ϕ, the h-curves are exhibited in Figure 2. It is pointed out that sufficient ranges for these parameters, namely ℏ_f, ℏ_θ and ℏ_ϕ, are −1.7 ≤ ℏ_f ≤ −0.1 and −1.7 ≤ ℏ_θ ≤ 0.0 and −1.8 ≤ ℏ_ϕ ≤ − 0.1.

FIGURE 2

Figure 2. Regions of convergence for f(η), θ(η), and ϕ(η).

Analysis

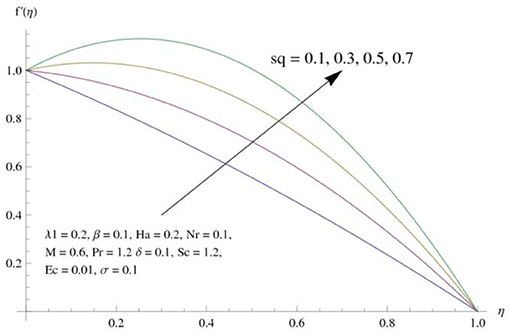
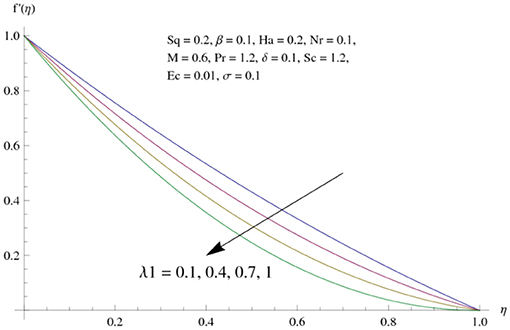
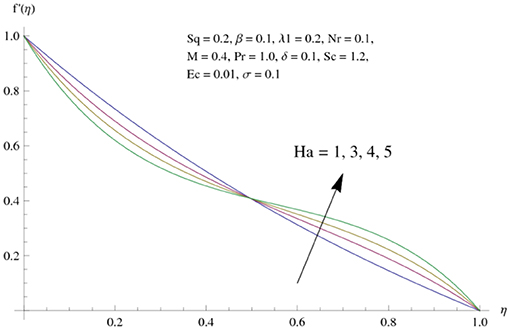
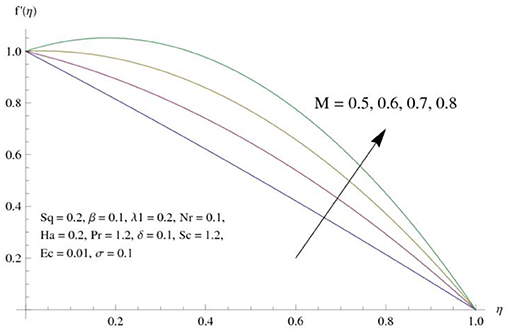
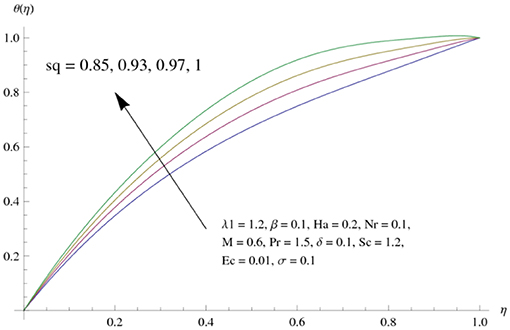
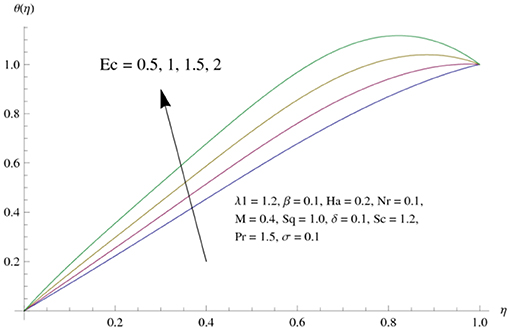
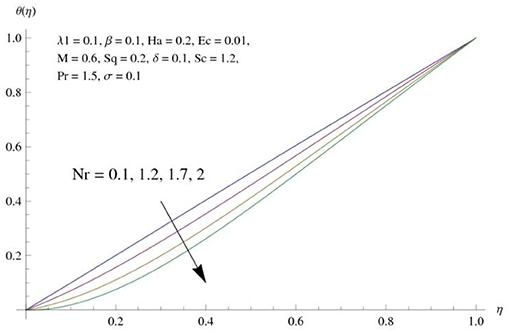
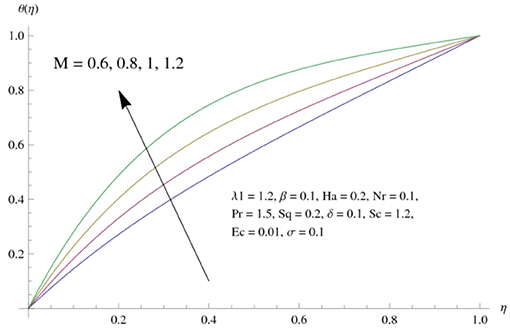
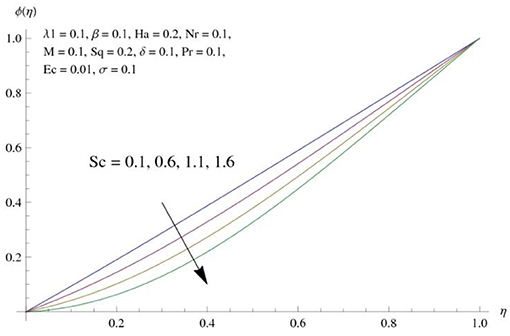
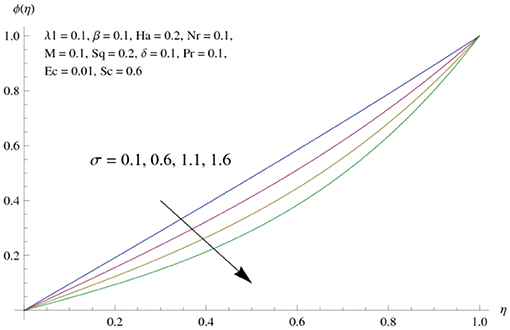
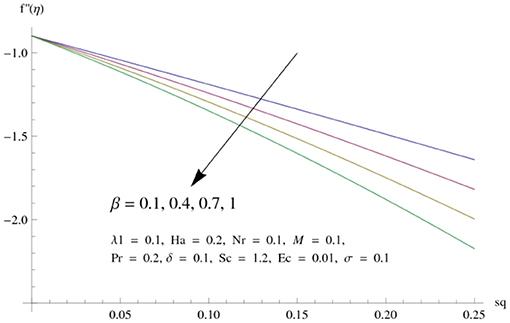
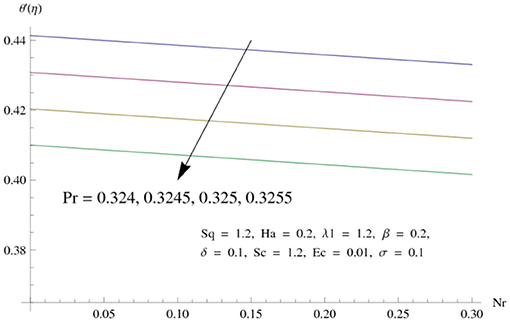
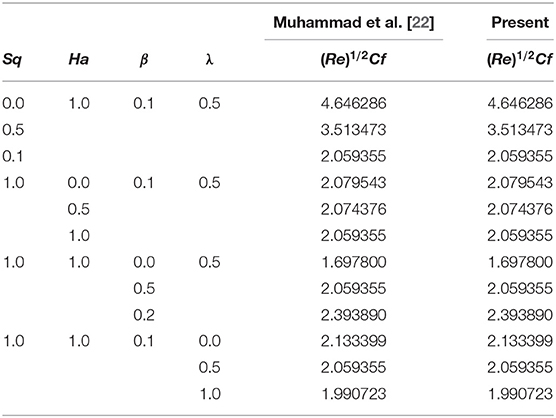
The main attraction here is to discuss the stimulus of emerging parameters in flow fields (i.e., velocity, temperature, concentration) under consideration. Figure 3 represents the impact of squeeze parameter (S_q) on the vertical and horizontal velocity fields. It is seen that increase in S_q guarantees an increase in both velocity distributions, respectively. Physically, it is justified that higher squeezing parameter corresponded to larger deformation in fluid particles. Hence, the growing behavior of velocity is noted. Figure 4 elucidates the impacts of the ratio between relaxation and retardation time parameter λ₁ on the horizontal component of velocity. It is delineated that horizontal velocity component decays for growing λ₁. Physically, greater values of λ₁ correspond to higher relaxation time. So, perturbed fluids require more time to take their original shape. Therefore, the velocity profile decreased. The variation in velocity distribution for diverse values of the Hartman number is exhibited in Figure 5. The velocity of the consider liquid exhibits decreasing trend in a region 0 ≤ η ≤ 0.5, whereas it shows opposite behavior in the region 0.5 ≤ η ≤ 1. Further, no variation is noticed in the fluid velocity at η = 0.5. Larger Hartman number values correspond to more intensity of the Lorentz force, resulting resistance in fluid's motion. Hence, velocity distribution decays. Figure 6 represents the behavior of horizontal velocity for varying melting parameter. It is evident that horizontal velocity enhances in increments in the melting parameter. A physically enlarged melting parameter is responsible for a more convective flow in the transaction of fluid, which is heated toward the cold plate surface, and as a consequence, horizontal velocity component increases. Analysis of the temperature field against the squeezing parameter is depicted in Figure 7. Here, the temperature field becomes dominant for greater values of the squeezing parameter. Further, higher temperature exists near the upper wall. In fact, the higher squeezing parameter corresponds to a greater squeeze force on the fluid, which leads to an increase in temperature profile. To capture the effects of the Eckert number on temperature distribution, Figure 8 is portrayed. With an increase in Eckert number, temperature field grows. Higher Eckert number is corresponding to higher friction force between the fluid particles which give rise to more heat generation. Hence liquid temperature amplifies. Description of thermal radiative parameter on liquid temperature is analyzed through Figure 9. Temperature field grows up for smaller thermal radiation parameter. Moreover, it is revealed that intensifies temperature occurs about upper plate surface. Physically, higher radiation parameter corresponds to lower absorption coefficient of the material. Thus, cold surface enhances more heat from heated fluid. Hence temperature field declines. Figure 10 addresses the variations of melting parameter in temperature field. It is reflected that temperature field goes up for higher melting parameter. Figure 11 exhibits the physical features of Schmidt number (Sc) on concentration curve. Decline is seen in concentration field with an increasing Schmidt number, which relates to momentum diffusivity and mass diffusivity. Thus, mass diffusivity diminishes for higher Schmidt number. Hence, liquid concentration weakens. Figure 12 exhibits the features of chemical reaction (destructive) parameter in concentration field. It demonstrates that higher chemical reaction parameter decays the concentration field. Figure 13 discloses the properties of squeezing parameter and the Deborah number on the skin friction. Skin friction intensifies for growing S_q and β. Influences of Pr and N_r on the Nussetl number are illustrated in Figure 14. It is seen that the Nussetl number weakens for greater Prandtl number and the thermal radiation parameter. To validate the current results, Table 1 displays a comparison of different values of skin friction with previously published work of Muhammad [22] for diverse values of S_q, Ha, β and λ₁. It is revealed that the outcome gives favorable agreement.

FIGURE 3

Figure 3. Behavior of S_q on f′(η).

FIGURE 4

Figure 4. Behavior of λ₁ on f′(η).

FIGURE 5

Figure 5. Behavior of Ha on f′(η).

FIGURE 6

Figure 6. Behavior of M on f′(η).

FIGURE 7

Figure 7. Behavior of S_q on θ(η).

FIGURE 8

Figure 8. Behavior of Ec on θ(η).

FIGURE 9

Figure 9. Behavior of N_r on θ(η).

FIGURE 10

Figure 10. Behavior of M on θ(η).

FIGURE 11

Figure 11. Behavior of Sc on ϕ(η).

FIGURE 12

Figure 12. Behavior of σ on ϕ(η).

FIGURE 13

Figure 13. Behavior of S_q & β on Cf.

FIGURE 14

Figure 14. Behavior of N_r & Pr on Nu.

TABLE 1

Table 1. Comparison of skin friction co-efficient (Cf) for different values of Sq, Ha, β, and λ₁.

Closing Remarks

Here, we have investigated heat and mass transport phenomenon effects on squeezed Jeffrey liquid flow between two parallel walls. Heat and mass transport are featured with melting heat transport and first order chemical reaction, respectively. The conclusions are as follows:

• Diverse values of relaxation to retardation parameter λ₁ decay the horizontal velocity profile.

• Higher values of melting parameter M enhance the horizontal velocity but vertical velocity shows decreasing behavior.

• Enhancing values of Eckert number Ec and melting parameter M lead to in the enhancement in temperature field.

• Concentration distribution shows decreasing behavior with increment in chemical reaction parameter σ.

It is expected that the present attempt relates the physical modeling under different flow conditions. It includes dynamical systems, lubrication mechanism, heating, cooling and energy estimation processes, etc. Further, as a future direction, the current investigation can tackle the different dynamical system [25–29].

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

SA collected the data and wrote the paper. MF made the analysis of the paper. MR, BA, and SR contributed in paper revision.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Stefen MJ. Versuch Uber die scheinbare adhesion. Sitzungsberichte der Akademie der Wissenschaften in Wien. Mathematik-Naturwissen. (1874) 69:713–21.

2. Muhammad N, Nadeem S, Mustafa T. Squeezed flow of a nanofluid with Cattaneo–Christov heat and mass fluxes. Results Phys. (2017) 7:862–9. doi: 10.1016/j.rinp.2016.12.028

CrossRef Full Text | Google Scholar

3. Adesanya SO, Ogunseye HA, Jangili S. Unsteady squeezing flow of a radiative Eyring-Powell fluid channel flow with chemical reactions. Int J Therm Sci. (2018) 125:440–7. doi: 10.1016/j.ijthermalsci.2017.12.013

CrossRef Full Text | Google Scholar

4. Su X, Yin Y. Effects of an inclined magnetic field on the unsteady squeezing flow between parallel plates with suction/injection. J Magn Magn Mater. (2019) 484:266–71. doi: 10.1016/j.jmmm.2019.04.041

CrossRef Full Text | Google Scholar

5. Naduvinamani NB, Shankar U. Radiative squeezing flow of unsteady magneto-hydrodynamic Casson fluid between two parallel plates. J Cent South Univ. (2019) 26:1184–204. doi: 10.1007/s11771-019-4080-0

CrossRef Full Text | Google Scholar

6. Ullah I, Rahim MT, Khan H, Qayyum M. Analysis of various semi-numerical schemes for magnetohydrodynamic (MHD) squeezing fluid flow in porous medium. Propul Power Res. (2019) 8:69–78. doi: 10.1016/j.jppr.2019.01.003

CrossRef Full Text | Google Scholar

7. Lahmar S, Kezzar M, Eid MR, Sari MR. Heat transfer of squeezing unsteady nanofluid flow under the effects of an inclined magnetic field and variable thermal conductivity. Physica A. (2020) 540:e123138. doi: 10.1016/j.physa.2019.123138

CrossRef Full Text | Google Scholar

8. Khan MI, ur Rahman M, Khan SA, Hayat T, Khan MI. Evaluation of entropy generation in cubic autocatalytic unsteady squeezing flow of nanofluid between two parallel plates. Comp Meth Prog Biomed. (2020) 185:e105149. doi: 10.1016/j.cmpb.2019.105149

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Hayat T, Farooq M, Alsaedi A. Melting heat transfer in the stagnation point flow of Maxwell fluid with double diffusive convection. Int J Num Meth Heat Fluid Flow. (2014) 24:760–74. doi: 10.1108/HFF-09-2012-0219

CrossRef Full Text | Google Scholar

10. Krishnamurthy MR, Prasannakumara BC, Gireesha BJ, Gorla RSR. Effect of chemical reaction on MHD boundary layer flow and melting heat transfer of Williamson nanofluid in porous medium. Eng Sci Tech Int J. (2016) 19:53–61. doi: 10.1016/j.jestch.2015.06.010

CrossRef Full Text | Google Scholar

11. Hashim, Khan M, Alshomrani AS. Characteristics of melting heat transfer during flow of Carreau fluid induced by a stretching cylinder. Eur Phys J Plus. (2017) 40:8. doi: 10.1140/epje/i2017-11495-6

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Soomro FA, Usman M, Haq R, Wang W. Melting heat transfer analysis of Sisko fluid over a moving surface with nonlinear thermal radiation via Collocation method. J Heat Mass Trans. (2018) 126:1034–42. doi: 10.1016/j.ijheatmasstransfer.2018.05.099

CrossRef Full Text | Google Scholar

13. Mabood F, Ibrahim SM, Khan WA. Effect of melting and heat generation/absorption on Sisko nanofluid over a stretching surface with nonlinear radiation. Phys Scr. (2019) 94:e065701. doi: 10.1088/1402-4896/ab1164

CrossRef Full Text | Google Scholar

14. Javed M, Alderremy AA, Farooq M, Anjum A, Ahmad S, Malik MY. Analysis of activation energy and melting heat transfer in MHD flow with chemical reaction. Eur Phys J Plus. (2019) 134:256. doi: 10.1140/epjp/i2019-12744-5

CrossRef Full Text | Google Scholar

15. Hayat T, Muhammad K, Alsaedi A, Ahmed B. Melting effect in squeezing flow of third-garde fluid with non-Fourier heat flux model. Phys Scr. (2019) 94:e105705. doi: 10.1088/1402-4896/ab1c2c

CrossRef Full Text | Google Scholar

16. Hayat T, Shah F, Alsaedi A, Ahmad B. Entropy optimized dissipative flow of effective Prandtl number with melting heat transport and Joule heating. Int Commun Heat Mass Transf. (2020) 111:e104454. doi: 10.1016/j.icheatmasstransfer.2019.104454

CrossRef Full Text | Google Scholar

17. Dinh MT, Tlili I, Dara RN, Shafee A, Al-Jahmany YY, Nguyen-Thoi T. Nanomaterial treatment due to imposing MHD flow considering melting surface heat transfer. Physica A. (2020) 541:e123036. doi: 10.1016/j.physa.2019.123036

CrossRef Full Text | Google Scholar

18. Hajipour M, Jajarmi A, Malek A, Baleanu D. Positivity-preserving sixth-order implicit finite difference weighted essentially non-oscillatory scheme for the nonlinear heat equation. Appl Math Comput. (2018) 325:146–58. doi: 10.1016/j.amc.2017.12.026

CrossRef Full Text | Google Scholar

19. Hajipour M, Jajarmi A, Baleanu D, Sun H. On an accurate discretization of a variable-order fractional reaction-diffusion equation. Commun Nonlinear Sci Numerical Simul. (2019) 69:119–33. doi: 10.1016/j.cnsns.2018.09.004

CrossRef Full Text | Google Scholar

20. Liao SJ. Homotopy Analysis Method in Non-linear Differential Equations. Heidelberg: Springer and Higher Education Press (2012).

Google Scholar

21. Turkyilmazoglu M. An effective approach for evaluation of the optimal convergence control parameter in the homotopy analysis method. Filomat. (2016) 30:1633–50. doi: 10.2298/FIL1606633T

CrossRef Full Text | Google Scholar

22. Muhammad T, Hayat T, Alsaedi A, Qayyum A. Hydromagnetic unsteady squeezing flow of Jeffrey fluid between two parallel plates. Chin J Phys. (2017) 55:1511–22. doi: 10.1016/j.cjph.2017.05.008

CrossRef Full Text | Google Scholar

23. Hayat T, Rashid M, Khan MI, Alsaedi A. Melting heat transfer and induced magnetic field effects on flow of water based nanofluid over a rotating disk with variable thickness. Results Phys. (2018) 9:1618–30. doi: 10.1016/j.rinp.2018.04.054

CrossRef Full Text | Google Scholar

24. Farooq M, Ahmad S, Javed M, Anjum A. Melting heat transfer in squeezed nanofluid flow through Darcy Forchheimer medium. J Heat Transf. (2019) 141:e012402. doi: 10.1115/1.4041497

CrossRef Full Text | Google Scholar

25. Baleanu D, Asad JH, Jajarmi A. New aspects of the motion of a particle in a circular cavity. Proc Rom Acad Ser A. (2018)19:361–7. Available online at: https://scholar.ptuk.edu.ps/handle/123456789/625

Google Scholar

26. Jajarmi A, Baleanu D, Sajjadi SS, Asad JH. A new feature of the fractional euler-lagrange equations for a coupled oscillator using a nonsingular operator approach. Front Phys. (2019) 7:196. doi: 10.3389/fphy.2019.00196

CrossRef Full Text | Google Scholar

27. Baleanu D, Sajjadi SS, Jajarmi A, Asad JH. New features of the fractional Euler-Lagrange equations for a physical system within non-singular derivative operator. Eur Phys J Plus. (2019) 134:181. doi: 10.1140/epjp/i2019-12561-x

CrossRef Full Text | Google Scholar

28. Baleanu D, Jajarmi A, Asad JH. The fractional model of spring pendulum: new features within different kernels. Proc Rom Acad Ser A. (2018) 19:447–54. Available online at: https://scholar.ptuk.edu.ps/handle/123456789/626

Google Scholar

29. Waqas M, Shehzad SA, Hayat T, Khan MI, Alsaedi A. Simulation of magnetohydrodynamics and radiative heat transport in convectively heated stratified flow of Jeffrey nanofluid. J Phys Chem Solids. (2019) 133:45–51. doi: 10.1016/j.jpcs.2019.03.031

CrossRef Full Text | Google Scholar