An Efficient Analytical Technique for Time-Fractional Parabolic Partial Differential Equations

Introduction

The physical behaviors of fractional order differential and integral equations have been studied in fractional calculus (FC). Fractional calculus deals with more general behavior than classical calculus. However, in the present era FC has got more attention for its vast applications in many fields such as science and engineering. Spanier and Oldham [1], Podlubny [2], and Miller and Rose [3], have studied this subject in detail and developed the theoretical explanation of the subject. During the last few decades, a large number of researchers have noted that the role of fractional differential or integral operators are unavoidable in representing the characteristics of physical phenomena like traffic flow, viscoelasticity, fluid flow, signal processing, etc., [4–10]. Many processes and equipment have been efficiently explained by FC. Furthermore, comparative studies have been done for fractional and total differential models. In conclusion, the fractional models are more effective than classical models. Fourth ordered linear PDE

$\begin{array}{ll}{\partial }_t^{2}v(s,t)+\mu {\partial }_s^{4}v(s,t)=h(s,t),& (1)\end{array}$

is very important in engineering and modern science. Bridge slabs, floor systems etc. are examples of fourth order PDEs. Where v is the beam transversal displacement, μ the is ratio of flexural stiffness to mass per unit length, t is the time, s is the space variable and h is the dynamic deriving force acting on unit mass.

In this study, the problem of undamped transverse vibrations of a flexible straight beam is considered. The support of the beam does not contribute to the strain energy of the system. The mathematical model of the problem is expressed in the form of the following time-fractional fourth-order parabolic partial differential equation as

$\begin{array}{ll}{\partial }_t^{\alpha }v(s,t)+\mu {\partial }_s^{4}v(s,t)=f(s,t),s\in \left[0,1\right],t>0,1<\alpha \le 2,& (2)\end{array}$

where ∂_t and ∂_s represents the partial derivatives with respect to t and s, respectively. The initial and boundary conditions are

$\begin{array}{l}v(s;0)=g_0,v_t(s;0)=g_1,\\ v(0;t)=f_0,v_t(s;0)=f_1,\\ v_{ss}(0;t)=p_0,v_{ss}(1;t)=p_1,& (3)\end{array}$

where ${\partial }_t^{\alpha }$ denotes the fractional order derivative operator, v(s, t) is the displacement of the beam in s direction, μ is the ratio of flexural stiffness to mass per unit length, t the is time, s is the space variable and f(s, t) is the dynamic deriving force acting on per unit mass, and g₀(s), g₁(s), f₀(t), f₁(t), p₀(t) and p₁(t) are continuous functions.

The concept of homotopy has been merged with perturbation in order to solve non-linear problems. Liao [11] conducted the basic work by utilizing the homotopy analysis method (HAM). He [12] presented the homotopy perturbation method and its applications. Marinca et al. [13–15] developed a novel computational scheme known as OHAM. The OHAM established a convergence criteria similar to HAM, but OHAM is more flexible. In various research papers Iqbal et al. [16–18] and Sarwar et al. [19, 20] have demonstrated the usefulness extension and trust of this technique and have achieved trustworthy solutions. In this paper, the Idea of OHAM has been explained. It gives logical, trustworthy solutions to linear and non-linear mathematical model fractional orders.

Very recently, some new definitions of fractional derivatives have been introduced and many physical medical problems have been modeled based on fractional derivatives, e.g., the SIRS-SI model describes the transmission of malaria disease [21]. The fractional extension of partial differential equations occurring in physical sciences was studied by Dubey et al. [22]. Other real-life problems with fractional calculus can be seen in a recent work by Gao et al. [23].

The homotopy asymptotic method (HAM) is also effective in solving a differential equation. Some result work comprises linear and nonlinear fractional differential equations considering different constraints without a singular kernel [24, 25]. The model shows that OHAM/HAM guarantee good approximation and better convergence rate than other numerical techniques.

The paper is structured as follows: The basic definition of fractional calculus is given in Section Basic Definitions. The method is described in Section Solution Procedure of OHAM. Section Solutions of Fractional Models of Parabolic PDEs gives the model problems and detailed results. Section Discussion of Results provides a discussion of the results. The conclusion is outlined in Section Conclusions.

Basic Definitions

Let g(t), t > 0 is a function of real value considered to be in space c_λ, λ ∈ R, which is very useful for the study in FC. If there exists, p > λ is a real number such that $g(t)=t^p{g}_1(t),$ where g₁(t) ∈ c(0, ∞), supposed to be in space $c_{\lambda }^m$ if and only if $g^m\in c_{\lambda }$,m ∈ N.

Definition 2.1. Riemann-Liouville form of integral operator of a function g ∈ c_λ, of fractional order β > 0,λ ≥ − 1 is expressed as

$\begin{array}{l}{{}^{RL}D}_{a,t}^{-\beta }g\left(t\right)=\frac{1}{\Gamma \left(\beta \right)}{\int }_a^t{\left(t-\lambda \right)}^{\beta -1}g(\lambda )d\lambda ,t>0,\beta >0,\\ k-1<\beta <k,k\in Z^{+}& (4)\end{array}$

Definition 2.2. Riemann-Liouville form of integral operator of a functiong(t) of fractional order β > 0 is given as

$\begin{array}{l}{{}^{RL}D}_{a,t}^{\beta }g\left(t\right)=\frac{1}{\Gamma \left(n-\beta \right)}\frac{d^k}{d{t}^k}{\int }_a^t{\left(t-\lambda \right)}^{k-\beta -1}g(\lambda )d\lambda ,t>0,\beta >0,\\ k-1<\beta <k,k\in Z^{+}.& (5)\end{array}$

Definition 2.3. The Caputo fractional derivative of order β > 0 is expressed as

$\begin{array}{l}{{}^{C}D}_{a,t}^{\beta }g\left(t\right)=\frac{1}{\Gamma \left(n-\beta \right)}{\int }_a^t{\left(t-\lambda \right)}^{k-\beta -1}{g}^{\left(k\right)}(\lambda )d\lambda ,t>0,\beta >0,\\ k-1<\beta <k,k\in Z^{+}.& (6)\end{array}$

If j − 1 < β < j, and $g\in c_{\lambda }^m,\lambda \ge -1$, then

$\begin{array}{ll}{{}^{RL}D}_{a,t}^{-\beta }\left({{}^{C}D}_{a,t}^{\beta }g\left(t\right)\right)=g\left(t\right)-{\displaystyle \sum _{i=0}^{j-1}{g}^i\left(a\right)\frac{{\left(t-a\right)}^j}{\Gamma \left(i+1\right)},}t>0.& (7)\end{array}$

Solution Procedure of OHAM

Based on the OHAM scheme [18, 19], we will extend this approach for time-fractional parabolic partial differential equations (TFPPDE) in the subsequent steps.

Step I. Write the governing time fractional order parabolic equation in the subsequent way

$\begin{array}{ll}Q(v(s,t))-f(s,t)=0;s\in \left[0,1\right],t>0.& (8)\end{array}$

Ω is domain. Equation (8) is bifurcated in to Q(v) = J(v) + T(v). In this expression J is a fractional component and T is a non-fractional component. $J_i=\frac{{\partial }^{\alpha }{\Phi }_i(s,t)}{\partial t^{\alpha }},i\ge 0$, $T_i=\frac{{\partial }^4\phi }{\partial s^4},i\ge 0.$

Step II. Develop an optimal homotopy for time-fractional partial deferential equation (TFPDE), φ(s, t; p) : Ω × [0, 1] → R which satisfies

$\begin{array}{ll}(1-p)(J(v)-f(s,t))-H(s,p;c)(Q(v)-f(s,t))=0.& (9)\end{array}$

In Equation (9) p ∈ [0, 1] and s ∈ Ω is a parameter, for p ≠ 0, H(s, p; c) is a non-zero auxiliary function and H(0, p; c) = 0 when p increases in the interval [0, 1] the solution φ(s, t) guarantees the rapidly convergent to the exact solution.

$\begin{array}{l}H(s,p;c)=p{j}_1(s,c_i)+p^2{j}_2(s,c_i)+p^3{j}_3(s,c_i)+\dots \\ +p^m{j}_m(s,c_i),& (10)\end{array}$

Where the auxiliary convergence control parameters are c_i, i = 0, 1, 2, 3, …, m and J_i(s), i = 0, 1, 2, 3, …, m can be a function on the variables. The J_m(s, c_i) may be selected in the form of polynomial, exponential and so on. It is very important to note that the crucial step is to select an appropriate function as the convergence rate depends on the initial guess of the solutions.

Step III. Expand φ(s, t; p, c) in Taylor's series for p to develop an approximate result as

$\begin{array}{ll}\phi (s,t;p,c_i)=v_0(s,t)+{\displaystyle \sum _{j=1}^m}{v}_k(s,t;c_i)p^j,1\le i\le m.& (11)\end{array}$

It has been clarified that the rate of convergence of the (11) depends upon auxiliary constants c_i. If the Equation (11), at p = 1 is convergent, then one has:

$\begin{array}{ll}\tilde{v}(s,t;p,c_i)=v_0(s,t)+{\displaystyle \sum _{j=1}^m}{v}_k(s,t;c_i).& (12)\end{array}$

Step IV. Compare the coefficients of identical powers p after substituting Equations (11) in (9), we can get 0th, 1st, 2nd and higher order problems if needed.

$\begin{array}{ll}{p}^0:J_0-f(s,t)=0.& (13)\end{array}$

$\begin{array}{ll}{p}^1:J_0-J_1+f(s,t)-c_1(J_0+T_1-f(s,t))=0.& (14)\end{array}$

$\begin{array}{ll}{p}^2:J_2-J_1-c_1(J_1+T_0)-c_2(T_0-f(s,t))=0.& (15)\end{array}$

$\begin{array}{l}{p}^3:J_3-J_2-c_1(J_2+T_2)-c_2(J_1+T_1)-c_3(J_0\hfill \\ +T_0-f\left(s,t\right))=0.& (16)\end{array}$

And so on

Step V. Substitute Equations (12) in (8), the outcome will be residual.

Create the δ(c_i)

$\begin{array}{l}\delta (c_i)={\displaystyle {\int }_0^t}{\displaystyle {\int }_{\Omega }}{R}^2(s,t;c_i)dsdt.\end{array}$

Residual of Problem Is R

Convergence auxiliary control (c_i) constants can be acquired as follows.

$\begin{array}{ll}\frac{\partial \delta }{\partial c_1}=\frac{\partial \delta }{\partial c_2}=\dots =\frac{\partial \delta }{\partial c_m}=0.& (17)\end{array}$

If R(s; j_i) = 0 then v(s; j_i) = 0 must be exact solution of the TFPDE. Normally it does not happen for non-linear problems.

Step VI. Using the convergence auxiliary control constants in Equation (12), we can develop an approximate solution.

Step VII. Accuracy of the technique is presented as

Error norm L₂

$\begin{array}{ll}\Vert v^{exact}-v_n\Vert =\sqrt{\frac{b-a}{n}{\displaystyle \sum _{i=0}^N}|v^{exact}-v_n{|}^2}.& (18)\end{array}$

Error normL^∞

$\begin{array}{ll}\begin{array}{l}\Vert v^{exact}-v_n\Vert =\hfill \end{array}|v_i^{exact}-{\left(v_n\right)}_i|.& (19)\end{array}$

Solutions of Fractional Models of Parabolic PDEs

In the current section, we take the two examples and solve them with the aid of OHAM and demonstrate the accuracy, validity, and suitability of the suggested computational scheme.

Example 1

Let us take the fourth order TFPPDE of the form

$\begin{array}{l}\frac{{\partial }^{\alpha }v(s,t)}{\partial t^{\alpha }}+\frac{{\partial }^{4}v(s,t)}{\partial s^4}=({\pi }^4-1)sin\pi scost.\\ s\in \left[0,1\right],t>0,\mu =1,1<\alpha \le 2.& (20)\end{array}$

Initial conditions (ICs)

$\begin{array}{l}v(s,0)=sin\pi s,v_t(s,0)=0.\end{array}$

Boundary conditions (BCs)

$\begin{array}{l}\begin{array}{c}v(0,t)=0,v_{ss}(0,t)=0.\\ v(1,t)=0,v_{ss}(1,t)=0.\end{array}\end{array}$

Exact solution of problem is

$\begin{array}{ll}v(s,t)=costsin\pi s& (21)\end{array}$

Compare the coefficients of equal powers of embedding parameter p, after substituting ϕ(s, p) in to optimal homotopy equation to get zero-order, 1st-order, and 2nd-order and higher-order series problems.

$\begin{array}{ll}{p}^0:\frac{{\partial }^{\alpha }{v}_0(s,t)}{\partial t^{\alpha }}=0,& (22)\end{array}$

$\begin{array}{ll}\begin{array}{l}{p}^1:(\cos \left(t\right)\sin \left(\pi s\right)+{\pi }^4\cos \left(t\right)\sin \left(\pi s\right)-\frac{{\partial }^4{v}_0\left(s,t\right)}{\partial s^4}\hfill \\ -\frac{{\partial }^{\alpha }{v}_0(s,t)}{\partial t^{\alpha }})c_1-\frac{{\partial }^{\alpha }{v}_0(s,t)}{\partial t^{\alpha }}+\frac{{\partial }^{\alpha }{v}_1(s,t)}{\partial t^{\alpha }}=0,\hfill \\ p^2:(-\cos \left(t\right)\sin \left(\pi s\right)+{\pi }^4\sin \left(\pi s\right)\cos (t)-\frac{{\partial }^4{v}_0\left(s,t\right)}{\partial s^4}\hfill \\ -\frac{{\partial }^{\alpha }{v}_0(s,t)}{\partial t^{\alpha }})c_2\hfill \end{array}& (23)\end{array}$

$\begin{array}{ll}-& c_1\left(\frac{{\partial }^{\alpha }{v}_0(s,t)}{\partial t^{\alpha }}+\frac{{\partial }^{\alpha }{v}_1(s,t)}{\partial t^{\alpha }}\right)-\frac{{\partial }^{\alpha }{v}_1(s,t)}{\partial t^{\alpha }}\\ +& \frac{{\partial }^{\alpha }{v}_2(s,t)}{\partial t^{\alpha }}=0.& (24)\end{array}$

After implementing the step-5 of sec-3 on Equations (22–24), we get following zero-order, 1st-order and 2nd-order results:

$\begin{array}{ll}{v}_0(s,t)=sin(\pi s),& (25)\end{array}$

$\begin{array}{ll}{v}_1(s,t)=\frac{c_1({\pi }^4-\frac{1}{4}(1+{\pi }^4)(-t^2))sin(\pi s)t^{\alpha }}{\Gamma (\alpha +1)},& (26)\end{array}$

$\begin{array}{l}{v}_2(s,t)=\frac{((1+{\pi }^4)c_1(c_1+1)+({\pi }^4-1)c_2)sin(\pi s)t^{\alpha +2}}{4\Gamma (\alpha +1)}\\ +\frac{{\pi }^8{c}_1^{2}sin(\pi s)t^{2\alpha }+\frac{{\pi }^4(1+{\pi }^4)(\alpha +2)c_1^{2}sin(\pi s)t^{2\alpha +2}}{8(2\alpha +1)}}{\Gamma (2\alpha +1)}\\ +\frac{{\pi }^4{c}_1(c_1+1)sin(\pi s)t^{\alpha }}{\Gamma (\alpha +1)}+\frac{{\pi }^4{c}_{2}sin(\pi s)t^{\alpha }}{\Gamma (\alpha +1)}.& (27)\end{array}$

After using Equations (25–27), we get the second order solution as follows

$\begin{array}{ll}\begin{array}{l}v(s,t)=\frac{1}{8}\sin \left(\pi s\right)(\frac{{\pi }^4{c}_1^2\left(\left(\alpha +2\right)t^2+{\pi }^4\left(16\alpha +\left(\alpha +2\right)t^2+8\right)\right)t^{2\alpha }}{\Gamma \left(2\alpha +2\right)}\hfill \\ +\frac{2\left(c_1\left(c_1+2\right)\left(t^2+{\pi }^4\left(t^2+4\right)\right)+c_2\left({\pi }^4\left(t^2+4\right)-t^2\right)\right)t^{\alpha }}{\Gamma \left(\alpha +1\right)}+8).\hfill \end{array}& (28)\end{array}$

Example 2

We take the 4rth-order TFPPDE of the form

$\begin{array}{l}\frac{{\partial }^{\alpha }v(s,t)}{\partial t^{\alpha }}+\frac{{\partial }^{4}v(s,t)}{\partial s^4}=({\pi }^4-1)e^{t}sin\pi s,\\ s\in \left[0,1\right],t>0,\mu =1,1<\alpha \le 2.& (29)\end{array}$

Initial conditions

$\begin{array}{l}v(s,0)=sin(\pi s),v_t(s,0)=sin(\pi s).\end{array}$

Boundary conditions

$\begin{array}{l}v(0,t)=0,v_{ss}(0,t)=0,\\ v(1,t)=0,v_{ss}(1,t)=0.\end{array}$

Exact solution is

$\begin{array}{ll}v(s,t)=e^{t}sin(\pi s).& (30)\end{array}$

Compare the coefficients of like powers of embedding parameter p, after substituting ϕ(s, p) in to optimal homotopy equation to get zero-order, 1st-order, 2nd-order and higher-order (if needed) deformed problems as under:

$\begin{array}{ll}{p}^0:\frac{{\partial }^{\alpha }{v}_0(s,t)}{\partial t^{\alpha }}=0,& (31)\end{array}$

$\begin{array}{l}{p}^1:\left(e^{t}sin(\pi s)+e^t{\pi }^{4}sin(\pi s)-\frac{{\partial }^4{v}_0(s,t)}{\partial s^4}-\frac{{\partial }^{\alpha }{v}_0(s,t)}{\partial t^{\alpha }}\right)\\ c_1-\frac{{\partial }^{\alpha }{v}_0(s,t)}{\partial t^{\alpha }}+\frac{{\partial }^{\alpha }{v}_1(s,t)}{\partial t^{\alpha }}=0,& (32)\end{array}$

$\begin{array}{l}{p}^2:\left(e^{t}sin(\pi s)+{\pi }^{4}sin(\pi s)cos(t)-\frac{{\partial }^4{v}_0(s,t)}{\partial s^4}-\frac{{\partial }^{\alpha }{v}_0(s,t)}{\partial t^{\alpha }}\right)c_2\\ -c_1\left(\frac{{\partial }^4{v}_1(s,t)}{\partial s^4}+\frac{{\partial }^{\alpha }{v}_1(s,t)}{\partial t^{\alpha }}\right)-\frac{{\partial }^{\alpha }{v}_1(s,t)}{\partial t^{\alpha }}+\frac{{\partial }^{\alpha }{v}_2(s,t)}{\partial t^{\alpha }}=0.& (33)\end{array}$

After implementing the step-5 of sec-3 on Equations (31–33), we develop the following zero-order, 1st-order and 2nd-order results.

$\begin{array}{ll}{v}_0(s,t)=tsin(\pi s)+sin(\pi s),& (34)\end{array}$

$\begin{array}{ll}{v}_1(s,t)=\frac{\sqrt{\pi }{c}_1{t}^{\alpha }\sin (\pi s)(2{\pi }^{\frac{7}{2}}(\alpha +t+1)-(1+{\pi }^4)2^{-\alpha }(\frac{2t^2}{4}+\frac{t^{2}t}{4})\Gamma (\alpha +2))}{2\Gamma (\alpha +2)},& (35)\end{array}$

$\begin{array}{l}{v}_2(s,t)=\frac{1}{8}{t}^{\alpha }\sin (\pi s)(\frac{8{\pi }^8{c}_1^2{t}^{\alpha +1}}{\Gamma (2\alpha +2)}\hfill \\ -\frac{{\pi }^{\frac{9}{2}}(1+{\pi }^4)2^{1-\alpha }{c}_1^2\Gamma (\alpha +3)t^{\alpha +2}}{\Gamma (2\alpha +3)}-\frac{{\pi }^{\frac{9}{2}}(1+{\pi }^4)2^{-\alpha }{c}_1^2\Gamma (\alpha +4)t^{\alpha +3}}{\Gamma (2\alpha +4)}\hfill \\ +\frac{8{\pi }^8{c}_1^2{t}^{\alpha }}{\Gamma (2\alpha +1)}+\frac{8(c_1^2+c_1+c_2)(\frac{{\pi }^4(\alpha +t+1)-\frac{1}{4}(1+{\pi }^4)t^3}{\alpha +1}-\frac{1}{4}(1+{\pi }^4)t^2)}{\Gamma (\alpha +1)}).\hfill & (36)\end{array}$

After using Equations (34–36), we get the second order solution as follows:

$\begin{array}{ll}\begin{array}{l}v\left(s,t\right)\hfill \\ =\frac{1}{8}\sin \left(\pi s\right)(-\frac{\begin{array}{l}{2}^{-\alpha }{c}_1{t}^{\alpha }(2^{\alpha +1}(t^2+{\pi }^4(t^2-8))(\alpha +t+1)\hfill \\ +(1+{\pi }^4)\sqrt{\pi }(t+2)t^2\Gamma (\alpha +2))\hfill \end{array}}{\Gamma \left(\alpha +2\right)}\hfill \\ -\frac{2c_2(t^2+{\pi }^4(t^2-4))(\alpha +t+1)t^{\alpha }}{\Gamma \left(\alpha +2\right)}\hfill \\ +c_1^2{t}^{\alpha }(-\frac{{\pi }^{\frac{9}{2}}(1+{\pi }^4)2^{-\alpha }\Gamma (\alpha +3)(4\alpha +(\alpha +3)t+6)t^{\alpha +2}}{\Gamma (2\alpha +4)}\hfill \\ +\frac{8{\pi }^8(2\alpha +t+1)t^{\alpha }}{\Gamma (2\alpha +2)}\hfill \\ -\frac{2(t^2+{\pi }^4(t^2-4))(\alpha +t+1)}{\Gamma (\alpha +2)})+8t+8).\hfill \end{array}& (37)\end{array}$

Discussion of Results

In the last section, a detailed algorithm for OHAM is presented for parabolic equations of arbitrary fractional order, and a description is designed for the examples in the above section which gives remarkably valid results for the TFPPDEs without domain discretization. OHAM does not require any higher order solutions to initiate the process.

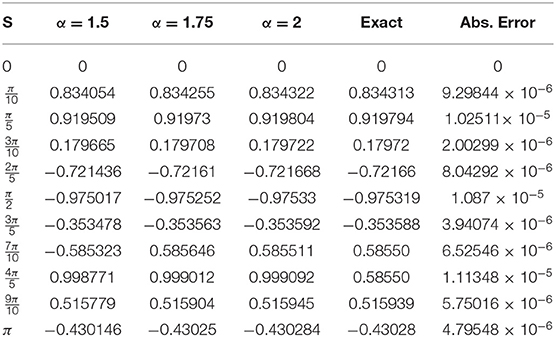
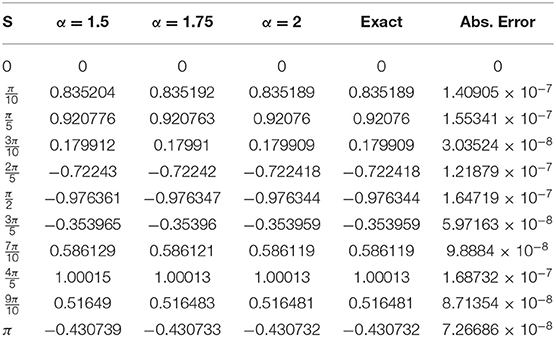
In the Tables 1A, 2A for examples 1 and 2 represent the values of auxiliary constants c₁ and c₂ for distinct values of α, α = 1.5, 1.75, and 2. Tables 1B, 2B for examples 1 and 2 represent the approximate and exact solutions with absolute error for distinct values of α at fixed time t = 0.01, and also error norms of example 1 are $L_2=2.48306\times 10^{-5},L_{\infty }=1.11348\times 10^{-5}$ and error norms of example 2 are $L_2=3.76272\times 10^{-7},L_{\infty }=1.68732\times 10^{-7}$, which demonstrates the validity and accuracy of the suggested scheme.

TABLE 1A

Table 1A. Shows the order of solution of problem-1 with α.

TABLE 1B

Table 1B. Shows the solutions and absolute error of problem-1 for various values of α.

TABLE 2A

Table 2A. Shows the order of solution of problem-2 with α.

TABLE 2B

Table 2B. Shows the solution and absolute error of problem-2 for distinct values of α.

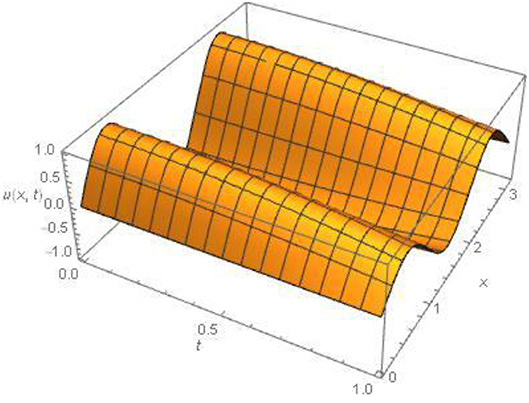
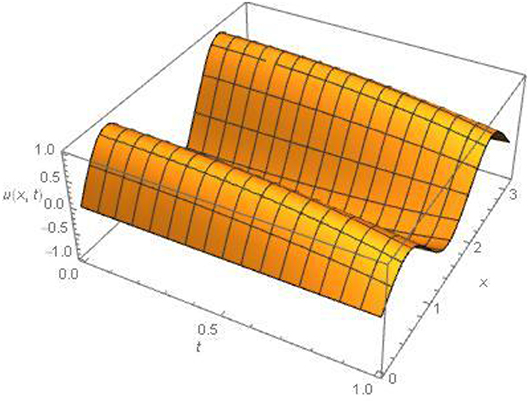
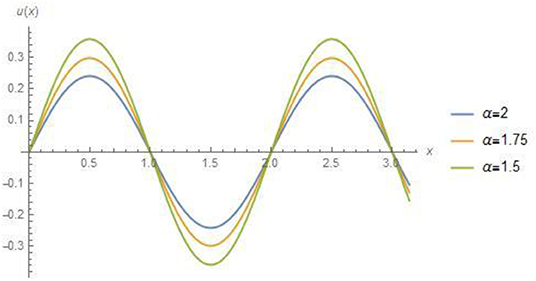
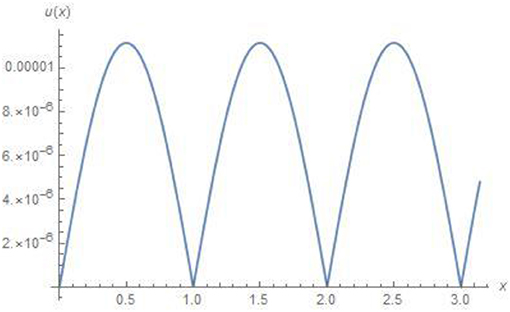
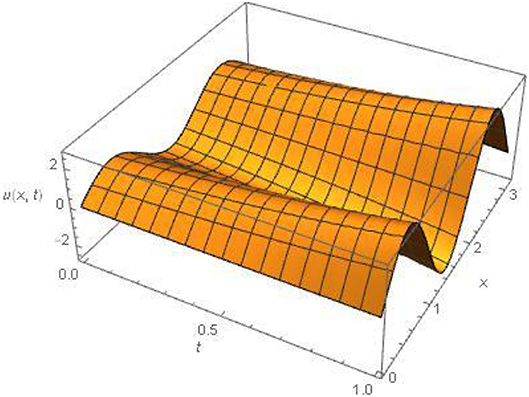
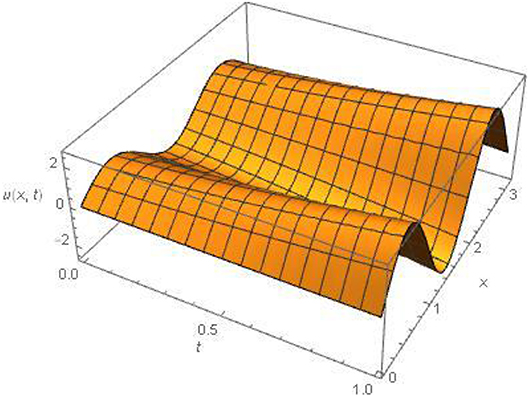
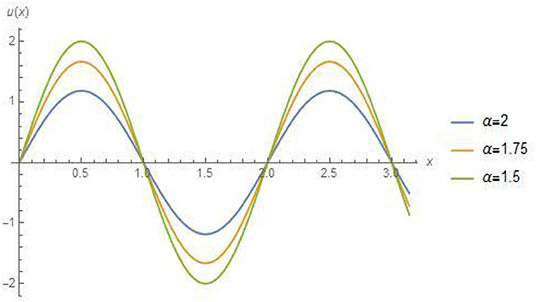
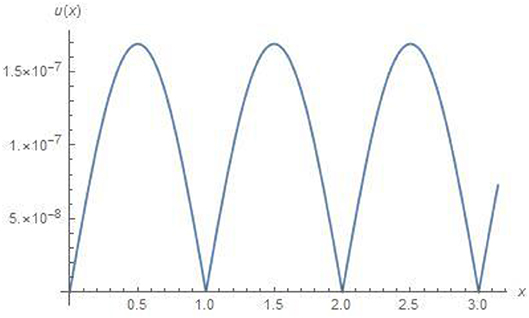
Figures 1, 2, 4 for example 1 represent the exact solution, approximate result and absolute error for fixed value α = 2. Figure 3 for example 1 represents the 2D results for different values of α, α = 1.5, 1.75 and 2 at fixed value of t = 0.01. Figures 5, 6, 8 for example 2 represent the exact solution, approximate result and absolute error for fixed value α = 2. Figure 7 for example 2 represents the 2D results for different

FIGURE 1

Figure 1. Surface of Exact solution for TFPPDE (20) with α = 2.

FIGURE 2

Figure 2. Surface of Approximate solution for TFPPDE (20) with α = 2.

FIGURE 3

Figure 3. Approximate solutions for TFPPDE (20) for distinct values of α = 1.5, 1.75, 2.

FIGURE 4

Figure 4. Absolute error for TFPPDE (20) at α = 2.

FIGURE 5

Figure 5. Surface of Exact solution for TFPPDE (29) with α = 2.

FIGURE 6

Figure 6. Surface of Approximate solution for TFPPDE (29) with α = 2.

FIGURE 7

Figure 7. Approximate solutions of TFPPDE (29) for distinct values of α = 1.5, 1.75, 2.

FIGURE 8

Figure 8. Absolute error for TFPPDE (29) at α = 2.

values of α, α = 1.5, 1.75 and 2 at fixed value of t = 0.01. All the above figures indicate the accuracy, suitability and effectiveness of the suggested algorithm. It is clear that as we proceed along the domain, we obtain consistent validity. In the above discussion (Tables 1B, 2B) show an excellent agreement between the approximate and exact solutions.

Conclusions

In this work, the TFPDE are examined by a semi-analytical scheme. The problems in hand are solved by OHAM. OHAM is incredibly effective for fractional order parabolic partial differential equations. The solutions obtained from OHAM are smooth enough to be compared with the exact solutions. The graphical reviews show the smoothness of the solutions. The error estimations with the exact solutions are of order 10⁻⁶. The tabular and graphical reviews of the solutions and errors are presented for different values of 1 < α ≤ 2 which are convergent. L² error and L^∞ error norms are calculated which show the error bounds. The error bound is of order 10⁻⁷. This is incredibly excellent.

This article focuses on the approximate solution of the parabolic equation which has many applications in engineering and physical sciences. The contribution of this article is 3-fold: first, we briefly defined the concept of fractional derivative, then developed the mathematical model. In the last step we implemented OHAM to find the solution of the model. The results are graphically represented and shown in tabular form to show the novelty and credibility of our method. In the future, we are interested in implementing OHAM on the system of fractional order partial differential equations in a more general way.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Oldham KB, Spanier J. The Fractional Calculus. New York, NY: Academic Press (1974).

Google Scholar

2. Podlubny I. Fractional Differential Equations. New York, NY: Academic Press (1999).

Google Scholar

3. Miller KS, Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations. New York, NY: Wiley (1993).

4. Kumar D, Singh J, Tanwar K, Baleanu D. A new fractional exothermic reactions model having constant heat source in porous media with power, exponential and Mittag-Leffler Laws. Int J Heat Mass Transfer. (2019) 138:1222–7. doi: 10.1016/j.ijheatmasstransfer.2019.04.094

CrossRef Full Text | Google Scholar

5. Kumar D, Singh J, Baleanu D. On the analysis of vibration equation involving a fractional derivative with Mittag-Leffler law. Math Methods Appl Sci. (2019) 43:443–57. doi: 10.1002/mma.5903

CrossRef Full Text | Google Scholar

6. Bhatter S, Mathur A, Kumar D, Singh J. A new analysis of fractional Drinfeld–Sokolov–Wilson model with exponential memory. Physica A. (2020) 537:122578. doi: 10.1016/j.physa.2019.122578

CrossRef Full Text | Google Scholar

7. Kumar D, Singh J, Purohit SD, Swroop R. A hybrid analytical algorithm for nonlinear fractional wave-like equations. Math Model Nat Phenom. (2019) 14:304. doi: 10.1051/mmnp/2018063

CrossRef Full Text | Google Scholar

8. Singh J, Kumar D, Baleanu D. New aspects of fractional Biswas-Milovic model with Mittag-Leffler law. Math Model Nat Phenom. (2019) 14:303. doi: 10.1051/mmnp/2018068

CrossRef Full Text | Google Scholar

9. Goswami A, Singh J, Kumar D, Sushila. An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma. Physica A. (2019) 524:563–75. doi: 10.1016/j.physa.2019.04.058

CrossRef Full Text | Google Scholar

10. Goswami A, Singh J, Kumar D, Gupta S, Sushila. An efficient analytical technique for fractional partial differential equations occurring in ion acoustic waves in plasma. J Ocean Eng Sci. (2019) 4:85–99. doi: 10.1016/j.joes.2019.01.003

CrossRef Full Text | Google Scholar

11. Liao SJ. On the Proposed Homotopy Analysis Technique for Nonlinear Problems and Its Applications (Ph. D. Dissertation). Shanghai Jio Tong University, Shanghai, China (1992).

12. He JH. An approximation solution technique depending upon an artificial parameter. Commun Nonlinear Sci Numerical Simul. (1998) 3:92–7. doi: 10.1016/S1007-5704(98)90070-3

CrossRef Full Text | Google Scholar

13. Marinca V, Herisanu N. The optimal homotopy asymptotic method for solving Blasius equation. Appl Math Comput. (2014) 231:134–9. doi: 10.1016/j.amc.2013.12.121

CrossRef Full Text | Google Scholar

14. Marinca V, Herisanu N. Application of homotopy asymptotic method for solving non-linear equations arising in heat transfer, I, Comm. Heat Mass Transfer. (2008) 35:710–5. doi: 10.1016/j.icheatmasstransfer.2008.02.010

CrossRef Full Text | Google Scholar

15. Marinca V, Herisanu N. Determination of periodic solutions for the motion of a particle on a rotating parabola by means of the optimal homotopy asymptotic method, J Sound Vib. (2010) 329:1450–9. doi: 10.1016/j.jsv.2009.11.005

CrossRef Full Text | Google Scholar

16. Iqbal S, Idrees M, Siddiqui AM, Ansari AR. Some solutions of the linear and nonlinear Klein Gordon equations using the optimal homotopy asymptotic method. Appl Math Comput. (2010) 216:2898–909. doi: 10.1016/j.amc.2010.04.001

CrossRef Full Text | Google Scholar

17. Iqbal S, Javed A. Application of optimal homotopy asymptotic method for the analytic solution of singular Lane-Emden type equation. Appl Math Comput. (2011) 217:7753–61. doi: 10.1016/j.amc.2011.02.083

CrossRef Full Text | Google Scholar

18. Iqbal S, Sarwar F, Rafiq M, Mufti Siddique I. Use of optimal homotopy asymptotic method for fractional order nonlinear Fredholm integro-differential equations. Sci Int. (2015) 27:3033−40.

Google Scholar

19. Sarwar S, Salem Alkhalaf. Iqbal S, Zahid MA. A note on optimal homotopy asymptotic method for the solutions of fractional order heat-and wave-like partial differential equations. Comp Math Appl. (2015) 70:942–53. doi: 10.1016/j.camwa.2015.06.017

CrossRef Full Text | Google Scholar

20. Sarwar S, Rashidi MM. Approximate solution of two term fractional order diffusion, wave diffusion and telegraph models arising in mathematical physics using optimal homotopy asymptotic method. Waves Random Complex Media. (2016) 26:365–82. doi: 10.1080/17455030.2016.1158436

CrossRef Full Text | Google Scholar

21. Kumar D, Singh J, Al Qurashi M, Baleanu D. A new fractional SIRS-SI malaria disease model with application of vaccines, antimalarial drugs, and spraying. Adv Differ Equ. (2019) 2019:278. doi: 10.1186/s13662-019-2199-9

CrossRef Full Text | Google Scholar

22. Dubey VP, Kumar R, Kumar D, Khan I, Singh J. An efficient computational scheme for nonlinear time fractional systems of partial differential equations arising in physical sciences. Adv Diff Eq. (2020) 2020:46. doi: 10.1186/s13662-020-2505-6

CrossRef Full Text | Google Scholar

23. Gao W, Yel G, Baskonus HM, Cattani C. Complex solitons in the conformable (2+1)-dimensional Ablowitz-Kaup-Newell-Segur equation. AIMS Math. (2020) 5:507–21. doi: 10.3934/math.2020034

CrossRef Full Text | Google Scholar

24. Yavuz M. Characterizations of two different fractional operators without singular kernel. Math Model Nat Phenom. (2019) 14:302. doi: 10.1051/mmnp/2018070

CrossRef Full Text | Google Scholar

25. Keten A, Yavuz M, Baleanu D. Nonlocal Cauchy problem via a fractional operator involving power kernel in Banach spaces. Fractal Fract. (2019) 3:27. doi: 10.3390/fractalfract3020027

CrossRef Full Text | Google Scholar