The Time-Dependent Lead-Lag Relationship Between WTI and Brent Crude Oil Spot Markets

Based on daily returns, we comprehensively characterize the lead-lag relationship between Brent and WTI crude oil spot markets from 1987 to 2017 with the non-parametric symmetric thermal optimal path (TOPS) method. The empirical results indicate that WTI spot price leads Brent spot price slightly, which provides support to the price leadership of WTI over Brent. However, the lead-lag relationship is volatile and sensitive to extreme events like geopolitical conflict and policy shift. Due to the concerns about future oil supply triggered by the two Gulf wars, both WTI and Brent experienced extreme uncertainty and co-moved closely during wartime. Notably, the TOPS method captures the structural break in the WTI-Brent price spread in 2011 which is influenced by the U.S. oil export ban and transportation bottleneck. After the lift of the ban, the two benchmark prices have reconnected. The lead-lag signals basically coincide with major influential changes in the oil markets, which suggests that the TOPS method provides a viable approach to reflecting the impact of extreme events on the crude oil prices motion.

1. Introduction

Brent and Western Texas Intermediate (WTI) are the two predominant benchmarks for crude oil in global markets. Their price relationship has been changeable all the time. Research on properties of their movements have been continually growing. Using copulas, Reboredo [1] reports evidence of symmetric upper and lower tail dependence structure between crude oil prices. Adopting a rolling estimation, Kao and Wang [2] trace the changing path of WTI information share from 1991 to 2009. Their results demonstrate that WTI has lost the status of leading price to Brent since 2004. While Liu et al. [3] utilize high-frequency data from 2008 to 2011 and show that WTI is more important than Brent for price discovery process when they are co-integrated. Elder et al. [4] also find WTI maintains a dominant role over Brent in price discovery from 2007 to 2012. Coronado et al. [5] apply a one-tailed non-parametric Granger causality test to study the co-movements for oil prices and alert a bi-directional feedback pattern between Brent and WTI from 2013 to 2015.

Moreover, the price spread between WTI and Brent is also essential to reflect the competitiveness among the two benchmarks. Chen et al. [6] verify the structural change of WTI-Brent spread process (December 2010). Scheitrum et al. [7] identify a breakpoint in January 2011. Caporin et al. [8] document two structural breaks in February 2011 and October 2014. Ye and Karali [9] detect three structural breaks in February 2005, the second is in December 2010 and the third is in April 2013.

Additionally, crude oil market is strongly associated to global economy, energy policy and financial market [10–12]. Correspondingly, crude oil price is fragile and subject to sudden incidents and shocks, such as political events, economic events (the Asian financial crisis in 1997), energy policies (the lift of U.S. crude oil export ban) and military conflicts (the Gulf War in 1990, the Iraq War in 2003, etc.). Thus, extensive interest has been devoted to the evident impacts of extreme and irregular events on crude oil markets. Zhang et al. [13] apply an empirical mode decomposition (EMD) based event analysis to evaluate the effects of the Persian Gulf War and the Iraq War on WTI and Brent. They find that impact of extreme events between the two prices exhibits no significant difference. Charles and Darné [14] discern that particular events have a bearing on large shocks in the crude oil prices based on the generalized autoregressive conditional heteroskedasticity (GARCH) models. Similarly, Basistha and Kurov [15] examine the impact of monetary policy shocks on energy prices and find different response patterns. Luong et al. [16] document that WTI and Brent have reintegrated since the lift of the U.S. crude oil export ban.

Though numerous researchers have investigated the crude oil markets and their interaction, the interlinkages and dynamics between WTI and Brent during extreme events is still a substantial point of discussion. In this paper, we investigate the time-dependent lead-lag relationship between the Brent and WTI crude oil spot price during 1987–2017 via the symmetric thermal optimal path (TOPS) method developed by Meng et al. [17]. The two non-parametric approaches can effectively identify the time-dependent lead-lag correlation between two time series, which have been applied to financial market [12, 18–23]. The TOPS method is an improved version of the novel thermal optimal path (TOP) method [24–26] with smaller biases and higher accuracy.

The TOP/TOPS method does not confirm the genuine causality but provides information on the time lag between two series [17, 24]. Moreover, crude oil price is highly sensitive to a variety of factors like policy changes and geopolitical events. Therefore, one should be careful when examining the price discovery of crude oil market via TOPS method. Further information is needed to determine the price leadership relationship. In this manuscript, we mainly focus on the time dependent lead-lag relationship between the two markets. Inspired by Jiang et al. [27], we separate the whole sample into four time periods by the outbreak of the Gulf War, the Iraq War and the lift of U.S. crude oil export ban to examine the lead-lag relationship during different periods. To test the significance of the lead-lag structure, we implement the self-consistency test introduced by Meng et al. [17].

The paper is organized as follows. In section 2, data and summary statistics are presented. Section 3 depicts the methodology. Section 4 provides the empirical results, and section 5 concludes the paper.

2. Data Description

This study uses daily data collected from the US Energy Information Administration (EIA) website. The data is given in the U.S. dollar per barrel spanning from 20 May 1987 to 10 October 2017 and illustrated in Figure 1. Note that the three vertical solid lines in Figure 1A divide the whole period into four segments: before the Gulf War, before the Iraq War, after the Iraq War and after the lift of export ban.

FIGURE 1

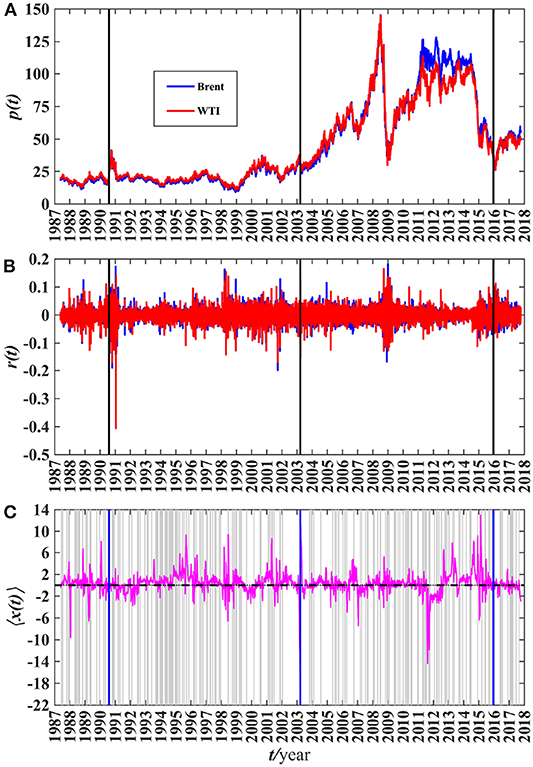
Figure 1. Spot price, returns, and lead-lag path 〈x(t)〉 from 20 May 1987 to 10 October 2017, respectively labeled by (A–C). The vertical lines mark the outbreaks of the Gulf War and the Iraq War as well as the lift of export ban. (A) Brent and WTI spot price. (B) Returns. (C) Lead-lag path 〈x(t)〉. The gray shades represent the periods when the consistency test is significant at the 5% level.

We use logarithmic returns for the analysis. The logarithmic returns of the spot price are defined as follows:

$\begin{array}{ll}r(t)=lnp(t)-lnp(t-1),& (1)\end{array}$

where p(t) represents the crude oil spot price at time t. The logarithm returns are in illustrated in Figure 1B.

Table 1 summarizes the statistics for the two return series. The descriptive statistics are quite similar across the two markets. The ADF test shows the stationarity of daily Brent and WTI crude oil spot returns. In comparison with Brent spot returns, WTI spot returns offer slightly higher volatility levels. Both of the returns are left-skewed and leptokurtic. The high values for the kurtosis statistic suggest that the distribution of returns has larger, thicker tails than normal distribution. The Jarque–Bera test results also suggest that both returns are not normally distributed.

TABLE 1

Table 1. Descriptive statistics for Brent and WTI spot returns.

Specifically, the Pearson correlation coefficient between spot returns of Brent and WTI is 0.60047, which indicates that Brent spot returns are slightly positive correlated to WTI spot returns.

3. Methodology

Meng et al. [17] improve the TOP method [24–26] and propose the TOPS method. The TOPS method is briefly described as below.

Consider two standardized time series X(t₁) : t₁ = 1, 2, ⋯ , N − 1 and Y(t₂) : t₁ = 1, 2, ⋯ , N − 1, the distance matrix between X(t₁) and Y(t₂), denoted by E_X,Y, is defined as

$\begin{array}{ll}ϵ(t_1,t_2)=|X(t_1)-Y(t_2)|.& (2)\end{array}$

The lead–lag structure between two time series is detected by searching for the one-to-one mapping t₁ → t₂ = ϕ(t₁) that satisfies

$\begin{array}{ll}{\displaystyle \underset{\left\{\varphi (t_1),t_1=0,1,\dots ,N-1\right\}}{min}}E:\; ={\displaystyle \sum _{t_1=0}^{N-1}}|X(t_1)-Y(\varphi (t_1))|,& (3)\end{array}$

which is a global minimization with continuity constraint

$\begin{array}{ll}0\le \varphi (t_1+1)-\varphi (t_1)\le 1.& (4)\end{array}$

And rotate the coordinate system (t₁, t₂) to (t, x)

$\begin{array}{ll}\{\begin{array}{l}t=t_2+t_1\hfill \\ x=t_2-t_1.\hfill \end{array}& (5)\end{array}$

Denote the probability for a path through (x, t) as W(t, x)/W(t), where W(t, x) is the partition function of x at fixed t and

$\begin{array}{ll}W(t)={\displaystyle \sum _x}W(t,x).& (6)\end{array}$

Notice that, the partition function W(t, x) obeys the following recursion relation:

$\begin{array}{ll}W(t,x)=\left[W(t-1,x-1)+W(t-1,x+1)+W(t-2,x)\right]e^{-ϵ(t,x)/T}.& (7)\end{array}$

Then implement a time-reversed invariant node weight process by averaging the weights determined along the time-forward and time-backward directions:

$\begin{array}{ll}\langle x(t)\rangle ={\displaystyle \sum _x}x\frac{\vec{W}(t,x)/\vec{W}(t)+\stackrel{⃖}{W}(t,x)/\stackrel{⃖}{W}(t)}{2},& (8)\end{array}$

where the arrow → represents the recursive weight process in a time-forward direction, and the arrow ← refers to the recursive weight process in a time-backward direction. Therefore, one can obtain the optimal thermal averaged path trajectory 〈x(t)〉.

4. Results

This section presents analysis results for the lead-lag features between Brent and WTI from 20 May 1987 to 10 October 2017. Based on the empirical experiment [17], we implement the TOPS analysis with temperature T = 2, which is the optimal parameter.

To examine the lead-lag structure during extreme events, we divide the full-sample period into four sub-samples by the outbreaks of the Gulf War (2 August 1990), the Iraq War (20 March 2003), and the lift of export ban (18 December 2015). We further carry out self-consistency tests in a moving window with size of 10 days to assess whether the lead-lag path is significant, and illustrate the result in Figure 1C. Periods that pass the test are marked in gray shades. Basically the consistency test is significant. Explanatorily, the four different subsamples are denoted as Sub 1, Sub 2, Sub 3, and Sub 4 based on their chronological orders, respectively. Table 2 shows the summary of 〈x(t)〉 during the sample period and Figure 2 shows the boxplots and probability density curves of 〈x(t)〉.

TABLE 2

Table 2. Summary of the 〈x(t)〉 during whole period and the four sub-periods.

FIGURE 2

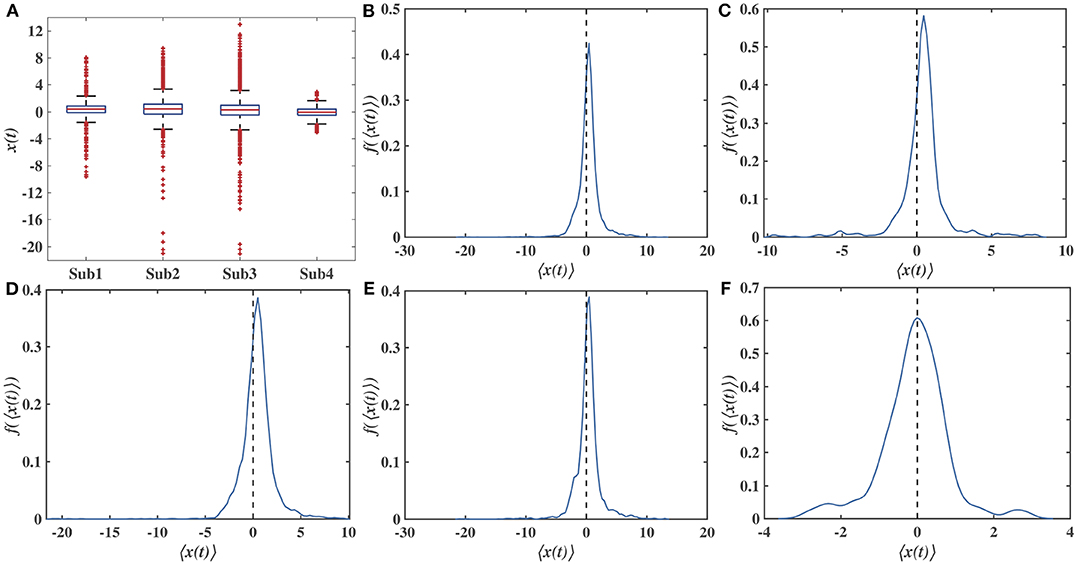
Figure 2. Boxplots and probability density curve based on kernel density estimation of the 〈x(t)〉. (A) Boxplots of 4 subsamples. The box plots illustrate the 25 and 75% quartiles, the median and outliers. (B–E) Probability density curve of four subsamples. (F) Probability density curve of the whole sample period.

As illustrated by the boxplots in Figure 2A, the 4 subsamples paths are highly similar except the outliers. See in Figures 2B–F, the probability density curve of the whole sample period TOPS path is almost symmetrical around 0. More accurately, positive 〈x(t)〉 takes more percentage of the whole paths (64.06%). The positive lead-lag paths reveal that WTI spot price is ahead of Brent spot price slightly with certain time lags, which means the price changes in WTI preceded the price changes in Brent. This is in accord with the fact that WTI holds the predominant position in the crude oil market except several episodes [3, 4, 7].

During the Sub 1 period from 20 May 1987 to 2 August 1990, the TOPS paths 〈x(t)〉 have 71.29% positive values, which indicates that Brent spot returns lag behind WTI spot returns over this period. The Iraq's invasion of Kuwait on 2 August, 1990 caused immediate disruption of the oil supply and triggered the oil price shock. The price of oil almost doubled in 2 months. WTI price peaked above $40 per barrel in October, while Brent price has risen to $41.45 per barrel on 27 September (see in Figure 1A). The alternate lead-lag dependence in September and October also suggests that the crude oil prices of WTI and Brent co-moved closely during periods of extreme market uncertainty [13].

As the situation gradually became clear, the uncertainty was eased and the market calmed down. From 1991 to the second half of 1992, Brent leads WTI (see in Figure 1C). Whereas, Brent is still lagged behind WTI in most cases during the Sub 2 period (with 66.42% positive 〈x(t)〉). Remarkably, the 〈x(t)〉 has two vibrations around the financial crises in 1995 and 1998, which coincides with the 1995 Russian crisis and the 1997 Asian financial crisis. Most intriguingly, we could observe a sharp vibration on 20 March 2003 in Figure 1C. The vibration is strong and temporal, which reflects the nervousness in the crude oil market triggered by the war. The weak alternate lead-lag relationship after the vibration implies that, the two markets react similarly under stress [13]. As concerns about long-term supply shortages eased and prices began to fall, a positive lead-lag path is observed in 2004.

In the Sub 3 period, the percentage that WTI spot leads Brent spot is 66.42%. The positive paths imply that WTI plays a leading role in most times while occasionally Brent takes the lead. For instance, the lead-lag relation reversion in 2007 might be associated with the financial crisis. Until 2011, WTI is more important than Brent for price discovery process [3, 4]. However, starting in 2011 the spread in the U.S. and international crude prices was enlarging, even reached -$29 per barrel (see in Figure 1A). WTI was trading at a large discount to Brent. Though several pipeline projects from Cushing to the Gulf Coast were built to expand transportation capacity after 2012 [16, 28], the U.S. crude oil could not be exported to the global marketplace to arbitrage away the spread due to the export ban [7] and transportation bottleneck [29]. Subsequently WTI was actually more a localized market than a globalized market. Then Energy Information Administration (EIA) replaced WTI with the North Sea Brent contract as the reference oil price [7]. The dramatic fluctuation of lead-lag path in 2011 (see in Figure 1C) supports the structural break that occurred in the WTI-Brent price spread around 2000–2011 [6–9]. At this time, WTI is “viewed as a broken benchmark” [7]. Since 2013 the lead-lag paths switch to an upward oscillation, which implies Brent changes are lagging behind WTI changes with increasing time lag. However, WTI was disconnected from the global market due to the export ban and transportation bottlenecks, it might not be reasonable to claim that WTI serves as a price discovery center during this time.

However, things have changed in 2015. The significant Brent-WTI spread, the sharp drop in oil prices and a Congressional budget deal led to the U.S. policy shift on oil export [30]. On 18 December of this year, the forty-decades-old crude oil export ban was finally lifted. Since then US oil could be transported abroad. Also, trade and efficiency in the oil market increased [31]. Consequently, sustainable increases in pipeline capacity together with the lift helped WTI reconnect with international crude oil prices [16]. After the lift of export ban, WTI spot almost evolves simultaneously with Brent (see in Figure 1A). The WTI and Brent crude oil returns display a bi-directional lead-lag structure (see in Figure 1C) with 48.24% positive 〈x(t)〉 in the Sub 4 period, which is consistent with the fact that WTI and Brent have reconnected ever since the lift of the ban [16].

Basically, WTI leads Brent during the whole sample period except the last sub-period, when the two benchmark prices align closely and exhibit an alternate lead-lag structure. Percent of positive 〈x(t)〉 is highest during Sub 1 period, then decreases in the following periods, which might suggest that WTI and Brent are more and more connected.

5. Conclusion

This paper comprehensively investigates the lead-lag relationship between Brent and WTI crude oil spot prices from 20 May 1987 to 10 October 2017 based on the TOPS method. To examine the lead-lag structure at different periods, we divide the whole series into four sub-series by the outbreaks of the Gulf War, the Iraq War, and the lift of the U.S. export ban.

The results show that the WTI spot market is leading the Brent spot market slightly during the whole period, which is in line with the fact that WTI oil price plays the dominant role in the international oil market [3, 4, 7]. However, the lead-lag relationship is volatile and subject to economic events, geopolitical events and policy shifts. The percentage of positive 〈x(t)〉 during different sub-periods increases successively, which may indicate that WTI and Brent prices are reintegrating gradually.

Additionally, extreme events affected the path in varying degrees. Political events like the two Gulf wars triggered concerns about future oil supply. Both of the two benchmark prices experienced extreme uncertainty [13], which is reflected in the sharp but temporary increase of oil price. During wartime WTI and Brent co-move closely. A violent fluctuation of the 〈x(t)〉 is observed on the outbreak of the Iraq war, which might be related to the Iraq's oil output collapse at that time. The U.S. export ban also affected the WTI-Brent lead-lag relationship. The ban [7] together with transportation bottleneck [29] have long influenced the WTI-Brent spread. The turning point of the WTI-Brent spread structure [6–9] in 2011 accords with the upheaval of the 〈x(t)〉. The shift of energy policy, i.e., the lift of the export ban in 2015, has reconnected WTI to Brent [16]. The alternate lead-lag relationship lasts until the end of the sample.

These results are in line with other related studies, which reveal that The TOPS method has the potential to investigate the impact of extreme events on correlations between two time series. However, oil market is extremely fragile and affected by numerous factors. There still needs further exploration and stronger support to make the TOPS method a more active and convincing approach to event analysis. Given this, we will focus on these issues in future research.

Data Availability Statement

The datasets for this study can be found in the https://www.eia.gov/ US Energy Information Administration (EIA) website.

Author Contributions

All authors analyzed and discussed the results, contributed to the draft paper, and revisions. YS and XS conceived, designed the research, and wrote the manuscript. YY have implemented the empirical analysis. HS participated on the writing and editing of the paper.

Funding

This work was supported by the Peak Discipline Construction Project of Education at East China Normal University, and the National Natural Science Foundation of China (Grant No. 11805119).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past supervisory role with the author YY.

Acknowledgments

We would like to acknowledge the reviewers for their constructive comments.

References

1. Reboredo JC. How do crude oil prices co-move? A copula approach. Energy Econ. (2011) 33:948–55. doi: 10.1016/j.eneco.2011.04.006

CrossRef Full Text | Google Scholar

2. Kao CW, Wan JY. Price discount, inventories and the distortion of WTI benchmark. Energy Econ. (2012) 34:117–24. doi: 10.1016/j.eneco.2011.03.004

CrossRef Full Text | Google Scholar

3. Liu WM, Schultz E, Swieringa J. Price dynamics in global crude oil markets. J Futures Mark. (2015) 35:148–62. doi: 10.1002/fut.21658

CrossRef Full Text | Google Scholar

4. Elder J, Miao H, Ramchander S. Price discovery in crude oil futures. Energy Econ. (2014) 46:S18–27. doi: 10.1016/j.eneco.2014.09.012

CrossRef Full Text | Google Scholar

5. Coronado S, Fullerton TM Jr, Rojas O. Causality patterns for brent, WTI, and argus oil prices. Appl Econ Lett. (2017) 24:982–6. doi: 10.1080/13504851.2016.1245830

CrossRef Full Text | Google Scholar

6. Chen W, Huang Z, Yi Y. Is there a structural change in the persistence of WTI-Brent oil price spreads in the post-2010 period? Econ Model. (2015) 50:64–71. doi: 10.1016/j.econmod.2015.06.007

CrossRef Full Text | Google Scholar

7. Scheitrum DP, Carter CA, Revoredo-Giha C. WTI and Brent futures pricing structure. Energy Econ. (2018) 72:462–9. doi: 10.1016/j.eneco.2018.04.039

CrossRef Full Text | Google Scholar

8. Caporin M, Fontini F, Talebbeydokhti E. Testing persistence of WTI and Brent long-run relationship after the shale oil supply shock. Energy Econ. (2019) 79:21–31. doi: 10.1016/j.eneco.2018.08.022

CrossRef Full Text | Google Scholar

9. Ye S, Karali B. Estimating Relative Price Impact: The Case of Brent and WTI. No 235728, 2016 Annual Meeting, July 31–August 2. Boston, MA: Agricultural and Applied Economics Association (2016).

Google Scholar

10. Zhu H, Guo Y, You W. An empirical research of crude oil price changes and stock market in China: evidence from the structural breaks and quantile regression. Appl Econ. (2015) 47:6055–74. doi: 10.1080/00036846.2015.1064076

CrossRef Full Text | Google Scholar

11. Kang W, Ratti RA, Yoon KH. Time-varying effect of oil market shocks on the stock market. J Bank Finance. (2015) 61:S150–63. doi: 10.1016/j.jbankfin.2015.08.027

CrossRef Full Text | Google Scholar

12. Yao CZ, Kuang PC. A study of lead-lag structure between international crude oil price and several financial markets. Phys A Stat Mech Appl. (2019) 531:121755. doi: 10.1016/j.physa.2019.121755

CrossRef Full Text | Google Scholar

13. Zhang X, Yu L, Wang S, Lai KK. Estimating the impact of extreme events on crude oil price: an EMD-based event analysis method. Energy Econ. (2009) 31:768–78. doi: 10.1016/j.eneco.2009.04.003

CrossRef Full Text | Google Scholar

14. Charles A, Darné O. Volatility persistence in crude oil markets. Energy Policy. (2014) 65:729–42. doi: 10.1016/j.enpol.2013.10.042

CrossRef Full Text | Google Scholar

15. Basistha A, Kurov A. The impact of monetary policy surprises on energy prices. J Futures Mark. (2015) 35:87–103. doi: 10.1002/fut.21639

CrossRef Full Text | Google Scholar

16. Luong PV, Mizrach B, Otsubo Y. Location basis differentials in crude oil prices. Energy J. (2019) 40:41–58. doi: 10.5547/01956574.40.SI2.pluo

CrossRef Full Text | Google Scholar

17. Meng H, Xu HC, Zhou WX, Sornette D. Symmetric thermal optimal path and time-dependent lead-lag relationship: Novel statistical tests and application to UK and US real-estate and monetary policies. Quant Financ. (2017) 17:959–77. doi: 10.1080/14697688.2016.1241424

CrossRef Full Text | Google Scholar

18. Guo K, Zhou WX, Cheng SW, Sornette D. The US stock market leads the Federal funds rate and treasury bond yields. PLoS ONE. (2011) 6:e22794. doi: 10.1371/journal.pone.0022794

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Wang D, Tu J, Chang X, Li S. The lead-lag relationship between the spot and futures markets in China. Quant Financ. (2017) 17:1447–56. doi: 10.1080/14697688.2016.1264616

CrossRef Full Text | Google Scholar

20. Xu HC, Zhou WX, Sornette D. Time-dependent lead-lag relationship between the onshore and offshore Renminbi exchange rates. J Int Financ Mark Inst Money. (2017) 49:173–83. doi: 10.1016/j.intfin.2017.05.001

CrossRef Full Text | Google Scholar

21. Shao YH, Yang YH, Shao HL, Stanley HE. Time-varying lead-lag structure between the crude oil spot and futures markets. Phys A. (2019) 523:723–33. doi: 10.1016/j.physa.2019.03.002

CrossRef Full Text | Google Scholar

22. Jiang T, Bao S, Li L. The linear and nonlinear lead-lag relationship among three SSE 50 Index markets: the index futures, 50ETF spot and options markets. Phys A. (2019) 525:878–93. doi: 10.1016/j.physa.2019.04.056

CrossRef Full Text | Google Scholar

23. Yang YH, Shao YH. Time-dependent lead-lag relationships between the VIX and VIX futures markets. The North American Journal of Economics and Finance. (2019) 191013729. doi: 10.1016/j.najef.2020.101196

CrossRef Full Text | Google Scholar

24. Sornette D, Zhou WX. Non-parametric determination of real-time lag structure between two time series: the “optimal thermal causal path” method. Quant Financ. (2005) 5:577–91. doi: 10.1080/14697680500383763

CrossRef Full Text | Google Scholar

25. Zhou WX, Sornette D. Non-parametric determination of real-time lag structure between two time series: the “optimal thermal causal path” method with application to economic data. J Macroecon. (2006) 28:195–224. doi: 10.1016/j.jmacro.2005.10.015

CrossRef Full Text | Google Scholar

26. Zhou WX, Sornette D. Lead-lag cross-sectional structure and detection of correlated-anticorrelated regime shifts: application to the volatilities of inflation and economic growth rates. Phys A. (2007) 380:287–96. doi: 10.1016/j.physa.2007.02.114

CrossRef Full Text | Google Scholar

27. Jiang ZQ, Xie WJ, Zhou WX. Testing the weak-form efficiency of the WTI crude oil futures market. Phys A. (2014) 405:235–44. doi: 10.1016/j.physa.2014.02.042

CrossRef Full Text | Google Scholar

28. Tian HZ, Lai WD. The causes of stage expansion of WTI/Brent spread. Petrol Sci. (2019) 16:1493–505. doi: 10.1007/s12182-019-00379-z

CrossRef Full Text | Google Scholar

29. Buyuksahin B, Lee TK, Moser JT, Robe MA. Physical markets, paper markets and the WTI-Brent spread. Energy J. (2013) 34:129–51. doi: 10.5547/01956574.34.3.7

CrossRef Full Text | Google Scholar

30. Colgan JD, de Graaf T. A crude reversal: The political economy of the United States crude oil export policy. Energy Res Soc Sci. (2017) 24:30–5. doi: 10.1016/j.erss.2016.12.012

CrossRef Full Text | Google Scholar

31. Melek NÇ, Ojeda E. Lifting the US crude oil export ban: prospects for increasing oil market efficiency. Econ Rev. (2017) 102:51–74. doi: 10.18651/ER/2q17CakirMelekOjeda

CrossRef Full Text | Google Scholar