Renormalization Group Approach to Pandemics: The COVID-19 Case

We investigate the spreading dynamics of infected cases for SARS-2013 and COVID-19 epidemics for different regions of the world, in terms of the renormalization group language. The latter provides an alternative way to describe the underlying dynamics of disease spread. This allows us to introduce important quantities, for a given disease, such as the slope of the beta function at fixed points and the time scale of the epidemic spread inflection point. We discover that for COVID-19 the epidemic slope is of order one inverse week and the inflection point occurs roughly 4 weeks after the outbreak. We use these results to attempt long term estimates for the epidemic evolution in several regions of the world. The accuracy of the results vary depending on the epidemic stage for each region. We also provide a webpage where we daily update our analyses.

1. Introducing the Framework

Prompted by the COVID-19 pandemic outbreak we investigate its spreading dynamics using the language of the renormalization group approach that is extremely effective in statistical and high energy physics [1, 2]. Our approach is complementary to other traditional methods nicely summarized in Li et al. [3] and Zhan et al. [4] for complex network methods and in Perc et al. [5] and Wang et al. [6, 7] when taking into account also spatial effects. As for the widely adopted choice to represent the data by fit them to a logistic function we refer to Danby [8], Brauer [9], Miller [10], Murray[11], Fisman et al. [12], and Pell et al. [13].

We find convenient to discuss rather than the number of cases its logarithm which, being a slowly varying function, is more suited for modeling. We define through it an epidemic strength function whose derivative with respect to time provides a new quantity that we interpret as the beta-function of an underlying microscopic model. In statistical and high energy physics the latter governs the time (inverse energy) dependence of the interaction strength among fundamental particles. Here it regulates social interactions.

To establish and test the framework we use the epidemic data from China for COVID-19 and from Hong-Kong (HK) for SARS-2003 since they represent statistically significative and precise ensembles with, to date, over 80k infected cases and 3k deaths reported for China COVID-19 and around 2k infected cases for (HK) SARS-2003 data. We start empirically by collecting data¹ for the cumulative confirmed infected cases² from the World Health Organization (WHO) -China COVID-19 and for HK-SARS 2003 (https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports) from World Health Organization (WHO)-HK SARS-2003 (https://www.who.int/csr/sars/country/en/). For the remaining countries we also cross-check the data with Worldometers (https://www.worldometers.info/coronavirus/#countries).

As simple characterization of the logarithmic value of the number of infected data points we use the following function:

$\begin{array}{ll}{\alpha }_{\text{ES}}[t]=\frac{aexp[\gamma t]}{b+exp[\gamma t]}.& (1)\end{array}$

By construction the function grows quickly at small t and then it approaches rapidly the large t plateau of the data. Here t is time measured in weeks. The parameter a determines the height of the plateau, ln(b) the offsetting time of the spread of the disease whereas γ controls the slope and it is measured in inverse time units. Since we will be using weeks as time-unit, this means that γ has to be understood as given in inverse weeks. Naturally a encodes information about the number of next-neighbor infectious transmissions. This is the parameter that is directly affected, in a logarithmic manner, by containment measures and the size of the population. The analytic function in Equation (1) can be further extended at the cost of introducing new parameters. For example a can be itself made a function of time to model changes in containment measures.

Additionally, the number of infected cases, which is the exponential of Equation (1), has an inflection point at the time

$\begin{array}{ll}{t}_{\text{Infl}}={\gamma }^{-1}ln\left[\frac{b}{2}\left(a+\sqrt{4+a^2}\right)\right],& (2)\end{array}$

which corresponds to the point where the second derivative of the number of the infected cases vanishes. Physically it is associated to the time when the number of reported new cases starts decreasing. This means that the first derivative of the fitted function at the inflection point displays a maximum (second derivative vanishes). It is convenient to measure the inflection point relative to an initial arbitrary value of the time t₀ corresponding, for example, to the point when the number of infected cases is 10. We arrive at:

$\begin{array}{ll}\Delta t_{\text{Infl}}:=t_{\text{Infl}}-t_0={\gamma }^{-1}ln\left[\frac{a-ln[10]}{2ln[10]}\left(a+\sqrt{4+a^2}\right)\right].& (3)\end{array}$

which has the advantage of being b independent and that for sufficiently large a is approximately $\Delta t_{\mathrm{\text{Infl}}}\approx {\gamma }^{-1}ln\left[\frac{a^2-aln[10]}{ln[10]}\right]$. Since the dependence on a is only logarithmic we will see that this time scale is fairly constant across different regions of the world with respect to the COVID-19 epidemic. This, in turn, allows for a certain degree of predictive power to the model parameterization when the data approach the inflection point.

To better elucidate how our parameterization encodes the epidemic dynamics occurring in each region of the globe we better clarify the role played by the parameter γ in what is commonly known as flattening the curve. The latter has come a rallying cry in the COVID-19 battle. From Figure 1 we learn that the smaller γ the longer it takes to reach the peak of the number of new cases (right panel) which also decreases with decreasing γ. As a consequence the epidemic will last longer. This is the price to pay for trying to reduce the number of new cases per day required to minimize the impact on the health system.

FIGURE 1

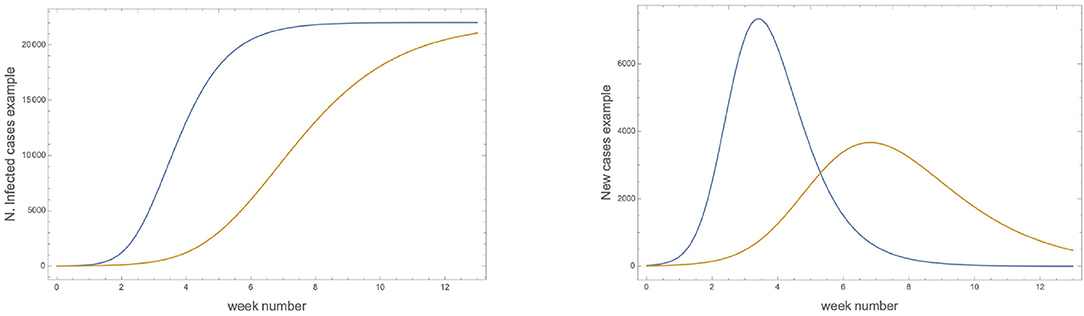
Figure 1. How to flatten the curve. (Left) Hypothetical number of infected cases for two values of γ, i.e., γ = 1 (blue) and 0.5 (orange) as function of time keeping fixed the total number of infected cases. (Right) The corresponding number of new cases.

1.1. Hong Kong SARS-2003

It is instructive to analyse first the Hong Kong (HK) SARS-2003 data to test the robustness of our approach before applying it to the evolving COVID-19 epidemic.

The number of infected cases as function of time as well as the epidemic strength (the logarithm of the number of infected cases) is depicted in Figure 2 along with the best fit that yields:

$\begin{array}{ll}{a}_{\text{H}K}=7.47,b_{\text{H}K}=1.11,{\gamma }_{\text{H}K}=0.60.& (4)\end{array}$

This is the final picture for the HK SARS-2003 epidemic, however it is interesting to learn about an evolving epidemic. This can be simulated by replaying the HK SARS-2003 data as function of time and for each given time obtain the time-dependent parameters a, b, and γ.

FIGURE 2

Figure 2. (Left) SARS-2003 infected cases in Hong Kong as function of the week number starting from March 17 2003. In red, we report the exponential of the epidemic strength model result. (Right) Epidemic strength (the logarithm of the number of infected cases) and the best fit result as in Equation (4).

The results are reported in Figure 3. We obtain excellent fits for each specific time. Nevertheless, as it is clear from the figures, unless the inflection point has occurred the time-dependent fitted parameters cannot be used to predict the entire evolution of the epidemic. The dashed-blue line in the plot corresponds to the time when the inflection occurs.

FIGURE 3

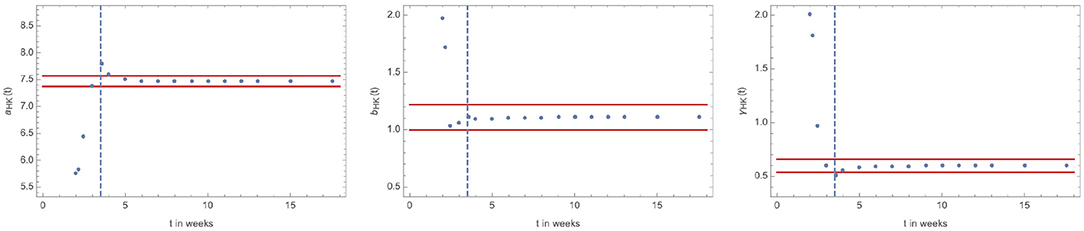
Figure 3. Fit parameters to HK SARS-2003 data as function of time. (Left) a(t) with the red band corresponding to a change of 0.1 in the asymptotic value of a. This translates into a 10% change in the asymptotic number of infected cases. (Center, Right) b(t) and γ(t) with the red band corresponding to a 10% change in their asymptotic value. The vertical dashed blue line marks the occurrence of the inflection point in the infected cases.

Another observation is that while b and γ are correlated they are anti-correlated with respect to a. Additionally, γ and b (a) decrease (increase) till near the inflection point where they overshoot (undershoot) the asymptotic value which is however quickly reached after the inflection point. We also discover that the inflection point occurs around 3.5 weeks after the first report.

Remarkably our analysis is able to reproduce the data with excellent accuracy.

1.2. China COVID-19

We now move to the China COVID-19 data to corroborate the findings above.

The outcome is reported in Figure 4 for the number of infected cases as function of time as well as the epidemic strength along with the best fit that yields

$\begin{array}{ll}{a}_{\text{C}hina}=11.35,b_{\text{C}hina}=2.55,{\gamma }_{\text{C}hina}=0.97.& (5)\end{array}$

We report in Figure 5 the time-evolution of the fit parameters a, b, and γ. Although the fit does not have the same quality as in the HK SARS-2003 case, the main features remain unchanged. Namely, the results stabilizes only when the inflection point has occurred and the parameters are still correlated as observed for the HK SARS-2003 case. The inflection point occurs after roughly 3.5 weeks from the outbreak. Another interesting observation is that the parameter a seems to stabilize earlier than the other parameters. This is a welcome news given that it gives us the log of the asymptotic number of infected cases. It will be interesting to test whether these trends persist for the epidemic spread in other regions of the world including whether the peak in the number of new cases also occurs between 3 and 4 weeks from the outbreak.

FIGURE 4

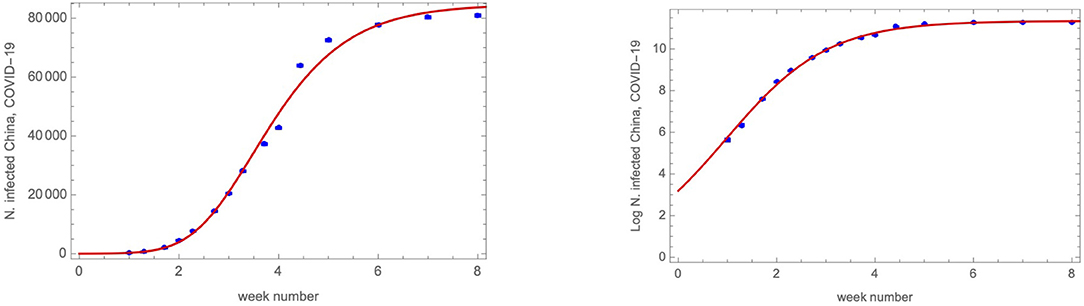
Figure 4. (Left) COVID-19 infected cases in China as function of the week number starting from January 21st 2019. In red, we report the exponential of the epidemic strength model result. (Right) Epidemic strength (the logarithm of the number of infected cases) and the best fit result as in Equation (5).

FIGURE 5

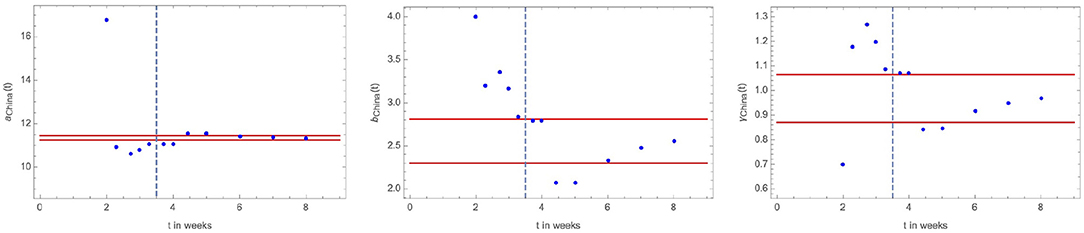
Figure 5. Fit parameters to China COVID-19 data as function of time. (Left) a(t) with the red band corresponding to a change of 0.1 in the asymptotic value of a. This translates into a 10% change in the asymptotic number of infected cases. (Center, Right) b(t) and γ(t) with the red band corresponding to a 10% change in their asymptotic value. The vertical dashed blue line marks the occurrence of the inflection point in the infected cases.

2. Renormalization Group Dictionary

Behavior such as the one in Figure 4 are common in physics from Fermi distributions to out-of-equilibrium thermodynamics to energy dependence of the interaction strengths in physical systems. We focus on the latter similarity with the goal to obtain an anatomic description of the epidemic strength as function of time and possibly identify universal quantities underlying disease spread mechanisms.

We now introduce the following dictionary: The time is naturally identified with t = −ln μ/μ₀ with μ an energy scale and μ₀ a reference energy scale; The epidemic coupling strength is identified with α_ES in Equation (1) and therefore we can now introduce the β_E function of the epidemic:

$\begin{array}{ll}{\beta }_E=\frac{d{\alpha }_{ES}}{dln(\mu /{\mu }_0)}=-\frac{d{\alpha }_{ES}}{dt}.& (6)\end{array}$

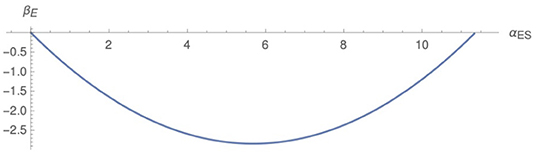
α_ES captures the essential information of the China data and it is shown in Figure 6. We now differentiate α_ES w.r.t. time and obtain β_E which we plot it in Figure 7 as a function of α_ES. The epidemic beta function has two zeros, one at α_ES = 0 corresponding to no disease and one for a finite value ${\alpha }_{ES}^{*}$ corresponding to the log of the plateau of the total infected cases. This is mapped into an underlying epidemic dynamics for which the system features two fixed points one of them being non-interacting and the other still interacting but time dilation invariant. This observation has important consequences in characterizing the universal properties of the underlying dynamics governing the epidemics as the critical theory of phase transitions teaches us [1, 2]. For example, the slope of the beta function evaluated in the infrared (i.e., at low energy/large times) is

$\begin{array}{ll}\frac{\partial {\beta }_E}{\partial {\alpha }_{\text{ES}}}{\displaystyle {|}_{{\alpha }_{\text{ES}}^{*}}}\equiv {\theta }_E=-\gamma ,& (7)\end{array}$

with ${\alpha }_{\text{ES}}^{*}=11.35$ (see Equation 5) the interacting fixed point which is approached at infinite time. The negative sign of the scaling epidemic exponent θ_E tells us that the fixed point is attractive, meaning that any small external perturbation will not destabilize the system. This is different from the fixed point at zero for which the scaling exponent _θE0 = γ is positive meaning that any external perturbation drives the system away from the non-disease limit. Intuitively this means that one has to work hard to stop the spreading of the disease.

FIGURE 6

Figure 6. α_ES[t] as function of time.

FIGURE 7

Figure 7. β_E as function of α_ES.

Additionally, the analytic time form of the epidemic strength encodes its history allowing us, for example, to estimate (taking the time for which α_ES = ln 10) when it actually started. From Figure 5 this can be estimated to be around end of November to beginning of December in agreement with the general expectations [14].

The above goes under the name of the Renormalization Group (RG) analysis in condensed matter and high energy physics.

One can actually construct an ab initio RG analysis for the spread of the pandemic to show that the model in Equation (1) reproduces the general qualitative behavior that we expect for the pandemic. The simplest model for the epidemic spread is

$\begin{array}{ll}\frac{dP}{dt}={\beta }_P(t)=r_{0}P(t)& (8)\end{array}$

where P(t) is the number of infections at time t and r₀ is a characteristic constant. This predicts an exponential growth modeling the first phase of the spread. The flow has a fixed point at P = 0, with critical exponent r₀: in RG parlance this is the ultraviolet (UV) repulsive fixed point.

Clearly this description is too naive. We can improve if we think of the RHS as of the first term in a polynomial expansion in P. Adding the next term we have

$\begin{array}{ll}{\beta }_P(t)=r_{0}P(t)\left(1-\frac{P(t)}{K}\right)& (9)\end{array}$

where K is a new constant. There are now two fixed points. Together with the initial P = 0, we have a new one at P = K. The latter is an infrared (IR) attractive fixed point. It models the later stages of the epidemy, when the number of infections reaches its final value P = K. The flow equation can be solved explicitly and reproduces a logistic growth:

$\begin{array}{ll}P(t)=\frac{K}{1+e^{-r_0(t-T_0)}},& (10)\end{array}$

where T₀ is a constant indicating the inflection point in time. Expanding around the two fixed points, we find that the corresponding critical exponents are the same, up the sign marking the fact that one is repulsive P = 0 and the other attractive P = K:

$\begin{array}{ll}\{\begin{array}{ll}\beta (P)~r_{0}P& \text{for }P~0\text{,}\\ \beta (P)~-r_0(P-K)& \text{for }P~K\text{.}\end{array}& (11)\end{array}$

The strength α_ES satisfies Equation (9) upon identifying a with K, γ with r₀ and exp(r₀T₀) with b. We have already noticed that our parameterization works fairly well and it will continue to do so for the other regions of the globe.

Nevertheless, it is possible to generalize the approach to allow for the exponents in the UV and the IR to differ. The UV describes the beginning of the epidemic, when no measures are taken, while the IR describes the end of it, which strongly depends on the social behavior of the population. To take this into account we add another term in the RG equation:

$\begin{array}{ll}{\beta }_P(t)=r_{0}P(t)\left(1-\frac{P(t)}{K}\right)\left(1-\frac{r_0-r_f}{r_0}\frac{P(t)}{K}\right).& (12)\end{array}$

without loss of generality we will assume r_f ≤ r₀. This model has three fixed points. The UV repulsive point at P = 0, the IR attractive at P = K and a new unphysical repulsive one at P = r₀K/(r₀ − r_f) = K₂ > K. A nice feature of this model is that now the critical exponents of the UV and IR are independent:

$\begin{array}{ll}\{\begin{array}{ll}\beta (P)~r_{0}P& \text{for }P~0\text{,}\\ \beta (P)~-r_f(P-K)& \text{for }P~K\text{.}\end{array}& (13)\end{array}$

[the spurious point is repulsive with β(P) ~ r₀r_f/(r₀ − r_f)(P − K₂)]. This allows for a more flexible description of the data at the price of adding a new parameter for the fit. Adding extra terms to the β function will not change this description qualitatively.

In fact, this RG-flow picture is useful in the sense that it clearly separates UV quantities, related to the beginning of the epidemic curve, such as r₀, from IR quantities, related to its end, such as r_f and the total number of infected K. We expect UV quantities to be universal, because they typically depend on the virus properties. On the other hand IR quantities, such as the total number of infected cases as well as the slope will depend on containment measures. The crossing point between the two behaviors is the inflection point t_Infl, where the derivative of the β-function changes sign. We are in the UV region if dβ/dP > 0 and in the IR region if dβ/dP < 0. It follows that before the inflection point, where the UV fixed point dominates, it is difficult to estimate IR quantities such as the total number of infected K.

As mentioned above, we will consider the simpler case with a single scaling exponent.

We have therefore provided a useful map between models of infectious diseases that are typically introduced directly for modeling P(t) and the epidemic strength α_ES(t).

3. COVID-19 in Other Regions of the World

We now employ the formalism above to analyse the epidemic spread in other regions of the world, namely South Korea, Italy, Denmark, the United States, and the United Kingdom. We chose these countries because they are at different stages of the epidemic evolution. However, at the end of the paper, we provide a link to a webpage in which other countries will be analyzed and all the data daily updated.

3.1. South Korea

We report the outcome for the fit adjourned to March 12th to the South Korea data in Figure 8 for the number of infected cases as function of time as well as the epidemic strength along with the best fit that yields

$\begin{array}{ll}{a}_{\text{K}or}=9.18,b_{\text{K}or}=727,{\gamma }_{\text{K}or}=1.29.& (14)\end{array}$

We report in Figure 9 the time-evolution of the fit parameters a, b, and γ. The time evolution of a and γ indicate that an almost stable value has been reached whereas the situation for b is still uncertain. However, the sensitivity of the data to b is very flat and therefore we can trust the observed stabilization of the other parameters and especially of a. Additionally, the latest-time value of a translates in the following number of asymptotic infected cases of about 9.7k±1k.

FIGURE 8

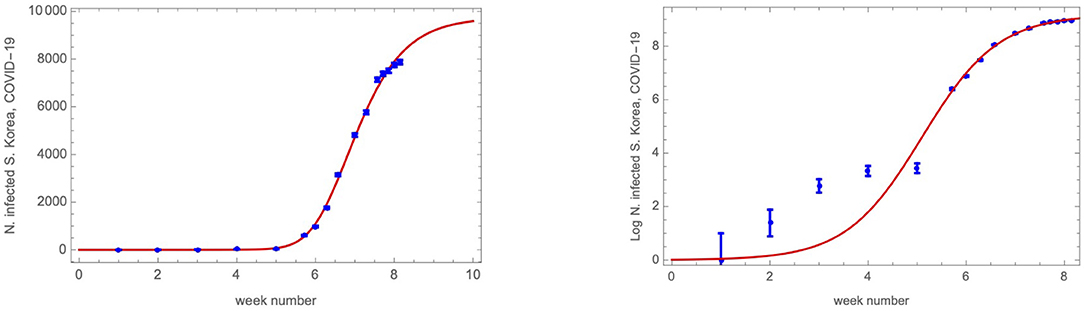
Figure 8. (Left) COVID-19 infected cases in South Korea as function of the week number starting from January 21st 2019. In red, we report the exponential of the epidemic strength model result. (Right) Epidemic strength (the logarithm of the number of infected cases) and the best fit result.

FIGURE 9

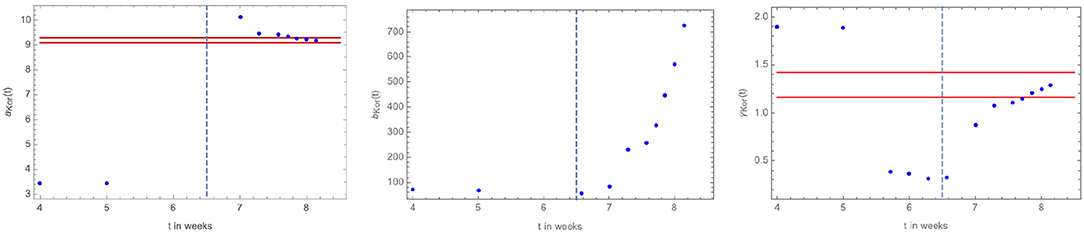
Figure 9. Fit parameters to South Korea COVID-19 data as function of time. (Left) a(t) with the red band corresponding to a change of 0.1 in the last value of a as function of time. This translates into a 10% change in the number of infected cases. (Center, Right) b(t) and γ(t) with the red band for γ corresponding to a 10% change w.r.t. its last value. The vertical dashed blue line marks the occurrence of the inflection point in the infected cases according to the overall fit.

Taking the starting point of the epidemic around the order of 10 reported cases (here occurring at week 2.5) we find that the inflection point is about 4 weeks after that in reasonable agreement with the China COVID-19 and HK SARS-2003 observations. Additionally, we can expect a stabilization in week 10–11 which corresponds to end of March beginning of April.

The data indicates that South Korea has implemented efficient containment measures when, as we shall see, we compare to other countries such as Italy, Denmark, US, and UK. We find convenient to introduce, for each country, denoted by X the parameter

$\begin{array}{ll}{a}_X^{Kor}=a_{Kor}+ln\left(\frac{{\text{pop}}_X}{{\text{pop}}_{Kor}}\right),& (15)\end{array}$

where “pop" stands for population. We believe that when fixing the parameter a to this value a_X it will allow us to measure the overall effects of the containment measures compared to the South Korean case. The following quantity

$\begin{array}{ll}{E}_X=exp\left[a_X-a_X^{Kor}\right],& (16)\end{array}$

measures the relative (in)efficiency of the containment policies enforced by a given county w.r.t. another country, such as South Korea. The measures adopted by a country are more efficient than the ones taken by South Korea if E_X is less than unity.

3.2. Italy

We report the outcome for the fit for the Italian data in Figure 10 for the number of infected cases as function of time. To see if we have reached the inflection point we provide in Figure 11 the evolution of a, b, and γ. It seems that if the current trends continues we have just approached the inflection point.

FIGURE 10

Figure 10. COVID-19 infected cases in Italy as function of the calendar week number. The curve and the band (90% confidence level) have been obtained by performing a fit w.r.t. a, b, and γ to the red data points.

FIGURE 11

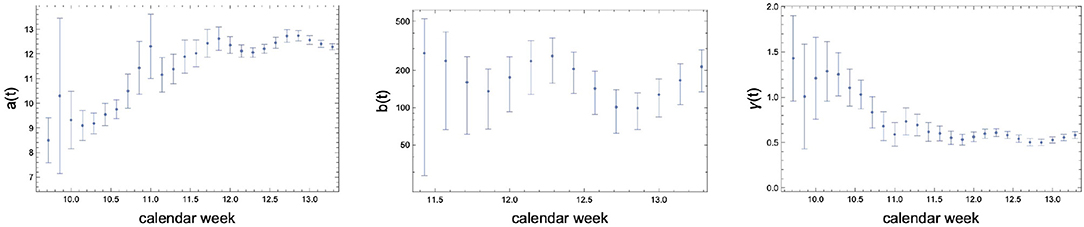
Figure 11. Fit parameters to Italy COVID-19 data as function of time. (Left) a(t). (Center) b(t). (Right) γ(t). The errors correspond to 90% confidence level.

The curve and the band (90% confidence level) in Figure 10 have been obtained by performing a fit with respect to a, b, and γ to the red data points. For the overall fit we have a_Ita = 12.29±0.12, b_Ita = 214±80, and γ_Ita = 0.58±0.04 with the errors estimated at 90% confidence level.

Currently, we therefore expect a minimal and maximal number of infected cases to be respectively 187k and 255k corresponding a 90% confidence level.

We also find the efficiency of the containment measures taken by Italy compared to Korea to be

$\begin{array}{ll}{E}_{Ita}=16-22.& (17)\end{array}$

3.3. Denmark

We report the outcome for Denmark in Figure 12 for the number of infected cases as function of time. The curve and the band, corresponding to 90% confidence level, have been obtained by performing a fit with respect to a, b, and γ to the red data points. The best values are: a = 9.30±0.23, b = (1.8±2.8) × 10⁴, and γ = 0.92±0.14. This corresponds to a variation in the number of asymptotic infected cases spanning from 8.7 to 14k. The inflection point is expected in between weeks 13 and 14 corresponding to end of March while stabilization around end of April.

FIGURE 12

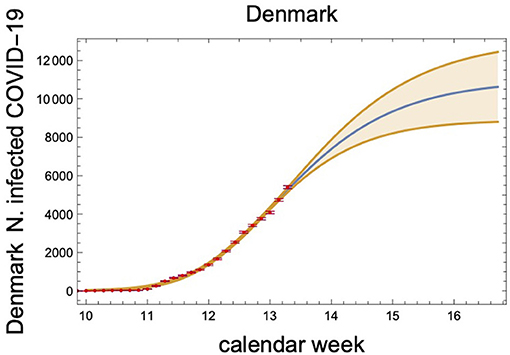
Figure 12. COVID-19 infected cases in Denmark as function of the calendar week number. The curve and the band (90% confidence level) have been obtained by performing a fit w.r.t. a, b, and γ to the red data points. Nota bene that after the 13th of March we multiplied the number of reported new cases by five to take into account the policy change in the way potential cases were tested.

With these very preliminary data we find the efficiency of the containment measures taken by Denmark to be

$\begin{array}{ll}{E}_{Denmark}=8-13,& (18)\end{array}$

at the 90% confidence level.

3.4. United States

The data and the fits for the United States are reported in Figure 13. The United States are still at the beginning of the exponential growth. The curve and the band, corresponding to 90% confidence level, have been obtained by performing a fit with respect to a, b, and γ to the red data points. The best values from the fit are: a = 13.3±0.5, b = (1.3±1.6) × 10⁴, and γ = 0.84 ± 0.11. This corresponds to a variation in the number of asymptotic infected cases spanning from 359 to 927k at the 90% confidence level. We are still far away from the inflection point.

FIGURE 13

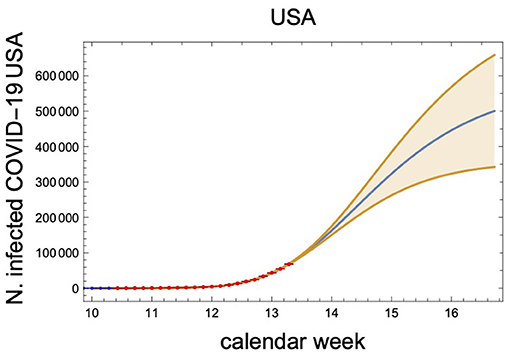
Figure 13. COVID-19 infected cases in the United States as function of the calendar week number. The curve and the band (90% confidence level) have been obtained by performing a fit w.r.t. a, b, and γ to the red data points.

With these very preliminary data we find the efficiency of the containment measures taken by the United States to be

$\begin{array}{ll}{E}_{US}=6-15,& (19)\end{array}$

at the 90% confidence level.

3.5. United Kingdom

Following the previous analyses the fit for the United Kingdom is given in Figure 14. We are still at the beginning of the exponential growth. The curve and the band, corresponding to 90% confidence level, have been obtained by performing a fit yielding a = 11.2 ± 0.5, b = (1.1 ± 1.1) × 10³, and γ = 0.64 ± 0.09 to the red data points. This corresponds to a variation in the number of asymptotic infected cases ranging from 43.5 to 124k at the 90% confidence level. We are still far away from the inflection point.

FIGURE 14

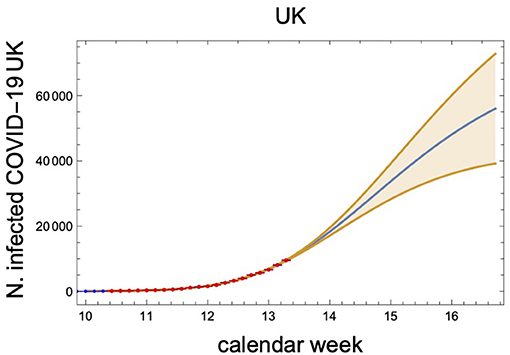
Figure 14. COVID-19 infected cases in the United Kingdom as function of the calendar week number. The curve and the band (90% confidence level) have been obtained by performing a fit w.r.t. a, b, and γ to the red data points.

With these very preliminary data we find the efficiency of the containment measures taken by the United Kingdom to be

$\begin{array}{ll}{E}_{UK}=3.5-9.7,& (20)\end{array}$

at the 90% confidence level.

3.6. A Preliminary Global Analysis

We now attempt to provide a very preliminary analysis for the world pandemic which must be taken cum grano salis. One of the advantages of performing such an analysis is that, given the large numbers involved, the results are less sensitive to individual countries ways of representing the data. As it is clear from Figure 15 the world is, overall, still at the beginning of the pandemic growth and far away from the inflection point. For this reason the predictions are only reasonable on a short time scale. The curve and the band, correspond to 90% confidence level. We stress that this band is for the current fit and it can very will be that when new data arrive the band moves up in the number of tested infected cases.

FIGURE 15

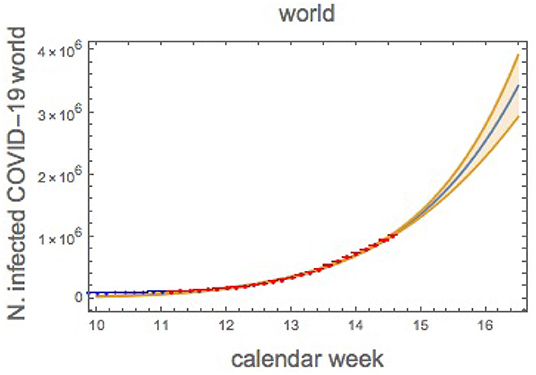
Figure 15. COVID-19 infected cases for the World as function of the calendar week number. The curve and the band (90% confidence level) have been obtained by performing a fit w.r.t. a, b, and γ to the red data points.

4. Conclusions and Online Updates

Summarizing, we interpreted the epidemic data in terms of a renormalization group approach which provides an alternative way to investigate the underlying dynamics of disease spread. We noticed, for example, that universal quantities, for a given disease, can be defined such as the slope of the beta function at fixed points and the time scale of the epidemic spread inflection point. The slope characterizes the speed with which the asymptotic number of infected cases is approached while the inflection point marks the deceleration in the number of new infected cases. Our results are corroborated by the experimental findings that show, indeed, that in the cases considered these quantities are of order one for the slope γ for COVID-19 and the inflection point typically occurs between 3 and 4 weeks after the outbreak. Encouraged by our findings we attempted long term estimates for Italy, Denmark, the United States, and United Kingdom. These countries are at different stages of the epidemic with Italy and to some extent Denmark being at or close to the inflection point and the United States and United Kingdom at the initial exponential growth phase. Consequently, the estimates for the asymptotic values of the corresponding number of infected cases are more accurate for Italy and for Denmark.

Additionally, we have shown that the parameter a which determines the final number of infected cases stabilizes earlier than the other two parameters (see Figures 3, 5, 9, 11). We used this parameter to compare the effects of the containment measures on the overall number of infected cases among different countries by defining an efficiency factor. The latter can also be employed to devise better control strategies [15]. For example, it is clear that the measures taken by South Korea have been highly impactful at the beginning of the outbreak. Other countries, such as Italy that didn't employ the South Korean model impose social distancing that affect the γ and a parameters. Additionally we have also seen that reducing γ flattens the curve of new infected cases. Therefore, control strategies are further naturally monitored by the value of this parameter. Being able to predict with a certain degree of confidence the inflection point and, once this is reached, when we expect the overall number of infected cases to be reached is key to devise control strategies such as either reducing or increasing social distancing.

Our work should be envisioned as a first step toward establishing a connection between epidemology and quantum field theory.

4.1. Online Updates

To keep up with the evolving situation you will find the updated analyses for several countries including the examples reported here on the following webpage: https://www.cp3-origins.dk/COVID-19.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^Although we are aware of possible inaccuracies and dishomogeneities in the data provided by each country we believe that the overall results of our analyses are robust when it comes to discuss the dynamics and temporal evolution of the epidemic. One check to ensure stability of our results has been to thin the data by either considering them weekly or daily, obtaining in the end results consistent within 90% confidence level.

2. ^There is only one exception and it deals with the Danish estimate for infected cases as detailed in the corresponding subsection.

References

1. Wilson KG. Renormalization group and critical phenomena. 1. Renormalization group and the Kadanoff scaling picture. Phys Rev B. (1971) 4:3174. doi: 10.1103/PhysRevB.4.3174

CrossRef Full Text | Google Scholar

2. Wilson KG. Renormalization group and critical phenomena. 2. Phase space cell analysis of critical behavior. Phys Rev B. (1971) 4:3184. doi: 10.1103/PhysRevB.4.3184

CrossRef Full Text | Google Scholar

3. Li L, Zhang J, Liu C, Zhang H-T, Wang Y, Wang Z. Analysis of transmission dynamics for Zika virus on networks. Appl Math Comput. (2019) 347:566–77. doi: 10.1016/j.amc.2018.11.042

CrossRef Full Text | Google Scholar

4. Zhan X-X, Liu C, Zhou G, Zhang Z-K, Sun G-Q, Zhu JJH, et al. Coupling dynamics of epidemic spreading and information diffusion on complex networks. Appl Math Comput. (2018) 332:437–48. doi: 10.1016/j.amc.2018.03.050

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Perc M, Jordan JJ, Rand DG, Wang Z, Boccaletti S, Szolnoki A. Statistical physics of human cooperation. Phys Rep. (2017) 687:1–51. doi: 10.1016/j.physrep.2017.05.004

CrossRef Full Text | Google Scholar

6. Wang Z, Andrews MA, Wu ZX, Wang L, Bauch CT. Coupled disease–behavior dynamics on complex networks: a review. Phys Life Rev. (2015) 15:1–29. doi: 10.1016/j.plrev.2015.07.006

CrossRef Full Text | Google Scholar

7. Wang Z, Bauch CT, Bhattacharyya S, d'Onofrio A, Manfredi P, Perc M, et al. Statistical physics of vaccination. Phys Rep. (2016) 664:1–113. doi: 10.1016/j.physrep.2016.10.006

CrossRef Full Text | Google Scholar

8. Danby JMA. Computing Applications to Differential Equations Modelling in the Physical and Social Sciences. Reston, VA: Reston Publishing Company (1985).

9. Brauer F. Early estimates of epidemic final sizes. J Biol Dyn. (2019) 13(Suppl.1):23–30. doi: 10.1080/17513758.2018.1469792

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Miller JC. A note on the derivation of epidemic final sizes. Bull Math Biol. (2012) 74:2125–41. doi: 10.1007/s11538-012-9749-6

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Murray JD. Mathematical Biology, Interdisciplinary Applied Mathematics. 3rd ed. New York, NY: Springer. (2002).

12. Fisman D, Khoo E, Tuite A. Early epidemic dynamics of the West African 2014 Ebola outbreak: estimates derived with a simple two-parameter model. PLoS Curr. (2014) 6. doi: 10.1371/currents.outbreaks.89c0d3783f36958d96ebbae97348d571

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Pell B, Kuang Y, Viboud C, Chowell G. Using phenomenological models for forecasting the 2015 Ebola challenge. Epidemics. (2018) 22:62–70. doi: 10.1016/j.epidem.2016.11.002

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Huang C, Wang Y, Li X, Ren L, Zhao J, Hu Y, et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet. (2020) 395:497–506. doi: 10.1016/S0140-6736(20)30183-5

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Xing Y, Song L, Sun G-Q, Jin Z, Zhang J. Assessing reappearance factors of H7N9 avian influenza in China. Appl Math Comput. (2017) 309:192–204. doi: 10.1016/j.amc.2017.04.007

CrossRef Full Text | Google Scholar