- 1School of Mathematics and Statistics, Hechi University, Yizhou, China
- 2School of Mathematics and Physics, Guangxi University for Nationalities, Nanning, China
- 3Department of Trial Production, North Institute of Automatic Control Technology, Taiyuan, China
In this study, an adaptive neural network (NN) command filtered control (CFC) method is proposed for a permanent magnet synchronous motor (PMSM) system with system uncertainties and external disturbance by means of a backstepping technique. At every backstepping step, a novel command filter is proposed, and the complicated virtual input and its derivative together can be approximated by this filter. The “explosion of complexity” problem in conventional backstepping design can be avoided because we do not need to calculate the derivative of the virtual input repeatedly. NNs are used to model system uncertainties and disturbances. Finally, an adaptive NN CFC is designed, and the convergence of the tracking error and the boundedness of all signals involved can be guaranteed. Finally, a simulation study is presented to verify the theoretical results.
1. Introduction
In the past several decades, adaptive backstepping control (ABC) has been used by more and more scholars due to its powerful ability in controlling non-linear systems. The ABC approach has some interesting properties. For example, it can achieve global ability and does not need a large amount of control energy. To increase the robustness of ABC, some other control methods, such as adaptive fuzzy control (AFC), adaptive neural network (NN) control, sliding mode control (SMC), etc., have been developed; the research results can be seen in references [1–10], and the references therein. However, the ABC approach has a drawback: the “explosion of complexity” problem, which is generated by differentiating the immediate virtual input repeatedly. Some efforts have been made to solve this problem, for example, in Liu et al. [6], virtual inputs were approximated by fuzzy systems, and in Ahn et al. [2], a sliding surface was used to avert the repeated calculation of the derivatives. Another approach, more powerful than these methods, is command filtered control (CFC), which was introduced by Farrell et al. [11] and Dong et al. [12], where several interesting results were presented to show that errors are of , with W being the frequency. To drive the tracking error toward a sufficiently small value, one can use large W. However, too large a W value usually means that too much control energy is used. Thus, some other control methods based on CFC have been developed, for example, in references [13–18], noting that the dimensions of the virtual signal should be enlarged to involve the desired signal and its derivative. Yet, the above-mentioned literature only studied the estimation of some command derivatives, i.e., the results do not correspond to the ABC design. Thus, it is meaningful to develop more approaches to solve the above problem.
For more than 30 years, the control of chaotic systems has been paid increasing attention as an important field in non-linear scientific research and has gradually become widely used in engineering and other fields. The permanent magnet synchronous motor (PMSM) has attracted widespread attention due to its rapid dynamics, wide speed range, and simple structure. However, because the PMSM is a multivariate non-linear system and the system exhibits phenomena, such as Hope bifurcation, limit cycles, and chaotic attractors when the system parameters are in some ranges, the control of PMSM systems is still a challenging problem. Chaos in the PMSM system can destroy the stability of the system and even crash it, so it is very important to control this chaos. At present, there are many methods to control chaos in PMSM, such as the OGY method, delayed feedback control method, sliding mode control method, ABC, AFC, and so on [19–23]. In the actual application process, the OGY method requires certain system parameters, some of which cannot be achieved in actual control, whereas the delayed feedback control method has achieved good results in the PMSM chaos control, but the delay is very difficult. In Yu et al. [23], the AFC method was used, and in each step, fuzzy systems were used to model system uncertainties to avoid the repeated calculation of the virtual signal and its derivative. In Sun et al. [24], an internal motion model was used to control PMSM systems with uncertainties. In Yang et al. [25], an AFC CFC method was used where the system uncertainties are not considered. In Niu et al. [26], an output feedback CFC method was proposed for PMSM. In Zou et al. [27], command filtering-based AFC was introduced for PMSM where input saturation is considered. Some related work can be seen in references [28–32]. However, in these studies, fully unknown system models are not considered.
Based on the above discussion, we will introduce an NN CFC method for PMSM systems with fully unknown system models. We combine ABC with CFC and propose a one-order filter to approximate the virtual signal and its derivative at each backstepping step. As the last step, a robust controller is designed, and adaptation laws are also presented. Compared with related works, our contributions are as follows. (1) A one-order filter is introduced. In each step, it can be used to approximate the virtual signal together with its derivative. In addition, the proposed filter has very good approximation ability, and the error can be made as small as possible. By doing this, the “explosion of complexity” problem is avoided. Compared with some related methods, for example, in references [23, 28, 31], our methods are simpler and can be implemented earlier. (2) The proposed control signals with adaptation laws have a very concise form relative to some related methods, for example, dynamic surface control.
This paper is arranged as follows. The description of the PMSM, the controller design, and the stability analysis are presented in section 2. Section 3 gives the simulation results of the proposed method. Finally, section 4 gives the conclusions of this paper.
2. Main Results
2.1. Problem Description
The mathematical model of a PMSM with a smooth air gap can be expressed as [23]
where ω, id, iq are system variables representing the angular velocity and shaft current of the motor, respectively, and , ũq, and ũd represent load torque and shaft voltage. When there are no external inputs, denoting x = ω, y = iq, z = id, and putting an input u(t) to the third equation, the PMSM system (1) can be written as
Let the tracking error be , with being a referenced signal. Our purpose is to implement a suitable control signal u such that ϵ1(t) becomes as small as possible.
2.2. Backstepping Control Signal Design
The backstepping control procedures can be divided into the following three steps.
Step 1. It follows from (2) that:
where Δg1(x) = −σx is assumed to be unknown. Then, Δg1(x) is estimated by using NN as
with being the adjustable parameter of the NN, being the optimal parameter, and ε1 being the optimal estimation error [33, 34]. Then, we can use the following virtual input
with being the estimation of ε1, k1, α1 > 0, and being a compensated tracking error. Thus, (3), (4), and (5) imply
with being the NN approximation error and being filtered error. We can define the following signal:
where ζ1 can be obtained by solving:
with ζ2 being defined in the next step and yc being the solution of the following equation:
with ϖ2 > 0. To solve (9), we can set yc(0) = 0. We can use the following adaptation law:
and
respectively, with a11, a12, a41, a42 > 0.
Step 2. According to the second equation of (2), we have
where Δg2 = −y + δx is unknown. We can use the NN to approximate it as
Define
with
with ζ2(0) = 0,
where k2, α2 > 0. W2 and are updated by
and
with a21, a22, a51, a52 > 0. Then we know
Step 3. According to the last equation of (2), we have
with Δg3(x) = −z + xy being unknown. It can be approximated by
We can implement the controller as
with k3, α3 > 0. Define
with
The parameters are updated by
with c31, c32, c61, c62 > 0. As a result,
Let us give the following reasonable assumption and lemma.
Assumption 1. The NN approximate error is bounded, i.e., there exists such that .
Lemma 1. [15] If α > 0 and κ = 0.27846, then we have
Then, we have
Theorem 1. When with b > 0, then (8), (15), and (25) imply
with , , and c = b + σ.
Proof. Let . It follows from (8), (15), and (25) that
As a result, it follows from (33) that (32) satisfies. ■
Theorem 2. Consider (2) satisfying Assumption 1. Virtual inputs are given by (5) and (17) under the filters (8), (9), (15), (16), and (25). The adaptation laws are (10), (18), (26), (11), (19), and (27). Then, the controller (23) ensures the convergences of , and to a small region.
Proof. Define
with . Then, (29), (30), (31), Assumption 1, and Lemma 1 imply
It follows from (10), (11), (18), (19), (26), and (27) that
As a result, (35), (36), and (37) imply
with d1 = 2 min{k1, k2, k3}, d2 = min{a11a12, a21a22, a31a32}, d3 = min{a41a42, a51a52, a61a62}, being non-negative constants. Apparently, the constants d1, d2, d3, d4 are determined by design parameters and some unknown constant variable (see, the optimal NN parameter). Thus, (38) implies , , . As a result, all variables are indeed bounded, and , and tend to a small region determined by design parameters. ■
Remark 1. It should be emphasized that the conclusion of Theorem 1 is very representative, and it can be widely used in the field of automatic control, finite-time control, and backstepping control. However, the proposed method can only guarantee the that tracking error tends to a very small region.
Remark 2. In the controller design, the proposed method is different from some related methods, for example, those detailed in references [4, 33, 34]. We introduce an auxiliary signal to approximate the virtual input, and the approximation error can be made as small as possible.
3. Simulation Study
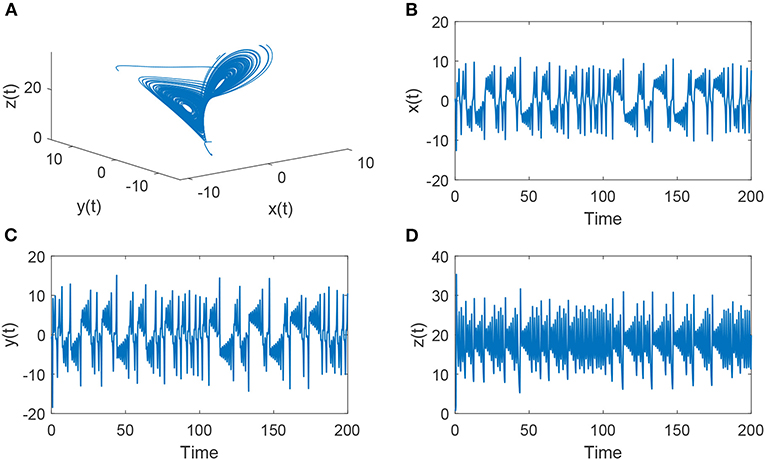
In system (2), let σ = 5.45, δ = 20.0, x(0) = 0.5, y(0) = −1, z(0) = 0. When u(t) ≡ 0, the chaotic behavior of (2) can be seen in Figure 1.
Let the desired signal be xc, defined by
With respect to the NNs, the basic functions are chosen on interval [-8 8], and five functions are used for each state. Their initial conditions are W1(0) = 01 × 2, W2(0) = 01 × 25, and W3(0) = 01 × 125. The design parameters are k1 = k2 = k3 = 1.5, ai1 = 6, ai2 = 0.05, i = 1, 2, 3, 4, 5, 6, α1 = α2 = α3 = 1.
The simulation results are presented in Figure 2. It can be seen in Figure 2 that the tracking error has rapid convergence and the signal x(t) tracks xc(t) tightly; the control input u(t) has a small amplitude, and it fluctuates very gently; the compensated error ϵ3 converges to zero very quickly, but ϵ2 does not converge to zero (in fact, in our method, it is not necessary for the compensated error to converge to zero); the parameters of the NNs also fluctuate gently.
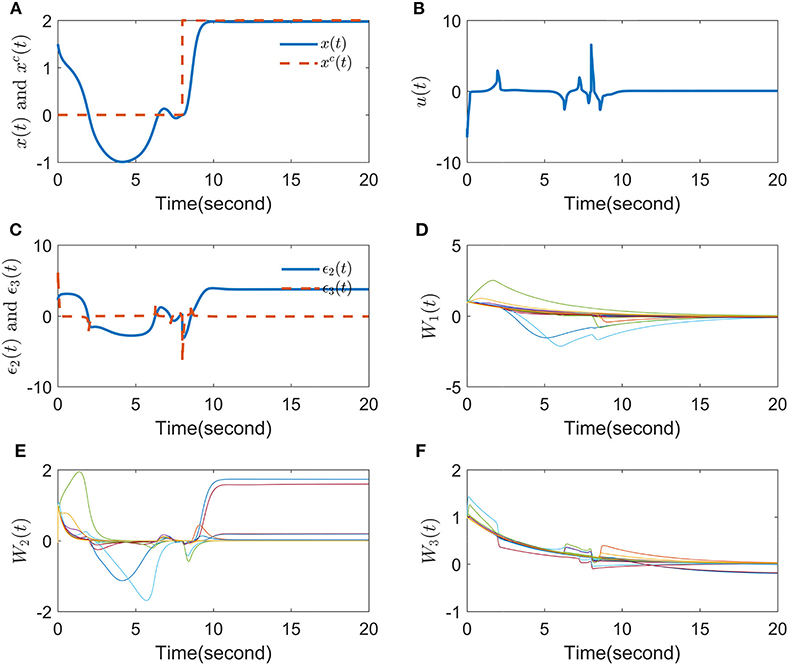
Figure 2. Simulation results in (A) tracking performance, (B) control input, (C) compensated errors, (D) W1(t), (E) W2(t), and (F) W3(t).
To show the robustness of the proposed method, let us add an external term 0.95 sin t into the third equation of the system (2). The simulation results are presented in Figure 3. Comparing Figures 2, 3, we can see that under the external disturbance, the proposed method has very good robustness.
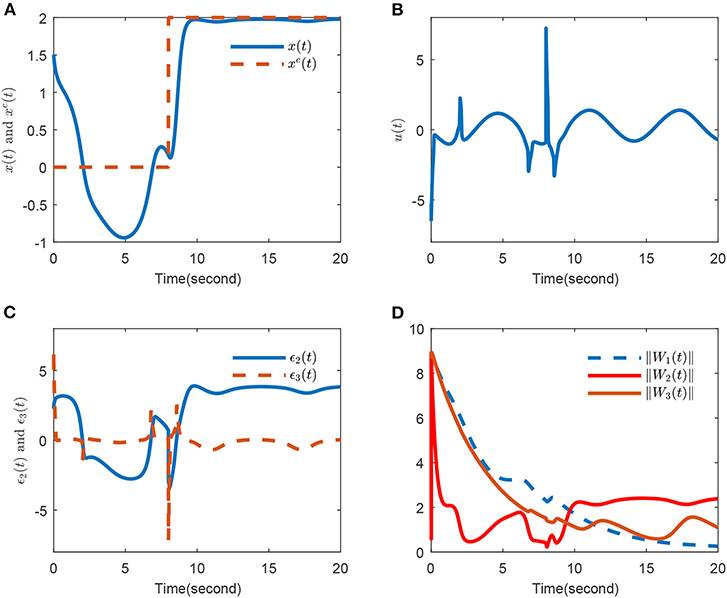
Figure 3. Simulation results with external disturbance in (A) tracking performance, (B) control input, (C) compensated errors, (D) ||W1(t)||, ||W2(t)|| and ||W3(t)||.
4. Conclusions
This paper presents an NN CFC method for PMSMs with fully unknown system models. To avoid the “explosion of complexity” problem, we propose a one-order command filter. It has been proven that the virtual input and its derivative can together be approximated by the proposed filter, and the approximation error can be made as small as possible. The proposed method is performed by using a backstepping technique. It is also shown that the proposed NN CFC can guarantee the boundedness of all signals. Investigating CFC for PMSMs with input constraints will be our future research direction.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
RL contributed the conception of the study. YD wrote the study and organized the literature analysis. YX wrote the simulation programs. RL and YX revised the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.
Funding
This work was supported by the Natural Science Foundation of Guangxi University for Nationalities (2019KJYB001), and the Guangxi Natural Science Foundation (2019GXNSFAA185007).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Lin FJ, Shen PH, Hsu SP. Adaptive backstepping sliding mode control for linear induction motor drive. IEEE Proc Electric Power Appl. (2002) 149:184–94. doi: 10.1049/ip-epa:20020138
2. Ahn KK, Nam DNC, Jin M. Adaptive backstepping control of an electrohydraulic actuator. IEEE/ASME Trans Mechatron. (2013) 19:987–995. doi: 10.1109/TMECH.2013.2265312
3. Liu JB, Shi ZY, Pan YH, Cao J, Abdel-Aty M, Al-Juboori U. Computing the Laplacian spectrum of linear octagonal-quadrilateral networks and its applications. Polycycl Aromat Comp. (2020). doi: 10.1080/10406638.2020.1748666. [Epub ahead of print].
4. Liu JB, Zhao J, He H, Shao Z. Valency-based topological descriptors and structural property of the generalized sierpiński networks. J Stat Phys. (2019) 177:1131–47. doi: 10.1007/s10955-019-02412-2
5. Zhou J, Wen C, Zhang Y. Adaptive backstepping control of a class of uncertain nonlinear systems with unknown backlash-like hysteresis. IEEE Trans Autom Control. (2004) 49:1751–9. doi: 10.1109/TAC.2004.835398
6. Liu H, Pan Y, Li S, Chen Y. Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans Syst Man Cybern Syst. (2017) 47:2209–17. doi: 10.1109/TSMC.2016.2640950
7. Liu H, Pan Y, Jinde C, Hongxing W, Yan Z. Adaptive neural network backstepping control of fractionial-order nonlinear systems with actuator faults. IEEE Trans Neural Netw Learn Syst. (2020). doi: 10.1109/TNNLS.2020.2964044. [Epub ahead of print].
8. Salimi M, Soltani J, Zakipour A. Experimental design of the adaptive backstepping control technique for single-phase shunt active power filters. IET Power Electron. (2017) 10:911–8. doi: 10.1049/iet-pel.2016.0366
9. Coban R. Adaptive backstepping sliding mode control with tuning functions for nonlinear uncertain systems. Int J Syst Sci. (2019) 50:1517–29. doi: 10.1080/00207721.2019.1615571
10. Thien TD, Ba DX, Ahn KK. Adaptive backstepping sliding mode control for equilibrium position tracking of an electrohydraulic elastic manipulator. IEEE Trans Ind Electron. (2019) 67:3860–9. doi: 10.1109/TIE.2019.2918475
11. Farrell JA, Polycarpou M, Sharma M, Dong W. Command filtered backstepping. IEEE Trans Autom Control. (2009) 54:1391–5. doi: 10.1109/TAC.2009.2015562
12. Dong W, Farrell JA, Polycarpou MM, Djapic V, Sharma M. Command filtered adaptive backstepping. IEEE Trans Control Syst Technol. (2011) 20:566–80. doi: 10.1109/TCST.2011.2121907
13. Liu H, Pan Y, Cao J. Composite learning adaptive dynamic surface control of fractional-order nonlinear systems. IEEE Trans Cybern. (2020) 50:2557–67. doi: 10.1109/TCYB.2019.2938754
14. Fu C, Zhao L, Yu J, Yu H, Lin C. Neural network-based command filtered control for induction motors with input saturation. IET Control Theory Appl. (2017) 11:2636–42. doi: 10.1049/iet-cta.2017.0059
15. Yu J, Shi P, Zhao L. Finite-time command filtered backstepping control for a class of nonlinear systems. Automatica. (2018) 92:173–80. doi: 10.1016/j.automatica.2018.03.033
16. Ahanda JJBM, Mbede JB, Melingui A, Zobo BE. Robust adaptive command filtered control of a robotic manipulator with uncertain dynamic and joint space constraints. Robotica. (2018) 36:767–86. doi: 10.1017/S0263574718000036
17. Pan Y, Wang H, Li X, Yu H. Adaptive command-filtered backstepping control of robot arms with compliant actuators. IEEE Trans Control Syst Technol. (2017) 26:1149–56. doi: 10.1109/TCST.2017.2695600
18. Pan Y, Sun T, Liu Y, Yu H. Composite learning from adaptive backstepping neural network control. Neural Netw. (2017) 95:134–42. doi: 10.1016/j.neunet.2017.08.005
19. Pillay P, Krishnan R. Modeling, simulation, and analysis of permanent-magnet motor drives. I. The permanent-magnet synchronous motor drive. IEEE Trans Ind Appl. (1989) 25:265–73. doi: 10.1109/28.25541
20. Kommuri SK, Defoort M, Karimi HR, Veluvolu KC. A robust observer-based sensor fault-tolerant control for PMSM in electric vehicles. IEEE Trans Ind Electron. (2016) 63:7671–81. doi: 10.1109/TIE.2016.2590993
21. Wang Y, Wang X, Xie W, Wang F, Dou M, Kennel RM, et al. Deadbeat model-predictive torque control with discrete space-vector modulation for PMSM drives. IEEE Trans Ind Electron. (2017) 64:3537–47. doi: 10.1109/TIE.2017.2652338
22. Cai B, Zhao Y, Liu H, Xie M. A data-driven fault diagnosis methodology in three-phase inverters for PMSM drive systems. IEEE Trans Power Electron. (2016) 32:5590–600. doi: 10.1109/TPEL.2016.2608842
23. Yu J, Chen B, Yu H, Gao J. Adaptive fuzzy tracking control for the chaotic permanent magnet synchronous motor drive system via backstepping. Nonlinear Anal Real World Appl. (2011) 12:671–81. doi: 10.1016/j.nonrwa.2010.07.009
24. Sun X, Shi Z, Chen L, Yang Z. Internal model control for a bearingless permanent magnet synchronous motor based on inverse system method. IEEE Trans Energy Convers. (2016) 31:1539–48. doi: 10.1109/TEC.2016.2591925
25. Yang X, Yu J, Wang QG, Zhao L, Yu H, Lin C. Adaptive fuzzy finite-time command filtered tracking control for permanent magnet synchronous motors. Neurocomputing. (2019) 337:110–9. doi: 10.1016/j.neucom.2019.01.057
26. Niu H, Yu J, Yu H, Lin C, Zhao L. Adaptive fuzzy output feedback and command filtering error compensation control for permanent magnet synchronous motors in electric vehicle drive systems. J Frankl Inst. (2017) 354:6610–29. doi: 10.1016/j.jfranklin.2017.08.021
27. Zou M, Yu J, Ma Y, Zhao L, Lin C. Command filtering-based adaptive fuzzy control for permanent magnet synchronous motors with full-state constraints. Inform Sci. (2020) 518:1–12. doi: 10.1016/j.ins.2020.01.004
28. Wang X, Chen Y, Lu Y, Li X, He W. Dynamic surface method-based adaptive backstepping control for the permanent magnet synchronous motor on parameter identification. Proc Inst Mech Eng I J Syst Control Eng. (2019) 233:1172–81. doi: 10.1177/0959651818819237
29. Singh JP, Roy BK, Kuznetsov NV. Multistability and hidden attractors in the dynamics of permanent magnet synchronous motor. Int J Bifurc Chaos. (2019) 29:1950056. doi: 10.1142/S0218127419500561
30. Wang M, Yu J, Ma Y, Yu H, Lin C. Discrete-time adaptive fuzzy speed regulation control for induction motors with input saturation via command filtering. J Frankl Inst. (2019) 356:6145–59. doi: 10.1016/j.jfranklin.2019.05.023
31. Xu D, Wang G, Yan W, Yan X. A novel adaptive command-filtered backstepping sliding mode control for PV grid-connected system with energy storage. Solar Energy. (2019) 178:222–30. doi: 10.1016/j.solener.2018.12.033
32. Errouissi R, Al-Durra A, Muyeen S, Leng S. Continuous-time model predictive control of a permanent magnet synchronous motor drive with disturbance decoupling. IET Electric Power Appl. (2017) 11:697–706. doi: 10.1049/iet-epa.2016.0499
33. Liu H, Wang H, Cao J, Alsaedi A, Hayat T. Composite learning adaptive sliding mode control of fractional-order nonlinear systems with actuator faults. J Frankl Inst. (2019) 356:9580–99. doi: 10.1016/j.jfranklin.2019.02.042
Keywords: adaptive neural network control, command filtered control, backstepping, permanent magnet synchronous motor, chaos control
Citation: Luo R, Deng Y and Xie Y (2020) Neural Network Backstepping Controller Design for Uncertain Permanent Magnet Synchronous Motor Drive Chaotic Systems via Command Filter. Front. Phys. 8:182. doi: 10.3389/fphy.2020.00182
Received: 11 April 2020; Accepted: 27 April 2020;
Published: 05 June 2020.
Edited by:
Jia-Bao Liu, Anhui Jianzhu University, ChinaReviewed by:
Guangming Xue, Guangxi University of Finance and Economics, ChinaShengda Zeng, Jagiellonian University, Poland
Ahmed Zarzour, British University in Egypt, Egypt
Copyright © 2020 Luo, Deng and Xie. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yanping Deng, eXBkZW5nZ3h1bkAxNjMuY29t
 Ricai Luo
Ricai Luo Yanping Deng
Yanping Deng Yuling Xie3
Yuling Xie3