- Institut für Theoretische Physik, Universität Heidelberg, Heidelberg, Germany
According to the asymptotic-safety conjecture, the gravitational renormalization group flow features an ultraviolet-attractive fixed point that makes the theory renormalizable and ultraviolet complete. The existence of this fixed point entails an antiscreening of the gravitational interaction at short distances. In this paper we review the state-of-the-art of phenomenology of Asymptotically Safe Gravity, focusing on the implications of the gravitational antiscreening in cosmology.
1. Gravitational Antiscreening: A Historical Perspective
Similarly to the case of Quantum Chromodynamics (QCD), the gravitational interaction might exhibit an antiscreening behavior at high energies [1]. A form of gravitational antiscreening was introduced in the 80s by Markov [2, 3] as a mechanism to cure the longstanding problem of gravitational singularities in General Relativity. In Markov and Mukhanov [4] and Markov [5], an ad hoc modification of the Einstein-Hilbert Lagrangian has been proposed, such that the corresponding field equations
admit a Newton coupling G(ρ) and cosmological constant Λ(ρ) whose strengths depend on the proper energy density ρ of matter fields, with G(ρ) → 0 as ρ → ∞. This latter assumption, which in Markov and Mukhanov [4] and Markov [5] is referred to as “asymptotic freedom of gravity,” has been introduced to render the gravitational interaction weaker at high energy densities. In a cosmological context, this could lead to a singularity-free cosmological evolution characterized by a deSitter initial state and a minimum radius of the order of the Planck length, amin ~ LPl. In this case the resolution of the cosmological singularity is due to the violation of the energy conditions, thus invalidating one of the key assumptions leading to the Hawking-Penrose singularity theorems [6]. Similar arguments could also apply to the case of black holes, where the gravitational antiscreening could lead to singularity-free black-hole spacetimes [7].
The “asymptotic freedom of gravity” discussed in Markov and Mukhanov [4] and Markov [5] was originally introduced as a modification of General Relativity at the classical level. It turns out that the gravitational antiscreening advocated in Markov and Mukhanov [4] and Markov [5] could be a natural consequence of the quantum properties of gravity. The “asymptotic safety” scenario for Quantum Gravity [8–10] aims at constructing a consistent quantum theory for the gravitational interaction within the well-established framework of Quantum Field Theory (QFT). As originally proposed by Weinberg [11, 12], in the light of the Wilsonian renormalization group [13, 14] and the related, generalized notion of renormalizability [15], a consistent QFT of gravity could be constructed if the gravitational renormalization group (RG) flow attains an interacting—non-Gaussian—fixed point (NGFP) in the ultraviolet limit. In this case, in the ultraviolet regime, gravity approaches a scale invariant regime where the dimensionless counterparts of all gravitational couplings attain finite, generally non-zero, values. The theory is thus interacting in the ultraviolet regime and the presence of the NGFP ensures the “non-perturbative” renormability [15] of gravity. While asymptotic safety of gravity remains a formally unproved conjecture, there are strong indications that a suitable gravitational fixed point indeed exists [16–34]. Moreover, despite its interacting nature, the fixed point could lie in the vicinity of the free-theory fixed point (Gaussian fixed point, GFP), making the theory near-perturbative [35]. Similarly to the case of non-abelian gauge theories like QCD, the existence of an ultraviolet fixed point is guaranteed whenever the “paramagnetic interactions” of the action dominate over the diamagnetic ones [1]. This mechanism is at the basis of the (quantum) gravitational antiscreening. The realization of the latter can be understood more intuitively from the RG running of the Newton coupling. The structure of the beta function of the dimensionless Newton coupling g(k) = G(k) k2 in d = 4 spacetime dimensions, k being the RG scale, is
where ηN = k∂k log G(k) is the anomalous dimension of the Newton coupling. The function ηN depends on g as well as on all other (dimensionless) gravitational couplings. Further note that ηN depends on the RG scale k only implicitly, i.e., only through the RG running of the dimensionless gravitational couplings. A necessary condition for the existence of a non-trivial fixed point is that ηN = −2 for some values of the gravitational couplings. Assuming that a non-trivial fixed point indeed exists in the full (not truncated) theory space, the simple fact that ηN < 0 at the non-trivial fixed point implies that the dimensionfull Newton coupling decreases with the RG scale k and vanishes as when g(k) → g*, where g* denotes the fixed-point value of the dimensionless Newton coupling.
Although in the context of asymptotically safe gravity (ASG) the gravitational antiscreening has a quantum origin and despite the different semantics [Markov's asymptotic freedom of G(k) vs asymptotic safety of g(k)], this is the same principle advocated by Markov and Mukhanov [4] and Markov [5] as one possible way to soften or even remove the singularities affecting the solutions of the Einstein equations. In the case of stellar black holes the mechanism of singularity-avoidance is very intuitive: when a collapsing star disappears behind its event horizon and its density reaches planckian values, the gravitational interaction driving the collapse becomes weaker. Therefore, under certain conditions, the gravitational antiscreening can potentially halt the collapse and prevent the formation of a spacetime singularity. Hints that the mechanism of singularity-avoidance could be realized within the Asymptotic Safety scenario for Quantum Gravity have been found in Bonanno and Reuter [36–38], Torres [39, 40], Torres and Fayos [41], Bonanno and Koch [42, 43], Bonanno et al. [44], Adeifeoba et al. [45], Platania [46], and Bonanno et al. [47] via the so-called RG-improvement procedure [see, e.g., [37, 48] and references therein], in Bosma et al. [49] by means of non-perturbative computations of quantum corrections to the Newtonian potential based on the functional renormalization group (FRG) method, and in Marunovic and Prokopec [50, 51] through a one-particle irreducible resummation of one-loop vacuum fluctuations of non-minimally coupled, massless, scalar matter. In analogy with the case of black-hole singularities, the gravitational antiscreening could provide a solution to the problem of the initial singularity [52–54] in cosmology. Moreover, the existence of a regime where gravity is approximately scale-invariant could be relevant in cosmology to provide a natural explanation for the nearly-scale-invariant distribution of temperature anisotropies in the Cosmic Microwave Background (CMB) radiation [55–61] [see also [62] for a recent review].
In this paper we review some of the main cosmological implications of ASG based on the running of the gravitational couplings. The rest of the present review is organized as follows. Section 2 summarizes the mechanism behind the renormalization group improvement and the scale-setting procedure. In sections 3 and 4 we review the main implications of the gravitational antiscreening in cosmology and inflation respectively. Finally, in section 5 we summarize the state-of-the-start of phenomenology of ASG, its main problems, and future perspectives.
2. Running Couplings and Renormalization Group Improvement
2.1. Decoupling Mechanism
One of the strengths of ASG is the possibility of constructing a quantum theory of gravity using the “language” of Quantum Field Theory—the standard framework to describe matter and all known fundamental interactions within the Standard Model of particle physics. On the one hand, this makes the connection between gravity and matter more straightforward than in other approaches to quantum gravity and allows to constrain the ultraviolet details of quantum gravity by verifying systematically its consistency with low-energy experiments and observations on the matter sector [see [63, 64] for recent reviews]. On the other hand, the computation of the quantum corrections to the classical solutions of General Relativity requires the knowledge of the gravitational quantum effective action . The classical Einstein equations are replaced by the fully quantum field equations
These are effectively classical field equations. Nonetheless, its solutions 〈gμν〉 actually incorporate all quantum gravitational effects.
The computation of the effective action comes along with several technical and conceptual issues. First, computing the effective action exactly would require either to solve the gravitational path integral over globally hyperbolic spacetimes or, equivalently, to solve the Functional Renormalization Group (FRG) equation for the effective average action Γk [65–67]
and take the limit k → 0. The mathematical tools currently available do not allow for an exact computation of the effective action, even if important progress in this direction has been made in Knorr and Saueressig [68] and Knorr et al. [69]. Secondly, the effective action is a gauge- and parametrization-dependent object: only physical observables will be independent of any gauge choice, parametrization and regularization schemes. A third key issue, related to the previous one, is that defining physical observables in quantum gravity is still an outstanding open problem [70, 71].
The decoupling mechanism [72] might provide a solution to some of the issues raised above. In what follows we will summarize how this mechanism works, mostly following the arguments and nomenclature in Reuter and Weyer [72]. As is clear from Equation (4), the RG running of the effective action is determined by the modified inverse propagator . The regulator is an effective mass-square term that implements the Wilsonian shell-by-shell integration of fast fluctuating modes: only fluctuations with momenta p2 ≳ k2 are integrated out, resulting in the partially-quantized effective action Γk. In the limit k → 0 all quantum fluctuations are integrated out, so that Γ0 coincides with the ordinary effective action. At the basis of the decoupling mechanism is the possibility that some infrared physical scales appearing in , such as a physical mass term, could compete and eventually overcome the effect of the unphysical mass term in in the infrared. In this case there will be a threshold value of k—a decoupling scale kdec—below which the running of Γk is essentially frozen. The “threshold effective action” Γkdec and the ordinary effective action are thus expected to be approximately the same. The identification of the infrared scale kdec, if any, could provide some of the (typically non-local) terms in Γ0. An emblematic example of this mechanism is massless scalar electrodynamics, where . The running of the quartic coupling λ(k) is logarithmic, λ(k) ~ log k and therefore the decoupling should occur at . The effective action Γ0 is thus expected to involve an effective non-local interaction of the form . To leading order, this leads to the ϕ4log(ϕ)-interaction appearing in the famous Coleman–Weinberg effective potential [73]. For other examples in QED and QCD see, e.g., [74–76] and references therein. When the effective action contains several competing infrared scales (particle momenta, field strengths, spacetime curvature, etc), identifying the threshold scale kdec becomes a more involved task: kdec might be a complicated non-linear function of all these scales or, in the best case, it might be given by the one physical infrared scale which dominates over the others. Conversely, a decoupling scale might not exist at all: this is the case if there are no dominant infrared scales acting as an actual physical cutoff. Therefore, the existence of kdec and its specific form strongly depend on the physical system under consideration.
The procedure of identifying and replacing the RG scale k with a physical infrared scale, supposedly acting as a decoupling scale kdec, is known as RG improvement. It aims at using the RG running in order to incorporate leading-order quantum effects in the dynamics of a classical system. In the example mentioned above, the RG improvement is used at the level of the action to obtain the leading-order terms in the quantum effective action Γ0. Other forms of RG improvement are the RG improvement at the level of the field equations and at the level of the classical solutions; the latter allows, e.g., to derive the Uehling potential from the RG-running of the electric charge [76]. Even if the idea behind the decoupling mechanism seems to suggest that the RG improvement should be performed at the level of the action, this is typically considered as a source of ambiguity. In the next subsection we will discuss the RG improvement in the case of gravity and how to constrain the scale setting k = k(x) based on the symmetries of the theory.
We remark that the RG running of the gravitational couplings extrapolated from FRG computations relies on the use of Euclidean metrics. The implications of ASG obviously involve Lorentzian spacetimes. It is thereby assumed that the scaling of the couplings and the existence of an ultraviolet-attractive fixed point are not affected, at least qualitatively, by the metric signature. Hints that this might indeed be the case have been found in Manrique et al. [77].
2.2. Renormalization Group Improvement and Scale-Setting Procedure
ASG relies on the existence of an ultraviolet-attractive fixed point of the gravitational RG flow. In the Einstein-Hilbert truncation, the scaling of the dimensionless Newton coupling g(k) = G(k) k2 and cosmological constant λ(k) = Λ(k)k−2 about the NGFP (g*, λ*) reads
where is the reduced Planck mass, the ci are integration constants labeling all possible RG trajectories, ei are the eigenvectors of the stability matrix ∂giβj|g* constructed using the beta functions βj of all dimensionless couplings gj, and (−θi) are its eigenvalues. The real part of the critical exponents θi determine the stability properties of the NGFP. In the case of pure gravity, the critical exponents θ1 and θ2 are typically a pair of complex conjugate numbers with positive real part: this implies that the NGFP is ultraviolet-attractive in the Einstein-Hilbert truncation. In extended truncations, involving higher-derivative operators, it has been shown that the NGFP comes with three relevant directions associated with the volume, R, and 4th-order derivative operators [20–22, 26, 30, 34, 78–81]. The number of relevant directions coincides with the number of free parameters (the integration constants ci) to be fixed by comparison with observations, e.g., by requiring that in the infrared and . Fixing the free parameters in this way allows to select the “RG trajectory realized by Nature” [82]. As it will be important in the applications of ASG in cosmology, it worth mentioning that the values of the critical exponents are influenced by the presence of matter: for instance, in the Einstein-Hilbert truncation, the presence of minimally-coupled free matter fields makes the critical exponents θ1, 2 real [32, 81, 83–85].
Neglecting the running of the matter couplings, the scale-dependent Einstein-Hilbert action reads
At some intermediate scale k = k(x), the RG running modifies the classical field equations by an effective energy-momentum tensor which could encode, at an effective level, the vacuum polarization effects of the quantum gravitational field [86],
If there is no energy-momentum flow between the gravitational and matter components of the theory, i.e., if the energy-momentum tensor Tμν is separately conserved, the cutoff function k = k(x) is constrained by the modified (contracted) Bianchi identities [82, 86–89]
The above equation provides a “consistency condition” [82, 86–89] which can be used, under certain assumptions and/or approximations, to determine the scale-dependence k = k(x). Specifically, we can identify the following cases
• CASE I: RG improvement at the level of the field equations
Performing the RG improvement at the level of the field equations or solutions is equivalent to neglecting Δtμν. Assuming that the matter energy-momentum tensor is covariantly conserved, , the shape of the function k(x) is dictated by the condition
The solution to this equation depends on the form of the energy-momentum tensor. As it will be important in cosmology, let us focus on the case of a perfect fluid with energy density ρ and pressure p. In this case , with p = w ρ, and the above equation yields the condition
with . In the fixed point regime, the scaling of the dimensionfull Newton coupling and cosmological constant reads
so that k can be related to the matter energy density ρ [87, 90],
In this setup the running gravitational couplings depend on the energy density ρ of the matter degrees of freedom: this is exactly the ad hoc assumption employed in Markov and Mukhanov [4] and Markov [5] to obtain a classical modification of General Relativity free of the problem of spacetime singularities.
The relation between k and the energy density ρ can also be understood in terms of the decoupling mechanism. If the spacetime is filled with a perfect fluid with energy density ρ, the gravitational action is complemented by a matter action . Due to the (minimal) coupling between the gravitational and matter degrees of freedom, the energy density ρ enters the modified inverse propagator and could thus provide a decoupling scale kdec for the flow of the scale-dependent effective action . We note that the Ricci scalar R enters the modified inverse propagator as well and therefore it could also provide a decoupling scale. However, as we will see below, a scale setting k2 ~ R satisfies the contracted Bianchi identities only if the RG improvement is performed at the level of the action.
In cosmology one can further limit the form of the effective metric to a Friedmann-Robertson-Walker (FRW) spacetime. Since Tμν is assumed to be separately conserved, the energy density ρ obeys the standard (i.e., classical) conservation equations and thus (note that the explicit time dependence of ρ is determined by the form of the scale factor, and therefore it could differ from the classical case). In this case
On the other hand, if Tμν is not separately conserved, the Bianchi identities
do not add any additional constraint on the form of the cutoff function k(x): the latter equation provides a generalized conservation equation allowing for an energy flow between the gravitational and matter degrees of freedom.
• CASE II: RG improvement at the level of the action
If the RG improvement is performed at the level of the action, the field equations contain an additional contribution encoded in the gravitational energy-momentum tensor Δtμν. Its variation reads [89]
The contracted Bianchi identities (8), together with the assumption that the energy-momentum tensor is separately conserved, thus yield the condition
Note that in this case, due to the presence of Δtμν, the contribution from the energy-momentum tensor Tμν cancels out. A scaling relation of the form k4 ~ ρ [87, 90], Equation (12), is only valid under the assumption that Δtμν is negligible. We are thus left with the condition
Diffeomorphism invariance thus requires [86, 88, 89]
In the proximity to the NGFP, the couplings scale as in (11) and the constraint (18) gives
This condition should also hold in the more general case of fk(R) theories, if the running of the gravitational couplings is approximated with the corresponding fixed-point scaling [88, 91].
It is worth noting that the replacement k2 ~ R in the scale-dependent action (6) generates an effective f(R) action, whose analytical expression is determined by the running of the gravitational couplings [48, 88, 92]. This fact is typically used to study effective inflationary models in ASG, as it will be discussed in section 4.
The RG improvement at the level of the field equations and at the level of the action lead to effective field equations which differ by a gravitational energy-momentum tensor Δtμν. Based on the idea behind the decoupling mechanism, performing the RG improvement at the level of the action would seem to be more natural. However, the possibility of choosing between different forms of RG improvement is considered as a source of ambiguity. The identification of the decoupling scale kdec is a second possible source of ambiguity: in the case of gravity, there are multiple scales that could potentially act as a decoupling scale for the flow of the scale-dependent gravitational effective action. However, if the matter energy-momentum tensor is covariantly conserved, the form of the cutoff function k(x) is constrained by the contracted Bianchi identities.
Phenomenological implications of ASG have been explored in the literature by means of RG-improved cosmological and astrophysical models. Although these models are not expected to provide precise and quantitative predictions, they are expected to capture qualitative features of the modifications of Einstein gravity induced by ASG.
Keeping strengths and limitations of the RG-improvement procedure in mind, in the next sections we will review some of the main phenomenological implications of ASG based on models of RG-improved cosmology.
3. RG-Improved Cosmologies
It is an old idea that the gravitational couplings could depend on the cosmic time and that this time-dependence could have implications in cosmology [93]. In the context of RG-improved cosmologies this time-dependence arises from the RG running of the gravitational couplings. In this section we will review some of the main cosmological implications of ASG [54–57, 94]. Each subsection focuses on the cosmological implications obtained in different regimes and/or under assumptions.
3.1. Early-Universe Cosmology: The NGFP Regime
We first focus on the RG-improved cosmological dynamics in the NGFP regime, following the analysis in Bonanno and Reuter [55]. The starting point is the assumption that the effective metric, solution to the fully quantum equation of motion, is a homogeneous and isotropic FRW universe,
The matter degrees of freedom are encoded in a perfect fluid with energy-momentum tensor and equation of state p = wρ. In this setup quantum-gravitational fluctuations can only modify the effective dynamics of the scale factor a(t). Performing an RG improvement at the level of the fields equations (in the Einstein-Hilbert truncation) yields the modified Friedmann equation
In this subsection we focus on the case where the energy-momentum tensor is separately conserved, as originally assumed in Bonanno and Reuter [55]. In this case no flow of energy between the gravitational and matter sector is possible [the case in which Tμν is not covariantly conserved has been studied in [57] and will be discussed in section 3.2]. The conditions and thus result in the “standard” conservation equation, , and in the consistency condition (9). The latter can be split in the following equations
where hμν = gμν + uμuν is the projection tensor onto the tangent 3-space orthogonal to the 4-velocity uμ of an observer comoving with the cosmological fluid. Provided that G and Λ do not vary along the hypersurfaces orthogonal to uμ, i.e., k = k(t), the latter relation is identically satisfied. The cosmological evolution of the universe is then (over-) determined by the system of equations [55]
The consistency condition (22) can thus be used to constrain the form of the cutoff function k(t). Assuming that in the early universe the growth of the scale factor follows a power law, Equation (22) is consistent with a scale dependence of the form , where ξt is a positive constant [55]. In particular, the consistency condition (22) fixes the value of the free parameter ξt in terms of fixed-point quantities. As it will become clear soon, the scale-setting k ~ t−1 employed in Bonanno and Reuter [55] is also compatible with the one in Equation (12), that was derived and discussed in subsequent studies [87, 90].
In what follows we will only consider the case of a spatially flat universe, K = 0. Approximating G(k) and Λ(k) with their fixed-point scaling, Equation (11), with , the cosmological system (24) can be solved analytically. The modified Friedmann and conservation equations admit a family of solutions where the scale factor a(t) and the density ρ(t) scale as power laws. Their dependence on the constant ξt can then be eliminated by imposing the consistency condition (22), which leads to the relation
Using this expression for ξt, the family of cosmological solutions associated with the RG-improved system (24) reads [55]
where M is an integration constant. These solutions depend on fixed-point quantities through the combination (λ*g*), which is known to be scheme independent [95, 96]. Moreover, the solutions do not depend on the infrared values of the gravitational couplings, reflecting the universal behavior of the RG flow at the NGFP. Note that, provided that the scale factor follows a power law scaling (i.e., w ≠ −1), the cutoff identification is equivalent to the scale settings k = ξhH(t) (even at a classical level), (due to the modified power law of the scale factor, and in accordance with the discussion in section 2) and, in a RG-improved radiation-dominated era, to , with
This magic can only occur in the proximity of a critical fixed point, where physical quantities should vary as power laws of a unique scale. Away from the NGFP, the complete solution to the cosmological system (24) can only be obtained numerically. This has been done in Reuter and Saueressig [56]. In this case the cutoff function k(t) is obtained by solving the full beta functions for the gravitational couplings and the consistency condition (22) numerically. In particular, in Reuter and Saueressig [56] it is shown that the dynamical cutoff k(t) is well approximated by the Hubble constant, k ~ H(t), for any value of the cosmic time t.
The fixed-point scaling of gravitational couplings modifies the power-law scaling of the scale factor, Equation (26), so that also the causal structure of the spacetime is modified at early times. At it can be easily seen, provided that w ≤ 1/3, there is no particle horizon [55]: quantum effects enlarge the extension of the light-cones such that events occurring at the decoupling era are causally influenced by all points belonging to the hypersurface t = 0 [55]. Nonetheless, if w = 1/3 the deceleration parameter is zero, i.e., no inflation occurs in a RG-improved radiation-dominated epoch. This problem can be overcome by relaxing the assumptions and/or improving the approximations made in Bonanno and Reuter [55]: a period of inflation can occur in RG-improved cosmologies if the gravitational and matter degrees of freedom can exchange energy [57] (this will be discussed in section 3.2) and/or when the gravitational effective energy-momentum tensor Δtμν discussed in section 2 is taken into account, i.e., when the RG improvement is performed at the level of the action [60, 61, 92, 97] (this point will be discussed in detail in section 4).
The gravitational effective energy-momentum tensor Δtμν is also crucial to make the cosmological evolution non-singular: in the setting introduced above, the RG-improved cosmological evolution (26) is still singular, as scale factor vanishes at t = 0. The Δtμν-term in the effective field Equations (7) might mimic the effect of higher-order operators in the gravitational effective action [60, 61, 92, 97] and, as discussed in Lehners and Stelle [98], higher-order operators could be crucial to explain the early-universe evolution and its initial conditions. As it will be discussed in section 3.3, starting from the Einstein-Hilbert truncation and performing the RG improvement at the level of the action gives rise to additional terms in the modified Friedmann equations [corresponding to the additional Δtμν-term in the effective field Equations (7)] which allow for a non-singular cosmological evolution for any value of the spatial curvature K [54].
3.2. Entropy Production
The results reviewed in the previous subsection are based on the assumption that the matter energy-momentum tensor is covariantly conserved. In a series of works [57, 59, 99], the possibility of an energy flow between the gravitational and matter sectors have been considered and its implications have been explored in detail. The main result is that, under certain assumptions, this energy flow could provide an explanation for the production of entropy during the primordial evolution of the universe.
If the matter energy-momentum tensor is not separately conserved, the continuity equation arising from the contracted Bianchi identity reads
and can be written in the form
Identifying U = ρa3 as the energy encapsulated in the proper volume V = a3, the latter equation assumes the form of the first law of thermodynamics
In classical cosmology and the evolution of the universe is regarded as an adiabatic process. The introduction of time-varying gravitational couplings entails instead a variation of the entropy generated by the continuous energy flow between the gravitational and matter sectors,
Specifically, the production of entropy during the expansion of the universe requires . As k(t) decreases with the cosmic time t, it follows that and Ġ ≥ 0. Entropy production thus requires the speed of variation of the running cosmological constant to overcome that of the Newton coupling, such that . Assuming that the universe is initially dominated by radiation and that the primordial evolution is an approximately adiabatic process, , the standard equilibrium conditions relating the thermodynamic variables (ρ, V, T) can still be used. In this case ρ(T) ∝ T4 and therefore S(t) ∝ a3ρ3/4 + const. The precise behavior of S(t) can be obtained by solving the RG-improved Friedmann and continuity equations. This requires to set the scaling relation k = k(t). Since the cosmological evolution is assumed to be approximately adiabatic, the consistency condition (22) should be approximately verified and, based on the results of Reuter and Saueressig [56], a cutoff function of the form k(t) = ξh H(t) could still be employed.
Focusing on the “NGFP era,” where and , the scale setting k(t) ~ ξh H(t) leads to an effective cosmological evolution where the scale factor varies as a power law a(t) ∝ tα, with
and . The corresponding deceleration parameter is q = α−1 − 1. Imposing the consistency condition (22) fixes and gives back the solution obtained in Bonanno and Reuter [55] and discussed in section 3.1: allowing for an energy flow between the gravitational and matter degrees of freedom, removes this additional constraint and leads to a family of cosmological solutions, each characterized by a fixed value of . However, since is assumed, the value of should not differ to much from that obtained by imposing the consistency condition, i.e., . As the value of λ* derived from FRG computations is of order , this also implies that . The transition to the classical FRW cosmology thus occurs when k(ttr) = ξhH(ttr) ~ MPl which, using the fact that ξh ~ 1, implies that the parameter α sets the ratio between the transition time ttr and the Planck time, ttr = α tPl. We thus learn that if α > 1 the transition to the classical regime occurs before the Planck time ttr > tPl.
In a RG-improved radiation-dominated epoch, the production of entropy is given by the power law , so that
In particular, the condition dS ≥ 0 is met if α ≥ 1. The case α = 1 () describes a universe where the gravitational and matter degrees of freedom are decoupled or, equivalently, . If instead α > 1, the variation of Λ dominates over the variation of G, resulting in a net entropy production during the Planck era (NGFP regime). Specifically, assuming S(0) = 0, within this model the entropy production can be entirely explained by the variation of Λ.
We highlight that the condition α > 1, necessary to generate entropy in the early-universe expansion, is the same condition needed in order to produce a period of power-law inflation. In a radiation-dominated epoch this is condition is satisfied for . If α = 1 [, case analyzed in [55]] no inflation occurs but, as in the case α > 1, no particle horizon exists. Therefore, within this simplified model, if (or, equivalently, α ≳ 1) the RG running of the gravitational couplings during the Planck epoch can explain the production of entropy and, at the same time, provide a period of power-law inflation.
3.3. Cosmological Singularities and Bouncing Cosmologies in ASG
The existence of an ultraviolet-attractive NGFP entails a weakening of the gravitational interaction at high energies. It is then natural to ask whether this weakening can lead to non-singular cosmologies. While a definite answer in the context of ASG is still out of reach, the mechanism underlying a possible singularity resolution might be captured by a simple model embedding the running of the gravitational couplings in the spacetime dynamics [54].
Following the discussion in section 2, the running of the gravitational couplings in the Einstein-Hilbert action generates an additional term Δtμν in the modified field equations. As we have seen, neglecting this term and introducing the running couplings at the level of the field equations leads to a family of RG-improved cosmologies admitting a period of power-law inflation and explaining the entropy production in terms of the energy flow between the gravitational and matter sectors [57]. These cosmologies are however singular. As shown explicitly in Bonanno et al. [54], taking into account the correction Δtμν to the effective field Equations (7) might modify this conclusion.
It is assumed that the universe is homogeneous and isotropic and that the energy-momentum tensor is covariantly conserved. Introducing the running of the gravitational couplings at the level of the (Einstein-Hilbert) action yields the modified Friedmann equation [54]
where . The key difference between this model [54] and the one analyzed in the previous subsections [55, 56] lies in the presence of an additional term, , in the modified Friedmann equation. Since ηN → 0 as the RG flow approaches the perturbative regime (a(t) ≫ LPl), Δ vanishes in this limit. Going back in time, ηG varies from its classical value ηN = 0 to the fixed-point value ηN = −2 (reached when k → ∞). In Bonanno et al. [54] a scaling k2 ∝ R ~ a−2 was assumed. This approximation is valid if the scale factor undergoes a period of exponential growth at early times—an assumption that can be verified a posteriori. Replacing the approximate relations [100]
in Equation (34), where (G0, Λ0) are the low-energy values of the gravitational couplings, and assuming that the universe is initially dominated by radiation, it can be easily seen [54] that the field Equations (34) admit non-singular cosmological solutions with minimum radius
where M is an integration constant. Depending on the values of the fixed-point parameters and on the spatial curvature K, both a bouncing cosmology or an emergent universe scenario could in principle be realized [54]. This happens if
and . In this case the universe undergoes a period of inflation at early times, where the scale factor grows exponentially [101]. Otherwise, if ab is not real, the universe is singular and a period of exponential growth of the scale factor is not possible (unless other degrees of freedom are introduced). However this would invalidate the initial assumption that k2 ∝ R ~ a−2 and a separate analysis would be required. This model thus shows how the gravitational antiscreening, encoded in the RG running of the gravitational couplings and in the presence of additional terms in the effective Friedmann equation, could lead to non-singular cosmologies and a period of exponential growth of the universe at early times.
4. Inflation in Asymptotically Safe Gravity
4.1. The Idea Behind “Asymptotically Safe Inflation”
Primordial quantum fluctuations occurring in the pre-inflationary epoch have left indelible imprints, which we measure today in the form of tiny temperature anisotropies, δT/T ~ 10−5, in the CMB radiation: according to the standard cosmological model, the inhomogeneities in the CMB can be traced back to the primordial quantum fluctuations in the pre-inflationary era. These fluctuations were subsequently amplified and smoothed out by the exponential growth of the universe, thus resulting in small density fluctuations at the last scattering surface. The distribution of temperature anisotropies in the sky could thus give us indirect information on the physics of the very early universe.
In momentum space, the power spectra of scalar and tensorial perturbations are written as follows
where k = |k| is the norm of the 3-momentum k and is a reference scale. The spectral index ns and the tensor-to-scalar ratio r ≡ At/As can be obtained from observational data. In particular, the most recent observations to date [102] constrain the spectral index to be ns = 0.9649±0.0042 at 68% confidence level, and limit the tensor-to-scalar ratio to values r < 0.064. Note that although the scalar power spectrum is almost scale invariant, perfect scale invariance (corresponding to ns = 1) is excluded.
The existence of a NGFP in the RG flow of gravity could provide a natural and intuitive explanation for the nearly-scale invariance of the power spectrum of temperature fluctuations in the CMB. Close to the NGFP, the effective background graviton propagator behaves as [103]. In d = 4, the asymptotic-safety condition requires the anomalous dimension of the Newton coupling to approach the value ηN = −2 in the ultraviolet limit. In this case the background graviton propagator in coordinate space scales as at the NGFP [103]. Assuming that the temperature fluctuations are entirely due to the amplification of the quantum fluctuation of the spacetime geometry during inflation and that these fluctuations are generated during the Planck era, the corresponding density fluctuations δρ are characterized by a two-point correlation function [57, 103, 104]
where is the fractional density fluctuation field and δR(y, t) stands for the fluctuation of the scalar curvature [or any component of the Riemann or Einstein tensor [55]], induced by a metric fluctuation. The power spectrum in momentum space is given by the 3-dimensional Fourier transform
The spectral index ns defines the power-law scaling of the power spectrum, . Thus the scaling ξ(x) ~ |x|−4 gives rise to a perfectly scale invariant power spectrum, with ns = 1 [57, 94, 103, 104]. The exact scale invariance of the power spectrum reflects the exact scale invariance of the theory at the NGFP. It is thereby possible that the nearly-scale-invariance of the scalar power spectrum is due to the nearly-scale invariant flow of RG trajectories in the proximity of the NGFP. This observation [57, 94, 103, 104] was the starting point for a number of studies looking for the existence of (unstable) deSitter solutions in ASG [58, 97, 105], giving rise to a sufficiently long period of “NGFP-driven inflation” [57]. The inflationary scenario arising from this mechanism is sometimes called “Asymptotically Safe Inflation.”
4.2. Starobinsky Model and RG-Running in Quadratic Gravity
Among all proposed inflationary models [106], the Starobinsky model is certainly one of the most appealing: it is a zero-parameters model and is compatible with the current observational data [102]. The Starobinsky model relies on the inclusion of an R2-term in the gravitational action. This is the minimal modification of Einstein gravity needed to produce inflation. From the point of view of ASG, focusing on an f(R)-truncation, the quadratic gravity Lagrangian
should comprise all relevant couplings of the theory (with respect to the NGFP): according to the studies of the renormalization group flow of f(R) theories (in pure gravity), the NGFP comes with three relevant directions—those associated with the couplings (G, Λ, B) [26, 34, 80, 81]. The latter are the only free parameters of the theory: every RG trajectory is uniquely identified by the infrared values of the scale-dependent couplings (G(k),Λ(k),B(k)). A key question is whether there exists an RG trajectory matching the infrared values of these couplings. Moreover, it is interesting to understand whether Starobinsky inflation can be realized naturally in the context of ASG. For this to happen the sign of the coupling B is crucial, as the Starobinsky model requires B to be negative. In addition, it is a key requirement that classical Einstein gravity is recovered at low energies. Studying the RG flow of the couplings (G(k),Λ(k),B(k)) in the quadratic truncation (41), it has been shown [107] that there exists an RG trajectory such that the observational constraints
are all fulfilled. We refer the reader to the original paper [107] for the details of the computation. The coupling B(k) is initially (k → ∞) positive, but it turns negative along the RG flow: the transition scale is k ~ 1023GeV (well above the Planck scale), so that at inflationary scales the action (41) matches that of the Starobinsky model [107]. Below the Planck scale, the couplings B(k) and G(k) vary by many orders of magnitude in a very short RG-time, t = log k. Their observed constant values are thus reached at inflationary scales. The cosmological constant instead keeps running even after the end of inflation: at inflationary scales its magnitude is ~ 4 · 1030eV2, while its observed constant value is only reached at k ~ 10−2eV [95, 107].
4.3. Constraints From Planck Data in Gravity-Matter Systems
In this subsection we review the results in Bonanno et al. [61] and Platania [91]. As the initial conditions for inflation are placed at trans-Planckian scales and since the effective action at inflationary scales depends on how the RG-trajectory realized by Nature emerges from the NGFP, the Planck data on CMB anisotropies can in principle put constraints on the universality properties of the gravitational RG flow. The latter are encoded in the critical exponents θi governing the scaling of the gravitational couplings in the vicinity of the NGFP. In turn, the specific values of the critical exponents depend on the number of scalar, Dirac and vectors fields in the theory [32, 81, 83]. The observational constraints on the spectral index ns and tensor-to-scalar ratio r could then be used to put constraints on the primordial matter content of the universe. Introducing the running of the gravitational couplings at the level of the (Einstein-Hilbert) action [48, 92] provides a simple toy model to understand whether and how this mechanism is realized [61, 91].
We restrict ourselves to the Einstein-Hilbert truncation, where the scaling of the gravitational couplings about the NGFP is that given in Equation (5). Following the discussion in section 2, close to the NGFP the consistency condition (16) imposes the scaling relation k2 = ξR, with . The RG running (5) thus yields an effective gravitational action of the form [91]
where fRG(R) is the part of the action generated as the RG trajectories flow away from the NGFP
with the coefficients bi being defined by
Here MPl is the reduced Planck mass, while the integration constants ci, the critical exponents θi and the eigenvectors ei are those introduced in section 2.2 (cf. Equation 5). The action
is the fixed-point action [88, 91]. This is compatible with the results in Benedetti and Caravelli [108], Dietz and Morris [109], and Demmel et al. [27] where, using the FRG Equation (4) to study the RG flow of fk(R)-gravity, it has been shown that the fixed-point Lagrangian is . Additional Rn-operators are generated along the RG flow. The effective action in (43) is thus expected to capture key features of the gravitational RG flow: at the fixed point the action is . Lowering the RG scale k down toward the infrared, additional operators are generated and . The set of operators appearing in depends on how the RG trajectories emerge from the NGFP. In the simplified model (43), this information lies in the critical exponents θi. In what follows we will explore the consequences of this fact in inflationary cosmology [61, 91].
Provided that , the gravitational action (43) is conformally equivalent to Einstein gravity, minimally coupled with a scalar field ϕ
where the subscript “E” indicates that these quantities are computed using the metric in the Einstein frame, and V(ϕ) = U(φ(ϕ)) φ(ϕ)−2, with
A period of exponential grow of the scale factor occurs if the dynamics of the scalar field ϕ is dominated by its potential energy V(ϕ). This happens under the slow-roll conditions
The violation of the slow-roll conditions, encoded in the equation ϵ(ϕf) = 1, defines the value of the field at the end of inflation, ϕf ≡ ϕ(tf). The initial condition ϕi ≡ ϕ(ti) is then obtained by fixing the number of e-folds
before the end of inflation. In the slow-roll approximation, the spectral index and tensor-to-scalar ratio characterizing the scalar power spectrum in Equation (38) can be easily computed by means of the following relations [110]
Moreover, every inflationary model has to be “normalized” [106], i.e., the inflation mass has to be fixed by requiring that the amplitude As of the scalar power spectrum (38) is
At the NGFP (k → ∞) fRG(R) = 0 and the effective action (43) reduces to the fixed-point action . In the Einstein frame, the corresponding fixed-point scalar potential is constant
and therefore it would generate an exactly scale-invariant power spectrum, with ns = 1. This is compatible with the discussion made in section 4.1 and based on the scaling of the background graviton propagator at the NGFP [57, 94, 103, 104]. The mass scale associated with the scalar degree of freedom ϕ can be read off from the potential V*(ϕ) and reads
This mass depends on fixed-point quantities only via the universal product (λ*g*) [96], as expected from the universality properties of the theory at the NGFP.
In the model (43) the departure from the exact scale invariance is due to the departure of the RG flow from the NGFP. Lowering the RG scale down toward the infrared, the gravitational Lagrangian is modified by the operators in and, in the Einstein frame, this corresponds to a variation of the scalar potential V(ϕ),
Its form is determined by the critical exponents θi, which are real numbers in the case of the most commonly studied gravity-matter systems [32, 81, 83]. The asymptotic-safety condition requires the real part of the critical exponents to be positive, Re(θi) > 0. As we are interested in the case of gravity-matter systems, we will only focus on the case where the critical exponents are real. It is assumed, in a first approximation, that the energy-density of the inflation field ϕ dominates. Under this assumption, the other matter fields do not contribute to the inflationary dynamics [61].
It is crucial to note that if all critical exponents are θi > 4, the effective Lagrangian reads
where R−p is the dominant correction in fRG(R) and b is the corresponding coefficient. Contributions of the form R−p are suppressed when R is large, so that the deviation from the exact scale invariance would be negligible (see Figure 1). Moreover in this case the R-operator is not generated by the flow. In the case θi = 4, the model (43) gives rise to an inflationary scenario compatible with the Planck data only under specific conditions [91].
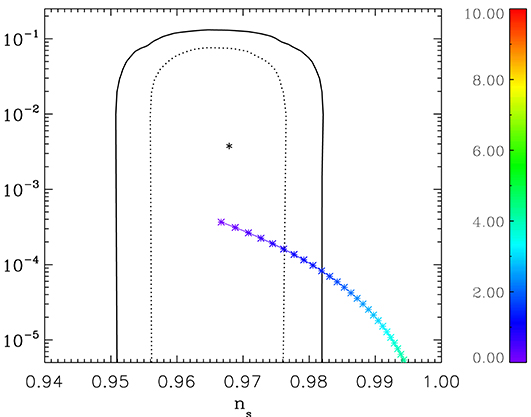
Figure 1. Spectral index and tensor-to-scalar ratio induced by the family of theories in Equation (57) as a function of the power index p for N = 60 e-folds and b = 1. Dashed and solid lines correspond to the 1σ and 2σ confidence levels on the values of (ns, r) extracted from the Planck data [102]. The Starobinsky model, denoted with a star symbol, is also shown for comparison. Only theories with p ≤ 1 are reasonably within the 2σ confidence-level line.
The agreement with the Planck data thus requires that at least one of the critical exponents is θi < 4. This condition is realized, e.g., when gravity is minimally-coupled to the fields of the Standard Model, at least in the approximation where these fields are free [32, 81, 83]. Within the simple model reviewed here, matter models making all gravitational critical exponents θi > 4 would not be compatible with observational data. In this sense, the Planck data on the CMB anisotropies could be used to constrain the primordial matter content of the universe [61].
The scalar potential V(ϕ) is shown in Figure 2 for various values of θ1 = θ2. All functions V(ϕ) approach the same constant value V* for ϕ ≫ MPl. In fact, as soon as θi ≠ 0, the coupling of the R2-term in Equation (43) is not modified by the presence of the additional operators in . Therefore, the height of the plateau and the inflation mass are those in Equations (54) and (55). This is an artifact of the simplified model in Bonanno et al. [61]: the coupling to the R2 operator is a running quantity and therefore also the value of the scalar potential at ϕ ≫ MPl should vary along the flow. In other words, in a more elaborate model accounting for the running of the coupling B in Equation (41), the family of effective potentials V(ϕ) should be characterized by a plateau with Vplateau ≠ V*: this decoupling would allow to set the initial conditions for inflation at Planckian scales and, at the same time, to reproduce the correct amplitude of scalar perturbations at the horizon exit [91].
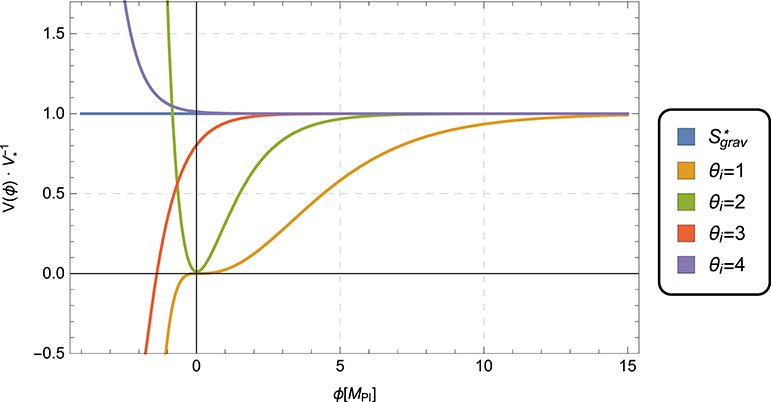
Figure 2. Inflationary potentials V(ϕ) produced by the conformal transformation of the action (43) for various values of the critical exponents θ1 = θ2 [91]. The fixed-point potential associated with the fixed-point action , Equation (46), is also shown for comparison. It corresponds to an exactly scale invariant scalar power spectrum, ns = 1. When the RG flow departs from the NGFP, additional operators are generated by the flow. These operators break the perfect scale invariance realized at the NGFP and destabilize the fixed-point potential, V*→V(ϕ) = V* + δV(ϕ), such that V′(ϕ) ≠ 0 at ϕ ~ MPl. The scalar field ϕ thus acquires a RG-induced kinetic energy, . The subsequent dynamics depends crucially on the critical exponents θi. In particular, the case θ1 = θ2 = 2 reproduces the well-known Starobinsky model.
As the RG flow moves way from the NGFP, the scalar potential V(ϕ) is dynamically modified such that V′(ϕ) is generally non-zero. The scalar field ϕ thus acquires a RG-running-induced kinetic energy . This provides the initial conditions for the subsequent evolution of the scale factor a(t), according to the modified Friedmann equations. Depending on the RG-induced variation of the scalar potential δV(ϕ), the dynamics of the scalar field ϕ can trigger a period of slow-roll inflation. For instance, the case θ1 = θ2 = 2 gives the scalar potential
i.e., a Starobinsky-like potential in the presence of an effective cosmological constant (see Figure 2). As it is well-known, this model leads to cosmic parameters
in good agreement with the current observational data. In the case θ1 ≈ 2 and θ2 ≈ 4, realized when gravity is minimally coupled with the (free) matter fields of the Standard Model [32, 81], the action (43) differs from the one of the Starobinsky model by subleading terms of the form R−p, with p > 0, which are suppressed for large R. The inflationary dynamics, as shown in Bonanno et al. [61], is thus very similar to that of the Starobinsky model (case θ1 = θ2 = 2). In the next subsection we will see how this scenario is modified when the RG-improved effective action is obtained by starting from the quadratic gravity action (41).
4.4. Comparison With the Planck Data in RG-Improved Quadratic Gravity
In Bonanno and Platania [60, 111], a class of inflationary models arising from the RG improvement of quadratic gravity (without matter) has been investigated [see also [48, 92]]. According to the studies of the non-perturbative RG flow of truncated f(R)-theories without matter [104, 112], the NGFP is attractive with respect to three relevant directions, those associated with the dimensionless couplings (gk, λk, βk), with βk = B(k)/G(k) [26, 34, 80, 81]. The question motivating the studies in Bonanno and Platania [60, 111] is whether the scale dependence of all relevant gravitational couplings can modify the classical Starobinsky model and if the RG-improved model is compatible with the Planck data. The ansatz for the gravitational action is
In order to derive an analytical form for the inflationary potential in the Einstein frame, the running of the gravitational couplings is approximated by [60, 111]
where μ is a reference scale and the three parameters (b0, c1, c2), corresponding to the three relevant directions of the theory, identify the RG trajectories terminating at the NGFP in the ultraviolet limit. These are free parameters of the theory and must be fixed by comparing the results with observations. Using the cutoff k2 = ξR [60, 111], the RG-improved effective action reads
with
The inflationary scenario generated in this model can be studied in the Einstein frame, where the f(R) action (62) can be written as in Equation (47). In this case the scalar potential V(ϕ) reads [60, 111]
with the dimensionless couplings Λ and α given by and . The existence of two solutions is due to the presence of the additional R3/2-term in the effective action, and the standard Starobinsky model is recovered by setting α = Λ = 0. Both functions V±(ϕ) define a two-parameters family of potentials, parameterized by the couple (α, Λ). The common feature of these potentials is the existence of a plateau for large positive values of the field ϕ, with . Note that the inclusion of the running of the coupling βk now allows for an effective potential with Vplateau ≠ V*, as mentioned in the previous section.
In order to fulfill the slow-roll conditions, the dynamical evolution of the inflation field must start from a quasi-deSitter state at V(ϕi) ~ Vplateau, and then proceed toward ϕ ≪ MPl. The inflationary dynamics depends on the values of (α, Λ). For any (α, Λ), the potential V±(ϕ) can either develop a minimum (Figure 3, right panel) or be unbounded from below (Figure 3, left panel). A standard reheating phase is only possible in the first case. In addition, in these models a “graceful exist” from inflation by violation of the slow-roll conditions is only possible when Vmin ≤ 0. The case Vmin > 0 leads instead to eternal inflation, as shown in the right panel of Figure 3.
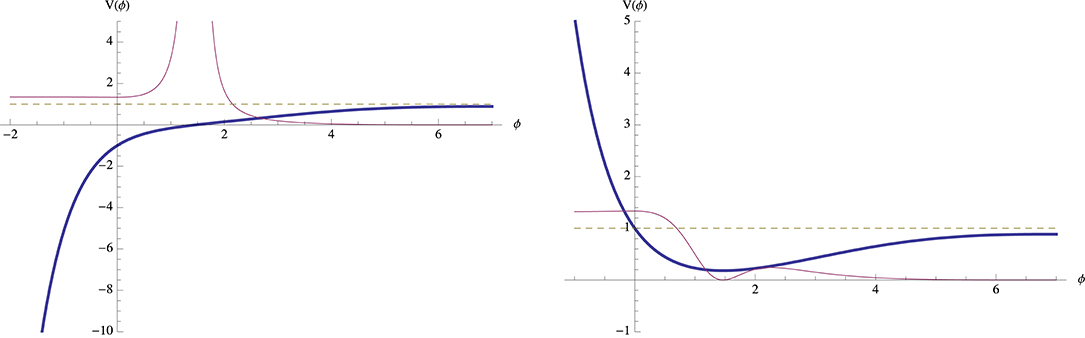
Figure 3. Scalar potential V−(ϕ) (blue thick line) and slow-roll function ϵ(ϕ) (red thin line) for α = −10 and Λ = −2 (potential unbounded from below, left panel) and Λ = 2 (potential with a minimum and Vmin > 0, right panel) [60, 111]. The slow-roll conditions are violated and inflation ends if ∃tf such that ϵ(ϕ(tf)) = 1 (thin dashed line) and ϵ(ϕ) > 1 for any t > tf. The dynamics induced by the potential V−(ϕ) in the right panel keeps the dynamical field ϕ(t) in the region where ϵ(ϕ) < 1 [60, 111], thus making it impossible to exit inflation by violation of the slow-roll conditions. The potential plotted on the left panel allows instead for a finite period of slow-roll inflation, but in this case the reheating of the universe after inflation cannot be described via the standard parametric oscillations of the inflation field.
We now focus on the class of inflationary potentials providing a well defined exit from inflation by violation of the slow-roll conditions, followed by a phase of parametric oscillations of the inflation field [60, 111]. These conditions are realized by the class of potentials V+(ϕ), with α ∈ [1, 3] and Λ ∈ [0, 1.5] [60, 111]. The corresponding potential is shown in Figure 4 for Λ = 1.4 and various values of α.
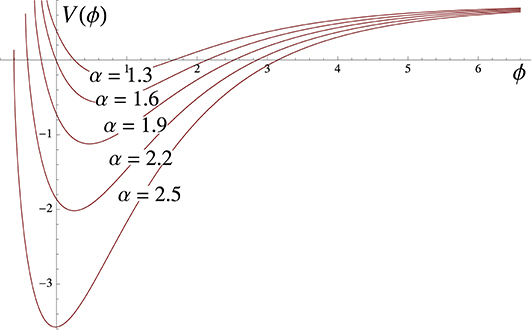
Figure 4. This figure depicts the potential V+(ϕ) for Λ = 1.4 and various values of α in the physically-interesting range, α ∈ [1, 3] [60, 111]. This is the class of potentials allowing for a (finite) period of slow-roll inflation, followed by a standard reheating phase.
As already mentioned, the constants (α, Λ) parameterize the deviations from the Starobinsky model due to the RG running of the gravitational couplings. It is thereby interesting to understand whether these modifications can affect the form of the power spectrum of temperature fluctuations in the CMB, and if the values of the spectral index ns and tensor-to-scalar ratio r are modified by this running. The results are summarized in Table 1 [111]. The range of values for the spectral index is ns ∈ [0.965, 0.972], in agreement with the value extracted from the Planck data, ns = 0.968±0.006. The tensor-to-scalar ratio is always compatible with their upper limit, but it is slightly higher than the one predicted within the Starobinsky model.
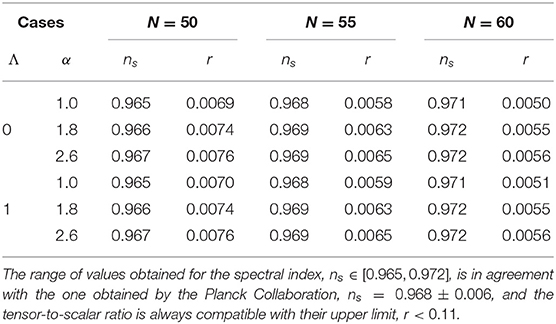
Table 1. Values of the spectral index ns and tensor-to-scalar ratio r obtained from the RG-improved model (62) for different values of (α, Λ) and number of e-folds N [111].
5. Discussion
The phenomenological consequences of Asymptotically Safe Gravity (ASG) are typically investigated within models that take the running of the gravitational couplings into account. Based on the decoupling mechanism [72], it is expected that these models can provide a qualitative, yet simple and intuitive, understanding of the effective modifications of General Relativity induced by quantum gravity in the asymptotic-safety approach. Nonetheless, the derivation of these “renormalization group (RG) improved” models is not free of ambiguities. Bearing in mind strengths and limitations of this approach, the scope of this review was to provide an overview of the main cosmological implications of ASG derived from models of RG-improved cosmology.
ASG is based on the existence of an interacting fixed point which is attained by the gravitational RG flow in the ultraviolet limit. The scale invariance of gravity at high energies and the consequent gravitational antiscreening can be regarded as the hallmarks of ASG. In particular the antiscreening character of gravity, rendering the gravitational interaction weaker at high energies, could lead to non-singular cosmological solutions: the classical singularity could be replaced by a bounce or an emergent universe [54]. The entropy production during inflation might be attributed to an energy flow from the gravitational to the matter degrees of freedom, which causes the primordial evolution of the universe to be approximately (but not exactly) adiabatic [57]. Moreover, the existence of a regime where gravity is approximately scale invariant (fixed-point regime and departure of the RG flow from it) provides a simple and natural interpretation for the nearly-scale-invariance of the power spectrum of temperature fluctuations in the Cosmic Microwave Background (CMB) radiation [57]. In the case of pure gravity, the spectral index and tensor-to-scalar ratio evaluated from models of “RG-improved” inflation are in agreement with the Planck data on CMB anisotropies [60]. When matter is minimally coupled to gravity, the universality properties of the gravitational RG flow are modified and this modification depends on the number and type (scalar, Dirac, vector, etc.) of matter fields: the observational data could thus be used to constrain the matter content of the theory in the early universe [61]. Finally, the running of the R2-coupling could also provide a mechanism to set the initial condition for inflation at trans-planckian scales, while being able to reproduce the amplitude of the scalar power spectrum at the horizon exit [91]. If this mechanism is realized, it could provide a solution to the “unlikeness problem” [113] of inflationary cosmology. A definite answer requires however more elaborate and extended studies, going beyond the simple models reviewed here.
Most of the results listed above have been obtained by including the running of the gravitational couplings within the Einstein-Hilbert truncation. As argued in Lehners et al. [98], fourth-derivatives operators are crucial for the understanding of the early-universe evolution. The inclusion of these operators in the models of RG-improved cosmologies could then be important to determine the phenomenological implications of the gravitational antiscreening.
One of the main problems of models of “RG-improved cosmologies” is the identification of the physical cutoff acting as a decoupling scale [72] for the RG flow of the effective average action [65]. The symmetries of theory play an important role, as they could provide a guideline for this scale-setting [87, 88, 90, 114, 115]. As shown in Reuter and Weyer [86], Reuter and Weyer [82], Babic et al. [87], Domazet and Stefancic [88], and Koch et al. [89], the contracted Bianchi identities typically lead to a “consistency condition” which can be used to determine the form of the cutoff scale. Close to a fixed point, the RG flow should be universal (no scheme or regulator dependence, at least for the flow of the full—not truncated—effective action) and all physical scales collapse into one: in this case the scale-setting is essentially unique. Away from the fixed point, the physical cutoff is dictated by the consistency condition. However, this condition requires the running of the gravitational couplings as an external input: since the RG flow obtained from the Wetterich equation [65] depends explicitly on the choice of the regulator, this dependence is inherited by the physical cutoff scale and it disappears only in the proximity of the fixed point (provided that no truncation of the effective action is employed).
While it is expected that the RG-improved models capture the qualitative features of the quantum modifications of General Relativity according to ASG, quantitative results require the knowledge of the fully-quantum gravitational effective action. This is expected to be non-local, due to the resummation of quantum fluctuations on all scales. Progress in this direction has been made in Codello and Jain [116], where the leading-order, quadratic part of the effective action has been derived within the framework of effective field theory, in Codello et al. [117], by studying the flow of the non-local part of the one-loop effective action, and, more recently, in Knorr et al. [69], where the beta functions for a specific non-local action have been computed using the functional renormalization group. Future developments of these programs could provide indications on the form of the gravitational effective action. On the phenomenological side, this could allow to derive more quantitative results on the implications of ASG in astrophysics and cosmology.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge financial support by the Baden-Württemberg Ministry of Science, Research, and the Arts and by Ruprecht-Karls-Universität Heidelberg. The author also thanks A. Bonanno and A. Eichhorn for their comments on this manuscript. The research of AP is supported by the Alexander von Humboldt Foundation.
References
1. Nink A, Reuter M. On the physical mechanism underlying asymptotic safety. J High Energy Phys. (2013) 1:62. doi: 10.1007/JHEP01(2013)062
2. Markov MA. Limiting density of matter as a universal law of nature. Soviet J Exp Theor Phys Lett. (1982) 36:265–67.
3. Markov MA. Asymptotic freedom and entropy in a perpetually oscillating universe. Phys Lett A. (1983) 94:427–9. doi: 10.1016/0375-9601(83)90845-9
4. Markov MA, Mukhanov VF. De Sitter-like initial state of the universe as a result of asymptotical disappearance of gravitational interactions of matter. Nuovo Cim. (1985) B86:97–102. doi: 10.1007/BF02732276
5. Markov MA. Possible existence of asymptotic freedom of gravitational interactions in nature. Phys Usp. (1994) 37:57. doi: 10.1070/PU1994v037n01ABEH000002
6. Hawking SW, Penrose R. The singularities of gravitational collapse and cosmology. Proc R Soc Lond Ser A. (1970) 314:529–48. doi: 10.1098/rspa.1970.0021
7. Frolov VP, Markov MA, Mukhanov VF. Through a black hole into a new universe? Phys Lett B. (1989) 216:272–6. doi: 10.1016/0370-2693(89)91114-3
8. Reuter M, Saueressig F. Quantum Einstein gravity. New J Phys. (2012) 14:055022. doi: 10.1088/1367-2630/14/5/055022
9. Percacci R. An Introduction to Covariant Quantum Gravity and Asymptotic Safety. Vol. 3. Singapore: World Scientific (2017). doi: 10.1142/10369
10. Reuter M, Saueressig F. Quantum Gravity and the Functional Renormalization Group. Cambridge, UK: Cambridge University Press (2019). doi: 10.1017/9781316227596
12. Weinberg S. Ultraviolet divergences in quantum theories of gravitation. In: Hawking SW, Israel W, editors. General Relativity: An Einstein Centenary Survey. Cambridge, UK: Cambridge University Press (1979). p. 790–831.
13. Wilson KG. Renormalization group and critical phenomena. I. Renormalization group and the kadanoff scaling picture. Phys Rev B. (1971) 4:3174–83. doi: 10.1103/PhysRevB.4.3174
14. Wilson KG. Renormalization group and critical phenomena. II. Phase-space cell analysis of critical behavior. Phys Rev B. (1971) 4:3184–205. doi: 10.1103/PhysRevB.4.3184
15. Wilson KG, Kogut JB. The Renormalization group and the epsilon expansion. Phys Rept. (1974) 12:75–199. doi: 10.1016/0370-1573(74)90023-4
16. Reuter M. Nonperturbative evolution equation for quantum gravity. Phys Rev D. (1998) 57:971–85. doi: 10.1103/PhysRevD.57.971
17. Souma W. Non-trivial ultraviolet fixed point in quantum gravity. Prog Theor Phys. (1999) 102:181–95. doi: 10.1143/PTP.102.181
18. Reuter M, Saueressig F. Renormalization group flow of quantum gravity in the Einstein-Hilbert truncation. Phys Rev D. (2002) 65:065016. doi: 10.1103/PhysRevD.65.065016
19. Litim DF. Fixed points of quantum gravity. Phys Rev Lett. (2004) 92:201301. doi: 10.1103/PhysRevLett.92.201301
20. Codello A, Percacci R, Rahmede C. Ultraviolet Properties of f(R)-gravity. Int J Modern Phys A. (2008) 23:143–50. doi: 10.1142/S0217751X08038135
21. Benedetti D, Machado PF, Saueressig F. Taming perturbative divergences in asymptotically safe gravity. Nucl Phys B. (2010) 824:168–91. doi: 10.1016/j.nuclphysb.2009.08.023
22. Saueressig F, Groh K, Rechenberger S, Zanusso O. Higher derivative gravity from the universal renormalization group machine. ArXiv e-prints. (2011).
23. Donkin I, Pawlowski JM. The phase diagram of quantum gravity from diffeomorphism-invariant RG-flows. arXiv [Preprint]. arXiv:1203.4207. (2012).
24. Benedetti D. On the number of relevant operators in asymptotically safe gravity. Europhys Lett. (2013) 102:20007. doi: 10.1209/0295-5075/102/20007
25. Eichhorn A. On unimodular quantum gravity. Class Quant Grav. (2013) 30:115016. doi: 10.1088/0264-9381/30/11/115016
26. Falls K, Litim D, Nikolakopoulos K, Rahmede C. Further evidence for asymptotic safety of quantum gravity. Phys Rev D. (2016) 93:104022. doi: 10.1103/PhysRevD.93.104022
27. Demmel M, Saueressig F, Zanusso O. A proper fixed functional for four-dimensional Quantum Einstein Gravity. J High Energy Phys. (2015) 8:113. doi: 10.1007/JHEP08(2015)113
28. Eichhorn A. The Renormalization Group flow of unimodular f(R) gravity. J High Energy Phys. (2015) 04:096. doi: 10.1007/JHEP04(2015)096
29. Biemans J, Platania A, Saueressig F. Quantum gravity on foliated spacetimes: asymptotically safe and sound. Phys Rev D. (2017) 95:086013. doi: 10.1103/PhysRevD.95.086013
30. Gies H, Knorr B, Lippoldt S, Saueressig F. Gravitational two-loop counterterm is asymptotically safe. Phys Rev Lett. (2016) 116:211302. doi: 10.1103/PhysRevLett.116.211302
31. Hamada Y, Yamada M. Asymptotic safety of higher derivative quantum gravity non-minimally coupled with a matter system. J High Energy Phys. (2017) 8:070. doi: 10.1007/JHEP08(2017)070
32. Biemans J, Platania A, Saueressig F. Renormalization group fixed points of foliated gravity-matter systems. J High Energy Phys. (2017) 5:093. doi: 10.1007/JHEP05(2017)093
33. Platania A, Saueressig F. Functional renormalization group flows on Friedmann-Lemaitre-Robertson-Walker backgrounds. Found Phys. (2018) 48:1291–304. doi: 10.1007/s10701-018-0181-0
34. Falls KG, Litim DF, Schröder J. Aspects of asymptotic safety for quantum gravity. Phys Rev D. (2019) 99:126015. doi: 10.1103/PhysRevD.99.126015
35. Eichhorn A, Lippoldt S, Pawlowski JM, Reichert M, Schiffer M. How perturbative is quantum gravity? Phys Lett B. (2018) 792:310–4. doi: 10.1016/j.physletb.2019.01.071
36. Bonanno A, Reuter M. Quantum gravity effects near the null black hole singularity. Phys Rev D. (1999) 60:084011. doi: 10.1103/PhysRevD.60.084011
37. Bonanno A, Reuter M. Renormalization group improved black hole space-times. Phys Rev D. (2000) 62:043008. doi: 10.1103/PhysRevD.62.043008
38. Bonanno A, Reuter M. Spacetime structure of an evaporating black hole in quantum gravity. Phys Rev D. (2006) 73:083005. doi: 10.1103/PhysRevD.73.083005
39. Torres R. Singularity-free gravitational collapse and asymptotic safety. Phys Lett B. (2014) 733:21–4. doi: 10.1016/j.physletb.2014.04.010
40. Torres R. Nonsingular black holes, the cosmological constant, and asymptotic safety. Phys Rev D. (2017) 95:124004. doi: 10.1103/PhysRevD.95.124004
41. Torres R, Fayos F. Singularity free gravitational collapse in an effective dynamical quantum spacetime. Phys Lett B. (2014) 733:169–75. doi: 10.1016/j.physletb.2014.04.038
42. Bonanno A, Koch B, Platania A. Cosmic censorship in quantum Einstein gravity. Class Quant Grav. (2017) 34:095012. doi: 10.1088/1361-6382/aa6788
43. Bonanno A, Koch B, Platania A. Asymptotically safe gravitational collapse: Kuroda-Papapetrou RG-improved model. PoS. (2017) corfu2016:058. doi: 10.22323/1.292.0058
44. Bonanno A, Koch B, Platania A. Gravitational collapse in quantum einstein gravity. Found Phys. (2018) 48:1393–406. doi: 10.1007/s10701-018-0195-7
45. Adeifeoba A, Eichhorn A, Platania A. Towards conditions for black-hole singularity-resolution in asymptotically safe quantum gravity. Class Quant Grav. (2018) 35:225007. doi: 10.1088/1361-6382/aae6ef
46. Platania A. Dynamical renormalization of black-hole spacetimes. Eur Phys J. (2019) C79:470. doi: 10.1140/epjc/s10052-019-6990-2
47. Bonanno A, Casadio R, Platania A. Gravitational antiscreening in stellar interiors. J Cosmol Astropart Phys. (2020) 2001:022. doi: 10.1088/1475-7516/2020/01/022
48. Bonanno A. An effective action for asymptotically safe gravity. Phys Rev D. (2012) 85:081503. doi: 10.1103/PhysRevD.85.081503
49. Bosma L, Knorr B, Saueressig F. Resolving spacetime singularities within asymptotic safety. Phys Rev Lett. (2019) 123:101301. doi: 10.1103/PhysRevLett.123.101301
50. Marunovic A, Prokopec T. Time transients in the quantum corrected Newtonian potential induced by a massless nonminimally coupled scalar field. Phys Rev D. (2011) 83:104039. doi: 10.1103/PhysRevD.83.104039
51. Marunovic A, Prokopec T. Antiscreening in perturbative quantum gravity and resolving the Newtonian singularity. Phys Rev D. (2013) 87:104027. doi: 10.1103/PhysRevD.87.104027
52. Kofinas G, Zarikas V. Avoidance of singularities in asymptotically safe Quantum Einstein Gravity. J Cosmol Astropart Phys. (2015) 1510:069. doi: 10.1088/1475-7516/2015/10/069
53. Kofinas G, Zarikas V. Asymptotically Safe gravity and non-singular inflationary Big Bang with vacuum birth. Phys Rev D. (2016) 94:103514. doi: 10.1103/PhysRevD.94.103514
54. Bonanno A, Gabriele Gionti SJ, Platania A. Bouncing and emergent cosmologies from Arnowitt-Deser-Misner RG flows. Class Quant Grav. (2018) 35:065004. doi: 10.1088/1361-6382/aaa535
55. Bonanno A, Reuter M. Cosmology of the Planck era from a renormalization group for quantum gravity. Phys Rev D. (2002) 65:043508. doi: 10.1103/PhysRevD.65.043508
56. Reuter M, Saueressig F. From big bang to asymptotic de Sitter: complete cosmologies in a quantum gravity framework. J Cosmol Astropart Phys. (2005) 0509:012. doi: 10.1088/1475-7516/2005/09/012
57. Bonanno A, Reuter M. Entropy signature of the running cosmological constant. J Cosmol Astropart Phys. (2007) 0708:024. doi: 10.1088/1475-7516/2007/08/024
58. Weinberg S. Asymptotically safe inflation. Phys Rev D. (2010) 81:083535. doi: 10.1103/PhysRevD.81.083535
59. Bonanno A, Reuter M. Entropy production during asymptotically safe inflation. Entropy. (2011) 13:274. doi: 10.3390/e13010274
60. Bonanno A, Platania A. Asymptotically safe inflation from quadratic gravity. Phys Lett B. (2015) 750:638–42. doi: 10.1016/j.physletb.2015.10.005
61. Bonanno A, Platania A, Saueressig F. Cosmological bounds on the field content of asymptotically safe gravity-matter models. Phys Lett B. (2018) 784:229–36. doi: 10.1016/j.physletb.2018.06.047
62. Bonanno A, Saueressig F. Asymptotically safe cosmology - A status report. Comptes Rendus Phys. (2017) 18:254–64. doi: 10.1016/j.crhy.2017.02.002
63. Eichhorn A. Status of the asymptotic safety paradigm for quantum gravity and matter. Found Phys. (2018) 48:1407–29. doi: 10.1007/s10701-018-0196-6
64. Eichhorn A. An asymptotically safe guide to quantum gravity and matter. Front Astron Space Sci. (2019) 5:47. doi: 10.3389/fspas.2018.00047
65. Wetterich C. Exact evolution equation for the effective potential. Phys Lett B. (1993) 301:90–4. doi: 10.1016/0370-2693(93)90726-X
66. Morris TR. The exact renormalization group and approximate solutions. Int J Modern Phys A. (1994) 9:2411–49. doi: 10.1142/S0217751X94000972
67. Reuter M, Wetterich C. Effective average action for gauge theories and exact evolution equations. Nucl Phys B. (1994) 417:181–214. doi: 10.1016/0550-3213(94)90543-6
68. Knorr B, Saueressig F. Towards reconstructing the quantum effective action of gravity. Phys Rev Lett. (2018) 121:161304. doi: 10.1103/PhysRevLett.121.161304
69. Knorr B, Ripken C, Saueressig F. Form factors in asymptotic safety: conceptual ideas and computational toolbox. Class Quant Grav. (2019) 36:234001. doi: 10.1088/1361-6382/ab4a53
70. Ambjorn J, Jurkiewicz J, Loll R. Spectral dimension of the universe. Phys Rev Lett. (2005) 95:171301. doi: 10.1103/PhysRevLett.95.171301
71. Ambjorn J, Goerlich A, Jurkiewicz J, Loll R. Nonperturbative quantum gravity. Phys Rept. (2012) 519:127–210. doi: 10.1016/j.physrep.2012.03.007
72. Reuter M, Weyer H. Renormalization group improved gravitational actions: a Brans-Dicke approach. Phys Rev D. (2004) 69:104022. doi: 10.1103/PhysRevD.69.104022
73. Coleman S, Weinberg E. Radiative corrections as the origin of spontaneous symmetry breaking. Phys Rev D. (1973) 7:1888–910. doi: 10.1103/PhysRevD.7.1888
74. Migdal AB. Vacuum polarization in strong non-homogeneous fields. Nucl Phys B. (1973) 52:483–505. doi: 10.1016/0550-3213(73)90575-0
75. Adler SL. Short-distance perturbation theory for the leading logarithm models. Nucl Phys B. (1983) 217:381–94. doi: 10.1016/0550-3213(83)90153-0
76. Dittrich W, Reuter M. Effective Lagrangians in quantum electrodynamics. Lect Notes Phys. (1985) 220:1–244. doi: 10.1007/3-540-15182-6
77. Manrique E, Rechenberger S, Saueressig F. Asymptotically safe lorentzian gravity. Phys Rev Lett. (2011) 106:251302. doi: 10.1103/PhysRevLett.106.251302
78. Codello A, Percacci R. Fixed points of higher-derivative gravity. Phys Rev Lett. (2006) 97:221301. doi: 10.1103/PhysRevLett.97.221301
79. Benedetti D, Machado PF, Saueressig F. Asymptotic safety in higher-derivative gravity. Modern Phys Lett A. (2009) 24:2233–41. doi: 10.1142/S0217732309031521
80. Falls K, King CR, Litim DF, Nikolakopoulos K, Rahmede C. Asymptotic safety of quantum gravity beyond Ricci scalars. Phys Rev D. (2018) 97:086006. doi: 10.1103/PhysRevD.97.086006
81. Alkofer N, Saueressig F. Asymptotically safe f(R)-gravity coupled to matter I: the polynomial case. Ann Phys. (2018) 396:173–201. doi: 10.1016/j.aop.2018.07.017
82. Reuter M, Weyer H. Quantum gravity at astrophysical distances? JCAP. (2004) 12:001. doi: 10.1088/1475-7516/2004/12/001
83. Doná P, Eichhorn A, Percacci R. Matter matters in asymptotically safe quantum gravity. Phys Rev D. (2014) 89:084035. doi: 10.1103/PhysRevD.89.084035
84. Doná P, Eichhorn A, Percacci R. Consistency of matter models with asymptotically safe quantum gravity. Can J Phys. (2015) 93:988–94. doi: 10.1139/cjp-2014-0574
85. Christiansen N, Litim DF, Pawlowski JM, Reichert M. Asymptotic safety of gravity with matter. Phys Rev D. (2018) 97:106012. doi: 10.1103/PhysRevD.97.106012
86. Reuter M, Weyer H. Running Newton constant, improved gravitational actions, and galaxy rotation curves. Phys Rev D. (2004) 70:124028. doi: 10.1103/PhysRevD.70.124028
87. Babic A, Guberina B, Horvat R, Stefancic H. Renormalization-group running cosmologies. A Scale-setting procedure. Phys Rev D. (2005) 71:124041. doi: 10.1103/PhysRevD.71.124041
88. Domazet S, Stefancic H. Renormalization group scale-setting from the action - a road to modified gravity theories. Class Quant Grav. (2012) 29:235005. doi: 10.1088/0264-9381/29/23/235005
89. Koch B, Rioseco P, Contreras C. Scale setting for self-consistent backgrounds. Phys Rev D. (2015) 91:025009. doi: 10.1103/PhysRevD.91.025009
90. Domazet S, Stefancic H. Renormalization group scale-setting in astrophysical systems. Phys Lett B. (2011) 703:1–6. doi: 10.1016/j.physletb.2011.07.038
91. Platania A. The inflationary mechanism in Asymptotically Safe Gravity. Universe. (2019) 5:189. doi: 10.3390/universe5080189
92. Hindmarsh M, Saltas ID. f(R) Gravity from the renormalisation group. Phys Rev D. (2012) 86:064029. doi: 10.1103/PhysRevD.86.064029
93. Reuter M, Wetterich C. Time evolution of the cosmological 'constant'. Phys Lett B. (1987) 188:38–43. doi: 10.1016/0370-2693(87)90702-7
94. Bonanno A, Reuter M. Cosmological perturbations in renormalization group derived cosmologies. Int J Mod Phys D. (2004) 13:107–22. doi: 10.1142/S0218271804003809
95. Dou D, Percacci R. The running gravitational couplings. Class Quant Grav. (1998) 15:3449–68. doi: 10.1088/0264-9381/15/11/011
96. Lauscher O, Reuter M. Ultraviolet fixed point and generalized flow equation of quantum gravity. Phys Rev D. (2002) 65:025013. doi: 10.1103/PhysRevD.65.025013
97. Bonanno A, Contillo A, Percacci R. Inflationary solutions in asymptotically safe f(R) theories. Class Quant Grav. (2011) 28:145026. doi: 10.1088/0264-9381/28/14/145026
98. Lehners JL, Stelle KS. A Safe beginning for the universe? Phys Rev D. (2019) 100:083540. doi: 10.1103/PhysRevD.100.083540
99. Bonanno A, Reuter M. Primordial entropy production and lambda-driven inflation from quantum einstein gravity. J Phys Conf Ser. (2008) 140:012008. doi: 10.1088/1742-6596/140/1/012008
100. Bonanno A, Reuter M. Proper time flow equation for gravity. J High Energy Phys. (2005) 2:035. doi: 10.1088/1126-6708/2005/02/035
101. Novello M, Bergliaffa SEP. Bouncing cosmologies. Phys Rept. (2008) 463:127–213. doi: 10.1016/j.physrep.2008.04.006
102. Akrami Y, Arroja F, Ashdown M, Aumont J, Baccigalupi C, Ballardini M, et al. Planck 2018 Results. X. Constraints on Inflation. (2018). Available online at: https://hal.archives-ouvertes.fr/hal-01871780
103. Lauscher O, Reuter M. Fractal spacetime structure in asymptotically safe gravity. J High Energy Phys. (2005) 10:050. doi: 10.1088/1126-6708/2005/10/050
104. Lauscher O, Reuter M. Flow equation of quantum Einstein gravity in a higher-derivative truncation. Phys Rev D. (2002) 66:025026. doi: 10.1103/PhysRevD.66.025026
105. Falls K, Litim DF, Nikolakopoulos K, Rahmede C. On de Sitter solutions in asymptotically safe f(R) theories. Class Quant Grav. (2018) 35:135006. doi: 10.1088/1361-6382/aac440
106. Martin J, Ringeval C, Vennin V. Encyclopedia inflationaris. Phys Dark Universe. (2014) 5:75–235. doi: 10.1016/j.dark.2014.01.003
107. Gubitosi G, Ooijer R, Ripken C, Saueressig F. Consistent early and late time cosmology from the RG flow of gravity. JCAP. (2018) 1812:004. doi: 10.1088/1475-7516/2018/12/004
108. Benedetti D, Caravelli F. The local potential approximation in quantum gravity. J High Energy Phys. (2012) 6:17. doi: 10.1007/JHEP06(2012)017
109. Dietz JA, Morris TR. Asymptotic safety in the f(R) approximation. J High Energy Phys. (2013) 1:108. doi: 10.1007/JHEP01(2013)108
110. Baumann D. Inflation. In: Csaki C, Dodelson S, editors. Physics of the Large and the Small: TASI. Singapore: World Scientific (2009). p. 523–686.
111. Bonanno A, Platania A. Asymptotically safe R+R2 GRAVITY. PoS. (2016) corfu2015:159. doi: 10.22323/1.263.0159
112. Rechenberger S, Saueressig F. R2 phase diagram of quantum Einstein gravity and its spectral dimension. Phys Rev D. (2012) 86:024018. doi: 10.1103/PhysRevD.86.024018
113. Ijjas A, Steinhardt PJ, Loeb A. Inflationary paradigm in trouble after Planck2013. Phys Lett B. (2013) 723:261–6. doi: 10.1016/j.physletb.2013.05.023
114. Koch B, Ramirez I. Exact renormalization group with optimal scale and its application to cosmology. Class Quant Grav. (2011) 28:055008. doi: 10.1088/0264-9381/28/5/055008
115. Contreras C, Koch B, Rioseco P. Setting the renormalization scale in QFT. J Phys Conf Ser. (2016) 720:012020. doi: 10.1088/1742-6596/720/1/012020
116. Codello A, Jain RK. On the covariant formalism of the effective field theory of gravity and leading order corrections. Class Quant Grav. (2016) 33:225006. doi: 10.1088/0264-9381/33/22/225006
Keywords: cosmology–theory, quantum gravitation, renormalization group, singularity, inflation
Citation: Platania A (2020) From Renormalization Group Flows to Cosmology. Front. Phys. 8:188. doi: 10.3389/fphy.2020.00188
Received: 12 March 2020; Accepted: 29 April 2020;
Published: 27 May 2020.
Edited by:
Antonio D. Pereira, Universidade Federal Fluminense, BrazilReviewed by:
Roberto Percacci, International School for Advanced Studies (SISSA), ItalyNobuyoshi Ohta, Kindai University, Japan
Copyright © 2020 Platania. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alessia Platania, YS5wbGF0YW5pYUB0aHBoeXMudW5pLWhlaWRlbGJlcmcuZGU=
 Alessia Platania
Alessia Platania