Perturbation Theory for Time-Dependent Quantum Systems Involving Complex Potentials

1. Introduction

In the case that we are unable to derive exact quantum solutions for a perturbed system, perturbation theory is a useful tool for obtaining approximate quantum solutions. When we apply perturbation theory, it should be supposed that the scale of the perturbed terms in the potential is relatively small. The perturbation theory is valid only when the quantum solutions of the system in which the perturbation potentials have been removed are exactly known or derivable. The perturbation theory was originally developed for Hermitian systems in which the potential is real. Hence, in conventional quantum mechanics, the perturbation theory has, in large, been developed for the systems in which the potentials are real Hermitian that allows only the spectrum of real expectation values for quantum observables. Whereas the eigenvalue problem and the effects of perturbations on stationary Hamiltonian systems are well known in non-relativistic quantum physics, the perturbation techniques for the time-dependent Hamiltonian systems (TDHSs) with complex potentials have been investigated much less. This is partly due to the difficulty of mathematical procedures when we apply perturbation techniques in TDHSs.

Time-independent perturbation theory is a mathematical tool for treating quantum systems whose Hamiltonian involves small static perturbing terms which do not induce transitions to other quantum states. In a case that the Hamiltonian is a function of time, transitions between quantum states may take place. Then, we should consider time-dependent perturbation theory instead of time-independent one. Provided that the perturbing Hamiltonian is differentiable with respect to time in that case, the transition probability is determined from the time derivative of the perturbing Hamiltonian [1]. Hence, if the perturbing Hamiltonian is slowly varying, we can adopt adiabatic theorem which assumes that the quantum system remains in its instantaneous eigenstate [2]. This allows the use of time-independent perturbation theory as an approximation in that situation. For more details of time-dependent perturbation theory and its relevance to time-independent perturbation theory, refer to Mandal and Hunt [1, 3] and Langhoff et al. [4].

On account of recent attention to the quantum problem of physical systems characterized by complex potentials, the necessity for the extension of perturbation theory to complex potential systems has gradually emerged. The data in some of the processes of elastic scattering such as nucleus-nucleus scattering [5] and electron scattering from solid crystals [6] fit better if one adopts complex potentials involving a non-positive imaginary part. Moreover, according to the advancement of techniques for unfolding quantum theory, the necessity of quantum manipulation with complex potentials takes place in many different areas of physics and related topics such as optics [7–11], statistical physics [12, 13], relativistic quantum field theory [14–16], nuclear physics [17], condensed matter physics [18–20], and biology [21]. To analyze the stability and nonlinear modes of optical beams propagating along an asymmetric waveguide, an imaginary potential has been adopted [11]. The structures of the energy band in elastic scattering processes governed by a periodic complex potential have also been studied [22].

According to such a research trend, we will investigate, in this work, how to apply perturbation theory to complex potential systems. We will adopt a general Hamiltonian that corresponds to a time-dependent harmonic oscillator to which complex potentials are coupled as perturbation terms. We will consider adiabatic evolution [23–25] of the states under slow variations of parameters while the magnitudes of perturbation terms are quite small compared to the unperturbed term at all times. Then, there will be no transition between eigenstates and, as a consequence, we can use usual time-independent perturbation theory. The wave functions corrected by perturbed potentials will be analytically evaluated. Using the wave functions involving correction terms, quantum characteristics of the system will be investigated. Furthermore, the spectrum of the expectation values of the Hamiltonian (EVH) will be rigorously evaluated. We will apply our development to some particular cases and analyze the time evolution of the corresponding wave functions and the EVH.

2. Theoretical Framework for a Complex Potential System

In this section, we outline the quantum structure for a TDHS which involves complex potentials as perturbations to the system. The equation of motion for lots of actual physical models in quantum mechanics are described not only by linear terms which allow us to have exact mathematical solutions, but also by nonlinear terms associated with interactions of the system with various subsystems. If the coupling parameters of the nonlinear parts are sufficiently small compared to others, we can treat them as perturbation terms. Regarding this, we consider the system of which Hamiltonian is represented as

$\begin{array}{ll}\widehat{{H}}=\widehat{H}+ϵ{\widehat{H}}_{\text{p}},& (1)\end{array}$

where Ĥ is a time-dependent quadratic Hamiltonian and Ĥ_p is a perturbing Hamiltonian, while ϵ is a small coupling parameter. In this case, the perturbation theory is available only when the second term on the right hand side of Equation (1) is very small relative to the first term. We assume that Ĥ and Ĥ_p are given by

$\begin{array}{llll}\widehat{H}& =& f(t)\frac{{\widehat{p}}^2}{2m_0}+g(t)(\widehat{q}\widehat{p}+\widehat{p}\widehat{q})+\frac{1}{2}h(t)m_0{\omega }^2(t){\widehat{q}}^2,& (2)\end{array}$

$\begin{array}{llll}{\widehat{H}}_{\text{p}}& =& {\displaystyle \sum _j}{k}_{\text{R},j}(t){\widehat{q}}^j+i{\displaystyle \sum _l}{k}_{\text{I},l}(t){\widehat{q}}^l,& (3)\end{array}$

where f(t), g(t), h(t), k_{R, j}(t), and k_{I, l}(t) are time functions that are differentiable with respect to time, and f(t)≠0. m₀ is the mass and ω(t) is a time-dependent angular frequency. Although this is a one-dimensional Hamiltonian, we can apply it to various different kinds of oscillators depending on the choice of the explicit formulae of time functions. As examples for such, we will apply it to two special cases at later by choosing the time functions being particular forms. In the case where the mass of the system varies over time, we can regard m₀ as the initial mass. Notice that the additional term Ĥ_p in the Hamiltonian makes the system be an anharmonic oscillator.

The Schrödinger solutions of the system are different depending on the choice of the time functions in the Hamiltonian. If we consider a discrete spectrum of solutions, the Schrödinger equation for the overall Hamiltonian $\widehat{{H}}$ can be written as

$\begin{array}{ll}i\hslash \partial {\text{Ψ}}_n(q,t)/\partial t=\widehat{{H}}{\text{Ψ}}_n(q,t).& (4)\end{array}$

To apply the perturbation theory at this stage, it is necessary to know complete quantum solutions associated with the unperturbed Hamiltonian Ĥ as mentioned in the introductory part. For this reason, we first derive exact solutions of the Schrödinger equation for Ĥ from

$\begin{array}{ll}i\hslash \partial {\psi }_n(q,t)/\partial t=\widehat{H}{\psi }_n(q,t).& (5)\end{array}$

Let us take a moment to review the theory for solving this equation exactly. Because Ĥ involves time functions, it is very difficult to solve this equation relying on the conventional method. For such TDHSs, it is known based on the invariant operator theory that the Schrödinger solutions are expressed in terms of the solutions of a classical equation associated with the system [26, 27]. Hence, let us consider a time function ρ(t) which is the solution of the following nonlinear equation

$\begin{array}{ll}\ddot{\rho }(t)+{\omega }_{\rho }^2(t)\rho (t)-\frac{{\Omega }^2}{{\rho }^3(t)}=0,& (6)\end{array}$

where

$\begin{array}{ll}{\omega }_{\rho }^2(t)=f(t)h(t){\omega }^2(t)+\frac{2\dot{f}(t)g(t)}{f(t)}+\frac{\ddot{f}(t)}{2f(t)}-\frac{3{\dot{f}}^2(t)}{4f^2(t)}-4g^2(t)-2\dot{g}(t).& (7)\end{array}$

Then, we can define the annihilation operator of the system in terms of ρ(t) as

$\begin{array}{ll}\widehat{a}=\sqrt{\frac{1}{2\hslash \Omega }}\left[\sqrt{\frac{m_0}{f(t)}}\left(\frac{\Omega }{\rho (t)}+iG(t)\right)\widehat{q}+i\sqrt{\frac{f\left(t\right)}{m_0}}\rho (t)\widehat{p}\right],& (8)\end{array}$

where Ω is an arbitrary real positive constant, and

$\begin{array}{ll}G(t)=\left(2g(t)-\frac{\dot{f}(t)}{2f(t)}\right)\rho (t)-\dot{\rho }(t).& (9)\end{array}$

Of course, the Hermitian adjoint of Equation (8), â^†, is the creation operator. These ladder operators obey the commutation relation [â, â^†] = 1. The time evolution of â(t) can be simply represented as â(t) = â(0)e^{−i[η(t)−η(0)]}, where

$\begin{array}{ll}\eta (t)=\Omega {\displaystyle {\int }_0^t}\frac{d\tau }{{\rho }^2(\tau )}+\eta (0).& (10)\end{array}$

It is also possible to define an invariant operator using the ladder operators, such that [27, 28]

$\begin{array}{ll}\hat{I}=\hslash \Omega ({â}^{†}â+\frac{1}{2}).& (11)\end{array}$

We can check that the direct differentiation of Î with respect to time results in zero, which means that Î(t) is a time-invariant. If we write the eigenfunctions of Î as ϕ_n(q, t), they can be derived from the eigenvalue equation:

$\begin{array}{ll}\hat{I}{\varphi }_n(q,t)={\lambda }_n{\varphi }_n(q,t).& (12)\end{array}$

This is analogous to the time-independent Schrödinger equation in a stationary system. We can easily solve this equation from a minor evaluation; the exact results are given in Appendix A. According to the invariant operator theory, the wave functions of the unperturbed system are expressed in terms of ϕ_n(q, t) as [27, 28]

$\begin{array}{ll}{\psi }_n(q,t)={\varphi }_n(q,t)e^{i{\theta }_n(t)},& (13)\end{array}$

where

$\begin{array}{ll}{\theta }_n(t)=-(n+1/2)\eta (t)+{\tilde{\theta }}_n,& (14)\end{array}$

while ${\tilde{\theta }}_n$ is an arbitrary constant phase. Because ϕ_n(q, t) given in Appendix A are described by ρ(t), the wave functions are also represented in terms of it. In fact, the reason why ρ(t) has been introduced is that it is necessary in the expression of the quantum solutions of the unperturbed system of which Hamiltonian Ĥ is dependent on time.

We can easily check that the ladder operators yield

$\begin{array}{ll}\hat{a}|{\varphi }_n(t)\rangle =\sqrt{n}|{\varphi }_{n-1}(t)\rangle ,& (15)\end{array}$

$\begin{array}{ll}{\hat{a}}^{†}|{\varphi }_n(t)\rangle =\sqrt{n+1}|{\varphi }_{n+1}(t)\rangle .& (16)\end{array}$

The quantum theory for a TDHS represented above will be used in the subsequent section in order to develop the perturbation theory of the system associated with the complex potentials.

3. Perturbation Theory With the Complex Potentials

Although perturbation theory does not give the spectrum of exact analytical quantum solutions for a dynamical system, it enables us to solve difficult problems in quantum mechanics from a series of routine calculations. If we regard that we cannot derive exact Schrödinger solutions in many cases of quantum mechanical problems, perturbation theory is quite useful in quantum mechanics. We will show how to manage perturbation theory for the case where the Hamiltonian involves time-dependent complex potentials on the basis of the associated theory represented in the previous section.

By expressing Equation (8) and its Hermitian adjoint â^† inversely, we obtain the representation of canonical variables $\widehat{q}$ and $\widehat{p}$ in terms of â and â^†. Then we can easily derive the expectation values of Ĥ using Equations (13), (15), and (16), leading to

$\begin{array}{ll}\langle {\psi }_n\left|\widehat{H}\right|{\psi }_n\rangle =\hslash W(t)\left(n+\frac{1}{2}\right),& (17)\end{array}$

where

$\begin{array}{ll}W(t)=\frac{1}{2\Omega }[G^2(t)+\frac{{\Omega }^2}{{\rho }^2(t)}+f(t)h(t){\omega }^2(t){\rho }^2(t)-4g(t)\rho (t)G(t)].& (18)\end{array}$

The purpose of using perturbation techniques is to find the effects of small perturbed potentials on the whole system. In general, perturbation expansion gives a power series representation of a resultant quantity with respect to the perturbing parameter ϵ. The results of a calculation considering perturbations agree quite well with experimental data, but entails an infinite number of minor terms. However, the higher orders of such minor terms can, in general, be negligible from the perturbation corrections because their numeric scales are small enough.

Our theory is based on time-independent perturbation theory that is usually managed in terms of the eigenstates where the phases are not considered [29], as mentioned earlier. Hence, if we do not care about the minor phases of the wave functions contributed from the perturbing Hamiltonian, we can represent the overall wave functions of the system as

$\begin{array}{ll}\langle q|{\text{Ψ}}_n\rangle =\langle q|{\Phi }_n\rangle e^{i{\theta }_n(t)},& (19)\end{array}$

where 〈q|Φ_n〉 are eigenstates and θ_n(t) are the phases. According to the perturbation theory, the eigenstates take the form

$\begin{array}{l}\langle q|{\Phi }_n\rangle =\langle q|{\varphi }_n\rangle \\ +ϵ{\displaystyle \sum _{n^{\prime },(n^{\prime }\ne n)}}{\Pi }_1\langle q|{\varphi }_{n^{\prime }}\rangle +{ϵ}^2{\displaystyle \sum _{n^{\prime },(n^{\prime }\ne n)}}{\Pi }_2\langle q|{\varphi }_{n^{\prime }}\rangle +\cdots ,& (20)\end{array}$

where 〈q|ϕ_n〉 = ϕ_n(q, t), which are given in Appendix A, and

$\begin{array}{ll}{\Pi }_1=\frac{\langle {\varphi }_{n^{\prime }}\left|{\widehat{H}}_{\text{p}}\right|{\varphi }_n\rangle }{\langle {\varphi }_n\left|\widehat{H}\right|{\varphi }_n\rangle -\langle {\varphi }_{n^{\prime }}\left|\widehat{H}\right|{\varphi }_{n^{\prime }}\rangle },& (21)\end{array}$

$\begin{array}{ll}{\Pi }_2={\Pi }_2^{(1)}+{\Pi }_2^{(2)},& (22)\end{array}$

with

$\begin{array}{ll}{\Pi }_2^{(1)}={\displaystyle \sum _{n^{″},(n^{″}\ne n)}}\frac{\langle {\varphi }_{n^{\prime }}\left|{\widehat{H}}_{\text{p}}\right|{\varphi }_{n^{″}}\rangle \langle {\varphi }_{n^{″}}\left|{\widehat{H}}_{\text{p}}\right|{\varphi }_n\rangle }{(\langle {\varphi }_n\left|\widehat{H}\right|{\varphi }_n\rangle -\langle {\varphi }_{n^{\prime }}\left|\widehat{H}\right|{\varphi }_{n^{\prime }}\rangle )(\langle {\varphi }_n\left|\widehat{H}\right|{\varphi }_n\rangle -\langle {\varphi }_{n^{″}}\left|\widehat{H}\right|{\varphi }_{n^{″}}\rangle )},& (23)\end{array}$

$\begin{array}{ll}{\Pi }_2^{(2)}=-\frac{\langle {\varphi }_{n^{\prime }}\left|{\widehat{H}}_{\text{p}}\right|{\varphi }_n\rangle \langle {\varphi }_n\left|{\widehat{H}}_{\text{p}}\right|{\varphi }_n\rangle }{{(\langle {\varphi }_n\left|\widehat{H}\right|{\varphi }_n\rangle -\langle {\varphi }_{n^{\prime }}\left|\widehat{H}\right|{\varphi }_{n^{\prime }}\rangle )}^2}.& (24)\end{array}$

By perturbation theory, the EVH are represented as

$\begin{array}{ll}\langle {\Phi }_n\left|\widehat{{H}}\right|{\Phi }_n\rangle ={ϵ}^0{\Lambda }_0+{ϵ}^1{\Lambda }_1+{ϵ}^2{\Lambda }_2+\cdots ,& (25)\end{array}$

where

$\begin{array}{ll}{\Lambda }_0=\langle {\varphi }_n\left|\widehat{H}\right|{\varphi }_n\rangle ,& (26)\end{array}$

$\begin{array}{ll}{\Lambda }_1=\langle {\varphi }_n\left|{\widehat{H}}_{\text{p}}\right|{\varphi }_n\rangle ,& (27)\end{array}$

$\begin{array}{ll}{\Lambda }_2={\displaystyle \sum _{n^{\prime },(n^{\prime }\ne n)}}\frac{\langle {\varphi }_n\left|{\widehat{H}}_{\text{p}}\right|{\varphi }_{n^{\prime }}\rangle \langle {\varphi }_{n^{\prime }}\left|{\widehat{H}}_{\text{p}}\right|{\varphi }_n\rangle }{\langle {\varphi }_n\left|\widehat{H}\right|{\varphi }_n\rangle -\langle {\varphi }_{n^{\prime }}\left|\widehat{H}\right|{\varphi }_{n^{\prime }}\rangle }.& (28)\end{array}$

Up until now, we have developed perturbation theory for the general time-dependent Hamiltonian system which involves complex potentials. In order to see the applicability of our theory to particular systems, let us consider the case where k_{R, 1}(t)≠0 and k_{I, 3}(t)≠0, while all other k_{R, j}(t) and k_{I, l}(t) are zero. In this case, Equation (3) can be written in the form

$\begin{array}{ll}{\widehat{H}}_{\text{p}}=k_{\text{R},1}(t)\widehat{q}+i{k}_{\text{I},3}(t){\widehat{q}}^3.& (29)\end{array}$

Now, from Equations (20)–(22), the corresponding wave functions are derived to be

$\begin{array}{ll}\langle q|{\Phi }_n\rangle =\langle q|{\varphi }_n\rangle +ϵ{\tilde{\Pi }}_1+{ϵ}^2{\tilde{\Pi }}_2+\cdots ,& (30)\end{array}$

where, ${\tilde{\Pi }}_1$ is given by

$\begin{array}{ll}{\tilde{\Pi }}_1=\frac{1}{\hslash W(t)}\left[A(t)k_{\text{R},1}(t){\phi }_{\text{R},1}+i{A}^3(t)k_{\text{I},3}(t){\phi }_{\text{I},3}\right],& (31)\end{array}$

with

$\begin{array}{ll}A(t)=\sqrt{\frac{\hslash f(t)}{2\Omega m_0}}\rho (t),& (32)\end{array}$

$\begin{array}{ll}{\phi }_{\text{R},1}=\sqrt{n}\langle q|{\varphi }_{n-1}\rangle -\sqrt{n+1}\langle q|{\varphi }_{n+1}\rangle ,& (33)\end{array}$

$\begin{array}{l}{\phi }_{\text{I},3}=\frac{\sqrt{n(n-1)(n-2)}}{3}\langle q|{\varphi }_{n-3}\rangle \\ -\frac{\sqrt{(n+1)(n+2)(n+3)}}{3}\langle q|{\varphi }_{n+3}\rangle \\ +3n^{3/2}\langle q|{\varphi }_{n-1}\rangle -3{(n+1)}^{3/2}\langle q|{\varphi }_{n+1}\rangle .& (34)\end{array}$

Because ${\tilde{\Pi }}_2$ in Equation (30) is a somewhat complicated form, we have represented it in Appendix B.

On the other hand, the EVH become

$\begin{array}{l}\langle {\Phi }_n\left|\widehat{\mathscr{H}}\right|{\Phi }_n\rangle =\hslash W(t)\left(n+\frac{1}{2}\right)\\ +\frac{{ϵ}^2}{\hslash W(t)}[A^6(t)k_{\text{I},3}^2(t)(30n^2+30n+11)\\ -A^2(t)k_{\text{R},1}^2(t)\\ -6i{A}^4(t)k_{\text{R},1}(t)k_{\text{I},3}(t)(2n+1)]+\cdots .& (35)\end{array}$

If large-scale perturbation expansions regarding higher order terms are required in the solutions, it is necessary to take the aid of computer algebra [30]. The last term in Equation (35) is an imaginary part of the energy. We can elucidate the time-dependent evolution of the probability density in a quantum state based on non-Hermitian quantum theory, where imaginary terms of the energy levels take place [10, 31–34] as well as the real ones. The novel outcome of non-Hermitian analyses is excluded in the problem of conventional quantization methods relevant to Hermitian Hamiltonians. The eigenvalues of Hermitian Hamiltonians and/or Pseudo Hermitian Hamiltonians are always real from a mathematical point of view. However, some systems/subsystems can violate the requirement of Hermiticity of Hamiltonians [35]. As can be seen from Equation (35), the expectation values of the Hamiltonian are complex. The possible existence of imaginary energy has a considerable interest from several decades ago [33]. Zhu and Cukier [34] adopted an imaginary energy method in order to formulate quantum rate theories. They have obtained a rate constant that can be used to explain the WKB quantum tunneling rate at low temperature and the quantum state transition rate at high temperature. Further, they have shown that their quantum rate constant has the same structure as the Miller's theory [36, 37] of quantum transition state at high temperature limit. Meanwhile, imaginary energy gaps between the complex eigenvalues of a system have been used to analyze cooperative effects such as superconductivity and superradiance [32]

Now let's turn to a special case where the unperturbed Hamiltonian corresponds to the Caldirola-Kanai oscillator [38, 39]:

$\begin{array}{ll}\widehat{H}=e^{\beta t}\frac{{\widehat{p}}^2}{2m_0}+\frac{1}{2}{e}^{-\beta t}{m}_0{\omega }_0^2{\widehat{q}}^2,& (36)\end{array}$

which can be obtained from the choice of time functions as f(t) = h⁻¹(t) = e^βt, g(t) = 0, and ω(t) = ω₀, where β and ω₀ are real positive constants. In addition, we choose

$\begin{array}{ll}{k}_{\text{R},1}(t)=a{k}_{\text{I},3}(t)=b,& (37)\end{array}$

where a and b are real constants. Then, the solution of the nonlinear equation, Equation (6), is given by

$\begin{array}{ll}\rho (t)={\left[c_1{cos}^2(\bar{\Omega }t)+c_2{sin}^2(\bar{\Omega }t)\right]}^{1/2},& (38)\end{array}$

provided that $\Omega ={(c_1{c}_2)}^{1/2}\bar{\Omega }$, where $\bar{\Omega }={({\omega }_0^2-{\beta }^2/4)}^{1/2}$, and c₁ and c₂ are arbitrary real positive constants.

We have depicted the probability density $|\langle q|{\text{Ψ}}_n\rangle {|}^2$ for the system described above in Figure 1. Due to the choice of c₁ = c₂ = 1 in this figure, ρ(t) is a uniform function having the value 1. This figure shows that the deviation of the probability densities for the perturbed wave functions, Equation (19), at an initial time can be negligible and, as a consequence, they are almost the same as $|\langle q|{\psi }_n\rangle {|}^2$ which are probabilities associated to the unperturbed wave functions. However, such deviation increases gradually as time goes by. We can also confirm from this figure that $|\langle q|{\text{Ψ}}_n\rangle {|}^2$ considered ϵ up to the second order are nearly the same as those considered ϵ up to the first order. This means that we can neglect the terms which are higher order in ϵ in the wave functions, as expected.

FIGURE 1

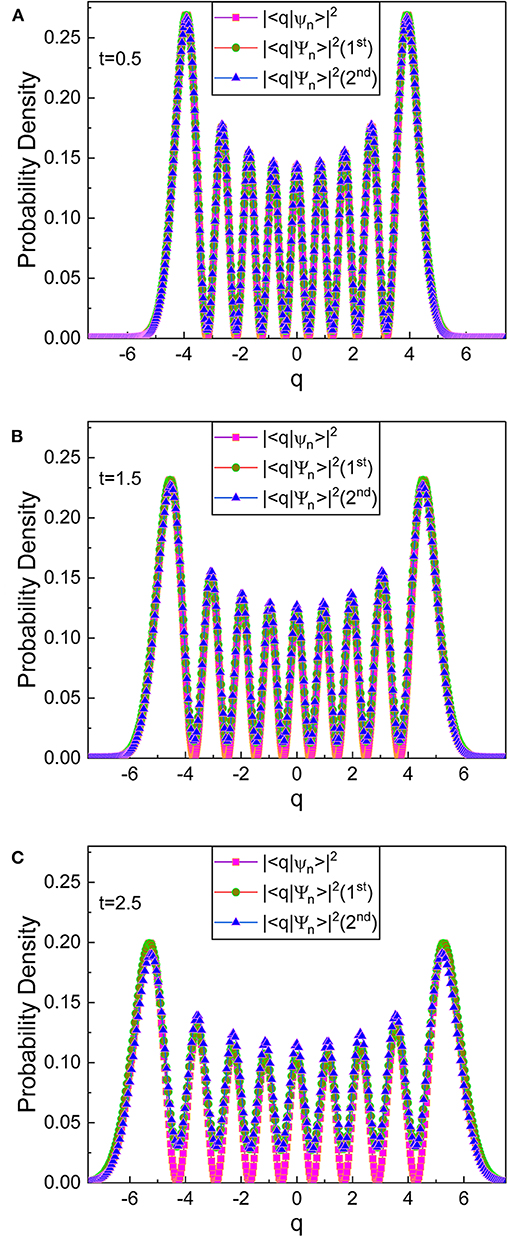
Figure 1. The probability densities $|\langle q|{\psi }_n\rangle {|}^2$ (for the wave functions Equation 14) and $|\langle q|{\text{Ψ}}_n\rangle {|}^2$ (for the wave functions Equation 20) for the system described in Equations (37)–(39), where t is 0.5 for (A), 1.5 for (B), and 2.5 for (C). The characters 1^st and 2^nd in the figure legends mean that the corresponding figure has been plotted with the consideration up to the first order and up to the second order of ϵ, respectively. The parameters are chosen as ℏ = 1, β = 0.3, ω₀ = 1, m₀ = 1, n = 8, c₁ = c₂ = 1, ϵ = 0.0035, and a = b = 1.

Figure 2 shows the time evolution of the real and the imaginary parts of the expectation values of the Hamiltonian $\widehat{{H}}$ considering up to the second order of ϵ for the system described by Equations (36)–(38). From Figure 2A, we can confirm that the deviation of both the real and the imaginary parts of the EVH from those of the unperturbed Hamiltonian is, largely, not so significant, but is not zero. Figures 2B,C are enlarged graphs of the real and the imaginary parts of $|\langle {\Phi }_n\left|\widehat{{H}}\right|{\Phi }_n\rangle {|}^2$, respectively. If β is large, the expectation values of the real part of the Hamiltonian are also large. Real parts deviate toward the positive direction whereas imaginary parts toward the negative one and such deviations increase over time.

FIGURE 2

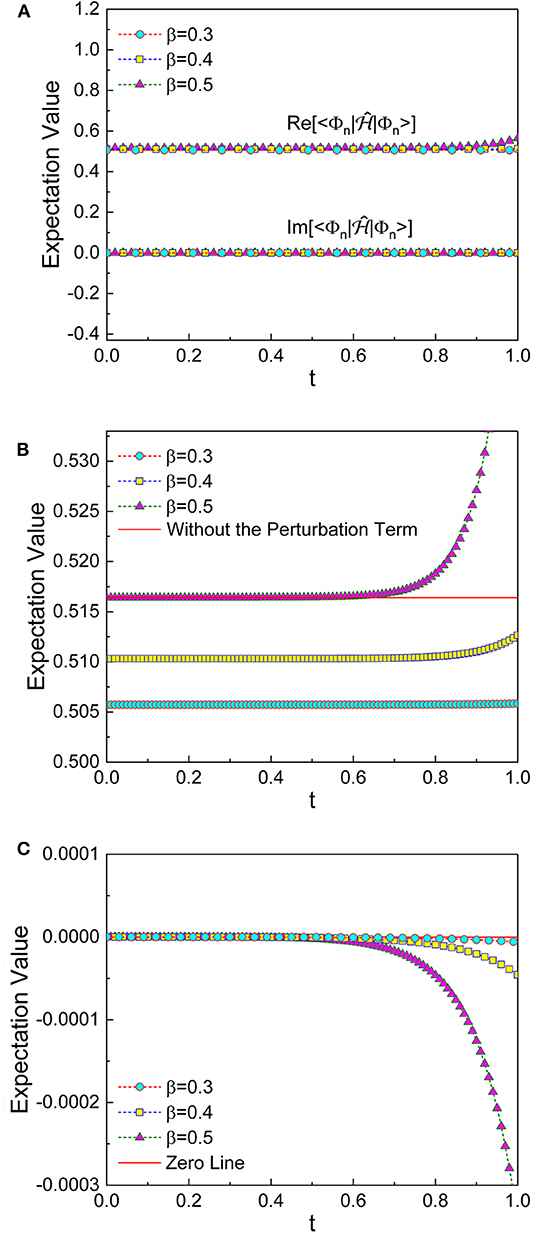
Figure 2. (A) The time evolutions of the real and the imaginary parts of the expectation values, Equation (36), for the system described in Equations (37)–(39), for three different values of β. The parameters are chosen as ℏ = 1, ω₀ = 1, m₀ = 1, n = 0, c₁ = c₂ = 1, ϵ = 0.0001, and a = b = 1. (B) Enlargement of the real parts in (A). The reference solid red line is the expectation value of the Hamiltonian without the perturbation term, given in Equation (18), under the choice of β = 0.5. (C) Enlargement of the imaginary parts in (A). The reference solid red line indicates zero of the vertical axis.

Let us show that the results, Equations (30)–(35), become well-known ones for a particular case. For this purpose, we put β = 0 from Equation (36) and b = 0 from Equation (37) while a ≠ 0. Then, the system becomes a simple one that is described by the Hamiltonian

$\begin{array}{ll}\widehat{{H}}=\frac{{\widehat{p}}^2}{2m_0}+\frac{1}{2}{m}_0{\omega }_0^2{\widehat{q}}^2+\delta \widehat{q},& (39)\end{array}$

where δ = ϵa. Then, under the choice c₁ = c₂ = 1, we have ρ = 1, W = Ω = ω₀, G = 0, and $A={\left[\hslash /(2m_0{\omega }_0)\right]}^{1/2}$. From these, we easily confirm that Equations (31) and (36) reduce in this situation to

$\begin{array}{l}\langle q|{\Phi }_n\rangle =\langle q|{\varphi }_n\rangle +\frac{\delta }{{\omega }_0}\sqrt{\frac{1}{2{\omega }_0{m}_0\hslash }}(\sqrt{n}\langle q|{\varphi }_{n-1}\rangle \\ -\sqrt{n+1}\langle q|{\varphi }_{n+1}\rangle )\\ +\frac{{\delta }^2}{4\hslash m_0{\omega }_0^3}(\sqrt{n+1}\sqrt{n+2}\langle q|{\varphi }_{n+2}\rangle \\ +\sqrt{n}\sqrt{n-1}\langle q|{\varphi }_{n-2}\rangle )+\cdots ,& (40)\end{array}$

$\begin{array}{ll}\langle {\Phi }_n\left|\widehat{{H}}\right|{\Phi }_n\rangle =\hslash {\omega }_0\left(n+\frac{1}{2}\right)-\frac{{\delta }^2}{2m_0{\omega }_0^2}+\cdots ,& (41)\end{array}$

where

$\begin{array}{ll}\langle q|{\varphi }_n\rangle =\sqrt[4]{\frac{m_0{\omega }_0}{\hslash \pi }}\frac{1}{\sqrt{2^{n}n!}}{H}_n(Q)e^{-Q^2/2},& (42)\end{array}$

with $Q=\sqrt{m_0{\omega }_0/\hslash }q$. The results Equations (40) and (41) are well-known in the literature [see, for example [40]]. If we choose c₁≠1 and/or c₂≠1, the quantum solutions for the unperturbed Hamiltonian Ĥ are somewhat different from the standard ones and the result given in Equation (41) becomes different; however, the quantum solutions for Ĥ still satisfy the Schrödinger equation in that case and the corresponding solutions approximated by the perturbation theory for the entire Hamiltonian are also allowed. Although we have chosen a simple reduced Hamiltonian, Equation (39), in order to show that our results become well-known ones for a particular case, the quantum solutions of the system described by this Hamiltonian can also be derived completely without using perturbation theory.

Now let us see another special case where the unperturbed Hamiltonian is given by

$\begin{array}{ll}\widehat{H}=\frac{{\widehat{p}}^2}{2m_0}+\frac{1}{2}{m}_0{\omega }_0^2{t}^4{\widehat{q}}^2.& (43)\end{array}$

This corresponds to the case where the time functions are given by f(t) = h(t) = 1, g(t) = 0, and ${\omega }^2(t)={\omega }_0^2{t}^4.$ Meanwhile, we put the time functions in Equation (30) as

$\begin{array}{ll}{k}_{\text{R},1}(t)=e^{-\alpha t}{k}_{\text{I},3}(t)=c+dcos(\gamma t),& (44)\end{array}$

where c ≥ d. Then the solution of the nonlinear equation given in Equation (6) can be written in the form

$\begin{array}{ll}\rho (t)={\left[{\rho }_1^2(t)+{\rho }_2^2(t)\right]}^{1/2},& (45)\end{array}$

with

$\begin{array}{ll}{\rho }_1(t)={\rho }_{1,0}{t}^{1/2}{J}_{\nu }(\frac{1}{3}{\omega }_0{t}^3),& (46)\end{array}$

$\begin{array}{ll}{\rho }_2(t)={\rho }_{2,0}{t}^{1/2}{N}_{\nu }(\frac{1}{3}{\omega }_0{t}^3),& (47)\end{array}$

provided that $\Omega ={\rho }_1(t){\stackrel{\bullet }{\rho }}_2(t)-{\stackrel{\bullet }{\rho }}_1(t){\rho }_2(t),$ where ρ_{1, 0} and ρ_{2, 0} are real positive constants, J_ν and N_ν are Bessel functions of the first and second kind, respectively, while ν = 1/6.

In Figure 3, we have plotted the EVH for the system described in Equations (43)–(47) considering up to the second order of ϵ. The imaginary part of the EVH does not vary much over time, whereas the real part increases as time goes by. This shows that the imaginary part is small but not zero, while the real part does not significantly deviate from the unperturbed one. We have enlarged the real and the imaginary parts of the expectation value in Figures 3B,C, respectively. It is interesting that both the real and the imaginary parts of the EVH oscillate over time, provided that γ is sufficiently large. The period of such oscillation becomes short as the angular frequency γ increases. In the case of α → ∞, we have k_{R, 1}(t) → 0, while the spectrum of the EVH is real and positive as conjectured by Bessis from numerical studies [see [41] and references therein].

FIGURE 3

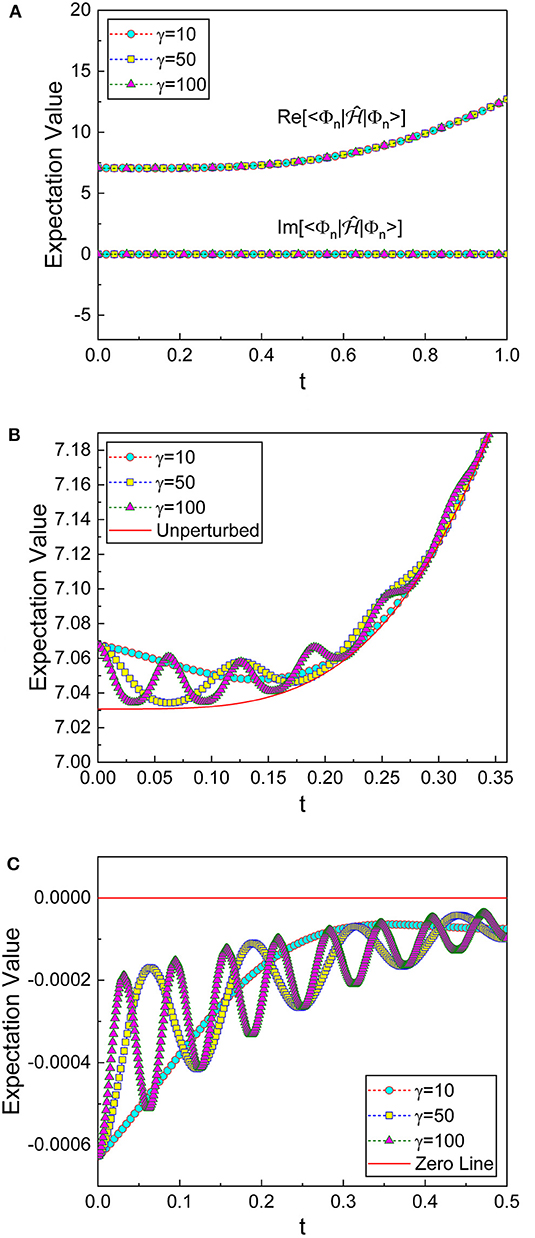
Figure 3. (A) The time evolutions of the real and the imaginary parts of the expectation values, Equation (36), for the system described in Equations (44)–(48) for three different values of γ. The parameters are chosen as ℏ = 1, ω₀ = 1, m₀ = 1, n = 10, ρ_{1, 0} = ρ_{2, 0} = 1, α = 1, c = 1, d = 0.5, and ϵ = 0.001. (B) Enlargement of the real parts in (A). The reference solid red line is the expectation value of the unperturbed Hamiltonian, given in Equation (18). (C) Enlargement of the imaginary parts in (A). The reference solid red line indicates zero of the vertical axis.

4. Conclusion

The properties of the quantum states for perturbed Hamiltonian systems involving complex potentials were investigated. We have considered time-dependence of the imaginary part of the perturbing potentials as well as that of the real part, which are both coupled to a generalized harmonic oscillator through a weak coupling constant. The solutions of the Schrödinger equation of the system in the Fock state have been obtained using the perturbation theory. The effects of the perturbation on time behavior of the system have been analyzed. The perturbation corrections on the wave functions and on the EVH have been analytically investigated. Because we have considered complicated time-dependent Hamiltonian systems as a generalization, the EVH for each particular case is nonconservative. However, when we remove the time dependence of the Hamiltonian, our quantum solutions reduce to stationary states where the corresponding energy spectrum is conservative.

We have applied our theory to particular cases, such as the perturbed systems of which the unperturbed part is described by the Caldirola-Kanai Hamiltonian, and by a potential in which the angular frequency increases in proportion to the square of time. We see that the deviation of the probability densities and the EVH from those of the unperturbed system is, in large, not significant due to the weakness of the coupling. However, the deviation of the probability densities from those of the unperturbed system becomes large with the lapse of time. The imaginary part of the EVH is very small, but not zero, whereas the real part deviates slightly from that of the unperturbed system. In the case where the unperturbed part of the Hamiltonian corresponds to the Caldirola-Kanai oscillator, such deviation increases as the damping factor β grows. We have confirmed that the EVH for the system whose angular frequency is proportional to the square of t oscillate over time due to the time-variation of the chosen perturbing term in the Hamiltonian. The period of such oscillation becomes short as the angular frequency γ that appears in the perturbing term increases.

The development of the perturbation theory represented here may also be possibly applied to diverse different quantum systems which contain time-dependent complex perturbation potentials beyond those studied in the text. Some insights for characterizing complex potential systems are necessary in the light of the fact that a complex potential is receiving due attention in analyzing actual physical states, such as elastic scattering processes [5, 6], gain and loss in waveguides [11], band structures [22], and tunneling in absorptive media [42]. In a unified description of resonance and decay phenomena in open quantum systems, imaginary energy implies decay widths of resonance states, while decay widths are inversely proportional to resonance lifetimes [31, 43]. On the other hand, in a description of quantum and/or classical waves propagating across a complex potential, the imaginary energy plays the role of gain which is the degree of amplification of the transmitted waves [10]. Model-independent investigations of usual and unusual quantum features of complex potential systems may be a very interesting topic for subsequent research as a further generalization of conventional quantum mechanics. In addition, PT based study for a perturbation theory of time-dependent Hamiltonian systems may also be a good research topic as a next task.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This research was supported by the Basic Science Research Programs through the National Research Foundation of Korea (NRF) grants funded by the Korea government (Ministry of Education) (No. NRF-2016R1D1A1A09919503) and funded by the Korea government(MSIT) (No. NRF-2020R1F1A1075322).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Mandal A, Hunt KLC. Adiabatic and nonadiabatic contributions to the energy of a system subject to a time-dependent perturbation: complete separation and physical interpretation. J Chem Phys. (2012) 137:164109. doi: 10.1063/1.4750045

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Born M, Fock VA. Beweis des adiabatensatzes. Z Phys A. (1928) 51:165–80. doi: 10.1007/BF01343193

CrossRef Full Text | Google Scholar

3. Mandal A, Hunt KLC. Quantum transition probabilities during a perturbing pulse: Differences between the nonadiabatic results and Fermi's golden rule forms. J Chem Phys. (2018) 148:194107. doi: 10.1063/1.5019172

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Langhoff PW, Epstein ST, Karplus M. Aspects of time-dependent perturbation theory. Rev Mod Phys. (1972) 44:602–44. doi: 10.1103/RevModPhys.44.602

CrossRef Full Text | Google Scholar

5. Schiff LI. Quantum Mechanics. 3rd Edn. New York, NY: McGraw-Hill (1968). p. 129–38.

6. Buxton BF, Berry MV. Bloch wave degeneracies in systematic high energy electron diffraction. Philos Trans R Soc Lond A. (1976) 282:485–525. doi: 10.1098/rsta.1976.0062

CrossRef Full Text | Google Scholar

7. Zhang C, Bai R, Gu X, Jin XR, Zhang YQ, Lee YP. Dual-band unidirectional reflectionless phenomena in an ultracompact non-Hermitian plasmonic waveguide system based on near-field coupling. Opt Exp. (2017) 25:24281. doi: 10.1364/OE.25.024281

CrossRef Full Text | Google Scholar

8. Konotop VV, Zezyulin DA. Families of stationary modes in complex potentials. Opt Lett. (2014) 39:5535–8. doi: 10.1364/OL.39.005535

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Miri MA, Heinrich M, Christodoulides DN. Supersymmetry-generated complex optical potentials with real spectra. Phys Rev A. (2013) 87:043819. doi: 10.1103/PhysRevA.87.043819

CrossRef Full Text | Google Scholar

10. Ma X, Soukoulis CM. Schrödinger equation with imaginary potential. Phys B. (2001) 296:107–11. doi: 10.1016/S0921-4526(00)00786-9

CrossRef Full Text | Google Scholar

11. Tsoy EN, Allayarov IM, Abdullaev FKh. Stable localized modes in asymmetric waveguides with gain and loss. Opt Lett. (2014) 39:4215–8. doi: 10.1364/OL.39.004215

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Hang C, Huang G. Parity-time symmetry with coherent atomic gases. Adv Phys X. (2017) 2:737–83. doi: 10.1080/23746149.2017.1352457

CrossRef Full Text | Google Scholar

13. Peng X, Zhou H, Wei BB, Cui J, Du J, Liu RB. Experimental observation of Lee-Yang zeros. Phys Rev Lett. (2015) 114:010601. doi: 10.1103/PhysRevLett.114.010601

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Bender CM, Milton KA. Nonperturbative calculation of symmetry breaking in quantum field theory. Phys Rev D. (1997) 55:R3255–9. doi: 10.1103/PhysRevD.55.R3255

CrossRef Full Text | Google Scholar

15. Bender CM, Milton KA. Model of supersymmetric quantum field theory with broken parity symmetry. Phys Rev D. (1998) 57:3595–608. doi: 10.1103/PhysRevD.57.3595

CrossRef Full Text | Google Scholar

16. Bender CM, Milton KA. A nonunitary version of massless quantum electrodynamics possessing a critical point. J Phys A. (1999) 32:L87–92. doi: 10.1088/0305-4470/32/7/001

CrossRef Full Text | Google Scholar

17. Mostafazadeh A. Pseudo-supersymmetric quantum mechanics and isospectral pseudo-Hermitian Hamiltonians. Nucl Phys B. (2002) 640:419–34. doi: 10.1016/S0550-3213(02)00347-4

CrossRef Full Text | Google Scholar

18. Zhu X, He Y. Vector solitons in nonparity-time-symmetric complex potentials. Opt Exp. (2018) 26:26511–9. doi: 10.1364/OE.26.026511

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Hatano N, Nelson DR. Localization transitions in non-Hermitian quantum mechanics. Phys Rev Lett. (1996) 77:570–3. doi: 10.1103/PhysRevLett.77.570

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hatano N, Nelson DR. Vortex pinning and non-Hermitian quantum mechanics. Phys Rev B. (1997) 56:8651–73. doi: 10.1103/PhysRevB.56.8651

CrossRef Full Text | Google Scholar

21. Nelson DR, Shnerb NM. Non-Hermitian localization and population biology. Phys Rev E. (1998) 58:1383–403. doi: 10.1103/PhysRevE.58.1383

CrossRef Full Text | Google Scholar

22. Ahmed Z. Energy band structure due to a complex, periodic, PT -invariant potential. Phys Lett A. (2001) 286:231–5. doi: 10.1016/S0375-9601(01)00426-1

CrossRef Full Text | Google Scholar

23. Wang W, Hou SC, Yi XX. Adiabatic evolution under quantum control. Ann Phys. (2012) 327:1293–303. doi: 10.1016/j.aop.2012.01.001

CrossRef Full Text | Google Scholar

24. Ye MY, Zhou XF, Zhang YS, Guo GC. Two kinds of quantum adiabatic approximation. Phys Lett A. (2007) 368:18–24. doi: 10.1016/j.physleta.2007.03.056

CrossRef Full Text | Google Scholar

25. Wei Z, Ying M. A relation between fidelity and quantum adiabatic evolution. Phys Lett A. (2006) 356:312–5. doi: 10.1016/j.physleta.2006.03.064

CrossRef Full Text | Google Scholar

26. Lewis HR Jr. Classical and Quantum systems with time-dependent harmonic-oscillator-type Hamiltonians. Phys Rev Lett. (1967) 18:510–2. doi: 10.1103/PhysRevLett.18.510

CrossRef Full Text | Google Scholar

27. Lewis HR Jr, Riesenfeld WB. An exact quantum theory of the time-dependent harmonic oscillator and of a charged particle in a time-dependent electromagnetic field. J Math Phys. (1969) 10:1458–73. doi: 10.1063/1.1664991

CrossRef Full Text | Google Scholar

28. Choi JR, Gweon BH. Operator method for a nonconservative harmonic oscillator with and without singular perturbation. Int J Mod Phys B. (2002) 16:4733–42. doi: 10.1142/S0217979202014723

CrossRef Full Text | Google Scholar

29. Landau LD, Lifshitz EM. Quantum Mechanics: Non-relativistic Theory. Vol. 3, 3rd Edn. Translated by J. B. Sykes and J. S. Bell. Oxford: Pergamon Press (1977), p. 133–8.

Google Scholar

30. Fernández FM, Guardiola R, Ros J. Computer algebra and large scale perturbation theory. Comput Phys Commun. (1998) 115:170–82. doi: 10.1016/S0010-4655(98)00135-0

CrossRef Full Text | Google Scholar

31. Tellander F, Berggren KF. Spectra, current flow, and wave-function morphology in a model PT-symmetric quantum dot with external interactions. Phys Rev A. (2017) 95:042115. doi: 10.1103/PhysRevA.95.042115

CrossRef Full Text | Google Scholar

32. Chávez NC, Mattiotti F, Méndez-Bermúdez JA, Borgonovi F, Celardo GL. Real and imaginary energy gaps: a comparison between single excitation superradiance and superconductivity and robustness to disorder. Eur Phys J B. (2019) 92:1–12. doi: 10.1140/epjb/e2019-100016-3

CrossRef Full Text | Google Scholar

33. Fox R. Possible existence of particles of imaginary mass, energy and momentum. Nat Phys Sci. (1971) 232:129–30. doi: 10.1038/physci232129a0

CrossRef Full Text | Google Scholar

34. Zhu J, Cukier RI. An imaginary energy method-based formulation of a quantum rate theory. J Chem Phys. (1995) 102:4123–30. doi: 10.1063/1.468540

CrossRef Full Text | Google Scholar

35. Weisz JF. Perturbation theory of a dissipative quantum subsystem. Rep Math Phys. (2006) 58:15–20. doi: 10.1016/S0034-4877(06)80037-6

CrossRef Full Text | Google Scholar

36. Miller W. Quantum mechanical transition state theory and a new semiclassical model for reaction rate constants. J Chem Phys. (1974) 61:1823–34. doi: 10.1063/1.1682181

CrossRef Full Text | Google Scholar

37. Miller W. Semiclassical limit of quantum mechanical transition state theory for nonseparable systems. J Chem Phys. (1975) 62:1899–906. doi: 10.1063/1.430676

CrossRef Full Text | Google Scholar

38. Caldirola P. Porze non conservative nella meccanica quantistica. Nuovo Cim. (1941) 18:393–400. doi: 10.1007/BF02960144

CrossRef Full Text | Google Scholar

39. Kanai E. On the quantization of dissipative systems. Progr Theor Phys. (1948) 3:440–2. doi: 10.1143/ptp/3.4.440

CrossRef Full Text | Google Scholar

40. Cohen-Tannoudji C, Diu B, Laloë F. Quantum Mechanics. Paris: Hermann (1977). p. 1110–2.

41. Bender CM, Boettcher S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys Rev Lett. (1998) 80:5243–6. doi: 10.1103/PhysRevLett.80.5243

CrossRef Full Text | Google Scholar

42. Lj S, Kočinac S, Milanović V. Tunneling times in complex potentials. Phys Lett A. (2008) 372:191–6. doi: 10.1016/j.physleta.2007.07.021

CrossRef Full Text | Google Scholar

43. Rotter I. A non-Hermitian Hamilton operator and the physics of open quantum systems. J Phys A Math Theor. (2009) 42:153001. doi: 10.1088/1751-8113/42/15/153001

CrossRef Full Text | Google Scholar

44. Malkin IA, Man'ko VI, Trifonov DA. Coherent states and transition probabilities in a time-dependent electromagnetic field. Phys Rev D. (1970) 2:1371–84. doi: 10.1103/PhysRevD.2.1371

CrossRef Full Text | Google Scholar

45. de Lima AL, Rosas A, Pedrosa IA. Quantum dynamics of a particle trapped by oscillating fields. J Mod Opt. (2009) 56:75–80. doi: 10.1080/09500340802495834

CrossRef Full Text | Google Scholar

Appendix A: Solutions of Equation (12)

The eigenstates of the invariant operator for the system are obtained by directly solving Equation (12) or by using the properties of Equations (15) and (16) [28, 44, 45]. In our case, the results are given by

$\begin{array}{l}{\varphi }_n(q,t)={\left(\frac{m_0\Omega }{f(t){\rho }^2(t)\hslash \pi }\right)}^{1/4}{(2^{n}n!)}^{-1/2}{H}_n\left[{\left(\frac{m_0\Omega }{f(t){\rho }^2(t)\hslash }\right)}^{1/2}q\right]\\ \times exp\left[-\frac{m_0}{2f(t)\rho (t)\hslash }\left(\frac{\Omega }{\rho (t)}+iG(t)\right)q^2\right],& (\mathrm{A1})\end{array}$

$\begin{array}{ll}{\lambda }_n=\hslash \Omega \left(n+\frac{1}{2}\right).& (\mathrm{A2})\end{array}$

Appendix B: The Formula of ${\tilde{\Pi }}_2$ in Equation (30)

${\tilde{\Pi }}_2$ is obtained by evaluating the summation ${\tilde{\Pi }}_2=\sum _{n^{\prime },(n^{\prime }\ne n)}{\Pi }_2\langle q|{\varphi }_{n^{\prime }}\rangle .$ Since Π₂ given in Equation (22) is composed of two terms, let us express ${\tilde{\Pi }}_2$ in the form

$\begin{array}{ll}{\tilde{\Pi }}_2={\tilde{\Pi }}_2^{(1)}+{\tilde{\Pi }}_2^{(2)},& (\mathrm{B1})\end{array}$

where

$\begin{array}{ll}{\tilde{\Pi }}_2^{(1)}={\displaystyle \sum _{n^{\prime },(n^{\prime }\ne n)}}{\Pi }_2^{(1)}\langle q|{\varphi }_{n^{\prime }}\rangle ,& (\mathrm{B2})\end{array}$

$\begin{array}{ll}{\tilde{\Pi }}_2^{(2)}={\displaystyle \sum _{n^{\prime },(n^{\prime }\ne n)}}{\Pi }_2^{(2)}\langle q|{\varphi }_{n^{\prime }}\rangle .& (\mathrm{B3})\end{array}$

The second term ${\tilde{\Pi }}_2^{(2)}$ is zero because the expectation values 〈ϕ_n|Ĥ_p|ϕ_n〉 which are involved in it are zero. On the other hand, a rigorous evaluation of the first term using Equation (23) gives

$\begin{array}{l}{\tilde{\Pi }}_2^{(1)}=\frac{A^2(t)}{{\hslash }^2{W}^2(t)}\{\frac{i}{3}{A}^2(t)k_{\text{I},3}\sqrt{(n+1)(n+2)(n+3)}\\ \times (\frac{i}{6}{A}^2(t)k_{\text{I},3}\sqrt{(n+4)(n+5)(n+6)}\langle q|{\varphi }_{n+6}\rangle \\ +\frac{1}{4}[k_{\text{R},1}\sqrt{n+4}+3i{A}^2(t)k_{\text{I},3}{(n+4)}^{3/2}]\langle q|{\varphi }_{n+4}\rangle \\ +\frac{1}{2}[k_{\text{R},1}\sqrt{n+3}+3i{A}^2(t)k_{\text{I},3}{(n+3)}^{3/2}]\langle q|{\varphi }_{n+2}\rangle )\\ +\frac{i}{3}{A}^2(t)k_{\text{I},3}\sqrt{n(n-1)(n-2)}\\ \times (\frac{i}{6}{A}^2(t)k_{\text{I},3}\sqrt{(n-3)(n-4)(n-5)}\langle q|{\varphi }_{n-6}\rangle \\ +\frac{1}{2}[k_{\text{R},1}\sqrt{n-2}+3i{A}^2(t)k_{\text{I},3}{(n-2)}^{3/2}]\langle q|{\varphi }_{n-2}\rangle \\ +\frac{1}{4}[k_{\text{R},1}\sqrt{n-3}+3i{A}^2(t)k_{\text{I},3}{(n-3)}^{3/2}]\langle q|{\varphi }_{n-4}\rangle )\\ +[k_{\text{R},1}\sqrt{n+1}+3i{A}^2(t)k_{\text{I},3}{(n+1)}^{3/2}]\\ \times (\frac{i}{4}{A}^2(t)k_{\text{I},3}\sqrt{(n+2)(n+3)(n+4)}\langle q|{\varphi }_{n+4}\rangle \\ -\frac{i}{2}{A}^2(t)k_{\text{I},3}\sqrt{(n+1)n(n-1)}\langle q|{\varphi }_{n-2}\rangle \\ +\frac{1}{2}[k_{\text{R},1}\sqrt{n+2}+3i{A}^2(t)k_{\text{I},3}{(n+2)}^{3/2}]\langle q|{\varphi }_{n+2}\rangle )\\ +[k_{\text{R},1}\sqrt{n}+3i{A}^2(t)k_{\text{I},3}{n}^{3/2}]\\ \times (-\frac{i}{2}{A}^2(t)k_{\text{I},3}\sqrt{n(n+1)(n+2)}\langle q|{\varphi }_{n+2}\rangle \\ +\frac{i}{4}{A}^2(t)k_{\text{I},3}\sqrt{(n-1)(n-2)(n-3)}\langle q|{\varphi }_{n-4}\rangle \\ +\frac{1}{2}[k_{\text{R},1}\sqrt{n-1}+3i{A}^2(t)k_{\text{I},3}{(n-1)}^{3/2}]\langle q|{\varphi }_{n-2}\rangle )\}.& (\mathrm{B4})\end{array}$