Effective Transfer Entropy Approach to Information Flow Among EPU, Investor Sentiment and Stock Market

In contrast to the traditional view that economic policy affects investor sentiment and eventually causes stock price fluctuations, we reveal that investor sentiment is a reflection of both economic policy and stock market information. This article first proposes an improved ETE method with a sliding window. We verify that this new method can capture the dynamic orders effectively by validating this method with the linear TE method. Furthermore, using the improved method, we investigate the strength and direction of information flow among economic policy uncertainty (EPU), investor sentiment and stock market by the novel concept of dynamic effective transfer entropy. The EPU and investor sentiment results show that EPU influenced investor sentiment mainly from August 2015 to June 2016. Among different policies, China's exchange rate reform policy and “circuit-breaker” policy in the stock market played an important role. Moreover, the analysis of sentiment and stock price returns shows that investor sentiment is more a reflection of changes in stock price returns with a 1-month lag order and that the stock market has a significant bargainer effect and a weaker bandwagon effect. Finally, there is no significant information flow transmission relationship between EPU and stock market volatility, indicating that stock market fluctuations are essentially not affected by national policy fluctuations. Although investor sentiment is affected by changes, such as exchange rate reform and stock market policies, many investors do not form consensus expectations.

Introduction

Transfer entropy arises from the formulation of conditional mutual information. When conditioning on past values of variables, it quantifies the reduction in uncertainty provided by these past values in predicting the dependent variable, which presents a natural way to model statistical causality between variables in multivariate distributions. In the general formulation, transfer entropy is a model-free statistic that is able to measure the time-directed transfer of information between stochastic variables and therefore provides an asymmetric method to measure information transfer.

The information transfer method has been widely used in the finance field. Kwon & Yang [1] employed it to measure the relationship between equities indices, showing that the information transfer was greatest from the US and toward the Asia Pacific region. In particular, the S&P 500 was shown to be the strongest driver of other stock indices. In earlier and somewhat related work, Marschinski and Kantz [2] defined and used effective transfer entropy to quantify contagion in financial markets. Kyrtsou et al. [3] proposed a Granger causality method based on partial transfer entropy to explore the complex relationships among the S&P 500, VIX and volume. Dimpfl and Peter [4] proposed an appropriate bootstrap to derive confidence bounds and showed in a simulation study that standard linear approaches in economics and finance, such as vector autoregressions and Granger causality tests, are not well-suited to detect information transfer. Garcia-Medina et al. [5] used random matrix theory and information theory to analyze the correlations and flow of information between 64,939 news items from The New York Times and 40 world financial indices over 10 months during the 2015–2016 period. Their results suggested a deep relationship between news and world indices and showed that the news drives world market movement. Sensoy et al. [6] explored the strength of information flow between exchange rates and stock prices by the effective transfer entropy with symbolic encoding methodology. Yang et al. [7] proposed an effective phase transfer entropy method based on the transfer entropy method. These scholars also analyzed the relationship among 9 stock indices from the U.S., Europe and China by using transfer entropy, effective transfer entropy, Rényi transfer entropy, and effective Rényi transfer entropy [8].

The vast influential literature focuses on the correlation between EPU and its impact of investment [9–21]. Many new studies investigated the fluctuation characteristics of China's uncertainty index and its impact on the economy [22–24].

Additionally, many other studies focused on the impact of investor sentiment on stock prices. A study investigating the correlation between investor sentiment and the equity market was conducted following De long's research [25]. Baker and Wurgler [26] investigated investor sentiment using a principal component method. Subsequently, a large number of studies emerged, suggesting that investor sentiment has a significant impact on stock returns [27–40]. In addition, some studies reveal a complex correlation between online investor sentiment and stock market volatility [35, 36, 41, 42].

Although there are many studies on the correlation between EPU and financial or economic indices, there are few studies on the influence of EPU on investor sentiment. There is also a lack of research on the transmission pathways of the EPU, investor sentiment and stock market.

It is widely considered that national economic policies will pass relevant information to influence investor sentiment, affect investment decisions, and ultimately cause stock price fluctuations. However, the real situation may be more complicated especially in China. Motivated by previous studies, we follow the theorizing on information flow to reveal the transmission path of information among these three variables and to provide more references for macro policy makers.

The rest of this paper is organized as follows. In section Data Description, we describe the time series data used in the models. In section Methodology, we introduce the effective transfer entropy (ETE) method. In section An Improved Effective Transfer Entropy Method Based on a Sliding Window, we propose an improved ETE method based on sliding windows. In section Empirical Results, we present the empirical results of EPU, trade and the exchange rate obtained using the improved ETE model. Finally, we provide the conclusion of this paper.

Data Description

The economic uncertainty index used in this article is an index compiled by Paul Luk's research team [43] from Hong Kong Baptist University. These authors construct the index using words from 10 Hong Kong newspapers, including Wen Wei Po, Sing Pao, etc. For each newspaper, the research group counts articles containing Chinese words related to economics, uncertainty and policy to formulate the economic policy uncertainty index. The latest data of the index and related papers can be downloaded from the web: https://economicpolicyuncertaintyinchina.weebly.com/.

The investment sentiment index is constructed with the principal component method based on four underlying proxie, i.e., the relative strength index, the psychological line index, the trading volume and the adjusted turnover rate [40]. The Shanghai Composite Index mostly reflects the performance of the Chinese stock market. The data of this index are from the China Stock Market & Accounting Research Database. The data period for all three time series is from February 2005 to May 2019 (Figure 1).

FIGURE 1

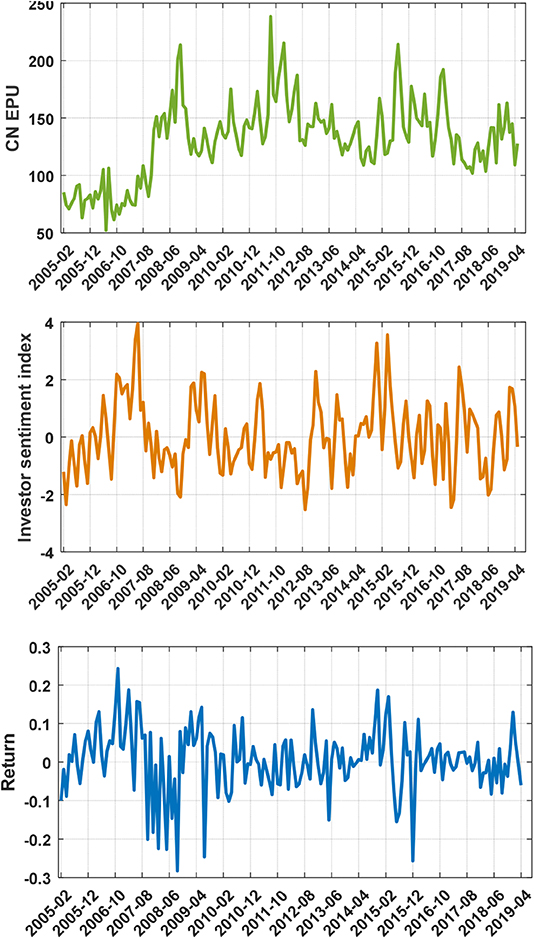
Figure 1. Time series of the CN EPU index, Investor sentiment and Return of the Shanghai Composite Index's closing price.

Methodology

We calculate the statistical causality between time series using two different approaches. The first assumes linearity and employs vector autoregressive techniques to estimate the extent to which knowing the driving time series can help predict the dependent series. The second technique compares the difference in mutual information between the independent case and the joint case to describe the success of predicting the dependent series. When predictability is increased by considering the past values of the driving variable, statistical causality is observed.

Linear Causality

We model a time series as autoregressive by expressing its value Y_t at time t as a sum of the contributions over m distinct lagged series using the following linear equation:

$\begin{array}{ll}{Y}_t={\displaystyle \sum _{k=1}^m}{\beta }_k^{(Y)}{Y}_{t-k}+{\epsilon }_t& (1)\end{array}$

Where ${\beta }_k^{(Y)}$ is a general coefficient term and ε_t is the residual. Linear regression estimates coefficient parameters ${\beta }_k^{(Y)}$, which minimize the sum of squared residuals.

To detect whether the values of some second time series X anticipate the future values of Y, we can compare Equation (1) with

$\begin{array}{ll}{Y}_t={\displaystyle \sum _{k=1}^m}{\beta }_k^{\prime (Y)}{Y}_{t-k}+{\displaystyle \sum _{k=1}^m}{\beta }_k^{\prime (X)}{X}_{t-k}+{\epsilon }_t^{\prime }& (2)\end{array}$

We determine that distribution Y is Granger caused by X if the residual in the second regression is significantly smaller than the residual in the first regression. When this distribution holds, then there must be some information transfer from X to Y. Following Geweke [44], we can represent the information transfer by

$\begin{array}{ll}T{E}_{X\to Y}=\frac{1}{2}log\left(\frac{var({\epsilon }_t)}{var({\epsilon }_t^{\prime })}\right)& (3)\end{array}$

where we adopt the transfer entropy notation (TE) following Barnett et al. [45], whose result shows Granger causality to be equivalent to transfer entropy for multivariate normal distributions.

Non-linear Causality

To detect non-linear causality, we apply an information-theoretic approach. Equation (3) measures the extent to which the additional information in the lagged variable reduces the variance in the model residuals. Transfer entropy extends this concept by considering the uncertainty instead of the variance. Adopting Shannon's measure of information [46], we can express the uncertainty associated with random variable X by

$\begin{array}{ll}H(X)=-{\displaystyle \sum _x}p(x).logp(x)& (4)\end{array}$

where H(x) is the Shannon entropy of the distribution, and p(x) represents the probability of X = x, which can be conditioned on a second variable to give the conditional entropy:

$\begin{array}{ll}H(Y|X)=H(X,Y)-H(X)& (5)\end{array}$

When two random variables share information, the mutual information is given by

$\begin{array}{ll}I(X;Y)=H(Y)-H(Y|X)=H(X)-H(X|Y)& (6)\end{array}$

The entropy of Y conditioned on two variables is

$\begin{array}{ll}H(Y|X,Z)=H(X,Y,Z)-H(X,Z)& (7)\end{array}$

and the conditional mutual information is therefore

$\begin{array}{ll}I(X;Y|Z)=H(Y|Z)-H(Y|X,Z)& (8)\end{array}$

Now, for each lag k, we can describe the information transfer from X_t−k to Y_t in terms of the following conditional mutual information:

$\begin{array}{l}T{E}_{X\to Y}^{(k)}=I\left(Y_t;X_{t-k}|Y_{t-k}\right)=H\left(Y_t|Y_{t-k}\right)\\ -H\left(Y_t|X_{t-k},Y_{t-k}\right)& (9)\end{array}$

This equation represents the resolution of uncertainty in predicting Y when considering the past values of both Y and X compared with considering the past values of Y alone.

Considering Equations (5) and (7), we can therefore represent the transfer entropy for a single lag k, which is shown in Equation (9), in terms of four separate joint entropy terms. Following equation (4), these terms may be estimated from the data using a non-parametric density estimation of the probability distributions. For multivariate normal statistics, Equations (9) and (3) coincide [45].

Effective Transfer Entropy (ETE)

It is a feature of the non-parametric estimation of entropy that the absolute scale of the transfer entropy measure has only limited meaning; to detect causality, a relative position must be considered. A simple technique proposed by Marschinski and Kantz [2] is the ETE, derived by subtracting from the observed transfer entropy an average transfer entropy figure calculated over independently shuffled time series, which destroys the temporal order and hence any possible causality. We adopt a shuffling approach producing 50 null-hypothesis transfer entropy values from independently shuffled time series over the same domain containing no causality. By calculating the mean and standard deviation of the shuffled transfer entropy figures, we estimate the significance of a causal result as the distance between the result and the average shuffled result standardized by the shuffled standard deviation:

$\begin{array}{l}ETE=TE-{\overline{TE}}_{shuffle}\\ Z:=\frac{TE-{\overline{TE}}_{shuffle}}{{\sigma }_{shuffle}}& (10)\end{array}$

where ${\overline{TE}}_{shuffle}$ is the mean of the shuffled values, and σ_shuffle is the standard deviation. The shuffling of the time series destroys temporality and should ensure that the mean is approximately zero; therefore, the spread of the data dictates the significance of the result. Assuming that the distribution is close to Gaussian, we can say that a result with Z > 3 is roughly in the top 1% of results and hence is comparable to a p-value of 0.01. The nature of the method typically enables clearer significance to be observed with fewer shuffles, even without a strict Gaussian distribution; thus, this method is computationally more attractive than the p-value.

This expression corresponds to the degree to which the result lies in the right tail of the distribution of the zero-causality shuffled samples and hence how unlikely the result is due to chance. Therefore, the Z-score figure represents the significance of the excess transfer entropy in the unshuffled case. We compute the Z-score in Equation (10) for both linear and non-linear results.

An Improved Effective Transfer Entropy Method Based on a Sliding Window

Improved Method Based on a Sliding Window and Comparison With a Traditional Linear Method

Keskin and Aste [47] validated that the non-linear TE method would be useful for detecting a non-linear process. However, the lag order they found was global and unique and thus was unsuitable for capturing the accurate order between two non-stationary series. For non-stationary time series, the data structure changes over time, which means that the causal relationships also evolve dynamically. In addition, due to policy or unexpected events, the causal structure of real financial sequences tends to change over time. Therefore, it would be inaccurate to use a single k to measure global causality.

Considering that the locality of non-stationary data may be stationary or approximately stationary, this paper proposes an improved transfer entropy method based on a sliding window to solve the influence of a non-stationary data structure on traditional transfer entropy. The improved method calculates the transfer entropy as described in section Non-linear Causality but is limited to a certain time segment. Through forward scrolling, the transfer entropy at each time point is obtained, and the causal relationship between the two times series can be revealed. In addition to its ability to capture the structural changes between two time series, the improved method can help us trace the specific time period of the structural change, which cannot be achieved using the traditional linear TE method. We next verify the validity of the algorithm.

First, we generate a time series X following the geometric Brownian motion according to Equation (11) as follows:

$\begin{array}{ll}{X}_{t+1}=(1+\mu )X_t+\sigma X_t{\eta }_t& (11)\end{array}$

where η_t is a noise obeying the standard normal distribution, η_t ~ N(0, 1), and μ and σ represent the drift coefficient and the diffusion coefficient, respectively. Y depends on X, and the equation is constructed as follows (Equation 12):

$\begin{array}{ll}{Y}_t=(1-\alpha )X_{t-k}+\alpha X_{t-k}^{\prime }& (12)\end{array}$

where $X_{t-k}^{\prime }$ is another time series generated according to Equation (11). k is the given lag order, and α ∈ (0, 1) determines the dependence strength between the series Y and X, i.e., the values of the transfer entropy.

Assuming k = 2, α = 0.5;k = 4, α = 0.5; and k = 5, α = 0.5, we can obtain three time series with a length of 200, i.e., $X_t,Y_t^{k=2};X_t,Y_t^{k=4}$ and $X_t,Y_t^{k=5}$ according to Equations (11) and (12).

As shown in Figure 2, for a correlation series with a single lag structure, both the traditional transfer entropy, i.e., the linear TE, and the improved TE method can capture the lag order accurately. However, according to the Z-score significance test, we can observe that when the temporal order is destroyed, the linear TE does not show significance in the relevant order; thus, the linear TE method depends on time evolution. As shown in Figure 3, the linear TE could only identify the order k = 4, which is the highest corresponding transfer entropy value (Z-score indicates that the value is above a significant level). However, the improved TE could detect both k = 4 and k = 5. Moreover, as shown in Figure 4, we can also track the specific time period during which the lead-lag order fluctuates with the improved method.

FIGURE 2

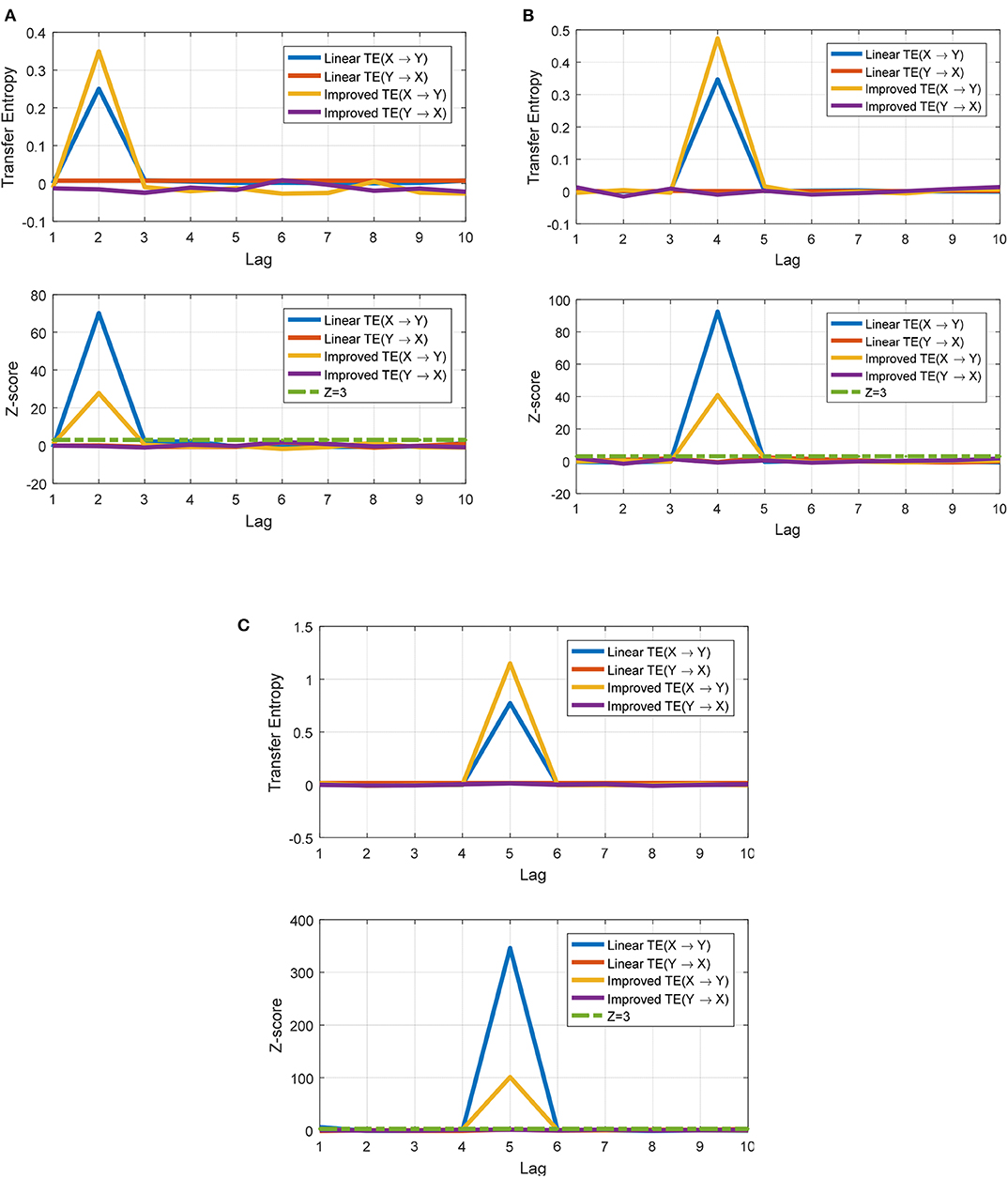
Figure 2. Demonstration that both methods identify the true lag values with maximal transfer entropy. Non-linear transfer entropy is calculated using a quantile-binned histogram, of 6 classes per dimension over 2,500 points. The Z-score for each result is also plotted for both methods. According to the z > 3 principle, it can be concluded that for two time series with a single lag order, the two methods can both identify the lag orders accurately. (A) k = 2, α = 0.5. (B) k = 4, α = 0.5. (C) k = 5, α = 0.5.

FIGURE 3

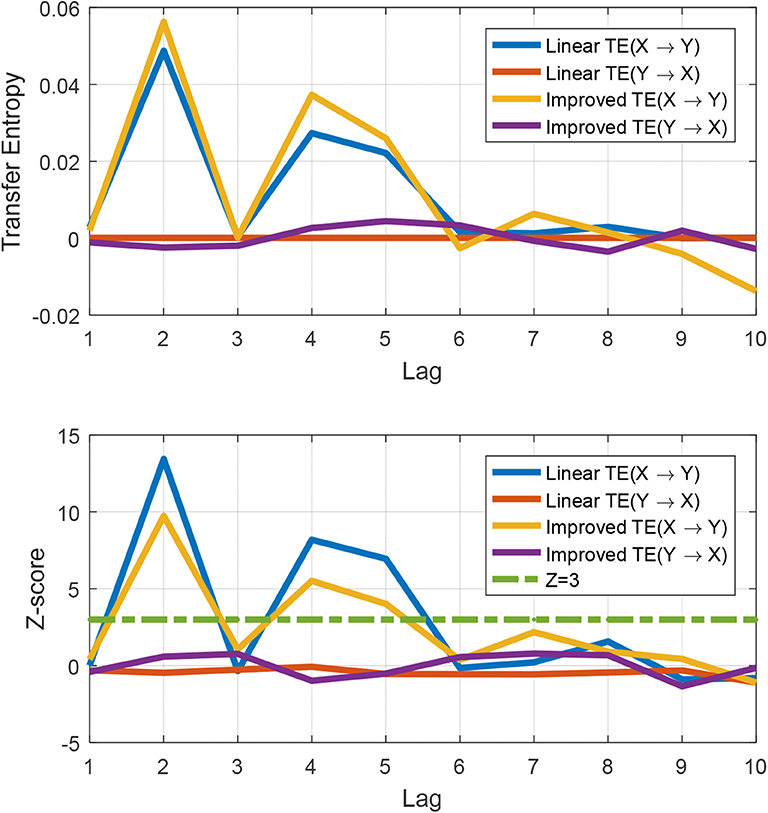
Figure 3. Demonstration that both methods identify the true lag values with maximal transfer entropy. The linear TE could only capture k = 2, corresponding to the highest transfer entropy value (Z-score indicates that the value is above a significant level), while the improved TE method could detect k = 2, 4, and 5.

FIGURE 4

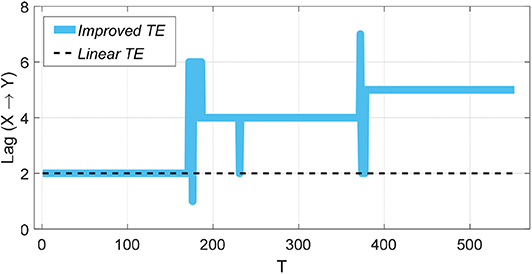
Figure 4. Order identification by the two transfer entropy methods. The dashed line k = 2 corresponds to the lag order when the transfer entropy value is the largest in the linear TE method in Figure 3.

We reshape $X_t,Y_t^{k=2};X_t,Y_t^{k=4}$ and $X_t,Y_t^{k=5}$ into two new time series $X_t^{\prime },Y_t^{\prime }$, where $X_t^{\prime }=\left[X_t,X_t,X_t\right]$ and $Y_t^{\prime }=\left[Y_t^{k=2},Y_t^{k=4},Y_t^{k=5}\right]$. These new series show obvious structure fluctuations, and the features are more consistent with the characteristics of real financial data.

Due to the shortcomings of traditional linear methods in revealing dynamic orders, in the empirical analysis in section Empirical Results, we apply the improved transfer entropy to explore the information flow between all sequences. The sliding window length of all structures is 36 months with a forward step size of 1 month.

Comparison With the Granger Causality Test

The Granger causality test is essentially a test used to determine whether a lagging variable can be introduced into an equation containing other variables. If a variable is affected by the lag of other variables, the variables are considered to have Granger causality. For the sequences X and Y, using different lag orders, we obtain the causality test results of the two sequences (Table 1).

TABLE 1

Table 1. Granger causality test results.

Granger causality is a regression-based interpretation of Wiener's causality definition [48]. In this section, the Granger causality test is employed as a comparison with the improved TE to detect the true lag orders. Following Granger's work [49], we model the Granger causality test with the following two regression equations:

$\begin{array}{ll}{X}_t={\displaystyle \sum _{i=1}^p}{\alpha }_i{X}_{t-i}+u_i& (13)\end{array}$

$\begin{array}{ll}{X}_t={\displaystyle \sum _{i=1}^p}{b}_i{X}_{t-i}+{\displaystyle \sum _{i=1}^p}{c}_i{Y}_{t-i}+v_t& (14)\end{array}$

where X denotes the object needed to find the Granger cause, Y denotes the object needed to determine whether it can Granger cause X, and residuals u_t and v_t are assumed to be mutually independent and individually distributed with a zero mean and constant variance. These equations were tested using the following hypothesis:

H₀ : Y does not Granger cause X(c₁ = c₂ = … = c_p = 0).

The F − test can be expressed as follows:

$\begin{array}{ll}F=\frac{(RS{S}_0-RS{S}_1)/p}{RS{S}_1/(n-2p-1)}~F(p,n-2p-1)& (15)\end{array}$

where RSS₀ is the residual sum of squares of Equation (13), RSS₁ is the residual sum of squares of Equation (14), n is the number of observations, and p is a lag value. We reject the hypothesis H₀ and accept that Y is a Granger cause of X if and only if F > F(p, n − 2p − 1). The model order p can be determined by minimizing the AIC [50], which is defined as follows:

$\begin{array}{ll}AIC(p)=2log(|\sigma |)+\frac{2m^{2}p}{\widehat{n}}& (16)\end{array}$

where σ is the estimated noise covariance, m is the dimension of the stochastic process and $\widehat{n}$ is the length of the data window used to estimate the model. For example, to detect the causal relationship from exports to US EPU, Y should be set to the exports sequence, while X should be set to the US EPU sequence. In contrast, Y should be set to the US EPU before detecting the causal relationship between US EPU and the exports.

The Granger causality test based on the sliding window method can also obtain the order and significance of two series' correlation. Using Y and X as an example, we elaborate upon the processes of the Granger model estimation within a fixed window as follows:

(a) The maximum of the lag value p is set to a fixed number, such as 10.

(b) By calculating the total AIC of Equations (13) and (14) by traversing the p value from 1 to 10, we obtain the corresponding p of the minimum AIC. The experimental results show that the optimal p is 5.

(c) Equations (13) and (14) are estimated by OLS with p = 5.

(d) F and F(p, n − 2p − 1) are calculated according to Equation (15). The results show that F = 4.0635 and F(p, n − 2p − 1) = 3.8549 (at the 99% confidence level).

(e) If F > F(p,n–2p − 1), we conclude that Y can significantly Granger cause X.

(f) The window is moved forward by a 1-month step, and steps (a–e) are repeated.

Using the process described above, we obtained the Granger causality test results based on a window length W = 36 (Figure 5A). As shown in Figure 5A, although the Granger causality test can identify k = 2, it cannot effectively capture the two orders of 4 and 5. Using k = 4 cannot pass the significance test; although using k = 5 can pass the significance test, there may be other orders, such as k = 8. The improved TE method can accurately identify three different orders (Figure 5B). In addition, the stage during which the order jumps cannot pass the significance test.

FIGURE 5

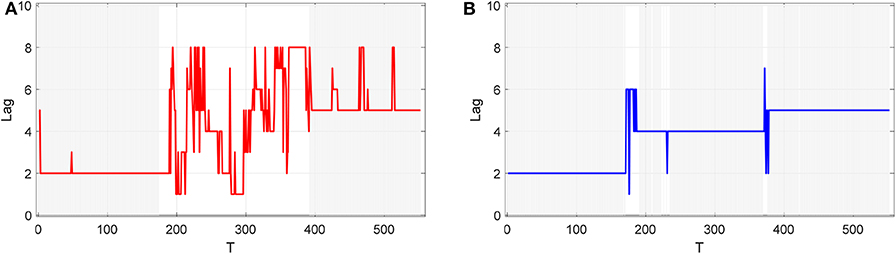
Figure 5. Comparison of the Granger causality method based on a sliding window and the improved TE method. The widow length in both methods is W = 36, and the significant level is 1%. The Granger method can clearly identify k = 2 but cannot identify k = 4, and there is considerable noise interference when identifying k = 5. The improved TE method can clearly identify the three orders 2, 4, and 5. (A) Granger causality test based on the sliding window method. The gray part indicates that the p-value of the F statistic is <1%, indicating that the causal relationship is significant in this area. (B) The result based on the improved TE method. The gray part indicates that the Z-score is higher than 3, which is equivalent to a significance level of p_val < 0.01 [section Effective Transfer Entropy (ETE)].

Empirical Results

Since traditional linear methods cannot identify dynamic orders between time series or track specific lead-lag orders when structural fluctuations occur, we apply the improved transfer entropy to explore the information flow among EPU, investor sentiment and the stock market.

EPU and Investor Sentiment

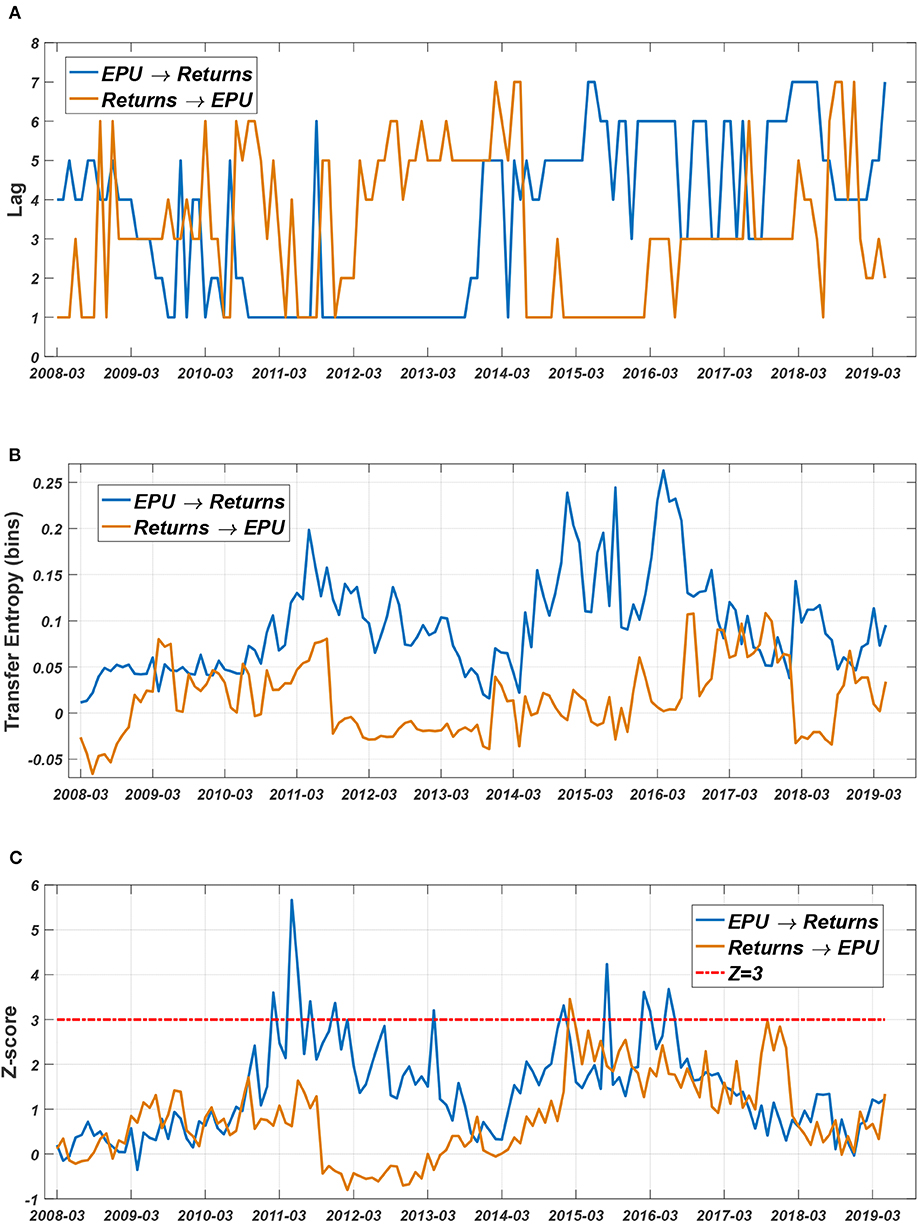
Based on the dynamic TE method, we analyze the causal relationship between EPU and investor sentiment. As shown in Figure 6A, there is an obvious dynamic order in the correlation between EPU and investor sentiment.

FIGURE 6

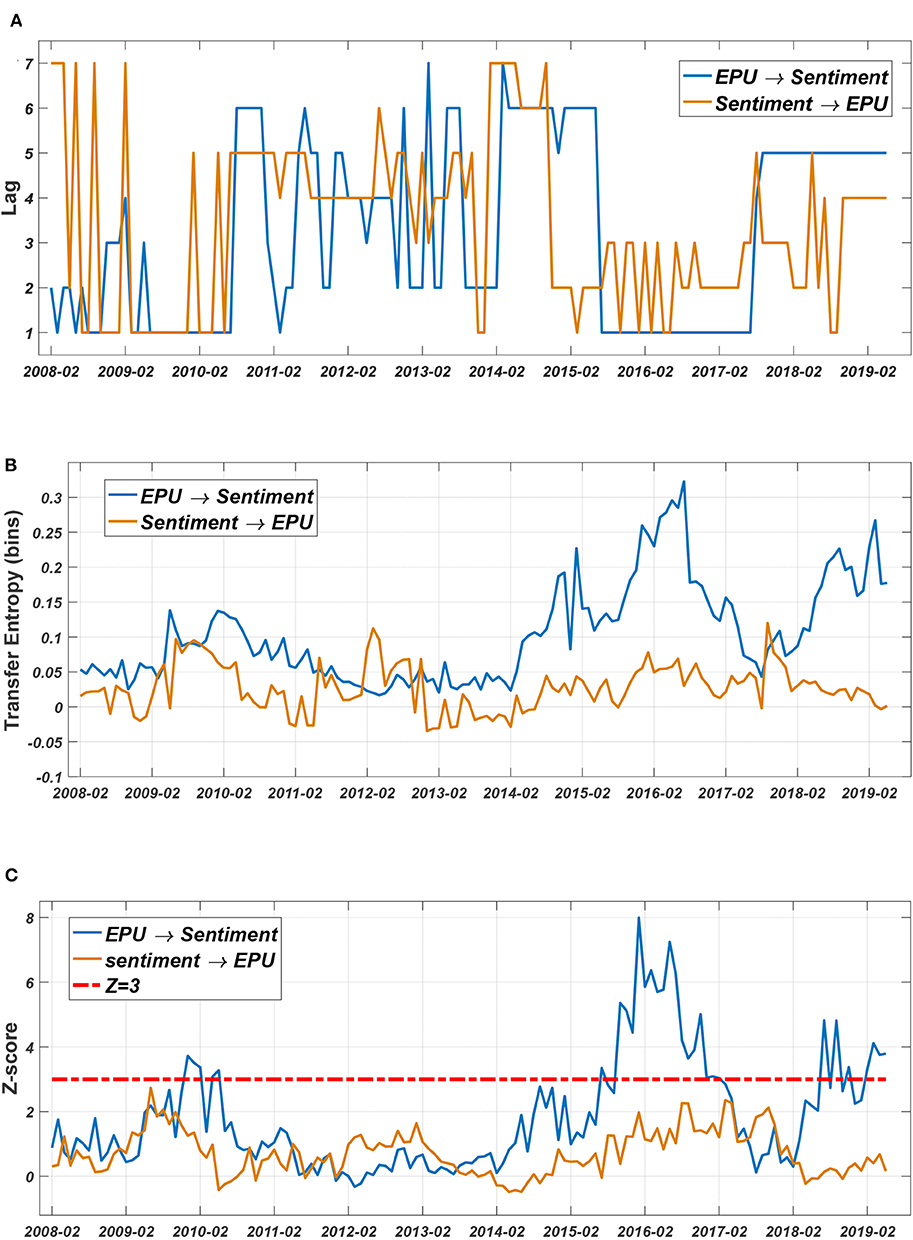
Figure 6. Dynamic Entropy results between EPU and investor sentiment. (A) Lag structure. (B) TE fluctuation. (C) Z-score.

As shown in Figure 6C, a Z-score > 3 is mainly located in August 2015–June 2016. This means that during this time period, EPU had a significant impact on investor sentiment, and uncertain information about national economic policies significantly affected investor sentiment. From Figure 6B, it can also be seen that in this stage, the EPU's transfer entropy to investor sentiment was significantly higher than the impact of investor sentiment on EPU.

The impact on investor sentiment is related to the nature of the policy, i.e., whether the policy is a domestic policy or a foreign policy. During this period, China's economic policy involved the following two important measures: a change in the CNY fixing mechanism and the launch of the “circuit-breaker” mechanism.

On August 11, 2015, the central bank made more reference to the closing price of the previous day in the daily CNY-USD mid-price quotation formation mechanism. This change makes the method of forming the middle price more market-oriented, which more closely reflects the actual supply-demand relationship of the market compared to the previous method.

The circuit-breaker benchmark index is the CSI 300 Index, which uses two thresholds of 5 and 7%. When the CSI 300 Index triggers a 5% breaking threshold, the three exchanges suspend trading for 15 min, and if the 5% is triggered late in the day or 7% is triggered at any time throughout the day, trading is suspended until the market closes. From January 4th to January 7th, the breaking mechanism was implemented for only 3 days, and it became the shortest-lived stock market policy in the history of Chinese securities. This policy uncertainty had a great impact on investor sentiment.

Before August 2015, there were incidents such as the bankruptcy of Lehman Brothers (September 2008), the downgrade of the US sovereign credit rating (August 2011), and the European debt crisis (January 2011–January 2014). However, probably because these events did not occur in China, their impact on consumer sentiment was not significant.

Investment Sentiment Index and the Stock Market

The correlation between sentiment and stock price returns is illustrated in Figure 7. As shown in Figure 7C, the impact of sentiment on stock returns is non-significant; in contrast, the fluctuation in stock price returns has a significant impact on investor sentiment throughout the time period. This shows that in the Chinese stock market, using emotions to predict changes in stock prices is useless, and investor sentiment is more a lagging reflection of stock price returns. Figure 7A shows that the lag time is approximately 1 month. Our results further verify the long-term correlation characteristics suggesting that investor sentiment is mainly affected by fluctuation in the market, which may be related to the existence of cyclical fluctuations in the market and futures arbitrage [40].

FIGURE 7

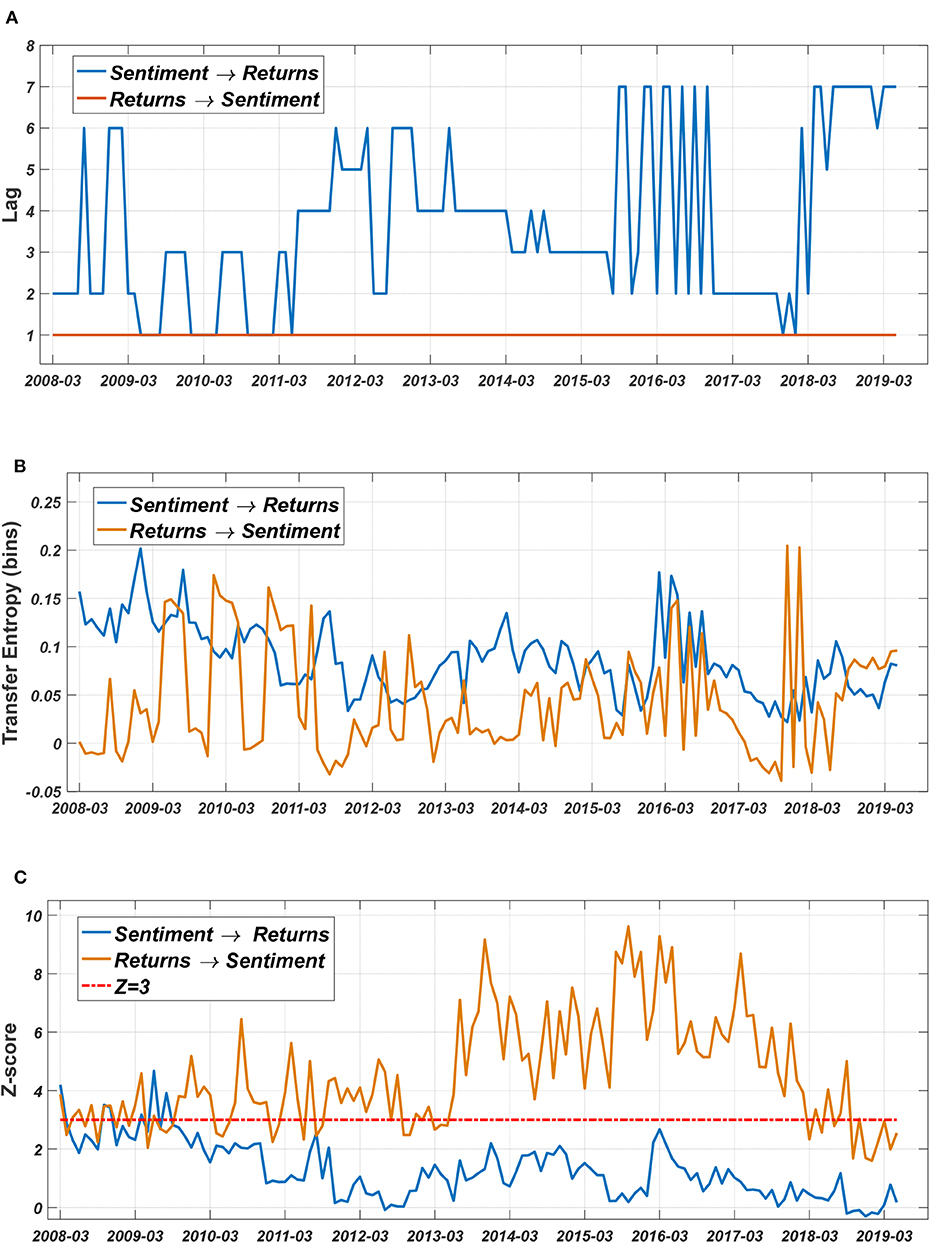
Figure 7. Entropy between investor sentiment and stock market. (A) Lag structure. (B) TE fluctuation. (C) Z-score.

The study conducted by Brown and Cliff [29, 51] revealed that the bandwagon effect and bargain shopper effect can offset each other, reducing the predictability of stock returns. The bandwagon effect indicates that higher investor sentiment could increase the stock price, which is reflected in the positive correlation between stock prices and sentiment during the same period; in contrast, the bargain shopper effect indicates that investors optimistically believe the shares at a relatively low price represent a purchase opportunity; therefore, their sentiment negatively changes the returns.

The bargain shopper and bandwagon effect make it difficult to explore the causality between investor sentiment and stock returns. In our analysis results, the bandwagon effect is weaker, and the bargain shopper effect is more significant. The bandwagon effect reflects the herd effect of investors. This effect makes the stock market prone to sudden rises and falls in the short term; it cannot reflect the true value of a company and is not conducive to the healthy and stable development of the stock market.

EPU and Stock Market

If investor sentiment has a significant impact on the stock price, then according to our expectations, national policy information will be transmitted to the stock price through investors' expectations and eventually cause stock price fluctuations; in other words, EPU also has some kind of information transmission relationship with the stock price. However, the results now show that both stock price fluctuations and EPU have an effect on investor sentiment and are not affected by investor sentiment. Therefore, either the stock price fluctuations and EPU have a weak information transmission effect or there is a mutually offsetting effect.

To further verify our assumptions, we explore the information transfer relationship between EPU and stock price returns (Figure 8). As shown from the results of Figure 8C, there are only a few discontinuous time points with a Z-score > 3 in the entire event period. Overall, the information transmitted by the EPU to the stock market is non-significant; in other words, the EPU has no obvious information transmission relationship with the stock market.

FIGURE 8

Figure 8. Entropy between EPU and stock market. (A) Lag structure. (B) TE fluctuation. (C) Z-score.

A considerable number of related studies showed that the stock market and EPU are significantly negatively correlated [11, 12, 21, 52]. Regarding the relationship between China's EPU and the stock market, Chen and Chiang [21] also verified that the stock returns in China are negatively correlated with EPU. Notably, the main correlation revealed by Chen and Chiang based on the GARCH method is the overall correlation between sequences. However, we reveal a time-varying relationship between sequences based on non-linear methods. As shown in Figure 8C, it can be concluded that in the short term, China's EPU also significantly impacts the stock market during the period from 2011 to 2012 and in 2016, but in the long run, this effect is generally not significant.

Discussion

According to the efficient market hypothesis theory, an efficient market (Figure 9A) should reflect all changes in information, including regular investor sentiment changes and shocking policy fluctuations. Therefore, the information flow should flow from the EPU and investor sentiment to the stock market. In addition, since policy shocks often affect sentiment in the short term, information flow should flow from policy to sentiment, but this is uncertain.

FIGURE 9

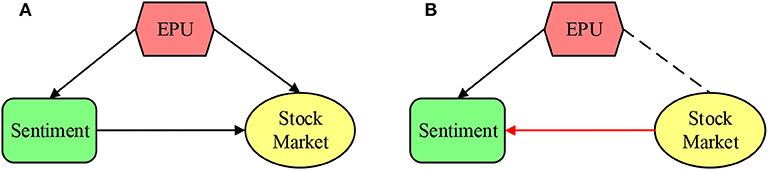
Figure 9. The correlation among CN EPU, investor sentiment and the stock market. (A) The efficient market hypothesis. The stock market may be able to effectively reflect information regarding conventional investment and policy shocks. (B) China's stock market is an inefficient market, and stock market volatility is an important factor affecting emotional volatility.

The results show that the Shanghai Stock market is not yet an efficient market (Figure 9B) and cannot reflect information from regular investment and low-frequency policy shocks. Therefore, investors can reap potential excess profits through operations. Furthermore, the stock market cannot form an effective path to reflect investor sentiment information; thus, in the long run, EPU cannot affect the stock market.

Compared with the market and policy factors, investor sentiment has a certain lag (Figure 9B), reflecting the volatility information of the two. Therefore, we should consider policy factors when studying the construction of investor sentiment indicators, which is rarely investigated in research concerning the factors affecting investor sentiment.

Conclusion

A widely accepted fact is that economic policy affects investor sentiment and will be ultimately reflected in the stock market through investment decisions, causing stock price volatility. Therefore, is this really the case?

Since traditional linear methods cannot identify the dynamic orders between time series and are unable to track specific lead-lag orders when structural fluctuations occur, we proposed an improved transfer entropy method based on a sliding window. By comparing with the linear ETE method and Granger causality method, we verify the effectiveness of the improved method. The main advantages of this methodology are the easy implementation-interpretation by non-parametricity to capture the non-linear dynamics and the point in time when the structure changes. Therefore, this method is considered a nice and promising alternative to the standard measures. We further employ this improved method to examine the information flow among EPU, investor sentiment and stock market.

The results of the information flow analysis of EPU and investment sentiment show that EPU influenced investor sentiment mainly from August 2015 to June 2016. Among different policies, China's exchange rate reform policy and “circuit-breaker” policy have played an important role. For other time periods, there are also points in time when policies were highly uncertain, such as the bankruptcy of Lehman Brothers (September 2008), the downgrade of the US sovereign credit rating (August 2011), and the European debt crisis (January 2011–January 2014). However, likely because these events did not occur in China, their impact on consumer sentiment was non-significant.

The analysis of the information flow between sentiment and stock price returns shows that the impact of sentiment on returns is non-significant, while the fluctuation in stock price returns has a significant impact on investor sentiment. Therefore, using emotions to predict changes in stock prices is valueless. Investor sentiment is more a reflection of changes in stock price returns with a 1-month lag order. The results show that in the Chinese stock market, the bargainer effect is more significant and the bandwagon effect is weaker.

There is no direct information flow from EPU to stock market, and according to our previous analysis, there is no indirect information flow through which EPU transmits information to the stock market through investor sentiment. Therefore, stock market fluctuations are basically not affected by national policy fluctuations. Although investor sentiment is affected by changes such as exchange rate reform and stock market policies, this effect is reflected only at the emotional level. Many investors can digest and neutralize extreme emotions. Therefore, a final consensus is not easy to form.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors analyzed and discussed the results, and contributed to the draft paper and revisions.

Funding

This work was supported by the National Social Science Foundation of China (Grant No. 19BJL086), Natural Science Foundation of Guangdong Province of China (Grant Nos. 2019A1515010471, 2017A030313396), MOE (Ministry of Education in China) Project of Humanities and Social Sciences (Project No. 17YJAZH109), Fundamental Research Funds for the Central Universities (Grant Nos. 2019MS082, 2020ZDPY19), and Guangzhou National Innovation-oriented City Development Research Center (Grant No. 2017IC02).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to acknowledge the reviewers for their constructive comments.

References

1. Kwon O, Yang J-S. Information flow between stock indices. EPL. (2008) 82:68003. doi: 10.1209/0295-5075/82/68003

CrossRef Full Text | Google Scholar

2. Marschinski R, Kantz H. Analysing the information flow between financial time series. Eur Phys J B. (2002) 30:275–81. doi: 10.1140/epjb/e2002-00379-2

CrossRef Full Text | Google Scholar

3. Kyrtsou C, Kugiumtzis D, Papana A. Further insights on the relationship between SP500, VIX and volume: a new asymmetric causality test. Europ J Finance. (2019) 25:1402–19. doi: 10.1080/1351847X.2019.1599406

CrossRef Full Text | Google Scholar

4. Dimpfl T, Peter FJ. Group transfer entropy with an application to cryptocurrencies. Phys A Stat Mech Appl. (2019) 516:543–51. doi: 10.1016/j.physa.2018.10.048

CrossRef Full Text | Google Scholar

5. García-Medina A, Sandoval L, Bañuelos EU, Martínez-Argüello AM. Correlations and flow of information between the New York times and stock markets. Phys A Stat Mech Appl. (2018) 502:403–15. doi: 10.1016/j.physa.2018.02.154

CrossRef Full Text | Google Scholar

6. Sensoy A, Sobaci C, Sensoy S, Alali F. Effective transfer entropy approach to information flow between exchange rates and stock markets. Chaos Soliton Fract. (2014) 68:180–5. doi: 10.1016/j.chaos.2014.08.007

CrossRef Full Text | Google Scholar

7. Yang PB, Shang PJ, Lin AJ. Financial time series analysis based on effective phase transfer entropy. Phys A Stat Mech Appl. (2017) 468:398–408. doi: 10.1016/j.physa.2016.10.085

CrossRef Full Text | Google Scholar

8. He JY, Shang PJ. Comparison of transfer entropy methods for financial time series. Phys A Stat Mech Appl. (2017) 482:772–85. doi: 10.1016/j.physa.2017.04.089

CrossRef Full Text | Google Scholar

9. Chung SL, Hung CH, Yeh CY. When does investor sentiment predict stock returns? J Empir Finance. (2012) 19:217–40. doi: 10.1016/j.jempfin.2012.01.002

CrossRef Full Text | Google Scholar

10. Dakhlaoui I, Aloui C. The interactive relationship between the US economic policy uncertainty and BRIC stock markets. Int Econ. (2016) 146:141–57. doi: 10.1016/j.inteco.2015.12.002

CrossRef Full Text | Google Scholar

11. Arouri M, Estay C, Rault C, Roubaud D. Economic policy uncertainty and stock markets: long-run evidence from the US. Finance Res Lett. (2016) 18:136–−41. doi: 10.1016/j.frl.2016.04.011

CrossRef Full Text | Google Scholar

12. Antonakakis N, Chatziantoniou I, Filis G. Dynamic co-movements of stock market returns, implied volatility and policy uncertainty. Econ Lett. (2013) 120:87–92. doi: 10.1016/j.econlet.2013.04.004

CrossRef Full Text | Google Scholar

13. Antonakakis N, André C, Gupta R. Dynamic co-movements between economic policy uncertainty and housing market returns. J Real Estate Portfol Manage. (2015) 21:53–60. doi: 10.5555/1083-5547-21.1.53

CrossRef Full Text | Google Scholar

14. Wisniewski TP, Lambe BJ. Does economic policy uncertainty drive CDS spreads? Int Rev Finan Anal. (2015) 42:447–58. doi: 10.1016/j.irfa.2015.09.009

CrossRef Full Text | Google Scholar

15. Li XM, Peng L. US economic policy uncertainty and co-movements between Chinese and US stock markets. Econ Model. (2017) 61:27–39. doi: 10.1016/j.econmod.2016.11.019

CrossRef Full Text | Google Scholar

16. Hammoudeh S, Kim WJ, Sarafrazi S. Sources of fluctuations in islamic US, EU, and Asia equity markets: the roles of economic uncertainty, interest rates, and stock indexes. Emerg Mark Financ Tr. (2015) 52:1–15. doi: 10.1080/1540496X.2014.998561

CrossRef Full Text | Google Scholar

17. Sarwar G, Khan W. The effect of US stock market uncertainty on emerging market returns. Emerg Mark Financ Tr. (2017) 53:1796–811. doi: 10.1080/1540496X.2016.1180592

CrossRef Full Text | Google Scholar

18. Tsai IC. The source of global stock market risk: a viewpoint of economic policy uncertainty. Econ Model. (2017) 60:122–31. doi: 10.1016/j.econmod.2016.09.002

CrossRef Full Text | Google Scholar

19. Li XL, Balcilar M, Gupta R, Chang T. The causal relationship between economic policy uncertainty and stock returns in China and India: evidence from a bootstrap rolling window approach. Emerg Mark Financ Tr. (2016) 52:674–89. doi: 10.1080/1540496X.2014.998564

CrossRef Full Text | Google Scholar

20. Yao CZ, Liu C, Ju WJ. Multifractal analysis of the WTI crude oil market, US stock market and EPU. Phys A Stat Mech Appl. (2020) 550:124096. doi: 10.1016/j.physa.2019.124096

CrossRef Full Text | Google Scholar

21. Chen X, Chiang TC. Empirical investigation of changes in policy uncertainty on stock returns—evidence from China's market. Res Int Bus Finance. (2020) 53:101183. doi: 10.1016/j.ribaf.2020.101183

CrossRef Full Text | Google Scholar

22. Dai PF, Xiong X, Zhou WX. Visibility graph analysis of economy policy uncertainty indices. Phys A Stat Mech Appl. (2019) 531:121748. doi: 10.1016/j.physa.2019.121748

CrossRef Full Text | Google Scholar

23. Jiang YH, Zhu ZX, Tian GY, Nie H. Determinants of within and cross-country economic policy uncertainty spillovers: evidence from US and China. Finance Res Lett. (2019) 31:195–206. doi: 10.1016/j.frl.2019.08.004

CrossRef Full Text | Google Scholar

24. Chen L, Du Z, Hu Z. Impact of economic policy uncertainty on exchange rate volatility of China. Finance Res Lett. (2020) 32:101266. doi: 10.1016/j.frl.2019.08.014

CrossRef Full Text | Google Scholar

25. De Long JB, Andrei S, Lawrence HS, Robert JW. Noise trader risk in financial markets. J Polit Econ. (1990) 98:703–38. doi: 10.1086/261703

CrossRef Full Text | Google Scholar

26. Baker M, Wurgler J. Investor sentiment and the cross-section of stock returns. J Finance. (2006) 61:1645–80. doi: 10.1111/j.1540-6261.2006.00885.x

CrossRef Full Text | Google Scholar

27. Fisher KL, Statman M. Investor sentiment and stock returns. Financ Anal J. (2000) 56:16–23. doi: 10.2469/faj.v56.n2.2340

CrossRef Full Text | Google Scholar

28. Baker M, Stein JC. Market liquidity as a sentiment indicator. J Financial Mark. (2004) 7:271–99. doi: 10.1016/j.finmar.2003.11.005

CrossRef Full Text | Google Scholar

29. Brown GW, Cliff MT. Investor sentiment and asset valuation. J Bus. (2005) 78:405–40. doi: 10.1086/427633

CrossRef Full Text | Google Scholar

30. Baker M, Wurgler J. Investor sentiment in the stock market. J Econ Perspect. (2007) 21:129–52. doi: 10.3386/w13189

CrossRef Full Text | Google Scholar

31. Kaplanski G, Levy H. Sentiment and stock prices: the case of aviation disasters. J Finan Econ. (2010) 95:174–201. doi: 10.1016/j.jfineco.2009.10.002

CrossRef Full Text | Google Scholar

32. Corredor P, Ferrer E, Santamaria R. Investor sentiment effect in stock markets: stock characteristics or country-specific factors? Int Rev Econ Finance. (2013) 27:572–91. doi: 10.1016/j.iref.2013.02.001

CrossRef Full Text | Google Scholar

33. Yang C, Gao B. The term structure of sentiment effect in stock index futures market. N Amer J Econ Finance. (2014) 30:171–82. doi: 10.1016/j.najef.2014.09.001

CrossRef Full Text | Google Scholar

34. Yang C, Zhou L. Investor trading behavior, investor sentiment and asset prices. N Amer J Econ Finance. (2015) 34:42–62. doi: 10.1016/j.najef.2015.08.003

CrossRef Full Text | Google Scholar

35. Yao CZ, Sun BY, Lin JN. A study of correlation between investor sentiment and stock market based on copula model. Kybernetes. (2017) 46:550–71. doi: 10.1108/K-10-2016-0297

CrossRef Full Text | Google Scholar

36. Renault T. Intraday online investor sentiment and return patterns in the U.S. stock market. J Bank Finance. (2017) 84:25–40. doi: 10.1016/j.jbankfin.2017.07.002

CrossRef Full Text | Google Scholar

37. Xu Q, Wang L, Jiang C, Zhang X. A novel UMIDAS-SVQR model with mixed frequency investor sentiment for predicting stock market volatility. Expert Syst Appl. (2019) 132:12–27. doi: 10.1016/j.eswa.2019.04.066

CrossRef Full Text | Google Scholar

38. Mascio DA, Fabozzi F. Sentiment indices and their forecasting ability. Int J Forecast. (2019) 38:257–76. doi: 10.1002/for.2571

CrossRef Full Text | Google Scholar

39. David EA, Michael M, Abhay KS. Daily market news sentiment and stock prices. Appl Econ. (2019) 51:3212–35. doi: 10.1080/00036846.2018.1564115

CrossRef Full Text | Google Scholar

40. Yao CZ, Li HY. Time-varying lead–lag structure between investor sentiment and stock market. N Amer J Econ Finance. (2020) 52:101148. doi: 10.1016/j.najef.2020.101148

CrossRef Full Text | Google Scholar

41. Corea F. Can twitter proxy the investors' sentiment? The case for the technology sector. Big Data Res. (2016) 4:70–74. doi: 10.1016/j.bdr.2016.05.001

CrossRef Full Text | Google Scholar

42. Ballinari D, Behrendt S. Structural breaks in online investor sentiment: a note on the nonstationarity of financial chatter. Finance Res Lett. (2020). doi: 10.1016/j.frl.2020.101479. [Epub ahead of print].

CrossRef Full Text | Google Scholar

43. Huang Y, Luk P. Measuring economic policy uncertainty in China. China Econ Rev. (2020) 59:101367. doi: 10.1016/j.chieco.2019.101367

CrossRef Full Text | Google Scholar

44. Geweke JF. Measures of conditional linear dependence and feedback between time series. J Amer Statistical Assoc. (1984) 79:907–15. doi: 10.1080/01621459.1984.10477110

CrossRef Full Text | Google Scholar

45. Barnett L, Barrett A, Seth A. Granger causality and transfer entropy are equivalent for gaussian variables. Phys Rev Lett. (2009) 103:238701. doi: 10.1103/PhysRevLett.103.238701

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Shannon C. A mathematical theory of communication. Bell Syst Tech J. (1948) 27:379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x

CrossRef Full Text | Google Scholar

47. Keskin Z, Aste T. Information-theoretic measures for non-linear causality detection: application to social media sentiment and cryptocurrency prices. arXiv:1906.05740v2. (2019).

Google Scholar

48. Wiener N. The Theory of Prediction. Modern Mathematics for Engineers. New York, NY: McGraw-Hill Book Company Inc (1956).

Google Scholar

49. Granger C. Investigating causal relations by econometric models and cross-spectral methods. Econometrica. (1969) 37:424–38. doi: 10.2307/1912791

CrossRef Full Text | Google Scholar

50. Akaike H. Fitting autoregressive models for prediction. Ann Inst Stat Math. (1969) 21:243–7 doi: 10.1007/BF02532251

CrossRef Full Text | Google Scholar

51. Brown GW, Cliff MT. Investor sentiment and the near-term stock market. J Empir Finance. (2004) 11:1–27. doi: 10.1016/j.jempfin.2002.12.001

CrossRef Full Text | Google Scholar

52. Alexopoulos M, Cohen J. The power of print: uncertainty shocks, markets, and the economy. Int Rev Econ Finance. (2015) 40:8–28. doi: 10.1016/j.iref.2015.02.002

CrossRef Full Text | Google Scholar