- 1Department of Computer Science, The University of Hong Kong, Hong Kong, China
- 2CPT, Aix Marseille Univ, Université de Toulon, CNRS, Marseille, France
- 3Perimeter Institute for Theoretical Physics, Waterloo, ON, Canada
- 4The Rotman Institute of Philosophy, London, ON, Canada
The Bose-Marletto-Vedral (BMV) experiment tests a quantum gravitational effect predicted by low energy perturbative quantum gravity. It has received attention because it may soon be within observational reach in the lab. We point out that: (i) in relativistic language, the experiment tests an interference effect between proper-time intervals; (ii) the feasibility study by Bose et al. suggests that current technology could allow to probe differences of such proper-time intervals of the order of 10−38 seconds, about twenty orders of magnitude beyond the current resolution of the best atomic clocks; (iii) the difference of proper times approaches Planck time (10−44 s) if the masses of the particles in the experiment approach the Planck mass (~micrograms). This implies that the experiment might open a window on the structure of time at the Planck scale. We show that if time differences are discrete at the Planck scale—as research in quantum gravity may suggest—the Planckian discreteness of time would appear as quantum levels of an in principle measurable entanglement entropy.
1. Introduction
Bose et al. [1] and Marletto and Vedral [2, 3] have proposed an ingenious idea to amplify and observe minuscule quantum gravitational effects in a table-top experiment. The idea has received considerable attention [4–14]. In the version proposed in Bose et al. [1] the observable signal is given by Bell–like correlations among the spins of two particles. The correlations are produced by a gravitational interaction. If we assume the identification of gravity with spacetime geometry which is at the basis of general relativity, the observation of these correlations implies that spacetime geometry can be in a quantum superposition (in a non-semiclassical state), and therefore can be taken as evidence for quantum behavior of the geometry [10].
The Bose-Marletto-Vedral (BMV) effect is predicted by low energy perturbative quantum gravity, and hence by any approach to quantum gravity consistent with this low energy expansion, including string theory and loop quantum gravity. It is therefore plausibly real. If detected, it would provide indirect empirical evidence that spacetime geometry does obey quantum mechanics.
On the other hand, the BMV effect is insensitive to the limit c → ∞, hence the gravitational interaction involved can be described in a non–relativistic language. For this reason, it does not test the full relativistic quantum gravitational regime. In fact, the effect can be accounted for purely in terms of the scalar non-radiative modes of the gravitational field, hence it does not test the quantum dynamics of gravity. If we do not fold in the relativistic information provided by classical general relativity, the effect can be interpreted in terms of Newton's action at a distance, leading to objections on the relevance of the effect for the quantum properties of spacetime [4].
Here, we point out that a refinement of the BMV effect could open a window on a quantum gravitational effect that would definitely not be accounted for by non-relativistic quantum physics: time discreteness. The reason this is possible is that from the point of view of general relativity the BMV set up is a delicate interference apparatus that picks up a tiny difference δτ in proper time between two quantum branches, due to gravitationally-induced time dilatation. As derived below, the phase difference δϕ responsible for the gravity-mediated entanglement, and giving rise to the effect, can be written in a particularly simple form
where the experiment is performed with particles of mass m, mPl is the Planck mass and tPl the Planck time. This expression shows that the time scales probed are extremely small. With current technology, the BMV effect might be detected in the lab by probing relevant entanglement (generated when δϕ ~ 1) using mesoscopic particles, with masses of the order of a millionth of a Planck mass () [1]. The corresponding time dilation is of the order of a million Planck times, . This is about twenty orders of magnitude above current capabilities of direct time measurements with atomic clocks [15].
Now, it is often pointed out in quantum gravity research that the Planck time tPl could be a minimal observable time; this follows from relativity plus the fact that many approaches to quantum gravity predict a minimal length [16]. In loop quantum gravity for instance, there is indirect evidence of discretization of time coming from loop quantum cosmology [17, 18] and other arguments [19, 20]. The simplest possibility is to assume that a measurement of a time lapse can only yield multiples of the Planck time. If this holds for the time difference δτ, namely if δτ = n tPl, with integer n, then
That is, a discontinuity in δτ could be detected as a discontinuity in δϕ. As discussed below, such a discretization of the phase could be detected by the Bell–like correlations among the particles' spins, which would acquire a characteristic quantum band structure.
The extremely small time intervals probed by the current proposal to implement the BMV experiment are still too large to see time discreteness. But if the experiment can be pushed to work with more massive particles, further approaching the Planck mass, δτ will approach the Planck time [see (1)]. While the Planck time tP is at the—so far—deeply inaccessible scale , the Planck mass is an easily accessible scale (~ micrograms). Thus, by directly manipulating quantum superpositions of Planck mass particles, interference as a result of gravitational attraction we can indirectly probe time at the Planck scale. This is the key theoretical observation of this paper.
The analysis that follows is rough and the effect might be questioned by a more detailed investigation. It may turn out that the BMV apparatus does not measure eigenvalues but rather expectation values, or, that the scale of discreteness for differences in duration is actually smaller that Planckian. Nevertheless, a prospect of experimental access to the scale of the Planck time is so interesting to deserve full attention.
2. The BMV Experiment
Let us start by describing the version of the BMV experiment of Bose et al. [1] in relativistic language, as in Christodoulou et al. [10]. Two mesoscopic particles (a and b) of mass m and embedded [21] spin are quantum split (say with a Stern-Gerlach-like apparatus) and each is set in a superposition of two distinct states, say with spins + and − in some basis, with different positions in space. This gives rise to four different branches, which we denote |+ +〉, |+ −〉, |− +〉, and |− −〉 and a tensor state
After a time t the two components of each particle are recombined. The relative positions of the particles differ in the distinct branches during the time t, giving rise to different gravitational fields, namely different spacetime geometries. Therefore, during the interval t the quantum state of the geometry is in a superposition of four (semiclassical) spacetimes, each corresponding to a classical metric. In particular, the proper time τ along the worldline of one particle is affected by the presence of the other by relativistic time dilation. This effect is obviously very small, but, as we shall see, it may be picked up by interference.
For simplicity, consider the case in which the two particles are kept at a small distance d only in a single branch, say |− −〉, while in the other three branches the time dilation is negligible. According to general relativity, the gravitational time dilation is [10]
where G is the Newton constant and c the speed of light. The phase of the quantum state of a particle of mass m evolves in time as eiϕ = eimc2τ/ℏ. Therefore, after a (laboratory frame) time t the |− −〉 branch picks up a phase difference
with respect to the other branches. This equation is equivalent to Equation (1).
After the time t the state of the two particles has become
This is an entangled state. The amount of entanglement is measured by the entanglement entropy
where
the trace being on the spin states of one of the two particles. A quick calculation gives
This is correctly a hermitian matrix of unit trace. To compute the entropy we need to diagonalize ρ. A straightforward calculation gives the eigenvalues
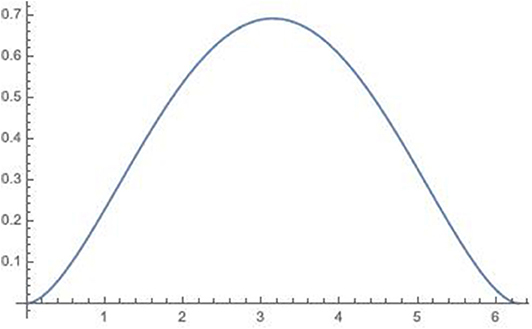
When δϕ = 0, the eigenvalues are ρ+ = 1 and ρ− = 0, thus giving vanishing entanglement entropy, i.e., there is no interference in the output. When δϕ = π, we have ρ+ = 1/2 and ρ− = 1/2; the state is maximally entangled and I = log 2, i.e., we observe the BMV effect. For a general δϕ, the entanglement entropy is
See Figure 1. In the lab, for a given mass m and distance d, δϕ can be controlled by modulating t via
that follows from (4) and (5). The entanglement entropy can be measured by repeated spin measurements on the recombined particles. A specific method would be the following: for a given t, and thus for a given δϕ through (12), one of the particles is discarded and state tomography is performed on the second particle. This would give a density matrix ρ′ of the form of Equation (9), where the cross terms would be some real numbers. Diagonalizing this matrix, an entanglement entropy I′ can be computed. Assuming all noise has been accounted for, I′ can be plotted against δϕ(t) and compared with I as given by (11) and (12). Any deviation of I′ from I could be a signal of a quantum gravity effect, and in particular the presence of plateaus in I′ would be a signal of time discreteness.
Consider now the hypothesis that time is discrete at the Planck scale. We consider here the simplest possible ansatz: that
with a non negative integer n. Writing m = αmP with α a dimensionless positive real parameter, we have that the only values of ϕ that are actually realized are
that is, the phase ends up taking only discrete quantized values, when t is varied continuously. It follows that the entropy is not anymore given by a continuous curve as in Figure 1, but has characteristic quantum steps. As long as α ≪ 1 the steps are too fine to be resolved, but if α approaches unit the steps become visible, as in Figure 2, where α =.2.
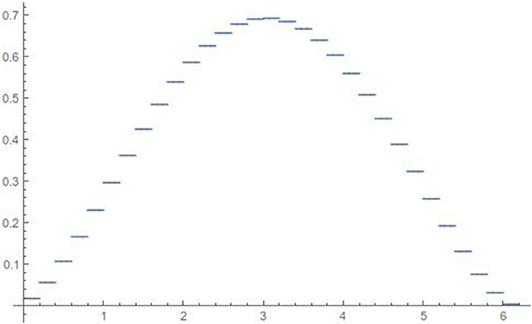
Figure 2. The entanglement entropy for δϕ ∈ {0, 2π} under the assumption that , for particles with mass one fifth of the Planck mass.
For particles with masses larger that the Planck mass interference is likely to disappear altogether, as is common in interference experiments when the wave frequency is much higher than the relevant scale of the apparatus. In this case wave theory goes to the Eikonal approximation. Wave mechanics goes to classical mechanics. The Compton frequency
of objects with mass larger than the Planck mass is formally larger than the Planck frequency and probably meaningless.
Notice that in this case an apparatus capable of detecting δϕ ~ 1 is going to be affected by genuine dynamical effects since we can also write
and if the left hand side and the first fraction are of order unit, so must be the second, with the consequence that the duration t of the interaction must be of the same order than the light travel time d/c between the particles. This would take us outside the static approximation used in the analysis (see also [22]).
3. Discussion
The current hope is to realize the BMV experiment in the lab with masses in the next few years [1]. Our key observation is that with masses at this scale, the BMV experiment is testing time differences of the order of . This is already an extraordinarily small time. For comparison, the most accurate direct measurements of time at our disposal make use of the frequencies corresponding to energy differences in atomic states, atomic clocks, with an accuracy corresponding at best to a period of the order ~10−19s [15]. It is this extraordinary sensitivity to small time intervals in the BMV interference that makes this experiment so interesting.
A relativistic language is not needed to derive the correlations that the BMV experiment is expected to detect. In the non-relativistic language no small time intervals are in play: instead of δϕ = mc2δτ/ℏ, the phase reads δϕ = tδE/ℏ, and the c2 makes all the difference, where the relevant time t at play is that of the laboratory frame.
But, if time discreteness is detected, the non-relativistic language becomes insufficient to describe the relevant physics. Time discreteness, according to current tentative theories, is a genuine relativistic effect arising from quantum gravity. On the other hand, this study does not go beyond the observation that the scales probed are possibly close to the relevant scale for such (naïve) models. Here we do not justify or discuss in depth a possible discretization of time and its implications. The effect discussed here however is a relativistic effect, and we do not think it could be relevant for systems in Newtonian gravity. In contrast for instance to Muller et al. [23], here the relativistic interpretation is used to discuss signatures of possible new physics associated with the discretization of time at the Planck-scale. These effects, if real, require the relativistic interpretation to be described. For completeness, although we are not aware of any such indication, let it be noted that as this is a yet unexplored time regime, there remains the logical possibility that there is time discreteness in this regime independently from quantum gravity.
As mentioned in the introduction, the analysis given here assumes the discreteness of δτ in Planck time multiples. It is possible, but it is not certain that this is implied by quantum gravity. Two reasons that could question this assumption are the following. First, the spectrum of τ could be less trivial and, as a consequence, differences of proper time could be much smaller. For instance, if the spacing between eigenvalues decreases when the eigenvalues are large, their differences may become small. Second, a more careful analysis might show that the interference depends on averages, or expectation values of time durations, and these may be continuous even if direct duration measurements are quantized. This issue in particular requires a more detailed quantum treatment of the phenomenon that will be developed elsewhere.
Even with these caveats, the possibility that quantum interference effects could depend on time differences of the order of Planck time, a scale so far considered totally out of reach, definitely deserves attention.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Pierre Martin-Dussaud and Andrea di Biagio for valuable discussions. The authors acknowledge support from the kind donors to the SM Center for Space, Time and the Quantum. This publication was made possible through the support of the ID 61466 grant from the John Templeton Foundation, as part of the The Quantum Information Structure of Spacetime (QISS) Project (qiss.fr). The opinions expressed in this publication are those of the author(s) and do not necessarily reflect the views of the John Templeton Foundation.
References
1. Bose S, Mazumdar A, Morley GW, Ulbricht H, Toroš M, Paternostro M, et al. Spin entanglement witness for quantum gravity. Phys Rev Lett. (2017) 119:240401. doi: 10.1103/PhysRevLett.119.240401
2. Marletto C, Vedral V. Witness gravity's quantum side in the lab. Nature. (2017) 547:156–8. doi: 10.1038/547156a
3. Marletto C, Vedral V. Gravitationally induced entanglement between two massive particles is sufficient evidence of quantum effects in gravity. Phys Rev Lett. (2017) 119:240402. doi: 10.1103/PhysRevLett.119.240402
4. Anastopoulos C, Hu BL. Comment on “a spin entanglement witness for quantum gravity” and on “gravitationally induced entanglement between two massive particles is sufficient evidence of quantum effects in gravity”. arXiv [Preprint]. arXiv:1804.11315.
5. Hall MJ, Reginatto M. On two recent proposals for witnessing nonclassical gravity. J Phys A. (2018) 51:085303. doi: 10.1088/1751-8121/aaa734
6. Belenchia A, Wald R, Giacomini F, Castro-Ruiz E, Brukner Č, Aspelmeyer M. Quantum superposition of massive objects and the quantization of gravity. ArXiv: 1807.07015. (2018). doi: 10.1103/PhysRevD.98.126009
7. Giampaolo SM, Macrì T. Entanglement, holonomic constraints, and the quantization of fundamental interactions. arXiv:1806.08383. (2018). doi: 10.1038/s41598-019-47844-8
8. Marletto C, Vedral V. When can gravity path-entangle two spatially superposed masses?. arXiv:1803.09124 (2018). doi: 10.1103/PhysRevD.98.046001
9. Albers M, Kiefer C, Reginatto M. Measurement analysis and quantum gravity. Phys Rev D. (2008) 78:064051. doi: 10.1103/PhysRevD.78.064051
10. Christodoulou M, Rovelli C. On the possibility of laboratory evidence for quantum superposition of geometries. Phys Lett B. (2018) 792:64–8. doi: 10.1016/j.physletb.2019.03.015
11. Reginatto M, Hall MJW. Entanglement of quantum fields via classical gravity. arXiv:1809.04989 (2018).
12. Carney D, Stamp PCE, Taylor JM. Tabletop experiments for quantum gravity: a user's manual. arXiv:1807.11494 (2018). doi: 10.1088/1361-6382/aaf9ca
13. Kosterina N, Wang R, Eriksson A, Gutierrez-Farewik EM. Force enhancement and force depression in a modified muscle model used for muscle activation prediction. J Electromyogr Kinesiol. (2013) 23:759–65. doi: 10.1016/j.jelekin.2013.02.008
14. Balushi AA, Cong W, Mann RB. Optomechanical quantum Cavendish experiment. Phys Rev A. (2018) 98:043811. doi: 10.1103/PhysRevA.98.043811
15. Marti GE, Hutson RB, Goban A, Campbell SL, Poli N, Ye J. Imaging Optical Frequencies with 100 μhz Precision and 1.1 μ m Resolution. Phys Rev Lett. (2018) 120:103201. doi: 10.1103/PhysRevLett.120.103201
16. Garay LJ. Quantum gravity and minimum length. Int J Mod Phys. (1994) A10:145–66. doi: 10.1142/S0217751X95000085
17. Bojowald M. Loop quantum cosmology. IV: Discrete time evolution. Class Quant Grav. (2001) 18:1071–88. doi: 10.1088/0264-9381/18/6/308
18. Ashtekar A, Singh P. Loop quantum cosmology: a status report. Class Quant Grav. (2011) 28:213001. doi: 10.1088/0264-9381/28/21/213001
19. Rovelli C, Vidotto F. Compact phase space, cosmological constant, and discrete time. Phys Rev D. (2015) 91:084037. doi: 10.1103/PhysRevD.91.084037
20. Gambini R, Pullin J. Canonical quantization of general relativity in discrete space-times. Phys Rev Lett. (2003) 90:21301. doi: 10.1103/PhysRevLett.90.021301
21. Wan C, Scala M, Morley GW, Rahman ATMA, Ulbricht H, Bateman J, et al. Free nano-object ramsey interferometry for large quantum superpositions. Phys Rev Lett. (2016) 117:143003. doi: 10.1103/PhysRevLett.117.143003
22. Mari A, De Palma G, Giovannetti V. Experiments testing macroscopic quantum superpositions must be slow. Sci Rep. (2016) 6:22777. doi: 10.1038/srep22777
Keywords: quantum gravity, time discreteness, entanglement, non perturbative effects, quantum gravity phenomenology
Citation: Christodoulou M and Rovelli C (2020) On the Possibility of Experimental Detection of the Discreteness of Time. Front. Phys. 8:207. doi: 10.3389/fphy.2020.00207
Received: 28 December 2019; Accepted: 14 May 2020;
Published: 03 July 2020.
Edited by:
Caslav Brukner, University of Vienna, AustriaReviewed by:
Igor Pikovski, Stockholm University, SwedenBhupal Dev, Washington University in St. Louis, United States
Copyright © 2020 Christodoulou and Rovelli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marios Christodoulou, Y2hyaXN0b2QubWFyaW9zQGdtYWlsLmNvbQ==
 Marios Christodoulou
Marios Christodoulou Carlo Rovelli
Carlo Rovelli