Abstract
The boundary value problems (BVPs) have attracted the attention of many scientists from both practical and theoretical points of view, for these problems have remarkable applications in different branches of pure and applied sciences. Due to this important property, this research aims to develop an efficient numerical method for solving a class of non-linear fractional BVPs. The proposed method is free from perturbation, discretization, linearization, or restrictive assumptions, and provides the exact solution in the form of a uniformly convergent series. Moreover, the exact solution is determined by solving only a sequence of linear BVPs of fractional-order. Hence, from practical viewpoint, the suggested technique is efficient and easy to implement. To achieve an approximate solution with enough accuracy, we provide an iterative algorithm that is also computationally efficient. Finally, four illustrative examples are given verifying the superiority of the new technique compared to the other existing results.
1. Introduction
The application of boundary value problems (BVPs) can be found in different fields of pure and applied sciences; for instance, the narrow converting layers bounded by stable layers, which are believed to surround A-type stars, may be modeled by BVPs [1]. Also, these problems may model the dynamo action in some stars [2]. More discussions on the application of BVPs have also been provided in Chandrasekhar [3], Baldwin [4], and Khalid et al. [5]. More to the point, the approximation schemes to solve non-linear BVPs can be found in different sources of numerical analysis [6, 7]. In Agarwal [8], Agarwal discussed the existence of unique solution for these problems; however, no numerical method is contained therein. Boutayeb and Twizell [9] developed the finite difference methods to solve the above-mentioned problems effectively. They also improved a second-order method in Twizell and Boutayeb [10] to solve the general and special BVPs. Besides, Twizell [11] advanced a finite difference scheme of order two to investigate the solution of these problems. However, the existing methods suffer from enormous computational effort. To solve this difficulty, some alternative schemes have been presented including the Adomian decomposition method (ADM) with Green's function [12], homotopy perturbation method (HPM) [13], and variational iteration method (VIM) [14].
During the past decades, many scientists have frequently shown that the mathematical equations with fractional calculus architectures can describe the reality more precisely than the classic integer models with ordinary time-derivatives [15–19]. Recently, the advantages of this approach have been extensively investigated for various practical applications [20–27]. Concerning the fractional BVPs, some noticeable efforts have been done in Ali et al. [28] and Ugurlu et al. [29]. The aforesaid problems have also noteworthy real applications in different areas of science and technology. For instance, a hybrid Caputo fractional modeling was considered in Baleanu et al. [30] for thermostat with hybrid boundary conditions. In Patnaik et al. [31], the application of a fractional-order non-local continuum model was studied for a Euler-Bernoulli beam. The authors in Salem et al. [32] analyzed the coupled system of non-linear fractional Langevin equations with multi-point and non-local integral boundary conditions. The existence of extremal solutions of fractional Langevin equation involving non-linear boundary conditions was also investigated in Fazli et al. [33]. However, the properties of fractional BVPs should be studied deeply and approximation schemes should be continuously improved solving the above-mentioned problems appropriately. To this end, some valuable studies have been carried out, and a number of noteworthy results have been achieved. For instance, an existence theorem was discussed in Zhang and Su [34] for a linear fractional differential equation (FDE) with non-linear boundary conditions by using the method of upper and lower solutions in reverse order. In Arqub et al. [35], a new kind of analytical method was proposed to predict and represent the multiplicity of solutions to non-linear fractional BVPs. In Khalil et al. [36], the authors studied a coupled system of non-linear FDEs whose approximate solution was achieved under two different types of boundary conditions. In Cui et al. [37], a monotone iterative method was investigated for non-linear fractional BVPs while the fractional order was considered between 2 and 3. In Asaduzzaman and Ali [38], the existence of positive solution was investigated to the BVPs for coupled system of non-linear FDEs.
Motivated by the aforementioned statement, this manuscript aims to design a new iterative method to generate the approximate solution of non-linear fractional BVPs in the form of uniformly convergent series. The proposed method is free from perturbation, discretization, linearization, or restrictive assumptions. Moreover, contrary to the VIM [14] or the ADM [12], the suggested technique provides the exact solution without identifying the Lagrange multipliers or calculating the Adomian's polynomials. The new scheme just requires solving a sequence of linear fractional-order BVPs. Finally, four numerical examples are solved to verify the efficiency of the new technique.
The rest of paper is structured in the following way. Hereinafter, we review the fractional calculus approach and its main definitions. Section 3 describes the problem statement. A numerical technique is extended in section 4 solving non-linear fractional BVPs. Numerical and comparative results are reported in section 5, and finally, the paper is finished in section 6 by some concluding remarks.
2. Preliminaries
This part is devoted to some preliminary results concerning the fractional operators. In the following, the Caputo derivative and the Riemann-Liouville integral are introduced, and their main properties are investigated as well [15].
Definition 2.1. For t ∈ (0, T) and n − 1 < α ≤ n, the αth-order Caputo derivative of a function x(t) is defined by
where Γ(·) is the gamma function. The corresponding Riemann-Liouville integral is also described as
With regard to the Caputo derivative (1), we can write
Furthermore, the Caputo derivative of a constant function is zero, i.e., if x(t) ≡ k, then we have . Additionally, the derivative and integral operators (1) and (2) satisfy the following anti-derivative property
More to the point, the Lipschitz condition is satisfied by the Caputo derivative (1)
where L > 0 is the Lipschitz constant.
For additional information, the interested readers can refer to Kilbas et al. [15].
3. The Statement of the Problem
To formulate a fractional BVP, consider the following FDE
where the function f(·) is analytic with regard to its arguments and f(0, t) = 0, ∀t ∈ (0, T). The expression denotes the αth-order Caputo derivative, and n is an even number. The boundary conditions for Equation (6) are given by
where a2k, b2k () are real finite numbers. As is well-known, the exact solution of the fractional BVP (6)-(7) can hardly be achieved except in very special cases. Hence, an efficient iterative technique will be developed hereinafter in order to derive the corresponding approximate solution.
4. The Iterative Method
In this section, an efficient iterative method is improved to solve the fractional BVP (6), (7). To this end, first the following lemma is presented and proved.
Lemma 4.1. The solution of the fractional BVP (6)-(7) is analytic with respect to the boundary conditions a2k, b2k, .
Proof: Let x(·) be the solution of the BVP (6)-(7). Define and , i, j = 0, …, n − 1. Then x(·) is the solution of the following initial value problems (IVPs)
Since f(x(t), t) is assumed to be analytic, x(·), as the solution of the IVPs (8) and (9), is analytic with respect to αi and βi, respectively [39]. Thus, x(·), as the solution of the BVP (6)-(7), is analytic with respect to a2k, b2k, .
Now, we state and prove the following theorem.
Theorem 4.1. The solution of the fractional BVP (6)-(7) is expressed by the uniformly convergent series, whereis attained by solving the sequence of linear fractional BVPs
and for i = 2, 3, 4, …
The non-homogeneous term Fiis determined by
, and the summationis taken over all combinations of non-negative integer indices k1through ki+1−jsuch that
Proof: By using the Maclaurin series of f(x(t), t) with respect to x(t), we have
where . Besides, the solution of the fractional BVP (6)-(7) for an arbitrary vector xb = (a0, a2, …, an, b0, b2, …, bn) is expressed by
where the vector function g : ℝn × (0, T) → ℝ is analytic based on Lemma 4.1. In addition, we have g(0, t) = 0, ∀t ∈ (0, T), since we have assumed that f(0, t) = 0 for all t ∈ (0, T). Therefore, by applying the Maclaurin series of g(xb, t) with respect to xb, from Equation (15) we derive
Since the function g(xb, t) is analytic with respect to xb, the Maclaurin series (16) exists and is uniformly convergent. Now, we perturb the boundary conditions by an arbitrary parameter ε > 0, i.e., xb → εxb. Then, Equation (16) is reformulated by
Substituting x(t) from Equation (17) into the expansion (14) yields
Rearranging Equation (18) with respect to the order of ε results
where
and the summation is taken over all combinations of non-negative integer indices k1 through ki+1−j such that
Since, Equation (19) must be satisfied for any ε > 0, we should equalize the coefficient of εi on the left-hand side of Equation (19) with its corresponding coefficient on the right-hand side. This procedure yields
Now, we put t = 0 and t = T in Equation (17) and in its second- and fourth-order derivatives in order to achieve the boundary conditions for the sequence (22)-(24). Again, we should equalize the coefficients of εi on the both sides of the resultant equations. Thus, we obtain
and the proof is complete.
As can be seen, Equation (10) formulates a homogeneous linear BVP of fractional-order. By solving this problem, is achieved in the first step. Following the proposed procedure in Theorem 4.1, we then obtain (i ≥ 2) by solving the non-homogeneous linear fractional BVP (11) in the ith step. Moreover, the non-homogeneous term in (11) is determined from Equation (12) by using the known functions provided in the previous steps. Thus, a recursive procedure should be employed here to solve the considered sequence.
4.1. Approximate Solution
Although Theorem 4.1 suggests a closed-form expression for the solution of BVP (6)-(7), it is almost impossible to compute this solution in its present form since it is an infinite series. Hence, for the purpose of practical implementation, we need to truncate the series by considering its first M components where M is a positive integer number. Thus, the Mth-order approximate solution xM(t) becomes
To evaluate the value of M in Equation (27), the following criterion is considered according to the required accuracy. Indeed, the Mth-order approximate solution (27) has enough accuracy if for δ > 0, a given positive constant, the two consecutive solutions yM−1(t) and yM(t) satisfy
Here, we present an iterative algorithm to design an approximate solution with enough accuracy.
Algorithm:
Step 1. Determine the first-order term from Equation (10) and set i = 2.
Step 2. Determine the ith-order term from Equation (11).
Step 3. Set M = i. By using the expression (27), compute xM(t).
Step 4. If the condition (28) holds for a given small enough constant δ > 0, go to Step 5; else, replace i by i + 1 and go to Step 2.
Step 5. Consider xM(t) as the appropriate approximate solution.
5. Numerical Simulations
In this part, four numerical examples are employed in order to verify the effectiveness of the new suggested technique. Here, we consider the examples form [13, 14] for the purpose of comparison with the other existing results.
Example 5.1. Consider a fractional BVP in the form below
whose exact solution is x(t) = etfor α = 6.
Following the new technique as in section 4, we solve the presented sequence of fractional BVPs (10)-(11) in a recursive manner. Simulation results up to 10th iteration for α = 6 are reported in Table 1. As is shown, the error is reduced further by considering more components of x(t). To achieve an approximate solution with enough accuracy, the new algorithm is applied with δ = 0.01. From Table 1, we observe that the convergence is achieved just in the second step, i.e., . Simulation curve of x2(t) and the exact solution are plotted in Figure 1. This figure indicates that the second-order approximate solution is in good agreement with the exact solution.
Table 1
| i (iteration time) | ||yi(t)−yi−1(t)||∞ |
|---|---|
| 1 | - |
| 2 | 2.2 ×10−3 |
| 3 | 4.6574 ×10−6 |
| 4 | 1.2394 ×10−8 |
| 5 | 3.7049 ×10−11 |
| 6 | 1.1878 ×10−13 |
| 7 | 3.9916 ×10−16 |
| 8 | 1.3874 ×10−18 |
| 9 | 4.9470 ×10−21 |
| 10 | 1.7993 ×10−23 |
The suggested technique at different iterations for Example 5.1.
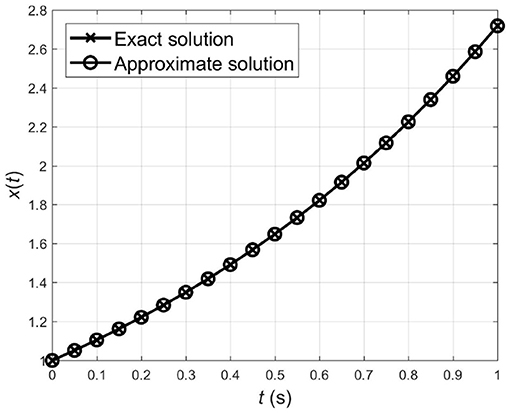
Figure 1
Simulation curves of the exact solution and the second-order approximate solution for Example 5.1.
The problem (31) for α = 6 has also been solved by using the HPM [13] and the VIM [14], respectively. Notice that the results of both methods are exactly the same as shown in Noor et al. [14]. Table 2 depicts the exact solution and the absolute errors achieved by applying two iterations of the HPM, VIM, and the proposed technique in this paper. Comparative results in this table verify the superiority of the suggested algorithm compared to the other approximation methods available in the literature.
Table 2
| Absolute error* | |||
|---|---|---|---|
| t | Exact solution | HPM [13] and | Proposed method |
| VIM [14] | (M = 2) | ||
| 0.0 | 1.000000000 | 0.000000 | 0.000000 |
| 0.1 | 1.105170918 | 4.56500 ×10−5 | 9.196986030 ×10−5 |
| 0.2 | 1.221402758 | 1.1522210 ×10−3 | 2.207276648 ×10−4 |
| 0.3 | 1.349858808 | 4.4830030 ×10−3 | 3.678794412 ×10−4 |
| 0.4 | 1.491824698 | 1.1323624 ×10−2 | 7.357588824 ×10−4 |
| 0.5 | 1.648721271 | 2.3094929 ×10−2 | 3.678794412 ×10−4 |
| 0.6 | 1.822118800 | 4.1367190 ×10−2 | 7.357588824 ×10−4 |
| 0.7 | 2.013752707 | 6.7875828 ×10−2 | 7.357588824 ×10−4 |
| 0.8 | 2.225540928 | 1.04538781 ×10−1 | 8.829106592 ×10−4 |
| 0.9 | 2.459603111 | 1.53475695 ×10−1 | 1.839397206 ×10−3 |
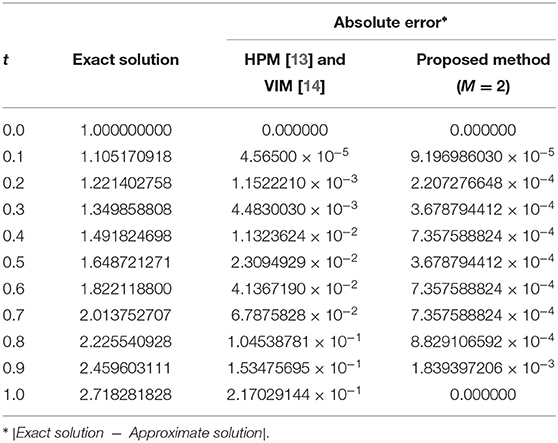
| 1.0 | 2.718281828 | 2.17029144 ×10−1 | 0.000000 |
Numerical comparison between the proposed iterative method and the other approximation techniques for Example 5.1.
|Exact solution−Approximate solution|.
Example 5.2. Consider the following non-linear BVP of fractional-order
whose exact solution is in the form x(t) = e−tfor α = 6.
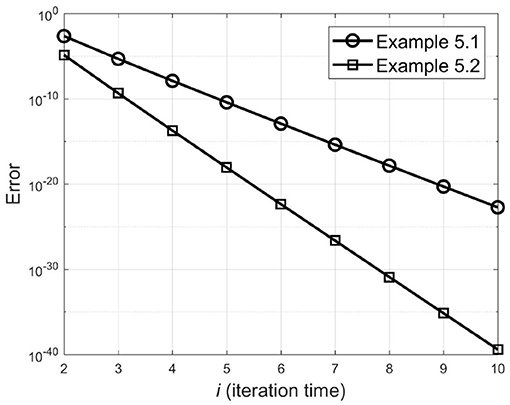
Following the same procedure as in Example 5.1, we report the simulation results up to 10th iteration in Table 3. This table shows that considering more components of x(t) provides more precise results. From this table, it is also indicated that the proposed algorithm with δ = 10−4 converges after only two iterations, i.e., . In Figure 2, the simulation curve of x2(t) is compared with the exact solution. Comparative results indicate that the second-order approximate solution is very close to the exact solution. Figure 3 shows the relation between the iteration time and the error given by the expression (28) using infinite norm for Examples 5.1 and 5.2. In this figure, the logarithmic scale is applied for the vertical axis. This figure verifies that the error decreases significantly as the iteration time increases.
Table 3
| i (iteration time) | |
|---|---|
| 1 | - |
| 2 | 1.3343 ×10−5 |
| 3 | 4.3500 ×10−10 |
| 4 | 1.8102 ×10−14 |
| 5 | 8.4664 ×10−19 |
| 6 | 4.2478 ×10−23 |
| 7 | 2.2340 ×10−27 |
| 8 | 1.2153 ×10−31 |
| 9 | 6.7823 ×10−36 |
| 10 | 3.8611 ×10−40 |
The suggested technique at different iterations for Example 5.2.
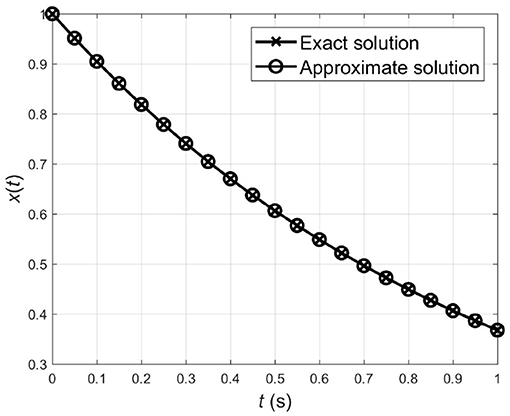
Figure 2
Simulation curves of the exact solution and the second-order approximate solution for Example 5.2.
Figure 3
Relation between the iteration time and the error for Examples 5.1 and 5.2.
The problem given by Equation (32) for α = 6 has also been solved by using the HPM and the VIM in Noor and Mohyud-Din [13] and Noor et al. [14], respectively. As can be seen in Noor et al. [14], the results of both methods are exactly the same. Table 4 exhibits the exact solution along with the absolute errors related to the HPM, VIM, and the proposed iterative algorithm. Comparing the results shows that the new approach is superior to the other existing methods.
Table 4
| Absolute error* | |||
|---|---|---|---|
| t | Exact solution | HPM [13] and | Proposed method |
| VIM [14] | (M = 2) | ||
| 0.0 | 1.000000000 | 0.000000 | 0.000000 |
| 0.1 | 0.9048374180 | 1.6258200 ×10−4 | 1.4715178 ×10−4 |
| 0.2 | 0.8187307531 | 1.2692469 ×10−3 | 1.2140022 ×10−3 |
| 0.3 | 0.7408182207 | 4.1817793 ×10−3 | 5.3342519 ×10−4 |
| 0.4 | 0.6703200460 | 9.6799540 ×10−3 | 8.8291066 ×10−4 |
| 0.5 | 0.6065306597 | 1.8469340 ×10−2 | 5.5181916 ×10−4 |
| 0.6 | 0.5488116361 | 3.1188364 ×10−2 | 0.000000 |
| 0.7 | 0.4965853038 | 4.8414696 ×10−2 | 5.5181916 ×10−4 |
| 0.8 | 0.4493289641 | 7.0671036 ×10−2 | 5.8860711 ×10−4 |
| 0.9 | 0.4065696597 | 9.8430340 ×10−2 | 3.3109150 ×10−3 |
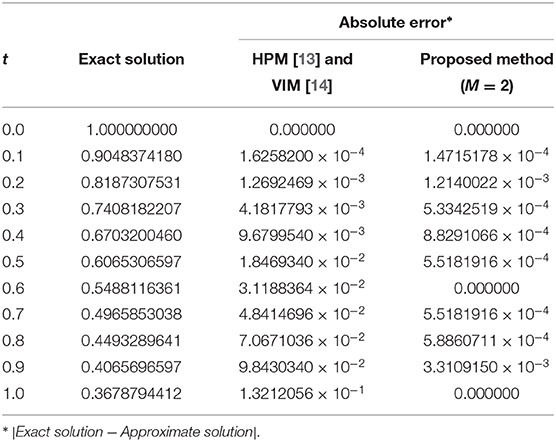
| 1.0 | 0.3678794412 | 1.3212056 ×10−1 | 0.000000 |
Numerical comparison between the proposed iterative method and the other approximation techniques for Example 5.2.
|Exact solution−Approximate solution|.
Example 5.3. Consider the following non-linear fractional BVP
whose exact solution iswhere Eα(·) is known as the Mittag-Leffler function.
Simulation curve of x2(t), i.e., the second-order approximate solution, for different values of α are plotted in Figure 4A. This figure indicates that the approximate solution tends to the classic integer solution for α = 6 when α → 6 as expected.
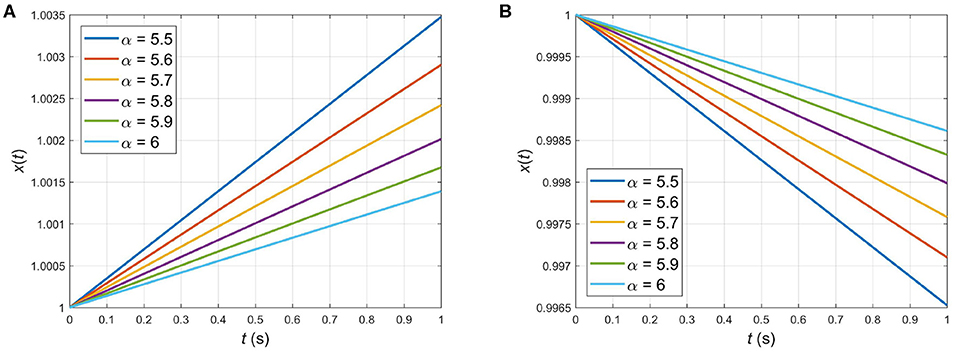
Figure 4
Simulation curves of the second-order approximate solution for α = 5.5, 5.6, 5.7, 5.8, 5.9, 6 [(A) Example 5.3 and (B) Example 5.4].
Example 5.4. Consider the non-linear fractional BVP
whose exact solution is.
In the same way as in Example 5.3, Figure 4B depicts the second-order approximate solution tending to the classic integer solution as α goes to 6.
6. Conclusion
This paper studied a new iterative scheme to provide the solution of non-linear fractional BVPs in terms of a uniformly convergent series. The proposed procedure was free from perturbation, discretization, linearization, or restrictive assumptions. Furthermore, contrary to the other approximation schemes such as ADM [12] and VIM [14], the suggested technique kept away from calculating the Adomian's polynomials or identifying the Lagrange multipliers, respectively. Hence, from practical viewpoint, the suggested technique is more efficient than the above-mentioned approximation methods. Simulation results, demonstrating the efficacy, high accuracy, and simplicity of the proposed method, were also included. In the following, we summarize the main aspects of our numerical findings. Tables 1, 3 provided the simulation results up to 10th iteration, and Figure 3 depicted the relation between the iteration time and the error given by the expression (28). From these results it is obvious that the error is reduced further by considering more components of x(t). Simulation curves in Figures 1, 2 also indicated that the second-order approximate solution is in good agreement with the exact solution. Tables 2, 4 exhibited the exact solution and the absolute error derived by employing two iterations of the HPM [13], VIM [14], and our new iterative algorithm. These tables clearly indicated the improvements made by employing the proposed method. The simulation curves for different values of α were given in Figures 4A,B verifying that the numerical approximate solution for α < 6 tends to the classic integer solution as α → 6. Future works can be focused on extending the suggested numerical technique to solve other types of BVPs.
Statements
Data availability statement
All datasets generated for this study are included in the article/supplementary material.
Author contributions
All authors contributed equally to each part of this work. All authors read and approved the final manuscript.
Funding
This research was in part supported by a grant from University of Bojnord (No. 97/367/18077).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1.
ToomoreJZahnJPLatourJSpiegelEA. Stellar convection theory II: single-mode study of the second convection zone in A-type stars. Astrophys J. (1976) 207:545–63. 10.1086/154522
2.
GlatzmaierGA. Numerical simulations of stellar convection dynamics III: at the base of the convection zone. Geophys Astrophys Fluid Dyn. (1985) 31:137–50. 10.1080/03091928508219267
3.
ChandrasekharS. Hydrodynamics and Hydromagnetic Stability. New York, NY: Dover (1981).
4.
BaldwinP. A localized instability in a Benard layer. Appl Anal. (1987) 24:1127–56. 10.1080/00036818708839658
5.
KhalidANaeemMNUllahZGhaffarABaleanuDNisarKSet al. Numerical solution of the boundary value problems arising in magnetic fields and cylindrical shells. Mathematics. (2019) 7:508. 10.3390/math7060508
6.
AkgulAAkgulEKKhanYBaleanuD. Solving the nonlinear system of third-order boundary value problems. In: TasKBaleanuDMachadoJ editors. Mathematical Methods in Engineering. Nonlinear Systems and Complexity. Cham: Springer (2019). p. 24. 10.1007/978-3-319-90972-1_8
7.
AkgulAAkgulEKBaleanuDIncM. New numerical method for solving tenth order boundary value problems. Mathematics. (2018) 6:245. 10.3390/math6110245
8.
AgarwalRP. Boundary Value Problems for Higher Order Differential Equations. Singapore: World Scientific (1986).
9.
BoutayebATwizellEH. Numerical methods for the solution of special sixth-order boundary value problems. Int J Comput Math. (1992) 45:207–233. 10.1080/00207169208804130
10.
TwizellEHBoutayebA. Numerical methods for the solution of special and general sixth-order boundary value problems, with applications to Benard layer eigen value problem. Proc R Soc A Math Phys Eng Sci. (1990) 431:433–50. 10.1098/rspa.1990.0142
11.
TwizellEH. Numerical methods for sixth-order boundary value problems. In: AgarwalRPChowYMWilsonSJ editors. Numerical Mathematics Singapore 1988. International Series of Numerical Mathematics. Basel: Birkhauser (1988). p. 495–506. 10.1007/978-3-0348-6303-2_40
12.
Al-HayaniW. Adomian decomposition method with Green's function for sixth-order boundary value problems. Comput Math Appl. (2011) 61:1567–75. 10.1016/j.camwa.2011.01.025
13.
NoorMAMohyud-DinST. Homotopy perturbation method for solving sixth order boundary value problems. Comput Math Appl. (2008) 55:2953–72. 10.1016/j.camwa.2007.11.026
14.
NoorMANoorKIMohyud-DinST. Variational iteration method for solving sixth-order boundary value problems. Commun Nonlinear Sci Num Simu. (2009) 14:2571–80. 10.1016/j.cnsns.2008.10.013
15.
KilbasAASrivastavaHHTrujilloJJ. Theory and Applications of Fractional Differential Equations. New York, NY: Elsevier (2006).
16.
BaleanuDAsadJHJajarmiA. The fractional model of spring pendulum: new features within different kernels. Proc Roman Acad Ser A. (2018) 19:447–54.
17.
BaleanuDAsadJHJajarmiA. New aspects of the motion of a particle in a circular cavity. Proc Roman Acad Ser A. (2018) 19:361–7.
18.
BaleanuDJajarmiAMohammadiHRezapourS. A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative. Chaos Solitons Fractals. (2020) 134:109705. 10.1016/j.chaos.2020.109705
19.
JajarmiAYusufABaleanuDIncM. A new fractional HRSV model and its optimal control: a non-singular operator approach. Phys A Stat Mech Appl. (2020) 547:123860. 10.1016/j.physa.2019.123860
20.
MohammadiFMoradiLBaleanuDJajarmiA. A hybrid functions numerical scheme for fractional optimal control problems: application to non-analytic dynamical systems. J Vibrat Control. (2018) 24:5030–43.
21.
JajarmiAArshadSBaleanuD. A new fractional modelling and control strategy for the outbreak of dengue fever. Phys A Stat Mech Appl. (2019) 535:122524. 10.1016/j.physa.2019.122524
22.
JajarmiABaleanuDSajjadiSSAsadJH. A new feature of the fractional Euler-Lagrange equations for a coupled oscillator using a nonsingular operator approach. Front Phys. (2019) 7:196. 10.3389/fphy.2019.00196
23.
JajarmiAGhanbariBBaleanuD. A new and efficient numerical method for the fractional modelling and optimal control of diabetes and tuberculosis co-existence. Chaos. (2019) 29:093111. 10.1063/1.5112177
24.
BaleanuDJajarmiASajjadiSSMozyrskaD. A new fractional model and optimal control of a tumor-immune surveillance with non-singular derivative operator. Chaos. (2019) 29:083127. 10.1063/1.5096159
25.
BaleanuDSajjadiSSJajarmiAAsadJH. New features of the fractional Euler-Lagrange equations for a physical system within non-singular derivative operator. Eur Phys J Plus. (2019) 134:181. 10.1140/epjp/i2019-12561-x
26.
BaleanuDJajarmiASajjadiSSAsadJH. The fractional features of a harmonic oscillator with position-dependent mass. Commun Theor Phys. (2020) 72:055002. 10.1088/1572-9494/ab7700
27.
YıldızTAJajarmiAYıldızBBaleanuD. New aspects of time fractional optimal control problems within operators with nonsingular kernel. Discrete Continuous Dyn Syst S. (2020) 13:407–28. 10.3934/dcdss.2020023
28.
AliAShahKBaleanuD. Ulam stability results to a class of nonlinear implicit boundary value problems of impulsive fractional differential equations. Adv Diff Equat. (2019) 2019:5. 10.1186/s13662-018-1940-0
29.
UgurluEBaleanuDTasK. On the solutions of a fractional boundary value problem. Turkish J Math. (2018) 42:1307–11. 10.3906/mat-1609-64
30.
BaleanuDEtemadSRezapourS. A hybrid Caputo fractional modeling for thermostat with hybrid boundary value conditions. Bound Value Probl. (2020) 2020:64. 10.1186/s13661-020-01361-0
31.
PatnaikSSidhardhSSemperlottiF. A Ritz-based finite element method for a fractional-order boundary value problem of nonlocal elasticity. arXiv preprint arXiv:200106885 (2020).
32.
SalemAAlzahraniFAlneggaM. Coupled system of nonlinear fractional Langevin equations with multipoint and nonlocal integral boundary conditions. Math Probl Eng. (2020) 2020:7345658. 10.1155/2020/7345658
33.
FazliHSunHAghchiS. Existence of extremal solutions of fractional Langevin equation involving nonlinear boundary conditions. Int J Comput Math. (2020) 10.1080/00207160.2020.1720662
34.
ZhangSSuX. The existence of a solution for a fractional differential equation with nonlinear boundary conditions considered using upper and lower solutions in reverse order. Comput Math Appl. (2011) 62:1269–1274. 10.1016/j.camwa.2011.03.008
35.
ArqubOAEl-AjouAZhourZAMomaniS. Multiple solutions of nonlinear boundary value problems of fractional order: a new analytic iterative technique. Entropy. (2014) 16:471–93. 10.3390/e16010471
36.
KhalilHAl-SmadiMMoaddyKKhanRAHashimI. Toward the approximate solution for fractional order nonlinear mixed derivative and nonlocal boundary value problems. Discrete Dyn Nat Soc. (2016) 2016:5601821. 10.1155/2016/5601821
37.
CuiYSunQSuX. Monotone iterative technique for nonlinear boundary value problems of fractional order p ∈ (2, 3]. Adv Diff Equat. (2017) 2017:248. 10.1186/s13662-017-1314-z
38.
AsaduzzamanMAliMZ. Existence of positive solution to the boundary value problems for coupled system of nonlinear fractional differential equations. AIMS Math. (2019) 4:880–95. 10.3934/math.2019.3.880
39.
DiethelmK. (2010). Multi-term caputo fractional differential equations. In: The Analysis of Fractional Differential Equations. Lecture Notes in Mathematics, Vol. 2004. Berlin; Heidelberg: Springer (2010). 10.1007/978-3-642-14574-2_8
Summary
Keywords
fractional calculus, boundary value problems, series expansion, uniform convergence, iterative method
Citation
Jajarmi A and Baleanu D (2020) A New Iterative Method for the Numerical Solution of High-Order Non-linear Fractional Boundary Value Problems. Front. Phys. 8:220. doi: 10.3389/fphy.2020.00220
Received
08 January 2020
Accepted
22 May 2020
Published
25 June 2020
Volume
8 - 2020
Edited by
Jordan Yankov Hristov, University of Chemical Technology and Metallurgy, Bulgaria
Reviewed by
Ahmed Elwakil, University of Sharjah, United Arab Emirates; Aydin Secer, Yildiz Technical University, Turkey
Updates
Copyright
© 2020 Jajarmi and Baleanu.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Amin Jajarmi a.jajarmi@ub.ac.ir
This article was submitted to Mathematical Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.