- 1Chair of Entrepreneurial Risks, ETH Zurich, Zurich, Switzerland
- 2Swiss Finance Institute, Zurich, Switzerland
We propose an extension of the class of rational expectations bubbles (REBs) to the more general rational beliefs setting of [1, 2]. In a potentially non-stationary but stationarizable environment, among a heterogenous population of agents, it is possible to hold more than one “rational” expectation. When rational but diverse beliefs converge (“correlated beliefs”), they do not cancel each other out in aggregate anymore. This can make them an object of rational speculation. Accounting for the fact that market efficiency has an intrinsic time-dimension, we show that diverse but correlated beliefs can thus account for speculative bubbles, without the need for irrational agents or limits to arbitrage. Many of the shortcomings of REBs that make rational bubbles implausible can be overcome once we relax the ergodicity requirement. In particular, we argue that the hitherto unexplained “bubble component” of REBs corresponds to the extension of the state space in [3].
1. Introduction
In the following, we provide some addenda and modifications to the work of Kurz and Motolese [3]. We show that their asset pricing model encompasses asset price bubbles, even though they did not intend for it. The significance of this lies in that theirs is an equilibrium model with perfectly rational agents in a frictionless competitive market—the economic equivalent of Euclidean geometry with perfect circles. The only other Euclidean account of bubbles we are aware of is the class of Rational Expectations bubbles (REBs) [4–6]. All other bubble theories rely on either irrational agents or frictions of some sort [see e.g., [7–9] for surveys of the bubble literature].
Just as lines and circles are useful abstractions even though they do not exist in the real world [10, 11], the “purity” of the setting in which bubbles are theorized is of practical import: If frictions are a necessary condition of bubbles, then the policy implication is that the regulator should focus on perfecting markets, pushing ever further the “financialization” of the economy [but see 12, 13]. If it is irrational behavior that causes them, then bubbles may only push the system to more efficient capital allocations [14, 15] or to new learning experiences [16, 17]. Either way, we should then expect to see bubbles never more than once in a generation (but see [18, 19]).
If, by contrast, bubbles can arise even in a perfectly rational, friction-free world, then they should be seen as an inherent feature of market economies, not as temporary aberrations. The regulatory imperative would be to guard, not to “lean,” against them—the difference between building dykes and trying to suppress the tides. The problem is that REBs as the only such account thus far are unexplained sunspot equilibria with strict conditions. For example, they must be present from the beginning of time1, cannot be negative, and, due to explosive conditional expectations, eventually dominate the economy [20–22]. Hence the preference in the literature for irrational or frictional explanations, which are more plausible at the cost of being less general (see however [9]).
The reduced form of Kurz and Motolese's [3] model corresponds to that of a noisy rational expectations equilibrium [23–25] but the model is derived under rational beliefs [1, 2, 26]. The rational beliefs framework widens the scope of expectational “rationality”2 from ergodic to non-ergodic, possibly non-stationary economic environments. As a consequence, rational beliefs are diverse—that is, diverse as a feature, not as a bug3. The persistent diversity of expectations adds a strategic element to the decision calculi of agents, enlarging the state space of the model by an endogenous variable called “market belief.” We contend that this endogenous state variable, which arises from the diversity of beliefs, corresponds to the unexplained “bubble component” in REBs.
There are two classical views on diverse beliefs. One is encapsulated by [28, 29], whose report from a weight-judging competition is the classic example of the “wisdom of crowds”4. The opposite view was set forth by [30, ch. 12] who said that, if agents disagreed too much about the future, speculation—betting on others's beliefs—would drive a wedge between price and value. The former leads to Hayek and the efficient market hypothesis (EMH); the latter underpins Minsky's financial instability hypothesis (FIH), and thereby most of the literature on bubbles outside of REBs5.
What makes the EMH and FIH seem so irreconcilable is that something is missing from the classical accounts, namely the dependence structure of beliefs. It is interesting to note therefore that both noisy rational expectations and the rational beliefs framework do take it into account but in opposite ways. Grossman [32], Hellwig [24], and Diamond and Verrecchia [25] all require independence between private signals (which implies independent beliefs) lest the aggregate signal lose its sufficiency6 and prices lose their informativeness. By contrast, Kurz and Motolese [3] require dependence between beliefs in order for the endogenous state variable to appear in the equilibrium price. One might say there is really only one model once we move up a level of abstraction: In the corner cases, when individual beliefs are either independent or comonotonic, the equilibrium price conforms to rational expectations; when they are (imperfectly) dependent, the market extends its state space through the endogenous market belief variable.
Accepting diverse beliefs as not the exception but the rule, and shifting the focus to their dependence structure instead, also changes our view of the role they play in the bubble literature thus far. The generic argument is that the broader the range of expectations, the more “confused” or “fantastical” about the future investors are, the more opportunity for speculation, and the bigger the bubble7. Historically, though, bubbles seem to have been associated with a reduction in diversity rather than an expansion of it [33]. People are literally “buying into” a, necessarily common, bubble narrative (see also [34]). It is interesting to note therefore that “correlated beliefs” in [3] actually refers to correlated innovations to individual beliefs. This means that, as the market belief variable appears, belief states converge, lending additional support to our contention that the endogenous state variable is the hitherto unexplained “bubble component” of rational bubbles.
Our approach is different from the idea of chaotic equilibrium cycles (see e.g., [35]). In the later works based on equilibrium cycles theory, the existence of a chaotic equilibrium growth may be derived, and “equilibrium bubbles” associated with transient excursions with nonlinear reversal (crashes) can be observed [36]. In contrast to the small number of “degrees of freedom” involved in the chaotic equilibrium growth models, our framework is based on a social graph representing a large number of individual agents with different but correlated beliefs.
Before we can re-interpret Kurz and Motolese's [3] market belief variable in this way, we need to add some detail. First, section 2 exemplifies the role of correlated beliefs and thus prepares for the subsequent developments. Then, we clarify what we mean when we speak of a bubble. After a quick summary of [3] in section 3, section 4 shows how their model relates to the definition we propose in [37]. Next, for market belief to explain the dynamic appearance of bubbles, we would like to be able to switch it “on” and “off” at will8. Kurz and Motolese [3] basically assume that it is always “on,” hence have little to say about the dependence structure that gives rise to it, other than that “due to correlation across agents, the law of large numbers is not operative.” But not only are there different variants of the law of large numbers (LLN), some LLNs can operate on correlated variates. We need more specificity about how much (or what kind of) dependence is necessary for market belief to emerge. Ideally, we would find a precise threshold in the parameter space fixing the dependence structure.
Section 5 introduces a simple graph model for the dependence of beliefs. This not only reduces the dimensionality of the problem but also creates a partition in the parameter space. The phase transition between small and giant components in the graph then effectively serves as the on/off switch for the market belief variable. The idea is to “rotate” the problem from one of identically distributed but correlated belief innovations to an independent but not identically distributed setting. This makes the problem accessible to LLNs of differently-sized variables [38, 39] via the eigenvalue distribution of the correlation matrix. In section 6, we then use linear aggregation [40, 41] to change the endogenous state variable from short- to long-memory. This “dramatizes” the emergence of bubbles. Section 7 concludes with a few suggestions regarding policy implications and empirical applications.
2. The Role of Correlated Beliefs: An Example
We begin with a re-examination of the introductory example of [42]. The chief distinction between rational belief bubbles and other heterogeneous belief bubbles [43] is our focus on the dependence structure, or correlation, of beliefs rather than their diversity. Lest the main idea get lost in technical details later, the simpler, stylized setting serves to highlight this distinction and provides some intuition about it before we embark on the main argument.
There is an asset that pays dividends d, which are iid with d ~ N(y, 1/a). Disregarding learning effects over time, each agent receives a signal xi = d + εi composed of a public element d and a private element εi ~ N(0, 1/b). Expectations are heterogeneous because agents mix the common prior with the signals they receive individually:
Aggregated over the set of investors I, these private expectations yield an average expectation of
Let agent i form a second-order belief
Aggregating again and comparing to Equation (3) now shows that the average expectations operator is not a “normal” expectations operator. It violates the law of iterated expectations:
This violation in turn leads to systematic pricing errors in the market. Insofar as the relevant expectations operator is furnished by “the average investor,” one can see this heuristically by expanding the basic asset pricing equation
where mt is the stochastic discount factor. A failure of the law of iterated expectations thus also means a breakdown of the basic asset price equation. Allen et al. [42] essentially blame the disagreement induced by the private signals for this failure: “if there is differential information between investors so that there is some role for the average expectations about payoffs, the folding back of future outcomes to the present cannot easily be achieved.” This is akin to Keynes's position.
Indeed, if one eliminates the private signals from the model [which amounts to taking the limit 1/a → 0 in expression (1)], the law of iterated expectations starts to work again: . It thus appears that investor disagreement introduced some sort of noise that prevented the law from operating. In reality, though, it was not the disagreement that induced the failure. If we go to the other extreme and eliminate the public signal instead: xi = y + εi, the information agents receive is still differential and still induces diversity of beliefs . Yet aggregating over the set I of agents now yields . Suddenly, we find ourselves in Galton's world!
The reason the law of iterated expectations for the average expectations operator failed is that the expectations were not only diverse or differential but also correlated. And the reason for this is that the signals xi were coordinated by the public element d:
To summarize, the (potential) wedge between price and value associated with the failure of basic asset pricing relations and identified by the failure of the law of iterated expectations was caused not by the diversity of beliefs but by the correlation between them.
3. Asset Pricing Under Rational Beliefs
Kurz and Motolese [3] present an infinite-horizon, discrete-time equilibrium asset pricing model. In order to be self-contained, we provide a brief summary9.
Let be an exogenous random sequence of payoffs of a risky asset. This random sequence has a true probability which is possibly non-stationary, unknown, and unknowable but assumed to be weak asymptotic mean stationary (WAMS). The agents have a large sample of historical data dt, t = −1, −2, … at their disposal from which they infer a unique empirical probability measure. This empirical measure generates data according to
This is the common reference point for all agents i ∈ I = {1, 2, …, n}, where n is the number of agents in the system. The law of motion (16) fixes the set of rational beliefs.
Subjective beliefs about the fundamentals dt are formed by augmenting the stationary measure with an individual belief state :
The individual beliefs are assumed to be rational, which means that fluctuates around 0:
The innovations to the individual belief states are coupled by a correlation matrix Σg.
As diverse expectations are readily ascertained by agents, the state space is “expanded” by the average state of belief, dubbed “market belief” Zt:
This is basically a measure of market sentiment, with Zt > 0 indicating that agents on average expect temporarily higher than normal payoffs (and vice versa). Market belief or sentiment Zt evolves according to
Since Σg may be time-varying, Zt may be non-stationary. It is, however, also assumed to be WAMS, yielding a stationary representation with
By assumption,
Given this setup, there exists a unique equilibrium map d × Z → p from the state space to prices.
Proposition 3.1. Under the conditions described above, there exists a unique equilibrium price map
from the state space of fundamentals dt and market belief Zt to prices pt.
Proof: See [3, theorem 2]. □
Our main interest lies in this map. Can we use market belief or sentiment Zt to explain bubbles?
We examine the origin as well as nature of correlations between individual beliefs that can lead to a natural explanation of bubbles in this rational belief framework. We use a formalism in terms of processes, which is coarse-grained compared with the field of strategic noncooperative games, for which it has been proved that there exists two classes of correlated equilibria, exogenous, and endogenous [44, 45]. Our derivation of correlated equilibria performed in section 6 does not require the game theoretical mathematics and can proceed more intuitively and transparently.
4. Bubbles vs. Efficient Markets
In contrast to topics of similar standing, bubbles are remarkably contentious even on an existential level. This is because even after centuries the term is still not well-defined. The problem stems from the use of “fundamental value” in many definitions—a highly contingent concept of its own. In our view, it is fine to construct a theory of value; it is a stretch to build definitions on top of it. This is why we proposed, in [37], to re-define bubbles not in “money-space” where value lives but in the time-domain where the efficient market lives. Before presenting the idea, we provide a brief review of various bubble definitions that have been proposed in the literature to contrast with our present approach.
4.1. Bubble Definitions in the Literature
4.1.1. Statistical Definitions
As a first group of bubble definitions, there are those that focus on the price trajectory or other observables such as trading volume, without reference to theoretical notions like fundamental value. For example, Kindleberger and Aliber [46] regard as bubbles “any upward price movement over an extended period of 15 to 40 months that then implodes.” Exchanging the specification of the time-horizon for a size requirement, as it were, Goetzmann [47] defines bubbles as a doubling in the market price followed by a 50% fall10. Presumably, then, bubbles cannot occur in fixed income or other markets where there is a natural upper bound on the market price! The fund manager GMO proposes that bubbles occur “when prices rise two standard deviations above their norm” [49, 50]. This is more flexible than an absolute size requirement but, alas, opens a whole other can of worms, like estimation issues, ergodicity assumptions, or the question if the second moment even exists for a given asset.
Brock, as cited in [51], defines bubbles as “a monotonically increasing sequence of prices.” Hüsler et al. [52] and Leiss et al. [53] cite super-exponential growth rates11 as the hallmark of a bubble. This chimes with [46] in that it also implies an unsustainable price path but differs in that it does not require an “implosion” or market crash.
What the definitions in this category have in common is that they neither imply nor necessitate a mispricing per se. They focus on the observable (the price series) and do not mix theoretical concepts into the definition. In particular, there is no notion of value here. This is an appealing feature for a definition, as explanandum and explanans then are clearly separated from each other. Bubbles, defined like this, can be tested without the problem of the joint hypothesis. On the downside, insofar as a definition depends on the full path, including a crash at the end, it can be guilty of post hoc ergo propter hoc in practice. Insofar as the theoretical underpinning is lacking, the definitions in this category can also be too broad in scope: Empirically, too many price series can fit a statistical bubble definition without necessarily corresponding to our intuition of what a bubble “should” be. For example, an interest rate sensitive stock might follow a rate cycle up “over an extended period of fifteen to forty months” only to then “implode” upon the revelation of a criminal investigation. Few would characterize this as a bubble. Context, as it were, is important.
4.1.2. Comparative Definitions
As a second category, there are bubble definitions based on comparisons, usually between price and some notion of value. For instance, the New Palgrave Dictionary of Economics defines bubbles as “asset prices that exceed an asset's fundamental value” [54]. Bland as it may appear, this excludes the possibility of negative bubbles, a significant restriction to make by definition, as it were. Temin and Voth [55] by contrast identify bubbles as “periods of substantial mispricing” which allows for undervaluations as well as overvaluations but adds a size requirement (“substantial”). Levine et al. [56] define bubbles as simply a “misfit between the market price and the true value of an asset” with no such qualification. This lack of specificity makes it hard to see where the line between excess volatility and bubbles should be drawn. The point is not to niggle or read too much into what may have been intended as merely passing remarks in a much longer work. It is to show that just because a definition is done casually does not mean it has no consequences—especially when we have to relate different studies to each other.
Apart from direct appeals to value, comparisons can also refer, more obliquely, to the information sets on which “true value” is presumably based. For instance, Blanchard and Watson [5] define bubbles as price movements which are “unjustified by information available at the time.” More emphatically, Asness [57] demands that the term should apply only when “no reasonable future outcome can justify” the price. This seems to posit a range of admissible price paths, defining bubbles negatively, or by exclusion.
For all their differences, comparative definitions always require a theory of asset pricing, if only implicitly, for a notion of what the correct price is supposed to be. This is their Achilles' heel and the chief criticism of efficient market proponents. For example, Santos and Woodford [58] compare the market price of an asset to the state-price weighted sum of its real payoffs, while [59] uses the realized return on an asset over a sufficiently long time after trading. Different studies can thus agree, in general terms, to define bubbles as a divergence of price from value and still disagree over whether a particular price series is a bubble or not. This can make it all seem a bit arbitrary.
4.1.3. Detailed Definitions
A third group of definitions goes beyond the perceived gap between price and value by tying it to specific explanations. For example, Kirman and Teyssière [60] require that the gap between price and value be “endogenous, i.e., not directly produced by exogenous shocks.” In other words, the mispricing must arise in a certain way in order for it to count as a bubble. Brunnermeier and Oehmke [31] concur that “not every temporary mispricing can be called a bubble.” In particular, it has to arise “because investors believe they can sell the asset at an even higher price to some other investor in the future,” so for them the speculative motive is essential. Roubini [61] even introduces a policy dimension by distinguishing between “endogenous” and “exogenous” bubbles, where the former are bubbles whose “probability and size can be affected by monetary policy” while the latter cannot12. As an extreme example of the involute nature of the definitions in this category, let us quote from [63]:
I would say that a speculative bubble is a peculiar kind of fad or social epidemic that is regularly seen in speculative markets; not a wild orgy of delusions but a natural consequence of the principles of social psychology coupled with imperfect news media and information channels. […] I offered a definition of bubble that I think represents the term's best use: A situation in which news of price increases spurs investor enthusiasm which spreads by psychological contagion from person to person, in the process amplifying stories that might justify the price increases and bringing in a larger and larger class of investors, who, despite doubts about the real value of an investment, are drawn to it partly through envy of others' successes and partly through a gambler's excitement.
Basically the obverse to our first category, it is not surprising then to find that detailed definitions tend to be too narrow in scope. Would a bubble that arose by a different mechanism, or in a market in which the proposed mechanism does not apply, also be a “bubble”? For example, would a “political bubble” [64] not count as a bubble to [31]? Or if it did, doesn't this mean that there must exist a less restrictive superset of bubbles, of which the two variants (political vs. speculative) are but particular cases? And if not, how are we to relate the results and policy implications of different studies to each other? Would a bubble indicator constructed for, say, speculative bubbles still be expected to detect politically driven ones?
The above quote also illustrates that the more detailed a definition, the more likely it is to mesh the notion of bubbles with behavioral assumptions or market frictions. Arguably it is this that makes bubbles such a loaded term. With respect to recessions, inflation or unemployment, the debates may be vigorous but at least their subjects are accepted. By contrast, bubbles remain “existentially controversial.” Perhaps this is because the more detailed a definition, the more it acts as a Trojan horse: the mere use of the term may already admit of assumptions one does not wish to make. It is thus that the rejection of behavioral hypotheses or doubt about the effectiveness of monetary policy may lead one to reject the concept of bubbles, almost as an unintended side effect. For the sake of discussion, we should therefore move away from such evocative definitions toward greater formalism and pithiness. In the words of Brock [65], “for the quality of a theory to improve over time, definitions must become more rigorous and less ambiguous.”
4.2. Market Efficiency and Time-Dependence of Market Efficiency
It remains commonly overlooked that the concept of market efficiency has a time-dimension. Markets essentially transform informational inputs, modeled by a filtration , into price signals . Markets thus act as a map from news to price changes. Market attributes are naturally defined in terms of these primitives. Eliding the discount factor for simplicity, the efficiency of markets has been characterized by the martingale property (cf. [66–68]), where
A market is efficient relative to the news process iff the map produces a martingale. This means that price is an unbiased predictor and that an efficient market does not allow trading profits based on the current information set [69].
But just as efficiency can only be defined relative to an information set, it also requires a time-scale. It is implicitly understood in Equation (27) that the time step 1 from t to t + 1 is the relevant time-scale. That is, if we take t0 to be the present, Equation (27) can be written like
with n = 1 and the understanding that the martingale condition holds for n ∈ ℕ. But any given discrete-time price process can be seen as merely a sampling from an underlying continuous-time process, which could have been sampled at a different rate or frequency, say τ or T with 0 < τ < t < T. That a process is a martingale on one time-scale neither necessitates nor implies that it is one on another13. This opens the possibility that a market is efficient on one time-scale but inefficient on another.
Such a disjunction between time-scales can be supported empirically14 as well as theoretically, from reading [72] “in reverse”: To recap his argument, as long as liquidity is not infinite and there is a strictly positive bid-ask spread s > 0 in the market, successive price changes Δp will exhibit serial dependence and the martingale property will not hold. Adapting his notation, let those price changes be measured at the time-scale τ < t, i.e., Δp2τ = p2τ − pτ, to make the connection to our discussion clearer. The bid-ask spread induces an asymmetry in the price path at the scale τ (see Figure 1): If the last transaction was conducted at the bid, then the next move can only be up (by the spread s) or 0. If the last transaction was conducted at the ask, then the next move can only be down (by s) or 0. One time-step further, the situation is reversed. If the last move was up or 0 (down or 0), then the next move can only be down or 0 (up or 0). The bid-ask spread thus introduces a serial dependence into successive price movements that is not compatible with the martingale condition of an efficient market.
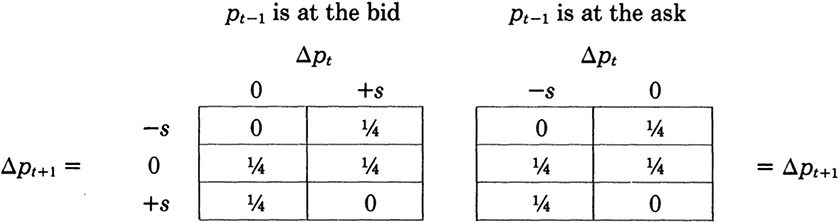
Figure 1. Table of transition probabilities, conditional on the last transaction having been conducted at the bid or at the ask price, adapted from [72, p. 1129].
At the same time, over a sufficient number n of time-steps τ, the transition probabilities converge to a (symmetric) steady state. This means that for t ≥ nτ, with n sufficiently large, the effect of the bid-ask spread (or, by extension, other microstructural factors) “washes out”: Measured on the micro-scale τ, the process exhibits serial dependence; measured on the macro-scale t ≥ nτ, the price process can conform to the martingale property again.
Let us illustrate this phenomenon analytically with a toy model, the two-step random walk in [73], a special case of the class of persistent random walks [cf. [74], section 5.2]. Let Δp ∈ {U, D} for up = +1, down = -1. Define πUU as the joint probability that the price goes up twice in a row; πUD as the probability that an up move is followed by a down move; and πDD, πDU as the probabilities of down-down and down-up moves. Let πUU = 1/6, πDU = πUD = 1/3, πDD = 1/6. Suppose the last move was up and start at time t0 with pt0 = 100. Then
where πU|U, πD|U are the corresponding conditional probabilities. That is, one time-step forward, this two-step random walk is not a martingale. However, if we perform the same calculation two time-steps forward,
The reason is that the memory gets lost at the time-scale t = 2τ,
As a result, even though the same price process exhibits serial correlation at the scale τ, it conforms to the martingale property at the scale t = 2τ.
4.3. Bubbles as Elongations of Characteristic Time-Scales of Markets
We call the time-scale at which the martingale property holds the characteristic time-scale of a market. It is inversely proportional to the speed with which a market can “digest” information. Not only do different markets process information at different speeds, the same market can slow down or speed up over time. Projected onto the time-line, bubbles appear as regimes in which the speed of a market slows down significantly from normal.
Definition 4.1. Given a market that is efficient relative to at the time-scale t, a t-bubble occurs when the price process changes such that the martingale condition now only holds at time-scales T > t. As a boundary case, we include regimes where T = ∞ or the condition never holds.
Colloquially, we may call t-bubbles simply “bubbles” so long as it is clear that the notion only makes sense when set in relation to the characteristic time-scale t of the market. Conversely, a bubble is a slowdown in the map from the “normal speed” ~1/t of the market to ~1/T—a sort of “informational constipation” if you will, as the “digestion” of news becomes slower15.
Our re-definition of bubbles is sufficiently general so as to be compatible with most of the existing definitions in the literature. The lengthening of the time-scale only serves to create space for a variety of bubble dynamics “in-between” the points at which the martingale property is restored. The general principle is to eliminate (the conditions for) the bubble from a model and inspect the time-scale t at which the market in the model is efficient. If the bubble component has a finite survival time, this can be taken as a lower bound for T. For example, under the limited arbitrage argument of [78], the duration of the bubble is finite with a survival time of (in their notation). Without the bubble, the market's characteristic time-scale is t; with a bubble, it slows down to .
To sum up, market efficiency has a time-dimension. It is therefore not enough to speak of a market as efficient. In addition to the news process relative to which efficiency is defined, one also needs to state at which time-scale efficiency is supposed to hold. The time it takes a market to fully absorb an information increment can be random but has a characteristic scale, in the sense that it fluctuates within certain bounds or that its mean is defined. In the following, we will take this characteristic time-scale of a market as a given16.
4.3.1. Application to REBs
Blanchard [4] constitutes an interesting example because even under a bubble the price path still follows a martingale. In equilibrium, the probability of a crash is supposed to exactly balance the added growth factor of the bubble component , where is the fundamental value, or
if we elide the discount factor for simplicity. That is, the price would simply incorporate the bubble component via
Note however that is generated by fundamental variables as well as the bubble component . But definition 4.1 relies on an efficient market as a benchmark. Therefore, the bubble according to 4.1 cannot be defined relative to . Instead, we must introduce a “copy” of the market, a hypothetical market in which all the elements are the same (agents and their preferences, assets, institutions, etc.) except the information process, which must exclude the bubble component bt. Denoting this filtration ,
That is, relative to the efficient market, the bubble component introduces an estimation or valuation error which survives with probability π and collapses with probability 1 − π in [4]. It thus has an expected length of π/(1 − π) time-steps, or T ≥ π/(1−π) time steps. For example, if π =.95, then T ≥ 19 time steps. As the probability (1 − π) of a crash approaches zero, T → ∞ in the limit.
4.3.2. Application to [3]
In accordance with definition 4.1, we must first specify an efficient benchmark against which a bubble can be defined. In [3], the natural benchmark is a market driven exclusively by the fundamentals (dt), or the price map pt = P0 + addt (see theorem 3.1). This relationship holds when the correlation of beliefs is sufficiently low for the law of large numbers to apply and market belief to vanish. Since the stable distribution of the dividend process is persistent (cf. Equation 16), we have
This means that any dividend shock will wash out exponentially fast, or that the market is (approximately) efficient at a time-scale T, where for any chosen tolerance ε > 0. For the sake of argument, let us fix λd = 1/4 and ε = 1/100. Then the market is efficient at the time-scale of 4 time steps.
If market belief Zt enters the equation because “due to correlation across agents, the law of large numbers is not operative,” ([3], p. 301) there are two scenarios. One, it has the same, or lower, persistence with 0 < λZ ≤ 1/4 in Equation (23). Then market belief increases the variance of the process but does not change the efficient time-scale. This was the original focus of [3]. Two, λZ > λd. Suppose, for instance, that λZ = 3/4. Now the innovations to market belief Zt affect the expected price (under the stable distribution) for T = 17 periods.
So far, we haven't done anything yet. It is simply an observation that if λZ > λd, market belief Zt potentially slows down the market or “interferes” with the fundamentals dt in the equilibrium price equation. This conforms to our re-definition of bubbles in terms of time-scales rather than price-value divergences but there is nothing in the original work of Kurz and Motolese [3] that would motivate a particular parameterization.
In the following, we now propose two extensions or modifications to the model: First, to find an “on/off” switch for market belief Zt in the parameter space of the dependence structure of beliefs, we propose to generate Σg from a “social graph.” This reduces the dimensionality of the problem and at the same time provides a natural partition of the parameter space. Then, to emphasize or perhaps motivate λZ > λd, we use linear aggregation [40, 41] to move the model beyond a simple parametrization. The aggregation of short-memory correlated belief transitions can lead to a long-memory series. The resulting divide between fast-moving fundamentals dt and slow-moving market belief Zt magnifies the bubble effect outlined above.
5. How Much Dependence Is Enough?
This section discusses the first modification to the model of [3], which consists in introducing a “social graph” to motivate the existence of a non-trivial correlation matrix Σg of the innovations to the individual belief states defined in Equation (19). In other words, we propose to generate Σg from a “social graph,” which represents the investor population. For simplicity, we use the Erdős-Renyi random graph model G(n, p), where n is the number of agents (or vertices) in the system and p ∈ [0, 1] is the probability with which a random pair of agents i, j is linked by an edge {i, j}. The edge is represented by a set as opposed to a tuple as we take the graph to be undirected. To keep things tractable, we also do not assign weights to links or distinguish between different degrees of correlation.
Whenever agents (or their nodes) are connected in the graph, we take their beliefs to be correlated17. Moreover, we let their beliefs be correlated by a constant , thereby abstracting not only from directions of influence (by the undirectedness of the graph) but also from variations in the degree of influence18. In our model, the pertinent fact is that (or whether) there exists some level of mutual influence or communication, regardless of its direction or strength. Formally, Σg is constructed via the rule ∀i ≠ j ∈ {1, …, n},
where is the (i, j)-th component of Σg. Since the social graph of the agents is random, so is Σg.
A group of agents that is connected to each other, or whose beliefs are correlated, is called a clique or “component” of the graph. One can distinguish between two kinds of cliques or components. If the size of a clique does not scale with the total number of agents in the system, or is independent of n, then we call it a “small component.” If a clique is such that it becomes larger the larger becomes n, it is called a “giant component.” This difference in the scaling behavior of cliques has an important consequence for Σg.
By construction, the correlation of beliefs is transitive: if agents i, j have correlated beliefs and agents j, k also have correlated beliefs, then so do agents i, k. Graphically, this means that every clique of agents can, after appropriate reshuffling of the indices, be represented by a block matrix in Σg. The size of a clique is the number of nodes or agents contained in it. If a clique of correlated agents has size m, say, then the corresponding block matrix in Σg is of m × m dimension. Obviously, if we pick any off-diagonal entry from such a block, its value is ; if we pick an entry of Σg that is not part of a clique, then its value is zero. But what about a random pick from Σg, i.e., the unconditional expectation ) or average correlation in the system as a whole?
The average correlation of beliefs depends on whether the agents are organized into many small separate components or into a giant connected component. The intuition is that components or cliques of correlated agents in the original space act like “composite agents” when transposed into eigenspace19. The law of large numbers then acts, or not, on these “composite agents,” which are independent but differently-sized, instead of the actual agents, which are equally-sized but correlated. A system with 1,000 isolated agents behaves essentially the same as a system with 2,000 agents who are organized into cliques of 2.
Small components do not scale with n. As the graph increases from, say, 100 to 1,000 agents, there are more cliques but of the same size (or size distribution) as before. A giant component, by contrast, scales with the system size n. Its size is a constant fraction S ∈ [0, 1] of n. As a giant connected component arises in the social graph of agents (or their beliefs), the weight of the non-zero correlations in Σg remains a constant fraction of the total, and the average correlation of beliefs in the system becomes positive.
Formally, the question is how the average correlation of beliefs behaves as the system becomes large, or
as n → ∞. Let c = (n − 1)p be the mean degree of the graph20. The average size of the small components is
The fraction S of the n agents or vertices contained in a giant connected component depends on c and is the solution or fixed point of
When c < 1, S = 0 or there is no giant component in the graph. This yields an average correlation coefficient of
As the system size n increases, the average correlation tends to 0, and in the limit, we can take .
When c ≥ 1, a giant component emerges in the graph and the system behaves differently. The reason is that unlike the small components, the giant component scales with the system size n. Then the average correlation of beliefs is
as n → ∞ which is strictly positive.
Our use of the Erdős-Renyi random graph theory has been made for the sake of simplicity and tractability. It will be interesting in the future to extend our treatment to the case of Barabasi-Albert networks and other random geometric graphs. However, our main point on the emergence of a non-zero average correlation of beliefs will not be changed. What will be modified are the specific control parameters and conditions under which a non-zero average correlation of beliefs emerges. Furthermore, the application to real-world social networks is reported to a future work.
6. The Emergence of Bubbles
We now make the following modification to [3]:
Axiom 6.1. Let the agents have coefficients λig in (19). In particular, we assume that the coefficients λig are drawn from a family of absolutely continuous distributions with support [0, 1) with density
with parameters −1/2 < b < 0 and 0 < cb < ∞.
The density in the axiom is only specified for values close to 1, so this is a flexible semiparametric specification. The only hard requirement is that the coefficients cannot be bounded away from 1 (although they can never attain it). Agents now differ from each other w.r.t. the persistence of their belief states . This means that agents differ in their trading horizons: Short-term day traders form subjective expectations that flit around much faster than long-term investors who form expectations over multi-year, even decade-long horizons.
As a result of this positive average correlation in the system, market belief Zt will assume long-memory and a price bubble develops, as we now show.
Proposition 6.1. Suppose that or that the average correlation of beliefs in Σg is positive. Then there exists a common component or “representative belief" πt ~ N(0, ϑ) iid in the innovations and the transition functions (19) of agent states of belief can be rewritten in terms of this representative belief to
As a consequence, the aggregate market belief Zt assumes long memory persistence.
Proof: Since Σg is symmetric and positive definite, we can perform a spectral decomposition
where S is the matrix of eigenvectors, Θ is the n-dimensional matrix with the eigenvalues ϑi, i = 1, …, n on the diagonal, , the n-dimensional identity matrix, , and ϑi ≠ ϑj, ∀i ≠ j.
According to [81], if , which we have shown above to be the case when a giant connected component arises in the social graph of the agents, then the biggest eigenvalue, ϑ1, is distributed according to
For correlation matrices, one needs to ensure positive definiteness of Σg and [82] show that the result remains valid under suitable restrictions on the support of the off-diagonal entries for large sample correlation matrices.
Given that , all other eigenvalues ϑi> 1 are therefore constrained to be of the order . That is, the larger the system, the greater the dominance of the largest eigenvalue, ϑ1, over all others, ϑi> 1. Furthermore, as the variance, unlike the mean, in (54) does not scale with n, this dominance also becomes more certain as n grows large.
We exploit this by rewriting the innovations in individual states of belief in terms of a factor model
where is the first principal component
and “factor loading" si1 is the (i, 1)-th component of eigenvector matrix S or the i-th component of the first eigenvector S1. Since is simply a linear combination of (multivariate) Gaussians with mean 0 and variance , it is itself ~ N(0, ϑ1). The belief transitions (19) now take the form
where L is the lag operator.
Hidden in the is the variation of all the other principal components in eigenspace. Since the system is orthogonal, all the summands are independent from each other. Again, each principal component is nothing but a different linear combination of the original innovations (Equation 56), hence . because the total variance is finite. Therefore, the series converges to zero as n → ∞ [83, thm. 22.6].
It follows that we can neglect the idiosyncratic terms and rewrite individual beliefs solely in terms of the common component
Accordingly, market belief (21) now takes the form
If we expand this expression,
A stochastic process has long memory if its spectral density is of the form L(ω)|ω|−2d, for some slowly varying function L at zero and [84]. Zaffaroni [41] shows that, for coefficients λig distributed according to expression (51) with b > −1/2, the coefficients in (63) converge
with
for some constant a as k → ∞, and that the limit process
has a spectral density ~ cω−2d if b < 0, for some constant c and d = −b. □
For example, what is the probability that the equilibrium price will lie at least one standard deviation of Zt above P0 for a period of 100 days? To isolate the effect of long memory on the bubble probability, we normalize the variance of Zt to a constant 1 for all t and calculate . Recalling that Zt is a Gaussian process, we note that
where 1 is the 100 × 1 vector of ones, ·′ indicates the transpose, and Σ100 is the 100 × 100-dimensional covariance matrix of (Z1, …, Z100) with (i, j)-entries .
Case 1: Independence. Under time independence, i.e., if Zt were iid, the entries in Σ100 are equal to 0 for i ≠ j and 1 for i = j. Then
and the probability .
Case 2: Short memory. Under the setup of [3], we have exponentially decaying autocorrelations and the (i, j)-th entry of Σ100 is
This corresponds to the yellow line in Figure 2. For comparison purposes, we choose a value of λZ ≃ .77, which yields
and the probability or less than 1 in 8,500.
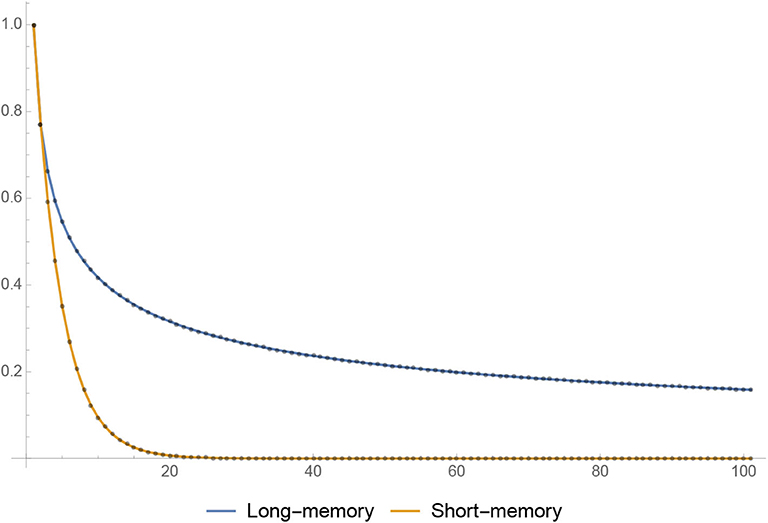
Figure 2. First 100 autocorrelations of the original, short-memory (yellow) and the modified, long-memory (blue) processes, where the parameters are chosen such that the first-order autocorrelation is equal.
Case 3: Long memory. By contrast with the previous cases, we see a significant probability of bubbles arising under the long memory specification of the previous section, with coefficients as in Equation (65). The (i, j)-th entry of Σ100 is now
Figure 2 plots the first 100 autocorrelations for a parametrization of b = −1/4 or λZ ≃ .77 (both yielding the same first-order autocorrelations).
The slowly decaying off-diagonal entries of Σ100 lead to a much higher dispersion of the sum,
and the probability or about 1 in 27. Ceteris paribus, introducing long memory increased the chances of a bubble by two orders of magnitude.
7. Conclusion
We mentioned in the introduction that the theoretical setting in which bubbles are conceived has practical implications. If bubbles can arise, as we have argued, even under idealized circumstances—in a world of perfectly rational agents acting in markets with no frictions or “limits of arbitrage”—then they should be recognized as a general and system-immanent feature of market economies. Continuing to view them as aberrations, due to specific faults or circumstances, implies that one can “lean against” or eradicate them by addressing said faults or circumstances. This strikes us as an attempt to suppress the tides. We favor building dykes instead, guarding against their inevitable recurrence by increasing the robustness of the system.
It is also not clear that bubbles are necessarily “bad.” Indeed, another way to look at them is as the free-market alternative of industrial policy, i.e. as a spontaneous and decentralized way to achieve coordination, instead of the controlled and centralized approach favored in statist economies. This would be another argument against efforts to suppress bubbles. Alas, it is undeniable that bubbles can have bad consequences, particularly if they end in “crashes” or sudden ruptures which can destabilize the system at large.
To make a rational policy tradeoff, we therefore need two further elements, apart from the bubble itself: One, a model of what might be termed “rational belief crashes,” noting that there is no violent ending inherent in rational belief bubbles themselves. This conforms to the view explored here that bubbles and crashes are separate events and require separate theories. A bubble does not have to end in a crash (it can deflate gently), just as an asset price can crash without a bubble (adverse news, e.g., in the form of a lawsuit, may arrive). The second element that is needed is a welfare analytical model of how rational belief bubbles and crashes fit into an economy with a production and a banking sector.
In terms of empirical applications, we would like to see an augmentation of current sentiment indicators with cross-sectional quantities [recall 32, lemma 1]. This could lead to a “real-time” bubble indicator based on disaggregated, contemporaneous expectations. As far as we are aware, current bubble indicators, which are used to monitor financial markets and systemic risk, are based on historical data and/or estimates of fundamental value.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author's Note
An earlier preliminary version of this manuscript has been released as a pre-print on July 2018 at http://ssrn.com/abstract=3176871 with the present authors (HS-U and DS). The present extended version has been released as a pre-print at http://ssrn.com/abstract=3530895 with the same authors [85].
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank (in alphabetical order) Thorsten Hens, Mordecai Kurz, Maurizio Motolese, Hiroyuki Nakata, and Carsten K. Nielsen, and seminar participants at the BIS for helpful comments. Financial support from the Institute for New Economic Thinking (INET) is gratefully acknowledged.
Footnotes
1. ^If a REB exists at any time t > 0, then it must also exist at t − 1.
2. ^To be distinguished from choice-theoretic rationality. See [27] for a critique of the terminology.
3. ^One way to think about it is that a non-stationary environment underdetermines the set of admissible, or rational, expectations (an expectation is inadmissible, or irrational, if it leads to systematic mistakes). If rational expectations are the fixed-point solution of a function, rational beliefs are the fixed-set solution of a correspondence.
4. ^Asked to guess the weight of an ox, none of the 787 individual estimates from the attending crowd were correct but the “middlemost” (presumably the median in today's terminology; the OED defines the word as “That […] in the very middle, or nearest the middle.”) came within less than one percent of the correct value (1,207 vs. 1,198 lbs.), beating all but a handful of presumably lucky individuals.
5. ^As Brunnermeier and Oehmke [31] point out, “much of the theoretical literature on bubbles can be seen as an attempt to formalize this [Minsky's] narrative.”
7. ^We identified the general mechanism behind this way of thinking as a form of explicit symmetry breaking, a notion borrowed from theoretical physics, in [8]. Breaking the symmetry inherent in a diverse set of beliefs explicitly (as opposed to spontaneously) also explains the need for frictions in these models.
8. ^Recall that REBs, by contrast, cannot be restarted once they are deflated.
9. ^For a quick overview of rational belief theory, we refer to its entry in Wikipedia which one of us (HS) contributed. For a survey, see [26].
10. ^One may recall here that [48] defined efficient markets as ones “in which price is within a factor of 2 of value. […] The factor of 2 is arbitrary, of course.”
11. ^faster than exponential growth, or growth rates that themselves grow.
12. ^A similar but more general argument, less focused on monetary policy, has been put forth in [62].
13. ^In [37], we use so-called n-step or persistent random walks as an example. Another way to see this is by letting the expectation cycle through a periodic function, e.g. a sine-curve: xt = sin(t) + ϵt with ϵ ~ N(0, σ2). Then Et(xt+2πn) = xt. As long as we sample at the frequency of (2π)−1, the series looks like a martingale but at any other frequency, it is not.
14. ^See for example [70] or, more plastically, the case study of [71]. The point being that a market, no matter how efficient, always needs some time to digest information.
15. ^An incarnation of this is provided by the Hawkes self-excited conditional Poisson process, which has been used to characterize the level of endogeneity or reflexivity of financial markets [75–77]. As the “branching ratio” approaches 1, the market becomes more and more endogenous and the response time to shocks diverges, so that news have a longer and longer lived impact.
16. ^It is also possible, though, to conceive of financial markets in which the mean time to digest news diverges. This could occur, for instance, when the absorption time is distributed according to a power law in the tail with tail exponent <1. As many response functions are power laws in the time domain with small exponent, this is indeed an interesting possibility. In this case, the market would never be efficient even at arbitrarily large time-scales.
17. ^For those unfamiliar with the terminology of graphs, note that there is a difference between two agents being “linked” by an edge and being “connected” by a path. Vertices i, j in the graph are said to be linked if the graph contains an edge {i, j} between them. For vertices to be connected, it suffices that there exist a path between them. Agents that are linked are also connected but agents may be connected without being linked. For example, if agents i and j are linked by {i, j} and agents j and k are linked by {j, k} but there is no edge between agents i and k, agents i and k are still considered connected via the path {{i, j}, {j, k}}.
18. ^That is chosen positive stems from the fact that sufficiently large groups of agents cannot be all negatively correlated. Suppose, for example, that there are three agents i, j, k all perfectly negatively correlated. If i becomes more optimistic, j must become more pessimistic, which means k must become more optimistic. But this belies the negative correlation between i and k. The same principle holds with less-than-perfect (negative) dependence in larger groups.
19. ^This is the basic idea of principal component analysis [79].
20. ^We skip calculations that do not add to the main point and refer interested readers to [80] instead.
References
1. Kurz M. On the structure and diversity of rational beliefs. Econ Theor. (1994) 4:877–900. doi: 10.1007/BF01213817
3. Kurz M, Motolese M. Diverse beliefs and time variability of risk premia. Econ Theor. (2011) 47:293–335. doi: 10.1007/s00199-010-0550-1
4. Blanchard OJ. Speculative bubbles, crashes and rational expectations. Econ Lett. (1979) 3:387–89. doi: 10.1016/0165-1765(79)90017-X
5. Blanchard O, Watson MW. Bubbles, rational expectations and financial markets. In: Wachtel P, editor. Crises in the Economic and Financial Structure. Lexington, MA: Lexington Books (1982) 5:295–315. doi: 10.3386/w0945
6. Tirole J. Asset bubbles and overlapping generations. Econometrica. (1985) 53:1499–528. doi: 10.2307/1913232
7. Kaizoji T, Sornette D. Bubbles and crashes. In R. Cont, editor, Encyclopedia of Quantitative Finance. Hoboken, NJ: Wiley. (2010).
9. Schatz M, Sornette D. Inefficient bubbles and efficient drawdowns in financial markets. Int J Theor Appl Fin. (2020). Available online at: https://ideas.repec.org/p/chf/rpseri/rp1849.html
10. Mandelbrot B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science. (1967) 156:636–8. doi: 10.1126/science.156.3775.636
12. Shin HS. Securitisation and financial stability. Econ J. (2009) 119:309–32. doi: 10.1111/j.1468-0297.2008.02239.x
13. Brock WA, Hommes CH, Wagener FOO. More hedging instruments may destabilize markets. J Econ Dyn Control. (2009) 33:1912–8. doi: 10.1016/j.jedc.2009.05.004
14. Farmer JD, Lo AW. Frontiers of finance: evolution and efficient markets. Proc Natl Acad Sci USA. (1999) 96:9991–2. doi: 10.1073/pnas.96.18.9991
15. Evstigneev IV, Hens T, Schenk-Hoppé K. Evolutionary finance. In: T. Hens and K. Schenk-Hoppé, editors. Handbook of Financial Markets: Dynamics and Evolution. North-Holland; Amsterdam. (2009).
17. Dufwenberg M, Lindqvist T, Moore E. Bubbles and experience: an experiment. Am Econ Rev. (2005) 95:1731–7. doi: 10.1257/000282805775014362
18. Sornette D, Cauwels P. 1980-2008: The Illusion of the Perpetual Money Machine and what it bodes for the future. Risks. (2014) 2:103–31. doi: 10.3390/risks2020103
19. Reid J, Nicol C, Burns N, Chanda S. The Next Financial Cri 2017. Deutsche Bank Markets Research.
20. Diba BT, Grossman HI. On the inception of rational bubbles. Q J Econ. (1987) 102:697–700. doi: 10.2307/1884225
21. Diba BT, Grossman HI. The theory of rational bubbles in stock prices. Econ J. (1988) 98:746–54. doi: 10.2307/2233912
22. Benhabib J, Farmer REA. Indeterminacy and sunspots in macroeconomics. In: Taylor JB, Woodford M, editors. Handbook of Macroeconomics. 1st ed. Amsterdam: Elseiver (1999). doi: 10.1016/S1574-0048(99)01009-5
23. Grossman SJ, Stiglitz JE. On the impossibility of informationally efficient markets. Am Econ Rev. (1980) 70:393–408.
24. Hellwig MF. On the aggregation of information in competitive markets. J Econ Theor. (1980) 22:477–98. doi: 10.1016/0022-0531(80)90056-3
25. Diamond DW, Verrecchia RE. Information aggregation in a noisy rational expectations economy. J Fin Econ. (1981) 9:221–35. doi: 10.1016/0304-405X(81)90026-X
26. Motolese M, Nielsen CK. Rational beliefs theory: a review. Rivista Internazionale di Scienze Sociali. (2007) 293–326.
27. Kurz M. Symposium: on the role of market belief in economic dynamics, an introduction. Econ Theor. (2011) 47:189–204. doi: 10.1007/s00199-010-0560-z
29. Galton F. Memories of My Life. North Yorkshire: Methuen & Co. (1908). doi: 10.5962/bhl.title.28398
30. Keynes JM. The General Theory of Employment Interest and Money. London: Palgrave Macmillan. (1936).
31. Brunnermeier MK, Oehmke M. Bubbles, financial crises, and systemic risk. In: Constantinides GM, Harris M, Stulz RM, editors. Handbook of the Economics of Finance. Vol. 2B. Handbooks in Economics. Amsterdam: Elseiver (2013). doi: 10.1016/B978-0-44-459406-8.00018-4
32. Grossman SJ. On the efficiency of competitive stock markets where traders have diverse information. J Fin. (1976) 31:573–85. doi: 10.1111/j.1540-6261.1976.tb01907.x
33. Chancellor E. Devil Take the Hindmost: A History of Financial Speculation. New York, NY: Plume. (1999).
35. Boldrin M, Nishimura K, Shigoka T, Makoto Y. Chaotic equilibrium dynamics in endogenous growth models. J Econ Theor. (2001) 96:97–132. doi: 10.1006/jeth.2000.2677
36. Corcos A, Eckmann JP, Malaspinas A, Malevergne Y, Sornette D. Imitation and contrarian behavior: hyperbolic bubbles, crashes and chaos. Quant Fin. (2002) 2:264–81. doi: 10.1088/1469-7688/2/4/303
38. Bingham NH, Rogers LCG. Summability Methods and almost-sure convergence. In: Bellow A, Jones RL, editors. Almost Everywhere Convergence II. Cambridge, MA: Academic Press. (1991). p. 69–83. doi: 10.1016/B978-0-12-085520-9.50012-5
40. Granger CWJ. Long memory relationships and the aggregation of dynamic models. J Econ. (1980) 14:227–38. doi: 10.1016/0304-4076(80)90092-5
41. Zaffaroni P. Contemporaneous aggregation of linear dynamic models in large economies. J Econ. (2004) 120:75–102. doi: 10.1016/S0304-4076(03)00207-0
42. Allen F, Morris S, Shin HS. Beauty contests and iterated expectations in asset markets. Rev Fin Stud. (2006) 19:161–77. doi: 10.1093/rfs/hhj036
43. Xiong W. Bubbles, crises, and heterogeneous beliefs. In: Fouque JP, Langsam JA, editors. Handbook on Systemic Risk. Cambridge, UK: Cambridge University Press (2013). p. 663–713. doi: 10.1017/CBO9781139151184.033
44. Kono N. Noncooperative game in cooperation: reformulation of correlated equilibria. Kyoto Econ Rev. (2008) 77:107–25. Available online at: https://www.jstor.org/stable/43213362
45. Kono N. Noncooperative game in cooperation: reformulation of correlated equilibria (II). Kyoto Econ Rev. (2008) 78:1–18. Available online at: https://www.jstor.org/stable/43213369
46. Kindleberger CP, Aliber RZ. Manias, Panics, and Crashes: A History of Financial Crises. 5th Edn. (2005). doi: 10.1057/9780230628045
47. Goetzmann WN. Bubble investing: learning from history. In: Chambers D, Dimson E, editors. Financial Market History: Reflections on the Past for Investors To. Charlottesville, Va: CFA Institute. (2017). pp. 149–69.
51. Veres B. Woody Brock's challenge to Krugman and the Keynesians. Advisor Perspectives. (2013). Available online at: https://www.advisorperspectives.com/newsletters13/pdfs/Woody_Brocks_Challenge_to_Krugman_and_the_Keynesians.pdf
52. Hüsler A, Sornette D, Hommes CH. Super-exponential bubbles in lab experiments: evidence for anchoring over-optimistic expectations on price. J Econ Behav Organ. (2013) 92:304–16. doi: 10.1016/j.jebo.2013.06.005
53. Leiss M, Nax HH, Sornette D. Super-exponential growth expectations and the global financial crisis. J Econ Dyn Control. (2015) 55:1–13. doi: 10.1016/j.jedc.2015.03.005
54. Brunnermeier MK. Bubbles. In: Durlauf SN, Blume LE, editors. The New Palgrave Dictionary of Economics. 2nd ed. London: Palgrave Macmillan. (2008). doi: 10.1057/978-1-349-95121-5_44-2
55. Temin P, Voth HJ. Riding the South Sea bubble. Am Econ Rev. (2004) 94:1654–68. doi: 10.1257/0002828043052268
56. Levine SS, Apfelbaum EP, Bernard M, Bartelt VL, Zajac EJ, Stark D. Ethnic diversity deflates price bubbles. Proc Natl Acad Sci USA. (2014) 111:18524–9. doi: 10.1073/pnas.1407301111
58. Santos M, Woodford M. Rational asset pricing bubbles. Econometrica. (1997) 65:19–57. doi: 10.2307/2171812
59. Siegel JJ. What is an asset price bubble? An operational definition. Eur Fin Manage. (2003) 9:11–24. doi: 10.1111/1468-036X.00206
60. Kirman AP, Teyssière G. Bubbles and long-range dependence in asset prices volatilities. In: Hommes CH, Ramer R, Withagen CA, editors. Equilibrium, Markets, and Dynamics: Essays in Honour of Claus Wedepohl. Hoboken, NJ: Wiley. (2002). doi: 10.1007/978-3-642-56131-3_22
61. Roubini N. Why central banks should burst bubbles. Int Fin. (2006) 9:87–107. doi: 10.1111/j.1468-2362.2006.00032.x
62. Johansen A, Sornette D. Shocks, Crashes and bubbles in financial markets. Brussels Econ Rev. (2010) 53:201–53.
63. Shiller RJ. Speculative asset prices. Am Econ Rev. (2014) 104:1486–517. doi: 10.1257/aer.104.6.1486
64. McCarty N, Poole KT, Rosenthal H. Political Bubbles: Financial Crises and the Failure of American Democracy. Princeton, NJ: Princeton University Press (2013). doi: 10.1515/9781400846399
65. Brock HW. Resolving the market efficiency paradox. SED: Strategic Economic Decisions. (2014). Available online at: http://www.sedinc.com/index.php?eID=tx_nawsecuredl&u=0&file=fileadmin/user_upload/reports/March_2014/March_2014_SED_PROFILE.pdf&t=1592843788&hash=b35ee8273298892f2132c4862380abd7
66. Samuelson PA. Proof that properly anticipated prices fluctuate randomly. Indus Manage Rev. (1965) 6:41–9.
67. Samuelson PA. Proof that properly discounted present values of assets vibrate randomly. Bell J Econ Manage Sci. (1973) 4:369–74. doi: 10.2307/3003046
69. Jensen MC. Some anomalous evidence regarding market efficiency. J Finan Econ. (1978) 6:95–101. doi: 10.1016/0304-405X(78)90025-9
70. Barany E, Beccar Varela MP. Long correlations applied to the study of memory effects in high frequency (tick) data, the dow jones index, and international indices. In: Viens FG, Mariani MC, Florescu I, editors. Handbook of Modeling High-Frequency Data in Finance. Hoboken, NJ: Wiley. (2012). doi: 10.1002/9781118204580.ch6
71. Maloney MT, Mulherin JH. The complexity of price discovery in an efficient market: the stock market reaction to the challenger crash. J Corpor Finan. (2003) 9:453–79. doi: 10.1016/S0929-1199(02)00055-X
72. Roll R. A simple implicit measure of the effective bid-ask spread in an efficient market. J Finan. (1984) 39:1127–39. doi: 10.1111/j.1540-6261.1984.tb03897.x
73. Sornette D and Arneodo A. Chaos, pseudo-random number generators and the random walk problem. J Phys. (1984) 45:1843. doi: 10.1051/jphys:0198400450120184300
74. Rudnick J, Gaspari G. Elements of the Random Walk: An introduction for Advanced Students and Researchers. Cambridge, UK: Cambridge University Press (2004). doi: 10.1017/CBO9780511610912
75. Filimonov VA, Sornette D. Quantifying reflexivity in financial markets: towards a prediction of flash crashes. Phys Rev E. (2012) 85:056108. doi: 10.1103/PhysRevE.85.056108
76. Filimonov V, Bicchetti D, Maystre N, Sornette D. Quantification of the high level of endogeneity and of structural regime shifts in commodity prices. J Int Money Finan. (2014) 42:174–92. doi: 10.1016/j.jimonfin.2013.08.010
77. Wheatley S, Wehrli A, Sornette D. The endo-exo problem in high frequency financial price fluctuations and rejecting criticality. Quant Finan. (2019) 19:1165–78. doi: 10.1080/14697688.2018.1550266
78. Abreu D, Brunnermeier MK. Bubbles and crashes. Econometrica. (2003) 71:173–204. doi: 10.1111/1468-0262.00393
79. Jolliffe IT. Principal Component Analysis. New York, NY: Springer Series in Statistics. 2nd ed. Springer (2002).
81. Füredi Z, Komlós J. The eigenvalue of random symmetric matrices. Combinatorica. (1981) 1:233–41.
82. Malevergne Y, Sornette D. Collective origin of the coexistence of apparent random matrix theory noise and of factors in large sample correlation matrices. Phys A. (2004) 331:660–8. doi: 10.1016/j.physa.2003.09.004
84. Beran J, Feng Y, Ghosh S, Kulik R. Long-Memory Processes: Probabilistic Properties and Statistical Methods. Berlin: Springer (2013).
85. Sohn H, Sornette D. Rational Belief Bubbles. Swiss Finance Institute Research Paper No. (2020) 20–05. Available online at: https://ssrn.com/abstract=3530895.
Keywords: asset pricing, bubbles, efficient markets, rational expectations, rational beliefs, aggregation, heterogeneous expectations, correlated beliefs,
JEL Classification: B20, D53, D58, D81, D83, D84, D85, E13, G00.
Citation: Sohn H-U and Sornette D (2020) Rational Belief Bubbles. Front. Phys. 8:230. doi: 10.3389/fphy.2020.00230
Received: 05 February 2020; Accepted: 28 May 2020;
Published: 10 August 2020.
Edited by:
Siew Ann Cheong, Nanyang Technological University, SingaporeReviewed by:
Satyam Mukherjee, Indian Institute of Management Udaipur, IndiaYuji Aruka, Chuo University, Japan
Copyright © 2020 Sohn and Sornette. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hyun-U Sohn, aHNvaG5AcG0ubWU=; Didier Sornette, ZHNvcm5ldHRlQGV0aHouY2g=
 Hyun-U Sohn
Hyun-U Sohn Didier Sornette
Didier Sornette