GGA and GGA Plus U Study of Half-Metallic Quaternary Heusler Compound CoCrScSn

Introduction

Spintronics, also known as magnetoelectronics, is a new discipline and technology that has developed rapidly since the 1990s [1, 2]. The information transport of traditional electronic devices mainly depends on the charge. Spintronics not only uses the charge transport, but also adds the spin and magnetic moment of the electron. Compared with traditional semiconductor electronic devices, spintronic devices have many advantages such as non-volatile, low power consumption and high integration. For spintronic materials, it is necessary to have higher electron polarizability and in this case, half-metallic magnetic materials become the best choice for spintronic applications. In the field of spintronics, half-metallic magnetic materials are widely used in spin diodes, spin valves, spin filters, and other devices due to their special electronic structure [3–5]. The most important feature of half-metallic magnetic materials is that the majority-spin (minority-spin) direction is metal property, and the minority-spin (majority-spin) direction is semiconductor or insulator property, leading to 100% spin polarization at the Fermi level [6, 7]. The unique electronic structure of half-metallic magnetic materials has become a research hotspot recently [8–10].

Heusler alloy compounds have always been one of the most important members of half-metallic magnetic materials. Since the first half-metallic magnetic material, ternary Heulser alloy NiMnSb [11] was predicted, researchers have paid great attention to the this kinds of compounds [12–25]. The crystal of Heusler compounds is generally cubic structure with four atoms. The four atoms occupy A(0,0,0), B(0.25,0.25,0.25), C(0.50, 0.50, 0.50), and D(0.75, 0.75, 0.75), respectively [26, 27]. According to the different ways of occupying atoms, Heusler compounds have derived many types of structures, including full-Heusler, half-Heuler, inverse-Heusler, and quaternary-Heusler, etc. There are many half-metallic magnetic materials in these different Heusler configurations, and they are widely concerned by researchers in experiments and theory [28–34].

In recent years, there are some reports about the CoCr-based quaternary Heusler compounds. In 2012, Gokoglu [35] found that quaternary Heusler compound NiCoCrGa displays a slightly disturbed half-metallic behavior with high-spin polarization ratio at Fermi level. In 2017, Xu et al. [36] found that the quaternary Heusler (Y, La, Lu)CoCr/FeMn(Al, Ga) containing rare earth elements has the characteristics of spin gapless semiconductors. In 2019, Wu et al. [37] found that the Curie temperature of CrCoScZ (Z = Si, Ge, Sn) based on mean field theory is higher than that of room temperature. Huang et al. [38] found that the bulk and surface states of CoCrScBi are half-metallic. In 2020, Khan et al. [39] studied the structural stability, band structure, density of states, magnetic and mechanical properties of CoCr-based quaternary Heusler compounds CoCrYZ (Z = Si, Ge, Ga, Al) and found all these materials possess half-metallic character.

Recent studies on quaternary Heusler compounds show that the Coulomb interaction of 3d electrons in transition metals has a significant effect on the electronic structure of alloys. Gao et al. [40] reveal that the half-metallicity is lost for both CoFeCrAl and CoFeCrGa but retentive for both CoFeCrSi and CoFeCrGe when the Coulomb interactions are considered. Paudel et al. [41] found the band gap width of CoFeZrGe, CoFeZrSb, and CoFeZrSi compounds under GGA + U changed a lot compared with that under GGA. Although CoCrScSn compound has been shown to have half-metallic behavior in previous studies [37], there has been no report on whether it has stable mechanical properties, nor on whether the Coulomb interactions between transition metal atoms in CoCrScSn affect its physical properties. Therefore, in order to reveal the effect of the coulomb interaction on the electronic structure of CoCrScSn, and also to understand its mechanical stability, so that CoCrScSn can be applied in spintronics. In this study, we perform a complete first-principles study of the ground state, mechanical, electronic, magnetic, and half-metallic properties of CoCrScSn compound based on the generalized gradient approximation (GGA) [42] with strong-correlated correction (GGA + U).

Calculation Methods

In this study, the GGA and GGA + U as implemented in the Vienna ab-initio simulation package (VASP) package [43], was used to calculate the physical and mechanical properties of the CoCrScSn compound. The effective U(U_eff) values of 2.7 eV for Co, 2.0 eV for Cr, and 0.5 eV for Sc [44, 45] were selected, respectively, as these values provides correct description magnetic moment and electronic structure in the Heusler compounds [46]. For the self-consistent calculation, the plane wave cutoff energy was chosen to be 500 eV. A mesh of 9 × 9 × 9 Monkhorst-Pack k-point was used. The convergence tolerances were selected as the difference in total energy and the maximum force within 1.0 × 10⁻⁵ eV and 1.0 × 10⁻² eV/atom, respectively.

Results and Discussions

Structural Properties

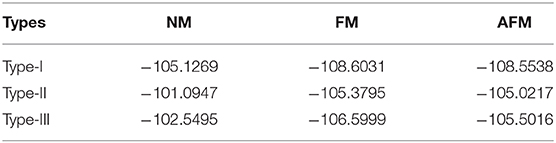
According to the results of earlier research, quaternary Heusler compounds usually have three different structures depending on the positions occupied by the atoms. The three structures are defined as type-I, type-II, and type-III, respectively [47–50]. For CoCrScSn compound, the occupancy positions of Co, Cr, Sc, and Sn atoms are shown in Table 1. We must first determine which of the three structures is the most stable. Therefore, we are very concerned about the relationship between the total energy of the three structures and the lattice constant. Through structural optimization, we have obtained the equilibrium lattice constants of three structures of CoCrScSn compounds as shown in Table 1. Table 2 shows the total energies of CoCrScSn compound in non-magnetic (NM), ferromagnetic (FM), and antiferromagnetic (AFM) states at the equilibrium structures. It can be seen that among these three structures, the energy of the ferromagnetic state with the type-I structure is the lowest, which means that the type-I structure of the CoCrScSn compound is the most stable, and the ground state of this stable structure is ferromagnetic. The next studies only consider the ferromagnetic type-I structure of CoCrScSn compound.

TABLE 1

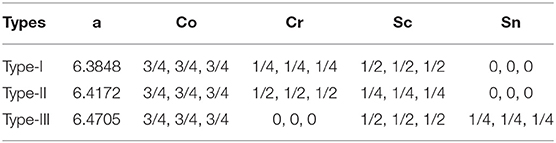
Table 1. Equilibrium lattice equilibrium constants (Å) and atomic positions for three different types of crystals.

TABLE 2

Table 2. Total energies (eV) of CoCrScSn compound in NM, FM, and AFM states.

So far, there are no experimental reports about CoCrScSn compound. In order to test the possibility of synthesizing CoCrScSn compound, we performed a calculation of formation energy, which is calculated as follows:

$\begin{array}{ll}{E}_f=E_{Tot}-E_{Co}-E_{Cr}-E_{Sc}-E_{Sn}& (1)\end{array}$

where E_Tot are the total energy of the CoCrScSn compound per formula unit at equilibrium lattice constants and E_Co, E_Cr, E_Sc, and E_Sn correspond to the total energy per atom for the Co, Cr, Sc, and Sn atoms, respectively. During calculation, Co, Cr, and Sc are taken as face-centered cubic structure (space group Fm-3m), Sn is taken as body-centered cubic structure (space group Im-3m). We use the ferromagnetic energy of the title compound as the E_Tot of formula (1) to obtain the formation energy of type-I, type-II, and type-III as −1.35, −0.55, and −0.85 eV, respectively. The negative values of the formation energy indicate that these three structures of CoCrScSn compounds are energetically stable and may be fabricated experimentally.

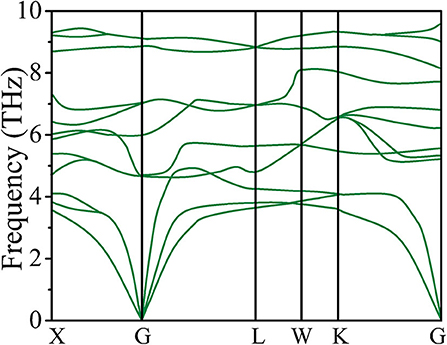
In order to examine the dynamical stability, the phonon dispersion curves of the type-I structure of CoCrScSn compound have been calculated and depicted in Figure 1. It is seen that the title compound have positive phonon frequency, which is an key indicator of the dynamical stability of the Heusle compound. There are no available experimental related to the quaternary Heusler compoud CoCrScSn to make a comparison with our data, and we are looking forward to the experimental synthesis of the title compound.

FIGURE 1

Figure 1. Phonon dispersion curves of the CoCrScSn compound at equilibrium lattice constants.

Mechanical Properties

The mechanical properties of cubic crystals are determined by three elastic constants, C₁₁, C₁₂, and C₄₄. The elastic constants C₁₁, C₁₂, and C₄₄ at are obtained by calculating the strain as a function of total energy. Born and Huang criteria give that the mechanical stability of cubic crystals is determined by the following formula [51, 52]:

$\begin{array}{ll}{C}_{11}-C_{12}>0C_{44}>0C_{11}+2C_{12}>0& (2)\end{array}$

The elastic constants C₁₁, C₁₂, and C₄₄ of CoCrScSn compound at equilibrium lattice constant were calculated to be 154.9 GPa, 61.5 GPa, and 62.7 GPa for GGA and 165.2 GPa, 70.3 GPa, and 74.2 GPa for GGA + U, respectively. As a comparison, we found that the C₁₁ and C₄₄ of CoCrScSn in this paper were larger than that of another similar compound CoCrScBi, while C₁₂ was smaller than that of CoCrScBi [38].

$\begin{array}{ll}B=\frac{C_{11}+2C_{12}}{3}& (3)\end{array}$

$\begin{array}{ll}{G}_V=\frac{C_{11}-C_{12}+3C_{44}}{5}& (4)\end{array}$

$\begin{array}{ll}{G}_R=\frac{5(C_{11}-C_{12})C_{44}}{4C_{44}+3(C_{11}-C_{12})}& (5)\end{array}$

$\begin{array}{ll}G=\frac{G_V+G_R}{2}& (6)\end{array}$

According to formula (3)–(6), the bulk modulus B and shear modulus G calculated are 92.63 GPa, 55.72 GPa for GGA, and 101.93 GPa, 62.02 GPa for GGA + U, respectively. The bulk modulus and shear modulus of CoCrScBi are reported as 127.03 GPa and 31.88 GPa, respectively. The bulk modulus of CoCrScSn is smaller than that of CoCrScBi, indicating that CoCrScSn is more prone to volume deformation than CoCrScBi. However, the larger shear modulus of CoCrScSn confirms its greater resistance to shear strain than CoCrScBi. The elastic constants obtained by using GGA and GGA + U all meet the elastic stability criteria and therefore, ferromagnetic type-I structure of CoCrScSn compound are mechanically stable.

As we all know, the physical properties of compounds will change with the change of crystal structure. The change of lattice constant of compounds under external pressure is one of the simplest ways to change the physical properties of compounds. Next, we study the mechanical stability of CoCrScSn compound when the lattice constant changes.

Under the uniform pressure P, the stress-strain coefficients will replace the elastic constants with the following expression:

$\begin{array}{ll}{B}_{11}=C_{11}-P,B_{12}=C_{12}+P,B_{44}=C_{44}-P& (7)\end{array}$

Accordingly, the mechanical stability of CoCrScSn compound under uniform pressure is determined by the following formula [53, 54]:

$\begin{array}{ll}{B}_{11}-B_{12}>0,B_{11}+2B_{12}>0,B_{44}>0& (8)\end{array}$

That is

$\begin{array}{ll}{C}_{11}-C_{12}-2P>0,C_{11}+2C_{12}+P>0,C_{44}-P>0& (9)\end{array}$

Figures 2A,B shows the change curve of the elastic modulus of CoCrScSn compound with the lattice constant under GGA and GGA + U, respectively. Under GGA, when the lattice constant of CoCrScSn compound is between 5.8 and 7.2 Å, C₁₁-C₁₂-2P, C₁₁+2C₁₂+P, and C₄₄-P are greater than zero, as shown in Figure 2A. This means that the mechanical properties of CoCrScSn compound in this lattice constant range are stable. One can see from Figure 2A that when the lattice constant is too large, it may cause negative values of C₁₁-C₁₂-2P, C₁₁+2C₁₂+P, and C₄₄-P. At this time, CoCrScSn compound will show unstable mechanical properties. This result is consistent with the fact that the interaction between atoms weakens and the stability is destroyed when the crystal expands. Under GGA + U, the mechanical properties of CoCrScSn are stable in the range of 5.6–6.7 Å as shown in Figure 2B. When the lattice constant is lower than 5.6 Å, C₁₁-C₁₂-2P appears a negative value, and when the lattice constant is > 6.7 Å, C₄₄-P may be a negative value, both of which will make the mechanical properties of the CoCrScSn compound unstable.

FIGURE 2

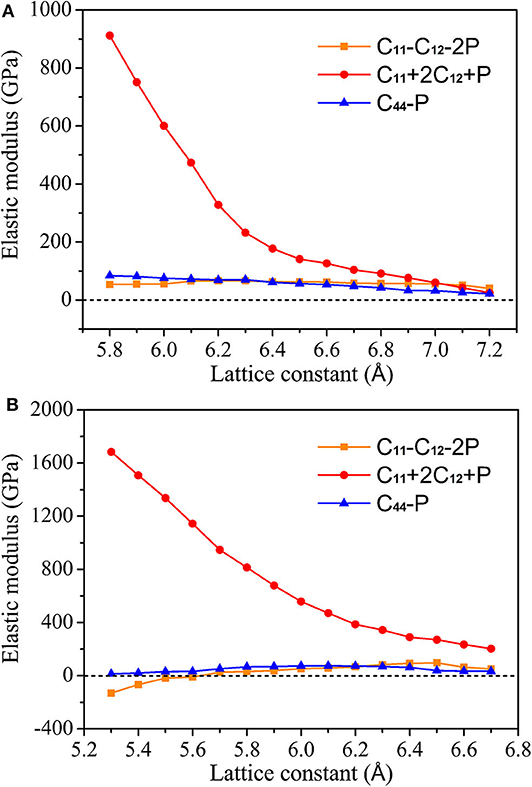
Figure 2. Elastic modulus of CoCrScSn compound under different lattice constant. (A) GGA, (B) GGA + U.

Electronic Properties

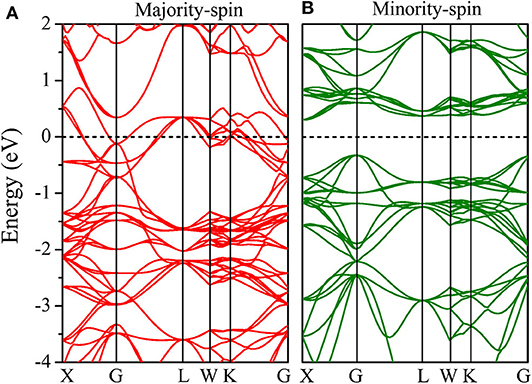
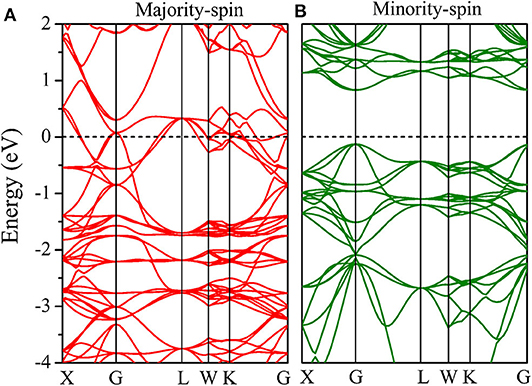
We further calculated the band structures of the CoCrScSn compound under GGA and GGA + U, as shown in Figures 3, 4, respectively. Under the cases of GGA and GGA + U, the majority-spin direction shows metal behavior, while minority-spin direction shows semiconductor behavior, which is a typical half-metal character. Furthermore, the band gap of minority-spin is an indirect under GGA, and direct (at the G point) under GGA + U. Under GGA and GGA + U, the minority-spin band gap of the title compound is 0.66 and 0.93 eV, respectively. The band gap considering Coulomb interaction is larger than that without Coulomb interaction. It shows that the Coulomb interaction has an obvious influence on the electronic structure of the CoCrScSn compound, so it is necessary to consider the Coulomb interaction when studying the electronic structure of the title compound.

FIGURE 3

Figure 3. Band structures of CoCrScSn compound under GGA. (A) Majority-spin, (B) minority-spin.

FIGURE 4

Figure 4. Band structures of CoCrScSn compound under GGA + U. (A) Majority-spin, (B) minority-spin.

Figure 5 shows the total and local density of states (DOSs) of CoCrScSn compound under GGA and GGA + U, respectively. Same as the result of the energy band structure, one spin direction is metallic, the other is semiconductor, and the title compound is a half-metal. By comparing the DOS distribution under GGA and GGA + U, it is clear that the shape of density of state in the two cases is roughly the same, but the local position is slightly different due to the Coulomb interaction. Obviously, the majority-spin below the Fermi level moves slightly to the low energy region, the minority-spin below the Fermi level moves toward the Fermi level, and the minority-spin above the Fermi level moves away from the Fermi level when the Coulomb interaction is considered.

FIGURE 5

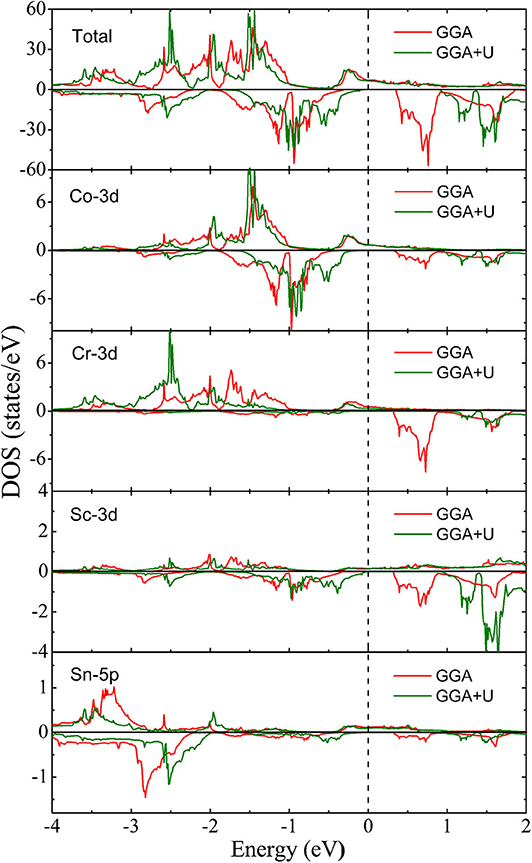
Figure 5. Total and local density of states of CoCrScSn compound under GGA and GGA + U, respectively.

The robustness of half-metallicity is a key factor for spintronic materials. For practical applications, it is particularly important whether the half-metallic properties can still exist under external pressure or strain. Next, we will study the stability of half-metallicity of CoCrScSn compound when the lattice constant changes. Figure 6 shows the curve of the minority-spin band gap width with the lattice constant of the CoCrScSn compound under GGA and GGA + U. The results show that the majority-spin direction always shows the metallic property when the lattice constant changes, therefore, the half-metallic property is determined by the minority-spin band gap. That is to say, when there is a band gap in minority-spin, the title compound has half-metallic property, when there is no band gap, the half-metallicity will disappears.

FIGURE 6

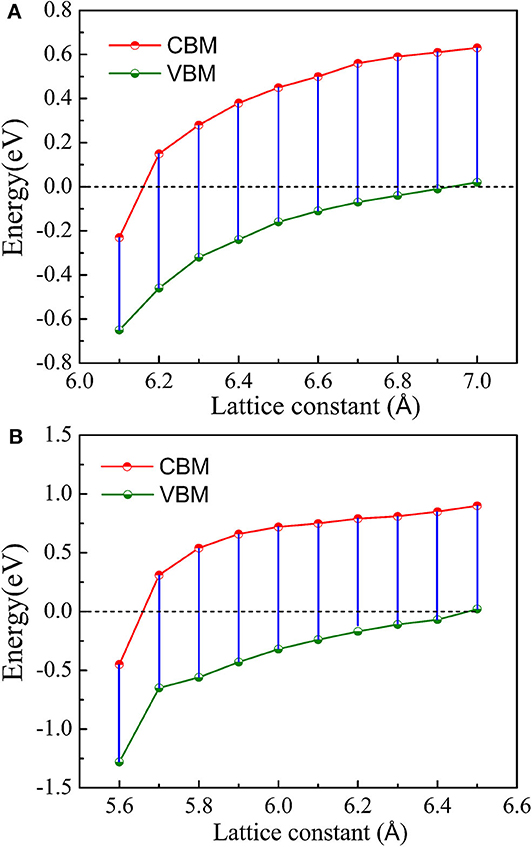
Figure 6. Minority-spin CBM and VBM of CoCrScSn compound at different lattice constant. (A) GGA, (B) GGA + U.

Figure 6 shows that under GGA and GGA + U, the conduction band minimum (CBM) and valence band maximum (VBM) in minority-spin change with the lattice constant. It can be seen that within the lattice constants region of 6.2–6.9 Å, the CBM and VBM are located on the two sides of the Fermi level under GGA. At this time, the semiconductor character of minority-spin is obvious, the title compound has stable half-metallic property. When the lattice constant is lower than 6.2 Å or higher than 6.9 Å, the minority-spin band gap disappears and the half-metallicity disappears.

In the case of GGA + U, the CoCrScSn compound also has similar characteristics, but due to the influence of Coulomb interaction, the lattice constant of the compound maintaining the half-metallicity region is from 5.7 to 6.4 Å. Combined with the mechanical properties research, we can find that in the case of GGA, the mechanical and half-metallic properties of the CoCrScSn compound are very stable within the lattice constant range of 6.2–6.9 Å. In the case of GGA + U, the mechanical properties and half-metallic properties exist stably in the range of 5.7–6.4 Å.

Magnetic Properties

Slater and Pauling in two pioneering papers show that if a minority-spin electron is added to a magnetic compound, the total magnetic moment of the compound will be reduced by 1 μ_B. If a majority-spin electron is added, the total magnetic moment of the compound will be increased by 1 μ_B [55–57]. This behavior called Slater-Pauling (SP) rule has been studied not only in binary magnetic compounds [58], but also in half-metallic Heusler compounds. So far, people have summarized some SP relation between the total magnetic moment (M_t) and number of valence electrons (Z_t) of per molecular unit in half-metallic Heusler compounds, such as M_t = Z_t-18 [59], M_t = Z_t-24 [4], and M_t = Z_t-28 [57]. Some half-metallic quaternary Heusler compounds mainly satisfy the SP rule of M_t = Z_t-18 [60–63] and M_t = Z_t-24 [64–66].

In CoCrScSn compound, the number of valence electrons of Co, Cr, Sc and Sn atoms are nine, six, three, and four, respectively, so the Z_t is twenty two. The calculations of GGA and GGA + U show that the M_t at equilibrium lattice constant is 4.0 μ_B. Obviously, the M_t and Z_t are in accordance with the SP relation M_t = Z_t-18, and CoCrScSn compound conform to the typical characteristics of half-metallic Heusler compound.

Figure 7 shows the total and local magnetic moments of CoCrScSn compound at different lattice constants under GGA and GGA + U, respectively. From 6.2 to 6.9 Å under GGA and from 5.7 to 6.4 Å under GGA + U, the M_t is an integral value 4.0 μ_B. Within this lattice constant range, the CoCrScSn compound has stable half-metallic character. When the lattice constant under GGA is lower than 6.2 Å or higher than 6.9 Å, the M_t is no longer an integral value, and the half-metallicity of the CoCrScSn compound will disappear.

FIGURE 7

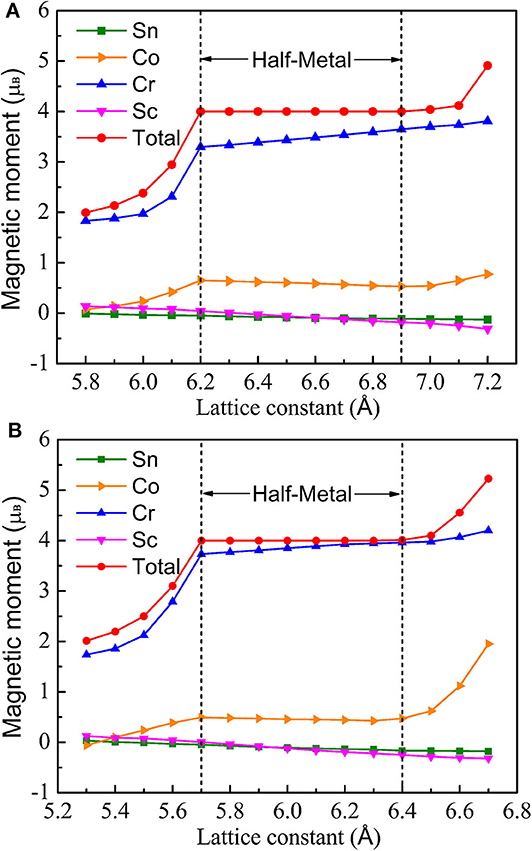
Figure 7. Total and atomic magnetic moments of CoCrScSn compound at different lattice constant. (A) GGA, (B) GGA + U.

The same situation also occurs when considering the Coulomb interaction. If the lattice constant is <5.7 Å or higher than 6.4 Å, the M_t does not meet the SP rule and the title compound will lose the half-metal character. It can be seen from the local magnetic moment distribution curve that Cr atom is the most important source of the magnetic properties of the title compound, and Co atom also contributes to the total magnetic moment, but the contribution degree is smaller than Cr atom. It seems that Sc and Sn atoms also have certain magnetic moments, but because Sc and Sn atoms are not magnetic themselves, they are induced magnetic moments due to the influence of Cr and Co atoms.

Higher Curie temperature is another key factor for the application of half-metallic magnetic materials in spintronics. Theoretically, the mean field approximation is often used to estimate the Curie temperature (T_c) of materials. The formula can be expressed as follows [37, 67]:

$\begin{array}{ll}{T}_c=\frac{2\Delta E_{AFM-FM}}{3C{K}_B}& (10)\end{array}$

where ΔE_AFM−FM is the total energy difference between antiferromagnetic and ferromagnetic states. C is the amount of the magnetic ion, and k_B is Boltzmann constant. The Curie temperature calculated based on formula (6) for CoCrScSn is 762 K, which is slightly less than the previous theoretical research result.

Furthermore, Wurmehl et al. [68] proposed a linear relation to estimate the Curie temperature of the half-metal Heusler compound by using the M_t, and the expression is [69]

$\begin{array}{ll}{T}_c=23+181M_t& (11)\end{array}$

The Curie temperature for CoCrScSn were estimated according to the model presented is 747K, which is very close to the result of mean field approximation. Although the theoretical estimate of the Curie temperature is often higher than the actual value, we conclude that the Curie temperature of CoCrScSn should be higher than room temperature, which make it interesting for technological applications in spintronics.

Conclusions

In this study, we focused on quaternary Heusler compound CoCrScSn, and showed a complete first-principles study on the structure, mechanical, electronic, magnetic, and half-metallic properties of this material. It was found that the type-I structure of quaternary Heusler compound CoCrScSn is the most stable, and the type-I structure has a stable ferromagnetic ground state. Elastic constant analysis shows that CoCrScSn compound have stable mechanical properties at the equilibrium lattice constant. The mechanical properties of CoCrScSn will change if the lattice constant changes. The further studies show that if the lattice constant can be maintained within the range of 5.8–7.2 Å under GGA, and 5.6–6.7 Å under GGA + U, the mechanical properties of CoCrScSn compound are also stable. At the equilibrium lattice constant, the electronic structure of CoCrScSn compound under GGA and GGA + U shows that it has obvious half-metal character. The half-metal robustness of the CoCrScSn compound can be maintained in the lattice constant range of 6.2–6.9 Å for GGA, 5.7–6.4 Å for GGA + U. At the equilibrium lattice constant, the molecular magnetic moment of the compound is an integer value of 4.0 μ_B. No matter how the lattice constant changes, as long as the compound has half-metallic character, the total magnetic moment of the CoCrScSn compound meets the Slater-Pauling rule. The mean field approximation shows that the Curie temperature is higher than room temperature, which makes the title compound a promising application in spintronics.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

CZ designed the research. HH analyzed the data and results. CZ and HH performed the research and wrote the paper. CW checked the article grammar. ZH, ZZ, and GL contributed to the revisions. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Natural Science Foundation of Hubei Province (No. 2017CFB740) and the Doctoral Scientific Research Foundation of Hubei University of Automotive Technology (No. BK201804).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Wolf SA, Awschalom DD, Buhrman RA, Daughton JM, von Molnar S, Roukes ML, et al. Spintronics: a spin-based electronics vision for the future. Science. (2001) 294:1488–95. doi: 10.1126/science.1065389

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zutic I, Fabian J, Das Sarma S. Spintronics: fundamentals and applications, Rev Mod Phys. (2004) 76:323–410. doi: 10.1103/RevModPhys.76.323

CrossRef Full Text | Google Scholar

3. Pickett WE, Moodera JS. Half Metallic Magnets. Phys Today. (2001) 54:39–44. doi: 10.1063/1.1381101

CrossRef Full Text | Google Scholar

4. Galanakis I, Dederichs PH, Papanikolaou N. Slater-Pauling behavior and origin of the half metallicity of the full-Heusler alloys. Phys Rev B. (2002) 66:174429. doi: 10.1103/PhysRevB.66.174429

CrossRef Full Text | Google Scholar

5. Song Y, Dai G. Spin filter and spin valve in ferromagnetic graphene. Appl Phys Lett. (2015) 106:223104. doi: 10.1063/1.4921668

CrossRef Full Text | Google Scholar

6. Bhat TM, Gupta DC. Robust thermoelectric performance and high spin polarisation in CoMnTiAl and FeMnTiAl compounds. RSC Adv. (2016) 6:80302–9. doi: 10.1039/c6ra18934b

CrossRef Full Text | Google Scholar

7. Gupta DC, Bhat IH. Magnetic, electronic, high-spin polarization and half-metallic properties of Ru₂VGe and Ru₂VSb Heusler alloys: An FP-LAPW study. J Magn Magn Mater. (2015) 374:209–13. doi: 10.1016/j.jmmm.2014.08.032

CrossRef Full Text | Google Scholar

8. Addadi Z, Doumi B, Mokaddem A, Elkeurti A, Sayede A, Tadjer A, et al. Electronic and ferromagnetic properties of 3d(V)-doped (BaS) barium sulfide. J Supercond Nov Magn. (2017) 30:917–23. doi: 10.1007/s10948-016-3894-3

CrossRef Full Text | Google Scholar

9. Dahmane F, Tadjer A, Doumia B, Mesria D, Aouragb H, Sayede A. First principles study of the electronic structures and magnetic properties of transition metal-doped cubic indium nitride. Mater Sci Semicond Process. (2014) 21:66–73. doi: 10.1016/j.mssp.2014.01.037

CrossRef Full Text | Google Scholar

10. Huang HM, Cao ML, Jiang ZY, Xiong YC, Zhang X, Luo SJ, et al. High spin polarization in formamidinium transition metal iodides: first principles prediction of novel half-metals and spin gapless semiconductors. Phys Chem Chem Phys. (2019) 21:16213. doi: 10.1039/c9cp00958b

PubMed Abstract | CrossRef Full Text | Google Scholar

11. De Groot RA, Mueller FM, Van Engen PG, Buschow KHJ. New class of materials: half-metallic ferromagnets. Phys Rev Lett. (1983) 50:2024. doi: 10.1103/PhysRevLett.50.2024

CrossRef Full Text | Google Scholar

12. Huang HM, Luo SJ, Yao KL. Half-metallicity and tetragonal distortion in semi-heusler alloy FeCrSe. J Appl Phys. (2014) 115:043713. doi: 10.1063/1.4863122

CrossRef Full Text | Google Scholar

13. Han Y, Bouhemadou A, Khenata R, Cheng Z, Yang T, Wang X. Prediction of possible martensitic transformations in all-d-metal zinc-based heusler alloys from first-principles. J Magn Magn Mater. (2019) 471:49–55. doi: 10.1016/j.jmmm.2018.09.053

CrossRef Full Text | Google Scholar

14. Chen Y, Chen S, Wang B, Wu B, Huang H, Qin X, et al. Half-Metallicity and magnetism of the quaternary Heusler compound TiZrCoIn_1−xGe_x from the first-principles calculations. Appl Sci. (2019) 9:620. doi: 10.3390/app9040620

CrossRef Full Text | Google Scholar

15. Tan X, You J, Liu PF, Wang Y. Theoretical study of the electronic, magnetic, mechanical and thermodynamic properties of the spin gapless semiconductor CoFeMnSi. Crystals. (2019) 9:678. doi: 10.3390/cryst9120678

CrossRef Full Text | Google Scholar

16. Li T, Wu Y, Han Y, Wang X. Tuning the topological nontrivial nature in a family of alkali-metal-based inverse heusler compounds: a first-principles study. J Magn Magn Mater. (2018) 463:44–9. doi: 10.1016/j.jmmm.2018.05.025

CrossRef Full Text | Google Scholar

17. Feng L, Ma J, Yang Y, Lin T, Wang L. The electronic, magnetic, half-metallic and mechanical properties of the equiatomic quaternary heusler compounds FeRhCrSi and FePdCrSi: a first-principles study. Appl Sci. (2018) 8:2370. doi: 10.3390/app8122370

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Sakon T, Yamasaki Y, Kodama H, Kanomata T, Nojiri H, Adachi Y. The characteristic properties of magnetostriction and magneto-volume effects of Ni₂MnGa-Type ferromagnetic heusler alloys. Materials. (2019) 12:3655. doi: 10.3390/ma12223655

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Faleev SV, Ferrante Y, Jeong J, Samant MG, Jones B, Stuart P. Origin of the tetragonal ground state of Heusler compounds. Phys Rev Appl. (2017) 7:034022. doi: 10.1103/PhysRevApplied.7.034022

CrossRef Full Text | Google Scholar

20. Wang XT, Dai XF, Wang LY, Liu XF, Wang WH, Wu GH, et al. Electronic structures and magnetism of Rh₃Z (Z=Al, Ga, In, Si, Ge, Sn, Pb, Sb) with DO₃ structures. J Magn Magn Mater. (2015) 378:16–23. doi: 10.1016/j.jmmm.2014.10.161

CrossRef Full Text | Google Scholar

21. Dahmane F, Mesri D, Tadjer A, Khenata R, Benalia S, Djoudi L, et al. Electronic structure, magnetism and stability of Co₂CrX (X=Al, Ga, In) ab initio study. Mod Phys Lett B. (2016) 30:1550265. doi: 10.1142/S0217984915502656

CrossRef Full Text | Google Scholar

22. Han YL, Wu MX, Kuang MQ, Yang T, Chen XB, Wang XT. All-d-metal equiatomic quaternary Heusler hypothetical alloys ZnCdTMn (T= Fe, Ru, Os, Rh, Ir, Ni, Pd, Pt): a first-principle investigation of electronic structures, magnetism, and possible martensitic transformations. Results Phys. (2018) 11:1134–41. doi: 10.1016/j.rinp.2018.11.024

CrossRef Full Text | Google Scholar

23. Li TZ, Khenata R, Cheng ZX, Chen H, Yuan HK, Yang T, et al. Martensitic transformation, electronic structure and magnetism in D03-ordered heusler Mn₃Z (Z=B, Al, Ga, Ge, Sb) alloys, Acta Cryst. (2018) B74:673–80. doi: 10.1107/S2052520618013525

CrossRef Full Text | Google Scholar

24. Berri S. First-principles calculations to investigate the structural, electronic, and half-metallic properties of Ti₂RhSn_1−xSi_x, Ti₂RhSn_1−xGe_x, and Ti₂RhGe_1−xSi_x(x=0, 0.25, 0.5, 0.75, and 1) quaternary heusler alloys. J Supercond Nov Magn. (2019) 32:2219–28. doi: 10.1007/s10948-018-4952-9

CrossRef Full Text | Google Scholar

25. Khalaf Al-zyadi JM, Kadhim AA, Yao KL. Half-metallicity of the (001), (111) and (110) surfaces of CoRuMnSi and interface half-metallicity of CoRuMnSi/CdS. RSC Adv. (2018) 8:25653. doi: 10.1039/c8ra02918k

CrossRef Full Text | Google Scholar

26. Huang H, Yang K, Zhao W, Zhou T, Yang X, Wu B. High-pressure-induced transition from ferromagnetic semiconductor to spin gapless semiconductor in quaternary heusler alloy VFeScZ (Z=Sb, As, P). Appl Sci. (2019) 9:2859. doi: 10.3390/app9142859

CrossRef Full Text | Google Scholar

27. Jin Y, Kharel P, Lukashev P, Valloppilly S, Staten B, Herran J, et al. Magnetism and electronic structure of CoFeCrX (X= Si, Ge) heusler alloys. J Appl Phys. (2016) 120:053903. doi: 10.1063/1.4960350

CrossRef Full Text | Google Scholar

28. Chen Z, Xu H, Gao Y, Wang X, Yang T. Site-Preference, electronic, magnetic, and half-metal properties of full-heusler Sc₂VGe and a discussion on the uniform strain and tetragonal deformation effects. Crystals. (2019) 9:445. doi: 10.3390/cryst9090445

CrossRef Full Text | Google Scholar

29. Wang XT, Zhao WQ, Cheng ZX, Dai XF, Khenata R. Electronic, magnetic,half-metallic and mechanical properties of a new quaternary heusler compound ZrRhTiT1: Insights from first-principles studies. Solid State Commun. (2018) 269:125–30. doi: 10.1016/j.ssc.2017.10.021

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Zhang HP, Liu WB, Lin TT, Wang WH, Liu GD. Phase stability and magnetic properties of Mn₃Z (Z=Al, Ga, In, Tl, Ge, Sn, Pb) heusler alloys. Appl Sci. (2019) 9:964. doi: 10.3390/app9050964

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Pourebrahim G, Ahmadian F, Momeni P. Robust half-metallicity in quaternary heusler compounds KSrNZ (Z=O, S, and Se). J Supercond Novel Magn. (2019) 32:3305–14. doi: 10.1007/s10948-019-5098-0

CrossRef Full Text | Google Scholar

32. Yousuf S, Gupta DC. Insight into half-metallicity, spin-polarization and mechanical properties of L2₁ structured MnY₂Z (Z=Al, Si, Ga, Ge, Sn, Sb) heusler alloys. J Alloy Compd. (2018) 735:1245–52. doi: 10.1016/j.jallcom.2017.11.239

CrossRef Full Text | Google Scholar

33. Benea D, Gavrea R, Coldea M, Isnard O, Pop V. Half-metallic compensated ferrimagnetism in the Mn-Co-V-Al Heusler alloys. J Magn Magn Mater. (2019) 475:229–33. doi: 10.1016/j.jmmm.2018.11.115

CrossRef Full Text | Google Scholar

34. Li Y, Liu GD, Wang XT, Liu EK, Xi XK, Wang WH, et al. First-principles study on electronic structure, magnetism and half-metallicity of the NbCoCrAl and NbRhCrAl compounds. Results Phys. (2017) 7:2248–54. doi: 10.1016/j.rinp.2017.06.047

CrossRef Full Text | Google Scholar

35. Gökoglu G. Ab initio electronic structure of NiCoCrGa half-metallic quaternary heusler compound. Solid State Sci. (2012) 14:1273–6. doi: 10.1016/j.solidstatesciences.2012.07.013

CrossRef Full Text | Google Scholar

36. Xu G, You Y, Gong Y, Liu E, Xu F, Wang W. Highly-dispersive spin gapless semiconductors in rare-earth-element contained quaternary heusler compounds. J Phys D Appl Phys. (2017) 50:105003. doi: 10.1088/1361-6463/aa57a3

CrossRef Full Text | Google Scholar

37. Wu B, Huang H, Zhou G, Yang X, Li P, Feng Y. Half-metallic ferrimagnets behavior of a new quaternary Heusler alloy CrCoScZ (Z = Si, Ge, Sn). Eur Phys J B. (2019) 92:119. doi: 10.1140/epjb/e2019-90646-4

CrossRef Full Text | Google Scholar

38. Huang HM, Jiang ZY, Hu YJ, Li W, Luo S. Effect of coulomb interaction on the electronic properties of bulk and surface of quaternary heusler CoCrScBi. Solid State Sci. (2019) 97:106018. doi: 10.1016/j.solidstatesciences.2019.106018

CrossRef Full Text | Google Scholar

39. Khan MI, Arshad H, Rizwan M, Gillani SSA, Zafar M, Ahmed S, et al. Investigation of structural, electronic, magnetic and mechanical properties of a new series of equiatomic quaternary Heusler alloys CoYCrZ (Z=Si, Ge, Ga, Al): a DFT study. J Alloy Comp. (2020) 819:152964. doi: 10.1016/j.jallcom.2019.152964

CrossRef Full Text | Google Scholar

40. Gao GY, Hu L, Yao KL, Luo B, Liu N. Large half-metallic gaps in the quaternary heusler alloys CoFeCrZ (Z=Al, Si, Ga, Ge): a first-principles study. J Alloy Comp. (2013) 551:539–43. doi: 10.1016/j.jallcom.2012.11.077

CrossRef Full Text | Google Scholar

41. Paudel R, Zhu J. Structural, electronic, magnetic, elastic, and thermal properties of co-based equiatomic quaternary Heusler alloys. J Magn Magn Mater. (2018) 453:10–6. doi: 10.1016/j.jmmm.2017.12.103

CrossRef Full Text | Google Scholar

42. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. (1996) 77:3865–8. doi: 10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Mater Sci. (1996) 6:15–50. doi: 10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

44. Rai DP, Thapa RK. An investigation of semiconducting behavior in the minority spin of Co₂CrZ (Z = Ga, Ge, As): LSDA and LSDA+U method. J Alloy Comp. (2012) 542:257–63. doi: 10.1016/j.jallcom.2012.07.059

CrossRef Full Text | Google Scholar

45. Rai DP, Thapa RK. An abinitio study of the half-metallic properties of Co₂TGe (T=Sc,Ti,V,Cr,Mn,Fe): LSDA+U method. J Korean Phys Soc. (2013) 62:1652–60. doi: 10.3938/jkps.62.1652

CrossRef Full Text | Google Scholar

46. Curtarolo S, Setyawan W, Hart GLW, Jahnatek M, Chepulskii RV, Taylor RH, et al. AFLOW: An automatic framework for high-throughput materials discovery. Comput Mater Sci. (2012) 58:218–26. doi: 10.1016/j.commatsci.2012.02.005

CrossRef Full Text | Google Scholar

47. Idrissia S, Khalladia R, Zitib S, El Mekkaouia N, Mtouguia S, Labrimc H, et al. The electronic and magnetic proprieties of the rare earth-based quaternary heusler compound LuCoVGe. Physica B Condens Matter. (2019) 562:116–23. doi: 10.1016/j.physb.2019.03.018

CrossRef Full Text | Google Scholar

48. Rani D, Bainsla L, Suresha KG, Alam A. Experimental and theoretical investigation on the possible half-metallic behaviour of equiatomic quaternary heusler alloys: CoRuMnGe and CoRuVZ (Z = Al, Ga). J Magn Magn Mater. (2019) 492:165662. doi: 10.1016/j.jmmm.2019.165662

CrossRef Full Text | Google Scholar

49. Forozani G, Abadi AAM, Baizaee SM, Gharaati A. Structural, electronic and magnetic properties of CoZrIrSi quaternary heusler alloy: first-principles study. J Alloy Comp. (2020) 815:152449. doi: 10.1016/j.jallcom.2019.152449

CrossRef Full Text | Google Scholar

50. Wei XP, Gao PF, Zhang YL. Investigations on gilbert damping, curie temperatures and thermoelectric properties in CoFeCrZ quaternary heusler alloys. Curr Appl Phys. (2020) 20:593–603. doi: 10.1016/j.cap.2020.02.007

CrossRef Full Text | Google Scholar

51. Mehmood N, Ahmad R, Murtaza G. Ab initio investigations of structural, elastic, mechanical, electronic, magnetic, and optical properties of half-heusler compounds RhCrZ (Z=Si, Ge). J Supercond Novel Magn. (2017) 30:2481–8. doi: 10.1007/s10948-017-4051-3

CrossRef Full Text | Google Scholar

52. Huang YC, Guo XF, Ma YL, Shao HB, Xiao ZB. Stabilities, electronic and elastic properties of L1₂-Al₃(Sc_1−x,Zr_x) with different Zr content: a first-principles study. Physica B Condens Matter. (2018) 548:27–33. doi: 10.1016/j.physb.2018.08.019

CrossRef Full Text | Google Scholar

53. Allali D, Bouhemadou A, Zerarga F, Ghebouli MA, Bin-Omran S. Prediction study of the elastic and thermodynamic properties of the SnMg₂O₄, SnZn₂O₄ and SnCd₂O₄ spinel oxides. Comput Mater Sci. (2012) 60:217–23. doi: 10.1016/j.commatsci.2012.03.044

CrossRef Full Text | Google Scholar

54. Gu JB, Wang CJ, Zhang WX, Sun B, Liu GQ, Liu DD, et al. High-pressure structure and elastic properties of tantalum single crystal: first principles investigation. Chin Phys B. (2016) 25:126103. doi: 10.1088/1674-1056/25/12/126103

CrossRef Full Text | Google Scholar

55. Slater JC. The ferromagnetism of nickel. II. Temperature effects. Phys Rev. (1936) 49:931. doi: 10.1103/PhysRev.49.931

CrossRef Full Text | Google Scholar

56. Pauling L. The nature of the interatomic forces in metals. Phys Rev. (1938) 54:899. doi: 10.1103/PhysRev.54.899

CrossRef Full Text | Google Scholar

57. Skaftouros S, Özdogan K, Saşioglu E, Galanakis I. Generalized slater-pauling rule for the inverse heusler compounds. Phys Rev B. (2013) 87:024420. doi: 10.1103/PhysRevB.87.024420

CrossRef Full Text | Google Scholar

58. Khalaf Al-zyadi JM, Samuel RM, Gao GY, Yao KL. The half-metallic characteristics of the (001) surface of zinc-blende TiTe. J Magn Magn Mater. (2013) 346:166–70. doi: 10.1016/j.jmmm.2013.07.032

CrossRef Full Text | Google Scholar

59. Galanakis I, Dederichs PH, Papanikolaou N. Origin and properties of the gap in the half-ferromagnetic heusler alloys, Phys Rev B. (2002) 66:134428. doi: 10.1103/PhysRevB.66.134428

CrossRef Full Text | Google Scholar

60. Berri S. Electronic structure and half-metallicity of the new heusler alloys PtZrTiAl, PdZrTiAl and Pt 0.5 Pd 0.5 ZrTiAl. Chin J Phys. (2017) 55:195–202. doi: 10.1016/j.cjph.2016.10.017

CrossRef Full Text | Google Scholar

61. Berri S, Ibrir M, Maouche D, Attallah M. Robust half-metallic ferromagnet of quaternary heusler compounds ZrCoTiZ(Z =Si, Ge, Ga and Al). Comput Condens Matter. (2017) 1:26–31. doi: 10.1016/j.cocom.2014.10.003

CrossRef Full Text | Google Scholar

62. Berri S, Ibrir M, Maouche D, Attallah M. First principles study of structural, electronic and magnetic propertiesof ZrFeTiAl, ZrFeTiSi, ZrFeTiGe and ZrNiTiAl. J Magn Magn Mater. (2014) 371:106–11. doi: 10.1016/j.jmmm.2014.07.033

CrossRef Full Text | Google Scholar

63. Xie HH, Gao Q, Li L, Lei G, Mao GY, Hu XR, Deng JB. First-principles study of four quaternary heusler alloys ZrMnVZ and ZrCoFeZ (Z=Si, Ge). Comput Mater Sci. (2015) 103:52–5. doi: 10.1016/j.commatsci.2015.03.010

CrossRef Full Text | Google Scholar

64. Berri S, Maouche D, Ibrir M, Zerarga F. A first-principle study of half-metallic ferrimagnetism in the CoFeTiSb quaternary heusler compound. J Magn Magn Mater. (2014) 354:65–9. doi: 10.1016/j.jmmm.2013.10.044

CrossRef Full Text | Google Scholar

65. Berri S. First-principles study on half-metallic properties of the CoMnCrSb quaternary Heusler compound. J Supercond Nov Magn. (2016) 29:1309–15. doi: 10.1007/s10948-016-3404-7

CrossRef Full Text | Google Scholar

66. Khalaf Al-zyadi JM, Kadhim AA, Yao KL. Electronic and magnetic properties of the (001) surface of the CoNbMnSi heusler alloy: first-principles calculations. J Electron Spectrosc Relat Phenom. (2018) 226:17–21. doi: 10.1016/j.elspec.2018.04.005

CrossRef Full Text | Google Scholar

67. Rostamia M, Afkania M, Torkamania MR, Kanjouri F. Bulk and surface DFT investigations of the electronic and magnetic properties of CsXNO (X=Mg, Ca and Sr) quaternary heusler alloys. Mater Chem Phys. (2020) 248:122923. doi: 10.1016/j.matchemphys.2020.122923

CrossRef Full Text | Google Scholar

68. Wurmehl S, Fecher GH, Kandpal HC, Ksenofontov V, Felser C, Lin HJ, et al., Geometric, electronic, and magnetic structure of Co₂FeSi: Curie temperature and magnetic moment measurements and calculations. Phys Rev B. (2005) 72:184434. doi: 10.1103/PhysRevB.72.184434

CrossRef Full Text | Google Scholar

69. Candan A, Ugur G, Charifi Z, Baaziz H, Ellialtioglu MR. Electronic structure and vibrational properties in cobalt-based full-Heusler compounds: a first principle study of Co₂MnX (X=Si, Ge, Al, Ga). J Alloy Comp. (2013) 560:215–22. doi: 10.1016/j.jallcom.2013.01.102

CrossRef Full Text | Google Scholar