- 1School of Automation, Southeast University, Nanjing, China
- 2School of Information Science and Engineering, Linyi University, Linyi, China
- 3School of Mathematics and Computing Science, Guilin University of Electronic Technology, Guilin, China
Many previous studies have indicated that pinning control and adaptive feedback control are two of most effective strategies for achieving synchronization. In this paper, we present a mixed method integrating the two control strategies to realize cluster synchronization in delayed networks with directed couplings. Based on Lyapunov stability theory and matrix theory, several criteria on cluster synchronization are obtained. Compared with the previous results on cluster synchronization, the obtained criteria can be applied to delayed network with non-identical nodes, directed couplings, and time-varying coupling strength. Finally, numerical simulations are performed to verify the theoretical results.
1. Introduction
In the past decade, more and more attention has been attracted to the problem of complex networks, which could be regarded as lots of dynamical nodes coupled with each other. As the result of the complex coupling effect, many different types of collective dynamical behaviors can be realized, such as complete synchronization [1, 2], cluster synchronization [3–5], exponential synchronization [6, 7], intermittent synchronization [8, 9], etc. Cluster synchronization, which is discussed in this paper, implies that the oscillators split into several clusters, and the oscillators in the same cluster synchronize with one another. Many researches have shown that there is a close interplay between cluster synchronization and network topologies. There are also some networks which can not realize a particular type of synchronization only via the inherent coupling effect of oneself. In order to realize cluster synchronization in networks without cluster structures, many various control schemes have been proposed during the past decades, for instance, adaptive feedback control [10, 11], pinning control [12, 13], intermittent control [14], and so on. The control approaches concerned in this paper are the famous pinning control and adaptive feedback control, both have been intensively investigated recently. First, we make a brief introduction to the background and related work of pinning control. Generally speaking, the node number of each complex network in the real world may be the massive level, and it is hard to control all nodes to realize a particular type of synchronization. In order to reduce the control gain and the number of controllers, pinning control is proposed as a more effective control approach [13]. The advantage of the pinning control approach is that it is only necessary to control a significantly smaller number of local controllers as compared to the randomly pinning scheme. Since the idea of pinning control was first developed, researchers concentrate their efforts on the popularization and application of the control approach [15–20]. For instance, by using the Schur complement and Lyapunov stability theory, several pinning schemes were designed to realize lag synchronization between two coupled networks in [15]. It is also shown that a directed network can realize pinning synchronization in [17]. Pinning control scheme was also applied to drive a directed dynamical network with non-identical nodes to cluster synchronization [18]. Similarly, the intermittent pinning-control problem of directed heterogeneous dynamical networks has also been discussed in [19]. Second, it is worth to point out that adaptive control scheme is a feasible approach to avoid larger feedback control gains. Notice that the coupling strength of many real network can not be arbitrarily large, adaptive feedback control should be a valid method for achieving synchronization. During the recent years, researchers have made some great achievements on adaptive feedback control. In [21], cluster synchronization of an adaptive dynamical network with non-identical nodes was discussed.
Motivated by the discussions above, this paper aims to provide several novel criteria on cluster synchronization of complex networks with adaptive coupling strength via pinning control. We carry out a new dynamical network model possessing four characteristics, i.e., delayed dynamics, non-identical nodes, directed topology and time-varying coupling strength. To the best of our knowledge, there is no previous research discussing the problem of cluster synchronization of such a network model. However, the problem mentioned above should be an important issue of complex networks because of its wide applications in practical problems. Then we design proper pinning controllers and adaptive coupling strength, and sufficient conditions are derived to realize cluster synchronization by using Lyapunov stability theory and matrix theory. In order to illustrate the feasibility and validity of the obtained theoretical results, several numerical simulations are presented.
The rest of this paper is designed as follows. The network model is described and some necessary lemmas and assumptions are stated in section 2. Via pinning and adaptive controls, cluster synchronization in a delayed network is discussed and then some sufficient conditions are given in section 3. Numerical examples are obtained in section 4. Finally, in section 5, conclusions are presented.
2. Model Description and Preliminaries
Consider a network consisting of N nodes, which are divided into m communities C1, C2, …, Cm, where 2 ≤ m ≤ N. It is easy to see that there holds If the ith node belongs to the jth cluster, then we define ϕi = j. The function can be employed to describe the local dynamics of each node in the ith cluster.
Now, we consider a delayed dynamic network described by the following equations,
where is the state variable of node i; fϕi is differentiable and capable of performing abundant dynamical behaviors. If ϕi ≠ ϕj, i.e., the ith node and the jth node belong to different clusters, then fϕi ≠ fϕj. δi(t) > 0 is a time-varying coupling strength. τ > 0 is a constant. δi(t) is the time-varying coupling strength. Γ ∈ Rn×n is an inner-coupling matrix. For simplicity, we suppose that Γ is a positive definite diagonal matrix, that is, Γ = diag(ρ1, ρ2, …, ρn) with ρi > 0. The asymmetric matrix A = (aij)N×N describes the topology of the directed network, where aij ≥ 0, i ≠ j, is the weight of the edge from j to i. Here, the coupling matrix A is supposed to be diffusive, that is, aii are defined as
At first, we give an assumption about the function fϕi, which has been widely employed in the previous researches on the problem of synchronization in complex networks. Most of the previous researches pointed out that many well-known chaotic systems have been checked to satisfy the following assumption, such as cellular neural networks and Chua's circuit [22].
Assumption 1 ([23]). For the vector-valued function , there exist a constant L such that
for any
By introducing the control inputs the controlled dynamical network with respect to the network (1) can be rewritten as
Definition 1. Let sϕi(t) = sϕi(t, t0, s0) be the solution of the following system
Defining the error variables by ei(t) = xi(t) − sϕi(t), i = 1, 2, …, N, the oscillator network (2) is said to realize cluster synchronization, if the synchronization errors satisfy
The following error system can be concluded from the Equations (2) and (3),
According to the definition of the diffusive coupling matrix A, one obtains that for i ∈ Gϕi − Ḡϕi, where Gϕi denotes the index set consisting of all nodes in the ϕith cluster and Ḡϕi represents the index set consisting of all nodes in the ϕith cluster which have direct connections with some nodes in other clusters. In view of this property, the pinning controller is designed as
where θi = 1 for i ∈ Ḡϕi, or θi = 0 for i ∈ Gϕi − Ḡϕi, and di > 0. The coupling strengths δi(t) are constructed by the following adaptive laws
where the constant σi > 0 is the control gain, δi(0) > 0, the 0 − 1 switching function γt is defined as follows,
T is a positive constant. Here, ui(t) and δi(t) are different from the corresponding functions of the previous papers, such as [3, 12, 14, 21]. It is easy to see that each node in the network has a different coupling strength. By intuition, the first term in the controller (5) is used to synchronize all nodes in the same cluster, while the second term in the controller (5) is to weaken the influences of the couplings among different clusters.
Remark: The controller (5) only works on the nodes which have direct connections with some nodes in other clusters since ui(t) = 0 for i ∈ Gϕi − Ḡϕi. That is to say, only the nodes which have direct connections with some nodes in other clusters need to be pinned. In addition, the coupling strengths δi(t) are constructed by the adaptive laws. Therefore, the controller (5) is an pinning controller with adaptive strength.
3. Sufficient Conditions on Realizing Cluster Synchronization
In this section, the problem of cluster synchronization in delayed networks will be investigated by designing proper pinning controllers and adaptive coupling strength. Based on Lyapunov functional method and matrix theory, the following theorem is established.
Theorem 1. Let δi ≜ δi(t). Under Assumption 1, if there exists a positive definite matrix Q, such that the matrix H1 is negative definite for t ≤ T, and the matrix H2 is negative definite for t > T, where
IN(In) is the N(n)-dimensional identity matrix,
then, by the local control (5) and the corresponding adaptive laws (6), the solutions e1(t), e2(t), …, eN(t) of the system (4) satisfy That is, cluster synchronization in the network system (2) is realized.
Proof. Let
Apparently, V(t) = 0 if and only if ei(t) ≡ 0, t ∈ [t − τ, t] and δi(T) − δi(t) = 0. Then, the derivate of V(t) along the solution of error system (4) under control (5) is
Denoting , we obtain
That is, for , we have
According to Assumption 1, we have
Denote ηT(t) = (eT(t), eT(t − τ)). For t ≤ T, γt = 1, that is Therefore, we have
Because of H1 < 0, we know that and the equality holds if and only if ei(t) = 0 and ei(t − τ) = 0 for i = 1, 2, …, N. For t > T, γt = 0, that is Then we obtain
As H2 < 0, we know that and the equality holds if and only if e(t) = 0 and ei(t − τ) = 0 for i = 1, 2, …, N.
Therefore, the solutions e1(t), e2(t), …, eN(t) of the system (4) satisfy for i = 1, 2, …, N. Thus, cluster synchronization in the network system (2) is realized under the local control (5) and the corresponding adaptive laws (6).
Let Q = Γ = In, we obtain the following corollary.
Corollary 1. Let δi ≜ δi(t). Under Assumption 1, if Γ = I, H3 is negative definite for t ≤ T, and H4 is negative definite for t > T, where
IN(In) is the N(n)-dimensional identity matrix,
F = diag(θ1δ1d1, θ2δ2d2, ⋯ , θNδNdN), W = diag(δ1(T) − δ1, δ2(T) − δ2, ⋯ , δN(T) − δN), then, by the local control (5) and the corresponding adaptive laws (6), the solutions e1(t), e2(t), …, eN(t) of the system (4) satisfy That is, cluster synchronization in the network system (2) is realized.
4. Numerical Simulations
In this section, we give a numerical example to verify the theorem given in the previous section.
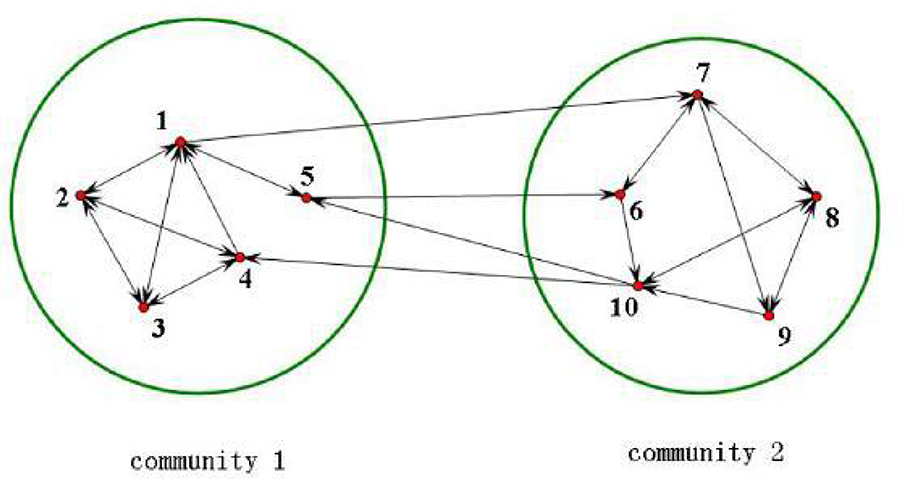
Consider a directed network consisting of 10 nodes with two communities, the topological structure of which is shown in Figure 1. Choose the node dynamics of the five nodes in the first cluster as the time-delayed Chua's circuit, which is described by the following equations,
where and i = 1, 2, …, 5. Choose the node dynamics of the five nodes in the second cluster as the time-delayed 3-D neural network which is described by the following equations,
where , i = 6, 7, ⋯, 10.
Matrices V1 and V2 are, respectively, defined by
Recalling that Ḡϕi denotes the set consisting of all nodes in the ϕith cluster which have direct connections to the nodes in other clusters. It is easy to see that Ḡ1 = {1, 5}, Ḡ2 = {10} and
According to the discussion in [18] and some simple calculations, Assumption 1 is satisfied for systems (7) and (8). And then we obtain L = 21. Let σi = 2, T = 2, δi(0) = 15, τ = 0.2, d1 = d5 = d10 = 20, d2 = d3 = d4 = d6 = d7 = d8 = d9 = 0, Γ = 12I3, Q = 22I3. It is easy to verify that H1 < 0 for 0 ≤ t ≤ 2 and H2 < 0 for t > 2.
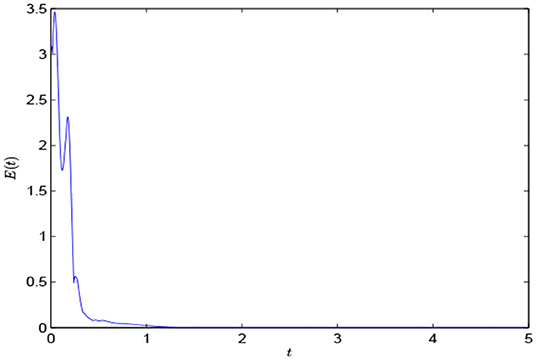
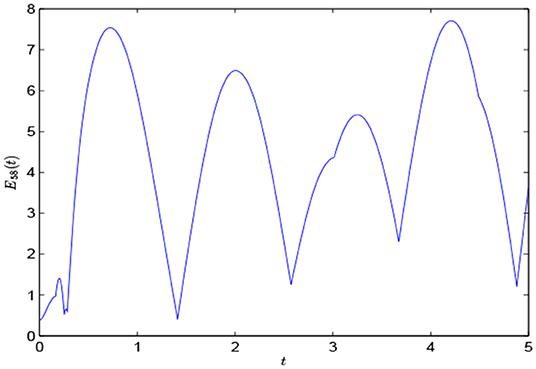
Let the state of the Chua's circuit under initial condition be t ∈ [−0.2, 0], and the state of the 3-D neural network under initial condition be t ∈ [−0.2, 0]. Initial states of all nodes are constant functions on [−0.2, 0]. Here, the values of the initial constant functions are randomly chosen on [−1, 1]. Now we define where the norm |·| of vector x is defined as |x| = (xTx)1/2. It is clear that the cluster synchronization is achieved if E(t) converges to zero and Eij(t) do not converge to zero as t → +∞.
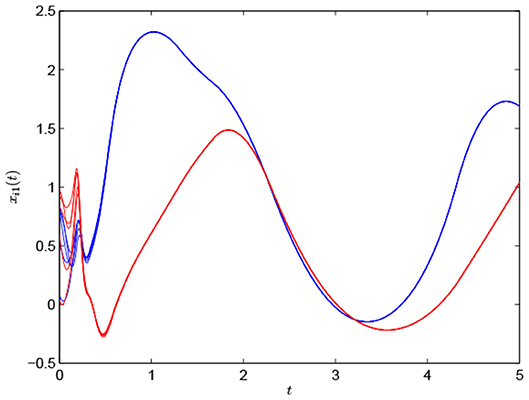
By the aid of Matlab, we obtain Figure 2, which shows the time evolutions of the component xi1, i = 1, …, 10. In Figure 2, the red lines represent the first five nodes, and the blue lines represent the latter five nodes. Figures 3, 4 show the time evolutions of E(t) and E58(t), respectively. It is easy to see that the error E(t) tends to zero, but E58 doesn't tend to zero when t → +∞. That is to say, 2-cluster synchronization is achieved, and the effectiveness of the theoretic results is verified.
5. Conclusions
In this paper, the problem of cluster synchronization in a complex network via pinning control has been investigated, and several novel criteria have been derived by utilizing the matrix theory and the stability analysis technique. The object of this research is a dynamical network possessing four characteristics, delayed dynamics, non-identical nodes, directed topology and time-varying coupling strength. And from the control schemes of this research, we present a novel mixed method, which integrated the pinning control and adaptive feedback control, to design proper pinning controllers and adaptive coupling strengths to realize cluster synchronization in such a dynamical network. For convenience, we also carried out a succinct and utilitarian corollary by simplifying the obtained conditions. Finally, numerical simulations are provided to illustrate the effectiveness of the proposed control methods.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
JZ performed the theory derivation and wrote the first draft of the paper. ZM and XL provided the numerical experiments and contributed to the modification of this paper. JQ revised the first draft and made many helpful suggestions, which improve this paper greatly. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by Natural Science Foundation of Guangxi Province (No. 2018GXNSFAA281068), Jiangsu Planned Projects for Postdoctoral Research Funds (No. 1701017A) and National Natural Science Foundation of China (Nos. 61877033, 11662001, and 11447005).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Li CG, Chen GR. Synchronization in general complex dynamical networks with coupling delays. Physica A. (2004) 343:263–78. doi: 10.1016/j.physa.2004.05.058
2. Daniel G, Birce O, Alyssa D, Hund TJ. Synchronization of pacemaking in the sinoatrial node: a mathematical modeling study. Front Phys. (2018) 6:63. doi: 10.3389/fphy.2018.00063
3. Qin J, Fu W, Shi Y, Gao H, Kang Y. Leader-following practical cluster synchronization for networks of generic linear systems: an event-based approach. IEEE T Neur Net Learn. (2018) 30:215–24. doi: 10.1109/TNNLS.2018.2817627
4. Blaha KA, Huang K, Rossa FD, Pecora L, Hossein-Zadeh M, Sorrentino F. Cluster synchronization in multilayer networks: a fully analog experiment with LC oscillators with physically dissimilar coupling. Phys Rev Lett. (2019) 122:014101. doi: 10.1103/PhysRevLett.122.014101
5. Zhang JB, Ma ZJ, Chen GR. Robustness of cluster synchronous patterns in small-world networks with inter-cluster co-competition balance. Chaos. (2014) 24:440–67. doi: 10.1063/1.4873524
6. Liu YJ, Guo BZ, Park JH, Lee SM. Nonfragile exponential synchronization of delayed complex dynamical networks with memory sampled-data control. IEEE T Neur Net Learn. (2018) 29:118–28. doi: 10.1109/TNNLS.2016.2614709
7. Yang CD, Qiu JL, He HB. Exponential synchronization for a class of complex spatio-temporal networks with space-varying coefficients. Neurocomputing. (2015) 151:401–7. doi: 10.1016/j.neucom.2014.09.025
8. Rubchinsky LL, Sungwoo A, Choongseok P. Dynamics of desynchronized episodes in intermittent synchronization. Front Phys. (2014) 2:38. doi: 10.3389/fphy.2014.00038
9. Cai SM, Lei XQ, Liu ZR. Outer synchronization between two hybrid-coupled delayed dynamical networks via aperiodically adaptive intermittent pinning control. Complexity. (2016) 21:593–605. doi: 10.1002/cplx.21837
10. Wu ZY, Xu XJ, Chen GR, Fu XC. Adaptive synchronization and pinning control of colored networks. Chaos. (2012) 22:043137. doi: 10.1063/1.4769991
11. Pham VT, Vaidyanathan S, Volos C, Jafari S, Alsaadi FE, Alsaadi FE. Chaos in a simple snap system with only one nonlinearity, its adaptive control and real circuit design. Arch Control Sci. (2019) 29:73–96. doi: 10.24425/acs.2019.127524
12. Liu ZX, Chen ZQ, Yuan ZZ. Pinning control of weighted general complex dynamical networks with delay. Phsica A. (2007) 375:345–54. doi: 10.1016/j.physa.2006.09.009
13. Wang XF, Chen GR. Pinning control of scale-free dynamical networks. Physica A. (2002) 310:521–31. doi: 10.1016/S0378-4371(02)00772-0
14. Xia WG, Cao JD. Pinning synchronization of delayed dynamical networks via periodically intermittent control. Chaos. (2009) 19:013120. doi: 10.1063/1.3071933
15. Sun WG, Wang S, Wang GH, Wu YQ. Lag synchronization via pinning control between two coupled networks. Nonlinear Dyn. (2015) 79:2659–66. doi: 10.1007/s11071-014-1838-7
16. DeLellis P, Garofalo F, Iudice FL. The partial pinning control strategy for large complex networks. Automatica. (2018) 89:111–6. doi: 10.1016/j.automatica.2017.11.025
17. Nian FZ, Wang XY. Optimal pinning synchronization on directed complex network. Chaos. (2011) 21:043131. doi: 10.1063/1.3665699
18. Wang G, Shen Y. Cluster synchronization of directed complex dynamical networks with nonidentical nodes via pinning control. Int J Syst Sci. (2012) 10:1–10. doi: 10.1080/00207721.2012.659699
19. Cai SM, Jia Q, Liu ZR. Cluster synchronization for directed heterogeneous dynamical networks via decentralized adaptive intermittent pinning control. Nonlinear Dynam. (2015) 82:689–702. doi: 10.1007/s11071-015-2187-x
20. Sun W, Sun M, Guan J, Jia Q. Robustness of coherence in noisy scale-free networks and applications to identification of influential spreaders. IEEE Trans Circ II Express Briefs. (2020) 67:1274–8. doi: 10.1109/TCSII.2019.2929139
21. Wu XJ, Lu HT. Cluster synchronization in the adaptive complex dynamical networks via a novel approach. Phys Lett A. (2011) 375:1559–65. doi: 10.1016/j.physleta.2011.02.052
22. Zhou J, Lu JA, Lv JH. Pinning adaptive synchronization of a general complex dynamical network. Automatica. (2008) 44:996–1003. doi: 10.1016/j.automatica.2007.08.016
Keywords: cluster synchronization, delayed network, pinning control, adaptive control, Lyapunov stability theory
Citation: Zhang J, Ma Z, Li X and Qiu J (2020) Cluster Synchronization in Delayed Networks With Adaptive Coupling Strength via Pinning Control. Front. Phys. 8:235. doi: 10.3389/fphy.2020.00235
Received: 30 March 2020; Accepted: 29 May 2020;
Published: 14 July 2020.
Edited by:
Muhammad Javaid, University of Management and Technology, PakistanCopyright © 2020 Zhang, Ma, Li and Qiu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jianbao Zhang, amlhbmJhb3poYW5nQDE2My5jb20=
 Jianbao Zhang
Jianbao Zhang Zhongjun Ma3
Zhongjun Ma3