Diamond Detectors for Timing Measurements in High Energy Physics

Timing detectors are a well-established part of High Energy Physics experimental instrumentation. The choice of sensors with fast (less than 10 ns) and precise (better than 100 ps) signals, together with radiation resistance considerations, are an essential part of the design of a timing detector. In this paper, the main characteristics that make single diamond crystal sensors ideal for timing applications will be described and an introduction to the design of fast front-end electronics will be given. Finally, two examples of diamond timing detectors used in High Energy Physics, the START detector of HADES and the TOTEM/CMS timing detector, will be discussed.

1. Introduction

In the last few years fast timing detectors have become more and more important for High Energy Physics (HEP) and for technological applications. ATLAS (A Toroidal LHC ApparatuS) and CMS (Compact Muon Solenoid) Collaborations plan to upgrade their experimental apparatus with the inclusion of a timing detector to extend their experiments capabilities in view of the High Luminosity LHC (HL-LHC) era [1, 2]. Furthermore, TOTEM has already operated a timing detector [3] in a special LHC run and other major Collaborations are currently undergoing R&D on timing detectors. In this review, an overview on modern timing detectors will be presented, with particular attention to diamond sensors. First, an overview on diamond detectors will be given in section 2. In section 3, the principles of front-end design for timing applications will be presented. Finally, two successful cases will be introduced and discussed in detail. The START detector of the HADES apparatus at GSI, one of the first diamond detectors with a time precision better than 100 ps on Minimum Ionizing Particles (MIPs) to be used in an HEP experiment, is described in section 4.1. The TOTEM and CMS timing detector, a diamond detector operated at few millimeters from the LHC beam and with a time precision on MIPs below 50 ps, is then described in section 4.2.

2. Diamond Sensors for Particle Detection

Modern solid state detectors often use silicon crystals as the sensitive element. However, other crystals can have interesting qualities that make them ideal for specific applications. In particular, diamond crystals can generate a signal faster than silicon in response to the passage of a particle. Moreover, diamond sensors, having superior radiation hardness, thermal properties and being able to operate in harsh conditions, are more robust then other sensors. They are thus ideal for high radiation environments or where appropriate cooling of the sensor is undesirable or impractical. In this section, a description of the main characteristics of diamond sensors will be given. The two main types of synthetic diamonds, with a short introduction to their manufacturing techniques, will be introduced in 2.1. In section 2.2, the crystal characteristics and the charge mobility are discussed. The effect of defects and the effect of radiation on defects concentration is introduced in section 2.3. A model of the signal for single crystal diamond sensors will be presented in section 2.4. Finally, the main diamond properties will be summarized and compared to silicon in section 2.5.

2.1. Crystal Production

Natural diamonds are not suitable to be used as particle detectors because of their high concentration of impurities which, as it will be discussed in section 2.3, greatly reduces the performance of the crystal as particle detector. On the other hand, synthetic diamonds with higher purity can be grown with two techniques: High Temperature High Pressure (HTHP) and Chemical Vapor Deposition (CVD). Both techniques were used for the first time in the 50's. The HTHP uses an high temperature (1,000–1,400 °C) high pressure (45–60 kBar) process, reproducing the condition of natural formation of diamond. The CVD technique, instead, uses a lower temperature (<1,000°C) and low pressure (~ 0.1 bar), producing the highest quality diamond to date. While many details on the CVD process can be found in [4, 5], considering that many manufacturers have their own proprietary technical procedure, only the main principles will be described here.

Almost all methods use a mixture of methane (CH₄), molecular hydrogen (H₂) and, optionally, an oxygen compound. The mixture is then heated with different techniques: hot filament, plasma generated with a microwave generator, combustion flames from an oxygen-acetylene brazing torch or high pressure direct-current plasma discharge (plasma jet). The best growth rate and crystal quality can be obtained with the plasma-assisted processes. In all cases, the goal is to continuously decompose the molecular hydrogen into atomic hydrogen during the entire process. Carbon atoms are then produced by stripping hydrogen atoms from the methane through the cascade reaction

$\begin{array}{ll}C{H}_x+H\to C{H}_{x-1}+H_2& (1)\end{array}$

which will then attach to the crystal.

A key role in the growth of ultra-pure diamond crystals is played by the substrate. If the substrate is not diamond (i.e., molybdenum, silicon nitride, tungsten carbide, …) nucleation has to take place before the crystal can grow [6]. Without a proper nucleation procedure, only a few small isolated diamond micro-crystals will be present in the sample (~ 10⁵−10⁶ cm⁻²), and it will instead be dominated by graphite and amorphous carbon, making the crystal unusable as particle detector. Even if the inclusion of non-diamond structures can be mitigated with a proper nucleation or by using a diamond as substrate, some graphite inclusions can still form. However, considering that diamond is more stable than graphite when directly exposed to hydrogen, hydrogen atoms can etch non-diamond bonded materials from the surface of the crystal. Moreover, hydrogen etching represents an efficient way to remove hydrogen atoms accidentally bonded to the surface, leaving the crystal surface free of impurities and ready to receive other carbon atoms. Diamond grown on hetero-substrates are poly-crystalline (pcCVD), since multiple nucleation regions will lead to multiple micro-crystals, with a columnar structure of grain. The column size typically increases during the process so that some seed crystals are naturally selected, eventually giving rise to a single crystal (scCVD) diamond. The use of scCVD diamond as a substrate, and a slower growth rate, increases the efficiency of the process at the expenses of an higher production costs. Moreover, large area scCVD cannot be easily produced and therefore the dimensions of scCVD crystals available on the market do not exceed 5 × 5 mm² with a thickness of 500 μm.

After the production, the diamond is cut and metalization is performed. The surfaces have to be coated with a conductive layer, usually a metal, to form the electrodes. These electrodes will then be connected to the front-end electronics. This connection, usually performed using one or more bonding wires, must be stable, non-volatile and resistant to mechanical stress. The metalization must ensure a uniform electric field when a bias voltage is applied and the contact between the diamond and the metal must be ohmic: the current across the junction must depend linearly on the applied voltage. To ensure all these properties, an alloy or a multi-layer metalization is commonly used. At room temperature the interface between the diamond and the deposed metal is abrupt and a Schottky (non-ohmic) contact is created. The sample must be heated (annealed) in order to obtain an ohmic contact. During the annealing certain metals (e.g., Al, Ti, Cr) react with the diamond and form carbides [7] resulting in a final ohmic contact. Annealing time and temperature depend on the type of metal. A detailed description for Cr layer is given in [8]. If a particular segmentation of the sensor is required, the sensor can be divided into pixels of the desired geometry during the metalization, using a mask or a lithographic process. It is interesting to note that the same crystal can be metalized more than once, chemically etching the previous electrodes.

Another notable procedure used to create contacts on diamond is called graphitization and consists of “burning” the surface of the diamond with a laser, creating a thin layer of graphite, which is conductive. This graphite layer can be directly connected to the front-end electronics, or protected by an additional metalization. With this technique it is possible to realize both microstrips [9] and pads with large area. In [10], electrodes with an area of 4 · 0.85 mm² have been created on a pcCVD diamond. The contact was ohmic with a constant resistivity of the order of 10⁻⁵ Ωm. Furthermore, graphitization can be used to create 3D structures in which cylindrical carbon electrodes are created in the bulk of the crystal [11]. In this case, the electrode density is mainly limited by the mechanical stress on the diamond structure: graphite electrodes, having a lower density with respect to diamond, will eventually break the crystal. In a 3D diamond the electrodes are usually arranged in quadratic cells consisting of bias electrodes in the four corners and a readout electrode in the center. Typical cell size is of the order of 100 · 100 μm². Electrode resistivity is of the order of 10⁻¹ Ωm and may have large fluctuations between different electrodes.

2.2. Diamond Crystals and Mobility

Carbon atoms that are arranged in diamond structure (fcc Bravis lattice) are bonded together through covalent bonds. Many others elements (including silicon, germanium, and gray tin) can crystallize in a diamond-like structure with a different lattice constant. This is why almost all properties of diamond can be described by the physics of semi-conductors.

Other properties of diamonds can be understood in terms of its band structure [12]. The band-gap, which is the difference between the minimum energy in the conduction band and the maximum energy in the valence band, is 5.47 eV in diamond, and it is the reason why diamonds are usually considered to be insulators.

Free electron-hole pairs (carriers) can be created by thermal excitation and reach a concentration equilibrium when recombination and formation rates are equal. The concentration of free carriers for a crystal (free of defects) is:

$\begin{array}{ll}{n}_i=\sqrt{n_c{n}_v}exp(-\frac{E_g}{2k_{B}T})& (2)\end{array}$

where n_c and n_v are the density of states in the conduction band and valence band, respectively, k_B the Boltzmann constant and T the temperature. In diamond $n_c~10^{20}{\text{ cm}}^{-3}$ and $n_v~10^{19}{\text{ cm}}^{-3}$, giving a carrier density of ~ 10⁻²⁷ cm⁻³ at room temperature. This value can be considered negligible in most cases and it is an important difference with respect to other materials, e.g., silicon, where it is necessary to create a region depleted of free carriers in order to use the device for particle detection.

Another important characteristics of the band structure is that the transition between valence and conduction bands is indirect, since a change in the particle momentum is needed. To allow the transition, an external agent (usually a phonon) must supply the momentum required. Direct transition is still possible, but with an higher energy gap (7.5 eV), and thus very rare.

An important parameter for timing measurements is the carrier drift velocity v_d, which determines the signal speed. It can be shown empirically [13] that the drift velocity depends on the electric field as:

$\begin{array}{ll}{\text{v}}_d(\text{E})=\frac{\mu \text{E}}{1+\frac{\mu \text{E}}{v_{sat}}}.& (3)\end{array}$

Where, E is the electric field, μ is the mobility of the charges and v_sat is the saturation velocity. With high enough electric fields (E > 10⁴V/cm), v_d becomes asymptotically equal to the saturation velocity, which depends only on the crystal characteristics. Physically, saturation occurs because a proportional fraction of the kinetic energy of the carriers is lost to the crystal by atomic collisions and phonons generation. Reaching the saturation velocity has several advantages for timing measurements. The fastest signal is achieved and non-uniformities of the electric field will have little to no effect on the shape and amplitude of the output signal. Among different diamond production techniques, higher mobilities are obtained with scCVD diamond. In particular, carrier mobility values for scCVD crystals are reported in Pernegger et al. [14], confirming Equation (3). Low field mobility of ${\mu }_e=1,714{\text{ cm}}^2/\text{Vs}$ and ${\mu }_h=2,064{\text{ cm}}^2/\text{Vs}$ and saturation velocities of 9.6 · 10⁶ cm/s and 14.1 · 10⁶ cm/s for electron and holes, respectively, have been observed. Mobility also depends on the concentration of crystal defects: mobilities of 4, 500 and 3, 800 cm²/Vs for electron and holes, respectively, have been measured in a special sample of ultra-pure scCVD diamond at room temperature [15], with electrons having higher mobility than holes. Similar results (${\mu }_e=4,551{\text{ cm}}^2/\text{Vs}$, ${\mu }_h=2,770{\text{ cm}}^2/\text{Vs}$) are reported in [16], with saturation velocities $v_{sat,e}~2.6·10^7\text{ cm}/\text{s}$ and $v_{sat,h}~1.6·10^7\text{ cm}/\text{s}$. This high values, even if clearly dependent on crystal quality, are very promising for timing applications. In section 2.4, carrier velocities will be used to model the signal induced on the electrodes of a diamond sensor by the passage of an ionizing particle.

2.3. Effects of Defects and Radiation

Even if synthetic diamonds have an higher purity than natural gems, defects cannot be completely avoided. For example, foreign atoms can be included in the crystal during the growth or additional defects can be created when the crystal is exposed to ionizing radiation. Planar defects, generated during the crystal growth when different micro-crystals merge together, are common in poly-crystalline sensors, while they do not exist in single crystals. Point defects usually involve only one or two atoms in the lattice. They can be caused both by carbon atoms which are not correctly placed in the crystal lattice or by non-carbon atoms embedded in the crystal (impurities).

While controlled impurities (doping) are intentionally added to silicon to create a pn junction and to obtain depleted regions, impurities in diamonds used for timing are usually cause of performance degradation. Indeed they create additional states in between the conduction and valence bands that will act as trapping and recombination centers for the carriers. The carrier lifetime, and thus the overall signal induced on the electrodes, is than reduced. Moreover, as seen in section 2.2, crystal with higher purity have higher mobility and saturation velocity, which are important parameters for timing applications. It is therefore crucial to produce scCVD diamonds with the highest purity achievable.

The exposure of a crystal to ionizing radiation triggers the formation of point defects named Frenkel pairs. A carbon atom leaves its place in the lattice, creating a vacancy, and becomes interstitial by lodging in a nearby location. The concentration of Frenkel defects is usually much lower than the other types of defects for a non-irradiated crystal, but they will increase when the crystal is exposed to radiation. The energy required to create a Frenkel pair is called the displacement threshold energy. Typical values for diamonds are in the range 37.5–47.6 eV depending on the crystal orientation [17], higher than is found in silicon (36 eV, [18]). This contributes to a better radiation resistance of diamond with respect to silicon sensors.

The RD42 Collaboration has recently performed irradiation studies [19] in which two groups of scCVD and pcCVD where irradiated with 800 MeV (at the Los Alamos LANSCE facility, [20]) and 24 GeV protons (at the CERN IRRAD facility, [21]) in steps up to ~ 10¹⁶ protons/cm². Their results show a signal reduction in both single (Figure 1, left) and poly-crystalline diamonds. The average distance traversed by a free carrier before being trapped λ can be modeled with the relation:

$\begin{array}{ll}\frac{1}{\lambda }=\frac{1}{{\lambda }_0}+k\varphi & (4)\end{array}$

Where λ₀ is the mean free path before irradiation, ϕ the particle fluence and k the damage coefficient. The damage coefficient has been found to be the same for both scCVD and pcCVD crystals (Figure 1, right). Furthermore, the scCVD uniformity does not change with an uniform irradiation, while for pcCVD irradiation is seen to improve signal uniformity.

FIGURE 1

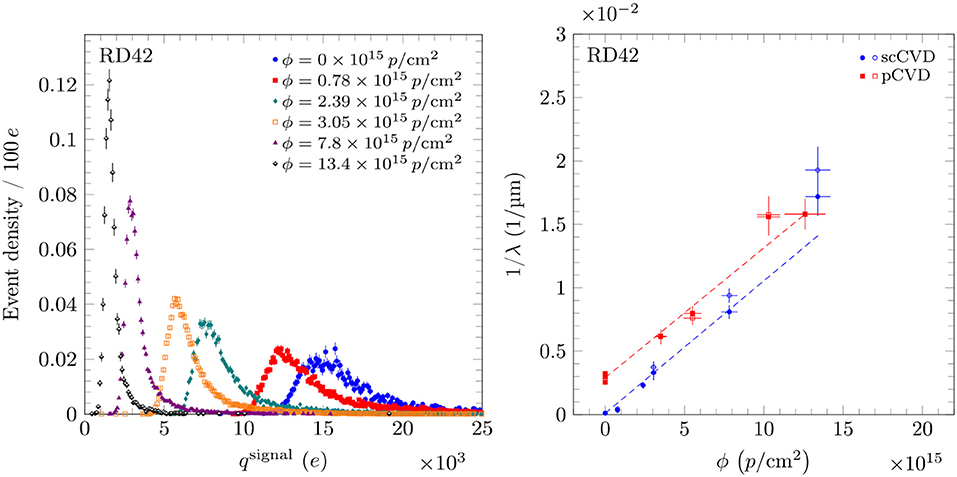
Figure 1. On the left pulse height evolution for a scCVD diamonds irradiated with 800 MeV protons (E =−2 V/μm). On the right the 1/λ for each type of diamond with 800 MeV protons. The two values for each fluence represent positive and negative biasing with E =±2 V/μm. Adapted from Bäni et al. [19] under the Creative Commons CC BY license.

2.4. Signal Generated at the Passage of a Particle

A particle passing through matter deposits, partially or fully, its energy into the material. In a semiconductor, like silicon or diamond, this energy creates pairs of electrons and holes. If the sensor is properly designed and biased, these pairs start drifting toward the electrodes, thereby inducing a current on them. In diamond the absence of free carriers ensures that under an external electric field no current flows across the device. Although in real life leakage current rises due to the presence of impurities and surface leakage, typical leakage currents remain of the order of few pA. This makes diamond an excellent candidate for charged particle detection.

The shape of the signal induced on the electrodes can be derived using the Shockley–Ramo theorem [22]. In particular, assuming a constant and uniform electric field in the crystal (or a regime of saturated velocity) and that the charge carriers drift with the same velocity, it can be shown [23] that the signal generated at the passage of a particle is:

$\begin{array}{ll}i(t)~2\frac{e{N}_{gen}}{t_{tr}}\left(1-\frac{t}{t_{tr}}\right)\theta (t-t_0)\theta (t_0+t_{tr}-t)& (5)\end{array}$

with:

• e is the electron charge;

• N_gen is the number of electron-holes pairs generated by the passage of the particle;

• θ is the Heaviside step function;

• t₀ is the time of crossing of the particle.

• t_tr = d/v_e,h is the transit time of the charge carriers, assuming electrons and holes drift with the same velocity v_e,h and that the diamond thickness is d.

To fully characterize the signal we need to estimate N_gen and t_tr. The mean energy release of a MIP for diamond is dE/dx ~ 470 keV/mm [24]. As discussed previously, diamond is an indirect semi-conductor. This implies that the energy needed for e-h generation is greater than the energy band gap of 5.47 eV, since some additional energy will be used to excite phonons. The mean excitation energy, E_eh, has been measured [25] to be ~ 16 eV. From this we define:

$\begin{array}{ll}{N}_{gen}=\frac{dE}{dx}·\frac{d}{E_{eh}},& (6)\end{array}$

For a diamond with a thickness of 500 μm, on average N_gen is ~ 18000, which corresponds to an induced charge, eN_gen, of 2.88 fC.

Finally, depending on the mobility and saturation values used in Equation (3), we obtain drift velocities on the order of 10⁷cm/s for an electric field of 1.6 V/μm. Hence, transit times are on the order of few nanoseconds.

A signal generated using Weightfield 2, a freeware 2D simulator for silicon and diamond detectors [26], is shown in Figure 2. This simulator computes the energy released every 1 μm by the passage of a particle using GEANT4 [27], a toolkit for the simulation of the passage of particles through matter. A simulation was performed with a 500 μm detector with a single pad with an applied external potential of 800 V (1.6 V/μm).

FIGURE 2

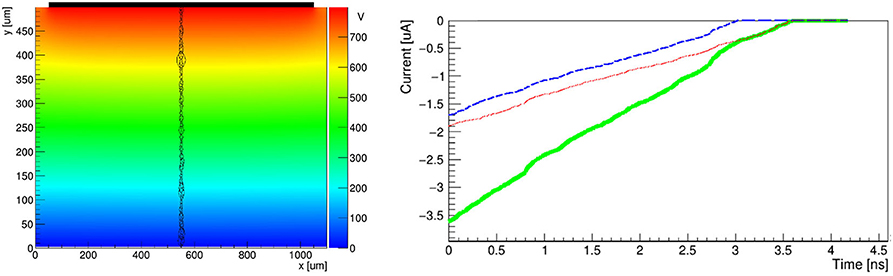
Figure 2. Signal produced by a MIP passing through a 500 μm diamond simulated using Weightfield2 [26]. On the left: the electric potential inside the diamond and the energy lost by a passing particle. The energy lost in a μm is represented as a black circle which radius is proportional to the charge released (Landau distribution). On the right are plotted the currents induced by the electrons (dotted red line), holes (dashed blue line) and the sum of the two contributions (solid green line).

While this model perfectly holds for single crystals diamond, poly-crystalline diamonds are slightly more complicated to model because of the reduced lifetime of the carriers. Due to recombination of charge carriers, not all of them are collected. This results in a reduction of the measured signal. A way to characterize this is to introduce the concept of Charge Collection Efficiency (CCE, the ratio between the generated charge and the total induced charge on the electrodes) or Charge Collection Distance (CCD = CCE · d, where d is the electrode distance). Thanks to the low impurity concentration and the absence of planar defects, CCE for a 500 μm scCVD crystal is close to 1. For pcCVD the value is much lower and the CCD is usually in between 200 and 300 μm, giving CCE ~ 50%. Hence, the signal generated by a 500 μm pcCVD diamond with a CCD 200 μm [28] can be assumed, in first approximation, to be similar to the signal generated by a 200 μm scCVD diamond.

The lower signal generated by pcCVD is the main reason why pcCVD is not the best solution for a timing detector for MIPs. For this reason single-crystal (scCVD) diamond sensors are preferred and will be the focus of this review. However, for low energy particles or for heavy ions, that release considerably more energy than a MIP, pcCVD are an attractive solution due to the lower cost and larger availability of pcCVD with respect to scCVD. For example, in a detector designed at GSI [29] for the Facility for Antiproton and Ion Research (FAIR) in Germany, the team achieved a time precision better than 50 ps utilizing a 35 MeV/u beam and a 300 μm pcCVD diamond with ~ 14 pF capacitance.

Finally, pcCVD can be used with a 3D architecture as described in section 2.1. Due to the 3D architecture, the distance between electrodes is shorter with respect to a planar configuration, leading to a better charge collection and radiation hardness. On the other hand, the resistivity of the electrodes and the non-uniform electric field limit timing performance. Results of recent tests of 3D pcCVD diamonds are available at [30].

2.5. Summary of Diamond Properties

Before describing the details of timing detectors based on scCVD, it is useful to summarize the main differences between silicon and diamond sensors. Due to the greater mobility of electrons and holes and to the combination of high resistivity and high breakdown field that allow a diamond sensor to operate with higher bias, i.e., higher internal electric field, scCVD diamond sensors have a faster signal with respect to silicon sensors. The lower relative permittivity of scCVD also simplifies the design of fast front-end electronics (see section 3.2). The main disadvantage of diamond is that the signal generated by the passage of a particle is smaller than the signal generated in silicon. The average number of electron-hole pairs created by the passage of a MIP, at ~ 36 per μm, is less than half the number created in silicon. Furthermore, diamonds are also more expensive due to the high purity needed for sensor applications and to the lack of large scale growth techniques, like for example the Czochralski process for silicon. A summary of the main properties of diamond crystals and silicon are compared in Table 1.

TABLE 1

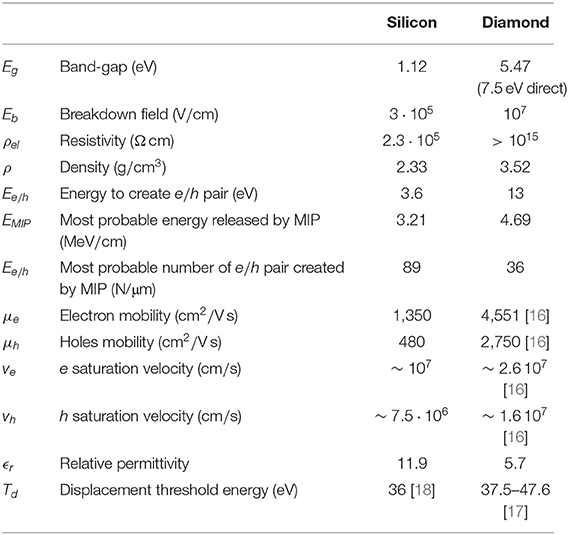
Table 1. Physical properties of silicon and diamond at room temperature [31].

3. Fast Timing Detectors

Timing detectors are designed to precisely measure the time of arrival of a particle. While in most applications the reduction of the noise on the signal is the main step to achieve a better precision, a fast signal is also required to achieve a good time precision (more details in section 3.1). For this reason, it is common to refer to this kind of technologies as “fast timing detectors.”

Precise timing is mostly used in Time Of Flight (TOF) applications for particle identification. New timing detector technologies opened the way for 4D tracking (spacial and temporal) like for example the Gigatraker developed by the NA62 Collaboration [32]. Other applications of fast time detectors include particle counting at very high rates for both Particle Physics experiments [33] and medical applications [34].

To achieve the best timing performance from scCVD diamonds, it is important to design the front-end electronics specifically for timing. The main contributions to time precision and accuracy will be investigated in section 3.1. Then, an overview of the front-end design will be presented in section 3.2 and an introduction the signal digitization techniques will be given in section 3.3.

3.1. Computation of the Arrival Time

The uncertainty, σ_t, in the arrival time is due to different contributions:

$\begin{array}{ll}{\sigma }_t^2={\sigma }_{sensor}^2+{\sigma }_{jitter}^2+{\sigma }_{walk}^2+{\sigma }_{digit}^2+{\sigma }_{drift}^2& (7)\end{array}$

Where,

• σ_sensor is the contribution due to statistical fluctuations in the sensor, like local Landau fluctuations on the deposited energy or the uncertainty on the first interaction point in the sensor;

• σ_jitter is the contribution due to the electronic noise, more details are discussed in section 3.2;

• σ_walk is the contribution due to the dependence of the measured time on the amplitude of the signal, more details are discussed in section 3.3;

• σ_digit is the contribution due to the digitization of the signal, more details are discussed in section 3.3;

• σ_drift is the contribution due to temperature changes and aging of the components.

Usually, σ_drift is negligible with respect to the other contributions since temperature and aging effects are typically several orders of magnitude slower than the passage of a particle through the sensor. Time walk and digitization noise can be optimized so that they are much smaller than the jitter. For diamond detectors σ_sensor is also considerably lower than the σ_jitter. Therefore, a quick rule of thumb to estimate the time precision is:

$\begin{array}{ll}{\sigma }_t~{\sigma }_{jitter}~\frac{{\sigma }_V}{dV/dt}~1.25\frac{\Delta t_{0.1-0.9}}{SNR}& (8)\end{array}$

Where the Signal to Noise Ratio (SNR) is defined as the ratio between the amplitude V_max and the noise σ_V:

$\begin{array}{ll}SNR=\frac{V_{max}}{{\sigma }_V}& (9)\end{array}$

The rise (fall) time Δt_0.1−0.9 is the time needed by a positive (negative) signal to rise (fall) from 0.1 V_max to 0.9 V_max.

3.2. Optimization of the Front-End Electronics

This section describes the main concepts needed to design a front-end amplifier for a diamond detector, with particular focus on timing applications. More detailed studies are discussed in [23] and [35].

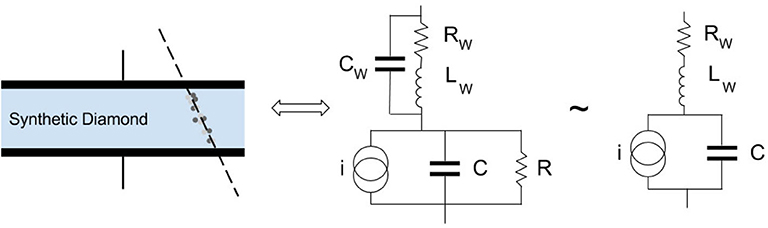
A reliable model of the sensor is the key to optimize the front-end electronics. A planar diamond sensor can be modeled as in Figure 3:

FIGURE 3

Figure 3. Equivalent model of a diamond detector with parallel plate geometry.

The capacitance of a diamond sensor is given by:

$\begin{array}{ll}C\left[\text{fF}\right]={ϵ}_{\text{r}}{ϵ}_0\frac{\text{S}}{\text{d}}~50\frac{\left[\text{fF}\right]}{\left[\text{mm}\right]}\frac{\text{S }\left[{\text{mm}}^2\right]}{\text{d }\left[\text{mm}\right]}& (10)\end{array}$

Where S and d are, respectively, the surface of the pad and the thickness of the diamond expressed in milimetres; ϵ₀ is the vacuum permittivity and ϵ_r is the relative permittivity of diamond that can be found in Table 1. The resistance R of the diamond is usually on the order of GΩ and can be approximated to an open circuit. R_W, L_W, and C_W are the parasitic contributions due to the line that connects the sensor to the amplifier, usually a bonding wire. Usual values are on the order of ~ Ω, ~ nH and ~ 0.1 pF respectively. Those values are usually negligible, hence the model can be further simplified, as shown on the rightmost part of Figure 3.

In principle, the simplest front-end is a single resistor, as shown in Figure 4. Clearly, without active amplification it is not possible to design a working detector. However, this simple model is useful to intuitively understand what are the main factor to optimize during the design of a front-end amplifier.

FIGURE 4

Figure 4. The simplest way to read the current generated by a diamond detector is using a resistor.

The signal produced by the RC is given by the convolution of the current generated by the diamond and the impulse response of the RC network:

$\begin{array}{ll}{V}_{RC}(t)=i(t)\star h_{RC}(t)=i(t)\star \frac{1}{C}{e}^{-\frac{t}{RC}}& (11)\end{array}$

Some examples of V_RC(t) are shown in Figure 5. With the same C, the signal is faster for low values of R, however its amplitude is lower.

FIGURE 5

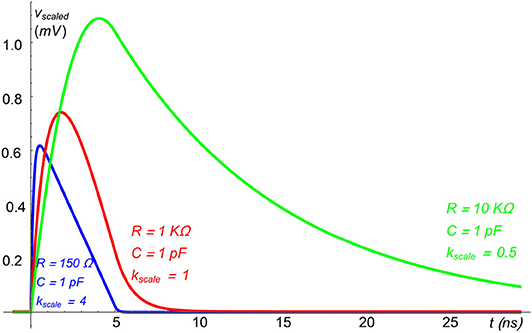
Figure 5. Examples of V_RC(t) for various values of R, computed using the toy model discussed in the text; the amplitude of the signals has been scaled for better displaying: V_scaled(t) = k_scale V_RC(t).

The main noise contribution is the Johnson-Nyquist noise on the resistor. In particular, the Signal to Noise Ratio (SNR) can be estimated as:

$\begin{array}{l}SNR=\frac{V_{max}}{{\sigma }_V}\\ \begin{array}{l}=\frac{2e{N}_{gen}}{t_{tr}^2}\frac{1}{\sqrt{k_{B}T}}\frac{1}{\sqrt{C}}RC\left(t_{tr}+RC\text{ ln }\left(\frac{RC}{RC+t_{tr}}\right)\right)\end{array}& (12)\end{array}$

where V_max, σ_V, and t_tr were previously defined, respectively, as: amplitude of the signal, noise and transit time of the charge carriers; k_B is the Boltzmann constant and T is the temperature.

Adjusting the value of the resistor to keep RC constant, the SNR then depends only on C. The behavior of this function vs. R is shown in Figure 6, for different values of C and at T = 300 K. For low values of R, the SNR decreases for increasing capacitance, then it saturates to:

$\begin{array}{ll}{\displaystyle \underset{R\to \infty }{\text{lim}}}SNR=\frac{e{N}_{gen}}{\sqrt{k_{B}T}}\frac{1}{\sqrt{C}}\propto \frac{1}{\sqrt{C}}& (13)\end{array}$

To understand intuitively why SNR saturates, it is useful to consider the RC as an integrator. The signal produced by the detector has a finite integral (the collected charge) and a finite duration (t_tr). Hence, for RC ≲ t_tr the integration time is not enough to integrate the whole signal and for RC≫t_tr the collected information cannot increase further.

FIGURE 6

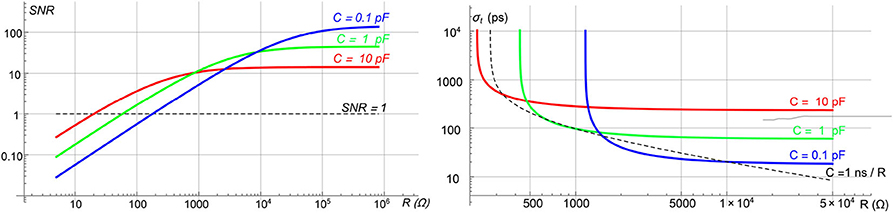
Figure 6. SNR (left) and time precision (right) of a diamond detector vs. the resistor R for different values of C at T = 300 K. The bashed black line on the left indicates SNR = 1. On the right, the dashed black line represents the time precision achievable for various C, varying accordingly R to have RC = 1 ns.

As an example, a typical case can be represented by a sensor with a pad of 10 mm² and a thickness of 500 μm (C = 1 pF using Equation 10). The amplitude of the signal is larger than the noise for R ≳ 60 Ω. To have some margin over the noise, considering the stochastic nature of the energy deposition, a good choice could be to require a SNR ≳ 6, which corresponds to R ≳ 430 Ω.

To design a tracking or counting detector, the SNR is the most important parameter to optimize. However, for a timing detector, a fast signal is also needed. Starting from Equation (8), the time precision can be approximated to:

$\begin{array}{ll}{\sigma }_t~\frac{{\sigma }_v}{dV/dt}{|}_{t=t_{th}}=\frac{\sqrt{k_{B}T}{t}_{tr}^2}{2Q_{gen}}\frac{\sqrt{C}}{RC}\frac{1}{(1+\frac{t_{tr}}{RC})e^{-\frac{t_{th}}{RC}}-1}& (14)\end{array}$

where t_th the time when the signal crosses the threshold. Since dV/dt is decreasing with t, the threshold should be set as low as possible and still be above the noise. The choice of the threshold depends on the particular application, but, as an example, it is possible to use V_RC(t_th) = 6 σ_V.

The time precision computed with Equation (14) is shown on the right in Figure 6. It is clear that the precision achievable is limited. The value of this limit depends on the capacitance of the detector, and it is about 100 ps for a diamond detector with C = 1 pF. It should also be noted that with the increasing value of R the total duration of the signal is increasing, limiting the maximum rate sustainable by the detector. Hence, R should be chosen to be the smallest value before the saturation of the time precision, for example R ~ 1 KΩ for C = 1 pF.

It is advisable to have a detector with the lowest possible capacitance. The detector, then, has to be read out using a resistance large enough to integrate all the signal generated by the diamond: RC ≲ t_tr. A good rule of thumb is to chose a resistor such that a RC time constant of ~ 1 ns is achieved.

The addition of an active component, i.e., a transistor, complicates a bit the situation. However, the overall behavior is similar using the input impedance of the amplifier as R. In order to have the best time precision, it is necessary to design an amplifier with high (about kΩ) input impedance. This strategy was successfully applied by the Hades and CMS/TOTEM Collaborations and more details will be discussed, respectively, in sections 4.1 and 4.2.

3.3. Computation of the Time of Arrival

Once the signal generated by the sensor at the passage of a particle is amplified, it needs to be digitized. We can then use digital processing (hardware or software) to compute precisely the time of arrival. The most accurate way to digitize a signal is to use a digital oscilloscope with a bandwidth and a sampling frequency high enough to preserve the information of the waveform. Considering the number of channels, scalability, and cost a digital oscilloscope is often not an ideal solution. In the last few years fast digitizers have become more and more common in timing applications. For example, the SAMpler for PICosecond time pick-off (SAMPIC) chip [36], designed and realized by a collaboration including IRFU/SEDI, Saclay and LAL, Orsay, is capable of sampling up to 10 GSa/s at a cost per channel that is comparable to a Time to Digital Converter (TDC). The SAMPIC chip was used in the TOTEM Timing Detector [3, 37]. While this sampling technique gives the best results in terms of performance, some times a sampler cannot cope with the dead-time and input rate required by the experiment. Moreover, this approach produces a large amount of data per channel that the data acquisition system must be able to handle.

Another widely used approach for digitization requires the use of a discriminator and a TDC. This approach drastically simplifies the hardware required and it reduces the amount of data to be processed, a maximum of two time measurements are performed on each signal, allowing higher acquisition rates. Both detectors described in the following sections use this approach. However, the reduced amount of data produced comes at the cost of timing performance. It has been measured [38] that this approach leads to a time precision degradation of about 30% when applied to sensors discussed in section 4.2. However, it should be noted that this value is strongly dependent on the particular case studied.

Once the waveform is digitized, several techniques can be applied to measure the time of arrival. The main goal is to develop an algorithm that removes the dependence of the time of arrival on the amplitude of the signal (time walk). The energy released by a particle when passing through the sensor is heavily dependent on the type and the energy of the particle. Moreover, due to statistical fluctuations, for the same particle the energy release in a thin detector follows a Landau distribution. As a result, even a particle passing through two consecutive sensors can release a different energies. The output signal of the sensor where more energy is released reaches the threshold level before the other sensor. Time walk can be the dominant source of uncertainty if not properly corrected, especially when large fluctuations of energy release are possible.

An extensive discussion of the correction strategies is impractical in this review, therefore only the two main techniques will be quickly discussed:

• Constant Fraction Discriminator (CFD)

• Time Over Threshold (TOT)

More details and other techniques are discussed in [39] and [40].

3.3.1. Constant Fraction Discriminator

In the standard CFD technique each signal waveform is inverted, attenuated, delayed and finally added to the original one. The time of zero crossing of the resulting function does not depend on the amplitude of the signal and can be used as time of arrival.

While this technique can be implemented with analog electronics, similar results can be obtained offline with a normalized threshold algorithm after digitizing the signal: the signal time is computed as the crossing time of a threshold proportional to the amplitude. To reduce the dependency of the jitter on low frequency fluctuations, a number of samples before the signal can be used to compute the baseline to which the threshold is referred. Furthermore, it is possible to reduce the digitization uncertainty by interpolating the sampled points. The choice between the different implementations of this technique depends on the resources available and on the precision required.

3.3.2. Time Over Threshold

The Time Over Threshold (TOT) technique can be applied when performing only two time measurements and, therefore, it is often used when the digitization is done through a discriminator and a TDC. In the classic approach, the discriminator signal begins when the signal crosses a given threshold and ends when it goes back below the same threshold, hence the name Time Over Threshold.

More generally, the TOT technique can be applied with any discriminator whose output duration is correlated to the total charge of the signal. Of course, the TDC must be able to tag and measure both leading and trailing edges of the output of the discriminator. It is possible to find a function of the TOT that, added to the time of the leading edge, removes the dependency of the time of arrival on the TOT, correcting for the time walk. In this case, the digitization noise is due to the TDC characteristics and the residual time walk contribution, usually larger than the digitization noise, depends on several factors, mainly the correction algorithm and the precision on the TOT measurement.

4. Timing Diamond Detectors in HEP

In this section two noticeable examples of diamond detectors used in HEP will be discussed. In particular, section 4.1 describes the detector that is providing the starting time for TOF measurements with the HADES detector at GSI and section 4.2 describes the CMS/TOTEM timing detector at CERN.

4.1. The HADES Start Detector

The High Acceptance Di-Electron Spectrometer (HADES) at GSI was one of the first Collaborations to pioneer diamond timing detectors capable of good timing performance with single MIPs. A general description of the experiment is available in [41]. In this review the focus will be on their diamond detector used for beam optimization and to measure the starting time T₀ for TOF measurements. In order to be placed in close proximity to the target in a vacuum chamber, the detector needs to be thin and radiation resistant. Moreover, the detector has must meet the following specific requirements [42]:

1. Timing precision δt ≤ 100 ps for MIPs;

2. Stable operations for particle fluxes J ≥ 10 · 10⁶ cm²s¹;

3. Efficiency for MIPS ϵ ≃ 100%;

4. Material budget as low as possible;

5. Spacial resolution of δx < 1 mm;

6. Possibility of operation in vacuum;

7. Sensitive area A = 1 cm².

As a compromise between material budget and SNR, scCVD diamonds with a thickness of 300 μm were used. Depending on the experimental configuration, several versions of the detector were designed. In particular, a detector composed by 9 diamonds with an active area of 4.3 · 4.3 mm², each segmented into 4 quadrants is described in Adamczewski-Musch et al. [42]. A version with a single diamond but with higher segmentation, 16 strips on each side of the crystal, is shown in Figure 7.

FIGURE 7

Figure 7. Picture of one of the HADES start detector (Courtesy of Dr. Jerzy Pietraszko).

As discussed in section 3.2, the input capacitance of the front-end amplifier is one of the main limiting factors to the timing performance of the detector. This capacitance is not only determined by the sensor, but also by the lines that are connecting the sensor to the first stage of amplification and by the amplifier itself. This is one of the key optimization points addressed by the HADES Collaboration in the design of their diamond timing detector. In fact, the first stage of amplification is located at few millimeters from the sensor, minimizing the parasitic capacitance. The first stage is based on SiGe:C transistors with 3 resistors in series as feedback to the input stage to further minimize the parasitic capacitance. The input impedance of few kΩ is in line with the approach described in section 3.2.

The following stages of amplification and shaping are placed outside the vacuum chamber where signal discrimination is done using the NINO chip [43], an 8 channel ultra-fast low-power differential amplifier and fixed threshold discriminator. The chip can encode the input charge, Q, collected from the detector in the output duration, W = K + f(Q), which can be used offline for TOT correction techniques. The discriminated signal is read-out by a TRB3 board [44] that hosts up to 264 channels TDC on a FPGA. The TRB3 is capable of a time precision better than 10 ps and it can be reprogrammed to improve the performance down to few ps if fewer channels are needed [45]. It is worth noting that some prototypes were tested [46] where an FPGA was also used as discriminator. The extreme flexibility of this solution came with a small cost in terms of performance, but still had a time precision better than 25 ps.

The final performance of the complete detector, 2 stacked planes with 9 sensors, was tested with a proton beam of 2.95 GeV, and achieved a time resolution of 91 ps, as shown in Figure 8.

FIGURE 8

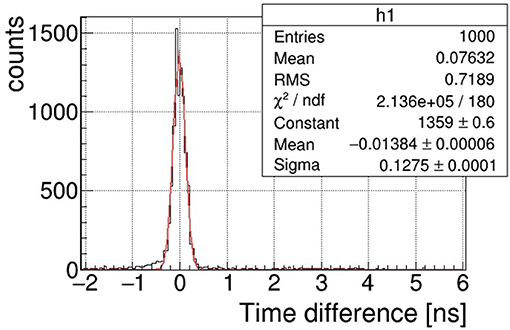
Figure 8. The time precision was estimated testing two identical detectors with a beam of 2.95 GeV protons. Assuming the two detectors have the same precision, $\sigma t=127\text{ ps}/\sqrt{(\text{2})}=91\text{ ps}$ (Courtesy of Dr. Jerzy Pietraszko).

A similar detector was also optimized for heavy ions operations to minimize the material budget. Reducing material budget, i.e., using a thinner sensor, also reduces the charge collection time. For example, the sensor tested in Pietraszko et al. [47] is a 70 μm scCVD crystal with a collection time of about 500 ps [16]. The single channel time precision of this detector was tested with 197Au beam at 1.25A GeV¹ for a non-irradiated detector and for the same detector after 5 days of operation when about 3.04 · 10¹¹ ions were detected, approximately corresponding to 87 MGy. The time precision, measured with respect to a reference detector, was 42 ps before irradiation and 54 ps after, showing excellent radiation resistance.

4.2. The CMS PPS Timing Detector

The Proton Precision Spectrometer [PPS, previously named CT-PPS [49]] is one of the CMS [50] subdetectors, developed in by the CMS and TOTEM [51] Collaborations. The PPS detector is designed to tag and measure the kinematics of protons produced in central exclusive processes from pp scattering at the LHC interaction point 5. The detected protons are scattered in the very forward regions where their detection requires sensors to be few millimeters from the LHC beam. This is possible thanks to special movable sections of the beam pipe, called Roman Pots (RP), symmetrically located at more than 200 m from the LHC IP5. RPs can be safely retracted during the critical phases of the LHC setup (injection, energy rump up, etc.) and approach the beam during data taking. Those RPs host detectors that can, thus, detect protons scattered down to few microradians from their nominal, i.e., without interacting, trajectory in the LHC.

At the LHC, protons are collected in bunches and bunch crossing occur with frequency up to 40 MHz. The average number of interactions per bunch crossing, called pile-up, was greater than 35 in 2018 and it is foreseen to above 100 in the Run 3 (2021–2024) of the LHC. The tracking system installed in the PPS RP can reconstruct the scattering angle and the fractional momentum loss, but it is not able to resolve the position of the interaction vertex. To discriminate pile-up events and reconstruct the protons vertex, PPS relies on the measurement of the time of arrival of the protons at the two sides of the interaction area. Measuring the time difference Δt of the protons, it is possible to reconstruct the longitudinal vertex position as Z_pp = cΔt/2 and correlate the two protons to one of the vertices reconstructed by the central CMS instrumentation.

The following requirements on the timing detector are quite strict but can be matched by diamond sensor technology:

• Resolution of few tens of ps and high efficiency in detection of 6–7 TeV protons (which can be considered as MIPs);

• Low density and thickness of the sensor to fit more planes in a single RP and to reduce the probability of background on the downstream RP stations due to secondary particles production;

• Capable to sustain an hit rate up to few MHz/mm²;

• Must be operated in vacuum;

• Active area ~ 80 mm²;

• High radiation hardness.

While the first few requirements can be met by other technologies, for example LGAD silicon sensors, the diamond sensors were selected due to their superior radiation resistance. The crystal must sustain an highly non-uniform irradiation, with a local peak of ~ 5 · 10¹⁵ protons/cm² in the region near the beam, for an integrated LHC luminosity of 100 fb⁻¹. This represents the radiation dose delivered by LHC with the RP in data taking position during Run 2. In future LHC operations (Run 3) the radiation dose is predicted to be increased a factor 3. The technology chosen by PPS is based on ultra-pure scCVD diamonds. During 2017 one detector plane based on Ultrafast Silicon Detectors [52] was used for R&D purpose. Diamond technology has been selected for all future data tacking.

4.3. Single Diamond Architecture

The PPS diamond sensors are made of scCVD crystals with a surface of 4.5 · 4.5 mm² and a thickness of 500 μm. They are arranged in a single column configuration of 4 crystals, with a total active surface coverage of about 20 · 4.5 mm² (Figure 9). Crystals are further segmented in pads of different sizes to minimize the possibility of having two simultaneous particles in the same pad while keeping the number of channel to the minimum. The segmentation is achieved with the metallization on the top face of the diamond while the bottom side of the crystal, where the bias voltage is applied, is metallized with a single pad. The pads located on the same crystal are separated by 100 μm and a clearance area of 150 μm is taken from the crystal edges to prevent discharges due to the bias voltage and to reduce the surface leakage current. Two different types of metallization have been used: Cr-50 nm + Au-150 or 100 nm Ti-W alloy. Test beam studies did not show any relevant difference in performance.

FIGURE 9

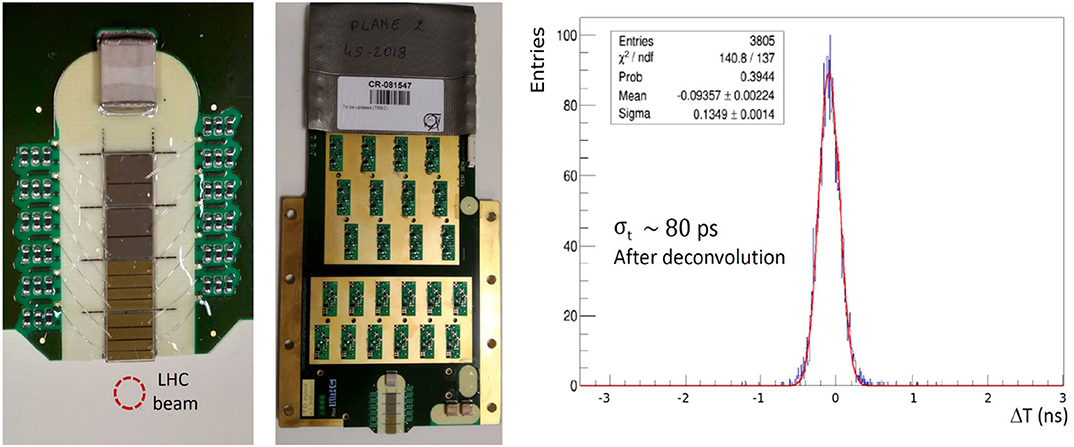
Figure 9. On the left, there is a closeup picture of the crystals were sensor segmentation and bonding wires are visible. On the center, the full detector board is shown. On the right, the measured time difference between a small pad (0.29 pF) and a big pad (2.0 pF) located in two consecutive layers is shown. After the deconvolution of the contribution of the time reference, 80 ps precision on one of the small pads is obtained. Adapted from [53] under the Creative Commons CC BY license.

The diamond sensors are glued to a hybrid board, that hosts both the sensors and the front-end electronics, designed and optimized for diamond signals, with 12 discrete multi-stage amplification channels. As discussed in section 3.2 and seen in section 4.1 for the HADES detector, care must be taken for the pre-amplification stage. The CMS/TOTEM Collaborations adapted the design of HADES, with a pre-amplification stage based on a discrete SiGe:C transistor (Infineon BFP840) in a common emitter configuration. The pre-amplifiers are placed a few millimeters from the crystals and the pads are directly connected to the pre-amplifier input via bonding wires to reduce the parasitic capacitance, estimated ~ 0.2 pF for 0.25 μm thick bonding wires. With this design, the input capacitance is dominated by the strip capacitance of 0.29 to 2 pF depending on its size.

To operate the detector with up to 500 V bias voltage, a coating is applied to sensitive areas to reduce the discharge probability. More details about sensors, amplification and test beam performance can be found in [53].

The output signal has a rise time ~ 1.7 ns and an amplitude of several hundreds of mV. This signal can be transmitted with negligible degradation over 2 m of coaxial cables. Efficiency measurements have been performed on a prototype board with a 5.6 GeV electron beam at DESY, where a tracking telescope was available. The two-dimensional scan showed a uniform efficiency above 98%. Efficiency in the inter-pad area is above 96%, when considering the combined overall efficiency of the two neighbor pad. Timing measurements were carried out at DESY and repeated with a 180 GeV π⁺ beam at the CERN SPS. The time precision is evaluated by measuring the time difference of a MIP passing through two consecutive, identical, diamond detectors. The output signal was collected with an Agilent DSO9254A oscilloscope (8 bits, 20 GSa/s, 2.5 GHz bandwidth) and a time walk correction was applied using the offline CFD algorithm, described in section 3.3.1. Results showed a precision in the range of 80 < σ_t < 108 ps, Figure 9 (right), correlated with the pad capacitance in the range of 0.29 < C < 2 pF.

4.4. Double Diamond Architecture

A new architecture, named Double Diamond (DD), was later developed for the 2018 data taking in which some layers of SD diamonds were replaced. DD architecture has been developed to achieve better time performance [54] with a single detector plane. In this design, two diamond crystals with the same metallization geometry are glued on both sides of the hybrid board, with corresponding pads connected to the same pre-amplification channel, as shown schematically in Figure 10.

FIGURE 10

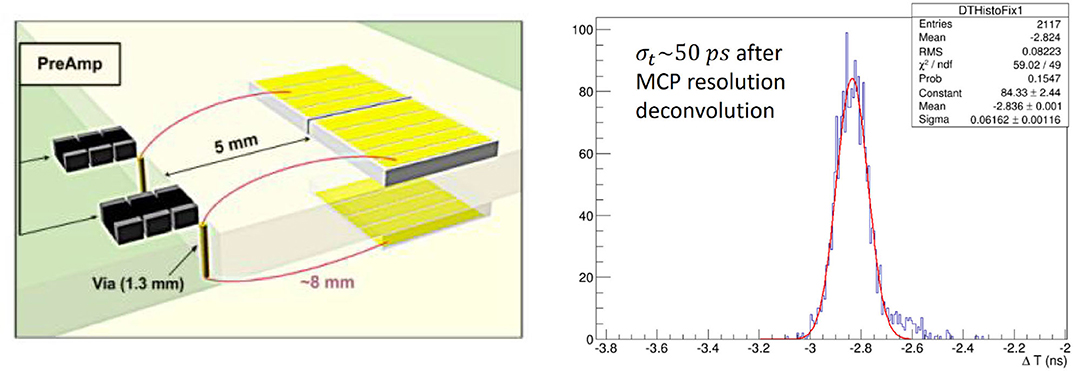
Figure 10. On the left, a scheme of the DD architecture, with corresponding strips on both sides connected to the same amplification input. On the right, time difference distribution between a DD plane and a reference Microchannel Plate photomultiplier tube (MCP-PMT). Adapted from Berretti et al. [54] under the Creative Commons CC BY license.

With this architecture, the electronic noise (dominated by the pre-amplifier) stays unchanged, while the collected charge is almost doubled. The higher sensor capacitance has a negative impact on the timing precision, but the performance loss is much lower with respect to the gain obtained due to the higher SNR. Another drawback of this technology is the need of a very precise alignment between crystals placed on the opposite sides of the hybrid board. During beam tests performed in the CERN North Area, in similar condition as for SD studies, a time precision of ~ 50 ps with a single plane of DD has been obtained, Figure 10. A MCP-PMT, with a precision better than 40 ps, was used as time reference for this study. The DD approach was shown to perform better than SD approach by a factor of ~ 1.7. It is worth noting that this performance increase is superior to the one achievable by doubling the detection layers by ~ 40% and at the same time the number of channels does not increase.

As introduced in section 3.3, the signal digitization is carried out using the NINO discriminator, as in the HADES design, and a TDC to perform the TOT time walk correction. The chosen TDC is the HPTDC [55], able to measure both leading and trailing edges of the signal with a binning of 25 ps and a resolution of about 7 ps.

DD sensors have been installed and used in the LHC Run 2. Detector calibration and radiation studies have been performed by the Collaborations [56], the resolution on the longitudinal vertex position is under study. The same technology has been confirmed for the upcoming Run 3 (2021-2024).

5. Conclusions

In this review the authors investigated diamond Minimum Ionizing Particles (MIPs) detectors with particular attention to timing applications. After an overview on diamond sensors, some ideas were proposed about design and optimization of front-end electronics. The precision of the time of arrival measurement, generally referred to as time resolution, is affected by several contributions. While the contribution of diamond sensors is usually negligible, the jitter due to the noise of the front-end electronics is the main contribution, because of the relatively small signal produced. To reduce this contribution it is important to find a compromise between a clean, but slow, signal and a fast rise time. The HADES Collaboration implemented a similar approach, designing a diamond detector capable of a time precision better than 100 ps, using an high input impedance amplifier placed at a few millimeters from the sensor to minimize parasitic capacitance and, hence, optimize the bandwidth. Those main ideas were further refined by the TOTEM and CMS Collaborations, reaching a 10% improvement on the time precision despite using larger pads than the HADES detector, and therefore larger capacitance. An improved version of this timing detector is based on the double diamond architecture reaching 50 ps precision. Finally, it is important to note that this review is focused on timing detectors that are fully operational at the moment of writing. However, some promising technologies are under investigation, like the 3D diamonds investigated by the TIMESPOT Collaboration [57], that could further improve performance of diamond timing detectors when some technological limits will be overcome.

Author Contributions

All authors contributed equally to the manuscript. All authors read and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank the CMS/TOTEM and HADES Collaborations for providing relevant material and useful advice for this article. In particular, we thank V. Avati, M. Bozzo, J. King, J. Pietraszko, and C. Rogan for their comments and suggestions.

Footnote

1. ^197Au ions at 1.25A GeV release in the sensor approximately 6,500 times more energy than a MIP [48]

References

1. ATLAS Collaboration. Technical Proposal: A High-Granularity Timing Detector for the ATLAS Phase-II Upgrade. (2018).

Google Scholar

2. CMS Collaboration. Technical Proposal for a MIP Timing Detector in the CMS Experiment Phase 2 Upgrade. (2017).

Google Scholar

3. Bossini E. The proton timing system of the TOTEM experiment at LHC. PoS. (2019) TWEPP2018:137. doi: 10.22323/1.343.0137

CrossRef Full Text | Google Scholar

4. Schwander MKP. A review of diamond synthesis by CVD processes. Diamond Relat Mater. (2011) 20:1287–301. doi: 10.1016/j.diamond.2011.08.005

CrossRef Full Text | Google Scholar

5. Gracio J, Fan Q, Madaleno J. Diamond growth by chemical vapour deposition. J Phys D Appl Phys. (2010) 43:374017. doi: 10.1088/0022-3727/43/37/374017

CrossRef Full Text | Google Scholar

6. Sunkara M, Angus JC, Hayman CC, Buck FA. Nucleation of diamond crystals. Carbon. (1990) 28:745–46. doi: 10.1016/0008-6223(90)90265-Z

CrossRef Full Text

7. Evans DA, Roberts OR, Williams GT, Vearey-Roberts AR, Bain F, Evans S. Diamond-metal contacts: interface barriers and real-time characterization. J Phys Condensed Matter. (2009) 21:36. doi: 10.1088/0953-8984/21/36/364223

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhu Y, Wang L, Yao W, Cao L. The interface diffusion and reaction between Cr layer and diamond particle during metallization. Appl Surface Sci. (2001) 171:143–50. doi: 10.1016/S0169-4332(00)00555-9

CrossRef Full Text | Google Scholar

9. Parrini G, Lagomarsino S, Scorzoni A, Fabbrizzi F, Sciortino S, Nunziati L. Laser graphitization for polarization of diamond sensors. PoS. (2011) RD11:17. doi: 10.22323/1.143.0017

CrossRef Full Text | Google Scholar

10. De Feudis M, Caricato A, Taurino A, Ossi P, Castiglioni C, Brambilla L, et al. Diamond graphitization by laser-writing for all-carbondetector applications. Diamond Relat Mater. (2017) 75:25–33. doi: 10.1016/j.diamond.2016.12.019

CrossRef Full Text | Google Scholar

11. Bachmair F, Bani L, Bergonzo P, Caylar B, Forcolin G, Haughton I, et al. A 3D diamond detector for particle tracking. Nuclear Instrum Methods Phys Res Sec A. (2015) 786:97–104. doi: 10.1016/j.nima.2015.03.033

CrossRef Full Text | Google Scholar

12. Pan LS, Kania DR. Diamond: Electronic Properties and Applications. New York, NY: Springer Science & Business Media (1995). doi: 10.1007/978-1-4615-2257-7

CrossRef Full Text | Google Scholar

13. Li Z, Kraner HW. Modeling and simulation of charge collection properties for neutron irradiated silicon detectors. Nuclear Phys B Proc Suppl. (1993) 32:398–409. doi: 10.1016/0920-5632(93)90052-8

CrossRef Full Text | Google Scholar

14. Pernegger H, Roe S, Weilhammer P, Eremin V, Frais-Kölbl H, Griesmayer E, et al. Charge-carrier properties in synthetic single-crystal diamond measured with the transient-current technique. J Appl Phys. (2005) 97:073704. doi: 10.1063/1.1863417

CrossRef Full Text | Google Scholar

15. Isberg J, Hammersberg J, Johansson E, Wikström T, Twitchen D, Whitehead A, et al. High carrier mobility in single-crystal plasma-deposited diamond. Science. (2002) 297:1670–2. doi: 10.1126/science.1074374

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Pomorski M. Electronic Properties of Single Crystal CVD Diamond and Its Suitability for Particle Detection in Hadron Physics Experiments. Wolfgang von Goethe University, Frankfurt am Main (2008).

Google Scholar

17. Koike J, Parkin D, Mitchell T. Displacement threshold energy for type IIa diamond. Appl Phys Lett. (1992) 60:1450–2. doi: 10.1063/1.107267

CrossRef Full Text | Google Scholar

18. Holmström E, Kuronen A, Nordlund K. Threshold defect production in silicon determined by density functional theory molecular dynamics simulations. Phys Rev B. (2008) 78:045202. doi: 10.1103/PhysRevB.78.045202

CrossRef Full Text | Google Scholar

19. Bäni L, Alexopoulos A, Artuso M, Bachmair F, Bartosik M, Beck H, et al. A study of the radiation tolerance of poly-crystalline and single-crystalline CVD diamond to 800 MeV and 24 GeV protons. J Phys D. (2019) 52:465103. doi: 10.1088/1361-6463/ab37c6

CrossRef Full Text | Google Scholar

20. LANL. Los Alamos Neutron Science Center (LANSCE). (2020). Available online at: http://wnr.lanl.gov/

Google Scholar

21. CERN. PS-IRRAD Proton Facility. (2020). Available online at: https://ps-irrad.web.cern.ch/

Google Scholar

22. Shockley W. Currents to conductors induced by a moving point charge. J Appl Phys. (1938) 9:635. doi: 10.1063/1.1710367

CrossRef Full Text | Google Scholar

23. Minafra N. Development of a timing detector for the TOTEM experiment at the LHC. Eur Phys J Plus. (2017) 132:402. doi: 10.1140/epjp/i2017-11707-2

CrossRef Full Text | Google Scholar

24. Tanabashi M, Hagiwara K, Hikasa K, Nakamura K, Sumino Y, Takahashi F, et al. Review of particle physics. Phys Rev D. (2018) 98:030001. doi: 10.1103/PhysRevD.98.030001

CrossRef Full Text | Google Scholar

25. Klein CA. Bandgap dependence and related features of radiation ionization energies in semiconductors. J Appl Phys. (1968) 39:2029–38. doi: 10.1063/1.1656484

CrossRef Full Text | Google Scholar

26. Cenna F, Cartiglia N, Friedl M, Kolbinger B, Sadrozinski HFW, Seiden A, et al. Weightfield2: a fast simulator for silicon and diamond solid state detector. Nuclear Instrum Methods Phys Res Sec A. (2015) 796:149–53. doi: 10.1016/j.nima.2015.04.015

CrossRef Full Text | Google Scholar

27. Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, Arce P, et al. Geant4 - a simulation toolkit. Nuclear Instrum Methods Phys Res Sec A. (2003) 506:250–303. doi: 10.1016/S0168-9002(03)01368-8

CrossRef Full Text | Google Scholar

28. Kagan H. Recent advances in diamond detector development. Nuclear Instrum Methods Phys Res Sec A. (2005) 541:221–7. doi: 10.1016/j.nima.2005.01.060

CrossRef Full Text | Google Scholar

29. Schirru F, Singh BN, Scruton L, Bentley M, Fox S, Lohstroh A, et al. Development of large area polycrystalline diamond detectors for fast timing application of high-energy heavy-ion beams. J Instrument. (2012) 7:P05005. doi: 10.1088/1748-0221/7/05/P05005

CrossRef Full Text | Google Scholar

30. Reichmann M, Alexopoulos A, Artuso M, Bachmair F, Bäni L, Bartosik M, et al. New test beam results of 3D and pad detectors constructed with poly-crystalline CVD diamond. Nuclear Instrum Methods Phys Res Sec A. (2020) 958:162675. doi: 10.1016/j.nima.2019.162675

CrossRef Full Text | Google Scholar

31. Pernegger H. High mobility diamonds and particle detectors. Physica Status Solidi. (2006) 203:3299–314. doi: 10.1002/pssa.200671404

CrossRef Full Text | Google Scholar

32. Rinella GA, Feito DA, Arcidiacono R, Biino C, Bonacini S, Ceccucci A, et al. The NA62 GigaTracker. Nuclear Instrum Methods Phys Res Sec A. (2017) 845:147–9. doi: 10.1016/j.nima.2016.06.045

CrossRef Full Text | Google Scholar

33. Minafra N, Royon C, Murray M, Camsonne A, Gaskell D, Hoskins J. Precision Electron Polarimetry at EIC. (2017). Available online at: https://agenda.infn.it/event/13037/contributions/17193/

Google Scholar

34. Minafra N, Royon C, Mcnulty R, Raab N, Mcclean B, Rock L, et al. Single Particle Detection for Medical Applications. (2018). Available online at: https://indico.desy.de/indico/event/18050/session/8/contribution/20

35. Minafra N. Development of a Timing Detector for the TOTEM Experiment at the LHC. (2016). Available online at: http://cds.cern.ch/record/2139815

Google Scholar

36. Royon C. SAMPIC: a readout chip for fast timing detectors in particle physics and medical imaging. arXiv preprint arXiv:150304625. (2015). doi: 10.1088/1742-6596/620/1/012008

CrossRef Full Text | Google Scholar

37. Bossini E. The timing system of the TOTEM experiment. Instruments. (2018) 2:21. doi: 10.3390/instruments2040021

CrossRef Full Text | Google Scholar

38. Bossini E. Development of a time of flight diamond detector and readout system for the TOTEM experiment at CERN. Ph.D. thesis (2016). Available online at: https://cds.cern.ch/record/2227688

Google Scholar

39. Berretti M, Bossini E, Minafra N. Timing Performances of Diamond Detectors with Charge Sensitive Amplifier Readout. (2015). Available online at: http://cds.cern.ch/record/2055747

Google Scholar

40. Breton D, De Cacqueray V, Delagnes E, Grabas H, Maalmi J, Minafra N, et al. Measurements of timing resolution of ultra-fast silicon detectors with the SAMPIC waveform digitizer. Nuclear Instrum Methods Phys Res Sec A. (2016) 835:51–60. doi: 10.1016/j.nima.2016.08.019

CrossRef Full Text | Google Scholar

41. Müntz C. The di-electron spectrometer HADES at GSI: a status report. Nuclear Phys B Proc Suppl. (1999) 78:139–44. doi: 10.1016/S0920-5632(99)00536-8

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Adamczewski-Musch J, Arnold O, Behnke C, Belounnas A, Belyaev A, Berger-Chen J, et al. A facility for pion-induced nuclear reaction studies with HADES. Eur Phys J. (2017) A53:188. doi: 10.1140/epja/i2017-12365-7

CrossRef Full Text | Google Scholar

43. Anghinolfi F, Jarron P, Krummenacher F, Usenko E, Williams C. NINO: an ultrafast low-power front-end amplifier discriminator for the time-of-flight detector in the ALICE experiment. IEEE Trans Nuclear Sci. (2004) 51:1974–8. doi: 10.1109/TNS.2004.836048

CrossRef Full Text | Google Scholar

44. Ugur C, Korcyl G, Michel J, Penschuk M, Traxler M. 264 channel TDC platform applying 65 channel high precision (7.2 psRMS) FPGA based TDCs. NoMe - TDC 2013 - 2013 IEEE Nordic Mediterranean Workshop on Time to Digital Converters, Proceedings. (2013). doi: 10.1109/NoMeTDC.2013.6658234

CrossRef Full Text | Google Scholar

45. Bayer E, Zipf P, Traxler M. A multichannel high-resolution (<5 ps RMS between two channels) Time-to-Digital Converter (TDC) implemented in a field programmable gate array (FPGA). In: 2011 IEEE Nuclear Science Symposium Conference Record. Valencia (2011). p. 876–9. doi: 10.1109/NSSMIC.2011.6154560

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Ugur C, Koening W, Michel J, Palka M, Traxler M. Field programmable gate array based data digitisation with commercial elements. J Instrument. (2013) 8:C01035. doi: 10.1088/1748-0221/8/01/C01035

CrossRef Full Text | Google Scholar

47. Pietraszko J, Galatyuk T, Grilj V, Koenig W, Spataro S, Trager M. Radiation damage in single crystal CVD diamond material investigated with a high current relativistic 197Au beam. Nuclear Instrum Methods Phys Res Sec A. (2014) 763:1–5. doi: 10.1016/j.nima.2014.06.006

CrossRef Full Text | Google Scholar

48. Nucleonica GmbH. Range & Stopping Power++. (2020). Available online at: http://www.nucleonica.net/Application/RangePlus.aspx

Google Scholar

49. Albrow M, Arneodo M, Avati V, Baechler J, Cartiglia N, Deile M, et al. CMS-TOTEM Precision Proton Spectrometer. Geneva: CERN (2014). Available online at: https://cds.cern.ch/record/1753795

Google Scholar

50. CMS Collaboration. The CMS experiment at the CERN LHC. J Instrument. (2008) 3:S08004. doi: 10.1088/1748-0221/3/08/s08004

CrossRef Full Text | Google Scholar

51. Anelli G, Antchev G, Aspell P, Avati V, Bagliesi MG, Berardi V, et al. The TOTEM experiment at the CERN large hadron collider. J Instrum. (2008) 3:S08007. doi: 10.1088/1748-0221/3/08/S08007

CrossRef Full Text | Google Scholar

52. Sadrozinski HFW, Seiden A, Cartiglia N. 4D tracking with ultra-fast silicon detectors. Rep Prog Phys. (2018). 81:026101. doi: 10.1088/1361-6633/aa94d3

PubMed Abstract | CrossRef Full Text | Google Scholar

53. TOTEM Collaboration. Diamond detectors for the TOTEM timing upgrade. J Instrument. (2017). 12:P03007. doi: 10.1088/1748-0221/12/03/p03007

CrossRef Full Text | Google Scholar

54. Berretti M, Bossini E, Bozzo M, Georgiev V, Isidori T, Linhart R, et al. Timing performance of a double layer diamond detector. J Instrument. (2017) 12:P03026. doi: 10.1088/1748-0221/12/03/P03026

CrossRef Full Text | Google Scholar

55. Christiansen J. HPTDC High Performance Time to Digital Converter. Geneva: CERN (2004). Available online at: https://cds.cern.ch/record/1067476

Google Scholar

56. Bossini E. The CMS Precision Proton Spectrometer timing system: performance in Run 2, future upgrades and sensor radiation hardness studies. J Instrument. (2020) 15:C05054. doi: 10.1088/1748-0221/15/05/C05054

CrossRef Full Text | Google Scholar

57. Morozzi A, Sciortino S, Anderlini L, Servoli L, Kanxheri K, Lagomarsino S, et al. 3D Diamond tracking detectors: numerical analysis for Timing applications with TCAD tools. J Instrument. (2020) 15:C01048. doi: 10.1088/1748-0221/15/01/C01048

CrossRef Full Text | Google Scholar