Photon-Assisted Transport Through a Quantum Dot Side-Coupled to Majorana Bound States

1. Introduction

In recent years, there is much interest in the newly emerged issue of how to prepare and detect Majorana bound states (MBSs) in solid platforms. In condensed matter physics, the MBSs refer to a kind of quasi-particle of Majorana fermions being of their own antiparticles with zero energy [1]. Due to these unique characters, the MBSs obey non-Abelian statistics instead of the usual Fermi-Dirac one. The quantum bits designed by MBSs then have some exotic properties besides all the merits of traditional bits. It has been demonstrated that the MBSs enable topologically protected quantum information with potential applications in quantum computation free from decoherence [2–6]. Besides, the MBSs are also promising in the research field of high-efficiency and energy-saving electronic devices [7]. The MBSs have been successfully prepared in some kinds of systems, such as the mainstream p-wave superconductors [1, 8], and non-centrosymmetric superconductors, topological insulators coupled to superconductors defects in topological superconductors, the semiconducting or ferromagnetic nanowires with intrinsic strong spin-orbit interaction proximitization to a conventional s-wave superconductors, Josephson junctions [5, 6, 8–13], and so on.

Due to the massless properties of the MBSs having no charge, the detection of it is also quite challenging. A vast of experimental works have been devoted to the detection of MBSs, relying on the signatures probably induced by the MBSs, including the 4π periodic Josephson current-phase in junctions between topological superconductors [13], half-integer conductance plateau at the coercive field in a hybrid structure composing of topological superconductors and topological quantum anomalous Hall insulator [6], tunneling spectroscopy using the Rashba nanowires coupled to the bulk s-wave superconductors [10], zero-bias of the differential conductance at the edges of the wires [14, 15], the non-locality [16–19] and Kondo effect [20] influenced by MBSs. Since the above signatures can also be brought about by other mechanisms, some alternative schemes then have been continually put forward, such as the optical detection ones [21–23]. In [21], the authors found that the MBSs will absorb(emit) photons and result in photon-assisted tunneling side band peaks. This process can split the MBSs and then induces non-zero MBSs mode, providing another detection scheme for the existence of MBSs which is quite different the currently adopted ones concerning zero-energy MBSs mode. They also found that the height of the photon-assisted tunneling side band peaks is related to the intensity of the microwave field, and the time-varying conductance induced by the MBSs shows negative values for a certain period of time. Three all-optical detection schemes for the MBSs were proposed in [22], including a single QD, a hybrid QD-nanomechanical resonators system, and a carbon nanotube resonator implanted in a single electron spin system with optical pump-probe, respectively. They investigated the signatures of the MBSs in terms of the probe absorption spectrum and non-linear optical Kerr effect, the coupling strength between MBSs and the QD or the single electron spin. In the hybrid QD-resonantors system, they found that the vibration of the nanomechanical resonators will enhance the non-linear optical effect, which makes the MBSs more sensitive for detection. In the carbon nanotube resonator with a single electron, the single electron spin can be considered as a sensitive probe, and the nanotube resonator behaved as a phonon cavity is robust for detecting of MBSs. The MBSs signatures in these optical schemes are quite different from electrical ones and are promising for the detection MBSs, as well as for new applications in manipulation of MBSs or quantum information processing based on MBSs.

In the present manuscript, we study electronic transport through a QD shelled by a photon field as shown in Figure 1. Quite different from the above optical detection schemes for the MBSs, we propose to insert a QD, which is coupled to a topological nanowire hosting MBSs at its two ends, between two normal metal leads. One of the advantages of our system, as compared to the ones in [21, 22], is that the transport processes occur between the leads and the QD. The electrons will not enter into the MBSs mode existed in the topological superconductor nanowire, and thus our system provides a signature of the MBSs without direct electron transport through it. Our numerical results show that the transmission function develops photon-induced peaks, which are split by the coupling between the QD and MBSs. The central peaks' height are suppressed to zero because of the photon absorbtion (emission) by MBSs. As a result of it, the MBSs are shifted to the non-zero energy mode, and thus provides another detection scheme based on non-zero MBSs mode. If the MBSs are overlapped, the central photon-assisted peaks in the transmission function reappear because the photon absorbed (emitted) by one mode of the MBSs are subsequently emitted (absorbed) by another MBSs' mode. Under this condition, the positions of the peaks induced by the MBS-MBS overlaping in the presence of the photon field are quite different from those without photon field.

FIGURE 1

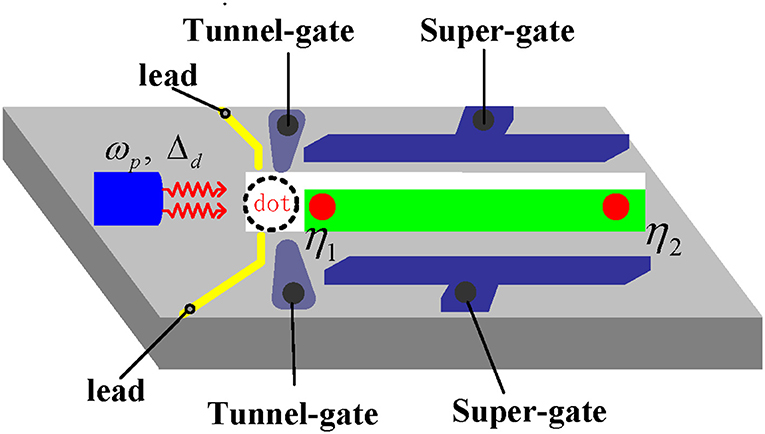
Figure 1. Schematic plot of a QD (white circle) coupled to MBSs (red circles) formed at the two ends of a topological superconductor nanowire (green). The dot is connected to two normal metal leads (golden), and is shelled by a microwave field of strength Δ_d and photon frequency ω_p. The dot and the superconductor nanowire are individually defined by tunnel- and super-gates.

2. Model and Methods

The Hamiltonian of the QD coupled to MBSs and is subjected to a photon field can be written as the following form [15, 24–26]

$\begin{array}{l}H={\displaystyle \sum _{k\alpha }}{\epsilon }_{k\alpha }{c}_{k\alpha }^{†}{c}_{k\alpha }+{\epsilon }_d(t)d^{†}d+{\displaystyle \sum _{k,\alpha =L,R}}(V_{k\alpha }{c}_{k\alpha }^{†}d+H.c)\\ +i{\epsilon }_M{\eta }_1{\eta }_2+\lambda (d-d^{†}){\eta }_1.& (1)\end{array}$

where $c_{k\alpha }^{†}$ (c_kα) creates (annihilates) an electron of momentum k, energy ε_kα in the lead α = L, R. For the QD, d^† (d) is the creation (annihilation) operator of an electron having energy level ε_d(t) = ε_d + Δ_d cos(ω_pt) [21]. Here, we have assumed that the photon field with strength Δ_d and frequency ω_p is applied only on the QD and the leads are free from its irradiation, and then only the dot's energy level is time-varying. In experiments, the dot level in the absence of photon field ε_d is tunable by external gate voltages. The coupling strength between the QD and the leads is described by V_kα. The last two terms in Equation (1) stand for the zero-energy MBSs with operators η₁ and η₂, as well as overlap strength between them ε_M. The MBSs locate on the opposite ends of the topological superconductor nanowire and are coupled to the QD with strength of λ [1, 6, 15]. In the present manuscript we assume that the dot is coupled only to the mode of the MBSs nearby to it with strength λ. The Majorana operators satisfy the relations of {η_i, η_j} = 2δ_ij and ${\eta }_i={\eta }_i^{†}$. We now follow previous work to switch from the Majorana fermion representation to the completely equivalent regular fermion one by defining [15] ${\eta }_1=(1/\sqrt{2})(f+f^{†})$, and ${\eta }_2=(-i/\sqrt{2})(f-f^{†})$, the Hamiltonian concerning about the MBSs in Equation (1) is rewritten as

$\begin{array}{ll}{H}_{MBSs}={\epsilon }_M(f^{†}f-\frac{1}{2})+\frac{\lambda }{\sqrt{2}}(d-d^{†})(f+f^{†}).& (2)\end{array}$

The time-averaged electric current through the system is calculated by following the standard Keldysh Green's function technique as [21, 25, 26]

$\begin{array}{ll}<J(t)>=\frac{e}{\hslash }{\displaystyle \int }\left[f_L(\epsilon )-f_R(\epsilon )\right]T(\epsilon )\frac{d\epsilon }{2\pi }& (3)\end{array}$

where e is the electron charge, ℏ the reduced Planck's constant, $f_{L/R}(\epsilon )={\left\{1+e^{(\epsilon -{\mu }_{L/R})/k_{B}T}\right\}}^{-1}$ the Fermi distribution function of the left/right electrode with chemical potential μ_L/R, temperature T and Boltzmann constant k_B. The transmission coefficient T(ε) can be expressed with the help of the retarded Green's function G^r(ε) as [25, 26]

$\begin{array}{ll}T(\epsilon )=\frac{{\Gamma }^L{\Gamma }^R}{{\Gamma }^L+{\Gamma }^R}[-2\text{Im}{\displaystyle \sum _k}{\tilde{G}}_{dd;k}^r(\epsilon )J_k^2(\frac{{\Delta }_d}{{\omega }_p})],& (4)\end{array}$

where ${\Gamma }^{\alpha }=2\pi \sum _k|V_{k\alpha }{|}^2\delta \left[\epsilon -{\epsilon }_{k\alpha }\right]$ is the line-width function for coupling strength between the dot and the leads. J_k(x) is the k-th (k = −∞, ∞) order Bessel function of argument x, and ${\tilde{G}}_{dd;k}^r(\epsilon )$ the retarded Green's function in the presence of photon field and QD-MBSs coupling. By applying the equation of motion method in [25] and adopting the truncation scheme introduced in [26], ${\tilde{G}}_{dd;k}^r(\epsilon )$ can be obtained as (detailed calculation processes are neglected here for the sake of conciseness):

$\begin{array}{ll}{\tilde{G}}_{dd;k}^r(\epsilon )=\frac{1}{g_{dd;k}^{r-1}(\epsilon )-{\displaystyle {\sum }_m}{J}_{k+m}^2(\frac{{\Delta }_d}{{\omega }_p}){\sum }_{mm}^r(\epsilon )-{\displaystyle {\sum }_{k^{\prime }}}\frac{{\tilde{\Sigma }}_{k{k}^{\prime }}^{r2}(\epsilon )}{{\tilde{g}}_{dd;k^{\prime }}^{r-1}(\epsilon )-{\tilde{\Sigma }}_{k^{\prime }}^r(\epsilon )}},& (5)\end{array}$

where the free electron and hole Green's functions are respectively given by,

$\begin{array}{ll}{g}_{dd;k}^r(\epsilon )=\frac{1}{\epsilon -{\epsilon }_d-k{\omega }_p+i({\Gamma }^L+{\Gamma }^R)/2},& (6)\end{array}$

and

$\begin{array}{ll}{\tilde{g}}_{dd;k}^r(\epsilon )=\frac{1}{\epsilon +{\epsilon }_d+k{\omega }_p+i({\Gamma }^L+{\Gamma }^R)/2}.& (7)\end{array}$

The self-energies in Equation (5) are given by ${\sum }_{mm}^r(\epsilon )={\lambda }^2(\epsilon +m{\omega }_p)/\left[{(\epsilon +m{\omega }_p)}^2+{\epsilon }_M^2\right]$,${\tilde{\Sigma }}_k^r(\epsilon )=\sum _k{J}_{k-m}(\frac{{\Delta }_d}{{\omega }_p}){\sum }_{mm}^r$, and ${\tilde{\Sigma }}_{k{k}^{\prime }}^r(\epsilon )=\sum _{k^{\prime }}{J}_{k+m}(\frac{{\Delta }_d}{{\omega }_p})J_{k^{\prime }-m}(\frac{{\Delta }_d}{{\omega }_p}){\sum }_{mm}^r(\epsilon )$. In the absence of the photon field (Δ_d = 0), because the Bessel function is J_k(0) = δ_{k, 0}, then the self-energies becomes ${\sum }_{00}^r(\epsilon )={\delta }_{m,0}{\sum }_{mm}^r(\epsilon )={\lambda }^2\epsilon /({\epsilon }^2+{\epsilon }_M^2)$, and ${\tilde{\Sigma }}_k^r(\epsilon )={\tilde{\Sigma }}_{k{k}^{\prime }}^r(\epsilon )={\sum }_{00}^r(\epsilon )$, now the above Green's function reduces to

$\begin{array}{ll}{\tilde{G}}_{dd;0}^r(\epsilon )=\frac{1}{g_{dd;0}^{r-1}(\epsilon )-{\sum }_{00}^r(\epsilon )-\frac{{\sum }_{00}^{r2}(\epsilon )}{{\tilde{g}}_{dd;0}^{r-1}(\epsilon )-{\sum }_{00}^r(\epsilon )}},& (8)\end{array}$

which is just the retarded Green's function derived in [15] with coupling between the QD and topological superconductor nanowire hosting MBSs at its ends.

3. Results and Discussion

In the following numerical calculations, we choose the photon frequency ω_p = 1 as the energy unit (ℏ = 1), and fix the values of Γ = Γ^L = Γ^R = 0.1 unless noted. We do not consider the case of finite bias voltage and then the leads' chemical potentials are se to be μ_L = μ_R = 0 as the zero-point of the energy. We first study in Figure 2 the case of zero photon field (Δ_d = 0). Under this condition, the retarded Green's is given in Equation (8). If there is no coupling between the QD and MBSs existed at the ends of the topological nanowire λ = 0, the transmission function T in Figure 2A shows the typical resonant tunneling feature, i.e., it develops a Lorentzian peak with height of 1 at zero energy state [27], T(ε → 0) = 1. This can be seen from the black solid line in Figure 2A, which denotes that the electrons can transport from one lead through the QD to the other lead if the electron energy in the leads (Fermi level μ_α) equals to the dot level ε_d. Turning on the coupling between the QD and MBSs at the ends of topological superconductor nanowire λ ≠ 0, we find that value of the zero-energy transmission function is reduced to half of its quantum value 1, i.e., T(0) = 1/2, showing the half-fermionic character of the MBSs. This is because now the retarded Green's function is ${\tilde{G}}_{dd;0}(\epsilon \to 0)=1/2(\epsilon +i\Gamma )$, and then the value of the zero-energy transmission function is reduced by a factor of 1/2, accordingly. This change of the value oftransmission function is believed to be the signature of existence of MBSs [15], and is also responsible for the zero-bias anomaly of the conductance peak, a kind of main detection means for the MBSs in tunneling spectroscopy. It is worth noting that as long as the coupling strength between the QD and MBSs λ ≠ 0, the result of T(0) = 1/2 remains unchanged regardless of the variation of it. For weak QD-MBSs coupling λ < Γ, the transmission function develops two peaks centered around ε ~ ±λ, induced by the splitting of the dot energy-level in the presence of coupling between the QD and the MBSs [15]. With increasing λ, the positions of the two peaks are shifted away from the zero-energy state, and the double-peak configuration in the transmission function evolves to a triple-peak one for λ ≥ Γ as shown in Figure 2A. The evolution of the peaks' configuration is a clear signature of the existence of MBSs. To show the evolution of the peak configuration in the transmission function by the relative strength between λ and Γ, we show the behavior of T(ε) in Figure 2B for fixed λ = 0.06 and different values of Γ. Under the condition of λ ≥ Γ, the transmission function shows the triple-peak configuration as indicated by the black solid, red dashed and blue dotted lines in Figure 2B. Whereas for Γ > λ, the transmission function shows the double-peak configuration.

FIGURE 2

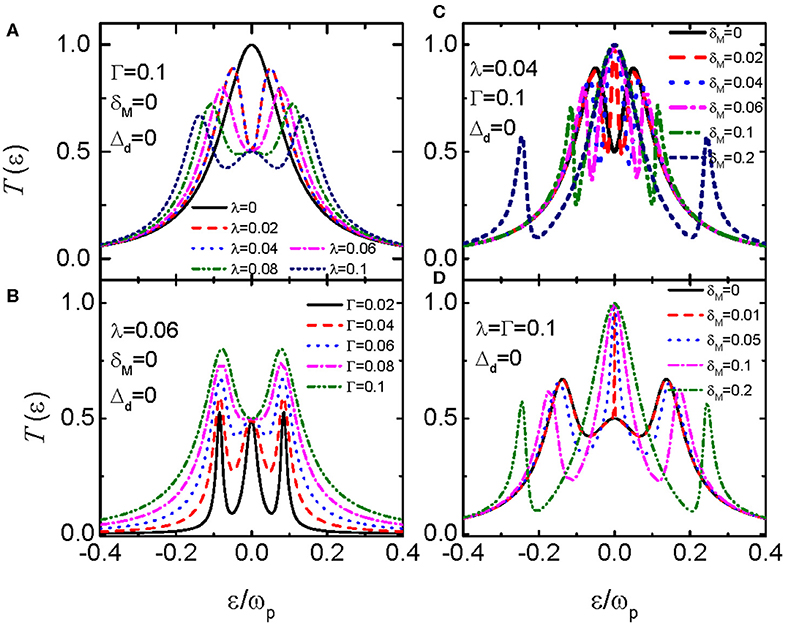
Figure 2. Transmission function T as a function of the electron energy ε in the absence of the photon field Δ_d = 0. Panels (A–D) correspond to different parameters, which are given in the figure.

The two modes of the MBSs at the two ends of the topological superconductor nanowire will overlap with each other, and the overlap strength between them δ_M depends on the length of the nanowire. In Figures 2C,D, we examine the influences of δ_M on the peak configurations of the transmission function T(ε). For the double-peak configuration in Figure 2C in which λ < Γ, the zero-energy transmission function shows peak of height T(0) = 1 not 1/2 even for very weak MBS-MBS hybridization δ_M = 0.02. The width of this zero-energy peak is proportional to the value of δ_M. Meanwhile, two additional peaks in T(ω) emerge around ε ~ ±(λ + δ_M) corresponding to the energy of the effective Dirac fermionic state f. For large coupling strength δ_M ≥ 0.1, the zero-energy transmission function reduces to the resonant level result. For sufficiently long nanowire in which the overlap strength between the two MBSs is weak enough as compared to the value of the QD-MBSs coupling λ and thermal energy k_BT, the signature of the MBSs T(0) = 1/2 will emerge. The behavior of the triple-peak configuration in the transmission function T(ε) in Figure 2D resembles that in Figure 2C because the peaks around ε ~ ±λ are merged into ε ~ ±(λ + δ_M) if the two modes of the MBSs are overlapped [15].

If the QD is shelled by a photon field of strength Δ_d = ω_p, a series of photon-assisted additional channels are opened [21–23, 25, 26, 28, 29]. Correspondingly, the transmission function T(ε) develops peaks at ε = ε_d ± nω_p, in which n = 0, ±1, ±2, ⋯⋯ . Now electrons can tunnel from one lead to the other through the dot whenever a channel enters into the conduction window. As a result of photon-induced additional transport channels (dot levels), the electron transport probability through each channel is weakened and the peak height of the transmission function in Figure 3A is lowered, accordingly. In the presence of coupling between the QD and MBSs (λ ≠ 0), we find that the peaks' value originally at the states of ε = ε_d ± nω_p are suppressed to zero accompanied by the emergence of two additional peaks roughly at ε = ε_d ± n(±λ + ω_p) [21–23, 25, 26, 28, 29]. It indicates that the two MBSs have absorbed the photon energy and then the character of its zero-energy mode is destroyed. The reason of the change of the transmission function can be explained as follows: Under the irradiation of the microwave field, the MBSs will absorb or emit n photons from the microwave field and jump to the states of ±nω_p. Accordingly, the energy levels of electrons on the QD is shifted to ε_d ± nω_p. If the chemical potential of the leads is aligned to these states, the electrons at them will transport through the QD, leading to peaks at ε = ε_d ± n(±λ + ω_p). The blowups of the peaks in the transmission function are given in Figures 3B–D, in which the disappearance and splitting of the peaks are clearly presented. Figures 3B–D also indicate that the application of the photon field may excite the zero-energy MBSs to non-zero-energy mode. This enables the probability of detection of the MBSs in not only the usual zero-energy mode but also in the non-zero one. Here we find that even the photon-induced peaks are destroyed by the existence of the MBSs, the splitting of these peaks still can serve as the signature of the MBSs, and provides another detection scheme. The peaks' height of the transmission function shown in Figures 3B–D are obviously lowered with increasing n because the electron transport probability through those channels are suppressed. For n = ±2, the transmission function in Figure 3D develops a sharp peak at ε = ε_d±2ω_p [25, 26, 28, 29]. The reason may be attributed to the fact that the MBSs have less probability of absorbing or emitting more than one photons and then the photon-induced peaks of n > 1 are relatively less influenced. The splitting of the peaks by the QD-MBSs coupling, however, is still prominent in Figure 3D. We have examined the cases of varying photon field strength Δ_d, and found that it will change the height of the peaks but not their splitting and suppression. Variation of the photon frequency induces the change of the peaks' positions, and will not change the essential influences of the photon field on the transmission function.

FIGURE 3

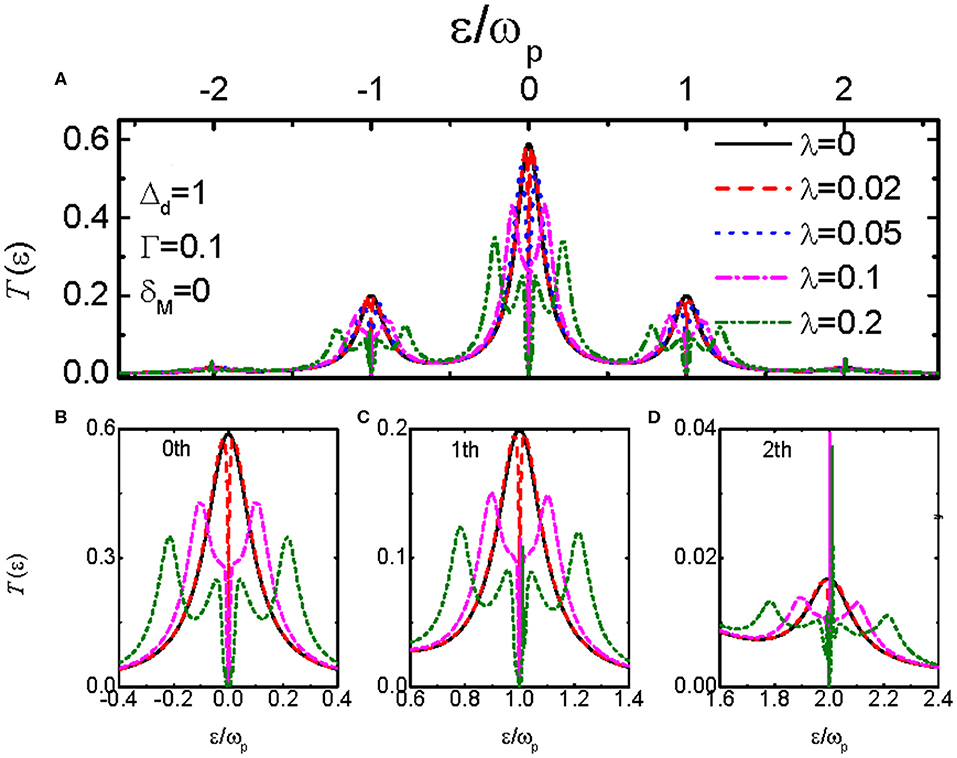
Figure 3. Transmission function T and its blowups as a function of the electron energy ε under fixed strength of the photon field Δ_d = ω_p, and different values of the coupling between the dot and the MBSs λ. Panel (A) correspond to the transmission coefficient in a large regime of the electron energy, and (B–D) denote the peaks in (A) for n=0,1,2, respectively.

We now study the impacts of the MBS-MBS direct overlap δ_M on the properties of the transmission function in Figure 4. The strength of the photon field is also set to be Δ_d = 1 and the coupling strength between the QD and the MBSs is weak than that between the QD and the leads, i.e., λ < Γ. In the absence of overlap between the MBSs δ_M = 0, the photon-assisted peaks in the transmission function are split by finite value of QD-MBSs coupling λ, which can be seen from the solid black lines in Figures 4A–D. Moreover, the value of the central peaks at ε = ε_d ± nω_p are suppressed to zero due to the photon absorbtion (emission) processes by the MBSs. For non-zero δ_M, we find that the peaks of the transmission function at ε = ε_d ± nω_p reappear, which resembles the result in Figure 2C in the absence of photon field. In other words, the impacts of the MBSs on the disappearance of the photon-assisted central peaks in the transmission function are eliminated by the overlap between the MBSs. We attribute this phenomenon to the fact that the photon absorbed (emitted) by one mode of the MBSs are immediately emitted (absorbed) by the other mode of the MBSs. Just by these two opposite processes, the photon energy are unchanged and then the MBSs remain the same. As compared to the case in Figure 2C, we find that the additional peaks induced by δ_M are positioned exactly at ε = ε_d ± n(±δ_M + ω_p), but not the expected positions of ε = ε_d ± n[±(λ + δ_M) + ω_p]. It may originates from the fact that the MBS-MBS overlaping dominates the transport processes and then the peaks in the transmission function are then determined by δ_M, accordingly.

FIGURE 4

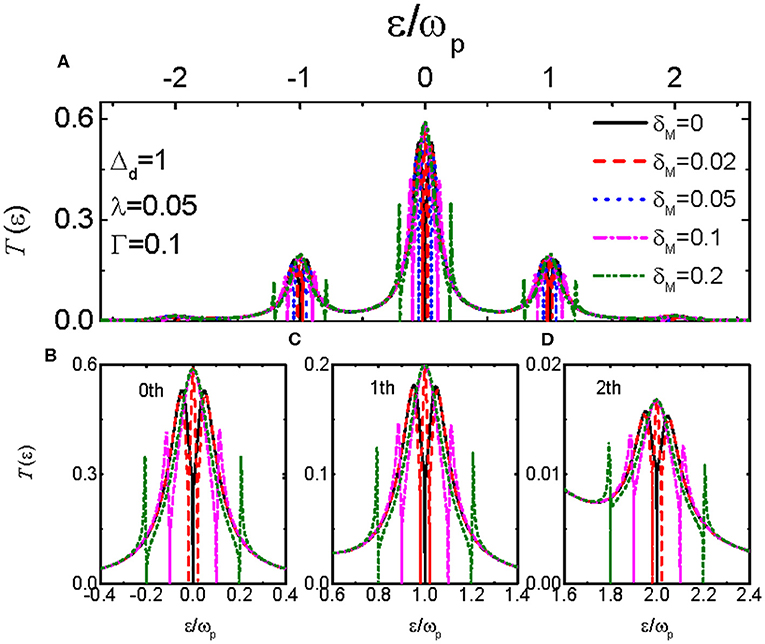
Figure 4. Transmission function and its blowups as a function of ε for Δ_d = ω_p, λ = 0.05 and different values of overlap strength between the MBSs δ_M. Panel (A) correspond to the transmission coefficient in a large regime of the electron energy, and (B–D) denote the peaks in Figure 4A for n=0,1,2, respectively.

4. Summary

In summary, we have studied photon-assisted transport through a QD side-coupled to a topological nanowire hosting MBSs at its two ends. It is found that the photon-induced peaks in the transmission function are split by the existence of the MBSs, and the value of the central peaks are suppressed to be zero. Such an abnormal change of the photon-assisted peaks may serve as the detection means for MBSs. If the two MBSs modes at the opposite ends of the nanowire are overlapped, the photon-assisted peaks are further split with the restoration of the central peaks, which may be induced by the opposite photon absorbtion (emission) processes of the two modes of the MBSs.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author/s.

Author Contributions

FC, Z-GF, and PZ contributed the ideas equally. FC, Z-GF, T-YH, JW, L-ML, and PL derived the formulae in the paper. FC, T-YH, JW, L-ML, and PL performed the numerical calculations. FC and Z-GF wrote the original manuscript. All authors contributed to the article and approved the submitted version.

Funding

FC was supported by the Initial Project of UEST of China, Zhongshan Institute (No. 415YKQ02), and Science and Technology Bureau of Zhongshan (Grant Nos. 2017B1116, 2017B1016, and 180809162197886). Z-GF was also supported by the Innovation Development Fund of the China Academy of Engineering Physics (CAEP; Grant No. ZYCX1921-02) and the Presidential Foundation of the CAEP (Grant No. YZ2015014). PL was supported by the NSF of China under Grant No. 11775047.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Fu L, Kane CL. Superconducting proximity effect and Majorana Fermions at the surface of a topological insulator. Phys Rev Lett. (2008) 100:096407. doi: 10.1103/PhysRevLett.100.096407

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Nayak C, Simon SH, Stern A. Non-Abelian anyons and topological quantum computation. Rev Mod Phys. (2008) 80:1083–159. doi: 10.1103/RevModPhys.80.1083

CrossRef Full Text | Google Scholar

3. Alicea J, Oreg Y, Refael G. Non-Abelian statistics and topological quantum information processing in 1D wire networks. Nat Phys. (2011) 7:412–7. doi: 10.1038/nphys1915

CrossRef Full Text | Google Scholar

4. Torsten Karzig RML, Christina Knapp. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. Phys Rev B. (2017) 95:235305. doi: 10.1103/PhysRevB.95.235305

CrossRef Full Text | Google Scholar

5. Sato M, Fujimoto S. Topological phases of noncentrosymmetric superconductors: edge states, Majorana fermions, and non-Abelian statistics. Phys Rev B. (2009) 79:094504. doi: 10.1103/PhysRevB.79.094504

CrossRef Full Text | Google Scholar

6. Qi XL, Zhang SC. Topological insulators and superconductors. Rev Mod Phys. (2011) 83:1057–110. doi: 10.1103/RevModPhys.83.1057

CrossRef Full Text | Google Scholar

7. Smirnov S. Universal Majorana thermoelectric noise. Phys Rev B. (2018) 97:165434. doi: 10.1103/PhysRevB.97.165434

CrossRef Full Text | Google Scholar

8. Wimmer M, Akhmerov AR, Medvedyeva MV. Majorana bound states without vortices in topological superconductors with electrostatic defects. Phys Rev Lett. (2010) 105:046803. doi: 10.1103/PhysRevLett.105.046803

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Sau JD, Lutchyn RM, Tewari S. Generic new platform for topological quantum computation using semiconductor heterostructures. Phys Rev Lett. (2010) 104:040502. doi: 10.1103/PhysRevLett.104.040502

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Lutchyn RM, Sau JD, Sarma SD. Majorana Fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys Rev Lett. (2010) 105:077001. doi: 10.1103/PhysRevLett.105.077001

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Choy TP, Edge JM, Akhmerov AR. Majorana fermions emerging from magnetic nanoparticles on a superconductor without spin-orbit coupling. Phys Rev B. (2011) 84:195442. doi: 10.1103/PhysRevB.84.195442

CrossRef Full Text | Google Scholar

12. San-Jose P, Prada E, Aguado R. AC Josephson effect in finite-length nanowire junctions with Majorana modes. Phys Rev Lett. (2012) 108:257001. doi: 10.1103/PhysRevLett.108.257001

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Mourik V, Zuo K, Frolov SM. Signatures of Majorana Fermions in hybrid superconductor-semiconductor nanowire devices. Science. (2012) 336:1003–7. doi: 10.1126/science.1222360

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ricco LS, de Souza M, Figueira MS. Spin-dependent zero-bias peak in a hybrid nanowire-quantum dot system: distinguishing isolated Majorana fermions from Andreev bound states. Phys Rev B. (2019) 99:155159. doi: 10.1103/PhysRevB.99.155159

CrossRef Full Text | Google Scholar

15. Liu DE, Baranger HU. Detecting a Majorana-fermion zero mode using a quantum dot. Phys Rev B. (2011) 84:201308R. doi: 10.1103/PhysRevB.84.201308

CrossRef Full Text | Google Scholar

16. Vernek E, Penteado PH, Seridonio AC, Egues JC. Subtle leakage of a Majorana mode into a quantum dot. Phys Rev B. (2014) 85:165304. doi: 10.1103/PhysRevB.89.165314

CrossRef Full Text | Google Scholar

17. Ruiz-Tijerina AD, Vernek E, da Silva LGGVD, Egues JC. Interaction effects on a Majorana zero mode leaking into a quantum dot. Phys Rev B. (2015) 91:115435. doi: 10.1103/PhysRevB.91.115435

CrossRef Full Text | Google Scholar

18. Prada E, Aguado R, San-Jose P. Measuring Majorana nonlocality and spin structure with a quantum dot. Phys Rev B. (2017) 96:085418. doi: 10.1103/PhysRevB.96.085418

CrossRef Full Text | Google Scholar

19. Deng MT, Vaitiekenas S, Prada E, San-Jose P, Nygard J, Krogstrup P, et al. Nonlocality of Majorana modes in hybrid nanowires. Phys Rev B. (2018) 98:085125. doi: 10.1103/PhysRevB.98.085125

CrossRef Full Text | Google Scholar

20. Wang R, Su W, Zhu JX. Kondo signatures of a quantum magnetic impurity in topological superconductors. Phys Rev Lett. (2019) 122:087001. doi: 10.1103/PhysRevLett.122.087001

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Tang HZ, Zhang YT, Liu JJ. Photon-assisted tunneling through a topological superconductor with Majorana bound states. AIP Adv. (2015) 5:127129. doi: 10.1063/1.4939096

CrossRef Full Text | Google Scholar

22. Chen HJ, Zhu KD. All-optical scheme for detecting the possible Majorana signature based on QD and nanomechanical resonator systems. Sci China Phys Mech Astron. (2015) 58:050301. doi: 10.1007/s11433-014-5637-4

CrossRef Full Text | Google Scholar

23. Väyrynen JI, Rastelli G, Belzig W, Glazman LI. Microwave signatures of Majorana states in a topological Josephson junction. Phys Rev B. (2015) 92:134508. doi: 10.1103/PhysRevB.92.134508

CrossRef Full Text | Google Scholar

24. Piotr S. Properties of the Majorana-state tunneling Josephson junction mediated by an interacting quantum dot. J Phys Condens Matter. (2019) 31:185301. doi: 10.1088/1361-648X/ab052a

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Jauho AP, Wingreen NS, Meir Y. Time-dependent transport in interacting and noninteracting resonant-tunneling systems. Phys Rev B. (1994) 50:5528–44. doi: 10.1103/PhysRevB.50.5528

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Sun QF, Wang J, Lin TH. Photon-assisted Andreev tunneling through a mesoscopic hybrid system. Phys Rev B. (1999) 59:13126–38. doi: 10.1103/PhysRevB.59.13126

CrossRef Full Text | Google Scholar

27. Pals P, MacKinnon A. Coherent tunnelling through two quantum dots with Coulomb interaction. J Phys Condens Matter. (1996) 8:5401–14. doi: 10.1088/0953-8984/8/29/015

CrossRef Full Text | Google Scholar

28. Chi F, Sun LL. Photon-assisted heat generation by electric current in a quantum dot attached to ferromagnetic leads. Chin Phys Lett. (2016) 33:117201. doi: 10.1088/0256-307X/33/11/117201

CrossRef Full Text | Google Scholar

29. Chi F, Liu LM, Sun LL. Photon-mediated spin-polarized current in a quantum dot under thermal bias. Chin Phys B. (2017) 26:037204. doi: 10.1088/1674-1056/26/3/037304

CrossRef Full Text | Google Scholar