Research on Geographic Location Prediction Algorithm Based on Improved Teaching and Learning Optimization ELM

Introduction

As a new swarm intelligence algorithm, Teaching Learning Based Optimization (TLBO) simulates the process of teachers' teaching to students and students' learning and the process of students' learning from each other. Through teachers' teaching and students' learning from each other, students' learning performance can be improved. Because TLBO has the advantages of few parameters, simple thinking, easy understanding and strong robustness [1–4], it has attracted the attention of many scholars since it was put forward and has been applied in many fields. Such as reactive power optimization of power system [5], LQR controller optimization [6], IIR digital filter design [7], steelmaking and continuous casting scheduling problem [8], PID controller parameter optimization problem [9, 10], feature selection problem [11], HVDC optimization of voltage source converter [12], extension of global optimization technology to constrained optimization [13], analysis of financial time series data [14], neural network optimization [15], etc. Compared with the existing swarm intelligence algorithm, the algorithm obtains better results. Firstly, the basic TLBO algorithm is introduced, then the improved TBLO algorithm is studied, and then the performance of ITLBO algorithm is tested by using F1–F4 four test functions. Finally, GPS data is used to verify the advantages of ITLBO-ELM algorithm.

Improved Teaching and Learning Optimization Algorithm

Basic TLBO Algorithm

TLBO algorithm is an optimization algorithm proposed by teachers' teaching and students' learning social activities in the process of inspired teaching. Both teachers and students are candidate solutions in TLBO algorithm population. Assuming that there are a total of N individuals in the class, the individuals with the best academic performance, that is, the best fitness, are regarded as teachers, and the rest are students. The specific implementation process of TLBO is described as follows:

A. Population initialization

Teachers and students are individuals in the class. Assuming that the solution space of the optimization problem is S-dimensional, any individual Xi in the population is initialized in a random way:

$\begin{array}{ll}{X}_i=L+r(U-L),i=1,2,\dots ,n& (1)\end{array}$

In the formula, U = (u₁, u₂, , …, u_s) and L = (l₁, l₂, , …, l_s) are vectors formed by the upper and lower bounds of each variable, respectively; r is a random number between [0, 1].

B. Teaching stage

The best individual in the population is the teacher, and students improve their performance through the difference between the average value of teachers and classes. The i-th student X_i generates a new individual according to Equation (2):

$\begin{array}{ll}{X}_i^{new}=X_i+D& (2)\end{array}$

Where $X_i^{new}$ is an updated individual, only if $f(X_i^{new})>f(X_i)$, $X_i^{new}$ is accepted, i.e., $X_i=X_i^{new}$, otherwise X_i is kept unchanged; D is the difference between teacher X_t and student average X_m, which is described as follows:

$\begin{array}{ll}D=r(X_t-T_f\times X_m)& (3)\end{array}$

Where $X_i^{new}$ is the teacher; $X_m=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{X}_i$ is the mean individual of the population; r is a random number between [0, 1]; the value of T_f teaching is only 0 or 1, which means that students may have learned all the knowledge of the teacher, or they may have learned nothing from the teacher. As a result, D may not be able to learn teachers' knowledge. T_f is a teaching factor and is generated by Equation (4):

$\begin{array}{ll}{T}_f=R_{ound}\left[1+rand(0,\text{1})\right]& (4)\end{array}$

Where R_ound represents the rounding function.

C. Learning Stage

In addition to learning from teachers, students also need to communicate with each other and learn from each other's strong points. Randomly select a student X_k(i ≠ k) from the class to carry out communication learning according to Equation (5):

$\begin{array}{ll}{X}_i^{new}=\{\begin{array}{cc}{X}_i+r(X_i-X_k),\hfill & iff(X_i)<f(X_k)\hfill \\ X_i+r(X_k-X_i),\hfill & \text{otherwise}\hfill \end{array}& (5)\end{array}$

Where r is a random number between [0, 1]; f(·) is a fitness function; $X_i^{new}$ is accepted only if $f(X_i^{new})>f(X_i)$.

ITLBO Algorithm

Aiming at the shortcomings of the original TLBO, which is easy to fall into local optimization and low precision in the optimization process, an improved TLBO algorithm is proposed, which is recorded as ITLBO. In the process of TLBO optimization, a remedial period for the worst students is added. For the students with the worst academic performance in the class, the teacher will guide the students alone to quickly improve their knowledge. On this basis, an interference operator is used to disturb the teacher to enhance the kinetic energy for the population to jump out of the local optimal. The improvements are described below:

D. Remedial period

Assuming that the worst student in the class is X_w, the remedial process is as follows Equation (6):

$\begin{array}{ll}{X}_w^{new}=r_1{X}_w+r_2(X_t-X_w)& (6)\end{array}$

Where r₁ and r₂ are random numbers between [0, 1]; $X_w^{new}$ is an individual updated by X_w, only if $f(X_w^{new})>f(X_w)$, $X_w^{new}$ replaces X_w; Otherwise, a reverse solution is generated to replace the original X_w, and the reverse solution is generated according to the following Equation (7):

$\begin{array}{ll}\overline{X_w}=U+L-X_w& (7)\end{array}$

Through tutoring or reverse learning for the worst students X_w, TLBO calculation points are used to speed up convergence and improve convergence accuracy. The strategy applied by X_w is to coach the worst students, which can directly improve the average value of the whole students. It is difficult to coach the best students to improve the average value of the whole students.

When TLBO algorithm solves complex multi-dimensional optimization problems, it is easy to fall into local optimization under finite iteration times. In order to further improve the global optimization capability of TLBO, interference operators are added in the search process p_ert(t):

$\begin{array}{ll}{p}_{ert}(t)=0.1\times r_3\times (1-t/t_{\text{max}})& (8)\end{array}$

The effect of interference operator p_ert(t) on teacher X_t is as follow Equation (9):

$\begin{array}{ll}{X}_t^{new}=X_t+p_{ert}(t)\times (U-L)& (9)\end{array}$

Where r₃ is a random number between [0, 1]; p_ert(t) is the disturbance coefficient of the t-th iteration process. With the increase of t, p_ert(t) gradually decreases, and the disturbance degree of interference operator to teachers gradually decreases. In the early stage of the search, p_ert(t) is larger, which causes greater disturbance to the update of teachers' positions, increases population diversity, and effectively enhances X_t to jump out of the local optimization. In the later stage of search, p_ert(t) gradually decreases to 0 to avoid affecting the local optimization and convergence of TLBO algorithm in the later stage.

The implementation process of ITLBO algorithm is shown in follow steps.

Step 1: Initialization parameters: class size n, dimension s, t_max, t = 1 and Initialize the population according to Equation (1).

Step 2: Calculate X_max and calculate D according to Equation (3) and calculate the new individual according to Equation (2) and update X_i.

Step 3: Individual X_j is randomly selected, new individuals are calculated according to Equation (5), and X_i is updated. Calculate $X_w^{new}$according to Equation (6); calculate the Directional Solution of X_w by Equation (7).

Step 4: Update X_w with New Individual or Reverse Solution, Choose the optimal individual X_w and calculate the interference operator according to Equation (8); according to Equation (9), update X_t.

Step 5: If t > t_max t = t+1; go to Step 2; or Output optimal solution.

Extreme Learning Machine (ELM)

ELM has the advantages of simple structure, fast operation, and strong generalization ability and so on, and avoids the problem of local optimization. No matter in theoretical research or in practical application, ELM has attracted the attention of many machine learning researchers. However, ELM still has some difficult problems to solve. The input weight thresholds of ELM are given randomly. How to ensure that they are the optimal model parameters? Appropriate number of hidden layer nodes and hidden layer activation function can ensure the generalization ability and running speed of ELM, but the setting of hidden layer node number and selection of hidden layer activation function of ELM are difficult problems.

Extreme Learning Machine (ELM) is a novel learning algorithm for single-hidden layer feedforward neural networks (SLFNs). Compared neural network learning methods (such as BP neural network) have complicated parameter design in the training model and are easy to fall into local optimization. However, ELM only sets a reasonable number of hidden layer neurons, and the algorithm execution process does not need to iterate the hidden layer. Input weights and hidden layer thresholds are randomly generated and do not rely on training sample data. The weight matrix of the output layer is obtained through one-step analytical calculation, which avoids the complicated calculation process of repeated iteration of the traditional neural network and greatly improves the training speed of the network.

For any N random samples (x_i, t_i),$x_i={[x_{i1},x_{i2},...,x_{in}]}^T\in R^n$, n is the number of input layer nodes, $t_i={[t_{i1},t_{i2},...,t_{im}]}^T\in R^m$ the number of hidden layer nodes is m, and the hidden layer excitation function is g (x), then the mathematical model is as follows:

$\begin{array}{ll}{\displaystyle \sum _{i=1}^L}{\beta }_{i}g(W_i·X_j+b_i)=o_j& (10)\end{array}$

$\begin{array}{ll}W={\left[\begin{array}{cccc}{W}_{11}& W_{12}& \dots & W_{1n}\\ W_{21}& W_{22}& \dots & W_{2n}\\ \dots & \dots & \dots & \dots \\ W_{L1}& W_{L2}& \dots & W_{Ln}\end{array}\right]}_{L\times n}& (11)\end{array}$

$\begin{array}{ll}\beta ={\left[\begin{array}{cccc}{\beta }_{11}& {\beta }_{12}& \dots & {\beta }_{1n}\\ {\beta }_{21}& {\beta }_{22}& \dots & {\beta }_{2n}\\ \dots & \dots & \dots & \dots \\ {\beta }_{L1}& {\beta }_{L2}& \dots & {\beta }_{Ln}\end{array}\right]}_{L\times n}& (12)\end{array}$

Where X_j and o_j are the input and output of the extreme learning machine, respectively, i.e., The input amount of location information of geographic information; W and β are both connection weight matrices; g(x) is the excitation function; b is the bias matrix, b = [b₁, b₂, …, b_L], b_i is the i-th neuron bias.

In order to minimize the output error, define the learning objectives:

$\begin{array}{ll}\text{lim}{\displaystyle \sum _{j=1}^N}\Vert o_j-t_j\Vert =0& (13)\end{array}$

Through continuous learning and training, $W_{i\stackrel{~}{}},b_{i\stackrel{~}{}},{\beta }_{i\stackrel{~}{}}$ are obtained, see as Equation (14)

$\begin{array}{ll}\Vert H(W_i^{\stackrel{~}{}},b_i^{\stackrel{~}{}}){\beta }_i^{\stackrel{~}{}}-T^{\prime }\Vert ={\displaystyle \underset{W,b,\beta }{\text{min}}}\Vert H(W_i^{\stackrel{~}{}},b_i^{\stackrel{~}{}}){\beta }_i^{\stackrel{~}{}}-T^{\prime }\Vert ,i=1,2,...,L& (14)\end{array}$

Equation (14) is equal Equation (15).

$\begin{array}{ll}E={{\displaystyle \sum _{j=1}^N}\left[{\displaystyle \sum _{i=1}^L}{\beta }_{i}g(W_i·X_j+b_j)-t_j\right]}^2& (15)\end{array}$

The training process actually solves the linear process and is realized by outputting weights.

$\begin{array}{ll}{\beta }^{~}=H^{*}{T}^{″}& (16)\end{array}$

Where H is the output matrix and H^* is the generalized inverse matrix of Moore-Penrose.

Simulation Test and Algorithm Comparison

Benchmark Test Function

In this paper, four benchmark functions are selected to test the algorithm.

The test functions are as follows:

A. Ackley's Function f 1:

$\begin{array}{l}f(X)=-20\text{ exp}(-0.2\sqrt{{\displaystyle \sum _{i=1}^n}{x}_i^2/n})-\text{exp}({\displaystyle \sum _{i=1}^n}\text{cos}(2\pi x_i)/n)\\ \begin{array}{l}+20+e,\left|x_i\right|\le 32\end{array}& (17)\end{array}$

The optimal values are: min(f(X^*)) = f(0, 0, ..., 0) = 0.

The function is a unimodal function with only one optimal value, but the surface is uneven.

B. Schweffel's Problem 1.2 function f2:

$\begin{array}{ll}f(X)={{\displaystyle \sum _{i=1}^n}\left[{\displaystyle \sum _{j=1}^i}{x}_j\right]}^2,\left|x_i\right|\le 100& (18)\end{array}$

The optimal values are: min(f(X^*)) = f(0, 0, ..., 0) = 0

The function is a unimodal function, but the surface is smooth near the optimal value.

C. Generalized Schweffel's Problem 2.26 function f3:

$\begin{array}{ll}f(X)=-{\displaystyle \sum _{i=1}^n{x}_i\text{ sin}(\sqrt{|x_i|}))},|x_i|\le 500& (19)\end{array}$

The optimal values are: .

The function is a multimodal function with multiple optimal values and uneven surface.

D. Generalized Rastrigin's function f 4:

$\begin{array}{ll}f(X)={\displaystyle \sum _{i=1}^n}\left[x_i^2-10\text{ cos}(2\pi x_i)+10\right],\left|x_i\right|\le 5.2& (20)\end{array}$

The optimal values are: min(f(X^*)) = f(0, 0, ..., 0) = 0.

The function is a multimodal function with multiple optimal values and uneven surface.

Test Results

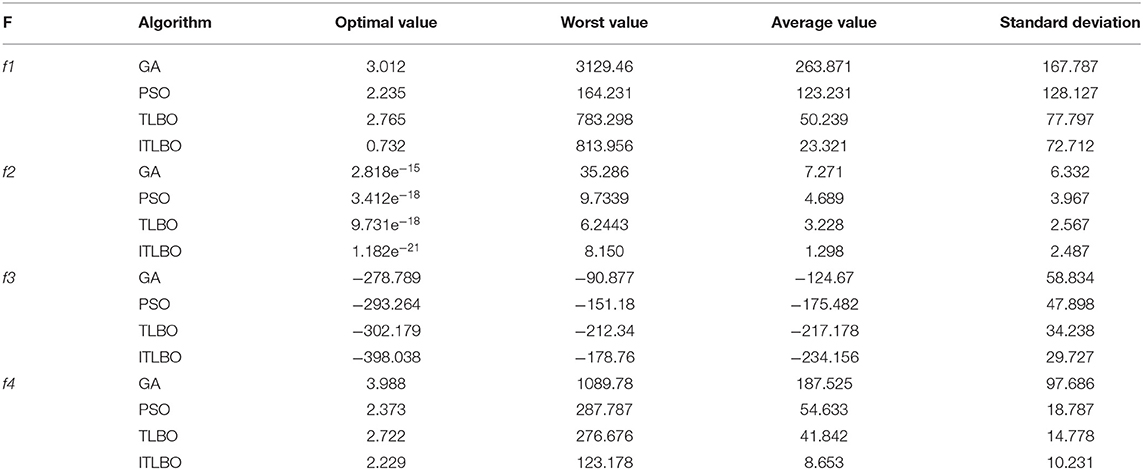
Verify the experimental results of TLBO-ELM algorithm, The algorithm uses Python language to implement the server Dell T610 operating system uses Ubuntu 64 bits, 2 CPU: x5650 main frequency 2.6G with 12 cores and 24 threads, memory 64G, The algorithm is run independently on four commonly used Benchmark functions for 30 times, The maximum number of iterations is 1,000, 100 iteration times are recorded, respectively, 200,., The average fitness value obtained 1,000 times describes the fitness value curve, The algorithms involved in the comparison include GA, PSO, TLBO and three commonly used swarm intelligence algorithms. The items to be compared include the average fitness value, the optimal result value, the worst result value and the standard deviation. The tested data are listed in detail in the test result comparison table. In order to compare the convergence performance of the four algorithms more vividly and clearly, the above three test functions are selected, and the convergence curves of the four algorithms on the selected functions are drawn, respectively. The test results are shown in Table 1 for example:

TABLE 1

Table 1. Comparison of four function sequencing.

Through the above test results and comparison tables, it can be seen that when testing functions f 4 and f 1, the optimal values found by ITLBO algorithm perform best and the curves are relatively smooth, TLBO is better and the curves fluctuate little, and PSO and GA perform poorly. The standard deviation of TLBO algorithm is similar to that of ITLBO algorithm, while the standard deviation of GA and PSO is larger, which shows that TLBO algorithm performs better in convergence stability. When testing f 3 function, ITLBO algorithm finds the best optimal value, the curve is smoother, the standard deviation is lower, TLBO curve is smoother, the standard deviation is lower, but the convergence result value is not accurate enough. PSO and GA algorithms find the best value, the curve fluctuates greatly, and the standard deviation is higher. When function f2 tests, ITLBO algorithm still shows better optimization accuracy and convergence stability than the other three algorithms.

On the four functions tested, ITLBO algorithm shows the advantages of good convergence stability, high optimization accuracy and so on, and shows good optimization ability. The accuracy of the optimal solution found by the artificial fish swarm algorithm is not high enough, but the stability is good. Genetic algorithm and particle swarm optimization algorithm have the worst performance in finding the optimal solution value of the four functions.

As we can see from that optimization graph, with the increase of iteration times, the optimization results of the algorithm also tend to be stable. The stable optimization values of genetic algorithm and particle swarm optimization algorithm are obviously higher than those of other algorithms. The curve of TLBO algorithm is relatively smooth, but the solution results are not very accurate. ITLBO algorithm has advantages in optimization speed, optimization accuracy and optimization stability compared with other three algorithms.

Random selection of iteration times is 100, 200, …, 1,000 times, respectively, to test the fitness value of the algorithm and the relationship between iteration times. See as Figure 1.

FIGURE 1

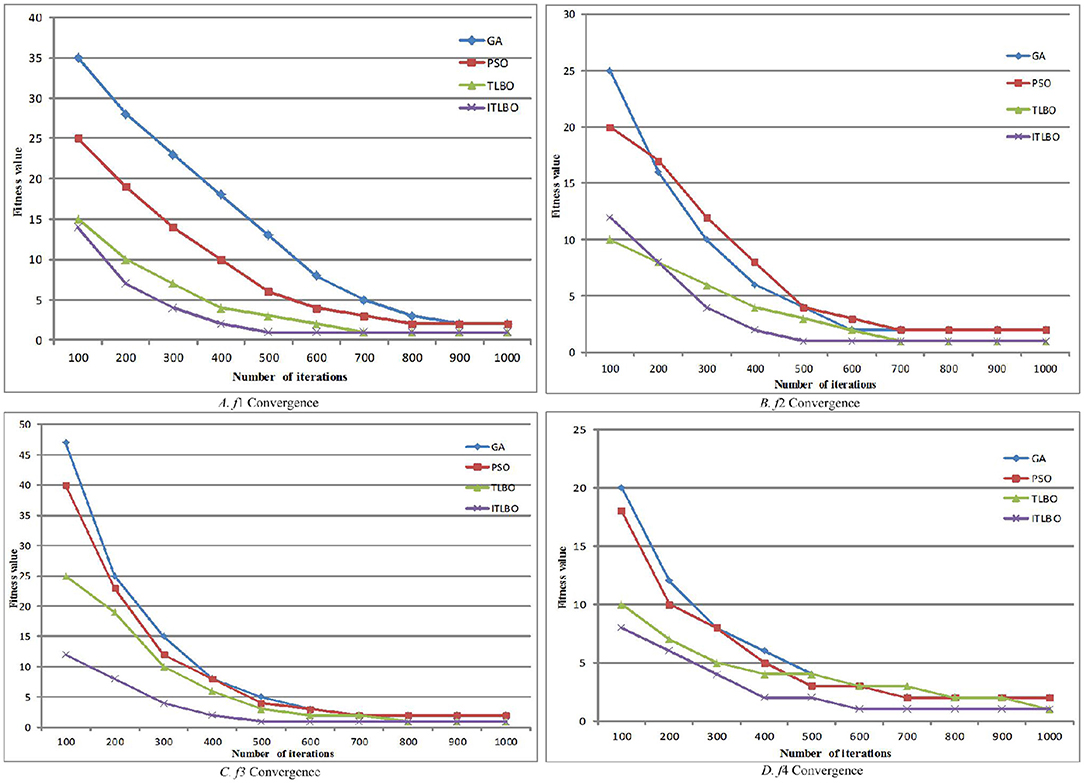
Figure 1. Convergence comparison of four functions. (A) f 1 Convergence. (B) f 2 Convergence. (C) f 3 Convergence. (D) f 4 Convergence.

Comparative Study on GPS Vehicle Data Position Prediction

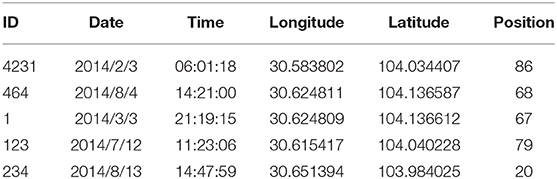
The data studied in this paper come from on-board GPS data. The data include: road number, vehicle ID, time, longitude, dimension, speed and position number. The data time is 15,000 on-board GPS data information from August 1, 2014 to August 31, 2014. Its data format is shown in Table 2 below:

TABLE 2

Table 2. Vehicle GPS data sheet.

Location numbering is based on the location range represented by dimensions. Different numbers differ in geographical locations. When the longitude and latitude of different geographical positions are numbered at the same number, it means that the two positions are identified as similar or the same position, i.e., the correct position is predicted. Based on the map division of this grid, different geographic location information is divided into the same or similar geographic spaces. The size of the grid also determines the accuracy of the prediction. When the grid is relatively large, the prediction effect is ideal. When there are many grids, the prediction effect may not be ideal. Under different grids, there may be two similar positions to deal with different grids. As a result, the grid size can also affect the accuracy of the experiment.

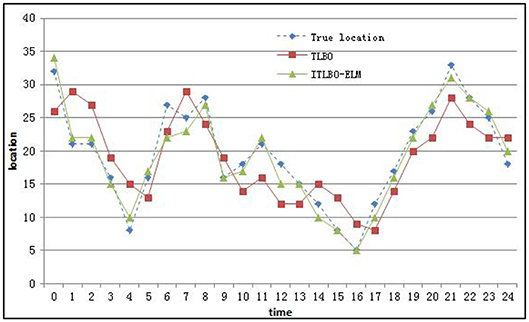
Through the processing and analysis of GPS data, this paper uses TLBO, ITLBO-ELM algorithms to compare the prediction results, and predicts different vehicle information from different road sections within the numbered range of the next position or related area. As shown in Figure 2.

FIGURE 2

Figure 2. Comparison of prediction effect of 1-day location.

Geographical locations are described by numerical numbers and different area numbers express different locations. The closer the data are, the shorter the distance between locations. As can be seen from Figure 2, ITLBO-ELM is closer to the real position than TLBO prediction method and ITLBO-ELM prediction method for prediction comparison of different positions at different time points. ITBLO combined with ELM algorithm is mainly to improve the convergence speed and accuracy of the algorithm. As can be seen from Figure 2, ITBLO-ELM algorithm has obvious advantages corresponding to other algorithms.

Geographic location information is encoded with specific area numbers and different area numbers express different geographic location information. There may be the same area numbers at different longitude and latitude. At this time, the location representation is similar. When judging from the effect of the actual position and the predicted position in Figure 2, there are obvious differences between the actual position and the TLBO prediction results, while in the whole prediction track process, the actual position area number is consistent with the ITLBO-ELM prediction results, and the two are relatively close. The experimental results show that ITLBO-ELM has good experimental results in overall performance.

Conclusion

In view of the poor prediction accuracy and effect in the geographic location information prediction algorithm, a prediction method based on improved teaching and learning optimization algorithm and ELM algorithm is proposed. The results show that ITLBO-ELM algorithm has high accuracy in predicting positions. The method proposed in this paper has good effect in predicting the position, considering the representation of position information under different coordinates. Further research work is carried out to predict the position information from different coordinates so as to reduce the prediction errors caused by coordinate differences. In the conclusion, in the future research work, whether more tests are considered in the algorithm to test the test effect of this paper. In the future research work, the convergence speed and position accuracy of the algorithm will be mainly considered.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors participated in the preparation and presentation of the manuscript.

Funding

This work was supported by the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJZD-K201902101).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Jiang W, Carter DR, Fu HL, Jacobson MG, Zipp KY, Jin J, et al. The impact of the biomass crop assistance program on the United States forest products market: an application of the global forest products model. Forests. (2019) 10:1–12. doi: 10.3390/f10030215

CrossRef Full Text | Google Scholar

2. Liu JB, Zhao J, Zhu ZX. On the number of spanning trees and normalized Laplacian of linear octagonal-quadrilateral networks. Int J Quantum Chem. (2019) 119:1–21. doi: 10.1002/qua.25971

CrossRef Full Text | Google Scholar

3. Liu JB, Zhao J, Cai Z. On the generalized adjacency, Laplacian and signless Laplacian spectra of the weighted edge corona networks. Physica A. (2020) 540:1–11. doi: 10.1016/j.physa.2019.123073

CrossRef Full Text | Google Scholar

4. Wei L, Li J, Ren L, Xu J. Exploring livelihood resilience and its impact on livelihood strategy in rural China. Social Indicat Res. (2020). doi: 10.1007/s11205-020-02347-2

CrossRef Full Text | Google Scholar

5. Ghasemi M, Taghizadeh M, Ghavidel S, Aghaei J, Abbasian A. Solving optimal reactive power dispatch problem using a novel teaching-learning-based optimization algorithm. Eng Appl Artif Intell. (2015) 39:100–8. doi: 10.1016/j.engappai.2014.12.001

CrossRef Full Text | Google Scholar

6. Lee J, Chang H-J. Analysis of explicit model predictive control for path-following control. PLoS ONE. (2018) 13:e0194110. doi: 10.1371/journal.pone.0194110

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Singh R, Verma HK. Teaching–learning-based Optimization Algorithm for Parameter Identification in the Design of IIR Filters. J Inst Eng. (2013) 94:285–94. doi: 10.1007/s40031-013-0063-y

CrossRef Full Text | Google Scholar

8. Pan Q-K. An effective co-evolutionary artificial bee colony algorithm for steelmaking-continuous casting scheduling. Eur J Operat Res. (2016) 250:702–14. doi: 10.1016/j.ejor.2015.10.007

CrossRef Full Text | Google Scholar

9. Dib F, Boumhidi I. Hybrid algorithm DE-TLBO for optimal and PID control for multi-machine power system. Int J Syst Assur Eng Manage. (2017) 8:S925–36. doi: 10.1007/s13198-016-0550-z

CrossRef Full Text | Google Scholar

10. Luo Z, Guo Q, Zhao J, Xu S. Tuning of a PID controller using modified dynamic group based TLBO algorithm. Int J Comput Appl. (2017) 157:17–23. doi: 10.5120/ijca2017912593

CrossRef Full Text | Google Scholar

11. Satapathy SC, Naik A, Parvathi K. Unsupervised feature selection using rough set and teaching learning-based optimisation. Int J Artif Intell Soft Comput. (2013) 3:244. doi: 10.1504/IJAISC.2013.053401

CrossRef Full Text | Google Scholar

12. Yang B, Shu HC, Zhang RY, Huang LN, Zhang XS, Yu T. Interactive teaching-learning optimization for VSC-HVDC systems. Kongzhi yu Juece/Control Decis. (2019) 34:325–34. doi: 10.13195/j.kzyjc.2017.1080

CrossRef Full Text | Google Scholar

13. Wang BC, Li HX, Feng Y. An improved teaching-learning-based optimization for constrained evolutionary optimization. Information Sci. (2018) 456:131–44 doi: 10.1016/j.ins.2018.04.083

CrossRef Full Text | Google Scholar

14. Das SP, Padhy S. A novel hybrid model using teaching-learning-based optimization and a support vector machine for commodity futures index forecasting. Int J Mach Learn Cybernet. (2018) 9:97–111. doi: 10.1007/s13042-015-0359-0

CrossRef Full Text | Google Scholar

15. Han B, Zhou L, Zhang Z. LIDAR:assisted radial basis function neural network optimization for wind turbines. IEEJ Trans Electr Electron Eng. (2018) 13:195–200. doi: 10.1002/tee.22514

CrossRef Full Text | Google Scholar