- 1GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
- 2MedAustron Ion Therapy Center, Wiener Neustadt, Austria
- 3Laboratori Nazionali di Legnaro, INFN Istituto Nazionale di Fisica Nucleare, Legnaro, Italy
- 4Vinča Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
The specific advantages of ion beams for application in tumor therapy are attributed to their different macroscopic and microscopic energy deposition pattern as compared to conventional photon radiation. On the macroscopic scale, the inverted dose profile with a Bragg peak and small lateral scattering allow a better conformation of the dose to the tumor. On the microscopic scale, the localized energy deposition around the trajectory of the particles leads to an enhanced biological effectiveness, typically expressed in terms of the relative biological effectiveness (RBE). Experimental investigations reveal complex dependencies of RBE on many physical and biological parameters, as e.g., ion species, dose, position in the field and cell or tissue type. In order to complement the experimental work, different approaches are used for the characterization of the specific physical and biological properties of ion beams. In a set of two papers, which are linked by activities within a European HORIZON 2020 project about nuclear science and application (ENSAR2), we describe recent developments in two fields playing a key role in characterizing the increased biological effectiveness. These comprise the biophysical modeling of RBE and the microdosimetric measurements in complex radiation fields. This first paper gives a brief introduction into these fields and then focuses on aspects of biophysical modeling of RBE, specifically on semi-empirical approaches that are currently used in treatment planning for ion beam therapy. It summarizes the status and recent developments of the Local Effect Model (LEM) and its conceptual framework and shows examples of model validation using recent experimental data. The model is compared to other approaches, e.g., to the Microdosimetric-Kinetic Model (MKM), that builds the bridge to the experimental microdosimetric work.
Introduction
The main motivation for the application of ion beams in radiotherapy is their advantageous depth dose profile, allowing maximizing the dose to the tumor by simultaneously sparing the surrounding normal tissue as compared to conventional photon radiation [1–3]. Whereas, all ion species share this macroscopic property, in particular heavier ions like carbon ions show an additional advantage with respect to their biological effectiveness. They exhibit an increased biological effectiveness in particular toward lower energies, i.e., in the region where they come to rest when penetrating tissue (the so-called “Bragg peak”) [4–6]. This increased effectiveness is expressed in terms of the relative biological effectiveness (RBE), which is defined by the doses required to achieve a given survival level with photons and ion beams, respectively, under otherwise identical conditions:
A major determinant of the RBE is the linear energy transfer (LET) of the ions, characterizing the energy released to the material surrounding the ion trajectory per unit path length. The LET of monoenergetic beams is represented by a single value and increases with decreasing energy; this generally leads to a corresponding increase of RBE toward the Bragg peak region.
In case of irradiation fields formed by particles of different types and energies, LET is represented by a distribution. However, in order to simplify the representation, typically averaged LET values are considered. There are two frequently applied ways of calculating the average LET, the track average and the dose average [7], where the in general is more closely related to RBE than values.
Regarding the biologic effects of radiation, the induced cell killing is a frequently used endpoint to characterize RBE. If cell survival S(D) after irradiation with dose D is described in terms of the linear-quadratic model
the changes of the parameters α and β after ion irradiation as compared to photon irradiation are typically characterized by [8]:
The changes primarily reflect the increase of the linear term α, i.e., the initial slope of the dose response curve. The impact on the quadratic term is less pronounced and subject to larger uncertainties. Overall, this results in more straightened dose response curves for high-LET radiation as compared to photon radiation.
For the dose prescription in ion beam therapy, the increased effectiveness needs to be adequately taken into account. However, although conceptually the definition of RBE is simple, it cannot be represented by a single fixed number in extended radiation fields, but actually depends in a complex way on several physical and biological parameters. Based on in-vitro studies, the fundamental RBE dependencies can be summarized as follows [8–11]:
1. RBE rises with LET up to a certain maximum and drops toward higher LET values.
2. The RBE(LET) curves are shifted toward higher LET values with increasing particle charge, i.e., for heavier particles.
3. RBE decreases with increasing dose and thus decreasing survival level.
4. RBE is higher for cells that are radioresistant against conventional photon radiation as compared to cells that are sensitive against photon radiation.
As a consequence of these relations, RBE values in typical treatment fields for ion beam therapy will vary with position in the target field and depend on the fractionation scheme used. Therefore, there is no single number for conversion of absorbed dose to RBE-weighted dose. To fully exploit the advantageous properties of ion beams, the systematic dependencies of the RBE have to be fully considered in treatment planning in ion beam therapy, allowing taking advantage of the vast experience made with conventional photon therapy.
Role of the Microscopic Energy Deposition Pattern
Careful analysis of the above-mentioned systematic dependencies of RBE clearly indicates that the increased effectiveness of ion beams is largely determined by their specific microscopic patterns of energy deposition: whereas photons deposit their energy by releasing secondary electrons almost randomly distributed within the irradiated volume, ions deposit their energy extremely localized and concentrated along the trajectory of the ion. Qualitatively, this localized higher energy density is expected to lead to more severe biological damages, e.g., clustered DNA damages, which finally result in a higher cell killing effect. The adequate characterization of the microscopic energy deposition patterns is thus a prerequisite for the detailed understanding of their biological effectiveness.
Although there is general agreement in the community about the relevance of the microscopic energy deposition pattern, it is less obvious at which spatial scales these patterns need to be characterized. For example, assuming the DNA within the cell nucleus to be a critical target for radiation damages points to the relevance of the nm scale [12–14]. In addition, analysis of the formation of radiation-induced chromosome aberrations suggests also the micrometer scale as particularly relevant [15]. Finally, early experimental data showed that the cell nucleus represents the gross sensitive target for most radiation effects [16], which points out the potential role of the 10 μm-scale. A recent combined experimental and modeling study further supports the importance of the 10 um-scale [17]. At the same time, this study revealed that the above mentioned three scales are not necessarily exclusive and that the relative importance of the different scales may strongly depend on the LET.
A wide range of experimental as well as theoretical approaches have been developed and discussed in order to address these aspects. Within a set of two papers, we discuss recent results obtained in two related fields: experimental microdosimetry and biophysical modeling. In the following, we briefly introduce some key aspects of both fields and in the main part of this manuscript then focus on recent results obtained with a specific biophysical model – the Local Effect Model.
Experimental Microdosimetry
Experimental microdosimetry aims at the accurate characterization of the energy deposition pattern in micrometer dimensions and particularly also their fluctuations and distributions. Major developments of this field were implemented in the framework of neutron therapy, since neutrons – as ion beams – exhibit an increased effectiveness as compared to conventional photon radiation.
The microdosimetric approach assumes that the quality of the radiation action, namely the biological effect per unit of absorbed dose, merely depends on the energy deposition within micrometer-sized critical target sites within the cell nucleus, so called single-event imparted-energy ε1. The ratio ε1/, where is the biological site mean-chord length of trajectories passing the site, is called lineal energy, y. Radiation fields as typical for ion beam therapy are characterized by a spectrum of y-values, and the distribution depends on the position in the radiation field. The biological effect is expected to be proportional to the dose delivered by each y-component of the spectrum, i.e., in general d(y) is indicative of the biological effect. RBE values can be obtained from the d(y)-spectrum by appropriate convolution with a weighting function r(y) that represents the increased effectiveness as a function of y [18]. A simplified exploitation of microdosimetric measurements is using the mean of the d(y) distribution, defined as: , or the mean corrected with a saturation function of y, which is called y* (ICRU 36).
Experimental measurements of microdosimetric spectra are frequently obtained using gas filled detectors, which actually have macroscopic sizes in the order of millimeter to centimeter. However, information on the micrometer scale is obtained by appropriate rescaling according to the different densities of gas and water. First microdosimeters were gas proportional counters made with tissue-equivalent plastic and filled with tissue-equivalent gas mixtures and were thus called TEPC (tissue-equivalent proportional-counter). TEPCs have a high detection efficiency, since they can detect also few ionization events thanks to the electron multiplication in the filling gas. However, they cannot operate in very high-intensity radiation fields, as their geometrical size is hardly < 1 mm. More recently, also solid-state detectors became available, made e.g., of silicon semiconductor material or of synthetic diamond. They are actually characterized by much smaller geometrical dimensions as compared to TEPCs; their geometrical size can be as small as 1 μm, making them fit to operate also in very intense radiation fields. However, this advantage has to be balanced with lower detection efficiency. The aspects of experimental microdosimetry will be developed more deeply in the second paper.
Biophysical Modeling
A thorough overview over the broad range of biophysical models addressing the aspects of high-LET radiation, covering extremely detailed so-called mechanistic models as well as semi-empirical and empirical approaches would be beyond the scope of this paper. We thus restrict here to some key aspects relevant for two models actually used in ion beam therapy at present, the Microdosimetric-Kinetic Model (MKM) [19, 20] and the Local Effect Model (LEM) [21–23].
The transition from the initial energy deposition to the final observable biological effect after a radiation insult includes numerous complex biological processes and pathways, from which many are still unknown or at least not yet accurately quantified, and any model thus can represent an approximation to reality only. One of the major challenges of modeling in the framework of treatment planning therefore is to find the right balance between accuracy and model complexity, i.e., number of different processes and mechanisms to be taken into account [24, 25].
Simplifications are made in both models typically with respect to two aspects:
1. Details of the stochastic distribution of energy deposition of ions around their trajectory on the level of individual secondary electrons are neglected.
2. The details of the complex biological processes, like e.g., the DNA damage signaling and repair pathways, and the corresponding uncertainties are “hidden” by making reference to the known photon dose response curve in a type of “black box” approach.
The models therefore do not aim at an ab-initio calculation/prediction of the biological effects of ion beams from first principles, but rather on a translation of what is known from photon radiation to the specific aspects of the microscopic energy deposition pattern of ion traversals through the cell nucleus.
The models mainly differ with respect to the level of detail on which the spatial distribution of energy deposition around the particle trajectory is taken into account. Whereas, e.g., the MKM is strongly linked to the facets of the experimental microdosimetry as described above and thus focuses on the energy deposition features on the micrometer scale, the LEM explicitly considers the impact of track structure on the nanometer, the micrometer and the 10-micrometer level [17].
Link Between Both Fields
The two aspects described above approach the problem of characterizing radiation quality from different directions and are, in a way, complementary. Microdosimetry focuses on the possibility to characterize experimentally the microcoscopic energy deposition in any complex radiation field, as it is typical for the superimposition of ion beams with different primary energies as required to form a spread-out Bragg-peak (SOBP). It is thus suitable to check radiation quality in typical patient plan like dose distributions and thus for quality assurance issues.
The modeling approach in contrast also makes use of some quantities and features of ion beam radiation, which cannot be directly measured in complex radiation fields. Instead, models make use of parametrizations, which are validated independently in specific experiments also under conditions which might even be beyond typical patient treatment conditions, e.g., by using also heavier ions than carbon or a larger energy regime. An advantage of the modeling approach is that it facilitates taking into account aspects of microscopic energy deposition on any spatial level, and thus potentially allows a more accurate description of the underlying mechanisms leading to the increased RBE.
Biophysical Modeling: General Aspects
In principle, protons as well as heavier ions exhibit an increased RBE toward the end of their range when penetrating tissue. However, the demand for RBE modeling for treatment planning in ion beam therapy is clearly more relevant in the case of heavier ions than for protons, since RBE values are substantially greater for heavy ions. Nevertheless, it is still under discussion whether a variable RBE instead of using a constant RBE = 1.1 could be beneficial in proton therapy [26–29]. Nonetheless, numerous simplified, empirical models have been proposed which are applicable solely to the case of protons, as they are based on certain simplified assumptions that are not valid for heavier ions [30].
At present, two different models are used in treatment planning for carbon-ion beam therapy: the Microdosimetric-Kinetic Model (MKM) is used in the Japanese facilities, whereas the Local Effect Model (LEM) is used in the European facilities. In both approaches, the characterization of the microscopic energy deposition pattern represents a major ingredient, although the details how this energy deposition pattern is translated into a biological response substantially differ. The characterization of the dose response curve after low-LET radiation represents the second pillar of these models. In the following, we briefly introduce the main concepts of these models. Although modeling results are presented in the results section only for the LEM, understanding the key aspects of the MKM is of relevance for the discussion and with respect to its link to the experimental microdosimetry approach presented in the second paper.
Basic Concepts of Models
Local Effect Model
The LEM in its original version (LEM I; 21) is used for treatment planning in the European carbon ion facilities. For this first version of the model an accurate representation of the effects of carbon ions was the major focus, and the application to other ion species required corresponding adaptation of input parameters. More recently improved versions of the model have been developed, and the most recent version (LEM IV; [22, 23]) now allows the simultaneous consistent prediction of RBE over a wide range of particles with similar accuracy based on a single set of input parameters. The basic idea of the LEM is to predict effects of high-LET radiation based on the known effects of low-LET radiation in combination with the characterization of the inhomogeneous, localized energy deposition pattern of charged particles. The effect calculation within the LEM IV includes the following major steps:
1. Characterization of the microscopic spatial energy deposition pattern by means of an amorphous track structure approach. This reflects the mean energy deposition (so called local dose) as a function of the distance from the particle trajectory, largely given by D(r) ~ 1/r2.
2. Determination of the spatial distribution of DSB of a single particle traversal through the cell nucleus derived from the amorphous track structure in combination with the known DSB yield of 30 DSB/Gy/nucleus after photon irradiation. Extremely high energy deposition in nanometer dimensions within the center of particle tracks can lead to correspondingly higher yields of DSB as compared to photon radiation by increased clustering of SSB leading to additional DSB.
3. Characterization of the clustering properties of DSB with respect to the giant loop substructure of the chromatin organization, containing typically 2 Mbp DNA and approximated by ~0.5 μm sized subvolumes of the nucleus. Chromatin loops containing just a single DSB are called isolated DSB (iDSB), chromatin loops with 2 or more DSB are called clustered DSB (cDSB).
4. Determination of the trend to form clustered DSB, captured by the cluster index C, which is the ratio of cDSB to the total number of DSB,
5. Determination of the photon dose leading to the same proportion of iDSB and cDSB, i.e., the same cluster index.
6. Calculation of the biological effect for this “iso-complexity” photon dose according to a (modified) LQ-approach.
7. Determination of the effect of ion irradiation from the effect of photons at the dose determined in the previous step by appropriate rescaling of the photon effect according to the total number of DSB induced by photon and ion irradiation, respectively.
LEM IV has been demonstrated to accurately represent experimental data in-vitro over a larger range of different ion species from protons to oxygen ions [22, 31–33]. Furthermore, besides in-vitro experiments also RBE for in-vivo experiments, e.g., the tolerance of the rat spinal cord, can be modeled with LEM IV [34, 35]. Interestingly, the concept of damage classification that has been developed for the LEM IV has been shown to be applicable also to other radiation qualities, and several key aspects like LQ-shape of survival curves, rejoining kinetics, dose rate effects and cell cycle effects are consistently modeled by this approach [36–38].
MKM
The MKM makes use of characterization of energy deposition in micrometer-sized volumes and of concepts implemented in the experimental microdosimetry branch. Its original version has been developed by Hawkins [19, 20], and subsequent further developments have been implemented in the framework of the Japanese heavy ion therapy projects [39, 40].
The key variable on which the MKM is based is the lineal energy y. However, predictions of the increased effectiveness do not use the details of the corresponding microdosimetric spectrum, but rather it's dose weighted mean value . The basic assumption of the MKM is, that in a first approximation the shape of the y-distribution can be ignored as long as the value of is identical for different distributions. The essential dependence reflecting the increased RBE in terms of the linear-quadratic parameters is then given by [41]:
Here, αIon represents the linear term of the dose response curve after ion irradiation, α0 the corresponding parameter for radiation qualities with LET→0 and d the diameter of the critical sensitive volume. The quantity β denotes the quadratic term of the dose response curves, which is identical to the value for photon radiation according to the MKM approach. Therefore, only the α-term is affected by high-LET radiation as compared to low-LET radiation. In a first approximation, α0 can be identified with the α value obtained after photon reference radiation.
As Equation (2) describes a continuously increasing α with increasing , it is not compatible with the drop of RBE toward very high LET values which results from the overkill effect. However, a saturation correction has been introduced [40] in order to account for this effect. The correspondingly corrected dose mean lineal energy is denoted by y*, and replacing by y* in Equation (2) then reflects the generally observed shape of RBE(LET) curves.
Equation (2) also allows the direct link to experimental microdosimetric measurements, from which can be obtained [e.g., 38]. Simulated spectra can be used as well, using e.g., amorphous track structure approaches to derive values for the use in conjunction with the MKM [42]. The MKM now serves as a replacement for the former experimentally based approach to characterize cellular RBE in-vitro within SOBPs in the Japanese treatment planning approach.
Other Models
Apart from the LEM and the MKM, other approaches are discussed for potential applications in ion beam therapy, as e.g., reported in [43–45]. However, a conceptual comparison of the models has revealed substantial differences e.g., with respect to the impact of overkill at very high LET and the change of the quadratic component with LET (see e.g., [46]). This underlines the need for a more detailed validation of the models by means of experimental data in order to assess the impact of these model differences on the accuracy of the model prediction.
Recent Results for LEM IV
In the following, we report about recent results obtained with the LEM IV with respect to a broad range of applications, comprising comparisons to experimental data in-vitro and in-vivo. In addition, we illustrate the impact of specific concepts underlying the LEM, highlighting the importance of different spatial scales to explain the systematic dependencies of RBE.
Comparison to Experimental Data at INFN-LNS
Brief Description of Experimental Conditions and Simulation With TRiP98
Irradiations of cell samples were performed in Istituto Nazionale di Fisica Nucleare, Laboratori Nazionali del Sud (INFN – LNS), Catania, Italy, with 62 MeV/u carbon ions at the 0° beam line and with 62 MeV therapeutic protons at the CATANA (Centro di AdroTerapia e Applicazioni Nucleari Avanzate) facility for treatment of eye melanoma. Details of the experimental results and the corresponding reference experiments using photon radiation are given elsewhere [47, 48], and here we only briefly report the main experimental conditions relevant for this contribution.
Four different tumor cell lines (CRL5876, HTB140, HTB177, MCF7) have been used, covering a broad range of radiosensitivities. Proton irradiations were performed using a 62 MeV proton beam in the center of a 15 mm SOBP, located at 10–25 mm depth [47]. The corresponding was 4.7 keV/μm. Carbon ion irradiations were performed with a 62 MeV/u beam for both a monoenergetic beam as well as a small, about 2 mm wide SOBP, which however does not deliver a homogeneous dose [48]. Details of the corresponding dose distributions are reported in Romano et al. [49] (see also Figure 1). Irradiation of the cells with monoenergetic beams was performed at the proximal side of the Bragg peak, where ~ 50% of the maximum relative dose are deposited (corresponding to 7.6 mm depth as marked in Figure 1 (left) 1; LET: 198 keV/μm). Irradiation under a very narrow, 2 mm SOBP condition was performed at the position where about 98% of the maximum relative dose are reached (corresponding to 5.4 mm as marked in Figure 1 (right); LET: 208 keV/μm). To obtain reliable statistics all irradiations with protons and carbon ions were performed in duplicate in three separate experiments, except those carried out with the monoenergetic carbon ions that were done in duplicate and repeated seven times. The increased repetition of irradiations with pristine carbon ions was necessary because of the delicate experimental conditions (positioning of cell samples) caused by a very narrow Bragg peak.
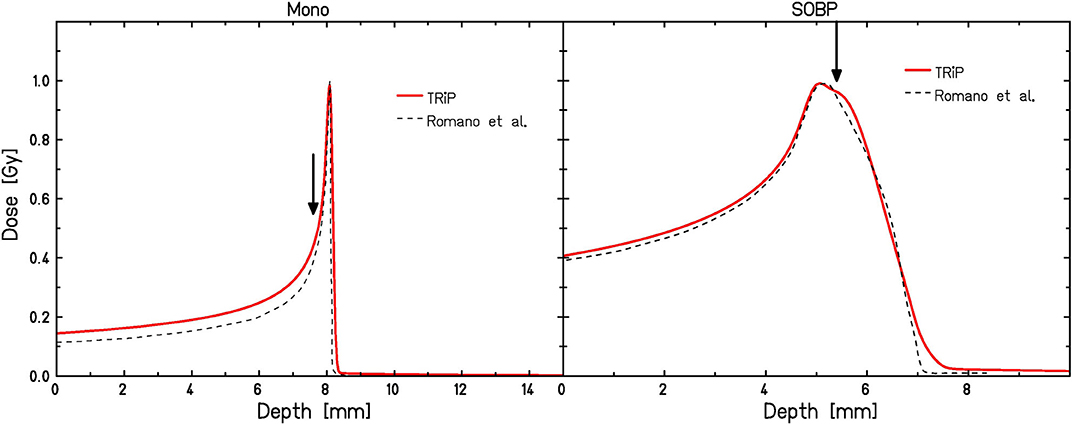
Figure 1. Depth dose distributions for monoenergetic (left) and SOBP (right) carbon ion irradiation according to TRiP calculations used in this paper as compared to those reported by Romano et al. [49]. Irradiation positions are marked by arrows.
The corresponding depth-dose distributions were simulated using the TRiP98 treatment planning environment [50, 51] (Figure 1). Since this system had been developed for planning under the conditions relevant for the GSI pilot project, i.e., base data are only available for beam energies >80 MeV/u, some approximations had to be used in order to mimic the conditions reflecting the INFN-LNS experiments. First, the lower energies have been mimicked by artificially introducing some bolus material in the treatment planning system. This, however, is not expected to have a large impact on the predicted RBE values, as the contribution of fragments is still low even with the additional bolus material, and the primary C ions will dominate the effectiveness. Therefore, as long as the dose is simulated correctly, also predicted RBE values are close to those expected in the “real” situation. Second, dose and LET values are subject to uncertainties, which are particularly relevant in the case of monoenergetic carbon-ion irradiation conditions due to the pronounced dose and LET gradients at this position in depth. We thus performed the model calculations also for a variation of ± 0.1 mm around the planning position of 7.6 mm depth in order to get some feeling for the corresponding uncertainties of survival curve predictions. Practically, we simulated the error of ± 100 μm in cell samples positioning, based on the 50 μm step width of the mechanical device that was used for sample positioning. For the carbon ion “SOBP” conditions depth dose profiles were simulated using a 2 mm ripple filter [52], which results in a depth-dose profile in reasonable agreement with the profile reported by Romano et al. [49].
Comparison With LEM Predictions
The parameters listed in Table 1 have been used as input for the LEM calculations [48]. For HTB140 cells, two different sets, a and b, have been used for comparison, since this cell line is characterized by an unusual, extreme radiation resistance, and thus very high doses are required to extract a reliable β-parameter. As experiments have been performed with γ-rays over different dose ranges, correspondingly different sets of LQ-parameters have been obtained and are used for the LEM calculations for that cell line.
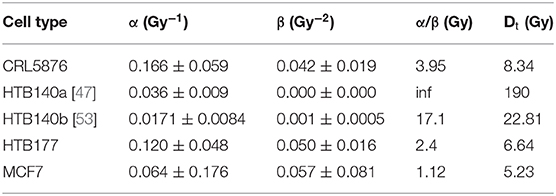
Table 1. Photon input parameters for the LEM calculations shown in Figure 2.
Predicted survival curves for the different conditions are shown in Figure 2 in comparison to the experimental data [48]. Surviving fractions are presented as mean values ± standard error of the mean of at least three (seven in the case of monoenergetic carbon ions) separate experiments. In general, standard error of the mean ranges from <5%, which is the case for smaller doses, to somewhat more than 15% for larger doses. This increase is the consequence of the fact that as the number of survived cell colonies falls (with the rise of dose) to 10−2 and further to 10−3 where there are only a few colonies that are counted, thus the statistics considerably deteriorates.
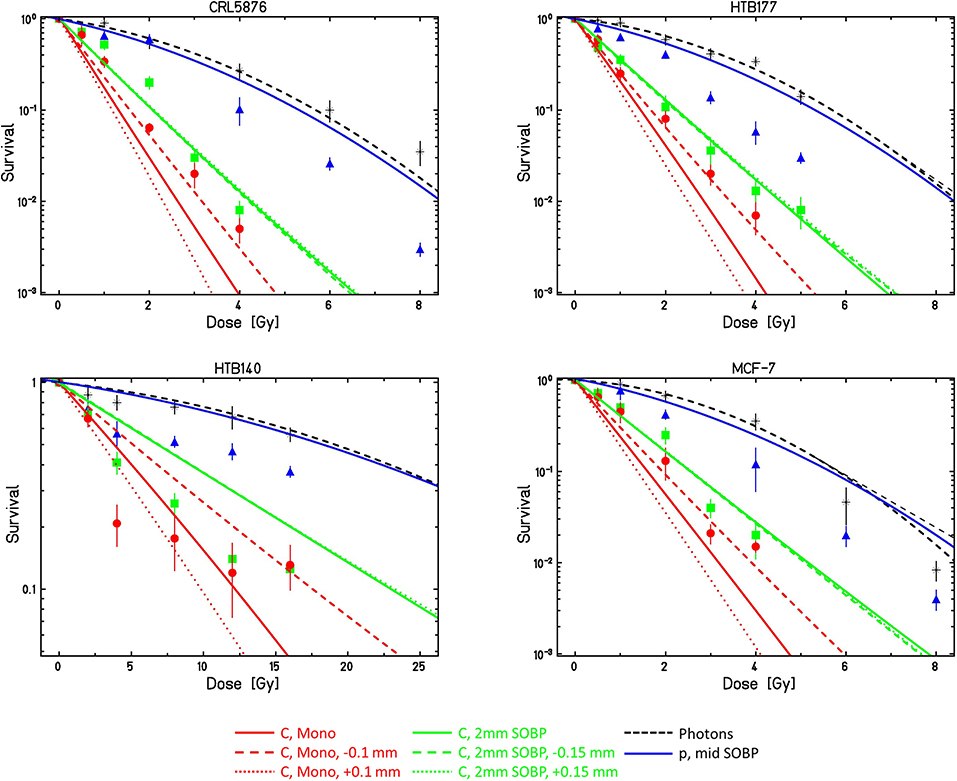
Figure 2. Comparison of LEMIV model calculations (lines) with experimental cell survival data (symbols) obtained at the INFN-LNS beamlines with different cell lines and different radiation qualities. For details see text. Calculations for ± 0.1 and ± 0.15 mm refer to potential positioning inaccuracies as compared to the desired depth.
For protons, measured survival in general is lower than predicted by the LEM.
For the monoenergetic carbon ions, as expected the calculations are very sensitive to the exact depth position; for all cell lines, the curves assuming a depth shift of −0.1 mm as compared to the desired position agree reasonably well with the experimental data. Also, the curves for the SOBP conditions show good agreement with the experimental data, and as expected they are also much less sensitive to the exact position in depth.
HTB140 cells are characterized by two special features: an extremely low sensitivity and an almost linear photon dose response curve. Model calculations have therefore been performed with two different parameter sets HTB140a and HTB140b (see Table 1), assuming either purely linear photon dose response or a small β-term of 0.001 Gy−2 according to Petrovic et al. [53]. As this latter parameter set better reflects the photon dose response curve at higher doses, this dataset also is expected to result in more accurate LEM predictions for high-LET radiation; the corresponding comparison is shown in Figure 2. Although the detailed shape of the experimental dose response curves is not predicted by the LEM, at least the order of magnitude of the spread of sensitivities between photon and high LET radiation is correctly predicted.
Contribution of Different Spatial Scales: DSB-Clustering vs. Increased Yield
The direct comparison of LEM predictions for HTB140 cells based on the two different data sets is shown in Figure 3. For protons, no substantial difference is observed for the different input data sets. In contrast, for carbon ion irradiation, the curves significantly differ, but already for β = 0 a clearly increased RBE is predicted. This can be attributed to the increased DSB yield resulting from the extremely high local doses in the track center of the particle trajectories, i.e., it is a consequence of processes at the nm-scale. This increased yield is in line with predictions of other models like e.g., PARTRAC [54].
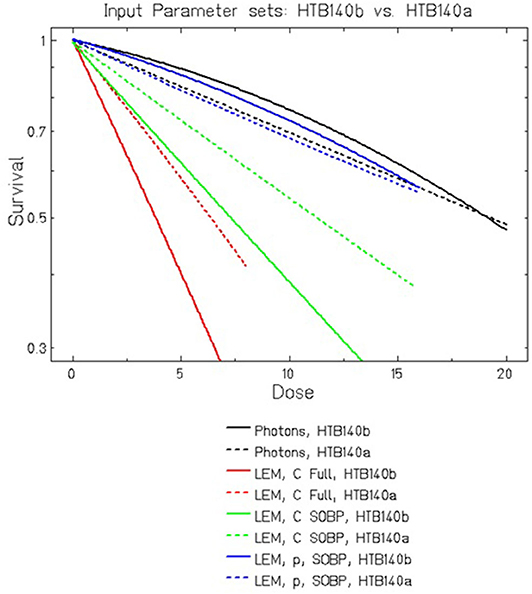
Figure 3. Comparison of LEMIV model calculations for cell killing of HTB140 cells using two different input data sets (see Table 1). For carbon ions at high LET, even in the case of βphoton = 0 Gy−2 a substantially increased RBE is predicted, which is further enhanced if βphoton > 0 is assumed.
In that respect, the LEM substantially differs from the MKM which would predict RBE = 1 in the case of β = 0 according to Equation (2). If a small β is assumed, as in the parameter set HTB140b, according to the LEM the RBE is further increased, which then can be attributed to the higher lethality of clustered DSB as compared to isolated DSB. This higher lethality is a direct consequence of β > 0 according to the LEM concept, reflecting processes at the μm scale. In general, RBE is due to contributions from multiple coexisting scales.
Use of Focused Low-LET Proton Beams to Mimic High-LET
The role of the contribution on different spatial scales has been further demonstrated recently using a special irradiation technique based on focused low-LET proton beams [17]. The basic idea of the experimental concept is to mimic high-LET radiation by focusing low-LET radiation to a small spot of about micrometer dimension, which reflects both the size of important biological structures within the cell as well as typical extensions of the radial dose distribution of high LET light ions. The experiments demonstrated that for identical average macroscopic doses, focused low-LET protons show a substantially increased effectiveness as compared to conventional broad beam irradiation. In the framework of the LEM concept, this is attributed to the clustering of DSB within giant loop chromatin compartments of about 0.5 μm size.
However, when comparing to e.g., carbon ions with the same energy deposition per spot, protons are still less effective. This difference arises from the extremely high local doses in the track centers of carbon ions, which lead to additional DSBs. Focusing low-LET protons to micrometer spots, however, is not sufficient to reach these high local doses – it would require to focus the protons on nm-sized spots, which is technically not feasible.
In Figure 4 we show the LEM predictions of RBE for a hypothetic cell line characterized by typical L-Q parameters for the impact of spot size of low LET protons. The figure clearly shows the transition to elevated RBE levels as soon as the spot size is decreased below ~1 μm. The figure also includes the information about the RBE that is expected for carbon ions for the same mean dose (arrow); the difference between the carbon ion and focused proton RBE values at small spot sizes is attributed to the increased DSB yield of C-ions as compared to protons, as explained above.
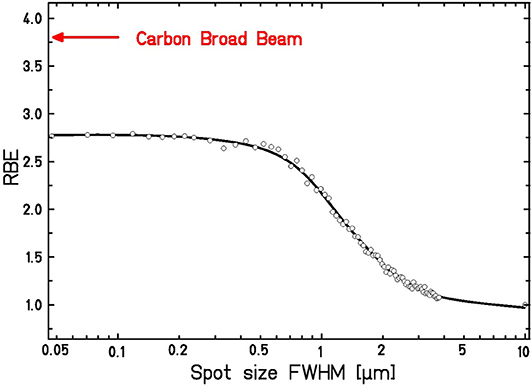
Figure 4. Expected dependence of RBE for a hypothetic cell line on the spot size of focused high-energy, low-LET protons at a mean dose of 1.0 Gy. For comparison, the RBE for broad beam carbon ion irradiation is shown. Calculations are based on the LEM input parameters: αPhoton = 0.1 Gy−1, βPhoton = 0.05 Gy−2, Dt = 8 Gy, Ep = 19.95 MeV, LETp = 2.67 keV/μm, EC = 4.05 MeV/u, LETC = 338 keV/μm.
Validation in-vivo: Tolerance of the Rat Spinal Cord to Proton Irradiation
Model validation based on in-vitro data as shown e.g. in section Comparison to Experimental Data at INFN-LNS and in Figure 2 is an important first step in testing a model that is considered for application in treatment planning for ion beam therapy. For the close link to the patient treatments, however, the validation by means of in-vivo experimental animal data is indispensable. First tests of the LEM in such preclinical experiments have been performed for carbon-ion irradiation of the skin of minipigs [55]. Larger systematic studies have then been performed based on the analysis of tolerance doses for the rat spinal cord [35, 56]. These studies also clearly demonstrated the better accuracy of the LEM IV as compared to the LEM I in particular in the critical high-dose/high-LET region. In the entrance channel at low LET, however, some systematic underestimation of the RBE by the LEM IV is observed. In order to clarify whether this is a general systematic effect at lower LET values or whether it is ion specific, comparison to data obtained with proton beams is an important pillar for the validation of the LEM.
Figure 5 shows a comparison of the LEM predictions with experimental data reported by Saager et al. for irradiation in typical therapy-like conditions, i.e., using a proton SOBP of 6 cm width located at 7–13 cm depth in water. RBE values were determined at different positions within the SOBP, corresponding to different LET values. LEM predictions are in reasonable agreement with the experimental data, demonstrating that, in general, the LEM IV allows RBE predictions also for lighter ions with correspondingly lower LET, and thus the systematic deviations found for carbon ions at low LET are specific for carbon ions and likely are a consequence of the high energy rather than the low LET itself.
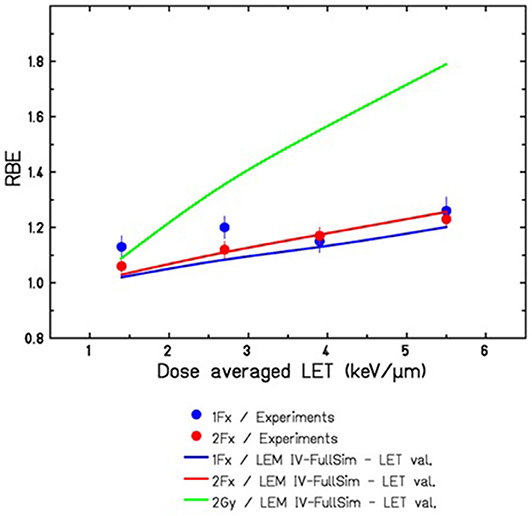
Figure 5. Comparison of LEMIV based RBE predictions for tolerance doses of the rat spinal cord in a 60 mm proton SOBP ranging from 70 to 130 mm water-equivalent depths. Experimental data for 1Fx and 2Fx were taken from [57], corresponding to TD50 values ranging from 21.7 to 19.5 Gy for 1Fx and from 32.3 to 27.9 Gy for 2Fx irradiation. The full green line indicates the expected RBE for lower doses of 2 Gy/Fx, as it is typically used in the therapeutic situation.
Both experimental data and model predictions shown in Figure 5 are in good agreement and support that also for protons at the distal edge of the SOBP elevated RBE values are observed, which are significantly above the RBE value of 1.1 that is currently assumed in treatment planning for proton therapy. Here, it has to be taken into account that the data were obtained for comparably high doses in 1 fraction (Fx) acute and 2Fx split-dose irradiations. Since the RBE is expected to further rise with decreasing doses, we have included in Figure 5 also the LEM IV prediction of RBE for the typical 2 Gy/Fx dose that is frequently used in therapy. Substantially higher RBE values are expected for these lower doses. Experiments with higher fraction number and correspondingly lower doses are currently under way at the Heidelberg ion beam therapy facility HIT, and the results will represent an important data set to further validate the LEM for application to proton irradiation.
Accuracy of as Descriptor for RBE
Potentially increased RBE values in proton therapy which are above the standard value of 1.1 that is currently used in treatment planning [58] are under vivid debate now since many years [26–28]. A wide range of models has been developed for taking these increased RBE values into account. In contrast to models like the MKM and LEM these models for proton RBE are mostly empirical and parameterize the increase of RBE as a function of . Rorvik et al. have compared 13 of these models, demonstrating that even when starting from identical conditions (i.e., assuming identical αX/βX-ratios for photon radiation) for all models there is a wide spread in the predicted RBE values. This might partially be because different sets of experimental data are used to calibrate the models. One important aspect in that respect is the use of as a predictor of RBE. As we have recently shown, values are not necessarily a good predictor of RBE, and for conditions resulting in the same but based on different actual distributions the expected RBE values might also substantially differ [59]. In order to illustrate this, Figure 6 shows RBE values along a typical SOBP as predicted with the LEM in conjunction with the TRiP98 treatment planning environment for protons and carbon ions in comparison to monoenergetic beams with identical . For both particle types the SOBP values differ from those expected for the corresponding monoenergetic beam under track-segment conditions, although in opposite directions. Whereas, for protons higher RBE values are expected in the case of SOBP, for carbon ions these values are lower. This can be explained by the non-linearities of the RBE(LET) relationship under track-segment conditions [59]. The LET values relevant for mixed SOBP fields in the proton case cover the LET region to the left side of the RBE maximum, and thus the non-linear increase of RBE with LET leads to correspondingly higher weights of the high-LET contribution. In contrast, highest LET values in the carbon case are linked to the LET region to the right side of the RBE maximum, where RBE already drops as a result of overkill effects. Therefore, the highest LET components get an effectively lower weight in the energy/LET spectra representative for typical carbon-ion treatment fields, and in general cannot be considered as a unique predictor of RBE.
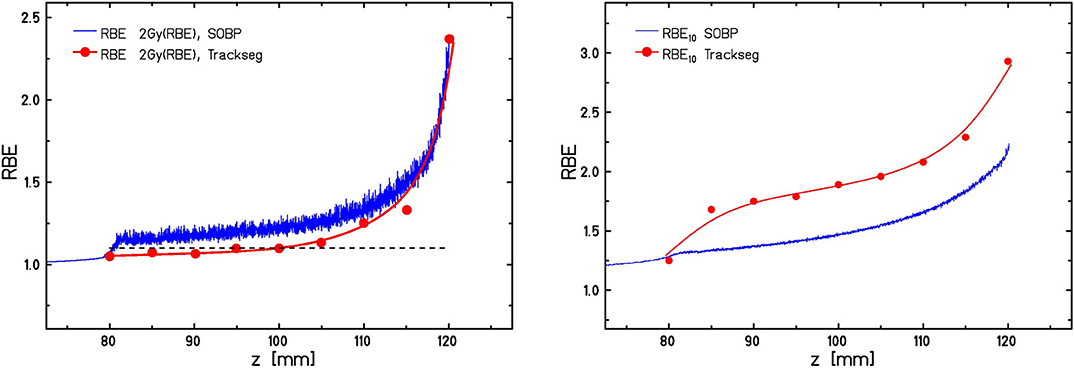
Figure 6. Comparison of predicted RBE10 values for HTB177 cells along a 40 mm proton SOBP (left) and carbon SOBP (right) from 80 to 120 mm with RBE10 values expected for track segment conditions (i.e., monoenergetic beams) at the same dose mean LET. The dashed line in the left panel indicates the RBE of 1.1, which is currently used in treatment planning for proton therapy.
Discussion
In Figure 2 we have demonstrated that the LEM is able to predict the general features of RBE for different cell lines and different radiation qualities. For monoenergetic carbon ions, the predictions significantly depend on the assumed depth position of the cell layer. Within the experimental uncertainties of positioning (estimated to be in the order of +/− 0.1 mm), however, the model predictions agree with the experimental data. Systematic underestimation of RBE has been observed for protons for doses > 2 Gy, whereas for doses ≤ 2 Gy the predicted effectiveness is still compatible with the experimental data. Previous comparisons of the LEM predictions for protons using a larger database have revealed mean deviations of <10% in the LET range up to 8–10 keV/μm [31], although individual experiments can show larger deviations similar to those seen in Figure 2.
Concerning the different cell lines, largest deviations between model prediction and experimental data are observed for the extremely radioresistant cell line HTB140. The experimental data indicate a trend to even negative bending of the dose response curves; this trend is not reflected by the LEM, although the order of magnitude of predicted RBE for the highest LET is compatible with the experimental data. One possible explanation for the somewhat unusual shape of the dose response curve could be the composition of subpopulations with substantially different radiosensitivities, as it occurs e.g., also for mixed oxic and hypoxic populations [60].
Concerning the general systematic dependencies, the results shown in Figures 3, 4 clearly demonstrate the impact of clustering effects on different spatial scales in the LEM; this aspect is particularly relevant for comparison with other models. Since apart from protons the LEM has been shown to also correctly reflect the systematic dependencies for focused carbon ions and lithium ions [17], which further supports the impact of clustering on different spatial scales. The corresponding contributions as a function of LET have been disentangled in more detail in Friedrich et al. [17].
The experiments using focused low-LET proton beams to mimic and explain high-LET effects represent an important pillar for benchmarking effect models and in particular for the validation of the LEM concept. However, although the LEM obviously correctly predicts the fundamental dependencies of RBE, its underlying concept is not necessarily the only possibility to explain the increased effectiveness. It would thus be of particular interest to compare also other models like the MKM or Repair-Misrepair-Fixation (RMF) model to the focused ion beam experiments and to analyze their predictive capacity for these conditions.
Apart from cell killing after acute ion beam radiation, the concept of damage clustering on the nm and μm level have been successfully applied also to other radiation types like high- and low-energy photon radiation [36, 61], to different conditions like e.g., cell cycle dependence of radiosensitivity [38] or the impact of dose rate [62] and to different end points like e.g., rejoining of DSB [37, 63]. As also in these cases in general good agreement between model predictions and experimental data has been found, this is taken as further support for the general concepts on which the LEM IV is based. The independent applicability to multiple endpoints and radiation phenomena within the same model framework using the same model parameters is a strong indication for the validity of the underlying mechanisms.
Modeling the effects of small focused beams might be in general also relevant for novel applications of so-called “spatially fractionated” irradiation like e.g., grid therapy. This therapy is characterized by extremely inhomogeneous lateral dose profiles, where peaks with very high doses are interlaced with valleys of almost zero dose. Both low-LET photon and proton irradiation as well as higher LET ion beam irradiation have been proposed in that respect [64–67]. Although this approach aims at reducing side effects in normal tissue by sparing the valley regions, the complementary higher effectiveness that is expected in the peak region will be relevant for a full characterization of this application. A general understanding of the impact on the biological effectiveness is thus of importance, but will presumably also require including geometrical properties of tissue repair processes that are not included in any RBE radiation effect model nor in any normal tissue complication model so far. This also requires correct modeling of in-vivo experimental systems that are frequently used to investigate the effectiveness of grid therapy [66]. An accurate prediction of biological effects in-vivo using standard broad beam irradiation is therefore a prerequisite for applications to more complex scenarios like grid therapy. Whereas, effects in the SOBP region of carbon ions are predicted by the LEM IV with reasonable accuracy, there is a trend to systematic underestimation of RBE in the entrance channel, i.e., at high energies [35]. Systematic comparison with larger data bases for in-vitro cell kill studies are currently ongoing in order to accurately quantify these deviations and to implement corresponding model improvements.
The correct representation of RBE also in the case of mixed fields, as they typically occur in the patient treatment situation, is of utmost importance in treatment planning. As shown in Figure 6, details of the energy/LET/particle spectrum can affect the RBE predicted by the LEM when compared to the corresponding mean values or single values representing track segment conditions. In that respect, it would be highly interesting to further investigate potential differences that would result from the corresponding microdosimetric concepts. For example, the approach using weighting functions makes use of the detailed y-spectrum, whereas the MKM uses the corresponding dose-mean y-values. Since y essentially represents a 1-dimensional representation of track structure, similar to LET, one would expect here also similar differences as observed in the case of dose-mean LET. A direct comparison and analysis of potential differences between these two approaches could shed light on the impact of the shape of distributions from the microdosimetric perspective.
Outlook
Comparing the two approaches used in the current and the accompanying paper, the major difference is that the modeling approach explicitly considers different spatial scales, whereas the microdosimetric approach focuses on aspects of the micrometer scale. It will thus be of major interest to further analyse the impact and relevance of the different scales for different irradiation scenarios. It would be particularly helpful to use the different approaches to develop hypothesis and specific scenarios that allow discriminating between the different aspects. In that respect, extension / translation of the microdosimetric concepts to the nanometer scale as described e.g., by Grosswendt [68], Selva et al. [69], and Mazzucconi et al. [70] are of further interest for a comparison with the LEM approach.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
MS drafted the manuscript. MS and TF performed the LEM calculations. AR-F and IP supplied the experimental data obtained at the INFN-LNS facility and all relevant information for the model comparison. GM and PC contributed to the microdosimetry aspects. All authors contributed to improvements/corrections and approved the final version.
Funding
This work was supported by the European HORIZON 2020 ENSAR2 project, GRANT AGREEMENT NUMBER: 654002.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
2. Schulz-Ertner D, Tsujii H. Particle radiation therapy using proton and heavier ion beams. J Clin Oncol. (2007) 25:953–64. doi: 10.1200/JCO.2006.09.7816
3. Schardt D, Elsässer T, Schulz-Ertner D. Heavy-ion tumor therapy: Physical and radiobiological benefits. Rev Mod Phys. (2010) 82:383–425. doi: 10.1103/RevModPhys.82.383
4. Blakely EA, Tobias CA, Yang TC, Smith KC, Lyman JT. Inactivation of human kidney cells by high-energy monoenergetic heavy-ion beams. Radiat Res. (1979) 80:122–60. doi: 10.2307/3575121
5. Tobias CA, Blakely EA, Alpen EL, Castro JR, Ainsworth EJ, Curtis SB, et al. Molecular and cellular radiobiology of heavy ions. Int J Radiat Oncol Biol Phys. (1982) 8:2109–20. doi: 10.1016/0360-3016(82)90554-5
6. Kraft G. Tumor therapy with heavy charged particles. Prog Part Nucl Phys. (2000) 45:S473–544. doi: 10.1016/S0146-6410(00)00112-5
8. Friedrich T, Scholz U, Elsässer T, Durante M, Scholz M. Systematic analysis of RBE and related quantities using a database of cell survival experiments with ion beam irradiation. J Radiat Res. (2013) 54:494–514. doi: 10.1093/jrr/rrs114
9. Tobias CA, Blakely EA, Chang PY, Lommel L, Roots R. Response of sensitive human ataxia and resistant T-1 cell lines to accelerated heavy ions. Br J Cancer Suppl. (1984) 6:175–85. doi: 10.2172/7005318
10. Weyrather WK, Ritter S, Scholz M, Kraft G. RBE for carbon track-segment irradiation in cell lines of differing repair capacity. Int J Radiat Biol. (1999) 75:1357–64. doi: 10.1080/095530099139232
11. Furusawa Y, Fukutsu K, Aoki M, Itsukaichi H, Eguchi-Kasai K, Ohara H, et al. Inactivation of aerobic and hypoxic cells from three different cell lines by accelerated (3)He-, (12)C- and (20)Ne-ion beams. Radiat Res. (2000) 154:485–96. doi: 10.1667/0033-758720001540485:IOAAHC2.0.CO;2
12. Ward JF. Mechanisms of DNA repair and their potential modification for radiotherapy. Int J Radiat Oncol Biol Phys. (1986) 12:1027–32. doi: 10.1016/0360-30168690220-8
13. Nikjoo H, Uehara S, Wilson WE, Hoshi M, Goodhead DT. Track structure in radiation biology: theory and applications. Int J Radiat Biol. (1998) 73:355–64. doi: 10.1080/095530098142176
14. Goodhead DT. Initial events in the cellular effects of ionizing radiations: clustered damage in DNA. Int J Radiat Biol. (1994) 65:7–17. doi: 10.1080/09553009414550021
15. Neary GJ, Preston RJ, Savage JR. Chromosome aberrations and the theory of RBE. 3. Evidence from experiments with soft x-rays, and a consideration of the effects of hard x-rays. Int J Radiat Biol Relat Stud Phys Chem Med. (1967) 12:317–45. doi: 10.1080/09553006714550881
16. Munro TR. The relative radiosensitivity of the nucleus and cytoplasm of Chinese hamster fibroblasts. Radiat Res. (1970) 42:451–70. doi: 10.2307/3572962
17. Friedrich T, Ilicic K, Greubel C, Girst S, Reindl J, Sammer M, et al. DNA damage interactions on both nanometer and micrometer scale determine overall cellular damage. Sci Rep. (2018) 8:16063. doi: 10.1038/s41598-018-34323-9
18. Wambersie A, Hendry JH, Andreo P, DeLuca PM, Gahbauer R, Menzel H, et al. The RBE issues in ionbeam therapy: conclusions of a joint IAEA/ICRU working group regarding quantities and units. Radiat Prot Dosimetry. (2006) 122:463–70. doi: 10.1093/rpd/ncl447
19. Hawkins RB. A microdosimetric-kinetic model of cell death from exposure to ionizing radiation of any LET, with experimental and clinical applications. Int J Radiat Biol. (1996) 69:739–55. doi: 10.1080/095530096145481
20. Hawkins RB. A microdosimetric-kinetic model for the effect of non-poisson distribution of lethal lesions on the variation of RBE with LET. Radiat Res. (2003) 160:61–9. doi: 10.1667/RR3010
21. Scholz M, Kellerer AM, Kraft-Weyrather W, Kraft G. Computation of cell survival in heavy ion beams for therapy. The model and its approximation. Radiat Environ Biophys. (1997) 36:59–66. doi: 10.1007/s004110050055
22. Elsässer T, Weyrather WK, Friedrich T, Durante M, Iancu G, Krämer M, et al. Quantification of the relative biological effectiveness for ion beam radiotherapy: direct experimental comparison of proton and carbon ion beams and a novel approach for treatment planning. Int J Radiat Oncol Biol Phys. (2010) 78:1177–83. doi: 10.1016/j.ijrobp.2010.05.014
23. Friedrich T, Scholz U, Elsässer T, Durante M, Scholz M. Calculation of the biological effects of ion beams based on the microscopic spatial damage distribution pattern. Int J Radiat Biol. (2012) 88:103–7. doi: 10.3109/09553002.2011.611213
24. van der Schaaf A, Langendijk JA, Fiorino C, Rancati T. Embracing phenomenological approaches to normal tissue complication probability modeling: a question of method. Int J Radiat Oncol Biol Phys. (2015) 91:468–71. doi: 10.1016/j.ijrobp.2014.10.017
25. Olsen CH, Ottesen JT, Smith RC, Olufsen MS. Parameter subset selection techniques for problems in mathematical biology. Biol Cybern. (2019) 113:121–38. doi: 10.1007/s00422-018-0784-8
26. Paganetti H. Relative biological effectiveness (RBE) values for proton beam therapy. Variations as a function of biological endpoint, dose, and linear energy transfer. Phys Med Biol. (2014) 59:R419–72. doi: 10.1088/0031-9155/59/22/R419
27. Peeler CR, Mirkovic D, Titt U, Blanchard P, Gunther JR, Mahajan A, et al. Clinical evidence of variable proton biological effectiveness in pediatric patients treated for ependymoma. Radiother Oncol. (2016) 121:395–401. doi: 10.1016/j.radonc.2016.11.001
28. Jones B. Why RBE must be a variable and not a constant in proton therapy. Br J Radiol. (2016) 89:20160116. doi: 10.1259/bjr.20160116
29. Gensheimer MF, Yock TI, Liebsch NJ, Sharp GC, Paganetti H, Madan N, et al. In vivo proton beam range verification using spine MRI changes. Int J Radiat Oncol Biol Phys. (2010) 78:268–75. doi: 10.1016/j.ijrobp.2009.11.060
30. Rørvik E, Fjæra LF, Dahle TJ, Dale JE, Engeseth GM, Stokkevåg CH, et al. Exploration and application of phenomenological RBE models for proton therapy. Phys Med Biol. (2018) 63:185013. doi: 10.1088/1361-6560/aad9db
31. Grün R, Friedrich T, Krämer M, Scholz M. Systematics of relative biological effectiveness measurements for proton radiation along the spread out Bragg peak: experimental validation of the local effect model. Phys Med Biol. (2017) 62:890–908. doi: 10.1088/1361-6560/62/3/890
32. Krämer M, Scifoni E, Schuy C, Rovituso M, Tinganelli W, Maier A, et al. Helium ions for radiotherapy? Physical and biological verifications of a novel treatment modality. Med Phys. (2016) 43:1995. doi: 10.1118/1.4944593
33. Sokol O, Scifoni E, Tinganelli W, Kraft-Weyrather W, Wiedemann J, Maier A, et al. Oxygen beams for therapy: advanced biological treatment planning and experimental verification. Phys Med Biol. (2017) 62:7798–813. doi: 10.1088/1361-6560/aa88a0
34. Saager M, Glowa C, Peschke P, Brons S, Scholz M, Huber PE, et al. Carbon ion irradiation of the rat spinal cord: dependence of the relative biological effectiveness on linear energy transfer. Int J Radiat Oncol Biol Phys. (2014) 90:63–70. doi: 10.1016/j.ijrobp.2014.05.008
35. Saager M, Glowa C, Peschke P, Brons S, Grün R, Scholz M, et al. Fractionated carbon ion irradiations of the rat spinal cord: comparison of the relative biological effectiveness with predictions of the local effect model. Radiat Oncol. (2020) 15:6. doi: 10.1186/s13014-019-1439-1
36. Friedrich T, Durante M, Scholz M. Modeling cell survival after photon irradiation based on double-strand break clustering in megabase pair chromatin loops. Radiat Res. (2012) 178:385–94. doi: 10.1667/RR2964.1
37. Tommasino F, Friedrich T, Scholz U, Taucher-Scholz G, Durante M, Scholz M. A DNA double-strand break kinetic rejoining model based on the local effect model. Radiat Res. (2013) 180:524–38. doi: 10.1667/RR13389.1
38. Hufnagl A, Herr L, Friedrich T, Durante M, Taucher-Scholz G, Scholz M. The link between cell-cycle dependent radiosensitivity and repair pathways: a model based on the local, sister-chromatid conformation dependent switch between NHEJ and HR. DNA Repair. (2015) 27:28–39. doi: 10.1016/j.dnarep.2015.01.002
39. Kase Y, Kanai T, Matsumoto Y, Furusawa Y, Okamoto H, Asaba T, et al. Microdosimetric measurements and estimation of human cell survival for heavy-ion beams. Radiat Res. (2006) 166:629–38. doi: 10.1667/RR0536.1
40. Inaniwa T, Furukawa T, Kase Y, Matsufuji N, Toshito T, Matsumoto Y, et al. Treatment planning for a scanned carbon beam with a modified microdosimetric kinetic model. Phys Med Biol. (2010) 55:6721–37. doi: 10.1088/0031-9155/55/22/008
41. Hawkins RB. The relationship between the sensitivity of cells to high-energy photons and the RBE of particle radiation used in radiotherapy. Radiat Res. (2009) 17:761–76. doi: 10.1667/RR1655.1
42. Kase Y, Kanai T, Matsufuji N, Furusawa Y, Elsässer T, Scholz M. Biophysical calculation of cell survival probabilities using amorphous track structure models for heavy-ion irradiation. Phys Med Biol. (2008) 53:37–59. doi: 10.1088/0031-9155/53/1/003
43. Waligórski MP, Hollmark M, Gudowska I, Lesia J. Cellular parameters and RBE-LET dependences for modelling heavy-ion radiotherapy. Radiother Oncol. (2004) 73(Suppl. 2):S173–5. doi: 10.1016/S0167-81400480043-4
44. Frese MC, Yu VK, Stewart RD, Carlson DJ. A mechanism-based approach to predict the relative biological effectiveness of protons and carbon ions in radiation therapy. Int J Radiat Oncol Biol Phys. (2012) 8:442–50. doi: 10.1016/j.ijrobp.2011.06.1983
45. Kamp F, Cabal G, Mairani A, Parodi K, Wilkens JJ, Carlson DJ. Fast biological modeling for voxel-based heavy ion treatment planning using the mechanistic repair-misrepair-fixation model and nuclear fragment spectra. Int J Radiat Oncol Biol Phys. (2015) 93:557–68. doi: 10.1016/j.ijrobp.2015.07.2264
46. Stewart RD, Carlson DJ, Butkus MP, Hawkins R, Friedrich T, Scholz M. A comparison of mechanism-inspired models for particle relative biological effectiveness (RBE). Med Phys. (2018) 45:e925–52. doi: 10.1002/mp.13207
47. Petrović I, Ristić-Fira A, Todorović D, Korićanac L, Valastro L, Cirrone P, et al. Response of a radioresistant human melanoma cell line along the proton spread-out Bragg peak. Int J Radiat Biol. (2010) 86:742–51. doi: 10.3109/09553002.2010.481322
48. Petrović I, Ristić-Fira A, Keta O, Petković V, Petringa G, Cirrone P, et al. A radiobiological study of carbon ions of different linear energy transfer in resistant human malignant cell lines. Int J Radiat Biol. BioRxiv [Preprint]. (2020).
49. Romano F, Cirrone GA, Cuttone G, Rosa FD, Mazzaglia SE, Petrovic I, et al. A monte carlo study for the calculation of the average linear energy transfer (LET) distributions for a clinical proton beam line and a radiobiological carbon ion beam line. Phys Med Biol. (2014) 59:2863–82. doi: 10.1088/0031-9155/59/12/2863
50. Krämer M, Scholz M. Treatment planning for heavy-ion radiotherapy: calculation and optimization of biologically effective dose. Phys Med Biol. (2000) 45:3319–30. doi: 10.1088/0031-9155/45/11/314
51. Krämer M, Scholz M. Rapid calculation of biological effects in ion radiotherapy. Phys Med Biol. (2006) 51:1959–70. doi: 10.1088/0031-9155/51/8/001
52. Weber U, Kraft G. Design and construction of a ripple filter for a smoothed depth dose distribution in conformal particle therapy. Phys Med Biol. (1999) 44:2765–75. doi: 10.1088/0031-9155/44/11/306
53. Petrović I, Ristić-Fira A, Todorović D, Valastro L, Cirrone P, Cuttone G. Radiobiological analysis of human melanoma cells on the 62 MeV CATANA proton beam. Int J Radiat Biol. (2006) 82:251–65. doi: 10.1080/09553000600669859
54. Friedland W, Dingfelder M, Kundrát P, Jacob P. Track structures, DNA targets and radiation effects in the biophysical monte carlo simulation code PARTRAC. Mutat Res. (2011) 711:28–40. doi: 10.1016/j.mrfmmm.2011.01.003
55. Zacharias T, Dörr W, Enghardt W, Haberer T, Krämer M, Kumpf R, et al. Acute response of pig skin to irradiation with 12C-ions or 200 kV X-rays. Acta Oncol. (1997) 36:637–42. doi: 10.3109/02841869709001328
56. Karger CP, Peschke P, Sanchez-Brandelik R, Scholz M, Debus J. Radiation tolerance of the rat spinal cord after 6 and 18 fractions of photons and carbon ions: experimental results and clinical implications. Int J Radiat Oncol Biol Phys. (2006) 66:1488–97. doi: 10.1016/j.ijrobp.2006.08.045
57. Saager M, Peschke P, Brons S, Debus J, Karger CP. Determination of the proton RBE in the rat spinal cord: Is there an increase towards the end of the spread-out Bragg peak? Radiother Oncol. (2018) 128:115–20. doi: 10.1016/j.radonc.2018.03.002
58. ICRU Report No. 78: Prescribing, Recording, and Reporting Proton-Beam Therapy. Bethesda, MD: International Commission on Radiation Units and Measurements Journal of the International Commission on Radiation Units and Measurements. (2007).
59. Grün R, Friedrich T, Traneus E, Scholz M. Is the dose-averaged LET a reliable predictor for the relative biological effectiveness? Med Phys. (2019) 46:1064–74. doi: 10.1002/mp.13347
60. Lindblom E, Dasu A, Lax I, Toma-Dasu I. Survival and tumour control probability in tumours with heterogeneous oxygenation: a comparison between the linear-quadratic and the universal survival curve models for high doses. Acta Oncol. (2014) 53:1035–40. doi: 10.3109/0284186X.2014.925582
61. Friedrich T, Durante M, Scholz M. Modeling cell survival after irradiation with ultrasoft X rays using the giant loop binary lesion model. Radiat Res. (2014) 181:485–94. doi: 10.1667/RR13518.1
62. Herr L, Friedrich T, Durante M, Scholz M. A model of photon cell killing based on the spatio-temporal clustering of DNA damage in higher order chromatin structures. PLoS ONE. (2014) 9:e83923. doi: 10.1371/journal.pone.0083923
63. Tommasino F, Friedrich T, Scholz U, Taucher-Scholz G, Durante M, Scholz M. Application of the local effect model to predict DNA double-strand break rejoining after photon and high-LET irradiation. Radiat Prot Dosimetry. (2015) 166:66–70. doi: 10.1093/rpd/ncv164
64. Dilmanian FA, Eley JG, Krishnan S. Minibeam therapy with protons and light ions: physical feasibility and potential to reduce radiation side effects and to facilitate hypofractionation. Int J Radiat Oncol Biol Phys. (2015) 92:469–74. doi: 10.1016/j.ijrobp.2015.01.018
65. Prezado Y, Jouvion G, Guardiola C, Gonzalez W, Juchaux M, Bergs J, et al. Tumor control in RG2 glioma-bearing rats: a comparison between proton minibeam therapy and standard proton therapy. Int J Radiat Oncol Biol Phys. (2019) 104:266–71. doi: 10.1016/j.ijrobp.2019.01.080
66. Girst S, Greubel C, Reindl J, Siebenwirth C, Zlobinskaya O, Walsh DW, et al. Proton minibeam radiation therapy reduces side effects in an in vivo mouse ear model. Int J Radiat Oncol Biol Phys. (2016) 95:234–41. doi: 10.1016/j.ijrobp.2015.10.020
67. Billena C, Khan AJ. A current review of spatial fractionation: back to the future. Int J Radiat Oncol Biol Phys. (2019) 104:177–87. doi: 10.1016/j.ijrobp.2019.01.073
68. Grosswendt B. Nanodosimetry, from radiation physics to radiation biology. Radiat Prot Dosimetry. (2005) 115:1–9. doi: 10.1093/rpd/nci152
69. Selva A, De Nadal V, Cherubini R, Colautti P, Conte V. Towards the use of nanodosimetry to predict cell survival. Radiat Prot Dosimetry. (2019) 183:192–6. doi: 10.1093/rpd/ncy274
Keywords: relative biological effectiveness (RBE), biophysical modeling, ion beam therapy, microdosimetry, heavy ion
Citation: Scholz M, Friedrich T, Magrin G, Colautti P, Ristić-Fira A and Petrović I (2020) Characterizing Radiation Effectiveness in Ion Beam Therapy Part I: Introduction and Biophysical Modeling of RBE Using the LEMIV. Front. Phys. 8:272. doi: 10.3389/fphy.2020.00272
Received: 03 April 2020; Accepted: 18 June 2020;
Published: 14 August 2020.
Edited by:
Yolanda Prezado, INSERM U1021 Signalisation normale et pathologique de l'embryon aux thérapies innovantes des cancers, FranceReviewed by:
Till Tobias Böhlen, Paul Scherrer Institut (PSI), SwitzerlandDimitris Emfietzoglou, University of Ioannina, Greece
Copyright © 2020 Scholz, Friedrich, Magrin, Colautti, Ristić-Fira and Petrović. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michael Scholz, bS5zY2hvbHpAZ3NpLmRl
 Michael Scholz
Michael Scholz Thomas Friedrich
Thomas Friedrich Giulio Magrin
Giulio Magrin Paolo Colautti
Paolo Colautti Aleksandra Ristić-Fira
Aleksandra Ristić-Fira Ivan Petrović
Ivan Petrović