- 1Dipartimento di Scienza e Alta Tecnologia, Center for Nonlinear and Complex Systems, Università degli Studi dell'Insubria, Como, Italy
- 2Istituto Nazionale di Fisica Nucleare, Sezione di Milano, Milan, Italy
- 3NEST, Istituto Nanoscienze-Consiglio Nazionale delle Ricerche, Pisa, Italy
- 4Consiglio Nazionale delle Ricerche, Istituto dei Sistemi Complessi, Florence, Italy
- 5Istituto Nazionale di Fisica Nucleare, Sezione di Firenze, Florence, Italy
- 6Dipartimento di Fisica e Astronomia and CSDC, Universitá di Firenze, Sesto Fiorentino, Italy
In this review paper we survey recent achievements in anomalous heat diffusion, while highlighting open problems and research perspectives. First, we briefly recall the main features of the phenomenon in low-dimensional classical anharmonic chains and outline some recent developments in the study of perturbed integrable systems and the effect of long-range forces and magnetic fields. Selected applications to heat transfer in material science at the nanoscale are described. In the second part, we discuss of the role of anomalous conduction in coupled transport and describe how systems with anomalous (thermal) diffusion allow a much better power-efficiency trade-off for the conversion of thermal to particle current.
1. Introduction
Anomalous diffusion is a well-established concept in statistical physics and has been used to describe many diverse kinetic phenomena. Detailed insights have been gained by generalizing the motion of Brownian particles, as done for the continuous-time random walk and for Lèvy flights and walks. A formidable body of literature on the topic exists; we refer to, for example, Klages et al. [1] as well as the present issue for an overview.
The above particle models are based on a single-particle description, whereby a single walker performs a non-standard diffusive motion. How do the features of anomalous diffusion emerge when dealing with a many-body problem? What are the conditions for a statistical system composed of many interacting particles to yield effectively anomalous diffusion of particles or quasi-particles? Another question concerns how such anomalies in diffusion are related to transport and whether they can somehow be exploited to achieve some design principle, such as efficiency of energy conversion. In fact, although thermoelectric phenomena have been known for centuries, it is only recently that a novel point of view on the problem has emerged [2]. Generally speaking, the renewed research activity is motivated also by the possibility of applying the thermodynamics and statistical mechanics to nano- and micro-sized systems, with applications in molecular biology, micro-mechanics, nano-phononics, etc. This involves dealing with systems far from the thermodynamic limit, where fluctuations and interactions with the environment are critically relevant and need to be understood in detail.
In this article, we first review how anomalous energy diffusion arises in lattices of classical oscillators as a joint effect of non-linear forces and reduced dimensionality (and in this respect we will mostly discuss one-dimensional chains). This amounts to saying that the anomalous dynamics of energy carriers is an emergent feature stemming from correlations of the full many-body dynamics. As a consequence, Fourier's law breaks down: the motion of energy carriers is so correlated that they are able to propagate faster than diffusively. In the second part of the paper, we discuss how this feature influences coupled transport and how it can be used to enhance the efficiency of thermodiffusive processes.
We conclude our review of the multifaceted problem of heat transport in classical systems with a short summary of possible extensions to the quantum domain, with reference to related open problems that merit attention in the near future.
2. Anomalous Heat Transport in Classical Anharmonic Lattices
The presence of a heat conductivity that diverges with the system size in a chain of coupled non-linear oscillators was first pointed out in Lepri et al. [3, 4]. This marked the beginning of a research endeavor that, over more than two decades, has been devoted to understanding the mechanisms giving rise to anomalous transport in low-dimensional systems. Far from being a purely academic exercise, this research has unveiled the possibility of observing such peculiar effects in nanomaterials, such as nanotubes, nanowires, or graphene [5, 6]. Extended review articles on this problem have existed for many years [7, 8], while a collection of works about more recent achievements can be found in Lepri [9] and a review article [10] in the present issue. Here it is useful to first provide a short summary of the state of the art in the field, while the main part of the paper will focus on recent achievements that point to promising and challenging directions for future investigations.
In any model where anomalous transport has been observed, it emerges as a hydrodynamic effect due to a combination of reduced space dimensionality and conservation laws, yielding non-standard relaxation properties even in a linear response regime. As a reference we consider the basic class of models represented by a Hamiltonian of the following form:
Typical choices for the interaction include the famous Fermi-Pasta-Ulam-Tsingou (FPUT) potential, where , and the rotor (or Hamiltonian XY) model, where V(x) = VXY(x) ≡ 1 − cos x. With regard to conservation laws, in d = 1 anomalous transport has been generically observed in Hamiltonian models of type (1), where energy, momentum, and the “stretch” variable are conserved. It is worth recalling that any approach aiming to describe out-of-equilibrium conditions, such as stationary transport processes, has to be based on the hydrodynamic equations associated with such locally conserved quantities. One-dimensional oscillator models with only one conserved quantity, such as the Frenkel-Kontorova or ϕ4 models [11], or two conserved quantities, such as the rotor model [12, 13] or the discrete non-linear Schrödinger lattice [14, 15], instead show standard diffusive transport. Intuitively, this is due to the presence of scattering sources for acoustic waves propagating through the lattice induced by the presence of a local non-linear potential, which breaks translation invariance (i.e., momentum conservation). This argument does not apply to the rotor model, where only the stretch variable is not conserved, owing to the angular nature of the qn variables; in any case standard diffusion is allowed because of the boundedness of the cosine potential. Concerning dimensionality, in d = 3 normal diffusion regimes are expected to characterize heat transport in non-linear lattices. Only in d = 2 can one find evidence of a diverging heat conductivity that exhibits a logarithmic dependence on the system size L [16–18].
The main distinctive feature of anomalous heat transport in one-dimensional Hamiltonian models of anharmonic lattices is that the finite-size heat conductivity κ(L) diverges in the limit L → ∞ of a large system size [3] as
with 0 < γ ≤ 1 (the γ = 1 case corresponds to integrable models, such as the Toda lattice discussed in section 2.2). This implies that this transport coefficient is, in the thermodynamic limit, not well-defined. In the linear response regime, this is equivalent to finding that the equilibrium correlator of the energy current J(t) displays, for long times t, a non-integrable power-law decay of the form
with 0 ≤ δ < 1. Accordingly, the Green-Kubo formula yields an infinite value of the heat conductivity and allows one to establish the equivalence of the exponents, i.e., γ = δ, provided that the sound velocity is finite [4]. In Figure 1 we show two typical simulations of the FPUT model demonstrating the results above.
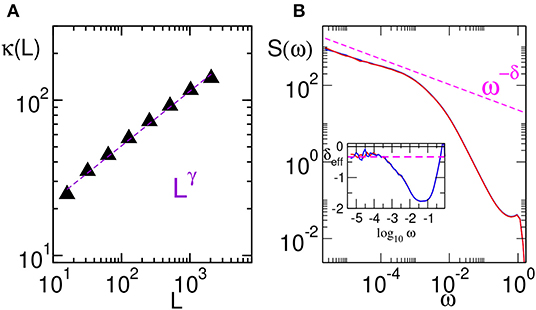
Figure 1. Anomalous thermal conductivity for the FPUT model with cubic and quartic potential terms (α = 0.25, β = 1): (A) finite-size conductivity measured in the non-equilibrium steady state; (B) power spectrum S(ω) of heat current fluctuations [i.e., the Fourier transform of 〈J(t)J(0)〉]. The long-time tail in (2) corresponds to a divergence ω−δ at small frequencies. The inset of (B) displays the logarithmic derivative δeff = dlog10S/dlog10ω. The data are compatible with δ = γ = 1/3 (dashed lines). Microcanonical simulations are performed at energy density 0.5.
The most basic issue of the anomalous feature relates to anomalous dynamical scaling of the equilibrium correlation of the hydrodynamic modes. A simple way to state this is that fluctuations of the conserved quantities with small wavenumber k evolve on time scales of order τ(k) ~ |k|−z. For standard diffusion one has z = 2. Within the non-linear fluctuating hydrodynamics approach it has been shown [19, 20] that models like (1) belong generically to the universality class of the famous Kardar-Parisi-Zhang (KPZ) equation, originally formulated in the context of growing interfaces. It is well-known that this equation in d = 1 is characterized by the dynamical exponent z = 3/2. The origin of this non-trivial dynamical exponent can be traced back to the non-linear interaction of long-wavelength modes. This leads to the prediction γ = (2 − z)/z = 1/3 (at least in the linear response regime), a value that should be largely universal, as confirmed by many numerical experiments.
The above consideration applies generically to anharmonic chains with three conservation laws [20]. There is, however, the possibility of having a different universality class depending on the number of conserved quantities [21] or on the non-linear coupling between the hydrodynamic modes [20]. For instance, model (1) with an even potential V(x) = V(−x) should belong to a different universality class having a different exponent γ. In fact, the precise value of γ is still somewhat controversial: the theoretical prediction from the mode-coupling approximation of the hydrodynamic theory yields γ = 1/2 [20, 22, 23], while kinetic theory yields γ = 2/5 [24], a value closer to that measured numerically [25, 26] (see also [27, 28] for related results on exactly solvable models). The existence of the two classes can be demonstrated either by direct measurement of the exponents [25] or via suitable changes of the thermodynamic parameters. For instance, a non-linear chain with a symmetric potential subject to a suitable pressure acting at its boundaries may exhibit a change from exponent γ = 1/2 to γ = 1/3 [29]. This observation is relevant to possible experimental verification of anomalous heat transport, as it indicates that the pressure or torque applied to any one-dimensional material should be taken into account for a correct comparison with theoretical predictions.
A physically intuitive way to describe anomalous heat transport is to think in terms of a Lévy walk, namely an ensemble of random walkers performing free ballistic steps with finite velocity for times that are power-law distributed [30]. This simple description accounts very well for many features of anharmonic lattices and fluids in various non-equilibrium settings [31–33]. For instance, energy perturbations propagate superdiffusively [31, 34, 35]: an initially localized perturbation of the energy broadens, and its variance grows in time as σ2 ∝ tη with η > 1. These empirical observations have a theoretical justification within the framework of non-linear fluctuating hydrodynamics. Indeed, the theory predicts a hydrodynamic “heat mode” that has the characteristic shape given by a Lévy-stable distribution [see [20, 36] for details]. Further support comes from mathematical results: superdiffusive behavior has been proven for one-dimensional infinite chains of harmonic oscillators undergoing stochastic collisions that conserve energy and momentum [37, 38]. In the same spirit, the more difficult case of non-linear oscillators with conservative noise has been discussed [39]. For exponential interactions (the Kac-van Moerbecke model), superdiffusion of energy has again been demonstrated, and a lower bound on the decay of the current correlation function has been obtained [40]. In reference [20] it is argued that such models should also belong to the KPZ class.
A related distinctive feature of anomalous transport is that the temperature profiles in non-equilibrium steady states are non-linear, even for vanishing applied temperature gradients [32, 41]. There is indeed a close connection with the fractional heat equation, which has been demonstrated and discussed in recent literature [10, 42].
2.1. The Importance of Being Small
As mentioned above, theoretical results on the problem of heat transport in anharmonic chains are based on the fundamental assumption that one should compute any relevant quantity in the limits L → ∞ and t → ∞, performed in that specific order. On the other hand, in any numerical simulation or for real low-dimensional heat conductors, such as nanowires, carbon nanotubes, polymers, or even thin fibers, one has to deal with finite size and finite time corrections. These can be controlled in a linear response regime if the mean free path of propagating excitations, λ, and their mean interaction time, τ, are such that λ ≪ L and τ ≪ t. It is a fact that when dealing with models of anharmonic chains, such control is often not guaranteed, mainly because of non-linear effects. This is a very relevant problem also for interpreting possible experimental verifications of anomalous transport in real systems as well as for designing nanomaterials that exhibit deviations from the standard diffusive conductivity.
In fact, severe finite size effects invariably arise when one tries to check predictions numerically. Very often, estimates of the relevant exponents γ and δ systematically deviate from the expected values and sometimes even seem to depend on parameters [43–46]. If universality were to hold (as we believe), these effects should be due to subleading corrective terms to the asymptotics that are still relevant on the scales accessible in simulations. Besides these issues, other unexpected effects arise. For instance, for the FPUT [47], Toda [43], and Kac-van Moerbecke [38] chains perturbed by conservative noise, the exponent γ increases with the noise strength. Apart from the problem of evaluating the precise exponents, this observation is quite surprising since it suggests that greater stochasticity in the model makes the system more diffusive, at least for finite systems.
Another example of finite size corrections being “amplified” by non-linear effects is the case of anharmonic chains with asymmetric potential, i.e., where V(x) ≠ V(−x) as in the FPUT model with α ≠ 0. As shown in Figure 1, both equilibrium and out-of-equilibrium measurements of the heat conductivity in the presence of an applied thermal gradient are usually consistent with KPZ scaling. However, in other temperature regimes Fourier's law appears to hold, i.e., thermal conductivity is constant over a large range of sizes [48]. This has been traced back to the relatively long relaxation time of mass inhomogeneities induced by the asymmetry of the interaction potential and acting as scatterers of phonons [48]. Actually, it was later shown in Wang et al. [49], Das et al. [50], and Chen et al. [51] that this is a strong finite size effect, as it persists for relatively large values of L and t. Yet, the expected theoretical prediction of a diverging heat conductivity can be recovered in simulations performed for sufficiently large values of L and t. It should be pointed out that all of these speculations are based on numerical results, and a theoretical approach capable of providing estimates for the combination of non-linear and finite size corrections to the hydrodynamics would be useful. Indeed, fluctuating hydrodynamics can provide some kind of prediction: subleading corrections to the leading asymptotic decay in (2) can be very large and decay very slowly [20].
There are other aspects to finite size effects. A remarkable example is the discrete non-linear Schrödinger equation, a well-known model for atomic condensates in periodic optical lattices. The model has two conserved quantities (energy and number density) and exhibits normal diffusive transport [14]. However, at very low temperatures another almost-conserved quantity (the phase difference between oscillators) appears, and for a finite chain and long times the dynamics is the same as that of a generic anharmonic model, leading to KPZ scaling of correlations and anomalous transport [52, 53]. Further unexpected features have been reported also in Xiong and Zhang [54], where the authors study this problem for the FPUT-β model (i.e., Equation 1) with V = VFPUT and α = 0) with an additional local, also called “pinning,” potential of the form
This term breaks translational invariance, making energy the sole conserved quantity. By varying the non-linear coupling β, one observes a crossover from ballistic transport, typical of an integrable model, to an anomalous diffusive regime governed by an exponent of the time correlation function, which corresponds to a value of γ ~ 0.2. The crossover occurs in the parameter region 0.1 < β < 1. Numerical simulations performed for a chain of a few thousands of oscillators show that further increasing β seems to yield an increasing γ. The overall outcome challenges the basic theoretical argument, which predicts that an anharmonic chain equipped with a local potential should exhibit normal diffusion. For the sake of completeness it is worth mentioning that in this paper the model under scrutiny is compared with the so-called ϕ4 model, where the non-linear term in Hamiltonian (1), i.e., , is replaced with . For this model one also observes, in the same parameter region, a crossover from a ballistic regime to an anomalous diffusive regime, but for β > 1 one eventually obtains numerical estimates yielding γ ~ 0, i.e., the expected diffusive behavior is recovered.
All of these results have a logical interpretation only if we take into account, once again, the role of finite size corrections combined with non-linearity. Actually, for the ϕ4 model there is no way to argue that a ballistic regime should be observed for any finite, even if small, value of β. The ballistic behavior observed in both models for β < 0.1 seems to suggest that for small non-linearities one needs to explore considerably larger chains and integrate the dynamics over much longer times than in Xiong and Zhang [54], before phonon-like waves in both chains may experience the scattering effects due to the local potential. Moreover, the weaker quadratic pinning potential of the original model seems to still be affected by finite size corrections, even in the region β > 1. A problem that should be investigated systematically is the dependence on β of the chain length and of the integration time necessary to recover standard diffusive transport, at least in the crossover region 0.1 < β < 1, where one can expect to perform proper numerical analysis in reasonable computational time.
2.2. Chimeras of Ballistic Regimes
In the light of the discussion in the previous subsection, one should not be surprised to encounter further non-linear chain models equipped with a pinning potential that exhibit a regime of ballistic transport of energy, compatible with a linearly divergent heat conductivity, κ(L) ~ L. Again, one might conjecture that this is due to the puzzling combination of non-linearity and finite size effects, although, as we shall see, the scenario that emerges is more intricate and interesting than the former statement indicates.
As a preliminary remark we recall that ballistic transport is the typical situation of an integrable Hamiltonian chain, the prototypical example of which is the harmonic lattice, with in Hamiltonian (1). It is worth pointing out that the addition of the harmonic pinning term (3) again keeps the harmonic chain integrable. With this in mind, it seems reasonable that for sufficiently small non-linearities both the FPUT-β and the ϕ4 chains, as discussed in the previous subsection, would exhibit a seemingly ballistic regime for β < 0.1 also in the presence of the pinning potential. Recovering the expected diffusive transport regime is a matter of simulating exceedingly large chains over extremely long times.
The special role played by the quadratic pinning potential (3) has been revealed also by a recent study of heat transport in the Toda chain [55]. It is worth recalling that the unpinned Toda chain is an integrable Hamiltonian model of the form (1) with V(x) = e−x + x − 1; in this model heat transport is ballistic due to the finite-speed propagation of solitons (rather than phonons, as in the harmonic chain). Toda solitons are localized non-linear excitations which are known to interact with each other by a non-dissipative diffusion mechanism; a soliton experiences a random sequence of spatial shifts as it moves through the lattice and interacts with other excitations without exchanging momentum [56]. In fact, the calculation of the transport coefficients by the Green-Kubo formula indicates the presence of a finite Onsager coefficient, which corresponds to a diffusive process on top of the dominant ballistic one [57, 58].
When the pinning term (3) is included, the Toda chain becomes chaotic, as one can easily see by measuring the spectrum of Lyapunov exponents [55]. Despite this, not only the energy but also the “center of mass”
are conserved quantities. The special role of the quadratic pinning potential (3) is evidenced by the fact that if one turns it into a quartic one, i.e., , the quantity hc is no longer conserved. Non-equilibrium simulations of the Toda chain with the addition of (3), with heat reservoirs at different temperatures T1 > T2 acting at its boundaries, yield a “flat” temperature profile at T = (T1 + T2)/2 in the bulk of the chain. This scenario would be expected for the pure Toda chain, but it is inconsistent with the basic consideration that the presence of (3) breaks translation invariance and total momentum is no longer conserved. This notwithstanding, in order to observe a temperature profile in the form of a linear interpolation between T1 and T2 (i.e., Fourier's law), one has to simulate the dynamics of very large chains over very long times, typically and , when all the parameters of the model are set to unity.
Equilibrium measurements based on the Green-Kubo relation, i.e., based on the behavior of the energy current correlator (2), lead to further interesting findings in this scenario. By comparing the Toda chain with quadratic and quartic pinning potentials, one observes in the latter case clear indications of a diffusive regime, i.e., a finite heat conductivity, and a practically negligible influence of finite size corrections, whereas in the former case the power spectrum [i.e., the Fourier transform of (2)] is found to exhibit a peculiar scaling regime (with power −5/3) before eventually reaching a plateau that indicates a standard diffusion. In the same region of the spectrum, the FPUT model (where the parameters α and β have been chosen in such a way to correspond to a Taylor series expansion of the Toda chain) with the addition of (3) is found to converge to a plateau, in the absence of any precursor of a power-law scaling.
Further details about the unexpected transport regimes encountered in the Toda chain equipped with the quadratic pinning can be found in Dhar et al. [59]. We point out that many of the observations still await a convincing theoretical interpretation.
2.3. Anomalous Transport in the Presence of a Magnetic Field
Recent contributions [60, 61] have dealt with the important problem of heat transport in chains of charged oscillators in the presence of a magnetic field B. The model is a one-dimensional polymer that allows transverse motion of the oscillators interacting via a harmonic potential. For B = 0 the exponent of the energy current correlator is , indicating the presence of anomalous transport and a divergent heat conductivity . Upon switching on B, the first basic consequence is the breaking of translation invariance, so that the total momentum is no longer conserved. This notwithstanding, the total pseudo-momentum is conserved, but the hydrodynamics of the model is definitely modified. In fact, numerical and analytical estimates indicate that the exponent δ may change to a value different from . In particular, in Tamaki et al. [60] two different cases were considered: one where oscillators have the same charge and one where oscillators have alternate charges of sign (−1)n, n being the integer index numbering oscillators along the chain. It can easily be shown that in the former case the sound velocity is null and the energy correlator exhibits a thermal peak centered at the origin and spreading in time. By contrast, in the latter case the sound velocity has a finite, B-dependent value and the thermal peak of the energy correlator is coupled to sound modes propagating through the chain. In the case of finite sound velocity (alternate charges), the exponent governing the divergence of the heat conductivity with the system size is found to remain the same as that for B = 0, i.e., . This is not surprising, since for B = 0 the sound velocity in the model is also finite. In the case of equally charged oscillators, on the other hand, a new exponent appears, which corresponds to a universality class different from all the others encountered in anomalous transport in non-linear chains of oscillators. An important remark about this new exponent is that in the absence of a finite sound velocity, the identification of the exponents δ and γ, introduced in section 2, is no longer correct. In fact, in this case the value of the exponent δ is found to be very close to . Rigorous estimates of all of these exponents, also for the d = 2 and d = 3 versions of the charged polymer model, have been obtained through the asymptotics of the corresponding Green-Kubo integrals, where the deterministic dynamics has been replaced with a stochastic version that conserves the same quantities [61]. For the different one-dimensional cases, these rigorous estimates agree with the previous findings, while in d = 2 and d = 3 dimensions the expected logarithmic divergence and finite heat conductivity have been singled out, respectively.
2.4. The Case of Long-Range Interactions
Long-range forces that slowly decay with the relative distance between particles are well-studied in statistical mechanics. They characterize a wide range of physical situations, such as self-gravitating systems, plasmas, interacting vortices in fluids, capillary effects of colloids at an interface, chemo-attractant dynamics, cold atoms in optical lattices, and colloidal active particles. Several unusual features are known: ensemble inequivalence, long-lived metastable states and anomalous energy diffusion [62, 63], inhomogeneous stationary states [64], lack of thermalization on interaction with a single external bath [65], etc. Moreover, perturbations can spread with infinite velocities, leading to qualitative differences from their short-range counterparts [66, 67].
Heat transport in chains with long-range interactions has been studied only recently [68–72]. The main question is to what extent the anomalous properties change as the spatial range of interactions between oscillators increases. In two recent papers [73, 74] this problem was investigated for Hamiltonian chains with a long-range potential of the form
where the generalized Kac factor
guarantees the extensivity of the Hamiltonian [62, 63]. In particular, the long-range versions of both the rotor chain, with v(x) = VXY(x), and the FPUT-β model, with , have been investigated. The reason for studying these two choices is that the nearest-neighbor version (i.e., α → +∞) of the former model exhibits standard diffusion of energy while that of the latter is characterized by anomalous diffusion.
For the rotor chain, non-equilibrium measurements with thermal reservoirs at different temperatures, T1 > T2, acting at the chain ends show that when α > 1, the resulting temperature profile interpolates linearly between T1 and T2. Despite the long-range nature of the interaction, this is a strong indication that a standard diffusive process still governs energy transport through the rotor chain, as in the limit α → +∞. In contrast, when α < 1 the temperature profile progressively flattens until it reaches a constant bulk temperature T = (T1 + T2)/2 in the “mean-field” limit α → 0+. It is important to note that, in contrast to the situation of chimeras of integrable models discussed in section 2.2, such flat temperature profiles have nothing to do with integrability, but rather are driven by the dominance of a “parallel” energy transport mechanism, which connects the heat baths at the chain boundaries with each other directly through the individual rotors in the bulk of the chain. Energy transport along the chain is practically immaterial, and the overall process is mediated by the rotors, which have to compromise between the two different temperatures imposed by the reservoirs. A sketch of this mechanism is presented in Figure 2. For small α, each lattice site in the bulk is directly coupled to both thermal baths, and its temperature tends to the average (T1+T2)/2 independently of the system size. Moreover, the average heat current exchanged with any other site is negligibly small.
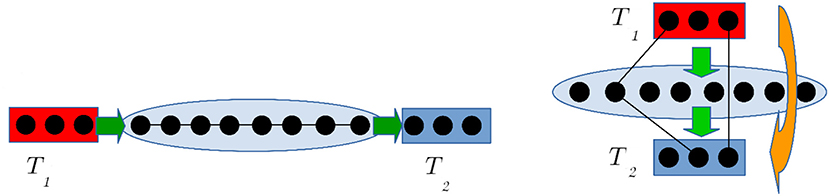
Figure 2. Pictorial representations of heat transfer processes for long-range interacting chains, in the limiting cases of α = ∞ (left) and α = 0 (right). Oscillators in contact with thermal reservoirs are enclosed in rectangular boxes while ones in the bulk are enclosed in the ellipse. The relevant transport channels are represented by black lines. Adapted with permission from Di Cintio et al. [74]. Copyright © 2019 American Physical Society.
At least for α < 1, a similar scenario seems to characterize the FPUT model: flat temperature profiles are observed also in this case, and one can verify that the same parallel transport mechanism as described for rotors is at work. On the other hand, the behavior is definitely more complicated for α > 1. Careful numerical studies exploring finite size effects give an overall picture in which an anomalous diffusion mechanism sets in, characterized by an exponent γ that is expected to increase up to that of the quartic FPUT model in the limit α → +∞. But one is faced with a first surprise at α = 2, where a flat temperature profile is restored, although, as the numerics clearly indicates, the mechanism of transport along the chain certainly dominates the parallel transport process. In the light of what was discussed in section 2.2, this would appear to be a possible manifestation of a chimera ballistic regime, although there is no simple argument allowing us to invoke a relation of this special case with an integrable approximation, if any. That the α = 2 case is characterized by a somewhat “weaker non-integrability” has been confirmed also for a related model [70, 72]. This can be traced back to the fact that in this case the lattice supports a special type of free-tail localized excitations (traveling discrete breathers) that enhance energy transfer [72].
A complementary approach is the analysis of space-time scaling of equilibrium correlations, which in the short-range case yields useful information via the dynamical exponent z [20]. A numerical study of the structure factors of the FPUT model [74] shows that for α > 1 the dynamical exponent z certainly depends on α in a different way from that expected from the theory of Lévy processes. Moreover, upon adding the cubic term to the potential, one recovers the same dependence of z on α, up to α = 5. This is again a surprise, because in the limit α → +∞ the cubic and quartic versions of the FPUT model should converge to different values of z. At present, no theoretical explanation exists for this challenging scenario; in particular, to the best of our knowledge, no hydrodynamic description is available.
2.5. Anomalous Transport via the Multi-Particle Collision Method
So far we have discussed the case of lattice models. To test the universality of the results, it is important to consider more general low-dimensional many-body systems, such as interacting fluids or even plasmas. Although molecular dynamics would be the natural choice, it is computationally convenient to consider effective stochastic processes capable of mimicking particle interactions through random collisions. A prominent example is the multi-particle collision (MPC) simulation scheme [75], proposed to simulate the mesoscopic dynamics of polymers in solution, as well as colloidal and complex fluids. Another application is the modeling of parallel heat transport in edge tokamak plasma [76]. Indeed, in the regimes of interest for magnetic fusion devices, large temperature gradients will build up along the field line joining the hot plasma region (hot source) and the colder one close to the wall (which acts as a sink). Besides this motivation, we mention some results that are pertinent to the problem of anomalous transport.
In brief, the MPC method consists in partitioning the set of Np point particles into Nc disjoint cells. Within each cell, the coordinates of the local center of mass and the velocity are computed, and a rotation of the particle velocities about a random axis in the cell's center-of-mass frame is performed. The rotation angles are fixed by requiring that the conserved quantities (energy, momentum) be locally preserved. All particles are then propagated freely. Physical details of the interaction can easily be included phenomenologically, for instance by introducing energy-dependent collision rates [18]. Interaction with external reservoirs can be also included by imposing Maxwellian distributions of velocity and chemical potentials on the thermostatted cells [77].
For a one-dimensional MPC fluid, since the conservation laws are the same as in, say, the FPUT model, we expect it to belong to the same KPZ universality class of anomalous transport. Indeed, numerical measurements of dynamical scaling fully confirm this prediction [78], and the result is quite robust. The same type of anomalies have been shown to occur also for quasi-one-dimensional MPC dynamics, namely in the case of a fluid confined in a box with a sufficiently large aspect ratio [18].
2.6. Anomalous Heat Transport in Material Science
The discovery of anomalous heat transport in anharmonic chains has triggered a search for this important physical effect in real low-dimensional materials. There is now a vast literature in which this kind of phenomenon has been predicted and experimentally observed; an overview of part of this growing research field is given in Lepri [9]. Here we just illustrate two recent contributions which will help the reader to appreciate the relevance of this phenomenon for nanowires and polymers. We point out that a review of the recent literature in both fields is contained in the bibliographies of these two contributions.
In Upadhyaya and Aksamija [79] the problem of lattice thermal conductivity in Si-Ge nanowires was tackled by solving the Boltzmann transport equation. More precisely, the authors used a Monte Carlo algorithm to sample the phonon mean free path, and combined this with phenomenological results concerning a suitable representation of realistic boundary conditions. It is quite remarkable that they found evidence of a heat transport mechanism ruled by a Lévy walk dynamics of phonon flights through the lattice structure. In particular, the phonon mean free paths are found to be characterized by a heavy-tailed distribution, which is associated with an anomalous diffusive behavior characterized by a size-divergent heat conductivity κ(L) ~ L0.33. This behavior has been checked for system sizes in the range of 10nm < L < 10μm. Notice that the phonon mean free path is orders of magnitude smaller than this size range. It is important to note that this scenario is robust across different alloy compositions, where the Ge component varies in the range [6, 86%]. All of these results fully agree with the theoretical expectation that anharmonic chains with leading cubic non-linearity should exhibit a divergent heat conductivity with an exponent .
In Crnjar et al. [80] atomistic simulations were performed for poly(3,4-ethylenedioxythiophene), abbreviated PEDOT, a conjugated polymer that is of interest in view of its tunable and large electrical conductivity, transparency, and air stability [81]. The authors simulated this polymer model in d = 1 and d = 3, in both equilibrium and non-equilibrium settings. More precisely, equilibrium measurements were performed by estimating the dependence of the heat conductivity κ on the system size L via the Green-Kubo formula, where one has to estimate the asymptotic decay in time of the correlator of the total energy current (2). The outcome of this analysis was compared with the numerics obtained in non-equilibrium conditions. The setup used in this case is based on a transient measurement of the effective heat diffusivity . The two halves of the system were initially prepared in two thermalized states at different temperatures T1 and T2. By running a molecular dynamics simulation, one can measure as a function of L during the transient evolution to the thermal equilibrium state at temperature (T1 + T2)/2. More precisely, the estimate of relies on the fit of the time-dependent temperature difference in the two regions (for details see Equation 9 in [80]). Finally, the thermal conductivity is obtained from the formula , where ρ is the polymer mass density and cV its specific heat. The authors obtained consistent results showing that for the polymer chain anomalous diffusion, κ(L) ~ Lγ with , is observed, whereas for the polymer crystal standard diffusion, i.e., a size-independent finite thermal conductivity κ, is recovered. These results are quite remarkable because they provide very clear confirmation of the role played by the space dimension in determining anomalous transport effects. On the other hand, the authors point out that the exponent does not agree with the expected theoretical value , since the phenomenological AMBER non-linear potential adopted for the PEDOT model is certainly asymmetric, dominated by a leading cubic non-linearity. Simulations of the polymer chain have been performed for quite large system sizes, namely 0.376μm < L < 7.526μm. This notwithstanding, we cannot exclude the possibility that, as discussed in the previous section, the combination of finite size effects and non-linearity might also be at work in this case, yielding a power-law divergence of κ(L) that should be compatible with a symmetric phenomenological potential.
These findings should be compared with those obtained for simpler models. For instance, in the case mentioned in section 2.3, the exponent was found in a chain model with a quadratic interaction potential between the beads [60] (notice that the possibility of displacements in both the horizontal and the vertical directions make this model non-integrable, in contrast to the harmonic chain). On the other hand, a three-dimensional anharmonic chain with cubic and quartic interactions has been shown to belong instead to the KPZ class with γ = 1/3 [82]. One could speculate that in any polymer model the basic scaling associated with anomalous transport is determined only by the quadratic term, and this is a conjecture that certainly merits further theoretical and numerical investigation.
To conclude this section, we briefly mention some experimental studies. Thermal properties of nanosized objects are of intrinsic technological interest for nanoscale thermal management. In this general context, nanowires and single-walled nanotubes have been analyzed to look for deviation from the standard Fourier's law [5]. Some experimental evidence of anomalous transport in very long carbon nanotubes has been reported [83], although the results are controversial [84]. Experiments demonstrating a non-trivial length dependence of thermal conductance for molecular chains have also been reported [85]. Admittedly, such experimental evidence of anomalous transport is rather limited and not exempt from criticism. Heat transfer measurements on nanosized objects are notoriously difficult but may be undertaken in the future, possibly guided by the theoretical insights summarized here.
3. Coupled Transport
In this section we discuss the relevance of anomalous diffusion in coupled transport. In particular, we focus on steady-state transport and for concreteness use the language of thermoelectricity [2, 86], in which the coupled flows are charge and heat flow (other examples where the flow coupled to heat is particle or magnetization flow could be treated similarly). Moreover, we shall limit our discussion to power production, even though many of the results and open problems highlighted below can be readily extended to refrigeration. Thermoelectricity is a steady-state heat engine. Relevant quantities for characterizing the performance of a generic heat engine, which operates between a hot reservoir at temperature Th and a cold one at Tc, are the following:
• The efficiency η = W/Qh, where W is the output work and Qh the heat extracted from the hot reservoir. For cyclic as well as for steady-state heat engines, the Carnot efficiency ηC = 1 − Tc/Th is an upper bound for the efficiency η.
• The output power P. It is a common belief that an engine attaining the Carnot efficiency would require a quasi-static transformation, i.e., an infinite cycle-time, implying vanishing power. For steady-state engines this argument is replaced by one saying that finite currents would imply dissipation, thus precluding Carnot efficiency for non-zero power. Hence, it is important to consider the power-efficiency trade-off. This is a key problem in the field of finite-time thermodynamics [87], in relation to the fundamental thermodynamic bounds on the performance of heat engines, as well as the practical purpose of designing engines that, for a given output power, work at the maximum possible efficiency. For classical cyclic heat engines, whose interactions with a heat bath can be described by a Markov process, it was proved [88] that the mean power P has an upper bound
where A is a system-specific pre-factor (see also [89] for an analogous linear response result within the framework of stochastic thermodynamics [90]). While at first sight this bound implies that P → 0 as η → ηc (and of course when η → 0), so that an engine of this kind with finite power never attains the Carnot efficiency, one cannot exclude the possibility that the amplitude A diverges as the efficiency approaches the Carnot value [91].
• The fluctuations in the power output about its mean value P. Indeed, large fluctuations render heat engines unreliable. Especially for heat engines at the nanoscale, one expects power fluctuations due to, e.g., thermal noise, which are not negligible in comparison with the mean output power. In general, one would like to obtain high efficiency (as close as possible to the Carnot efficiency), large power, and small fluctuations. However, a trade-off between these three quantities has been proved [92] for a broad class of steady-state heat engines (including machines described by suitable rate equations or modeled by overdamped Langevin dynamics):
where the (steady-state) power fluctuations are given by
with P(t) being the mean power delivered up to time t. For t → ∞, since P(t) converges to P as , an additional factor of t in (8) is needed to obtain a finite limit for ΔP. Equation (7) tells us that efficiency close to the Carnot value and high power entail large fluctuations. We note that the bound (8) has recently been generalized to periodically driven systems [93].
3.1. Linear Response
In the linear response setting, the relationship between currents and generalized forces is linear [94, 95]. In particular, for thermoelectric transport we have
where je is the electric current density, ju is the energy current density, and the conjugated generalized forces are and , with μ being the electrochemical potential and e the electron charge. The coefficients Lab (a, b = e, u) are known as kinetic or Onsager coefficients; we will denote by L the Onsager matrix with matrix elements Lab. Note that the (total) energy current ju = jh + (μ/e)je is the sum of the heat current jh and the electrochemical potential energy current (μ/e)je.
The Onsager coefficients must satisfy two fundamental constraints. First, the second law of thermodynamics, i.e., the positivity of the entropy production rate, , implies
Second, for systems with time-reversal symmetry, Onsager derived fundamental relations, Leu = Lue, known as Onsager reciprocal relations.
The kinetic coefficients Lab are related to the familiar thermoelectric transport coefficients, namely the electrical conductivity σ, the thermal conductivity κ, the thermopower (or Seebeck coefficient) S, and the Peltier coefficient Π:
For systems with time-reversal symmetry, the Onsager reciprocal relations give Π = TS.
The thermoelectric performance is governed by the thermoelectric figure of merit
Thermodynamics imposes a lower bound on the figure of merit: ZT ≥ 0. Moreover, the thermoelectric conversion efficiency is a monotonically increasing function of ZT, with η = 0 at ZT = 0 and η → ηC in the limit ZT → ∞. Nowadays, most efficient thermoelectric devices operate at around ZT ≈ 1. On the other hand, it is generally accepted that ZT > 3–5 is the target value for efficient, commercially competitive thermoelectric technology. It is a great challenge to increase the thermoelectric efficiency, since the transport coefficients S, σ, and κ are generally interdependent. For instance, in metals σ and κ are proportional according to the Wiedemann-Franz law, and the thermopower is small; these properties make metals poor thermoelectric materials. It is therefore of great importance to understand the physical mechanisms that might allow us to independently control the above transport coefficients.
3.2. Anomalous Transport and Efficiency
The theoretical discussion of the role of anomalous (thermal) diffusion in thermoelectric transport is based on the Green-Kubo formula. expresses the Onsager coefficients in terms of dynamic correlation functions of the corresponding currents, computed at thermodynamic equilibrium. If the current-current correlations 〈ja(0)jb(t)〉 (where 〈·〉 denotes the canonical average at a given temperature T) do not decay after time-averaging, then by definition the corresponding Drude weight
is different from zero. Here Ω is the system's volume and Λ is the system's size along the direction of the currents. It has been shown [96–99] that a non-zero Drude weight Dab is a signature of ballistic transport, i.e., in the thermodynamic limit the corresponding kinetic coefficient Lab diverges linearly with the system size. Non-zero Drude weights can be related to the existence of relevant conserved quantities, which determine a lower bound on Dab [100, 101]. By definition, a constant of motion Q is relevant if it is not orthogonal to the currents under consideration; in thermoelectricity this means 〈jeQ〉 ≠ 0 and 〈juQ〉 ≠ 0.
With regard to thermoelectric efficiency, a theoretical argument [102] predicts that for systems with a single relevant conserved quantity, as is the case for non-integrable systems with elastic collisions (momentum-conserving systems), the figure of merit ZT diverges at the thermodynamic limit, so that the Carnot efficiency is attained in that limit. Indeed, for systems in which the total momentum along the direction of the currents is the only relevant constant of motion, as a consequence of ballistic transport the Onsager coefficients Lab are proportional to Λ. Therefore, the electrical current is ballistic, σ ~ Lee ~ Λ, while the thermopower is asymptotically size-independent, . On the other hand, for such systems the ballistic contribution to det L is expected to vanish [102]. Hence the thermal conductivity κ ~ det L/Lee grows sub-ballistically, κ ~ Λγ with γ < 1. Since σ ~ Λ and S ~ Λ0, we can conclude that ZT ~ Λ1−γ; that is, ZT diverges in the thermodynamic limit Λ → ∞.
This result has been demonstrated in several models: in a diatomic chain of hard-point colliding particles [102] (see Figure 3), in a two-dimensional system [77] with dynamics simulated by the MPC method discussed in section 2.5 [75], and in a one-dimensional gas of particles with screened (nearest-neighbor) Coulomb interactions [104]. In all these (classical) models, the collisions are elastic and the only relevant constant of motion is the component of momentum in the direction of the charge and heat flows. In the numerical simulations, openings connect the system with two electrochemical reservoirs. The left (L) and right (R) reservoirs are modeled as ideal gases, at temperature Tγ and electrochemical potential μγ (γ = L, R). A stochastic model of the reservoirs [105, 106] is used: whenever a particle of the system crosses the opening that separates the system from the left or right reservoir, it is removed. Particles are injected into the system through the openings, with rates and energy distribution determined by the temperature and electrochemical potential (see e.g., [2]).
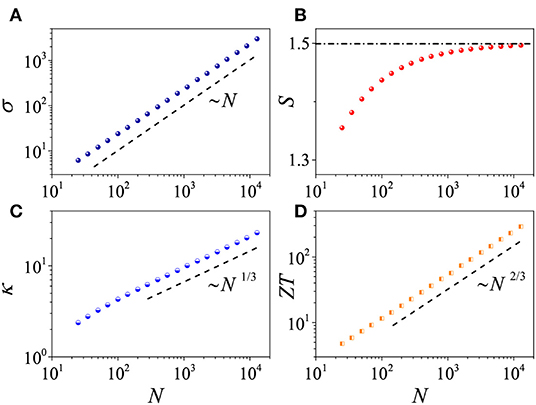
Figure 3. (A) Electrical conductivity σ, (B) Seebeck coefficient S, (C) thermal conductivity κ, and (D) thermoelectric figure of merit ZT plotted as functions of the mean number N of particles in the system, for a one-dimensional diatomic hard-point gas. Parameter values are m = 1 and M = 3 for the masses, T = 1, μ = 0, and kB = e = 1, with the system length Λ set equal to the number of particles. Adapted with permission from Luo et al. [103]. Copyright © 2018 American Physical Society.
We now show that systems with anomalous (thermal) diffusion allow a much better power-efficiency trade-off than is achievable by non-interacting systems or, more generally, by any system that can be described by the scattering theory.
We first briefly discuss non-interacting systems. In this case, we can express the charge current according to the Landauer-Büttiker scattering theory [107], adapted to classical physics:
where is the Maxwell-Boltzmann distribution function for reservoir γ and is the transmission probability of a particle with energy ϵ going from one reservoir to the other, so that . Similarly, we obtain the heat current from reservoir γ as
For a given output power P = (Δμ/e)Je (where Δμ = μR − μL > 0 and we set μL = 0 for simplicity), the transmission function that maximizes the efficiency of the heat engine, η(P) = P/Jh, L (with P, Jh, L > 0 and TL > TR) was determined in Luo et al. [103] by closely following the method developed for the quantum case in Whitney [108, 109]. The optimal transmission function is a boxcar function, for ϵ0 < ϵ < ϵ1 and otherwise. Here ϵ0 = Δμ/ηC is obtained from the condition fL(ϵ0) = fR(ϵ0) and corresponds to the special value of energy for which the flow of particles from left to right is the same as the flow from right to left. Thus, if particles only flow at energy ϵ0, the flow can be considered “reversible” in a thermodynamic sense. The energy ϵ1 and Δμ are determined numerically in the optimization procedure [103, 108, 109]. The maximum achievable power is obtained when ϵ1 → ∞:
where ΔT = TL − TR, A ≈ 0.0373, and the superscript “(st)” reminds us that the results are obtained within the scattering theory framework. At small output power, , we have
where B ≈ 0.493. Note that in the limit P → 0 the upper bound on efficiency achieves the Carnot value and the energy window for transmission, δ = ϵ1 − ϵ0, tends to 0. That is, we recover the celebrated delta-energy filtering mechanism for Carnot efficiency [110–112]. Hence, the Carnot limit corresponds to the aforementioned reversible, zero-power flow of particles.
It is clear that selecting transmission over a small energy window reduces power production. We would thus expect a different mechanism for reaching Carnot efficiency to be more favorable for power production. Such an expectation is supported by numerical data for the interacting momentum-conserving systems described above. For these systems, the Carnot efficiency can be reached without delta-energy filtering [113], and the power-efficiency trade-off can be improved. Figure 4 shows, for a given ΔT and different system sizes, η/ηC as a function of P/Pmax. The curves have two branches. Indeed, they are obtained by increasing Δμ from zero, where trivially P = 0, up to the stopping value, where again P = 0. In the latter case, the power vanishes because the electrochemical potential difference becomes too great to be overcome by the temperature difference. The power first increases with Δμ, up to its maximum value P = Pmax, and then decreases, leading to a two-branch curve. Note that, despite the relatively high value of ΔT/T = 0.2, the numerical results are in rather good agreement with the universal linear curves, which depend only on the figure of merit ZT [103]. Not surprisingly, the agreement improves with increasing system size, since |∇T| = ΔT/N decreases as N increases. In Figure 4 we also plot the limiting curve corresponding to ZT = ∞, obtained in momentum-conserving models in the thermodynamic limit N → ∞. The upper branch of this curve is the universal linear response upper bound on efficiency for a given power P. For P/Pmax ≪ 1, this bound reads
which is much less restrictive than the bound (20) obtained from scattering theory. Note that, by using the linear response result , from (21) we obtain P ∝ ΔT(ηC − η). Accordingly, when η ≈ ηC ∝ ΔT, we find the same dependence as in bound (6), which was obtained in a rather different context.
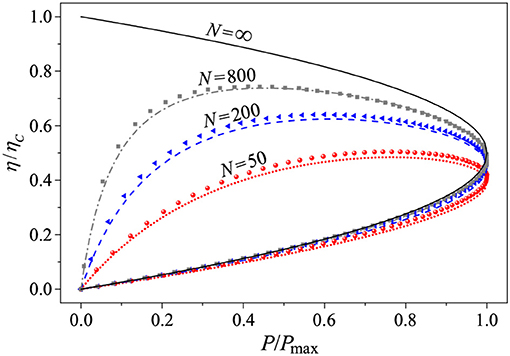
Figure 4. Relative efficiency η/ηC vs. normalized power P/Pmax at different system sizes. The dotted, dashed, and dot-dashed curves represent the linear response predictions at the ZT(N) value corresponding to the given system size Λ = N. The solid line is the linear response curve for ZT = ∞ (i.e., N = ∞). The model parameter values are as in Figure 3, with ΔT = 0.2 (TL = 1.1 and TR = 0.9). Adapted with permission from Luo et al. [103]. Copyright © 2019 American Physical Society.
3.3. Open Problems
Several open questions about the role of anomalous transport in coupled transport remain, notably the following:
• As discussed in section 2.4, heat transport in the presence of long-range interactions has been investigated recently. However, the effect of the range of interactions on coupled transport, and in particular on the power-efficiency trade-off, is unknown.
• While momentum-conserving systems greatly improve the power-efficiency trade-off relative to the non-interacting case, it is not known how they would behave with respect to the bound (7), which simultaneously involves the efficiency, power, and fluctuations. That bound was obtained within the framework of stochastic thermodynamics [90], with the transition rates between the system's states obeying the local detailed balance principle, and without precise modeling of the underlying particle-particle interactions. On the other hand, in the models described in the present paper, stochasticity is confined to the baths and the internal system dynamics plays a crucial role. This has allowed us to assess the impact of constants of motion and anomalous transport on the efficiency of heat-to-work conversion and could also be relevant to the bound (7).
• Although the results reviewed in this section have been corroborated by numerical simulations of several classical one- and two-dimensional systems, their extension to the quantum case remains a challenging problem for future investigation.
• The discussion in this section has neglected phonons. Nevertheless, besides being of fundamental interest, the results presented here could be of practical relevance to very clean systems where the elastic mean free path of the conducting particles is much longer than the length scale associated with elastic particle-particle collisions, for instance in high-mobility two-dimensional electron gases at very low temperatures. Phonon-free thermoelectricity (or, more precisely, thermodiffusion) has been experimentally realized in the context of cold atoms, first for weakly interacting particles [114] and more recently in a regime with strong interactions [115]. In the latter case, a strong violation of the Wiedemann-Franz law has been observed. Such violations cannot be explained by the Landauer-Büttiker scattering theory. It would be interesting to investigate whether in such systems where a high thermoelectric efficiency has been observed, the non-interacting bound on efficiency for a given power could be outperformed.
4. Overview
In spite of the significant progress made over the past few decades, the study of anomalous heat transport in non-linear systems remains a challenging research field. While this review has focused on some promising directions in regard to classical systems, a main avenue for future investigations should undoubtedly be sought in the quantum domain. At the quantum level, anomalous heat transport is considerably less well-understood than in the classical case, due to both conceptual and practical difficulties. The definitions of thermodynamic observables, such as temperature, heat, and work, and of the concept of local equilibrium, become problematic in nanoscale systems. For instance, in solid-state nanodevices we can have structures smaller than the length scale over which electrons relax to a local equilibrium due to electron-electron or electron-phonon interactions. Consequently, quantum interference effects, quantum correlations, and quantum fluctuation effects should be taken into account [2]. In particular, many-body localization provides a mechanism by which thermalization can fail in strongly disordered systems, with anomalous transport in the vicinity of the transition between many-body localized and ergodic phases [116, 117].
From a practical viewpoint, one faces challenges arising from the computational complexity of simulating many-body open quantum systems, with the size of the Hilbert space growing exponentially with the number of particles. Notwithstanding these difficulties, a time-dependent density matrix renormalization group method allows the computation of transport properties of integrable and non-integrable quantum spin chains driven by local (Lindblad) operators acting close to their boundaries [118]. Sizes up to n ~ 100 spins can be simulated, much larger than the n ~ 20 spins achievable with other methods, such as Monte Carlo wavefunction approaches [119]. The results obtained confirm the relevance of constants of motion to transport properties, with integrable systems that exhibit ballistic heat transport, whereas for quantum chaotic systems heat transport is normal (according to Fourier's law; see [120, 121]). In passing, we note that for magnetization transport in some integrable models like XXZ, one can obtain diffusive behavior (Fick's law; see [118]).
From a thermodynamic perspective, the use of local Lindblad operators is problematic. Except in quantum chaotic systems, such operators do not drive the system to a grand-canonical state [122]. Furthermore, the use of local Lindblad baths may result in apparent violations of the second law of thermodynamics [123]. Global Lindblad dissipators are free from such problems and can be used to simulate heat transport (see e.g., [124]), but are not practical in that they are limited to very small system sizes. Furthermore, for the description of quantum heat engines in the extreme case where the working medium may even consist of a single two-level quantum system, it is crucial to take into account medium-reservoir quantum correlations as well as non-Markovian effects, which are not included in the standard, weak-coupling Lindblad description of quantum open systems. For first steps in this challenging direction, see Carrega et al. [125], Tamascelli et al. [126], and Wiedmann et al. [127]. The investigation of anomalous heat transport in such regimes is terra incognita.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
SL and RL acknowledge partial support from project MIUR-PRIN2017 Coarse-grained description for non-equilibrium systems and transport phenomena (CO-NEST) N. 201798CZL. They thank P. Di Cintio and S. Iubini for invaluable help.
References
1. Klages R, Radons G, Sokolov IM. Anomalous Transport: Foundations and Applications. Weinheim: John Wiley & Sons (2008).
2. Benenti G, Casati G, Saito K, Whitney RS. Fundamental aspects of steady-state conversion of heat to work at the nanoscale. Phys Rep. (2017) 694:1–124. doi: 10.1016/j.physrep.2017.05.008
3. Lepri S, Livi R, Politi A. Heat conduction in chains of nonlinear oscillators. Phys Rev Lett. (1997) 78:1896–9. doi: 10.1103/PhysRevLett.78.1896
4. Lepri S, Livi R, Politi A. On the anomalous thermal conductivity of one-dimensional lattices. Europhys Lett. (1998) 43:271–6. doi: 10.1209/epl/i1998-00352-3
5. Chang CW. Experimental probing of non-fourier thermal conductors. In: Lepri S, editor. Thermal Transport in Low Dimensions: From Statistical Physics to Nanoscale Heat Transfer. Berlin; Heidelberg: Springer-Verlag (2016). p. 305–38. doi: 10.1007/978-3-319-29261-8_8
6. Balandin AA. Thermal properties of graphene and nanostructured carbon materials. Nat Mater. (2011) 10:569–81. doi: 10.1038/nmat3064
7. Lepri S, Livi R, Politi A. Thermal conduction in classical low-dimensional lattices. Phys Rep. (2003) 377:1. doi: 10.1016/S0370-1573(02)00558-6
8. Dhar A. Heat Transport in low-dimensional systems. Adv Phys. (2008) 57:457–537. doi: 10.1080/00018730802538522
9. Lepri S editor. Thermal Transport in Low Dimensions: From Statistical Physics to Nanoscale Heat Transfer. Vol. 921 of Lecture Notes in Physics. Berlin; Heidelberg: Springer-Verlag (2016) 1–407. doi: 10.1007/978-3-319-29261-8
10. Dhar A, Kundu A, Kundu A. Anomalous heat transport in one dimensional systems: a description using non-local fractional-type diffusion equation. Front Phys. (2019) 7:159. doi: 10.3389/fphy.2019.00159
11. Aoki K, Kusnezov D. Bulk properties of anharmonic chains in strong thermal gradients: non-equilibrium ϕ4 theory. Phys Lett A. (2000) 265:250. doi: 10.1016/S0375-9601(99)00899-3
12. Giardiná C, Livi R, Politi A, Vassalli M. Finite thermal conductivity in 1D lattices. Phys Rev Lett. (2000) 84:2144–7. doi: 10.1103/PhysRevLett.84.2144
13. Gendelman OV, Savin AV. Normal heat conductivity of the one-dimensional lattice with periodic potential of nearest-neighbor interaction. Phys Rev Lett. (2000) 84:2381–4. doi: 10.1103/PhysRevLett.84.2381
14. Iubini S, Lepri S, Politi A. Nonequilibrium discrete nonlinear Schrödinger equation. Phys Rev E. (2012) 86:011108. doi: 10.1103/PhysRevE.86.011108
15. Mendl CB, Spohn H. Low temperature dynamics of the one-dimensional discrete nonlinear Schroedinger equation. J Stat Mech: Theory Exp. (2015) 2015:P08028. doi: 10.1088/1742-5468/2015/08/P08028
16. Lippi A, Livi R. Heat conduction in two-dimensional nonlinear lattices. J Stat Phys. (2000) 100:1147–72. doi: 10.1023/A:1018721525900
17. Wang L, Hu B, Li B. Logarithmic divergent thermal conductivity in two-dimensional nonlinear lattices. Phys Rev E. (2012) 86:040101. doi: 10.1103/PhysRevE.86.040101
18. Di Cintio P, Livi R, Lepri S, Ciraolo G. Multiparticle collision simulations of two-dimensional one-component plasmas: anomalous transport and dimensional crossovers. Phys Rev E. (2017) 95:043203. doi: 10.1103/PhysRevE.95.043203
19. van Beijeren H. Exact results for anomalous transport in one-dimensional Hamiltonian systems. Phys Rev Lett. (2012) 108:180601. doi: 10.1103/PhysRevLett.108.180601
20. Spohn H. Nonlinear fluctuating hydrodynamics for anharmonic chains. J Stat Phys. (2014) 154:1191–227. doi: 10.1007/s10955-014-0933-y
21. Popkov V, Schadschneider A, Schmidt J, Schütz GM. Fibonacci family of dynamical universality classes. Proc Natl Acad Sci USA. (2015) 112:12645–50. doi: 10.1073/pnas.1512261112
22. Lee-Dadswell GR, Nickel BG, Gray CG. Thermal conductivity and bulk viscosity in quartic oscillator chains. Phys Rev E. (2005) 72:031202. doi: 10.1103/PhysRevE.72.031202
23. Delfini L, Lepri S, Livi R, Politi A. Anomalous kinetics and transport from 1D self-consistent mode-coupling theory. J Stat Mech Theory Exp. (2007) 2007:P02007. doi: 10.1088/1742-5468/2007/02/P02007
24. Lukkarinen J, Spohn H. Anomalous energy transport in the FPU-β chain. Commun Pure Appl Math. (2008) 61:1753–86. doi: 10.1002/cpa.20243
25. Lepri S, Livi R, Politi A. Universality of anomalous one-dimensional heat conductivity. Phys Rev E. (2003) 68:067102. doi: 10.1103/PhysRevE.68.067102
26. Wang L, Wang T. Power-law divergent heat conductivity in one-dimensional momentum-conserving nonlinear lattices. Europhys Lett. (2011) 93:54002. doi: 10.1209/0295-5075/93/54002
27. Basile G, Bernardin C, Olla S. Momentum conserving model with anomalous thermal conductivity in low dimensional systems. Phys Rev Lett. (2006) 96:204303. doi: 10.1103/PhysRevLett.96.204303
28. Lepri S, Mejía-Monasterio C, Politi A. Stochastic model of anomalous heat transport. J Phys A Math Theor. (2009) 42:025001. doi: 10.1088/1751-8113/42/2/025001
29. Lee-Dadswell G. Universality classes for thermal transport in one-dimensional oscillator systems. Phys Rev E. (2015) 91:032102. doi: 10.1103/PhysRevE.91.032102
30. Zaburdaev V, Denisov S, Klafter J. Lévy walks. Rev Mod Phys. (2015) 87:483. doi: 10.1103/RevModPhys.87.483
31. Cipriani P, Denisov S, Politi A. From anomalous energy diffusion to Lévy Walks and heat conductivity in one-dimensional systems. Phys Rev Lett. (2005) 94:244301. doi: 10.1103/PhysRevLett.94.244301
32. Lepri S, Politi A. Density profiles in open superdiffusive systems. Phys Rev E. (2011) 83:030107. doi: 10.1103/PhysRevE.83.030107
33. Dhar A, Saito K, Derrida B. Exact solution of a Lévy walk model for anomalous heat transport. Phys Rev E. (2013) 87:010103. doi: 10.1103/PhysRevE.87.010103
34. Denisov S, Klafter J, Urbakh M. Dynamical heat channels. Phys Rev Lett. (2003) 91:194301. doi: 10.1103/PhysRevLett.91.194301
35. Liu S, Haenggi P, Li N, Ren J, Li B. Anomalous heat diffusion. Phys Rev Lett. (2014) 112:040601. doi: 10.1103/PhysRevLett.112.040601
36. Mendl CB, Spohn H. Equilibrium time-correlation functions for one-dimensional hard-point systems. Phys Rev E. (2014) 90:012147. doi: 10.1103/PhysRevE.90.012147
37. Jara M, Komorowski T, Olla S. Superdiffusion of energy in a chain of harmonic oscillators with noise. Commun Math Phys. (2015) 339:407–53. doi: 10.1007/s00220-015-2417-6
38. Bernardin C, Gonçalves P, Jara M. 3/4-fractional superdiffusion in a system of harmonic oscillators perturbed by a conservative noise. Archiv Ration Mech Anal. (2016) 220:505–42. doi: 10.1007/s00205-015-0936-0
39. Bernardin C, Stoltz G. Anomalous diffusion for a class of systems with two conserved quantities. Nonlinearity. (2012) 25:1099. doi: 10.1088/0951-7715/25/4/1099
40. Bernardin C, Gonçalves P. Anomalous fluctuations for a perturbed Hamiltonian system with exponential interactions. Commun Math Phys. (2014) 325:291–332. doi: 10.1007/s00220-013-1860-5
41. Delfini L, Lepri S, Livi R, Mejia-Monasterio C, Politi A. Nonequilibrium dynamics of a stochastic model of anomalous heat transport: numerical analysis. J Phys A Math Theor. (2010) 43:145001. doi: 10.1088/1751-8113/43/14/145001
42. Kundu A, Bernardin C, Saito K, Kundu A, Dhar A. Fractional equation description of an open anomalous heat conduction set-up. J Stat Mech Theory Exp. (2019) 2019:013205. doi: 10.1088/1742-5468/aaf630
43. Iacobucci A, Legoll F, Olla S, Stoltz G. Thermal conductivity of the Toda lattice with conservative noise. J Stat Phys. (2010) 140:336–48. doi: 10.1007/s10955-010-9996-6
44. Hurtado PI, Garrido PL. A violation of universality in anomalous Fourier's law. Sci Rep. (2016) 6:38823. doi: 10.1038/srep38823
45. Xiong D. Underlying mechanisms for normal heat transport in one-dimensional anharmonic oscillator systems with a double-well interparticle interaction. J Stat Mech Theory Exp. (2016) 2016:043208. doi: 10.1088/1742-5468/2016/04/043208
46. Archana GR, Barik D. Temperature-dependent divergence of thermal conductivity in momentum-conserving one-dimensional lattices with asymmetric potential. Phys Rev E. (2019) 99:022103. doi: 10.1103/PhysRevE.99.022103
47. Basile G, Delfini L, Lepri S, Livi R, Olla S, Politi A. Anomalous transport and relaxation in classical one-dimensional models. Eur Phys J Spec Top. (2007) 151:85–93. doi: 10.1140/epjst/e2007-00364-7
48. Zhong Y, Zhang Y, Wang J, Zhao H. Normal heat conduction in one-dimensional momentum conserving lattices with asymmetric interactions. Phys Rev E. (2012) 85:060102. doi: 10.1103/PhysRevE.85.060102
49. Wang L, Hu B, Li B. Validity of Fourier's law in one-dimensional momentum-conserving lattices with asymmetric interparticle interactions. Phys Rev E. (2013) 88:052112. doi: 10.1103/PhysRevE.88.052112
50. Das S, Dhar A, Narayan O. Heat conduction in the α-β Fermi-Pasta-Ulam chain. J Stat Phys. (2014) 154:204–13. doi: 10.1007/s10955-013-0871-0
51. Chen S, Wang J, Casati G, Benenti G. Nonintegrability and the Fourier heat conduction law. Phys Rev E. (2014) 90:032134. doi: 10.1103/PhysRevE.90.032134
52. Spohn H. Fluctuating hydrodynamics for a chain of nonlinearly coupled rotators. (2014). arXiv[Preprint].arXiv:14113907.
53. Kulkarni M, Huse DA, Spohn H. Fluctuating hydrodynamics for a discrete Gross-Pitaevskii equation: mapping onto the Kardar-Parisi-Zhang universality class. Phys Rev A. (2015) 92:043612. doi: 10.1103/PhysRevA.92.043612
54. Xiong D, Zhang Y. One-dimensional superdiffusive heat propagation induced by optical phonon-phonon interactions. Phys Rev E. (2018) 98:012130. doi: 10.1103/PhysRevE.98.012130
55. Di Cintio P, Iubini S, Lepri S, Livi R. Transport in perturbed classical integrable systems: the pinned Toda chain. Chaos Solit Fract. (2018) 117:249–54. doi: 10.1016/j.chaos.2018.11.003
56. Theodorakopoulos N, Peyrard M. Solitons and nondissipative diffusion. Phys Rev Lett. (1999) 83:2293. doi: 10.1103/PhysRevLett.83.2293
57. Spohn H. Interacting and noninteracting integrable systems. J Math Phys. (2018) 59:091402. doi: 10.1063/1.5018624
58. Kundu A, Dhar A. Equilibrium dynamical correlations in the Toda chain and other integrable models. Phys Rev E. (2016) 94:062130. doi: 10.1103/PhysRevE.94.062130
59. Dhar A, Kundu A, Lebowitz JL, Scaramazza JA. Transport properties of the classical Toda chain: effect of a pinning potential. J Stat Phys. (2019) 175:1298–310. doi: 10.1007/s10955-019-02284-6
60. Tamaki S, Sasada M, Saito K. Heat transport via low-dimensional systems with broken time-reversal symmetry. Phys Rev Lett. (2017) 119:110602. doi: 10.1103/PhysRevLett.119.110602
61. Saito K, Sasada M. Thermal conductivity for coupled charged harmonic oscillators with noise in a magnetic field. Commun Math Phys. (2018) 361:951–95. doi: 10.1007/s00220-018-3198-5
62. Bouchet F, Gupta S, Mukamel D. Thermodynamics and dynamics of systems with long-range interactions. Phys A Stat Mech Appl. (2010) 389:4389–405. doi: 10.1016/j.physa.2010.02.024
63. Campa A, Dauxois T, Ruffo S. Statistical mechanics and dynamics of solvable models with long-range interactions. Phys Rep. (2009) 480:57–159. doi: 10.1016/j.physrep.2009.07.001
64. Gupta S, Casetti L. Surprises from quenches in long-range-interacting systems: temperature inversion and cooling. New J Phys. (2016) 18:103051. doi: 10.1088/1367-2630/18/10/103051
65. de Buyl P, De Ninno G, Fanelli D, Nardini C, Patelli A, Piazza F, et al. Absence of thermalization for systems with long-range interactions coupled to a thermal bath. Phys Rev E. (2013) 87:042110. doi: 10.1103/PhysRevE.87.042110
66. Torcini A, Lepri S. Disturbance propagation in chaotic extended systems with long-range coupling. Phys Rev E. (1997) 55:R3805. doi: 10.1103/PhysRevE.55.R3805
67. Métivier D, Bachelard R, Kastner M. Spreading of perturbations in long-range interacting classical lattice models. Phys Rev Lett. (2014) 112:210601. doi: 10.1103/PhysRevLett.112.210601
68. Ávila RR, Pereira E, Teixeira DL. Length dependence of heat conduction in (an) harmonic chains with asymmetries or long range interparticle interactions. Phys A Stat Mech Appl. (2015) 423:51–60. doi: 10.1016/j.physa.2014.12.018
69. Olivares C, Anteneodo C. Role of the range of the interactions in thermal conduction. Phys Rev E. (2016) 94:042117. doi: 10.1103/PhysRevE.94.042117
70. Bagchi D. Thermal transport in the Fermi-Pasta-Ulam model with long-range interactions. Phys Rev E. (2017) 95:032102. doi: 10.1103/PhysRevE.95.032102
71. Tamaki S, Saito K. Energy current correlation in solvable long-range interacting systems. (2019). arXiv[Preprint].arXiv:190608457. doi: 10.1103/PhysRevE.101.042118
72. Wang J, Dmitriev SV, Xiong D. Extremely high length-divergent thermal conductivity in long-range interacting Fermi-Pasta-Ulam Chains. (2019). arXiv[Preprint].arXiv:190611086. doi: 10.1103/PhysRevResearch.2.013179
73. Iubini S, Di Cintio P, Lepri S, Livi R, Casetti L. Heat transport in oscillator chains with long-range interactions coupled to thermal reservoirs. Phys Rev E. (2018) 97:032102. doi: 10.1103/PhysRevE.97.032102
74. Di Cintio P, Iubini S, Lepri S, Livi R. Equilibrium time-correlation functions of the long-range interacting Fermi-Pasta-Ulam model. J Phys A Math Theor. (2019) 52:274001. doi: 10.1088/1751-8121/ab22f7
75. Malevanets A, Kapral R. Mesoscopic model for solvent dynamics. J Chem Phys. (1999) 110:8605. doi: 10.1063/1.478857
76. Ciraolo G, Bufferand H, Di Cintio P, Ghendrih P, Lepri S, Livi R, et al. Fluid and kinetic modelling for non-local heat transport in magnetic fusion devices. Contrib Plasma Phys. (2018) 58:457–64. doi: 10.1002/ctpp.201700222
77. Benenti G, Casati G, Mejía-Monasterio C. Thermoelectric efficiency in momentum-conserving systems. New J Phys. (2014) 16:015014. doi: 10.1088/1367-2630/16/1/015014
78. Di Cintio P, Livi R, Bufferand H, Ciraolo G, Lepri S, Straka MJ. Anomalous dynamical scaling in anharmonic chains and plasma models with multiparticle collisions. Phys Rev E. (2015) 92:062108. doi: 10.1103/PhysRevE.92.062108
79. Upadhyaya M, Aksamija Z. Nondiffusive lattice thermal transport in Si-Ge alloy nanowires. Phys Rev B. (2016) 94:174303. doi: 10.1103/PhysRevB.94.174303
80. Crnjar A, Melis C, Colombo L. Assessing the anomalous superdiffusive heat transport in a single one-dimensional PEDOT chain. Phys Rev Mater. (2018) 2:015603. doi: 10.1103/PhysRevMaterials.2.015603
81. Sun K, Zhang S, Li P, Xia Y, Zhang X, Du D, et al. Review on application of PEDOTs and PEDOT:PSS in energy conversion and storage devices. J Mater Sci Mater Electron. (2015) 26:4438–62. doi: 10.1007/s10854-015-2895-5
82. Barreto R, Carusela M, Monastra A. Nonlinear fluctuating hydrodynamics with many conserved fields: the case of a three-dimensional anharmonic chain. Phys Rev E. (2019) 100:022118. doi: 10.1103/PhysRevE.100.022118
83. Lee V, Wu CH, Lou ZX, Lee WL, Chang CW. Divergent and ultrahigh thermal conductivity in millimeter-long nanotubes. Phys Rev Lett. (2017) 118:135901. doi: 10.1103/PhysRevLett.118.135901
84. Li QY, Takahashi K, Zhang X. Comment on “Divergent and ultrahigh thermal conductivity in millimeter-long nanotubes”. Phys Rev Lett. (2017) 119:179601. doi: 10.1103/PhysRevLett.119.179601
85. Meier T, Menges F, Nirmalraj P, Hölscher H, Riel H, Gotsmann B. Length-dependent thermal transport along molecular chains. Phys Rev Lett. (2014) 113:060801. doi: 10.1103/PhysRevLett.113.060801
86. Benenti G, Casati G, Mejía-Monasterio C, Peyrard M. From thermal rectifiers to thermoelectric devices. In: Lepri S, editor. Thermal Transport in Low Dimensions. Lecture Notes in Physics. Cham: Springer (2016) 365–407. doi: 10.1007/978-3-319-29261-8_10
87. Andresen B. Current trends in finite-time thermodynamics. Angew Chem Int Ed. (2011) 50:2690–704. doi: 10.1002/chin.201123258
88. Shiraishi N, Saito K, Tasaki H. Universal trade-off relation between power and efficiency for heat engines. Phys Rev Lett. (2016) 117:190601. doi: 10.1103/PhysRevLett.117.190601
89. Brandner K, Saito K, Seifert U. Thermodynamics of micro- and nano-systems driven by periodic temperature variations. Phys Rev X. (2015) 5:031019. doi: 10.1103/PhysRevX.5.031019
90. Seifert U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep Prog Phys. (2012) 75:126001. doi: 10.1088/0034-4885/75/12/126001
91. Campisi M, Fazio R. The power of a critical heat engine. Nat Commun. (2016) 7:11895. doi: 10.1038/ncomms11895
92. Pietzonka P, Seifert U. Universal trade-off between power, efficiency, and constancy in steady-state heat engines. Phys Rev Lett. (2018) 120:190602. doi: 10.1103/PhysRevLett.120.190602
93. Koyuk T, Seifert U. Operationally accessible bounds on fluctuations and entropy production in periodically driven systems. Phys Rev Lett. (2019) 122:230601. doi: 10.1103/PhysRevLett.122.230601
94. Callen HB. Thermodynamics and An Introduction to Thermostatics. New York, NY: John Wiley & Sons (1985).
96. Zotos X, Naef FP, Prelovšek P. Transport and conservation laws. Phys Rev E. (1997) 55:11029. doi: 10.1103/PhysRevB.55.11029
97. Zotos X, Prelovšek P. Transport in one dimensional quantum systems. In: Baeriswyl D, Degiorgi L, editors. Strong Interactions in Low Dimensions. Physics and Chemistry of Materials With Low-Dimens. Dordrecht: Kluwer Academic Piublishers (2004).
98. Garst M, Rosch A. Transport in a classical model of a one-dimensional Mott insulator: Influence of conservation laws. Europhys Lett. (2001) 55:66. doi: 10.1209/epl/i2001-00382-3
99. Heidrich-Meisner F, Hoenecker A, Brenig W. Thermal transport of the XXZ chain in a magnetic field. Phys Rev B. (2005) 71:184415. doi: 10.1103/PhysRevB.71.184415
100. Mazur P. Non-ergodicity of phase functions in certain systems. Physica. (1969) 43:533–45. doi: 10.1016/0031-8914(69)90185-2
101. Suzuki M. Ergodicity, constants of motion, and bounds for susceptibilities. Physica. (1971) 51:277. doi: 10.1016/0031-8914(71)90226-6
102. Benenti G, Casati G, Wang J. Conservation laws and thermodynamic efficiencies. Phys Rev Lett. (2013) 110:70604. doi: 10.1103/PhysRevLett.110.070604
103. Luo R, Benenti G, Casati G, Wang J. Thermodynamic bound on heat-to-power conversion. Phys Rev Lett. (2018) 121:080602. doi: 10.1103/PhysRevLett.121.080602
104. Chen S, Wang J, Casati G, Benenti G. Thermoelectricity of interacting particles: a numerical approach. Phys Rev E. (2015) 92:032139. doi: 10.1103/PhysRevE.92.032139
105. Mejía-Monasterio C, Larralde H, Leyvraz F. Coupled normal heat and matter transport in a simple model system. Phys Rev Lett. (2001) 86:5417–20. doi: 10.1103/PhysRevLett.86.5417
106. Larralde H, Leyvraz F, Mejía-Monasterio C. Transport properties of a modified Lorentz gas. J Stat Phys. (2003) 113:197–231. doi: 10.1023/A:1025726905782
107. Datta S. Electronic Transport in Mesoscopic Systems. Cambridge: Cambridge University Press (1995).
108. Whitney RS. Most efficient quantum thermoelectric at finite power output. Phys Rev Lett. (2014) 112:130601. doi: 10.1103/PhysRevLett.112.130601
109. Whitney RS. Finding the quantum thermoelectric with maximal efficiency and minimal entropy production at given power output. Phys Rev B. (2015) 91:115425. doi: 10.1103/PhysRevB.91.115425
110. Mahan GD, Sofo JO. The best thermoelectric. Proc Natl Acad Sci USA. (1996) 93:7436. doi: 10.1073/pnas.93.15.7436
111. Humphrey TE, Newbury R, Taylor RP, Linke H. Reversible quantum Brownian heat engines for electrons. Phys Rev Lett. (2002) 89:116801. doi: 10.1103/PhysRevLett.89.116801
112. Humphrey TE, Linke H. Reversible thermoelectric nanomaterials. Phys Rev Lett. (2005) 94:096601. doi: 10.1103/PhysRevLett.94.096601
113. Saito K, Benenti G, Casati G. A microscopic mechanism for increasing thermoelectric efficiency. Chem Phys. (2010) 375:508–13. doi: 10.1016/j.chemphys.2010.06.009
114. Brantut JP, Grenier C, Meineke J, Stadler D, Krinner S, Kollath C, et al. A thermoelectric heat engine with ultracold atoms. Science. (2013) 342:713. doi: 10.1126/science.1242308
115. Husmann D, Lebrat M, Häusler S, Brantut JP, Corman L, Esslinger T. Breakdown of the Wiedemann-Franz law in a unitary Fermi gas. Proc Natl Acad Sci USA. (2018) 115:8563–68. doi: 10.1073/pnas.1803336115
116. Vasseur R, Moore JE. Nonequilibrium quantum dynamics and transport: from integrability to many-body localization. J Stat Mech. (2016) 2016:064010. doi: 10.1088/1742-5468/2016/06/064010
117. Abanin DA, Altman E, Bloch I, Serbyn M. Many-body localization, thermalization, and entanglement. Rev Mod Phys. (2019) 91:021001. doi: 10.1103/RevModPhys.91.021001
118. Prosen T, Žnidarič M. Matrix product simulations of non-equilibrium steady states of quantum spin chains. J Stat Mech. (2009) 2009:P02035. doi: 10.1088/1742-5468/2009/02/P02035
119. Mejia-Monasterio C, Wichterich H. Heat transport in quantum spin chains. Eur Phys J Spec Top. (2007) 151:113–25. doi: 10.1140/epjst/e2007-00367-4
120. Saito K. Strong evidence of normal heat conduction in a one-dimensional quantum system. Europhys Lett. (2003) 61:34. doi: 10.1209/epl/i2003-00241-3
121. Mejía-Monasterio C, Casati G, Prosen T. Fourier's law in a quantum spin chain and the onset of quantum chaos. Europhys Lett. (2005) 72:520. doi: 10.1209/epl/i2005-10267-y
122. Znidarič M, Prosen T, Benenti G, Casati G, Rossini D. Thermalization and ergodicity in one-dimensional many-body open quantum systems. Phys Rev E. (2010) 81:051135. doi: 10.1103/PhysRevE.81.051135
123. Levy A, Kosloff R. The local approach to quantum transport may violate the second law of thermodynamics. Europhys Lett. (2014) 107:2004. doi: 10.1209/0295-5075/107/20004
124. Balachandran V, Benenti G, Pereira E, Casati G, Poletti D. Heat current rectification in segmented XXZ chains. Phys Rev E. (2019) 99:032136. doi: 10.1103/PhysRevE.99.032136
125. Carrega M, Solinas P, Braggio A, Sassetti M, Weiss U. Functional integral approach to time-dependent heat exchange in open quantum systems: general method and applications. New J Phys. (2015) 17:045030. doi: 10.1088/1367-2630/17/4/045030
126. Tamascelli D, Smirne A, Lim J, Huelga SF, Plenio MB. Efficient simulation of finite-temperature open quantum systems. Phys Rev Lett. (2019) 123:090402. doi: 10.1103/PhysRevLett.123.090402
Keywords: anomalous transport and diffusion, non-linear chains, Kardar Parisi Zhang equation, thermoelectricity, efficiency, multi-particle-collision
Citation: Benenti G, Lepri S and Livi R (2020) Anomalous Heat Transport in Classical Many-Body Systems: Overview and Perspectives. Front. Phys. 8:292. doi: 10.3389/fphy.2020.00292
Received: 12 February 2020; Accepted: 26 June 2020;
Published: 17 September 2020.
Edited by:
Carlos Mejía-Monasterio, Polytechnic University of Madrid, SpainReviewed by:
Hernán Larralde, National Autonomous University of Mexico, MexicoCédric Bernardin, Université Côte d'Azur, France
Copyright © 2020 Benenti, Lepri and Livi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stefano Lepri, c3RlZmFuby5sZXByaUBpc2MuY25yLml0
 Giuliano Benenti
Giuliano Benenti Stefano Lepri
Stefano Lepri Roberto Livi
Roberto Livi