Input Redundancy for Parameterized Quantum Circuits

1. Introduction

Quantum Information Processing proposes to exploit quantum physical phenomena for the purpose of data processing. Conceived in the early 80's [1, 2], recent breakthroughs in building controllable quantum mechanical systems have led to an explosion of activity in the field.

Building quantum computers is a formidable challenge—but so is designing algorithms which, when implemented on them, are able to exploit the advantage that quantum computing is widely believed by experts to have over classical computing on some computational tasks. A particularly compelling endeavor is to make use of near-term quantum computers, which suffer from limited size and the presence of debilitating levels of quantum noise. The field of algorithm design for Noisy Intermediate-Scale Quantum (NISQ) computers has scrambled over the last few years to identify fields of computing, paradigms of employing quantum information processing, and commercial use-cases in order to profit from recent progress in building programmable quantum mechanical devices—limited as they may be at present [3].

One use-case area where quantum advantage might materialize in the near term is that of Artificial Intelligence [3, 4]. The hope is best reasoned for generative tasks: several families of probability distributions have been theoretically proven to admit quantum algorithms for efficiently sampling from them, while no classical algorithm is able or is known to be able to perform that sampling task. Boson sampling is probably the most widely known of these sampling tasks, even though the advantage does not seem to persist in the presence of noise (cf. [5]); examples of some other sampling procedures can be found in references [6, 7].

Promising developments have also been made available in the case of quantum circuits that can be iteratively altered by manipulation of one or several parameters: Du et al. [8] consider so-called Parameterized Quantum Circuits (PQCs) and find that they, too, yield a theoretical advantage for generative tasks. PQCs are occasionally referred to as Quantum Neural Networks (QNNs) (e.g., in [9]) when aspects of non-linearity are emphasized, or as Variational Quantum Circuits [10]. We stick to the term PQC in this paper, without having in mind excluding QNNs or VQCs.

The PQC architectures which have been considered share some common characteristics, but an important design question is how the input data is presented. Input data refers either to a feature vector, or to output of another layer of a larger, potentially hybrid quantum-classical neural network. The fundamental choice is whether to encode digitally or in the amplitudes of a quantum state. Digital encoding usually entails preparing a quantum register in states |b^x〉, where b^x ∈ {0, 1}ⁿ is binary encoding of input datum x. Encoding in the amplitudes of a quantum state, on the other hand, refers to preparing a an n-bit quantum register in a state of the form $|{\varphi }^x\rangle :=\sum _{j=0}^{2^n-1}{\varphi }_j(x)|j\rangle$, where ϕ_j, j = 0, …, 2ⁿ − 1 is a family of encoding functions which must ensure that |ϕ^x〉 is a quantum state for each x, i.e., that $\sum _j{\left|{\varphi }_j(x)\right|}^2=1$ holds for all x. We refer the reader to the discussion of these concepts in Schuld and Petruccione [11] for further details.

The present paper deals with redundancy in the input data, i.e., giving the same datum several times. The most straightforward concept here is that of “tensorial” encoding [12]. Here, several quantum registers are prepared in a state which is the tensor product of the corresponding number of identical copies of a data-encoding state, i.e., |ϕ^x〉⊗⋯⊗|ϕ^x〉. For example, Mitarai et al. [13], propose the following construction: To encode a real number x close to 0, they choose the state

$\begin{array}{l}|{\varphi }^x\rangle =R_y(\arcsin (x)/2)|0\rangle =\sin (\arcsin (x)/2)|0\rangle \\ +\cos (\arcsin (x)/2)|1\rangle ,& (1)\end{array}$

where $R_y(\theta ):=e^{-i\theta {\sigma }_Y/2}$ is the 1-qubit Pauli rotation around the Y-axis (and σ_Y the Pauli matrix). But then, to construct a PQC that is able to learn polynomials of degree n in a single variable, they encode the polynomial variable x into n identical copies, ${\otimes }_{j=1}^n|{\varphi }^x\rangle$. It is noteworthy, and the starting point of our research, that the number of times that the input, x, is encoded redundantly, depends on the complexity of the learning task.

Encoding the input several times redundantly, as in tensorial encoding, is probably motivated by the quantum no-cloning principle. While classical circuits and classical neural networks can have fan-out—the output of one processing node (gate, neuron, …) can be the input to several others—the no-cloning principle of quantum mechanics forbids to duplicate data which is encoded in the amplitudes of a quantum state. This applies to PQCs, and, specifically, to the input that is fed into a PQC, if the input is encoded in the amplitudes of input states.

1.1. The Research Presented in This Paper

The no-cloning principle suggests that duplicating input data redundantly is unavoidable. The research presented in this paper aims to lower bound how often the data has to be redundantly encoded, if a given function is to be learned. The novelty in this paper lies in establishing that these lower bounds are possible. For that purpose, the cases for which we prove lower bounds are natural, but not overly complex, thus highlighting the principle over the application.

The objects of study of this paper are PQCs of the following form. The input consists of a single real number x, which is encoded into amplitudes by applying a multi-qubit Hamiltonian evolution of the form e^−iη(x)H at one point (no redundancy), or several points in the quantum circuit. The function η and Hamiltonian H may be different at the different points the quantum circuit.

Hence, our definition of “input” is quite general, and allows, for example, that the input is given in the middle of a quantum circuit—mimicking the way how algorithms for fault-tolerant quantum computing operate on continuous data: the subroutine for accessing the data be called repeatedly; cf., e.g., the description of the input oracles in van Apeldoorn and Gilyén [14]. It should be pointed out, however, that general state preparation procedures as in Harrow et al. [15] and Schuld et al. [12] cannot not be studied with the tools of this paper, because they apply many operations with parameters derived from a collection of inputs, instead of a single input.

Our lower bound technique is based on Fourier analysis.

1.2. Example

Take, as example, the parameterized quantum circuits of Mitarai et al. [13] mentioned above. Comparing with (1) shows: The single real input x close to 0 is prepared by performing, at n different positions in the quantum circuit, Hamiltonian evolution $e^{-i{\eta }_j(x)H_j}$ with η_j(x): = arcsin(x), and H_j: = σ_Y/2, for j = 1, …, n.

We say that the input x to the quantum circuits of Mitarai et al. are encoded with input redundancy n—meaning, the input is given n times.

The example highlights the ostensible wastefulness of giving the same data n times, and the question naturally arises whether a more clever application of possibly different rotations would have reduced the amount of input redundancy.

In the case of Mitarai et al.'s example, it can easily be seen—from algebraic arguments involving the quantum operations which are performed—that, in order to produce a polynomial of degree n, redundancy n is best possible for the particular way of encoding the value x by applying the Pauli rotation to distinct qubits, we leave that to the reader. However, already the question whether by re-using the same qubit a less “wasteful” encoding could have been achieved is quite not so easy. Our Fourier analysis based techniques give lower bounds for more general encodings, in particular, for applying arbitrary single-qubit Pauli rotations to an arbitrary set of qubits at arbitrary time during the quantum circuit.

Figure 1 next page shows the schematic of quantum circuits with input x. The setup resembles that of a neural network layer. The j'th “copy” of the input is made available in the quantum circuit by, at some time, performing the unitary operation $e^{2\pi i{\eta }_j(x)H_j}$ on one qubit, where η_j(x) = φ(a_jx + b_j), for an “activation function” φ. (We switch here to adding the factor 2π, to be compatible with our Fourier approach).

FIGURE 1

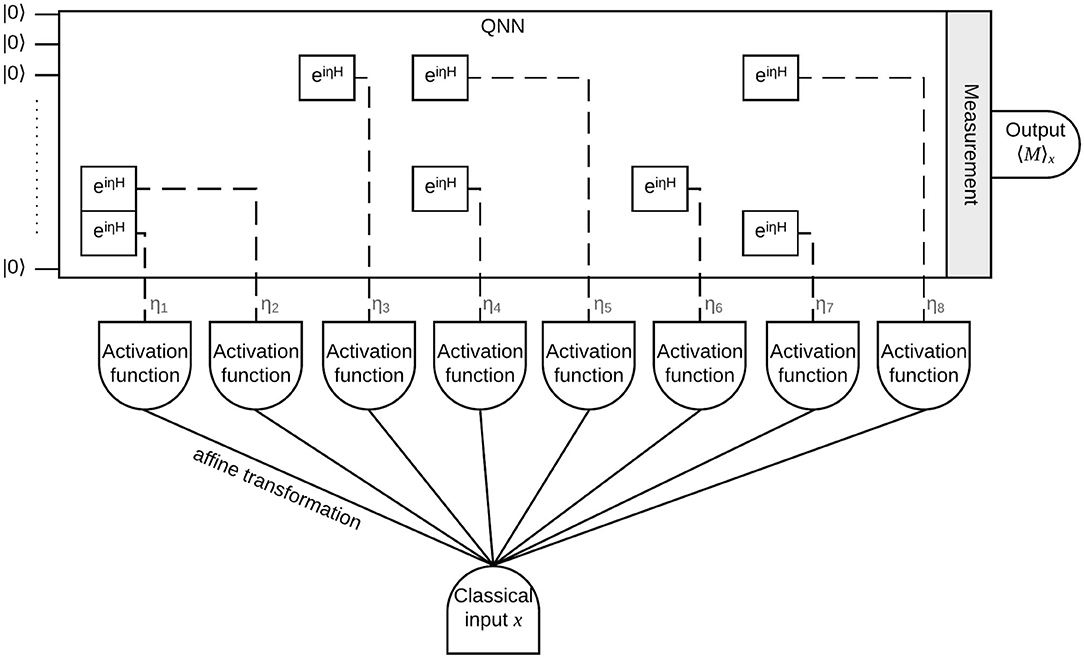
Figure 1. Schematic for the PQCs we consider. The classical input x, after being subjected to a transformations η_j(x) = φ(a_jx + b_j) with “activation function” φ, is fed into the QNN/PQC through Hamiltonian evolution operations $e^{2\pi i{\eta }_j(x)H_j}$. Quantum operations which do not participate in entering the input data into the quantum circuit are not shown; these include the operations which depend on the training parameters θ.

In the above-mentioned example in Mitarai et al. [13], the activation function is φ: = arcsin. Figure 1 aims at making clear that the input can be encoded by applying different unitary operations to different qubits, or to the same qubit several times, or any combination of these possibilities. Generalization of our results to several inputs is straightforward, if the activation functions in Figure 1 have a single input.

1.3. Our Results

As hinted above, our intention with this paper is to establish, in two natural examples, the possibility of proving lower bounds on input redundancy. The first example is what we call “linear” input encoding, where the activation function is φ(x) = x. The second example is Mitarai et al. [13] approach, where the activation function is φ(x) = arcsin(x).

For both examples, we prove lower bounds on the input redundancy in terms of linear-algebraic complexity measures of the target function. We find the lower bounds to be logarithmic, and the bounds are tight.

To the best of our knowledge, our results give the first quantitative lower bounds on input redundancy. These lower bounds, as well as other conclusions derived from our constructions, should directly influence design decisions for quantum neural network architectures.

1.4. Paper Organization

In the next section we review the background on the PQC model underlying our results. Sections 3 and 4 contain the results on linear and arcsine input encoding, respectively. We close with a discussion and directions of future work.

2. Background

2.1. MiNKiF PQCs

We now describe parameterized quantum circuits (PQCs) in more detail. Denote by

$\begin{array}{ll}{U}_H(\alpha ):\rho \mapsto e^{-2\pi i\alpha H}\rho e^{2\pi i\alpha H}& (2)\end{array}$

the quantum operations of an evolution with Hamiltonian H (operating on some set of qubits); the 2π factor is just a convenience for us and introduces no loss of generality. Following, in spirit, Mitarai et al. [13], in this paper we consider quantum circuits which apply quantum operations each of which is one of the following:

1. An operation as in (2), with a parameter α: = η which will encode input, x (i.e., η is determined by x);

2. An operation as in (2), with a parameter α: = θ which will be “trained” (we refer to these parameters as the training parameters);

3. Any quantum operation not defined by any parameter (although its effect can depend on θ, η, e.g., via dependency on measurement results).

Denote the concatenated quantum operation by ${E}(\eta ,\theta )$. Now let M be an observable, and consider its expectation value on the state which results if the parameterized quantum circuit is applied to a fixed input state ρ₀, e.g., ρ₀: = |0〉〈0|. We denote the expectation value with parameters set to η, θ by f(η, θ):

$\begin{array}{ll}f:{ℝ}^n\times {ℝ}^m\to ℝ:(\eta ,\theta )\mapsto =\text{tr}(M{E}(\eta ,\theta ){\rho }_0).& (3)\end{array}$

The PQCs could have multiple outputs, but we do not consider that in this paper. We refer to PQCs of this type as MiNKiF PQCs, as [13] realized the fundamental property

$\begin{array}{ll}{\partial }_{{\theta }_j}f(\eta ,\theta )=\pi \left(f(\eta ,\theta +\frac{1}{4}{e}_j)-f(\eta ,\theta -\frac{1}{4}{e}_j)\right),& (4)\end{array}$

where e_j is the vector with a 1 in position j and 0 otherwise. This equation characterizes trigonometric functions. (The same relation holds obviously for derivatives in η_j direction.)

The setting we consider in this paper is the following.

• The training parameters, θ, have been trained perfectly and are thus ignored, in other words, omitting the θ argument, we conveniently consider f to be a function defined on ℝⁿ (instead of on ℝⁿ × ℝ^m);

• The inputs, x, are real numbers;

• The parameters η of f are determined by x, i.e., η is replaced by (φ(a₁x + b₁), …, φ(a_nx + b_n)), where a, b ∈ ℝⁿ; in other words, we study the function

$\begin{array}{l}ℝ\to ℝ:x\mapsto f(\phi (a_{1}x+b_1),\dots ,\phi (a_{n}x+b_n)).\end{array}$

We allow a, b to depend on the target function¹.

This setting is restrictive only in as far as the input is one-dimensional; the reason for this restriction is that this paper aims to introduce and demonstrate a concept, and not be encyclopedic or obtain the best possible results.

This setting clearly includes the versions of amplitude encoding discussed in the introduction by applying operations U_Hj(φ(a_jx+b_j)) to |0〉〈0| states (of appropriately many qubits) for several j's, with suitable H_j's. However, the setting is more general in that it doesn't restrict to encode the input near the beginning of a quantum circuit, indeed, the order of the types of quantum operations is completely free.

To summarize, we study the functions

$\begin{array}{l}f:ℝ\to ℝ:\eta \mapsto f(\eta )\\ :=\text{ tr}(M{V}_n{U}_n({\eta }_n)V_{n-1}{U}_{n-1}({\eta }_{n-1})\dots V_1{U}_1({\eta }_1)V_0{\rho }_0)& (\mathrm{5a})\end{array}$

where

$\begin{array}{ll}{U}_1:=U_{H_1},\dots ,U_n:=U_{H_n}\text{for Hamiltonians }{H}_j,j\text{ = 1},\dots ,\text{n}.& (\mathrm{5b})\end{array}$

and

$\begin{array}{ll}ℝ\to ℝ:x\mapsto f(\eta (x))& (6)\end{array}$

where $\eta :ℝ\to {ℝ}^n:x\mapsto \phi (a_{1}x+b_1),\dots ,\phi (a_{n}x+b_n)$. Then we ask the question: How large is the space of the x : f(η(x)), for a fixed activation function φ, but variable vectors a, b ∈ ℝⁿ?

2.2. Fourier Calculus on MiNKiF Circuits

This paper builds on the simple observation of [16] that, under assumptions which are reasonable for near-term gate-based quantum computers, the Fourier spectrum, in the sense of the Fourier transform of tempered distributions, is finite and can be understood from the eigenvalues of the Hamiltonians. In particular, if, for each of the Hamiltonians H_j, j = 1, …, n, the differences of the eigenvalue of H_j are integer multiples of a positive number κ_j, then η↦f(η) is periodic.

Take, for example, the case of Pauli rotations ($e^{-2\pi i{\sigma }_{\star }/2}$ in our notation): There, each of the H_j is of the form σ_uj/2 (with u_j ∈ {x, y, z}). The eigenvalues of H_j are ±½, the eigenvalue differences are 0, ±1, and f : ℝⁿ → ℝ is 1-periodic² in every parameter, with Fourier spectrum contained in

$\begin{array}{ll}{\mathbb{Z}}_3^n:={\left\{0,\pm 1\right\}}^n.& (7)\end{array}$

More generally, if the H_j have eigenvalues, say, ${\lambda }_j^{(0)}\in ℝ$ and ${\lambda }_j^{(s)}={\lambda }_j^{(0)}+s$ for s = 1, …, K_j, then the eigenvalue differences are {−K_j, …, K_j}, and f : ℝⁿ → ℝ is 1-periodic in every parameter, with Fourier spectrum contained in ${\prod }_{j=1}^n\{-K_j,\dots ,K_j\}$.

We refer to [16] for the (easy) details. In this paper, focusing on the goal of demonstrating the possibility to prove lower bounds on the input redundancy, we mostly restrict to 2-level Hamiltonians with eigenvalue difference 1 (such as one-half times a tensor product of Pauli matrices), which gives us the nice Fourier spectrum (7), commenting on other spectra only en passant.

For easy reference, we summarize the discrete Fourier analysis properties of the expectation value functions that we consider in the following remark. The proof of the equivalence of the three conditions is contained in the above discussions, except for the existence of a quantum circuit for a given multi-linear trigonometric polynomial, for which we defer [17], as it is not the topic of this paper.

REMARK 1. The following three statements are equivalent. If they hold, we refer to the function as an expectation value function, for brevity (suppressing the condition on the eigenvalues of the Hamiltonians). The input redundancy of the function is n.

1. The function f is of the form 5, where the H_j, j = 1, …, n, have eigenvalues ±½.

2. The function f is a real-valued function ℝⁿ → ℝ which is 1-periodic in every parameter, and its Fourier spectrum is contained in ${\mathbb{Z}}_3^n$. Hence,

$\begin{array}{ll}f(\eta )={\displaystyle \sum _{w\in {\mathbb{Z}}_3^n}}\widehat{f}(w)e^{2\pi iw•\eta }& (8)\end{array}$

where $w•\eta :=\sum _{j=1}^n{\eta }_j{w}_j$ is the dot product (computed in ℝ), and $\widehat{f}$ the usual periodic Fourier transform of f, i.e., $\widehat{f}(w)={\int }_{{\left[0,1\right]}^n}{e}^{-2\pi iw•\eta }f(\eta )d\eta$.

3. The function f is a multi-linear polynomial in the sine and cosine functions, i.e.,

$\begin{array}{ll}f(\eta )={\displaystyle \sum _{\tau \in {\left\{1,cos,sin\right\}}^n}}{\tilde{f}}_{\tau }{\displaystyle \prod _{j=1}^n}{\tau }_j(2\pi {\eta }_j),& (9)\end{array}$

(where “1” under the sum denotes the all-1 function).

3. Linear Input Encoding

We start discussing the case where the input parameters are affine functions of the input variable, e.g., φ = id and η(x) = x · a + b for some a, b ∈ ℝⁿ, so the input redundancy is n.

For a ∈ ℝⁿ define

$\begin{array}{ll}{K}_a:=\left\{w•a|w\in {\mathbb{Z}}_3^n\right\},& (\mathrm{10a})\end{array}$

$\begin{array}{ll}\text{spread}(a):=\frac{1}{2}|K_a\backslash \left\{0\right\}|,& (\mathrm{10b})\end{array}$

with |·| denoting set cardinality; we refer to spread(a) as the spread of a. We point the reader to the fact that K_a is symmetric around 0 ∈ ℝ and 0 ∈ K_a, so that the spread is a non-negative integer.

For every k ∈ ℝ, consider the function

$\begin{array}{ll}{\chi }_k:ℝ\to ℂ:t\mapsto e^{2\pi ikt}.& (11)\end{array}$

These functions are elements of the vector space ℂ^ℝ of all complex-valued functions on the real line. We note the following well-known fact.

LEMMA 2. The functions χ_k,k ∈ ℝ, defined in (11) are linearly independent (in the algebraic sense, i.e., every finite subset is linearly independent).

Moreover, for every x₀ ∈ ℝ and ε > 0, the restrictions of these functions to the interval ]x₀ − ε, x₀ + ε[ are linearly independent.

Proof: We refer the reader to Appendix 1 for the first statement and only prove the second one.

Suppose that for some finite set K ⊂ ℝ and complex numbers α_k, k ∈ K we have $g(z):=\sum _{j=1}^m{\alpha }_j{\chi }_{k_j}(z)=0$ for all z ∈ ]x₀ − ε, x₀ + ε[. Since g is analytic and non-zero analytic functions can only vanish on a discrete set, we then must also have g(z) = 0 for all z ∈ ℂ. This means that the linear dependence on an interval implies linear dependence on the whole real line. This proves the second statement, and the proof of Lemma 2 is completed.

We can now give the definition of the quantity which will lower-bound the input redundancy for linear input encoding.

DEFINITION 3. The Fourier rank of a function h : ℝ → ℝ at a point x₀ ∈ ℝ is the infimum of the numbers r such that there exists an ε > 0, a set K ⊂ ℝ \ {0} of size 2r, and coefficients α_k ∈ ℂ, k ∈ {0}∪K such that

$\begin{array}{ll}h(x)={\displaystyle \sum _{k\in \{0\}\cup K}{\alpha }_k}{\chi }_k(x)forallx\in ]x_{\text{0}}-\epsilon ,x_{\text{0}}\text{+ }\epsilon [.& (12)\end{array}$

Note that the Fourier rank can be infinite, and if it is finite, then it is a non-negative integer. Indeed, from h^* = h it follows that $\sum _{k\in \left\{0\right\}\cup K}{\alpha }_k{\chi }_k=\sum _{k\in \left\{0\right\}\cup K}{\alpha }_k^{*}{\chi }_{-k}$, so that by the linear independence of the χ's (Lemma 2) we have ${\alpha }_{-k}={\alpha }_k^{*}$, which means that in a minimal representation of h, the set K is symmetric around 0 ∈ ℝ.

EXAMPLES.

• Constant functions have Fourier rank 0 at every point.

• The trigonometric functions x ↦ cos(κx + ϕ), with κ ≠ 0, have Fourier rank 1 at every point.

• Trigonometric polynomials of degree d, $x\mapsto \sum _{j=0}^d{\alpha }_j{cos}^j({\kappa }_{j}x+{\varphi }_j)$, have Fourier rank d at every point, if α_d ≠ 0, κ_d ≠ 0.

• The function x ↦ |sin(πx)| has Fourier rank 1 at every x₀ ∈ ℝ \ ℤ and infinite Fourier rank at the points x₀ ∈ ℤ.

• The function x ↦ x has infinite Fourier rank at every point.

THEOREM 4. Let f be an expectation value function, i.e., as in Remark 1. Moreover, let a, b ∈ ℝⁿ, and h : ℝ → ℝ : x ↦ f(x · a + b). For every x₀ ∈ ℝ, the Fourier rank of h at x₀ is less than or equal to the spread of a.

Proof: With the preparations above, this is now a piece of cake. Let x₀ ∈ ℝ and set ε : = 1. With K_a as defined in (10), for x ∈ ]x₀ − ε, x₀ + ε[, we have

$\begin{array}{l}h(x)=f(x\cdot a+b)={\displaystyle \sum _{w\in {\mathbb{Z}}_3^n}\widehat{f}}(w)e^{2\pi iw•(x·a+b)}\text{ [Remark 12]}\\ ={\displaystyle \sum _{w\in {\mathbb{Z}}_3^n}\widehat{f}}(w)e^{2\pi iw•b}{e}^{2\pi ix·w•a}\\ ={\displaystyle \sum _{k\in K_a}}{\displaystyle (}{\displaystyle \sum _{\begin{array}{c}w\in {\mathbb{Z}}_3^n,\\ w•a=k\end{array}}\widehat{f}}(w)e^{2\pi iw•b})e^{2\pi ix·k}\\ ={\displaystyle \sum _{k\in K_a}{\alpha }_k}{\chi }_k(x),\end{array}$

where we let

$\begin{array}{l}{\alpha }_k:={\displaystyle \sum _{\begin{array}{c}w\in {\mathbb{Z}}_3^n,\\ w•a=k\end{array}}}\widehat{f}(w)e^{2\pi iw•b}\end{array}$

This shows that h has a representation as in (12) with K: = K_a \ {0}. It follows that the Fourier rank of h is bounded from above by |K_a|/2 = spreada. This completes the proof of Theorem 4.

The theorem allows us to give the concrete lower bounds for the input redundancy.

COROLLARY 5. Let h be a real-valued function defined in some neighborhood of a point x₀ ∈ ℝ.

Suppose that in a neighborhood of x₀, h is equal to an expectation value function with linear input encoding, i.e., there is an n, a function f as in Remark 1, vectors a, b ∈ ℝⁿ, and an ε > 0 such that h(x) = f(x · a + b) holds for all x ∈ ]x₀ − ε, x₀ + ε[.

The input redundancy, n, is greater than or equal to log₃(r + 1), where r is the Fourier rank of h at x₀.

To represent a function h by a MiNKiF PQC with linear input encoding in a tiny neighborhood of a given point x₀, the input redundancy must be at least the logarithm of the Fourier rank of h at x₀.

Proof of Corollary 5: For every a ∈ ℝⁿ, we have $K_a\le 3^n$, by the definition of K_a, and hence spread(a) ≤ (3ⁿ − 1)/2.

We allow that a, b are chosen depending on h (see the Remark 6 below). Theorem 4 gives us the inequality

$\begin{array}{l}r\le {\displaystyle \underset{a}{max}}\text{ spread}(a)\le (3^n-1)/2,\end{array}$

which implies n ≥ log₃(2r + 1) ≥ log₃(r + 1), as claimed. (We put the +1 to make the expression well-defined for r = 0.) This concludes the proof of Corollary 5.

REMARK 6. If the entries of a are all equal up to sign, then we have spread(a) = n. It can be seen that if the entries of a are chosen uniformly at random in [0, 1], then spread(a) = (3ⁿ − 1)/2. Hence, it seems that some choices for a are better than others. Moreover, looking into the proof of Theorem 4 again, we see that the χ_k, k ∈ K_a, must suffice to represent (or approximate) the target function, and that the entries of b play a role in which coefficients α_k can be chosen for a given a. Hence, it is plausible that the choices of a, b should depend on h.

REMARK 7. Our restriction to Hamiltonians with two eigenvalues leads to the definition of the spread in (10). If the set of eigenvalue distances of the Hamiltonian encoding the input η_j is D_j ⊂ ℝ, then, for the definition of the spread, we must put this:

$\begin{array}{l}{K}_a:=\{w•a|w\in {\displaystyle \prod _{j=1}^n}{D}_j\}.\end{array}$

Theorem 4 and Corollary 5 remain valid, with essentially the same proofs, but with a higher base for the logarithm.

4. Arcsine Input Encoding

We now consider the original situation of the example in Mitarai et al. [13], where the activation function is φ = arcsin. More precisely, for a, b ∈ ℝⁿ, we consider

$\begin{array}{l}\eta (x):=arcsin((ax+b)/(2\pi )).\end{array}$

Abbreviating s_j: = a_jx + b_j and $c_j:=\sqrt{1-s_j^2}$ for j = 1, …, n, Remark 13, gives us that the expectation value functions with arcsine input encoding are of the form

$\begin{array}{l}h(x)=f(\eta (x))={\displaystyle \sum _{\begin{array}{c}S,C\subseteq [n]\\ S\cap C=\varnothing \end{array}}{\tilde{f}}_{S,C}}{\displaystyle \prod _{j\in S}{s}_j}{\displaystyle \prod _{j\in C}{c}_j}\\ ={\displaystyle \sum _{\begin{array}{c}S,C\subseteq [n]\\ S\cap C=\varnothing \end{array}}{\tilde{f}}_{S,C}}{\displaystyle \prod _{j\in S}(a_{j}x+b_j)}{\displaystyle \prod _{j\in C}\sqrt{1-{(a_{j}x+b_j)}^2}},& (13)\end{array}$

where we use the common shorthand [n]: = {1, …, n}, and set ${\tilde{f}}_{S,C}:={\tilde{f}}_{\tau (S,C)}$ with τ_j(S, C) = sin if j ∈ S, τ_j(S, C) = cos if j ∈ C, and τ_j(S, C) = id otherwise.

Consider a formal expression of the form

$\begin{array}{ll}{\mu }_{S,C}^{(a,b)}:={\displaystyle \prod _{j\in S}}(a_{j}x+b_j){\displaystyle \prod _{j\in C}}\sqrt{1-{(a_{j}x+b_j)}^2}& (14)\end{array}$

where x is a variable (for arbitrary a, b ∈ ℝⁿ and S, C ⊆ [n] with S ∩ C = Ø). We call it an sc-monomial of degree |S| + |C|. An sc-monomial can be evaluated at points x ∈ ℝ for which the expression under the square root is not a negative real number, i.e., in the interval

$\begin{array}{ll}{I}_{\mu }:={\displaystyle \underset{j\in C}{\cap }}\left]\frac{-1-b_j}{a_j},\frac{+1-b_j}{a_j}\right[& (15)\end{array}$

(which could be empty), and it defines an analytic function there. Note, though, that it can happen that an sc-monomial can be continued to an analytic function on a larger interval than I_μ. The obvious example where that happens is this: For j, j′ ∈ C with j ≠ j′ we have $(a_j,b_j)=\pm (a_{j^{\prime }},b_{j^{\prime }})$. In that case, the formal power series of the sc-monomial simplifies, and omitting the interval $\left]\frac{-1-b_j}{a_j},\frac{+1-b_j}{a_j}\right[$ (also for j′) from (15) makes the intersection larger.

The following technical fact can be shown (cf. [17]).

LEMMA 8. Let $g=\sum _j{\alpha }_j{\mu }_j$ be a linear combination of sc-monomials with degrees at most d, and suppose that ⋂_jI_μj ≠ Ø. If an analytic continuation of g to a function $\tilde{g}:ℝ\to ℝ$ exists, then $\tilde{g}$ is a polynomial of degree at most d.

From this lemma, we obtain the following result.

COROLLARY 9. Let h : ℝ → ℂ be an analytic function, and x₀ ∈ ℝ.

Suppose that in a neighborhood of x₀, h is equal to an expectation value function with arcsine input encoding, i.e., there is an n, a function f as in Remark 1, vectors a, b ∈ ℝⁿ, and an ε > 0 such that

1. −1 ≤ x · a_j + b_j ≤ +1 for all x ∈ ]x₀ − ε, x₀ + ε[, and

2. h(x) = f(arcsin(x · a + b)) holds for all x ∈ ]x₀ − ε, x₀ + ε[.

Then h is a polynomial, and the input redundancy, n, is greater than or equal to the degree of h.

To represent a polynomial h by a MiNKiF PQC with arcsine input encoding in a tiny neighborhood of a given point x₀, the input redundancy must be at least the degree of h.

Proof of Corollary 9: Let us abbreviate g : x ↦ f(arcsin(x · a + b)):]x₀ − ε, x₀ + ε[ → ℝ. From the discussion above, we know that g is a linear combination of sc-monomials.

Both functions h and g are analytic, and they coincide on an interval. Hence, g has an analytic continuation, h, to the real line so that Lemma 8 is applicable, and states that h is a polynomial with degree at most n. This completes the proof of Corollary 9.

As indicated in the introduction, in the special case which is considered in Mitarai et al. [13]—where the input amplitudes are stored (by rotations) in n distinct qubits before any other quantum operation is performed—this can be proved by looking directly at the effect of a Pauli transfer matrix on the mixed state vector in the Pauli basis. Our corollary shows that this effect persists no matter how the arcsine-encoded inputs are spread over the quantum circuit.

The corollary allows us to lower bound the input redundancy for some functions.

EXAMPLES. There is no PQC with arcsine input encoding that represents the function x ↦ sinx (exactly) in a neighborhood any point. Indeed, the same holds for any analytic function defined on the real line which is not a polynomial: the exponential function, the sigmoid function, arcus tangens, …

Unfortunately, from these impossibility results, no approximation error lower bounds can be derived. Indeed, in their paper [13], Mitarai et al. point out that, due to the $\sqrt{·}$ terms, the functions represented by the expectation values can more easily represent a larger class of functions than polynomials.

To give lower bounds for the representation of functions which are not analytic on the whole real line, we proceed as follows. For fixed n ≥ 1, x₀ ∈ ℝ and a, b ∈ ℝⁿ, denote by $M_{x_0}^{n;a,b}$ the vector space spanned by all functions of the form ]x₀ − ε, x₀+ε[ → ℝ : x ↦ f(arcsin(x · a + b)) for an³ ε > 0, where f ranges over all expectation value functions with input redundancy n, i.e., functions as in Remark 1, a, b ∈ ℝⁿ satisfy −1 < a_jx₀ + b_j < +1, and the arcsin is applied to each component of the vector.

PROPOSITION 10. The vector space $M_{x_0}^{n;a,b}$ has dimension at most 3ⁿ, and is spanned by the sc-monomials (14) of degree n.

Proof: With a, b fixed, there are at most 3ⁿ sc-monomials (14) of degree n, as S, C ⊆ [n] and S ∩ C = Ø hold. Hence, the statement about the dimension follows from the fact that the elements of $M_{x_0}^{n;a,b}$ are generated by sc-monomials.

The fact that the sc-monomials generate the expectation value functions with arcsine input-encoding of redundancy n is just the statement of (13) above. This concludes the proof of Proposition 10.

We can now proceed in analogy to the case of linear input encoding. Let us define the sc-rank at x₀ of a function h defined in a neighborhood of x₀ as the infimum over all r for which there exist sc-monomials μ₁, …, μ_r, an ε > 0, and real numbers α₁, …, α_r such that x₀∈⋂_jI_μu, and

$h(x)={\displaystyle \sum _{j=1}^r{\alpha }_j}{\mu }_j(x)\text{\hspace{1em}for all }x\in ]x_{\text{0}}-\epsilon ,x_{\text{0}}\text{+ }\epsilon [.$

Proposition 10 now directly implies the following result.

COROLLARY 11. Let h be a real-valued function defined in some neighborhood of a point x₀ ∈ ℝ.

Suppose that in a neighborhood of x₀, h is equal to an expectation value function with arcsine input encoding, i.e., there is an n, a function f as in Remark 1, vectors a, b ∈ ℝⁿ, and an ε > 0 such that h(x) = f(arcsin(x · a + b)/(2π)) holds for all x ∈ ]x₀ − ε, x₀ + ε[.

The input redundancy, n, is greater than or equal to log₃(r), where r is the sc-rank of h at x₀.

To represent a function h by a MiNKiF PQC with arcsine input encoding in a tiny neighborhood of a given point x₀, the input redundancy must be at least the logarithm of the sc-rank of h at x₀.

We conclude the section with a note on the choice of the parameters a, b.

REMARK 12. It can be seen [17] that the dimension of the space $M_{x_0}^n$ is 3ⁿ, if a_j, b_j j = 1, …, n are chosen in general position, but only O(n) if a is a constant multiple of the all-ones vector. Moreover, as indicated in Proposition 10, the basis elements which span the space depend on a, b, and hence the space $M_{x_0}^{n;a,b}$ will in general be different for different choices of a, b. Again, we find that it is plausible that the choices of a, b should depend on the target function.

5. Conclusions and Outlook

To the best of our knowledge, our results give the first rigorous theoretical quantitative justification of a routine decision for the design of parameterized quantum circuit architectures: Input redundancy must be present if good approximations of functions are the goal.

Both activation functions we have considered give clear evidence that input redundancy is necessary, and grows at least logarithmically with the “complexity” of the function: The complexity of a function f with respect to a family ${B}$ of “basis functions” is the number of functions from the family which are needed to obtain f as a linear combination. In our results, the function family ${B}$ depends on the activation function. In the case of linear input encoding (activation function “identity”), the basis functions are trigonometric functions t ↦ e^2πikt, whereas for the arcsin activation function, we obtain the basis monomials (14) already used, in a weaker form, in Mitarai et al. [13].

From Remarks 6 and 12 we see that the weights a, b, i.e., the coefficients in the affine transformation links in Figure 1, should have to be variable in order to ensure a reasonable amount of expressiveness in the function represented by the quantum circuit. We use the term variational input encoding to refer to the concept of training the parameters involved in the encoding with other model parameters. A recent set of limited experiments [18] indicate that variational input encoding improves the accuracy of Quantum Neural Networks in classification tasks.

While we emphasize the point that this paper demonstrates a concept—lower bounds for input redundancy can be proven—there are a few obvious avenues to improve our results.

Most importantly, our proofs rely on exactly representing a target function. This is an unrealistic scenario. The most pressing task is thus to give lower bounds on the input redundancy when an approximation of the target function with a desired accuracy ε > 0 in a suitable norm is sufficient.

Secondly, we thank an anonymous reviewer for pointing out to us that lower bounds for many more activation functions could be proved.

Finally, Remark 1 mentions that for every multi-linear trigonometric polynomial f, there is a PQC whose expectation value function is precisely f. It would be interesting to lower-bound a suitable quantum-complexity measure of the PQCs representing a function, e.g., circuit depth. While comparisons of the quantum vs. classical complexity of estimating expectation values have attracted some attention [19], to our knowledge, the same question in the “parameterized setting” has not been considered.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

DT contributed the realization that lower bounds could be obtained, and sketches of the proofs. FG contributed the details of the proofs and the literature overview. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the Estonian Research Council, ETAG (Eesti Teadusagentuur), through PUT Exploratory Grant #620. DT was partly supported by the Estonian Centre of Excellence in IT (EXCITE, 2014-2020.4.01.15-0018), funded by the European Regional Development Fund.

Conflict of Interest

DT was employed by the company Ketita Labs OÜ.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This manuscript has been released as a pre-print on arXiv (arXiv:1901.11434).

Footnotes

1. ^Cf. Remarks 6 and 12. Indeed, our analysis suggests that the a, b should be training parameters if the goal is to achieve high expressivity; see the Conclusions.

2. ^This is where the factor 2π in the exponent is used.

3. ^Mathematically rigorously speaking, $M_{x_0}^{n;a,b}$ is the germ of functions at x₀.

References

1. Feynman RP. Simulating physics with computers. Int J Theor Phys. (1982) 21:467–88. doi: 10.1007/BF02650179

CrossRef Full Text | Google Scholar

2. Manin II. Vychislimoe i nevychislimoe. Moscow: Sov. Radio (1980).

3. Mohseni M, Read P, Neven H, Boixo S, Denchev V, Babbush R, et al. Commercialize quantum technologies in five years. Nat News. (2017) 543:171. doi: 10.1038/543171a

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Perdomo-Ortiz A, Benedetti M, Realpe-Gómez J, Biswas R. Opportunities and challenges for quantum-assisted machine learning in near-term quantum computers. Quant Sci Technol. (2018) 3:030502. doi: 10.1088/2058-9565/aab859

CrossRef Full Text | Google Scholar

5. Neville A, Sparrow C, Clifford R, Johnston E, Birchall PM, Montanaro A, et al. Classical boson sampling algorithms with superior performance to near-term experiments. Nat Phys. (2017) 13:1153. doi: 10.1038/nphys4270

CrossRef Full Text | Google Scholar

6. Bremner MJ, Montanaro A, Shepherd DJ. Average-case complexity versus approximate simulation of commuting quantum computations. Phys Rev Lett. (2016) 117:080501. doi: 10.1103/PhysRevLett.117.080501

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Farhi E, Harrow AW. Quantum supremacy through the quantum approximate optimization algorithm. arXiv. (2016) 160207674.

Google Scholar

8. Du Y, Hsieh MH, Liu T, Tao D. The expressive power of parameterized quantum circuits. arXiv. (2018) 181011922.

Google Scholar

9. Farhi E, Neven H. Classification with quantum neural networks on near term processors. arXiv. (2018) 180206002.

Google Scholar

10. McClean JR, Romero J, Babbush R, Aspuru-Guzik A. The theory of variational hybrid quantum-classical algorithms. New J Phys. (2016) 18:023023. doi: 10.1088/1367-2630/18/2/023023

CrossRef Full Text | Google Scholar

11. Schuld M, Petruccione F. Supervised Learning with Quantum Computers. Vol. 17. Cham: Springer (2018).

PubMed Abstract | Google Scholar

12. Schuld M, Bocharov A, Svore K, Wiebe N. Circuit-centric quantum classifiers. arXiv. (2018) 180400633.

Google Scholar

13. Mitarai K, Negoro M, Kitagawa M, Fujii K. Quantum circuit learning. Phys Rev A. (2018) 98:032309. doi: 10.1103/PhysRevA.98.032309

CrossRef Full Text | Google Scholar

14. van Apeldoorn J, Gilyén A. Improvements in quantum SDP-solving with applications. arXiv. (2018) 180405058.

Google Scholar

15. Harrow AW, Hassidim A, Lloyd S. Quantum algorithm for linear systems of equations. Phys Rev Lett. (2009) 103:150502. doi: 10.1103/PhysRevLett.103.150502

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Vidal JG, Theis DO. Calculus on parameterized quantum circuits. arXiv. (2018) 181206323.

Google Scholar

17. Vidal JG. Analysis on Quantum Circuits. Tartu: University of Tartu (2020).

18. Lei AW. Comparisons of Input Encodings for Quantum Neural Networks. Tartu: University of Tartu (2020).

19. Bravyi S, Gosset D, Movassagh R. Classical algorithms for quantum mean values. arXiv. (2019) 190911485.

Google Scholar

Proof of Lemma 2

We have to prove that the functions χ_k, k ∈ ℝ, defined in (11) are linearly independent (in the algebraic sense, i.e., considering finite subsets of the functions at a time). There are several ways of proving this well-known fact; we give the proof that probably makes most sense to a physics readership: The Fourier transform (in the sense of tempered distributions) of the function χ_k is δ(k − *), the Dirac distribution centered on k. These generalized functions are clearly linearly independent for different values of k.