- 1Center for Gravitational Physics, Yukawa Institute for Theoretical Physics, Kyoto University, Kyoto, Japan
- 2Quantum Hadron Physics Laboratory, RIKEN Nishina Center, Wako, Japan
- 3Interdisciplinary Theoretical and Mathematical Sciences Program (iTHEMS), RIKEN, Wako, Japan
In this article, we review the HAL QCD method to investigate baryon-baryon interactions, such as nuclear forces in lattice QCD. We first explain our strategy in detail to investigate baryon-baryon interactions by defining potentials in field theories, such as QCD. We introduce the Nambu-Bethe-Salpeter (NBS) wave functions in QCD for two baryons below the inelastic threshold. We then define the potential from NBS wave functions in terms of the derivative expansion, which is shown to reproduce the scattering phase shifts correctly below the inelastic threshold. Using this definition, we formulate a method to extract the potential in lattice QCD. Secondly, we discuss pros and cons of the HAL QCD method, by comparing it with the conventional method, where one directly extracts the scattering phase shifts from the finite volume energies through the Lüscher's formula. We give several theoretical and numerical evidences that the conventional method combined with the naive plateau fitting for the finite volume energies in the literature so far fails to work on baryon-baryon interactions due to contaminations of elastic excited states. On the other hand, we show that such a serious problem can be avoided in the HAL QCD method by defining the potential in an energy-independent way. We also discuss systematics of the HAL QCD method, in particular errors associated with a truncation of the derivative expansion. Thirdly, we present several results obtained from the HAL QCD method, which include (central) nuclear force, tensor force, spin-orbital force, and three nucleon force. We finally show the latest results calculated at the nearly physical pion mass, mπ ≃ 146 MeV, including hyperon forces which lead to form ΩΩ and NΩ dibaryons.
1. Introduction
How do nuclear many-body systems emerge from the fundamental degrees of freedom, quarks and gluons? It has been a long-standing problem to establish a connection between nuclear physics and the fundamental theory of strong interaction, quantum chromodynamics (QCD). In particular, nuclear forces serve as one of the most basic constituents in nuclear physics, which are yet to be understood from QCD. While so-called realistic nuclear forces [1–3] have been established with a good precision, they are constructed phenomenologically based on scattering data experimentally obtained. Recent development in effective field theory (EFT) provides a more systematic approach for nuclear forces from a viewpoint of chiral symmetry in QCD [4–8], whose unknown low-energy constants, however, cannot be determined within its framework but are obtained only by the fit to the experimental data. Under these circumstances, it is most desirable to determine nuclear forces as well as general baryon-baryon interactions from first-principles calculations of QCD, the lattice QCD method. Once baryon forces are extracted from QCD, we can solve finite nuclei, hypernuclei and nuclear/hyperonic matter by employing various many-body techniques developed in nuclear physics. The outcome is expected to make a significant impact on our understanding of nuclear astrophysical phenomena, such as supernovae, binary neutron star merges and nucleosynthesis.
In this paper, we review the HAL QCD method to determine baryon-baryon interactions in lattice QCD. In this method, integral kernels, or so-called “potentials,” are first extracted from lattice QCD, and physical observables, such as scattering phase shifts and binding energies are calculated by solving the Schrödinger equation with obtained potentials in the infinite volume. We show that the notion of potential can be rigorously introduced as a representation of the S-matrix in quantum field theories as QCD. The essential point is that the potentials are defined through the Nambu-Bethe-Salpeter (NBS) wave functions, in which the information of phase shifts are encoded in their asymptotic behaviors. We employ a non-local and energy-independent potential where the non-locality is defined through the derivative expansion. In particular, energy-independence of the potential is useful since one can extract the potential from the ground state as well as elastic excited states simultaneously. This enables us to avoid the notorious signal-to-noise issue for multi-baryon systems in lattice QCD (or the ground state saturation problem), and to make a reliable determination of baryon-baryon interactions.
In lattice QCD, there also exists a conventional method, in which phase shifts are obtained from finite volume energies through the Lüscher's formula. For meson-meson systems, a number of works have been performed based on the Lüscher's formula [9], where finite volume energies are extracted utilizing the variational method [10]. The Lüscher's formula has been generalized for various systems, such as boosted systems [11], arbitrary spin/partial waves [12, 13], and three-particle systems [14, 15]. While theoretical bases are well-established for both conventional method and HAL QCD method, numerical results for baryon-baryon systems at heavy pion masses have shown inconsistencies with each other. In this paper, we make a detailed comparison between two methods, scrutinizing possible sources of systematic errors. In particular, we examine whether the systematic errors associated with excited state contaminations are controlled or not in the procedure of the conventional method in the literature (“the direct method”), namely, simple plateau fitting for the ground state at early Euclidean times. We also examine systematic errors in the HAL QCD method, in particular, the truncation error of the derivative expansion. We show theoretical and numerical evidences that the inconsistency between two methods originates from excited state contaminations in the direct method. We also demonstrate that the inconsistency can be actually resolved if and only if finite energy spectra are properly obtained with an improved method rather than the naive plateau fitting in the conventional method.
After establishing the reliability of the HAL QCD method, we present the numerical results of nuclear forces from the HAL QCD method at various lattice QCD setups. The results at heavy pion masses for central and tensor forces are shown and their quark mass dependence as well as physical implications are discussed. The calculations of spin-orbit forces and three-nucleon forces are also given. Once nuclear forces are obtained, one can solve nuclear many-body systems with the obtained potentials. We study finite nuclei, nuclear equation of state and structure of neutron stars based on lattice nuclear forces at heavy pion masses. Finally, the latest results of nuclear forces near the physical pion mass are presented, as well as hyperon forces, which are shown to generate ΩΩ and NΩ dibaryons.
This paper is organized as follows. In section 2, we discuss methods to study baryon-baryon interactions from lattice QCD. After briefly introducing the conventional method and its actual practice, called the “direct method,” we describe the detailed theoretical formulation as well as its practical demonstration for the newly developed method, the HAL QCD method. In section 3, we discuss pros and cons of these two methods, and compare the numerical results at heavy pion masses. We present evidences that the results from the direct method suffer from uncontrolled systematic errors associated with the excited state contaminations. In section 4, we summarize results on nuclear potentials in the HAL QCD method. After reviewing the results obtained at heavy pion masses for central and tensor forces in the parity-even channel as well as spin-orbit forces and three-nucleon forces, we present nuclear many-body calculations based on lattice nuclear forces for double-magic nuclei, equation of state and the structure of neutron stars. Latest results for nuclear forces near the physical pion mass are also given. In section 5, we present hyperon forces near the physical pion mass, which lead to ΩΩ and NΩ dibaryons. Section 6 is devoted to the summary and concluding remarks.
2. Two Baryon Systems in Lattice QCD
In lattice QCD, the 2-pt function for a hadron H, created by and annihilated by OH, is expressed as
where is the n-th one-particle state with a mass mn, a momentum and an energy , and ellipses represent contributions from multi particle states. We here assume m0 < mn>0, so that m0 is the hadron mass for the ground state, which can be extracted from the asymptotic behavior of the 2-pt function in the large t as
where finite volume artifact is exponentially suppressed and can be eliminated by an infinite volume extrapolation.
So far, this method in lattice QCD (and the extension to lattice QCD + QED) has successfully reproduced light hadron spectra [16] including the proton–neutron mass splitting [17]. A simple application of the method, however, does not work well for an investigation of hadron interactions. For example, the 2-pt function of two baryons in the center of mass system behaves in the large t as
where we obtain the lowest energy EBB. In the infinite volume limit, EBB behaves as EBB = 2mB or EBB = 2mB − ΔE depending on an absence or presence of bound state. Here mB is the corresponding baryon mass and ΔE > 0 is the binding energy of the lowest bound state. Only the binding energy of the bound state can be extracted by this simple method and thus more sophisticated methods are required. Currently there are two methods to investigate hadron interactions in lattice QCD, the direct method (or finite volume method) and the HAL QCD method, which are explained in this section.
2.1. Direct Method
The method most widely used to investigate hadron interactions in lattice QCD is to extract scattering phase shifts from energy eigenvalues in 3-dimensional finite boxes through the Lüscher's finite volume formula [18]. For example, in the case of the S-wave scattering phase shift, δ0(k), the formula reads
where k is determined through with EBB(L) being the energy of the two baryon measured in lattice QCD on a finite box with the spatial extension L as in Equation (3). We here neglect the partial wave mixing in the cubic group and spin degrees of freedom, for simplicity. Only the discrete sets of point , which satisfies Equation (4), are realized on a given volume L3. Thus, the scattering phase shift δ0(k) at the corresponding k can be extracted in lattice QCD, simply by measuring the finite volume energy, EBB(L). Note that the formula assumes that the hadron interaction is accommodated within the lattice box and is not distorted by the finite volume artifact, which condition should be examined numerically to be satisfied in actual calculations.
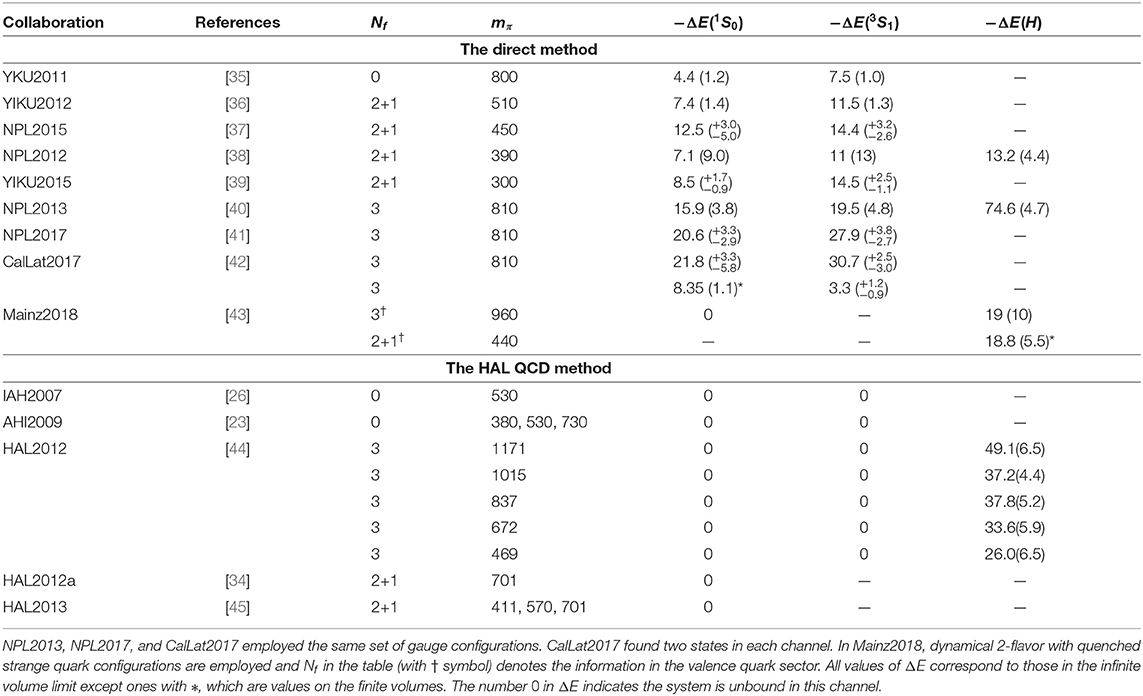
In Figure 1, we illustrate how scattering phase shifts and the bound state energy can be extracted by this method in the case of the NN scatterings. In the figure, the red solid line represents the effective range expansion (ERE) for k cot δ0(k)/mπ at the Next-to-Leading order (NLO) as
where the scattering length a0 and the effective range r0 are taken to be a0mπ = 16.8, r0mπ = 1.9 for (Left) or a0mπ = −3.8, r0mπ = 1.3 for (Right) with mπ = 140 MeV, while colored dashed lines represent the Lüscher's finite volume formula, Equation (4) on L = 10, 12, 14, 18 fm. Discrete points which satisfy both the Lüscher's finite volume formula and the ERE are realized on each volume, as shown by the open squares, up/down triangles and diamonds.
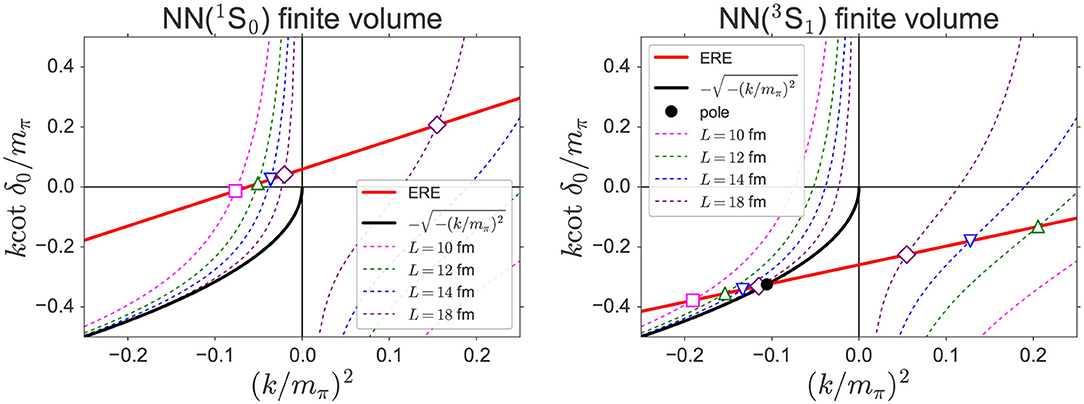
Figure 1. A determination of k cot δ0(k)/mπ from energies of the two nucleon state in the finite volume. Taken from Iritani et al. [19].
A distribution of the allowed k2 for k2 > 0 becomes denser as the volume increases, so as to be continuous in the infinite volume limit, while a sequence of discrete points for k2 < 0 leads to an accumulation point, which corresponds to the scattering state at k2 = 0 in the left figure or the bound state pole, denoted by the black solid circle in the right figure. It is noted here that the bound state pole appears as the intersection between the ERE and the bound state condition, (black solid line). To see this, we first write
where S(k) is the S-matrix for the NN elastic scattering. The bound state energy κb can be extracted from the pole of this S-matrix as
where is real and positive for physical poles [20]. Thus at , we have
which means that the binding momentum k = iκb is given by an intersection between k cot δ0(k) and . Moreover, since
the slope of k cot δ0(k) must be smaller than that of as a function of k2 at the bound state pole, as in the case of Figure 1 (right). The finite volume analysis thus provides not only an infinite volume extrapolation of the binding energy but also a novel way to examine the normality of the result in the direct method [19].
2.2. HAL QCD Method
2.2.1. Formulation
The HAL QCD method, another method to investigate hadron interactions in lattice QCD, employs the equal time Nambu-Bethe-Salpeter (NBS) wave function, defined by
where |NN, Wk〉 is the NN eigenstate in QCD with the center of mass energy and the nucleon mass mN, and N(x, t) is a nucleon (annihilation) operator, made of quarks. Other quantum numbers, such as spin/isospin of two nucleons are suppressed for simplicity. We mainly use
where C = γ2γ4 is the charge conjugation matrix, q = u(d) for proton (neutron). Other choices, such as smeared quarks are possible here, and such arbitrariness is considered to be a choice of the scheme for the definition of the NBS wave function or the potential (see [21] for such an example). Throughout this paper, we consider the NN elastic scattering, so that Wk < Wth ≡ 2mN + mπ, where mπ is the pion mass. Note that this condition is also necessary for the finite volume method in the previous subsection.
Since interactions among hadrons are all short-ranged in QCD, there exists some length scale R, beyond which (i.e., r ≡ |r| > R) the NBS wave function satisfies the Helmholtz equation as
Furthermore, it behaves for large r > R as
where Ylm is the spherical harmonic function for the solid angle Ωr of r, and we ignore spins of nucleon for simplicity1. Here it is important to note that the NBS wave function contains information of the phase δl(k) of the S-matrix for the orbital angular momentum l, which is a consequence of the unitarity of the S-matrix in QCD [24, 25].
In the HAL QCD method, the non-local but energy-independent potential is defined from the NBS wave function through the following equation,
for Wk < Wth, and Equation (12) implies U(r, r′) = 0 for r > R. While an existence of U(r, r′) has been shown in Ishii et al. [26] and Aoki et al. [23, 27], the non-local potential which satisfies Equation (14) is not unique. Thus we have to define the potential uniquely, by specifying how to extract it. For this purpose, we introduce the derivative expansion, U(r, r′) = V(r, ∇)δ(3)(r − r′), whose lowest few orders for the NN with a given isospin channel are written as
where V0(r) is the central potential, Vσ(r) is the spin dependent potential with σi being the Pauli matrix acting on the spinor index of the i-th nucleon, VT(r) is the tensor potential with the tensor operator (), and VLS(r) is the spin-orbit (LS) potential with the angular momentum L = r × p and the total spin S = (σ1 + σ2)/2. It is noted that an expansion of the non-local potential is not unique. For example, we may improve the convergence of the expansion by modifying the ∇ operator [28].
Once we obtain the approximated potential at lowest few orders, we can calculate the scattering phase shifts or the binding energies of possible bound states by solving the Schrödinger equation with this potential in the infinite volume. As is the case for the finite volume method, it is necessary that the potential is not distorted by the finite volume artifact, but this can be checked easily since the potential itself is explicitly obtained. We can also check how good the approximated potential is, by increasing the order of the expansion. Needless to say, the approximated potential depends on momenta of input wave functions. As pointed out in Aoki et al. [29], these dependences of the approximated potentials have been misidentified with those of the non-local potential in the literature [30]. In the next subsection, we will explicitly demonstrate how this procedure works.
2.2.2. Demonstration
In order to see how the scattering phase shifts can be obtained by the HAL QCD method, we consider the quantum mechanics for a spinless system with a separable potential, defined by
The S-wave solution of the Schrödinger equation with this potential is given exactly by
where
which is the 4-th order polynomials in k2. In order to make the scattering phase shift a more complicated function of k2, we artificially modify the wave function from to ϕk(r) which is defined by
where R is an infrared cutoff, and it is understood that the potential is modified accordingly. The continuity of ϕk(r) and at r = R gives
as well as C(k) = X/sin(kR + δR(k)). Hereafter, we study how the scattering phase shifts are obtained in the HAL QCD method.
The derivative expansion for the S-wave scatterings leads to
and we consider to determine the potential in each order from ϕk(r).
The leading order (LO) potential is given by
while the next-to-leading order (NLO) potential is extracted as
where
Note that the potential in each order in the derivative expansion {V0(r), V1(r), ⋯} are defined to be k-independent, while the potentials approximately obtained in each LO/NLO analysis, and , have implicit k-dependence due to the truncation error in the derivative expansion [29].
We calculate S-wave scattering phase shifts corresponding to these approximated potentials, and compare them with the exact phase shifts, δR(k). Considering μ as a typical inelastic threshold energy in this model, we take k = 0 and/or k = μ for the following analysis. Figure 2 shows the S-wave scattering phase shift δ(k) (Left) and k cot δ(k) (Right) as a function of k2, where all (dimensionful) quantities are measured in units of μ. In this example, we take ω = −0.017μ4, m = 3.30μ, and R = 2.5/μ. In the figures, the exact phase shift δR(k)(Left) or k cot δR(k) (Right) is given by the blue solid line, while the LO approximations at k = 0 or k = μ are represented by orange and green solid lines, respectively. As seen from the figures, the LO approximation at k = 0 (orange), exact at k2 = 0 by construction, gives a reasonable approximation at low energies (k2 ≃ 0) but deviates from the exact one at high energies near k2 ≃ μ2. On the other hand, the LO approximation at k = μ (green) becomes accurate at higher energies near k2 ≃ μ2 but inaccurate at low energies near k2 ≃ 0. Combining two NBS wave functions, ϕk1 = 0(r) and ϕk2 = μ(r), one can determine the approximated potential at the NLO, VNLO(r, ∇), whose scattering phase shifts are represented by the red solid lines in the figures. The phase shifts at the NLO (red lines) gives reasonable approximations of the exact results (blue solid lines) in the whole range (0 ≤ k2 ≤ μ2), as they are exact at k2 = 0 and k2 = μ2 by construction. If we increase the order of the expansion more and more, the approximation becomes better and better2.
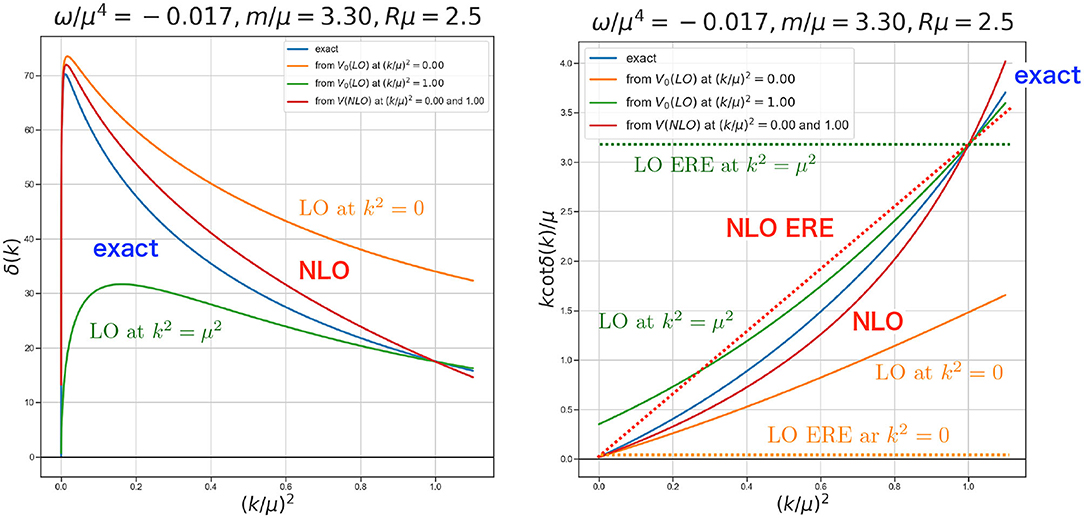
Figure 2. The scattering phase shifts δ(k) and k cot δ(k) as a function of k2. See the main text for more details.
Using this model, let us compare the direct method and the HAL QCD method. At the LO, the direct method gives either k cot δ(k) at k2 = 0 or k2 = μ2 without any information about the effective range, which only gives the LO ERE (an orange dashed line or a green dashed line in the right figure). Thus the LO potentials approximate the exact k cot δ(k) much better (the orange solid line or the green solid line). In the direct method, the ERE at NLO is obtained by combining the data at k2 = 0 and k2 = μ2 as
which is given by a red dashed line in the right figure. By comparing the HAL QCD method with potentials at NLO (the red solid line) and the direct method with NLO ERE (the red dashed line), the former leads to a better approximation of the exact result than the latter, since higher order effects in ERE in terms of k2 are included in the former. Note, however, that sufficiently precise data in the direct method can also evaluate higher order ERE terms than NLO, in principle.
2.2.3. Dependence of the LO NN Potential on Energy and Partial Waves
In this subsection, we consider effects of higher order terms in the derivative expansion for the NN in QCD.
Figure 3 shows three dimensional plots of the NBS wave functions ϕk(x, y, z = 0) for with the periodic boundary condition (PBC) at Ek ≃ 0 MeV (Left) and with the anti-periodic boundary condition (APBC) at Ek ≃ 45 MeV (Right), in quenched lattice QCD at a ≃ 0.137 fm on L ≃ 4.4 fm with mπ ≃ 530 MeV [33]. As seen from the figure, two NBS wave functions look very different from each other. In particular, the right one vanishes on the boundary due to the APBC constraint.
Figure 3. The NBS wave function for at Ek ≃ 0 MeV with the PBC (left) and at Ek ≃ 45 MeV with the APBC (right). Both are normalized to unity at r = 1 fm. Taken from Murano et al. [33].
Figure 4 (Left) compares the LO potentials for obtained from the corresponding NBS wave functions in Figure 3. While the NBS wave functions at different energies have different spatial structures, the potentials look very similar. This suggests that the higher order terms in the derivative expansion of the potential have negligible contributions at this energy interval, 0 ≤ Ek ≤ 45 MeV.
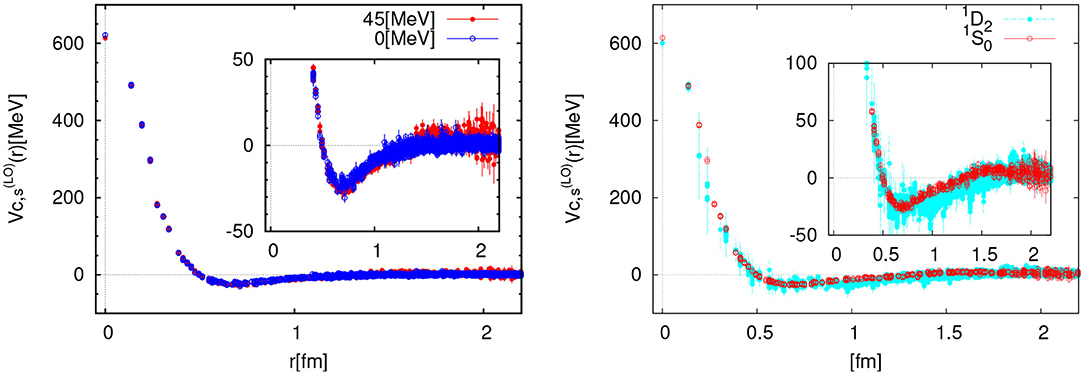
Figure 4. (Left) The LO potential for as a function of r at Ek ≃ 45 MeV (red solid circles) and at Ek ≃ 0 MeV (blue open circles). (Right) The LO potential as a function of r at Ek ≃ 45 MeV for (red open circles) and for (cyan solid circles). Taken from Murano et al. [33].
Figure 4 (Right) compares the LO potential for (red open circles) with the one for (cyan solid circles) at Ek ≃ 45 MeV. Although statistical fluctuations are larger for the latter, they look similar, suggesting that L2 dependence of the potential is also small in this setup. If more accurate data show a difference of potentials between and , one may determine the L2 dependent term of the potential in the spin-singlet channel.
2.2.4. Time-Dependent HAL QCD Method
In order to extract the NBS wave functions on the finite volume in lattice QCD, we consider the 4-pt function given by
where is an operator which creates two nucleon states at time t0, , and ellipses represent inelastic contributions, which become negligible at Wth(t − t0) ≫ 1. Like the direct method, one can extract the NBS wave function for the ground state from the above 4-pt function as
for (Wk1 − Wk0)t ≫ 1, where Wk0 (Wk1) is the lowest (second-lowest) energy on the finite volume. The LO potential from the NBS wave function for the ground state is then extracted from FJ(r, t) at large t. As will be discussed in the next section, however, it is numerically very difficult to determine FJ(r, t) for two nucleons at such large t due to the bad signal-to-noise (S/N) ratio.
Fortunately, an alternative extraction is available for the HAL QCD method [34]. Let us consider the ratio of 4-pt function to the 2-pt function squared as
which behaves
for Wth t ≫ 1, where inelastic contributions can be neglected. Noticing that
we obtain
We can approximately extract V(r, ∇) from RJ(r, t) for (different) J's, as long as t satisfies the condition that Wth t ≫ 1 (elastic state saturation), which is much easier than to achieve (Wk1 − Wk0)t ≫ 1 (ground state saturation). We call this alternative extraction the time-dependent HAL QCD method.
3. A Comparison of the Two Methods at Heavier Pion Masses
It is interesting to ask whether the attractions of the nuclear forces at low energies would become weaker or stronger if the pion mass were larger than the value in Nature. In principle, such a question can be answered by employing either the direct method or the HAL QCD method in lattice QCD. There exists, however, a qualitative discrepancy between the two methods on the answer to this question. As summarized in Table 1, the direct method tends to indicate that attractions between two nucleons become stronger as the pion mass increases, so that both deuteron and di-neutron form bound states, while the HAL QCD method suggests that the attractions become weaker and the bound deuteron does not exist at heavier pion masses. Note that the results from the direct method in the flavor SU(3) limit (Nf = 3 in the table), NPL2013/NPL2017, CalLat2017, and Mainz2018, exhibit discrepancies with each other [19]. In addition, while both methods lead to the bound H-dibaryon at heavier pion masses, in particular, in the flavor SU(3) limit, the predicted binding energies differ even within the direct method: NPL2013 [40] gives 75(5) MeV at mπ = 810 MeV, which is much larger than 19(10) MeV at mπ = 960 MeV by Mainz2018 [43]. On the other hand, HAL2012 [44] gives 38(5) MeV at mπ = 837 MeV from the HAL QCD method. These deviations seem to be too large to be explained by lattice artifacts.
In order to understand origins of these discrepancies, we have performed extensive investigations, whose results have been published in a series of papers [19, 46–48], which will be explained in the following subsections.
3.1. Operator Dependence in the Direct Method
In the direct method, reliable extractions of the two nucleon ground state energies are crucially important. As long as (Wk1 − Wk0)t ≫ 1, the two nucleon correlation function is dominated by the ground state as
so that the extracted ground state energy Wk0 depends neither the source operator nor the sink operator JNN, while magnitudes of contaminations from excited states are affected by the choices of these operators. Since on the finite box with the spacial extension L, t ≫ 4 fm is required, for example, for L ≃ 4 fm and mN ≃ 2 GeV at heavier pion masses. Due to the bad S/N ratio at such large t, however, authors in previous literature extracted the ground state energies at much smaller t, t ~ 1 fm, by tuning the source operators in order to achieve a plateau of the effective energy shift at such a small t, where
Unfortunately, such a naive plateau fitting at earlier t may not be reliable due to contaminations from nearby excited states, which may easily produce (incorrect) plateau-like behaviors in effective energies. It was indeed demonstrated that plateau-like behaviors in effective energy shifts at small t can depend not only on the source operator but also on the sink operator: Plateaux disagree between the wall source (red circle) and the smeared source (blue square) in the left of Figure 5, while plateaux depend on sink operators for the same smeared source in the right figure.
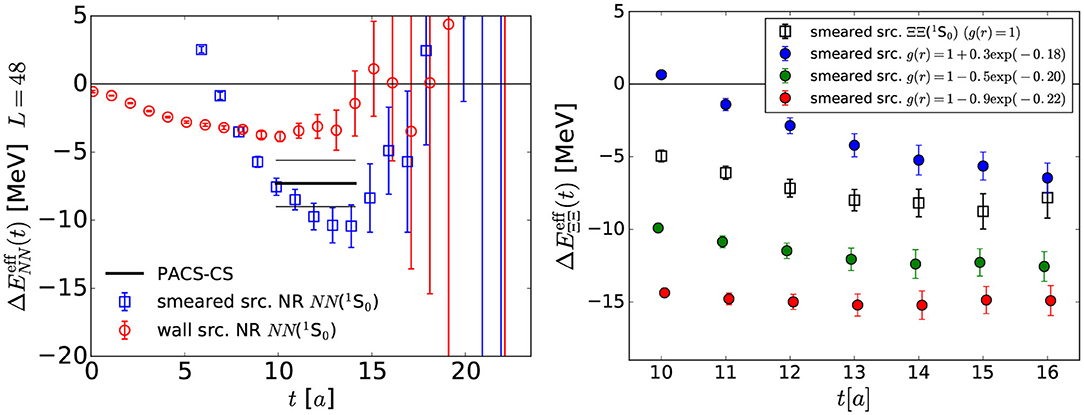
Figure 5. (Left) The effective energy shift for from the wall source (red circles) and the smeared source (blue squares) on L = 48a ≃ 4.3 fm at mπ = 0.51 GeV, mN = 1.32 GeV and mΞ = 1.46 GeV [46]. (Right) The effective energy shift for from the smeared source with different sink operators on the same gauge configurations [46].
In order to see how easily contaminations from elastic-excited states can produce plateau-like behaviors at earlier t, let us consider the effective energy shift from the mockup data for RNN(t), given by
where we take δEel. = 50 MeV for the typical lowest elastic excitation energy on L ≃ 4 fm at mN ≃ 1.5 GeV, and δEinel. ≃ mπ ≃ 500 MeV for the lowest inelastic energy. Naively, it is expected that the correct plateau at ΔENN for the ground state appears at t≫1/δEel. ≃ 4 fm, which however is too large to have good signals for two baryons, such as NN. By tuning the source operator, one may reduce coefficients b1 and c0. Since the NN operator does not strongly couple to NNπ state, we expect small c0 and take c0 = 0.01. On the other hand, NN operators easily couple to both ground and 1st elastic excited states as they become almost identical to each other in the infinite volume limit. We therefore take b1 = 0.01 (the highly tuned operator), b1 = ±0.1 (the tuned ones) as well as b1 = 0.5 (the untuned one). Figure 6 (Left) shows for these 4 examples with c0 = 0.01, where random fluctuations and errors whose magnitude increase exponentially in t are assigned to . All examples show plateau-like behaviors at t ≃ 1 fm, but these four plateaux disagree with each other. As |b1| increases, the deviation between the values of these “pseudo plateaux” and the true value becomes larger. Contaminations of the elastic excited states can easily produce the plateau-like behavior at earlier t, and the t dependence of data alone cannot tell us which plateau is correct, or in other words, cannot tell which tuning is good.
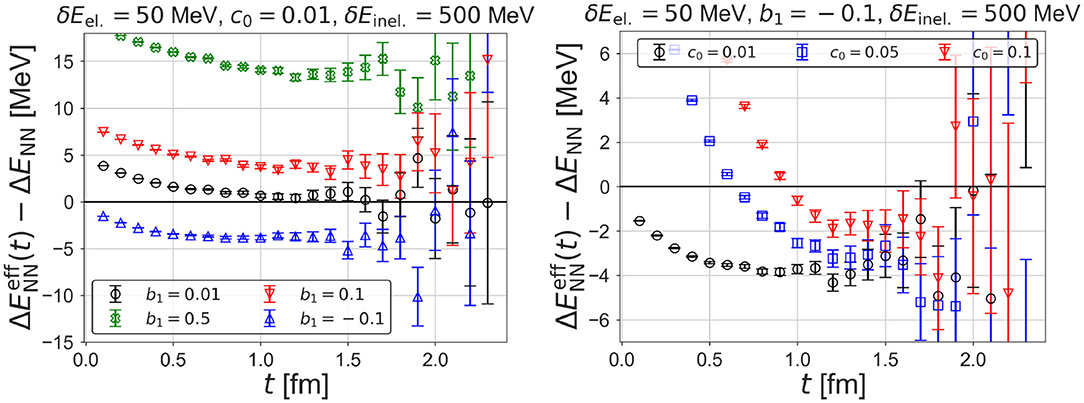
Figure 6. from the mockup data with fluctuations and errors as a function of t. (Left) b1 = 0.01, ±0.1, 0.5 and c0 = 0.01. (Right) c0 = 0.01, 0.05, 0.1 and b1 = −0.1.
Contaminations from inelastic states seem unimportant to produce the plateau-like behavior, as shown in Figure 6 (Right), where the effective energy shift for c0 = 0.01, 0.05, 0.1 with b1 = −0.1 is plotted. All cases converge to almost the same pseudo plateau, while a pseudo plateau starts at later t for larger c0. It is noted that the multi-exponential fit does not work in this case at t ≃ 1.0 fm, which is much smaller than the necessary t≫1/δEel.. The multi-exponential fit at such small t only separates the pseudo plateau from the inelastic contributions but is difficult to distinguish the ground state and the 1st excited state for the elastic states.
3.2. Normality Check in the Direct Method
While the check through operator dependence is useful, it requires extra calculations. We find that the finite volume formula in Equation (4) provides a simpler test, which tells us whether the ground state energies extracted by the plateau fitting give a reasonable ERE or not without extra calculations. We call this test a normality check [19]. Figure 7 (Left) shows k cot δ0(k)/mπ in YIKU2012 [36] as a function of for , where the solid red line represents the NLO ERE fit in Equation (5), and the light red bands shows statistical and systematic errors added in quadrature [19]. Contrary to a naive expectation from non-singular ERE behaviors, data align almost vertically, since ΔENN is almost independent of the volume. In other words, according to the finite volume formula, the claimed “binding energy” (open circle) is too shallow to have such volume independent ΔE. Not only the central value of the NLO ERE fit gives singular parameters as but also it violates the physical pole condition, Equation (9), at the crossing point (open circle). The singular and unphysical behaviors, in addition to the operator dependence of these data, strongly indicate that the naive plateau fitting employed in the direct method is unreliable. Another example is shown in Figure 7 (Right) for from NPL2015 [37]. In this case, two different NLO ERE fits (red line/band and blue line/band) are performed depending on the lattice data to be used for the fit. It turns out that two ERE are inconsistent with each other, indicating that their lattice data themselves are “self-inconsistent.” In addition, one of ERE (blue line/band) is found to violate the physical pole condition, Equation (9), at the crossing point (open circle). Similar symptoms are observed for all other data in the direct method claiming the existence of NN bound states at heavy quark masses [19]3.
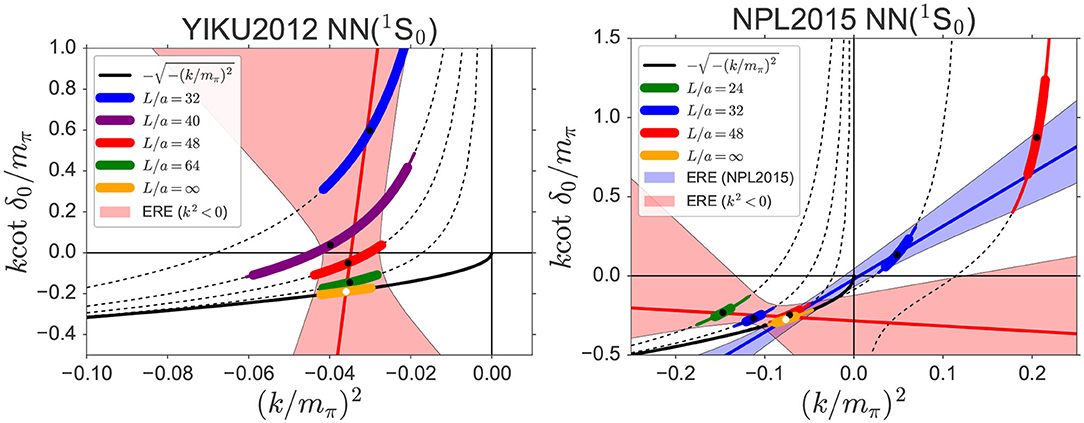
Figure 7. (Left) k cot δ0(k)/mπ in YIKU2012 [36] for as a function of . The solid red line and light red band represent the ERE fit and the corresponding error (statistical and systematic added in quadrature), respectively. The dashed lines are the finite volume formula for the corresponding volume. (Right) k cot δ0(k)/mπ in NPL2015 [37] for as a function of . Two ERE fits are performed depending on the lattice data to be used for the fit. The red line with the band represents the fit made by the authors in Iritani et al. [19], while the blue line with the band is plotted by the authors in Iritani et al. [19] using the fit result of NPL2015. Both figures are taken from Iritani et al. [19].
3.3. The Source Dependence and the Derivative Expansion in the HAL QCD Method
The source operator dependence of the HAL QCD potential has been investigated in Iritani et al. [47]. Figure 8 (Left) compares the LO potentials, , for between the wall source (red open circles) and the smeared source (blue open squares). We observe a small difference at short distances, from which one can determine the N2LO potential, Note that the NLO term, is absent in the channel. Figure 8 (Right) shows , which is non-zero only at r < 1.0 fm, where two LO potentials differ. We then extract the scattering phase shifts, using this N2LO potential.
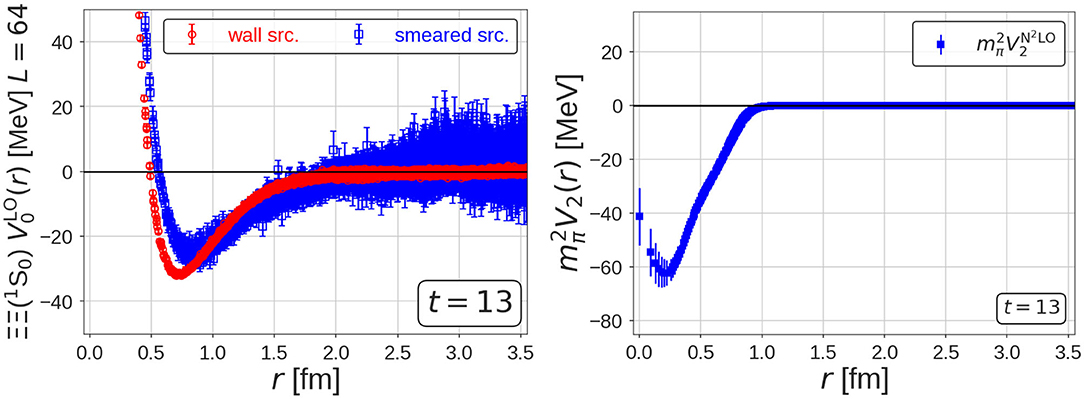
Figure 8. (Left) The LO potential, , for from the wall source (red open circles) and the smeared source (blue open square). (Right) The second order term, (blue solid squares), in the N2LO potential for . Both are taken from Iritani et al. [47].
The N2LO corrections turn out to be negligible at low energies, as shown in Figure 9 (Left), where k cot δ0(k) is almost identical between (r, ∇) (red solid circles) and (blue solid squares). Furthermore, even the LO analysis for the wall source, (black open diamond), is sufficiently good at low energies. As energy increases, the N2LO corrections become visible as seen in Figure 9 (Right), where corresponds to ΔE ≃ 90 MeV for the energy shift from the threshold. It is noted that (blue solid squares) gives a little closer results to N2LO results (red solid circles) than (black open diamond) does.
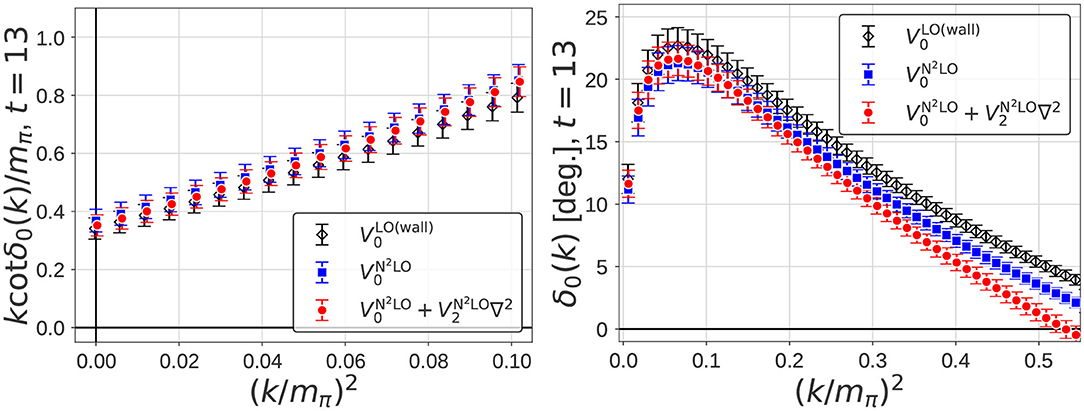
Figure 9. (Left) k cot δ0(k)/mπ as a function of at low energies, where δ0(k) is the scattering phase shift for , calculated from VN2LO(r, ∇) (red solid circles), (blue solid squares) and (black open diamond). (Right) The corresponding δ0(k). Both are taken from Iritani et al. [47].
3.4. Understanding Pseudo Plateaux
In this subsection, we explain why the wall source and the smeared source give inconsistent plateau behaviors, in the case of ΞΞ correlation functions as an example.
To this end, we consider the Hamiltonian , where we employ , the LO potential from the wall source, since it works rather well at low energies as shown in the previous subsection. We first decompose for J = wall/smear in terms of finite volume eigenfunctions of H as
where Ψn(r) and ΔEn are normalized-eigenfunction and eigenenergy in the finite volume, respectively, and is the overlapping coefficient extracted at t.
Then the correlation function for the source J in the direct method is given by
Finally, approximating a sum over n by the lowest few orders, we reconstruct the behavior of the effective energy shift as a function of t as
where we fix the overlapping coefficient at t = t0, and nmax is a number of excited states used in the approximation.
In Figure 10, we show reconstructed effective energy shift on L = 48a with nmax = 4, together with the effective energy shifts from , for the wall source (red bands and red open circles) and the smeared source (blue bands and blue open squares). The black dashed line represents the energy shift for the ground state of on L = 48a.
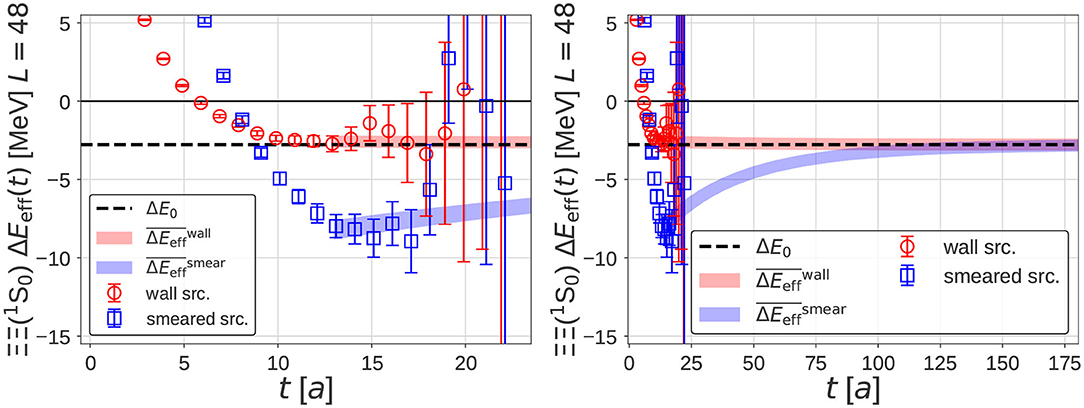
Figure 10. The reconstructed effective energy shift for the wall source (red bands) and the smeared source (blue bands) on L = 48a, while the effective energy shifts directly from are shown for J = wall (red open circles) and J = smear (blue open squares). The black dashed lines are the energy shifts for the ground state of H in the finite box. (Left) 0 ≤ t/a ≤ 24. (Right) 0 ≤ t/a ≤ 175. Taken from Iritani et al. [48].
We find that the plateau-like structures in the direct method around t/a = 15 are well-reproduced by for both sources in Figure 10 (Left). This indicates that the plateau-like structures in the direct method at this time interval are explained by the contributions from several low-lying states.
These plateau-like structures of course do not necessarily correspond to the true energy shift of the ground state. The fate of these structures is shown in Figure 10 (Right), where we plot at asymptotically large t. While the plateau-like structure for the wall source is almost unchanged, for the smeared source gradually increases and reaches to the true value at t/a ~ 100.
The above results clearly reveal that the plateau-like structures at t/a ~ 15 for the smeared source are pseudo-plateaux caused by the contaminations of the excited states. Large contaminations from excited states in the case of the smeared source are not caused by the smearing, but are indeed implied by putting two baryon operators on the same space-time point as
where the above source operator couples to all momentum modes with almost equal weight. Since almost all previous studies on NN interactions in the direct method employed this type of the source operator, their conclusions on the existences of both deuteron and di-neutron are not valid due to large contaminations4.
3.5. Consistency Between the Two Methods
Once eigenmodes of H in the finite box are obtained, we can construct an improved sink operator for a particular eigenstate, whose correlation function with the J source is given by
Figure 11 shows the effective energy shift calculated from on L = 48a with J = wall (black open up-triangles) and J = smear (purple open down-triangle), for the ground state (Left) and the 1st excited state (Right), together with ΔE0 or ΔE1, eigenvalues of H in the finite box (red bands) as well as those of H0 (black lines). For the ground state in Figure 11 (Left), the effective energy shift in the direct method without projection are also plotted for the wall source (red open circles) and the smeared source (blue open squares).
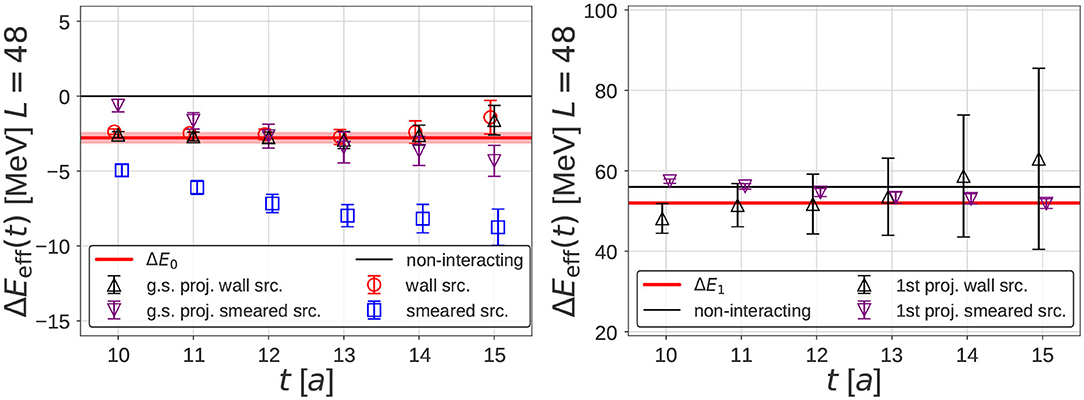
Figure 11. The effective energy shift from , the correlation function projected to the n-th eigenstate at the sink on L = 48a, for J = wall (black open up-triangles) and J = smear (purple open down-triangle). Red bands represent the energy shifts from the eigenvalues of H in the finite box, while black lines denote those of a free Hamiltonian H0. (Left) The projection to the ground state (n = 0), together with the effective energy shift in the direct method without projection for the wall source (red open circles) and the smeared source (blue open squares). (Right) The projection to the 1st excited state (n = 1). Taken from Iritani et al. [48].
After the sink projection, the effective energy shifts agree well between wall and smeared sources around t/a ~ 13, not only for the ground state but also for the 1st excited state. while the effective energy shifts for the ground state in the direct method without projection disagree between two sources. In particular, an agreement between two sources with sink projection for the 1st excited state is rather remarkable, since variational methods, usually mandatory for excited states in lattice QCD, are not used here. Furthermore, the plateaux of the effective energy shifts after the sink projection also agree with ΔE0,1 of H (red bands). Note that the effective energy shift for the 1st excited state, , has larger errors since the contribution of the 1st excited state in is much smaller.
Although the sink operator projection utilizes the information of the HAL QCD potential to construct eigenfunctions, agreements in the effective energy shifts for the ground state as well as the 1st excited state provide a non-trivial consistency check between the HAL QCD method and the Lüscher's finite volume formula (with proper projections to extract the finite volume spectra). We thus conclude from Figure 11 not only that the HAL QCD potential correctly describes the energy shifts of two baryons in the finite box for both ground and excited states but also that these energy shifts can be extracted even for baryon-baryon systems if and only if the sink/source operators are highly improved. We emphasize that improvement of operators has to be performed not by the tuning of the plateau-like structures but by a sophisticated method, such as the variational method [10]5 (or a method presented here). See Francis et al. [43] for a recent study toward such a direction.
4. Nuclear Potential
In this section, we summarize results on nuclear potentials in the HAL QCD method.
4.1. Parity-Even Channel With LO Analysis at Heavy Pion Masses
We first show the results of nuclear forces in the parity-even channel ( and - channels) at heavy quark masses obtained by the LO analysis for the derivative expansion of the potential. Since the statistical fluctuations are smaller at heavier quark masses in lattice QCD, this study is a good starting point to grasp the nature of lattice QCD nuclear forces. In addition, quark mass dependence of nuclear forces is of fundamental importance from a point of view of, e.g., anthropic principle, which cannot be studied by experiments.
In the case of channel, we obtain the LO central force following Equation (31). In the case of - channel, the LO potentials consist of the central and tensor forces, which can be obtained from the coupled channel analysis between the S- and D-wave components as
where ellipses represent higher order terms in the derivative expansion. Using the projection to the representation of the cubic group (S-wave projection), , and the orthogonal one (D wave projection), , the above equation reduces to two independent equations, from which VC(r) and VT(r) can be obtained [23]. Since the representation couples to the angular momentum l = 0, 4, 6, ⋯ , these projections are expected to serve as the relevant partial wave decomposition at low energies. We find that the NBS correlation functions after and are dominated by S-wave and D-wave components, respectively, indicating that the contaminations from l ≥ 4 components are indeed small. For a more advanced partial wave decomposition, see Miyamoto et al. [49].
We perform the calculations in quenched [23, 26], dynamical 2-flavor [50], dynamical 3-flavor [44, 51, 52], and dynamical (2+1)-flavor [34, 45, 47, 53] lattice QCD with various quark masses. We here present the results obtained in 3-flavor lattice QCD at (Mps, Moct)=(1171, 2274), (1015, 2031), (837, 1749), (672, 1484), (469, 1161) MeV [44, 51, 52]6. In the case of (Mps, Moct) = (837, 1749), the value of quark masses mu = md = ms nearly correspond to the physical strange quark mass. We generate gauge configurations with the RG-improved Iwasaki gauge action and non-perturbatively -improved Wilson quark action on a L3 × T = 323 × 32 lattice. The lattice spacing is a = 0.121(2) fm and hence lattice size L is 3.87 fm. In the calculation of the NBS correlation function, parity-even states are created by a two-baryon operator with a wall quark source, while a point operator is employed for each baryon at the sink.
Shown in Figure 12 (Upper) are the lattice QCD results for the potentials. We find that the results are insensitive to the Euclidean time t, at which the NBS correlation function is evaluated, indicating that the derivative expansion is well-converged. The obtained potentials are found to reproduce the qualitative features of the phenomenological NN potentials, namely, attractive wells at long and medium distances, central repulsive cores at short distance and strong tensor force with a negative sign. We also find intriguing features in the quark mass dependence of the potentials. At long distances, it is observed that the ranges of the tail structures in the central and tensor forces become longer at lighter quark masses. Such a behavior can be understood from the viewpoint of one-boson-exchange potential. At short distances, the repulsive cores in the central forces are found to be enhanced at lighter quark masses. This could be explained by the short-range repulsion due to the one-gluon-exchange in the quark model, whose strength is proportional to the inverse of the (constituent) quark mass. In fact, our systematic studies including hyperon forces with the same lattice setup revealed that the nature of repulsive core is well-described by the quark Pauli blocking effect together with the one-gluon-exchange effect [44, 51, 54].
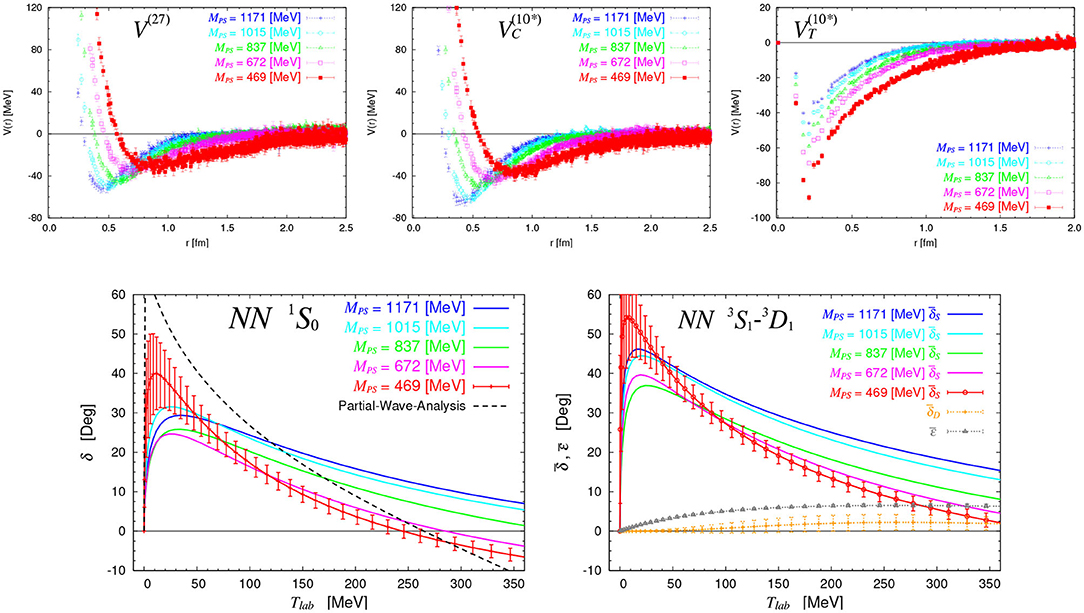
Figure 12. (Upper) Nuclear forces obtained from 3-flavor lattice QCD at Mps= 469–1171 MeV. (Left) Central force in the channel (27-plet in SU(3)f representation). (Middle) Central force in the - channel (10*-plet in SU(3)f representation). (Right) Tensor force in the - channel. (Lower) NN scattering phase shifts as a function of energy in the laboratory frame (colored solid lines), obtained from 3-flavor lattice QCD at Mps= 469-1171 MeV, together with those from experiments (black dashed lines). (Left) Results in the channel. (Right) Results in the - channel (with Stapp's convention). Figures are taken from Inoue et al. [44].
As noted before, the potentials themselves are not physical observables and quantitative lattice QCD predictions shall be given in terms of scattering observables. Shown in Figure 12 (Lower) are the scattering phase shifts (and mixing angles) obtained from lattice nuclear forces. We find that NN systems do not bound at these pseudoscalar masses as discussed in section 3. Behaviors of phase shifts are qualitatively similar to the experimental ones, while the strength of the attraction is weaker due to the heavy quark masses in this calculation. It is also observed that quark mass dependence of phase shifts is quite non-trivial. In fact, if we decrease the quark masses, there appear competing effects in the interaction: the long-range attraction becomes stronger and the short-range repulsive core also becomes stronger. We also note that lighter quark masses correspond to lighter nucleon mass, which leads to larger kinetic energies.
We also present the results obtained in (2+1)-flavor lattice QCD at quark masses corresponding to (mπ, mN) ≃ (701, 1584), (570, 1412), and (411, 1215) MeV [45]. Note that only up and down quark masses are varied with a strange quark mass being fixed to the physical value in this study. We employ the gauge configurations generated by the PACS-CS Collaboration with the RG-improved Iwasaki gauge action and non-perturbatively -improved Wilson quark action on a L3 × T = 323 × 64 lattice. The lattice spacing is a ≃ 0.091 fm (a−1 = 2.16(31)GeV), which leads to the spatial extension L ≃ 2.9 fm.
In Figure 13, we show the lattice QCD results for the potentials in the and - channels, together with the corresponding phase shifts in the channel. Qualitative features are similar to those in 3-flavor case: (i) the central forces have repulsive cores at short distance and attractive wells at long and medium distances, both of which are enhanced at lighter quark masses (ii) the tensor force is strong with a negative sign, which increases at lighter quark masses.
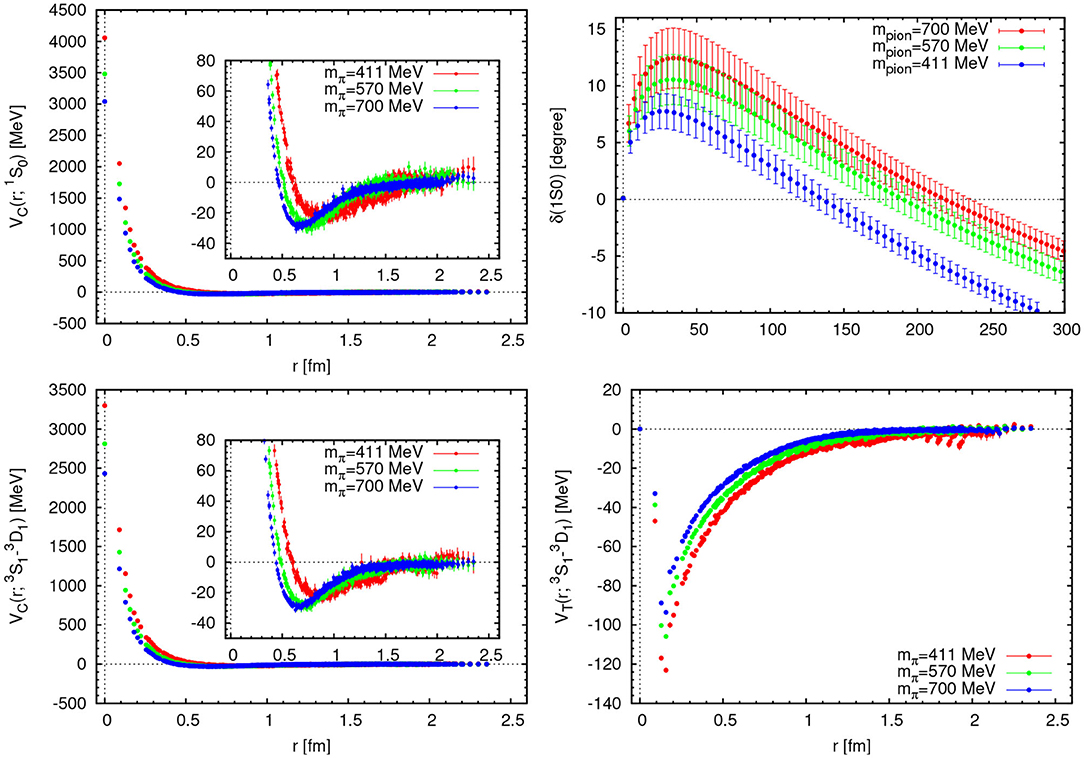
Figure 13. Nuclear forces obtained from (2+1)-flavor lattice QCD at mπ ≃ 411 (red), 570 (green), 701 (blue) MeV: (Upper-Left) Central forces in the channel (Lower) Central forces (left) and tensor forces (right) in the - channel. (Upper-Right) The scattering phase shifts in the channel at mπ ≃ 411 (blue), 570 (green), 701 (red) MeV. Figures are taken from Ishii [45].
4.2. More Structures: Spin-Orbit Forces in the Parity-Odd Channel and Three Nucleon Forces
If we consider an interaction at higher order terms in the derivative expansion, there appear more structures in the potentials. In particular, the extension from LO analysis to NLO analysis enables us to determine the spin-orbit (LS) force. The LS force is known to play an important role in the LS-splittings of nuclear spectra and the nuclear magic numbers. In addition, the LS force in the - channel attracts great interest in nuclear astrophysics, since it could lead to the P-wave superfluidity in the neutron stars and affect the cooling process of neutron stars.
We here present the calculation in parity-odd channels (, , , - channels) at heavy quark masses and show the results of LS forces as well as central/tensor forces [50]. In order to construct the source operator which couples to parity-odd states, we employ the two nucleon operators as
where N denotes a nucleon operator with a momentum,
with . A cubic group analysis shows that this source operator contains the orbital contribution , whose dominant components have l = 1, 0, 2, respectively, and thus covers all the two-nucleon channels with J ≤ 2. Combined with the spin degrees of freedom, we consider the representation in the spin singlet channel and the , , representations in the spin triplet channel. At low energies, these representations correspond to the channel and the , , and - channels, respectively, from which we extract the central force in the spin singlet channel (), and the central, tensor and LS forces () in the spin triplet channel.
Calculations are performed in 2-flavor lattice QCD at quark masses corresponding to (mπ, mN) ≃ (1133, 2158) MeV [50]. We employ the gauge configurations generated by the CP-PACS Collaboration with the RG-improved Iwasaki gauge action and a mean field -improved Wilson quark action on a 163 × 32 lattice. The lattice spacing a = 0.156(2) fm leads to the spatial extension L ≃ 2.5 fm.
Shown in Figure 14 (Upper-Left) are the lattice QCD results for the potential, , . We find that (i) the central forces and are repulsive, (ii) the tensor force is positive and weak compared to and , and (iii) the LS force is negative and strong. These features are qualitatively in line well with those of the phenomenological potential. One can also see these properties in terms of the potential in each channel. In Figure 14 (Upper-Right), we plot the potentials in the , , and channels, which are defined by , , , .
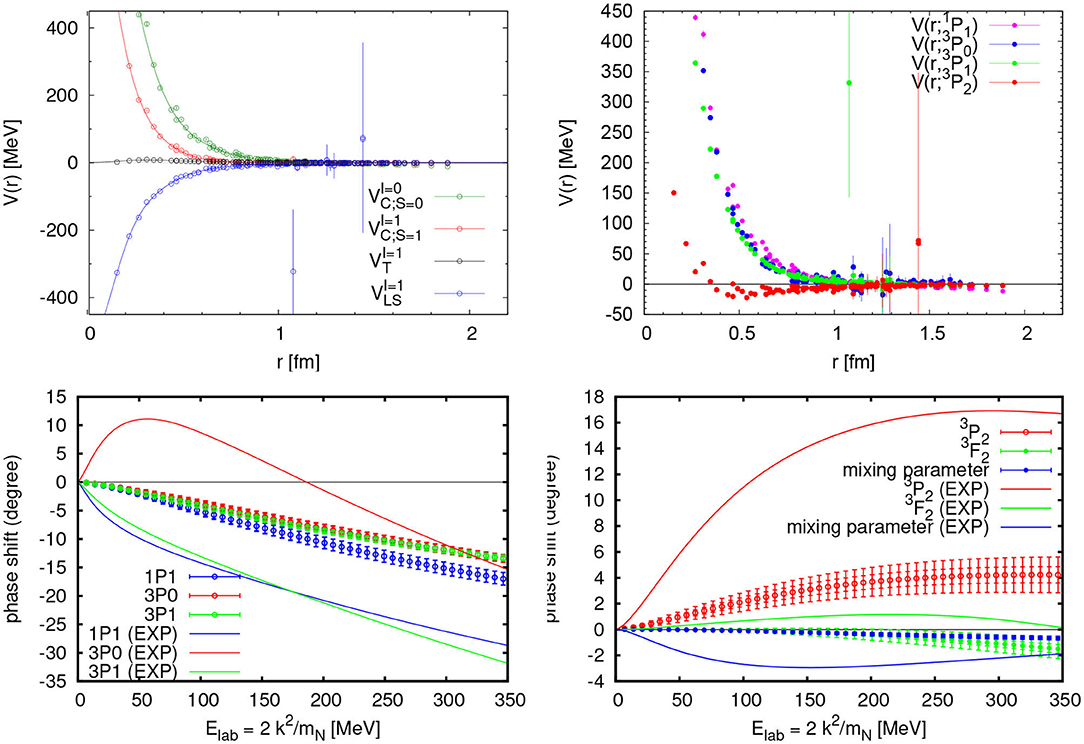
Figure 14. (Upper-Left) Central (S = 0 and 1), tensor and spin-orbit potentials in parity-odd channels obtained by 2-flavor lattice QCD at mπ ≃ 1133 MeV. (Upper-Right) The potentials for the , , , and channels. (Lower-Left) Phase shifts in the , , and channels, together with the experimental ones for comparisons. (Lower-Right) Phase shifts and mixing parameter (with Stapp's convention) in the – channel, together with the experimental ones. Figures are taken from Murano et al. [50].
To obtain the scattering observables, we fit the potentials and solve the Schrödinger equation in the infinite volume. In Figure 14 (Lower), we show the results for the scattering phase shifts. Compared with the experimental phase shifts, we find that behaviors of phase shifts are generally well-reproduced, while the magnitudes are smaller due to the heavier pion mass in lattice QCD calculations. In the channel, we observe that the attraction is missing compared with the experimental one, which however is also likely due to the weak tensor force VT caused by the heavier pion mass. Among others, the most interesting feature is the attraction in the channel as shown in Figure 14 (Lower-Right), originated from the strong (and negative) LS forces. As noted before, it is this interaction which is relevant to the paring correlation of the neutrons and possible P-wave superfluidity in the neutron stars.
We now turn to the study of three-nucleon forces. Determination of three-nucleon forces is one of the most challenging problems in nuclear physics: Three-nucleon forces are known to play important role in nuclear spectra/structures, such as the binding energies of (light) nuclei and properties of neutron-rich nuclei. They are also essential ingredients to understand properties of nuclear matters, such as the equation of state (EoS) at high density, which is relevant to the structures of neutron stars and nucleosynthesis at the binary neutron star mergers. While there have been many studies to construct three-nucleon forces by phenomenological approaches [55, 56] or by chiral EFT approaches [6–8, 57], it is most desirable to carry out the direct determination from QCD.
To study three-nucleon forces in lattice QCD, we consider the NBS wave function for a n(≥ 3)-particle system, |α〉,
where Wα is the center of mass energy of the system and we ignore the spins of nucleon for simplicity. In Aoki et al. [58, 59] and Gongyo and Aoki [60], we show that the asymptotic behavior of the NBS wave function with the non-relativistic approximation can be written as
where D = 3(n − 1) is the dimension of a n-particle system, ΔL = (2L + D − 3)π/4, is the radial component of the NBS wave function in D-dimension with R and Q being the hyper radius and momentum, respectively, and [L], [K] denotes the quantum numbers of the angular momentum in D-dimension. δ[N](Q) is the generalized “phase shift” for a n-particle system and U[L][N](Q) is a unitary matrix, which parameterize the T-matrix as
Therefore, as in the case of n = 2 system (see section 2.2.1), the information of T-matrix is encoded in the asymptotic behavior of the NBS wave function. Based on this property, we can define the energy-independent non-local potential for a n-particle system, which can be extracted from the (time-dependent) HAL QCD method.
We calculate the six-point correlation function divided by two-point correlation function cubed,
where , , are the Jacobi coordinates. In the time-dependent HAL QCD method at the LO analysis for the derivative expansion and with the non-relativistic approximation, we can extract the three-nucleon forces through the following Schrödinger equation,
where with denotes two-nucleon forces between (i, j)-pair, μr = mN/2, μρ = 2mN/3 the reduced masses.
In our first study of three-nucleon forces, we consider the total 3N quantum numbers of (I, JP) = (1/2, 1/2+), the triton channel. We also consider a particular spacial geometry of the 3N, i.e., the “linear setup” (), where 3N are aligned linearly with equal spacing of . This setup makes the analysis much simpler. In addition, we consider the following channel, and calculate the corresponding matrix element of V3NF, so that we can suppress the statistical fluctuations in subtracting the contribution from V2N.
One of the biggest challenges in the lattice QCD study of three-nucleon forces is the enormous computational cost required for the calculation of correlation functions. In fact, in terms of a mass number A, the cost grows with the multiplication of two factors, one of which scales factorially in A due to the Wick contraction (permutation of quarks), and the other of which scales exponentially in A due to the color/spinor contractions. On this point, we have developed a novel computational algorithm, called the unified contraction algorithm (UCA), in which two contractions are unified and redundant calculations are eliminated systematically [61]. In particular, the computation becomes faster by a factor of 192 for a calculation of three-nucleon forces.
We perform the calculation in 2-flavor lattice QCD at (mπ, mN) = (0.76, 1.81), (0.93, 1.85), (1.13, 2.15) GeV [62]. We employ the gauge configurations generated by CP-PACS Collaboration with mean field -improved Wilson fermion and RG-improved Iwasaki gauge action on a L3 × T = 163 × 32 lattice. The lattice spacing is a = 0.1555(17) fm and thus L = 2.5 fm. Shown in Figure 15 (Left) are the lattice QCD results for the three-nucleon forces. We find a repulsive interaction at short-distances, r2 ≃ 0.2–0.4 fm (results at r2 ≲ 0.2 fm would suffer from lattice discretization error). Note that a repulsive short-range three-nucleon force is phenomenologically required to explain the properties of high density matter. On the other hand, three nucleon forces are found to be suppressed at long distances. This is in accordance with the suppression of two-pion-exchange due to the heavier pion masses.
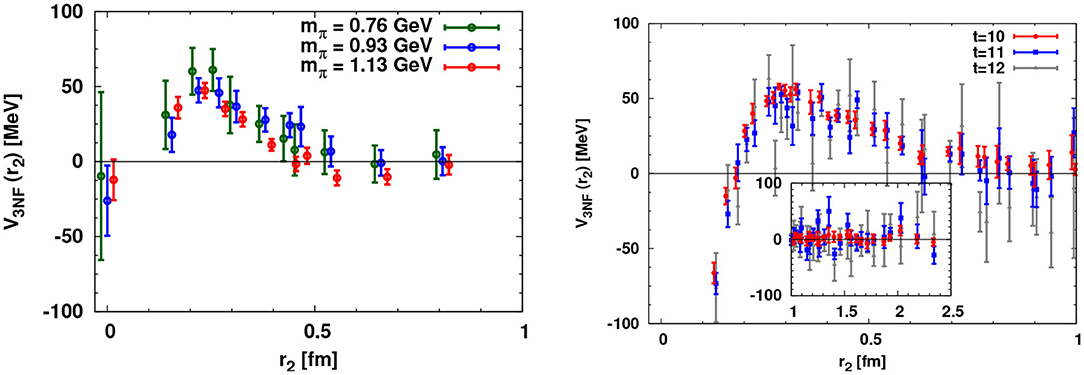
Figure 15. Three-nucleon forces in the triton channel with the linear setup. (Left) Results from 2-flavor lattice QCD at mπ= 0.76–1.13 GeV. (Right) Results from (2+1)-flavor lattice QCD at mπ = 0.51 GeV.
Shown in Figure 15 (Right) is the latest preliminary result obtained at mπ = 510 MeV. In this calculation, we employ (2+1)-flavor lattice QCD gauge configurations generated in Yamazaki et al. [36] with the RG-improved Iwasaki gauge action and non-perturbatively -improved Wilson quark action on a L3 × T = 643 × 64 lattice (work in progress). The lattice spacing is a = 0.090 fm and L = 5.8 fm. Avoiding the very short-distance region where lattice discretization error could affect the results, we again find the short-range repulsive three-nucleon forces at r2 ≃ 0.2–0.7 fm. We find that, while the pion mass dependence of three-nucleon forces is not significant at mπ= 0.76–1.13 GeV, the range of repulsive three-nucleon forces tend to be enlarged at mπ = 0.51 GeV. It is important to pursue the study at lighter pion masses toward the physical pion mass.
4.3. Applications to Nuclei, Nuclear Equation of State, and Structure of Neutron Stars
Once nuclear potentials are obtained by lattice QCD, we can use them to study various phenomena in nuclear physics and astrophysics. We here present the study of nuclear spectra/structures and Equation of State (EoS) of dense matter relevant to neutron star physics. Potentials used in this subsection are of the leading order only, and therefore are all hermitian. We can make non-hermitian higher order potentials in the HAL QCD method hermitian in the derivative expansion [63], which may be used for future applications in nuclear many body calculations.
In McIlroy et al. [64], binding energies and structures of doubly magic nuclei, 4He, 16O, 40Ca, are studied by an ab initio nuclear many-body calculation based on lattice nuclear forces. We employ the nuclear forces obtained in 3-flavor lattice QCD at Mps = 469 MeV (see Figure 12). We consider two-body nuclear forces in , , and channels, while nuclear forces in other channels and spin-orbit forces as well as three-nucleon forces are neglected. For simplicity, the Coulomb force between protons is not taken into account, either. As the ab initio many-body calculation, we employ self-consistent Green's function (SCGF) method, in which the single-particle propagator (Green's function) and the self-energy is solved self-consistently in a non-perturbative manner. In a practical calculation, the self-energy is calculated by Algebraic Diagrammatic Construction (ADC) formalism at third order for the so-called (low-momentum) P-space and Bethe-Goldstone equation (BGE) for the Q = 1 − P space. (see [64] for details.)
In Table 2, we summarize the results for the ground state energies, together with the results from Brueckner Hartree-Fock (BHF) calculation [65] and exact stochastic variational calculation [66] using the same lattice nuclear forces. For the results from SCGF, the first parentheses show the errors associated with the infrared (IR) extrapolation in the SCGF calculation. We also estimate the errors from many-body truncations using 4He as a benchmark. Since the SCGF result deviates from the exact solution by <10% for 4He, and the SCGF approach is size extensive, we take a conservative estimate of 10% error for 16O and 40Ca, which are quoted in the second parentheses. The BHF results are sensibly more bound than the SCGF results, and we interpret this as a limitation of BHF theory. For the results shown in Table 2, there exist additional errors associated with the statistical fluctuations in the input lattice nuclear forces, which are estimated to be ~10% [65]. Note that statistical fluctuations are correlated among nuclei, so we expect our observations described below are rather robust against statistical errors.
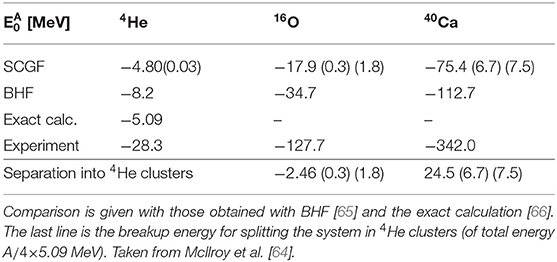
Table 2. Ground state energies of 4He, 16O, and 40Ca calculated by self-consistent Green's function (SCGF) method using nuclear forces at MPS = 469 MeV obtained from 3-flavor lattice QCD with the HAL QCD method.
We find that at Mps = 469 MeV in the SU(3) limit of QCD, both 4He and 40Ca have bound ground states while the deuteron is unbound. 16O is likely to decay into four separate alpha particles, though it is already close to become bound. Moreover, we find that asymmetric isotopes, like 28O, are strongly unbound systems. These results suggest that, when lowering the pion mass toward its physical value, closed shell isotopes are created at first around the traditional magic numbers and the region of Mps ~ 500 MeV marks a transition between an unbound nuclear chart and the emergence of bound isotopes.
We calculate the root mean square radii, which are given in Table 3, where we show only the central values. Although the total binding energies are 15–20% of the experimental value (Table 2), the computed charge radii are about the same as the experiment. We also find that the calculated one-nucleon spectral distributions are qualitatively close to those of real nuclei even for Mps = 469 MeV considered here. This is due to the fact that the heavy nucleon mass (mN = 1161.1 MeV) used here reduces the motion of the nucleons inside the nuclei and counterbalances the effect of weak attraction of the lattice nuclear forces at this pion mass.
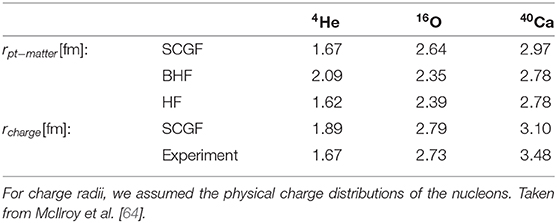
Table 3. Matter and charge radii of 4He, 16O, and 40Ca at MPS = 469 MeV computed by the SCGF method, which are compared with those by BHF [65], by Hartree-Fock (HF) and by experiments [67, 68].
We next present the study of properties of dense matter, namely, Equation of State (EoS) of nuclear matter. We again employ the nuclear forces in , , and channels obtained in 3-flavor lattice QCD. To study the quark mass dependence, we use lattice results for all five quark masses, at Mps = 469, 672, 837, 1015, 1171 MeV, which are shown in Figure 12. As a method for a many-body calculation, we employ the Brueckner-Hartree-Fock (BHF) theory [69], which is known to be quantitative enough to give the essential underlying physics for infinite matter.
In Figure 16 (Upper), we show the results of the ground state energy per nucleon (E/A) as a function of the Fermi momentum kF for the symmetric nuclear matter and the pure neutron matter. Shown together are the so-called APR EoS [70], which are obtained by the variational chain summation method from phenomenological nuclear forces with (APR(Full)) and without (APR(AV18)) three-nucleon forces. In Figure 16 (Upper-Left), we find that the symmetric nuclear matter becomes a self-bound system with a saturation point at the lightest quark mass (Mps = 469 MeV). This is the first time that the saturation in the symmetric nuclear matter is obtained through first-principles lattice QCD simulations. The saturation point, however, deviates from the empirical point primarily due to heavy pion (pseudo-scalar meson) mass in lattice simulation and the lack of three-nucleon forces in BHF calculation.
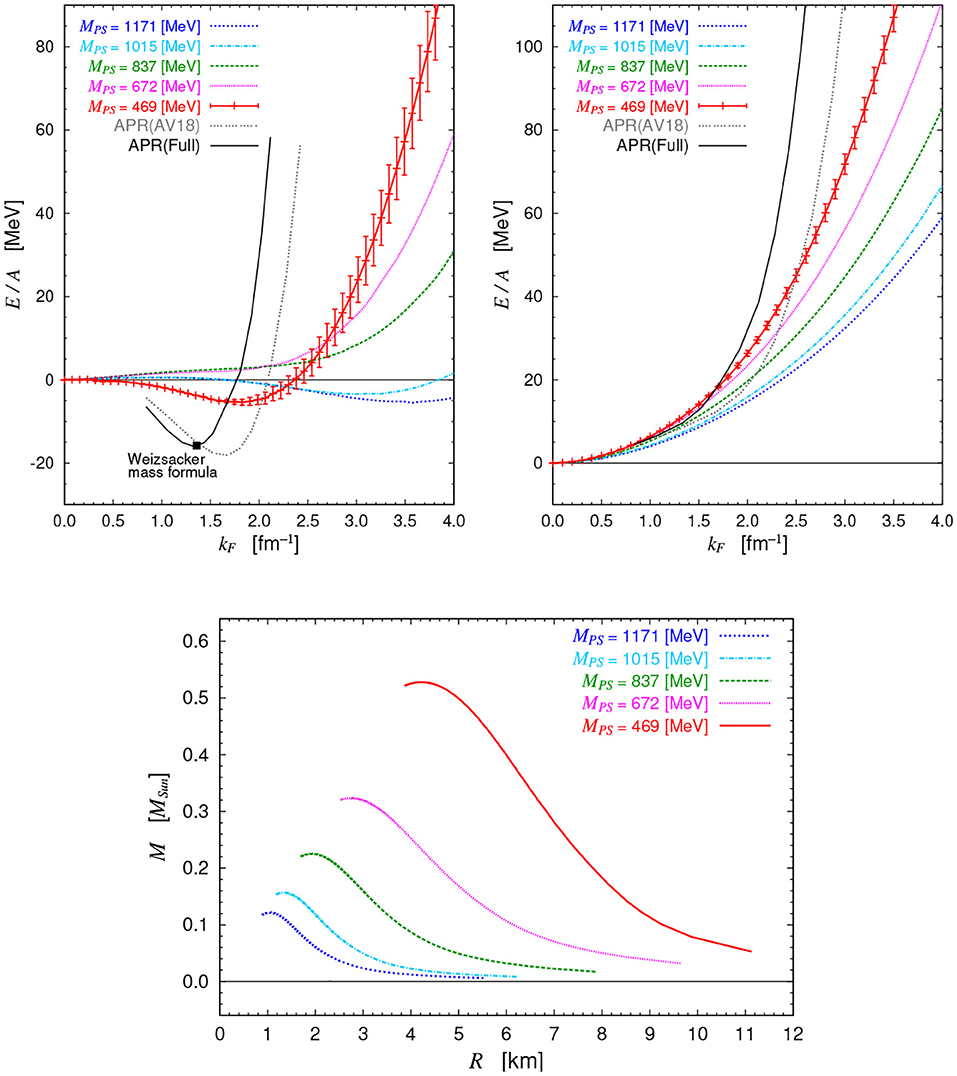
Figure 16. (Upper) Ground state energy per nucleon (E/A) as a function of the Fermi momentum kF by the BHF theory with nuclear forces from 3-flavor lattice QCD at Mps = 469–1,171 MeV, together with that from APR [70] with and without phenomenological three-nucleon forces. (Left) Results for the symmetric nuclear matter. filled square indicates the empirical saturation point. (Right) Results for the pure neutron matter. (Lower) Mass-radius relation of the neutron star based on EoS obtained by the BHF theory with nuclear forces from 3-flavor lattice QCD at Mps = 469–1,171 MeV. Figures are taken from Inoue et al. [69].
We also find a non-trivial Mps dependence of the EoS: the saturation disappears at intermediate pion masses (Mps = 672, 837 MeV) and possibly appears again at the heavy pion mass region (Mps = 1015, 1171 MeV). This implies that the saturation originates from a subtle balance between short-range repulsion and the intermediate attraction of the nuclear force, which have different mq dependence [44]. A similar non-trivial Mps dependence originated from the balance between repulsion and attraction is also observed for NN scattering phase shifts, as was discussed in section 4.1.
In Figure 16 (Upper-Right), we find that neutron matter is not self-bound due to large Fermi energy. If we decrease the pion mass, EoS is found to become stiffer. To further study the impact on phenomena in nuclear astrophysics, we calculate the mass (M) vs. the radius (R) relation of neutron stars at each pion mass. Here, we solve the Tolman-Oppenheimer-Volkoff (TOV) equation by using the EoS of the neutron-star matter with neutron, proton, electron and muon under the charge neutrality and beta equilibrium, where we use the standard parabolic approximation for asymmetric nuclear matters.
Shown in Figure 16 (Lower) is the M-R relation of the neutron star for different pion masses. As Mps decreases, the M-R curve shifts to the upper right direction, due to the stiffening of the EoS. While the maximum mass of the neutron star (Mmax) in this calculation is much smaller than the recent observations, Mmax ≃ 2M⊙, the deviation is most likely due to the heavy pion masses and lack of interactions as three-nucleon forces. A naive extrapolation of Mmax and the corresponding radius to Mps = 137 MeV would give Mmax ~ 2.2M⊙ and R ~ 12 km, which are encouraging for more quantitative studies in future. Another hottest topic in the context of neutron star physics is the effect of hyperon on the EoS at high density (so-called “hyperon puzzle”). Lattice QCD can play an unique role to study this effect by determining the hyperon forces which suffer from large uncertainties in experiments to date. For the on-going study in this direction, see Inoue [71].
4.4. Challenge: Nuclear Forces Near the Physical Pion Mass
While the results of nuclear forces at heavy pion masses are very intriguing and useful to extract the physical picture of nuclear forces, the quantitative results require the study at the physical pion mass. Note that the pion mass dependence of nuclear forces is quite non-trivial as discussed in sections 4.1 and 4.3, so the direct calculation near the physical point is desirable.
To this end, we have recently performed the first calculation of nuclear forces near the physical up, down and strange quark masses. Actually, our aim is to calculate not only nucleon forces but also hyperon forces, hereby achieve the comprehensive determination of two-baryon interactions from the strangeness S = 0 to −6 in parity-even channels (S- and D-waves). As mentioned before, the statistical fluctuations in lattice QCD are smaller (larger) for larger (smaller) quark masses, and thus the results have better precision in sectors involving more number of strange quarks (larger strangeness |S|). On the other hand, experiments in such larger |S| sectors are more difficult due to the short life time of hyperons. Therefore, lattice QCD studies and experiments are complementary with each other in the determination of baryon forces (see Figure 17).

Figure 17. An illustration of the complementary role of lattice QCD and experiments in the determination of baryon forces.
(2+1)-flavor gauge configurations are generated on a L3 × T = 963 × 96 lattice with the RG-improved Iwasaki gauge action and non-perturbatively -improved Wilson quark action and APE stout smearing. The lattice spacing is a ≃ 0.0846 fm (a−1 ≃ 2.333 GeV), so that spatial extent, L = 8.1 fm, is sufficiently large to accommodate two baryons in a box. Quark masses are tuned so as to be near the physical point, and the hadron masses are found to be (mπ, mK, mN) ≃ (146, 525, 955) MeV. NBS correlation functions for two-baryon systems are calculated for 55 channels in total and we extract the central and tensor forces in parity-even channel at the LO analysis for the derivative expansion (work in progress, and see also [72]). In order to make this first calculation a reality, “trinity” of state-of-the-art developments was crucial: (a) time-dependent HAL QCD method (theory), (b) unified contraction algorithm (software) and (c) K-computer, HOKUSAI and HA-PACS supercomputers (hardware).
Shown in Figure 18 are the results for the central force in the channel (Left), and the central force (Middle) and tensor force (Right) in the - channel. As noted above, nuclear forces are the most challenging interactions in lattice QCD calculation, and one can see that the results suffer from large statistical fluctuations. Nevertheless, the obtained results exhibit several interesting properties.
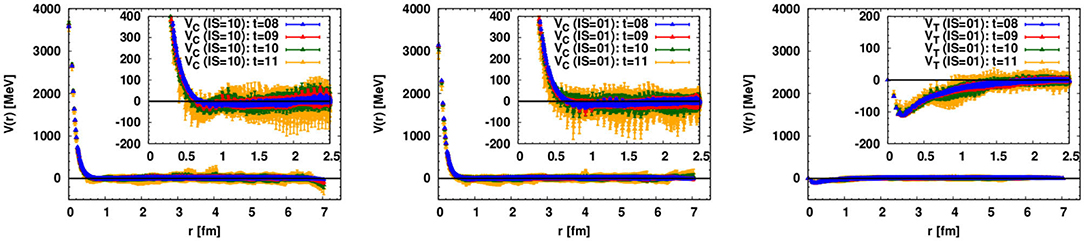
Figure 18. Nuclear forces from (2+1)-flavor lattice QCD near the physical point, mπ = 146 MeV. The central force in the channel (Left). The central force (Middle) and the tensor force (Right) in the - channel.
First of all, the repulsive core at short-range is clearly observed in central forces. In order to clarify the physical picture for the repulsive core, it is useful to compare them with hyperon forces obtained in the same lattice setup. We find that the strength of repulsive core (or attractive core) highly depends on the flavor SU(3) (SU(3)f) classification, in a consistent way with the quark Pauli blocking effect. In addition, if we compare interactions which belong to the same SU(3)f classification, such as and both of which belong to 27-plet, we find that the strength differs in a way which can be understood from the viewpoint of one-gluon-exchange (e.g., repulsive core in is stronger than that in ). These observations confirm the physical picture for the repulsive core obtained in the 3-flavor lattice QCD (section 4.1), the quark Pauli blocking effect and the one-gluon-exchange, is relevant even at physical quark masses. See also Park et al. [73] for a more detailed study on this point.
At middle and long distances, while statistical errors are quite large, we observe that the central force is attractive, resembling the phenomenological potential as one-pion-exchange potential (OPEP). The tensor force has relatively smaller statistical errors than the central forces, showing that the tensor force becomes stronger (with a negative sign) and has a longer tail, as compared with the tensor forces at heavier pion masses (section 4.1). This property can be understood by the picture of OPEP. These results are encouraging and serve as the first step to establish a direct connection between QCD and nuclear physics. At the same time, statistical errors remain to be large and there also exist systematic errors associated with inelastic state contaminations. The studies to resolve these issues are in progress, and the second generation calculation is planned on the forthcoming Exascale computer, “Fugaku” (see https://postk-web.r-ccs.riken.jp/).
5. Dibaryons
Before closing this review, we present our latest results on dibaryon searches in lattice QCD near the physical pion mass [72]. A dibaryon, a bound-state (or a resonance) with a baryon number B = 2 in QCD, can be classified in the SU(3)f as
for the octet-octet system, where the deuteron, the only stable dibaryon observed in nature so far, appears in the representation while H dibaryon has been predicted in the 1 representation [74] and actively investigated in lattice QCD [43, 44, 51, 52, 75]. For the decuplet-octet system, the classification leads to
and NΩ (NΔ) dibaryon has been predicted in the 8 (27) representation [76–78], and
for the decuplet-decuplet system, where ΩΩ dibaryon has been predicted in the 28 representation [79] while ΔΔ has been predicted in the [78, 80] and the corresponding d*(2380) was indeed observed [81]. Note that among decuplet baryons, only Ω is stable against strong decays.
5.1. The Most Strange Dibaryon
We first consider the ΩΩ system in the 28 representation of SU(3)f in the channel [82].
Figure 19 (Upper-Left) shows ΩΩ potentials at t/a = 16, 17, 18, which has qualitative features similar to the central potentials for NN but whose repulsion is weaker and attraction is shorter-ranged. This potential predicts an existence of one shallow bound state, whose binding energy is plotted in Figure 19 (Upper-Right) as a function of the root-mean-square distance, with (red) and without (blue) Coulomb repulsion between ΩΩ. We may call this ΩΩ bound state “the most strange dibaryon.” Such a system can be best searched experimentally by two-particle correlations in relativistic heavy-ion collisions [84].
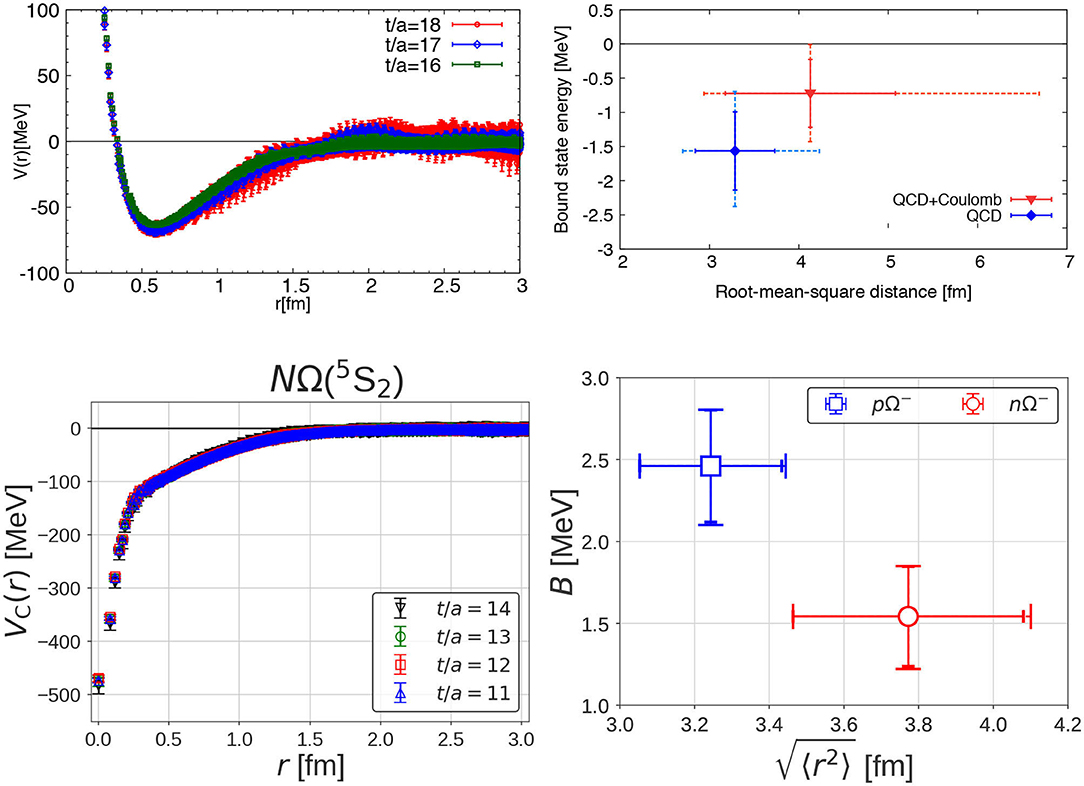
Figure 19. (Upper) The ΩΩ system in the channel in 2 + 1 flavor QCD at mπ ≃ 146 MeV and a ≃ 0.0846 fm on a (8.1 fm)3 box. (Left) The ΩΩ potential V(r) at t/a = 16, 17, 18. (Right) The binding energy of the ΩΩ system and the root-mean-square distance between two Ω's are shown by blue solid diamond (red solid triangle), calculated from the ΩΩ potential V(r) at t/a = 17 without (with) the Coulomb repulsion. Taken from Gongyo et al. [82]. (Lower) The NΩ system in the channel with the same lattice setup for ΩΩ. (Left) The NΩ potential VC(r) at t/a = 11, 12, 13, 14. (Right) The binding energy and the root-mean-square distance for the nΩ− (red open circle) and pΩ− (blue open square). Taken from Iritani et al. [83].
5.2. NΩ Dibaryon
We next consider the NΩ system with S = −3 in the 8 representation in the channel [83]. Near the physical point, NΩ(5S2) may couple to D-wave octet-octet channels below the NΩ threshold (ΛΞ and ΣΞ), but such couplings are assumed to be small in this calculation.
Figure 19 (Lower-Left) shows the NΩ potential at t/a = 11–14, which is attractive at all distances without repulsive core, so that one bound state appears in this channel. In Figure 19 (Lower-Right), the binding energy (vertical) and the the root-mean-square distance (horizontal) are plotted for NΩ− with no Coulomb interaction (red) and pΩ− with Coulomb attraction (blue). These binding energies are much smaller than MeV at heavy pion mass mπ = 875 MeV [85]. Such a NΩ state can be searched through two-particle correlations in relativistic nucleus-nucleus collisions [84] and an experimental indication was also reported [86].
5.3. Comparison Among Dibaryons
Let us consider the scattering length a0 and the effective range reff for ΩΩ(1S0) and NΩ(5S2). In Figure 20, the ratio reff/a0 as a function of reff are plotted for ΩΩ(1S0) and NΩ(5S2) obtained in lattice QCD near the physical pion mass, together with the experimental values for NN(3S1) (deuteron) and NN(1S0) (di-neutron). Small values of |reff/a0| in all cases indicate that these systems are located close to the unitary limit.
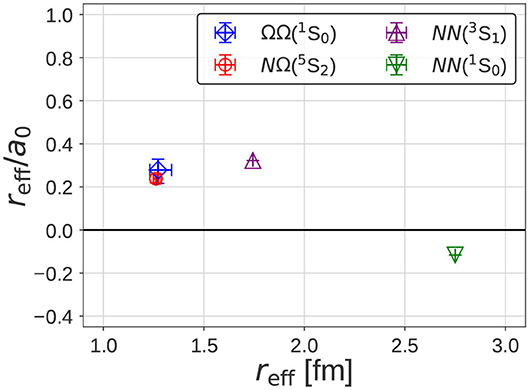
Figure 20. The ratio of the effective range and the scattering length reff/a0 as a function of reff for (blue open diamond) and (red open circle) obtained in lattice QCD, as well as for (purple open up-triangle) and (green open down-triangle) in experiments. Taken from Iritani et al. [83]. The sign convention for the scattering length is opposite to Eq. (5) in this figure.
6. Conclusions
In this paper, we have reviewed the recent progress in lattice QCD study of baryon-baryon interactions by the HAL QCD method. We first presented the detailed account on how to define the potentials in quantum field theories, such as QCD. The key observation is that the Nambu-Bethe-Salpeter (NBS) wave functions contain the information of scattering phase shifts below inelastic threshold in their asymptotic behaviors outside the range of the interactions. The potentials at the interaction region can then be defined through the NBS wave functions so as to be faithful to the phase shifts by construction, where the non-locality of the potential is defined by the derivative expansion. In addition, by constructing the potentials in energy-independent way, the potentials can be extracted from two-baryon correlation functions without the requirement of the ground state saturation.
We then made a detailed comparison between the HAL QCD method and the conventional method, in which phase shifts are obtained from the finite volume energies through the Lüscher's formula. We pointed out that, while the validity of the latter method relies on the ground state saturation of the correlation function, its practical procedure for multi-baryon systems (“direct method”) so far has utilized only the plateau-like structures of the effective energies at Euclidean times much earlier than the inverse of the lowest excitation energy. We showed theoretical and numerical evidences that such a procedure generally leads to unreliable results due to the contaminations from the elastic excited states: For instance, the results were found to be dependent on the operators and unphysical behaviors were exposed by the normality check. This invalidates the claim of the literature in the direct method that NN bound states exist for pion masses heavier than 300 MeV.
On the other hand, HAL QCD method is free from such a serious problem since the signal of potentials can be extracted from not only the ground state but also elastic excited states. While there instead exists the truncation error of the derivative expansion of the potential, the calculation of the higher order term in the derivative expansion showed that the convergence of the expansion is sufficiently good at low energies. Furthermore, utilizing the finite volume eigenmodes of the HAL QCD Hamiltonian, the excited state contaminations in the direct method were explicitly quantified. It turns out that the plateau-like structures of effective energies at early time slices are indeed pseudo-plateaux contaminated by elastic excited states and that the plateau for the ground state is realized only at a much larger time corresponding to the inverse of the lowest excitation energy gap. We also showed that, by employing an optimized operator utilizing the finite volume eigenmodes, the effective energies from the correlation functions give consistent results with those from the HAL QCD potential. Thus the long-standing issue on the consistency between the conventional method based on the Lüscher's formula and the HAL QCD method was positively resolved.
After establishing the reliability of the HAL QCD method, we presented the numerical results of nuclear forces from the HAL QCD method at various lattice QCD setups. At heavy pion masses, where good signal-to-noise ratio can be achieved in lattice QCD, we observed that the obtained NN potentials in the parity-even channel (, -) reproduce the qualitative features of the phenomenological potentials, namely, attractive wells at long and medium distances, accompanied with repulsive cores at short distance in the central potentials and the strong tensor force. The net interactions were found to be attractive, which however are not strong enough to form a bound NN state, probably due to the heavy pion masses. We observed that the tail structures are enhanced at lighter pion masses, which can be understood from the viewpoint of one-pion exchange contributions. We also found the repulsive cores are enhanced at lighter pion masses. Combined with our systematic studies including hyperon forces, the nature of repulsive cores was found to be well-described by the quark Pauli blocking effect together with the one-gluon-exchange contribution.
The HAL QCD method can be extended to determine more complicated nuclear forces, such as spin-orbit forces and three-nucleon forces. In this paper, we considered two-nucleon systems in the parity-odd channels (, , , - channels) and calculated spin-orbit forces as well as central and tensor forces. We found that qualitative features of experimental results are generally well-reproduced, while the magnitudes differ due to the heavy pion mass. In particular, we observed the strong (and negative) spin-orbit forces, which lead to the attraction in the channel. Three-nucleon forces were studied in the triton channel, (I, JP) = (1/2, 1/2+), thank to the unified contraction algorithm (UCA), which can enormously speed up calculations of multi-baryon correlation functions. It was found that there exists a repulsive three-nucleon forces at short distances. These observations are of interest in the context of not only the structures of nuclei but also those of neutron stars, e.g., P-wave superfluidity and the maximum mass of neutron stars.
We carried out the applications to nuclei, nuclear equation of state (EoS) and structure of neutron stars based on lattice nuclear forces at heavy quark masses. We performed ab initio self-consistent Green's function (SCGF) calculations for closed shell nuclei with nuclear forces at Mps=469 MeV in the SU(3) limit of QCD. We found that 4He, 40Ca nuclei are bound, and 16O is close to become bound, while asymmetric isotopes are strongly unbound. The results suggest that, when lowering the pion mass toward its physical value, islands of stability appear at first around the traditional doubly magic numbers. The nuclear EoS was also studied by the BHF theory with nuclear forces in the flavor SU(3) limit. We found that the saturation property appears in the symmetric nuclear matter at Mps = 469 MeV. A mass-radius relation of the neutron star was also studied based on the EoS obtained from lattice nuclear forces and we observed a tendency that the maximum mass of a neutron star increases as the pion mass decreases.
Finally, we presented the first lattice QCD study of baryon forces near the physical pion mass in the parity-even channel. The computation is quite challenging particularly for nuclear forces due to bad signal-to-noise ratio near the physical point. Nevertheless, we observed prominent characteristics of nuclear forces, such as repulsive cores at short distances as well as attractive interactions at mid and long distances in central forces, and a strong (and negative) tensor force. We also presented the results for the hyperon forces obtained near the physical point. We found that both and systems have strong attractions, and (quasi) bound dibaryons are formed near the unitary limit. These systems could be searched experimentally through two-particle correlations in relativistic nucleus-nucleus collisions.
Present results shown in this paper already indicate a clear pathway which connects nuclear physics with its underlying theory of the strong interaction, QCD. While there remain many challenges to accomplish researches in this direction, there is no doubt that successive theoretical developments together with next-generation supercomputers will further deepen the connection between the two. The outcome is also expected to play a crucial role to understand the nuclear astrophysical phenomena, such as supernova explosions and mergers of binary neutron stars, as well as the nucleosynthesis associated with these explosive phenomena.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author/s.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This work was supported in part by the Grant-in-Aid of the Japanese Ministry of Education, Sciences and Technology, Sports and Culture (MEXT) for Scientific Research (Nos. JP16H03978, JP18H05236, JP18H05407, and JP19K03879), by HPCI programs (hp120281, hp130023, hp140209, hp150223, hp150262, hp150085, hp160211, hp160093, hp170230, hp170170, hp180179, hp180117, hp190160, and hp190103), by a priority issue (Elucidation of the fundamental laws and evolution of the universe) to be tackled by using Post K Computer, and by Joint Institute for Computational Fundamental Science (JICFuS).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank members of the HAL QCD Collaboration for providing lattice QCD results and for fruitful collaborations based on which this paper was prepared. Figure 12 was reprinted from Inoue et al. [44] with permission from Elsevier. Figure 14 was taken from Murano et al. [50], and Figures 19, 20 were taken from Iritani et al. [83], under the term of the https://creativecommons.org/licenses/by/3.0/.
Footnotes
1. ^The formula becomes more complicated if the nucleon spins are considered [22, 23].
2. ^A similar attempt to represent an arbitrary potential in terms of a separable potential is given in Ernst et al. [31, 32].
3. ^After these problems were pointed out in Iritani et al. [19], revised data of NPL2013 have been presented in Wagman et al. [41], whose EREs are still marginal to satisfy/violate the physical pole condition.
4. ^Note that Mainz2018 employed a source operator as and they reported that “In the 27-plet (dineutron) sector, the finite volume analysis suggests that the existence of a bound state is unlikely.”
5. ^In lattice QCD studies for the meson-meson scatterings [9], serious systematics from the excited state contaminations in the simple plateau fitting have been widely recognized and the variational method has been utilized to obtain the finite volume spectra rather reliably, which can be combined with the Lüscher's finite volume formula to extract phase shifts.
6. ^Mps = mπ = mK and Moct = mN = mΛ = mΣ = mΞ in 3-flavor QCD.
References
1. Stoks VGJ, Klomp RAM, Terheggen CPF, de Swart JJ. Construction of high quality N N potential models. Phys Rev C. (1994) 49:2950–62. doi: 10.1103/PhysRevC.49.2950
2. Wiringa RB, Stoks VGJ, Schiavilla R. An Accurate nucleon-nucleon potential with charge independence breaking. Phys Rev C. (1995) 51:38–51. doi: 10.1103/PhysRevC.51.38
3. Machleidt R. The High precision, charge dependent Bonn nucleon-nucleon potential (CD-Bonn). Phys Rev C. (2001) 63:024001. doi: 10.1103/PhysRevC.63.024001
4. Weinberg S. Nuclear forces from chiral Lagrangians. Phys Lett B. (1990) 251:288–92. doi: 10.1016/0370-2693(90)90938-3
5. Weinberg S. Effective chiral Lagrangians for nucleon–pion interactions and nuclear forces. Nucl Phys B. (1991) 363:3–18. doi: 10.1016/0550-3213(91)90231-L
6. Epelbaum E, Hammer HW, Meissner UG. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773–825. doi: 10.1103/RevModPhys.81.1773
7. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rept. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001
8. Hammer HW, Koenig S, van Kolck U. Nuclear effective field theory: status and perspectives. Rev Mod Phys. (2019) 92:025004. doi: 10.1103/RevModPhys.92.025004
9. Briceno RA, Dudek JJ, Young RD. Scattering processes and resonances from lattice QCD. Rev Mod Phys. (2018) 90:025001. doi: 10.1103/RevModPhys.90.025001
10. Luscher M, Wolff U. How to calculate the elastic scattering matrix in two-dimensional quantum field theories by numerical simulation. Nucl Phys B. (1990) 339:222–52. doi: 10.1016/0550-3213(90)90540-T
11. Rummukainen K, Gottlieb SA. Resonance scattering phase shifts on a nonrest frame lattice. Nucl Phys B. (1995) 450:397–436. doi: 10.1016/0550-3213(95)00313-H
12. Briceno RA, Davoudi Z, Luu TC. Two-nucleon systems in a finite volume: (I) quantization conditions. Phys Rev D. (2013) 88:034502. doi: 10.1103/PhysRevD.88.034502
13. Briceno RA. Two-particle multichannel systems in a finite volume with arbitrary spin. Phys Rev D. (2014) 89:074507. doi: 10.1103/PhysRevD.89.074507
14. Hansen MT, Sharpe SR. Relativistic, model-independent, three-particle quantization condition. Phys Rev D. (2014) 90:116003. doi: 10.1103/PhysRevD.90.116003
15. Hansen MT, Sharpe SR. Lattice QCD and three-particle decays of resonances. Ann Rev Nucl Part Sci. (2019) 69:65–107. doi: 10.1146/annurev-nucl-101918-023723
16. Durr S, Fodor Z, Frison J, Hoelbling C, Hoffmann R, Katz SD, et al. Ab-initio determination of light hadron masses. Science. (2008) 322:1224–7. doi: 10.1126/science.1163233
17. Borsanyi S, Durr S, Fodor Z, Hoelbling C, Katz SD, Krieg S, et al. Ab initio calculation of the neutron-proton mass difference. Science. (2015) 347:1452–5. doi: 10.1126/science.1257050
18. Luscher M. Two particle states on a torus and their relation to the scattering matrix. Nucl Phys B. (1991) 354:531–78. doi: 10.1016/0550-3213(91)90366-6
19. Iritani T, Aoki S, Doi T, Hatsuda T, Ikeda Y, Inoue T, et al. Are two nucleons bound in lattice QCD for heavy quark masses? Consistency check with Lüscher's finite volume formula. Phys Rev D. (2017) 96:034521. doi: 10.1103/PhysRevD.96.034521
21. Kawai D, Aoki S, Doi T, Ikeda Y, Inoue T, Iritani T, et al. I = 2 ππ scattering phase shift from the HAL QCD method with the LapH smearing. PTEP. (2018) 2018:043B04. doi: 10.1093/ptep/pty032
22. Ishizuka N. Derivation of Luscher's finite size formula for N pi and NN system. PoS LAT. (2009) 2009:119. doi: 10.22323/1.091.0119
23. Aoki S, Hatsuda T, Ishii N. Theoretical foundation of the nuclear force in QCD and its applications to central and tensor forces in quenched lattice QCD simulations. Prog Theor Phys. (2010) 123:89–128. doi: 10.1143/PTP.123.89
24. Lin CJD, Martinelli G, Sachrajda CT, Testa M. K → ππ decays in a finite volume. Nucl Phys B. (2001) 619:467–98. doi: 10.1016/S0550-3213(01)00495-3
25. Aoki S, Fukugita M, Ishikawa KI, Ishizuka N, Iwasaki Y, Kanaya K, et al. I=2 pion scattering length from two-pion wave functions. Phys Rev D. (2005) 71:094504. doi: 10.1103/PhysRevD.71.094504
26. Ishii N, Aoki S, Hatsuda T. The nuclear force from lattice QCD. Phys Rev Lett. (2007) 99:022001. doi: 10.1103/PhysRevLett.99.022001
27. Aoki S, Doi T, Hatsuda T, Ikeda Y, Inoue T, Ishii N, et al. Lattice QCD approach to nuclear physics. PTEP. (2012) 2012:01A105. doi: 10.1093/ptep/pts010
28. Sugiura T, Ishii N, Oka M. Derivative expansion of wave function equivalent potentials. Phys Rev D. (2017) 95:074514. doi: 10.1103/PhysRevD.95.074514
29. Aoki S, Doi T, Hatsuda T, Ishii N. Comment on “Relation between scattering amplitude and Bethe-Salpeter wave function in quantum field theory”. Phys Rev D. (2018) 98:038501. doi: 10.1103/PhysRevD.98.038501
30. Yamazaki T, Kuramashi Y. Relation between scattering amplitude and Bethe-Salpeter wave function in quantum field theory. Phys Rev D. (2017) 96:114511. doi: 10.1103/PhysRevD.96.114511
31. Ernst DJ, Shakin CM, Thaler RM. Separable representations of two-body interactions. Phys Rev C. (1973) 8:46–52. doi: 10.1103/PhysRevC.8.46
32. Ernst DJ, Shakin CM, Thaler RM. Separable representations of T matrices valid in the vicinity of off-shell points. Phys Rev C. (1974) 9:1780–3. doi: 10.1103/PhysRevC.9.1780
33. Murano K, Ishii N, Aoki S, Hatsuda T. Nucleon-nucleon potential and its non-locality in lattice QCD. Prog Theor Phys. (2011) 125:1225–40. doi: 10.1143/PTP.125.1225
34. Ishii N, Aoki S, Doi T, Hatsuda T, Ikeda Y, Inoue T, et al. Hadron-hadron interactions from imaginary-time Nambu-Bethe-Salpeter wave function on the lattice. Phys Lett B. (2012) 712:437–41. doi: 10.1016/j.physletb.2012.04.076
35. Yamazaki T, Kuramashi Y, Ukawa A. Two-nucleon bound states in quenched lattice QCD. Phys Rev D. (2011) 84:054506. doi: 10.1103/PhysRevD.84.054506
36. Yamazaki T, Ishikawa Ki, Kuramashi Y, Ukawa A. Helium nuclei, deuteron and dineutron in 2+1 flavor lattice QCD. Phys Rev D. (2012) 86:074514. doi: 10.1103/PhysRevD.86.074514
37. Orginos K, Parreno A, Savage MJ, Beane SR, Chang E, Detmold W. Two nucleon systems at mπ ~ 450MeV from lattice QCD. Phys Rev D. (2015) 92:114512. doi: 10.1103/PhysRevD.92.114512
38. Beane SR, Chang E, Detmold W, Lin HW, Luu TC, Orginos K, et al. The deuteron and exotic two-body bound states from lattice QCD. Phys Rev D. (2012) 85:054511. doi: 10.1103/PhysRevD.85.054511
39. Yamazaki T, Ishikawa Ki, Kuramashi Y, Ukawa A. Study of quark mass dependence of binding energy for light nuclei in 2+1 flavor lattice QCD. Phys Rev D. (2015) 92:014501. doi: 10.1103/PhysRevD.92.014501
40. Beane SR, Chang E, Cohen SD, Detmold W, Lin HW, Luu TC, et al. Light nuclei and hypernuclei from quantum chromodynamics in the limit of SU(3) flavor symmetry. Phys Rev D. (2013) 87:034506. doi: 10.1103/PhysRevD.87.034506
41. Wagman ML, Winter F, Chang E, Davoudi Z, Detmold W, Orginos K, et al. Baryon-Baryon interactions and spin-flavor symmetry from lattice quantum chromodynamics. Phys Rev D. (2017) 96:114510. doi: 10.1103/PhysRevD.96.114510
42. Berkowitz E, Kurth T, Nicholson A, Joo B, Rinaldi E, Strother M, et al. Two-nucleon higher partial-wave scattering from lattice QCD. Phys Lett B. (2017) 765:285–92. doi: 10.1016/j.physletb.2016.12.024
43. Francis A, Green JR, Junnarkar PM, Miao C, Rae TD, Wittig H. Lattice QCD study of the H dibaryon using hexaquark and two-baryon interpolators. Phys Rev D. (2019) 99:074505. doi: 10.1103/PhysRevD.99.074505
44. Inoue T, Aoki S, Doi T, Hatsuda T, Ikeda Y, Ishii N, et al. Two-Baryon potentials and H-dibaryon from 3-flavor lattice QCD simulations. Nucl Phys A. (2012) 881:28–43. doi: 10.1016/j.nuclphysa.2012.02.008
45. Ishii N. Baryon-baryon interactions from lattice QCD. PoS CD. (2013) 12:025. doi: 10.22323/1.172.0025
46. Iritani T, Doi T, Aoki S, Gongyo S, Hatsuda T, Ikeda Y, et al. Mirage in temporal correlation functions for Baryon-Baryon interactions in lattice QCD. JHEP. (2016) 10:101. doi: 10.1007/JHEP10(2016)101
47. Iritani T, Aoki S, Doi T, Gongyo S, Hatsuda T, Ikeda Y, et al. Systematics of the HAL QCD potential at low energies in lattice QCD. Phys Rev D. (2019) 99:014514. doi: 10.1103/PhysRevD.99.014514
48. Iritani T, Aoki S, Doi T, Hatsuda T, Ikeda Y, Inoue T, et al. Consistency between Lüscher's finite volume method and HAL QCD method for two-baryon systems in lattice QCD. JHEP. (2019) 3:007. doi: 10.1007/JHEP03(2019)007
49. Miyamoto T, Akahoshi Y, Aoki S, Aoyama T, Doi T, Gongyo S, et al. Partial wave decomposition on the lattice and its applications to the HAL QCD method. Phys Rev D. (2019) 101:074514. doi: 10.1103/PhysRevD.101.074514
50. Murano K, Ishii N, Aoki S, Doi T, Hatsuda T, Ikeda Y, et al. Spin-orbit force from lattice QCD. Phys Lett B. (2014) 735:19–24. doi: 10.1016/j.physletb.2014.05.061
51. Inoue T, Ishii N, Aoki S, Doi T, Hatsuda T, Ikeda Y, et al. Baryon-Baryon interactions in the flavor SU(3) limit from full QCD simulations on the lattice. Prog Theor Phys. (2010) 124:591–603. doi: 10.1143/PTP.124.591
52. Inoue T, Ishii N, Aoki S, Doi T, Hatsuda T, Ikeda Y, et al. Bound H-dibaryon in flavor SU(3) limit of lattice QCD. Phys Rev Lett. (2011) 106:162002. doi: 10.1103/PhysRevLett.106.162002
53. Ishii N, Aoki S, Hatsuda T. Nuclear forces from quenched and 2+1 flavor lattice QCD using the PACS-CS gauge configurations. PoS Lattice. (2008) 2008:155. doi: 10.22323/1.066.0155
54. Oka M, Shimizu K, Yazaki K. Quark cluster model of baryon baryon interaction. Prog Theor Phys Suppl. (2000) 137:1–20. doi: 10.1143/PTPS.137.1
55. Coon SA, Han HK. Reworking the Tucson-Melbourne three nucleon potential. Few Body Syst. (2001) 30:131–41. doi: 10.1007/s006010170022
56. Pieper SC, Pandharipande VR, Wiringa RB, Carlson J. Realistic models of pion exchange three nucleon interactions. Phys Rev C. (2001) 64:014001. doi: 10.1103/PhysRevC.64.014001
57. Weinberg S. Three body interactions among nucleons and pions. Phys Lett B. (1992) 295:114–21. doi: 10.1016/0370-2693(92)90099-P
58. Aoki S, Charron B, Doi T, Hatsuda T, Inoue T, Ishii N. Construction of energy-independent potentials above inelastic thresholds in quantum field theories. Phys Rev D. (2013) 87:034512. doi: 10.1103/PhysRevD.87.034512
59. Aoki S, Ishii N, Doi T, Ikeda Y, Inoue T. Asymptotic behavior of Nambu-Bethe-Salpeter wave functions for multiparticles in quantum field theories. Phys Rev D. (2013) 88:014036. doi: 10.1103/PhysRevD.88.014036
60. Gongyo S, Aoki S. Asymptotic behavior of Nambu-Bethe-Salpeter wave functions for scalar systems with a bound state. PTEP. (2018) 2018:093B03. doi: 10.1093/ptep/pty097
61. Doi T, Endres MG. Unified contraction algorithm for multi-baryon correlators on the lattice. Comput Phys Commun. (2013) 184:117. doi: 10.1016/j.cpc.2012.09.004
62. Doi T, Aoki S, Hatsuda T, Ikeda Y, Inoue T, Ishii N, et al. Exploring three-nucleon forces in lattice QCD. Prog Theor Phys. (2012) 127:723–38. doi: 10.1143/PTP.127.723
63. Aoki S, Iritani T, Yazaki K. Hermitizing the HAL QCD potential in the derivative expansion. PTEP. (2020) 2:023. doi: 10.1093/ptep/ptz166
64. McIlroy C, Barbieri C, Inoue T, Doi T, Hatsuda T. Doubly magic nuclei from lattice QCD forces at MPS=469 MeV/c2. Phys Rev C. (2018) 97:021303. doi: 10.1103/PhysRevC.97.021303
65. Inoue T, Aoki S, Charron B, Doi T, Hatsuda T, Ikeda Y, et al. Medium-heavy nuclei from nucleon-nucleon interactions in lattice QCD. Phys Rev C. (2015) 91:011001. doi: 10.1103/PhysRevC.91.011001
66. Nemura H. Recent developments on LQCD studies of nuclear force. Int J Mod Phys E. (2014) 23:1461006. doi: 10.1142/S0218301314610060
67. De Vries H, De Jager CW, De Vries C. Nuclear charge and magnetization density distribution parameters from elastic electron scattering. Atom Data Nucl Data Tabl. (1987) 36:495–536. doi: 10.1016/0092-640X(87)90013-1
68. Angeli I, Marinova KP. Table of experimental nuclear ground state charge radii: an update. Atom Data Nucl Data Tabl. (2013) 99:69–95. doi: 10.1016/j.adt.2011.12.006
69. Inoue T, Aoki S, Doi T, Hatsuda T, Ikeda Y, Ishii N, et al. Equation of state for nucleonic matter and its quark mass dependence from the nuclear force in lattice QCD. Phys Rev Lett. (2013) 111:112503. doi: 10.1103/PhysRevLett.111.112503
70. Akmal A, Pandharipande VR, Ravenhall DG. The equation of state of nucleon matter and neutron star structure. Phys Rev C. (1998) 58:1804–28. doi: 10.1103/PhysRevC.58.1804
71. Inoue T. Strange nuclear physics from QCD on lattice. AIP Conf Proc. (2019) 2130:020002. doi: 10.1063/1.5118370
72. Doi T, Iritani T, Aoki S, Gongyo S, Hatsuda T, Ikeda Y, et al. Baryon interactions from lattice QCD with physical quark masses-Nuclear forces and ΞΞ forces. EPJ Web Conf. (2018) 175:05009. doi: 10.1051/epjconf/201817505009
73. Park A, Lee SH, Inoue T, Hatsuda T. Baryon-baryon interactions at short distances-constituent quark model meets lattice QCD. Eur Phys J A. (2019) 56:93. doi: 10.1140/epja/s10050-020-00078-z
74. Jaffe RL. Perhaps a stable dihyperon. Phys Rev Lett. (1977) 38:195–8. doi: 10.1103/PhysRevLett.38.195
75. Beane SR, Chang E, Detmold W, Joo B, Lin HW, Luu TC, et al. Evidence for a bound H-dibaryon from lattice QCD. Phys Rev Lett. (2011) 106:162001. doi: 10.1103/PhysRevLett.106.162001
76. Goldman JT, Maltman K, Stephenson GJ Jr, Schmidt KE, Wang F. Strangeness-3 dibaryons. Phys Rev Lett. (1987) 59:627. doi: 10.1103/PhysRevLett.59.627
77. Oka M. Flavor octet dibaryons in the Quark model. Phys Rev D. (1988) 38:298. doi: 10.1103/PhysRevD.38.298
78. Dyson F, Xuong NH. Y=2 states in Su(6) theory. Phys Rev Lett. (1964) 13:815–7. doi: 10.1103/PhysRevLett.13.815
79. Zhang ZY, Yu YW, Shen PN, Dai LR, Faessler A, Straub U. Hyperon nucleon interactions in a chiral SU(3) quark model. Nucl Phys A. (1997) 625:59–70. doi: 10.1016/S0375-9474(97)00033-X
80. Kamae T, Fujita T. Possible existence of a deeply bound delta-delta system. Phys Rev Lett. (1977) 38:471–5. doi: 10.1103/PhysRevLett.38.471
81. Adlarson P, Adolph C, Augustyniak W, Baru V, Bashkanov M, Bergmann FS, et al. ABC effect in basic double-pionic fusion–observation of a new resonance? Phys Rev Lett. (2011) 106:242302. doi: 10.1103/PhysRevLett.106.242302
82. Gongyo S, Sasaki K, Aoki S, Doi T, Hatsuda T, Ikeda Y, et al. Most strange dibaryon from lattice QCD. Phys Rev Lett. (2018) 120:212001. doi: 10.1103/PhysRevLett.120.212001
83. Iritani T, Aoki S, Doi T, Etminan F, Gongyo S, Hatsuda T, et al. NΩ dibaryon from lattice QCD near the physical point. Phys Lett B. (2019) 792:284–9. doi: 10.1016/j.physletb.2019.03.050
84. Morita K, Gongyo S, Hatsuda T, Hyodo T, Kamiya Y, Ohnishi A. Probing ΩΩ and pΩ dibaryons with femtoscopic correlations in relativistic heavy-ion collisions. Phys Rev C. (2020) 101:015201. doi: 10.1103/PhysRevC.101.015201
85. Etminan F, Nemura H, Aoki S, Doi T, Hatsuda T, Ikeda Y, et al. Spin-2 NΩ dibaryon from lattice QCD. Nucl Phys A. (2014) 928:89–98. doi: 10.1016/j.nuclphysa.2014.05.014
Keywords: lattice QCD, nuclear forces, baryon-baryon interactions, dibaryons, equation of state, neutron stars
Citation: Aoki S and Doi T (2020) Lattice QCD and Baryon-Baryon Interactions: HAL QCD Method. Front. Phys. 8:307. doi: 10.3389/fphy.2020.00307
Received: 13 January 2020; Accepted: 03 July 2020;
Published: 14 August 2020.
Edited by:
Laura Elisa Marcucci, University of Pisa, ItalyReviewed by:
Fiorella Burgio, National Institute of Nuclear Physics, ItalyRaul A. Briceno, Old Dominion University, United States
Copyright © 2020 Aoki and Doi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sinya Aoki, c2Fva2lAeXVrYXdhLmt5b3RvLXUuYWMuanA=
 Sinya Aoki
Sinya Aoki Takumi Doi2,3
Takumi Doi2,3