- Glorious Sun School of Business and Management, Donghua University, Shanghai, China
In recent years, shadow banking is considered to be one of the important factors that cause the financial crisis and destroy the stability of the banking system. However, in fact, macroeconomic fluctuation is closely related to the stability of the banking system. As an indispensable part of the decision-making of shadow banking, the shock of macroeconomic fluctuation plays a vital role as well. Therefore, based on the agent-based method in modern complex network theory, a model of a dynamic complex interbank network with shadow banking under macroeconomic fluctuation is proposed in this paper, in which the shock of macroeconomic fluctuation on the stability of the banking system with shadow banking and the effect of the shadow banking on the macroeconomic fluctuation are explored. The results show that in the boom, the liquidity of the banking system is expanded, the average bank profits are improved, the investment opportunities are increased, the survival bank ratio is high, and the systemic risk is low. The banking system stability is increased. While in the stable and the bust, the liquidity of the banking system is declined, average bank profits are shrunk, investment opportunities are gradually disappeared, and the survival bank ratio is decreased. Shadow banking starts to collapse, the systemic risk breaks out, and the banking system stability is seriously damaged. Furthermore, by analyzing the influence of shadow banking on the macroeconomic fluctuation, we find that shadow banking builds up the fragility of macroeconomic performance, and without external regulation, this impact is irreversible. This paper sheds light on the impact of macroeconomic fluctuation on the stability of the banking system with shadow banking, shows the risk problems brought by shadow banking for economic fluctuation, refines research of the banking system stability, and offers effective theoretical references for decision-makers and regulators.
Introduction
The frequent financial crises in recent years have aroused scholars and relevant regulatory agencies to pay more and more attention to the stability of the banking system [1–4]. Existing research on the stability of the banking system mainly focuses on the interbank market [5–7]. Allen and Gale [8] modeled financial contagion based on the interbank market and figured out that the possibility of contagion depends highly on the structure of interregional claims; the complete structure is more stable than the incomplete market structure. Freixas and Parigi [9] pointed out that in the event of a crisis, the higher the degree of interbank correlation, the stronger the banking network's resilience. Ladley [10] argued that interbank lending may increase the stability of the system with risk-sharing or provide a financial contagion channel. Moreover, Iori and Jafarey [11] revealed that the interbank market made the banking system more stable with homogeneous banks while there may be knock-on effects with heterogeneous banks. Gai and Kapadia [12] examined the impact of network structure, market liquidity, and idiosyncratic shocks on stability in the interbank market and found that the banking system exhibited a robust-yet-fragile tendency. Additionally, as a carrier of facilitating liquidity exchange [13, 14] and a potential path for risk contagion [15, 16], the interbank network plays an important role in maintaining the stability of the banking system [6].
In reality, many of current related studies adopt agent-based models in networked systems [17]. For example, Madey et al. [18] built an agent-based model of collaborative, Abbas [19] constructed an agent-based friendship links model, and Lu et al. [20] investigated community formation and consensus engineering by an agent- based model. Also, considering that the properties of the multi-agent network can help to formulate an effective networked system. Cao et al. [21] proposed a partially visible multi-agent system (PVMAS) based on the aggregation phenomenon to detect prosumer-community groups in smart grids from the multi-agent perspective. Bu et al. [22] from the perspective of the proximity relationship combined integrating survival analysis and game theory, built an autonomy-oriented-computing (AOC) multi-agent system to study the evolution mechanism of the real-world temporal networks. In terms of the banking network system, Lenzu and Tedeschi [23] constructed the interbank network model based on agent-based with a random network and a scale-free network structure and showed that in case of heterogeneity, the random network structure appears to be more stable than the scale-free one. Caccioli et al. [24] explored the stability of the banking system with different interbank network structures and found that the scale-free network has better flexibility, but its stability of the banking system is also significantly lower than other networks. Georg and Poschmann [25] and Georg [26] proposed an interbank network system that introduced the central banks as the lender of last resort and demonstrated that the money-center network is more resilient than the random network. Additionally, Lux [27] developed a simple dynamic interbank network model based on an elementary reinforcement learning algorithm and concluded that the evolution of the banking system presents a “core-periphery” structure that could maintain the stability of the banking system. By investigating the impact of the banking network concentration on the stability of banking system, Nier et al. [28] confirmed that the more concentrated banking system tended to be more fragile. Berardi and Tedeschi [29] built the interbank network model based on different banking strategies and stressed that the strategies might impact on the network topology and the stability of the banking system. Liu et al. [30] rebuilt the interbank network based on the banking decision-making rules and pointed out that banks' losses and bankruptcies caused by network contagion and liquidity turbulence in the loan market will impact the stability of the banking system.
Recently, it was discovered from the bubbles and crash in the financial market that the causes of the crisis are not only focused on the interconnections among the interbank market, but shadow banking is also one of the important factors that lead to crisis and destabilizing the stability of the banking system. The term shadow banking was coined by McCulley [31] and then was picked up by policymakers. The Financial Stability Board (FSB) [32] pointed out that the shadow banking system as a credit intermediary system is free from the formal banking system and may cause systemic financial risks and regulatory arbitrage risks. Adrian and Ashcraft [33] stressed that shadow banks are inherently fragile, unlike the commercial banks under the policy safety net. Pozsar et al. [34], and Tucker [35] found that the size of shadow banking showed a sudden increased pattern before the outbreak of the global financial crisis. By documenting the performance of shadow banking, Wiggers and Ashcraft [36] observed that shadow banks defaulted in large numbers following the financial crisis, which destroyed the banking system stability. Ross [37] and Allen and Gale [38] showed that the financing expansion of shadow banking system accords with Pareto's optimal improvement, which can share part of the systemic risk and maintain the stability of the banking system. Gennaioli et al. [39] proposed an improved shadow banking model and found that investors' neglect of tail risk would make the banking system vulnerable to crisis shocks, but under rational expectations, shadow banking would help withstand the systemic risk and maintain the stability of the system. Colombo et al. [40] constructed a model of shadow banking as well and emphasized that the propagation form after a crisis shock could reduce the ability of the financial system to resist risks and the corresponding stability level of the banking system. In addition, Adrian and Shin [41] proved that the pro-cyclical behavior of leverage is a hallmark of shadow banking and revealed that when balance sheets are large and credit intermediation is expanding, shadow banking leverage tends to be high, which shocks the stability of the banking system. Loayza and Rigolini [42] and Elias [43] qualitatively analyzed the impact of shadow banking on the stability of the banking system from the perspective of the labor market and money market funds, respectively.
In the existing research, the impact of shadow banking on the banking system stability has been viewed through the qualitative analysis related to the change in the characteristics of shadow banking and static analysis based on some simple models. However, as a vital role in the decision-making of shadow banking, the shock of macroeconomic fluctuation is not considered. In fact, the macroeconomic fluctuation is closely related to the stability of the banking system. As far as we know, at present, there is almost no quantitative analysis on the stability of the interbank market with shadow banking under macroeconomic fluctuation. Therefore, based on the agent-based method in modern complex network theory, a model of a dynamic complex interbank network with shadow banking under macroeconomic fluctuation, which approximates real-world banking network, is proposed in this paper. Traditional banks, shadow banks, and the central bank are included in the proposed model. Interbank lending network that contained the traditional interbank lending network among traditional banks and the new interbank lending network between traditional banks and shadow banks is established. In addition, the assistance network between the central bank and traditional banks is built. In the proposed model, the macroeconomy is divided into three situations: boom, stable, and bust. Under different economic situations, the dynamic evolution of assets and liabilities of traditional banks and shadow banking nodes follows different evolution rules. This makes it possible to analyze whether macroeconomic fluctuation maintains or shocks the stability of the banking system with shadow banking. In addition, the rise and fall of the number of shadow banking also play a central role in economic performance. Hence, in the proposed model, based on the Pareto principle, the proportion of default banks is set as the measurement index and then the economic situation of the banking system is determined based on the dynamic change of the proportion of default banks in the banking system to further explore the possible effect of the shadow banking on the macroeconomic fluctuation.
The main contribution of this paper is summarized in that it quantitatively examines the impact of macroeconomic fluctuation on the stability of the banking system with shadow banking for the first time. Compared with other qualitative and static studies, our paper fully considers the complex interaction between banks, as well as the impact between the macroeconomic and the banking system, and presents an effective method for modeling and simulating the dynamic operation and evolution of the interbank network. The remainder of this paper is organized as follows. The dynamic complex interbank network with shadow banking under the macroeconomic fluctuation model is constructed in section The Model. In section Simulation Analysis, simulation of experimental results and relative analysis are presented. Finally, conclusions are conducted in section Conclusion.
The Model
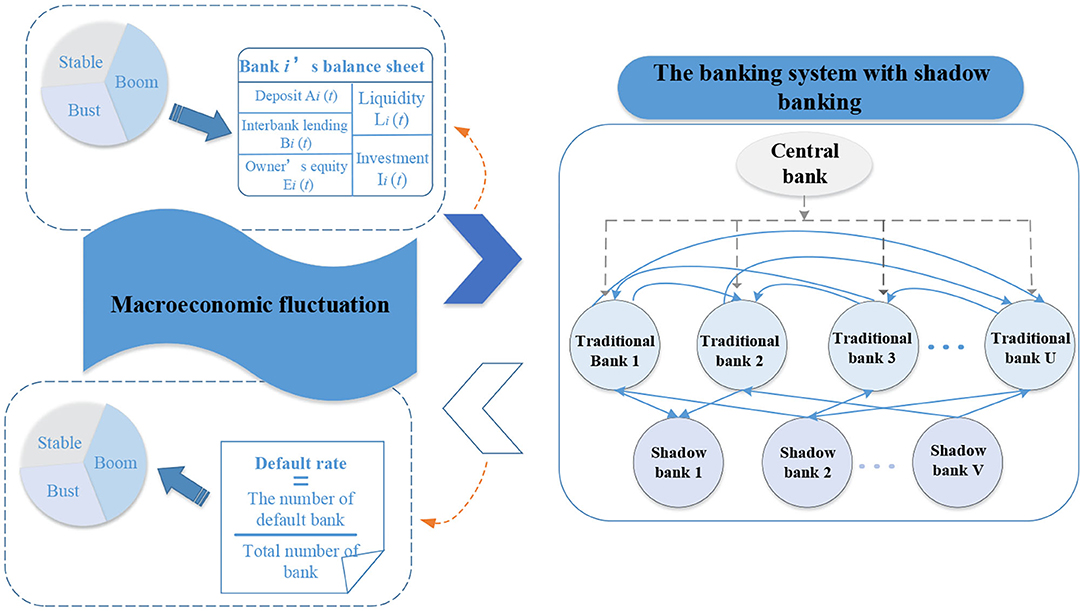
In order to investigate the stability of the banking system with shadow banking under macroeconomic fluctuation, a dynamic complex interbank network with shadow banking under the macroeconomic fluctuation model based on the agent-based method is developed in this paper. The model structure is shown in Figure 1. The proposed model mainly consists of two components, which include the banking system with shadow banking and macroeconomic fluctuation.
The Banking System With Shadow Banking
Traditional banks, shadow banks, and the central bank are included in the proposed model. Apart from the central bank, there are G bank agents in the banking system, among which the number of traditional bank agents is U, and the number of shadow bank agents is V, that is, G = U + V. Referring the works of Iori et al. [11], Georg and Poschmann [25], Georg [26], and Caccioli et al. [44, 45], the banking network in this paper is assumed to be a random network. The interbank credit lending relationship is represented by a binary matrix X, where Xi, j = 1 or Xi, j = 0. Xi, j = 1 indicates that there is a credit connection between bank i and bank j, and Xi, j = 0 shows that there is no credit connection. Bank i and bank j are connected by probability ci,j. It should be noted that due to the independent and opacity characteristics of shadow banks [46], matrix X only established between traditional banks and between traditional banks and shadow banks shown in Figure 1.
The behaviors of each bank agent are described through the bank balance sheet, which changes dynamically over time. The initial bank balance sheet of bank i is described as follows:
where Li(t – 1) is the liquidity of bank i at time t – 1; Ai(t – 1) is the deposit of bank i at time t – 1; Ei(t – 1) is the owner's equity of bank i at time t – 1; is the total investment of bank i in τ investment periods; is the total borrowing amount of bank i at time t – 1, gi, j(t – 1) describes the connection relationship between bank i and bank j at time t – 1; if there is a loan relationship between bank i and bank j, gi, j(t – 1) = 1; otherwise, gi, j(t – 1) = 0 (it should be noted that g is not equal to X and g is the real loan relationship, while X indicates a possible credit connection); bi, j (t – 1) > 0 if bank i borrows from bank j, and bi, j (t – 1) < 0 if bank j loans to bank i, where bi, j(t – 1) = −bj, i(t – 1). bi, j (t – 1) = −bj, i(t – 1) = 0 if there is no lending relationship between banks.
It is assumed that interbank lending between banks within the system only relies on the latest bank balance sheet. As the interbank network evolves with time, the balance sheet of the bank will change dynamically. At time t, the liquidity of bank i is updated to:
where raAi(t – 1) is the interest paid by the bank to depositors (for simplicity, we use the same terminology “deposits” to represent deposits for traditional banks and funding for shadow banks), ra is the deposit interest rate, and li (t – τ) are the income from the investment and the expiry investment, τ is the investment cycle, and ρ is the return on investment of each period. The return on investment ρ can be expressed as:
where q is the investment recovery probability. We use the normal distribution to update the deposits (t) of bank i by the following equation:
where Ā is the mean of random deposits of all banks, ĀδA is the standard deviation of random deposits of all banks, and εt~N(0,1).
Banks with adequate liquidity possess the ability to pay the dividend and reinvest. The dividend payment and reinvestment behaviors of traditional banks refer to the research of Iori et al. [11]. This paper focuses on the business activities of shadow banks. The dividend Di(t) of shadow bank i at time t can be calculated as follows:
where θ is the deposit ratio of shadow banks. The reinvestment Ii(t) of shadow bank i at time t can be decided by the following equation:
where ωi(t) is the investment opportunity of shadow bank i at time t, which follows a normal distribution and can be described:
where is the mean value of all shadow banks investment opportunities, is the standard deviation of all shadow banks' investment opportunities, and ηt~N(0,1).
After completing the above dividend distribution and reinvestment, if the bank i still has adequate liquidity Li(t) ≥ 0, it continues interbank lending. Conversely, if Li(t) < 0, it is labeled to be a member of the default set D at time t and wait for central bank aid or clearing.
Given that the key difference between traditional banks and shadow banks is that the business activities of shadow banks are free from the scope of central bank supervision [35], only traditional banks can receive assistance from the central bank. The assistance of the central bank to the traditional bank i at time t can be expressed as:
where Ri(t) = βAi(t) is the legal deposit reserve required by traditional bank i at time t and β is the deposit reserve ratio. Ri(t)-Li(t) is the assistance of the central bank to traditional bank i, when Ri(t) > Li(t). Then, the liquidity and debts of the assisted traditional bank i both update to 0 [Bi(t) = 0 and Li(t) = 0], and it evolves into the next time step. Otherwise, the traditional bank i pays legal deposit reserve by itself and evolves to the next time step.
Meanwhile, the insufficient liquidity shadow bank i is cleared by the central bank and pays its debts proportionally [47]. The debt repayment is calculated as follows:
where Ei (t) represents the owner's equity of the shadow bank i, gi, j(t)bi, j(t) represents the interbank borrowing amount between the shadow bank i and traditional bank j, and represents the total amount of the shadow bank i borrowed from no more than f traditional banks (f is the maximum number of traditional banks that can be borrowed by a shadow bank). Then, the debts of shadow bank i update to 0, and it remains a member of default set D for all subsequent time.
Macroeconomic Fluctuation
Recently, the performance of macroeconomic fluctuation presents a process of boom, bust, and a slow recovery alternating. In fact, the macroeconomic fluctuation is closely related to the stability of the banking system. Therefore, the macroeconomic fluctuation is introduced into the present model. We assume that the set M of macroeconomic fluctuation includes three macroeconomy states: the boom M1, the stable M2, and the bust M3, that is, M = {M1, M2, M3}. Figure 1 shows the interaction diagram between the macroeconomic fluctuation and the banking system with shadow banking. Under different macroeconomy states, the dynamic evolution of assets and liabilities of banks follow different evolution rules. The macroeconomic fluctuation influences the banking system with shadow banking by determining the bank balance sheet across different macroeconomy states. This makes it possible to analyze whether macroeconomic fluctuation maintains or shocks the stability of the banking system with shadow banking.
In addition, the banking system and macroeconomy states feature a two-sided interaction. The rise and fall of the shadow banking also play a central role in recent economic performance. Assume that the impact of shadow banking on the states of macroeconomy depends on the bank default rate (the ratio of the number of default banks to the total number of banks). Thus, according to Pareto's principle [48] and Pareto's economic model [49], using the bank default rate as a measure, the three critical values in the banking system for dividing the macroeconomy states are made sure. When the bank default rate in the system is <10%, it is in a boom state M1; when the bank default rate in the system is between 10 and 20%, it is in a stable state M2; when the bank default rate in the system exceeds 20%, it is in a bust state M3. By observing the change of the macroeconomy state Mn with the dynamic evolution of the bank default rate in the system, the impact of the banking system with shadow banking on the macroeconomic fluctuation is further explored.
Dynamic Process Algorithm
The dynamic process algorithm of the interbank network with shadow banking under macroeconomic fluctuation can be specifically described as follows:
Step 1: Determine and set the state of macroeconomy Mn. The corresponding initial parameters and variables are respectively performed. Then, the initial balance sheet of the bank i is determined.
Step 2: Update the liquidity Li(t) of the bank i at time t. If the bank i has sufficient liquidity [Li(t) ≥ 0], it carries out dividend distribution Di(t) and reinvestment li(t). If the bank i has liquidity shortage [Li(t) < 0], it waits for the interbank lending.
Step 3: After dividend distribution Di(t) and reinvestment li (t) are operated, the liquidity of bank i updates to Li(t) = Li(t) – Di(t) – li(t). If the liquidity of bank i is still positive, then the bank i is a creditor bank, which can lend its liquidity to debt banks; otherwise, the bank i is a debt bank. Then interbank lending begins according to the liquidity of the banks. If the debt bank i can borrow sufficient funds from the creditor banks to repay the previous loan and interest, i.e., Li(t) – (1 + rb)Bi(t – 1) ≥ 0 (rb is the interbank market interest rate), it can evolve to the next time step; if the debt bank i cannot borrow sufficient funds to repay the previous loan and interest, i.e., Li(t) – (1 + rb)Bi(t – 1) < 0, it becomes a member of the default set D and then assisted or cleared by the central bank.
Step 4: The default bank i is assisted or cleared by the central bank at time t. If the default bank i is a traditional bank, it is assisted by the central bank and then evolves into the next time step. If the default bank i is a shadow bank, it is cleared by the central bank and then remains a member of default set D for all subsequent time steps. The assisted or cleared bank i's liquidity and debts are both updated to 0, i.e., Li(t) = 0 and Bi(t) = 0.
Compared with the dynamic process algorithm of the interbank network with shadow banking under macroeconomic fluctuation, the dynamic process algorithm of the effect of shadow banking on the states of macroeconomy only changes in Step 1 and Step 2 as follows:
Step 1: Set the state of macroeconomy Mn = M1 at time t = 1. The corresponding initial parameters and variables are, respectively performed. Then, the initial balance sheet of the bank i is determined.
Step 2: According to the number of default banks in the system at time t – 1, the default rate is calculated to determine the state of macroeconomy Mn (n = 1, 2, or 3) at time, and the value of relevant parameters and variables are set. Update the liquidity Li(t) of the bank i at time t. If the bank i has sufficient liquidity [Li(t) ≥ 0], it carries out dividend distribution Di(t) and reinvestment li (t). If the bank i has liquidity shortage [Li(t) < 0], it waits for the interbank lending.
Steps 3 and 4 are the same as the dynamic process algorithm of the interbank network with shadow banking under macroeconomic fluctuation.
For the initial banking network with shadow banking, the number of bank nodes is G and n is the number of the activity feature associated with each node. The time cost of calculating the initial balance sheet of bank nodes is dominated by Step 1, which is O (G). The main time cost of the algorithm comes from Steps 2 and 3: updating bank liquidity and activity transformation will cost O (nG), and it will take O (G2) time for interbank lending. Therefore, the time complexity of the algorithm in this paper is O [T(G2)], where T indicates the number of iterations in the evolution of the system.
Simulation Analysis
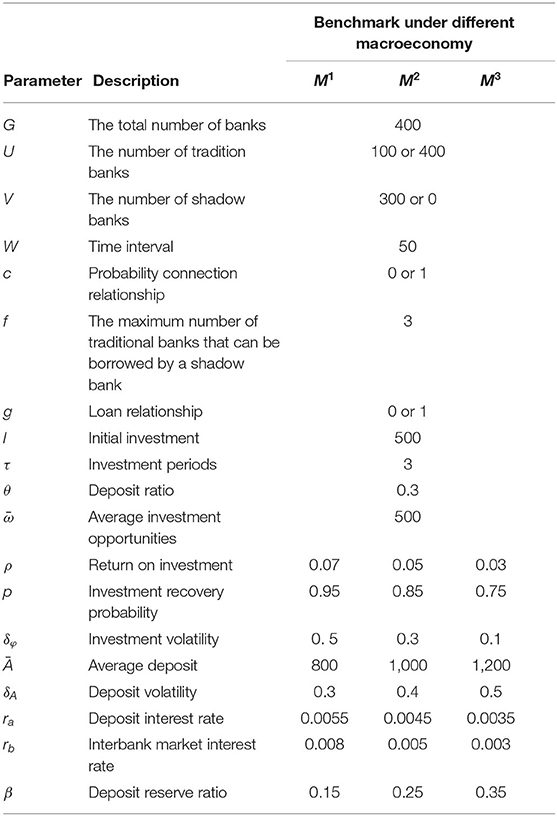
The interbank network with shadow banking under macroeconomic fluctuation constructed in our study evolves with time t. The macroeconomy, the bank balance sheet, and the related indicators are dynamically evolved over time t. We perform our simulation experiments via the proposed model with a total time step T = 500 as stopping criterion. To test the effectiveness of the proposed model, this paper mainly simulates the model from two aspects: (i) the shock of macroeconomic fluctuation on the stability of the banking system with shadow banking and (ii) the effect of the banking system with shadow banking on the macroeconomic fluctuation. Referring to the parameters in the actual banking network system, the benchmark values of the parameters are set as Table 1. Different parameters will lead to changes in the evolution of the banking network system, which is very consistent in line with the actual operation process of the banking system.
The Shock of Macroeconomic Fluctuation on the Stability of the Banking System With Shadow Banking
As we all know, economic fluctuation has an impact on the banking system [50]. To better explore the shock of macroeconomic fluctuation on the banking system with shadow banking (U = 100 and V = 300), we added the traditional banking system for comparison (U = 400 and V = 0). Figure 2 shows the changes in liquidity, average bank profits, and investment opportunities in the banking system under macroeconomic fluctuation. In Figures 2A–C, the changes in liquidity in the banking systems under macroeconomic fluctuation are described. Compared with the traditional banking system, the liquidity of the banking system with shadow banking is significantly more abundant in the boom. However, the liquidity of the banking system with shadow banking begins to be lower than that of the traditional banking system, continues to decline in the stable, and then reaches a low point in the bust. This is because in the boom, the spreads are narrow and shadow banking attracts more investors, thus increasing the liquidity of funds and reducing the deposit demand of households. Yet, shadow banking can be described as fragile liquidity transformation. With the accumulation of liquidity, the fragility of the banking system with shadow banking increases dramatically. When the macroeconomy becomes stable, the fragility of shadow banking begins to be highlighted and breaks out in the bust. The changes in average bank profits in the banking systems under macroeconomic fluctuation are shown in Figures 2D–F. Similar to the changing law of liquidity in the banking system under macroeconomic fluctuation, the average bank profits also continue to decrease as the macroeconomy state goes from good to bad. However, the difference is that there is a short buffer period for the change in average bank profits caused by macroeconomy changes. During the period, the average bank profits of the banking system with shadow banking are higher than that of the traditional banking system. This may be due to the time lag from investment to return, which forms a short buffer period. Figures 2G–I draw the changes in investment opportunities in the banking systems under macroeconomic fluctuation. The investment opportunities of the banking system with shadow banking are more advantageous in the boom, but in the stable, the investment opportunities begin to decline, and rapidly decline and disappear in the bust. This shows in the boom that abundant liquidity allows investors to distribute wealth when it is more valuable. However, the liquidity contraction in the stable and bust results in raising discount rates, and as a result, investment opportunities fall and growth turns negative.
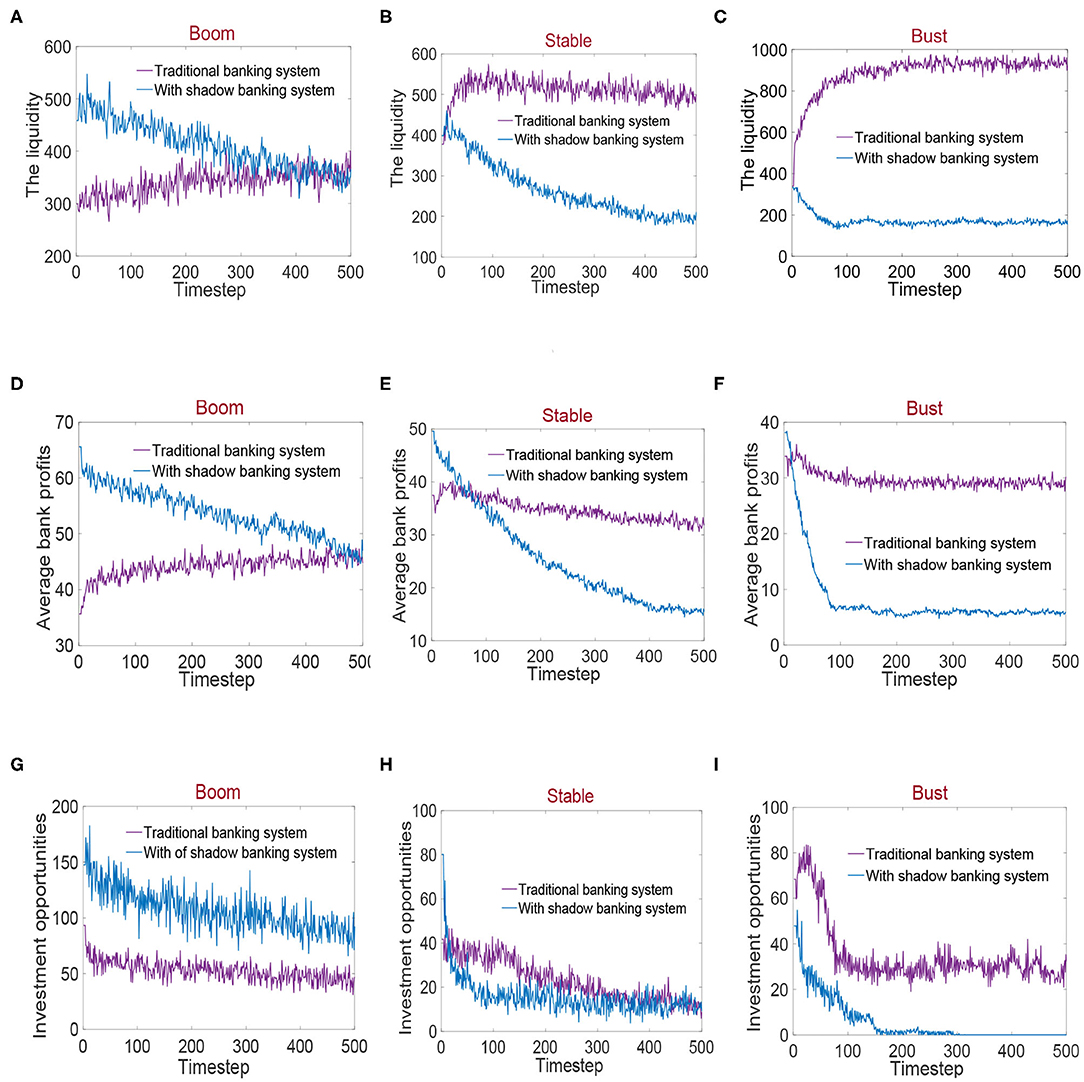
Figure 2. (A–C) Representation of the changes in liquidity in the banking systems under macroeconomic fluctuation. (D–F) Representation of the changes in average bank profits in the banking systems under macroeconomic fluctuation. (G–I) Representation of the changes in investment opportunities in the banking systems under macroeconomic fluctuation.
The number of survival banks in the banking system can measure the ability of the banking system to resist risks and examine the stability of the banking system. Figure 3 describes the changes in the survival bank ratio in the banking systems under macroeconomic fluctuation. Protected and aided by the central bank, the survival bank ratio of the traditional banking system is higher than 95%, which is less affected by macroeconomic changes. Different from the traditional banking system, Figures 3A–C show that the survival bank ratio of the banking system with shadow banking has a significant decline under macroeconomic fluctuation and is positively related to the macroeconomy states. This presents that independent shadow banks, while enjoying higher benefits, also bear higher default risk. A boom state is conducive to the shadow banking business activities, enabling them to timely repay debts and then reduce the bank default rate. However, in the stable and bust, liquidity contraction and high-risk business activities prevent shadow banking from repaying debts, which induces a debt crisis, resulting in a large number of related bank defaults, and then the survival bank ratio of the banking system with shadow banking drops sharply. Thus, the changes in macroeconomy states can make a remarkable effect on the stability of the banking system with shadow banking.
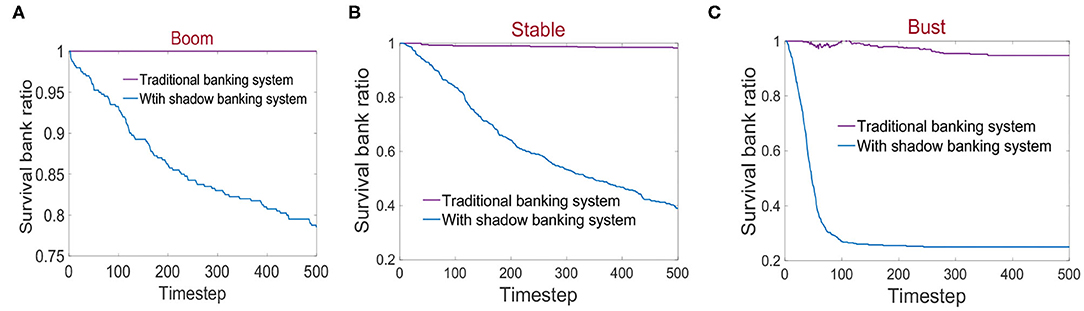
Figure 3. (A–C) Representation of the changes in the survival bank ratio in the banking systems under macroeconomic fluctuation.
Intuitively, systemic risk reflects the stability of the banking system. Therefore, in this paper, the average number of default bank in the [t + 1, t + W] time range is normalized, and the calculated value is recorded as SR(t):
where W is the time interval, and the average proportion of default bank in the future W time can indicate the systemic risk of the system at a certain moment. Oe is the time number of the simulation. and are the number of default bank and survival bank at time j in the ith simulation, respectively.
Using Equation 10, the curve of systemic risk in the banking system under macroeconomic fluctuation is calculated and shown in Figure 4. It is easy to find that the systemic risk of the traditional banking system is less affected by the changes of the macroeconomy states and has been maintained at a level close to 0. It mainly stems from the strict supervision of the policy department and the protection and rescue of the central bank. On the contrary, the systemic risk of the banking system with shadow banking is obviously affected by macroeconomic fluctuation. As can be seen from Figure 4A, the systemic risk in the boom is <5% and tends to decline, which is relatively low. This is because sufficient liquidity improves the ability of the banking system with shadow banking to resist risks and maintains its stability. In the stable (as shown in Figure 4B), the systemic risk rises to 5–15% and a small peak appears. This shows that as shadow banking starts to contract, exposure to uncertainty shocks and systemic risk rises. However, with default banks cleared and aided by the central bank, the systemic risk gradually decreases. In the bust, as seen in Figure 4C, systemic risk erupts, peaks at 95% at time step 20, and then declines. This is because shadow banking is no longer prosperous in the bust, a large number of illiquidity shadow banks default, and there is systemic risk outbreak. Later, as the contagion related to shadow banks ceases in the interbank network, systemic risk is alleviated and decreased.
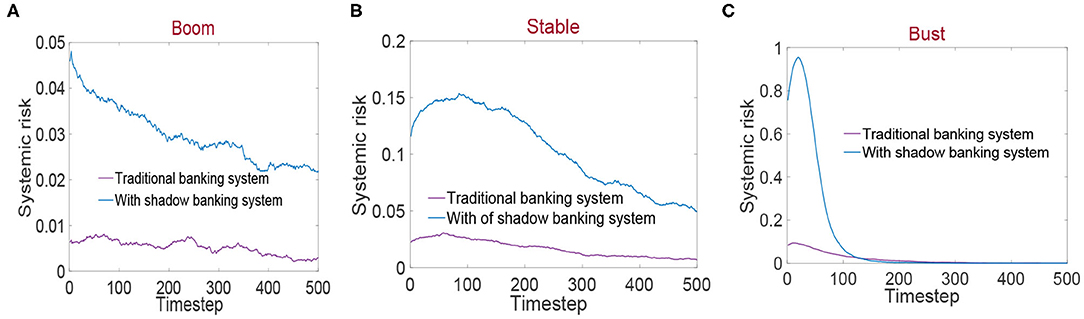
Figure 4. (A–C) Representation of the systemic risk changes in the banking systems under the macroeconomic fluctuation.
The Effect of the Banking System With Shadow Banking on the Macroeconomic Fluctuation
As we have shown above, the stability of the banking system with shadow banking is affected by macroeconomic fluctuation. Because the relationship between the banking system and the macroeconomy states is not one sided, we will next investigate the effect of the banking system with shadow banking on the states of macroeconomy.
We set the initial state of the macroeconomy as a boom M1, and then the macroeconomy state will dynamically evolve based on the changes in the bank default rate of the banking system with shadow banking. Figure 5 depicts the changes in liquidity, investment opportunities, and average bank profits under the two-sided interaction between the banking system with shadow banking and the macroeconomy states. Considering the change range of the indicators, we put liquidity and investment opportunities in Figure 5A and investment opportunities and average bank profits in Figure 5B to show the changes of the three more clearly. It can be seen that the liquidity changes from a highly stable state to a rapid decline state at about time 200 and does not stabilize at a low level until about time 270. Similarly, the change point and trend of the average bank profit curve are almost the same as that of the liquidity curve. For the change of investment opportunities, in addition to the short-term small increase at about time 200, the overall trend is also showing a downward trend. As can be seen from the evolution of the banking system with shadow banking, there are two obvious change points in the curves of liquidity, investment opportunities, and average bank profits (marked by the red circle in Figure 5). We believe that the internal evolution of the banking system with shadow banking is not sufficient to produce such significant changes, and the occurrence of the change points must be related to the changes in the macroeconomy states. Therefore, we carry out statistics on the corresponding real macroeconomy states during the evolution of the banking system with shadow banking. At the same time, we further examine the changes in the survival bank ratio and systemic risk in the system.
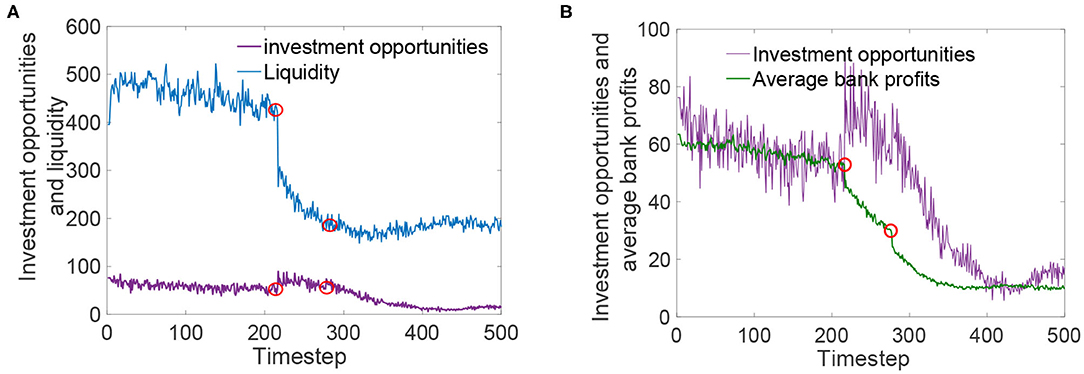
Figure 5. (A,B) Representation of the changes in liquidity, investment opportunities, and average bank profits under the two-sided interaction between the banking system with shadow banking and the macro- economy states.
Figure 6A shows the changes in macroeconomy states with the evolution of the banking system with shadow banking. We can find that with the evolution of the banking system with shadow banking, there are two changes in the macroeconomy states: the change from the boom M1 to the stable M2 at time 217 and the change from the stable M2 to the bust M3 at time 278. These two changes are consistent with the two changing points in Figure 5. This shows that the banking system with shadow banking does have an effect on the macroeconomic fluctuation. Further, from Figure 6B, we find that the system risk surges before and after the macroeconomy state changing from the boom M1 to M2. This is due to the fact that during the boom period, shadow banks with rich liquidity concentrated their investments on high-risk assets and accumulated fragility, which affects the macroeconomy state and changes it. As the fragility continues to increase, the shadow banking boom gradually disappears, and its liquidity begins to evaporate, leading to severe bank default, the survival bank ratio plummets and triggers the outbreak of systemic risk, which affects the macroeconomic fluctuation and makes the macroeconomy state change from the stable M2 to the bust M3. Over time, the bust M3 does not change again, because the serious impact caused by shadow banking leads to slow recoveries. In conclusion, we find that shadow banking has a negative effect on the macroeconomic fluctuation without other intervening factors, and this effect is irreversible.
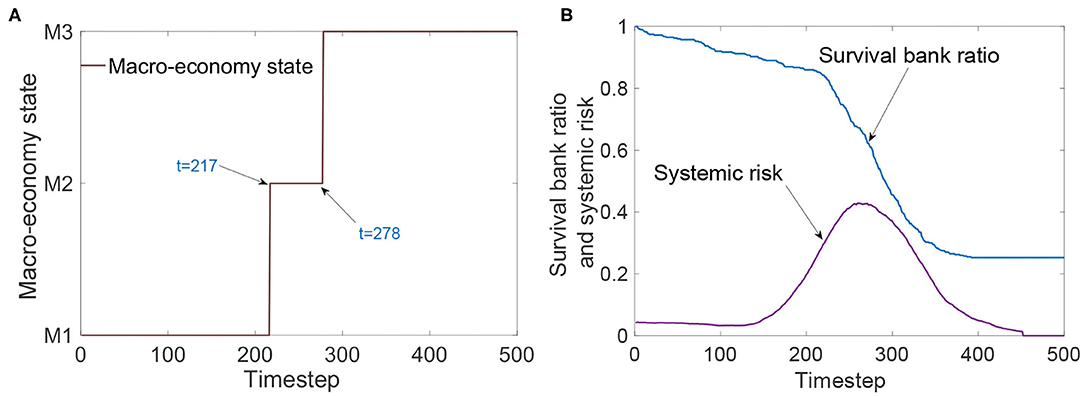
Figure 6. (A) Representation of the changes in macroeconomy states with the evolution of the banking system with shadow banking. (B) Representation of the changes in bank survival ratio and systemic risk of the banking system with shadow banking.
Conclusion
With the development of the financial market, shadow banking has become an essential part of the modern complex financial system, and it has led to fundamental changes in the global financial system. Shadow banking is considered to be one of the most principal factors that cause financial contagion and destroy the stability of the banking system. At present, research on the impact of shadow banking on the system stability mainly focuses on qualitative analysis related to monetary policy and static analysis based on some specific models like regression analysis. However, as a vital role in the decision-making of shadow banking, the shock of macroeconomic fluctuation is not considered. In order to better reflect the system stability of the banking system with shadow banking, based on the agent-based method in modern complex network theory, a model of a dynamic complex interbank network with shadow banking under macroeconomic fluctuation is proposed in this paper. The model includes two parts: the banking system with shadow banking and the macroeconomic fluctuation. The interbank lending network, which includes the traditional interbank lending network among traditional banks and the new interbank lending network between traditional banks and shadow banking, and the assistance network between the central bank and traditional banks as well are built in the banking system with shadow banking. Macroeconomy is divided into three states, and under different macroeconomy states, the dynamic evolution of assets and liabilities of bank nodes follows different evolution rules. This makes it possible to analyze whether macroeconomic fluctuation maintains or shocks the stability of the banking system with shadow banking. In addition, according to the Pareto principle and economic model, the dynamic changing bank default rate in the system is used as a measure to further explore the effect of shadow banking on the macroeconomic fluctuation.
The simulation results show that in the boom, the liquidity of the banking system with shadow banking is expanded, the average bank profits are improved, the investment opportunities are increased, and the survival bank ratio is high. Shadow banking can bear part of systemic risk. The systemic risk is decreased and the stability of the banking system is increased. In the circumstances of the stable and the bust, the liquidity of the banking system is declined, average bank profits are shrunk, investment opportunities are gradually disappeared, and the survival bank ratio is decreased. Shadow banking starts to collapse, the systemic risk breaks out, and the stability of the banking system is seriously damaged. Furthermore, by analyzing the influence of shadow banking on the macroeconomy, we find that shadow banking builds up the fragility of macroeconomic performance, and without external regulation, this impact is irreversible. This paper sheds light on the impact of macroeconomic fluctuation on the stability of the banking system with shadow banking, shows the risk problems brought by shadow banking for macroeconomic fluctuation, refines research of the banking system stability, and offers effective theoretical references for decision-makers and regulators.
The real banking network system is very complex; the simulation experiment can only reflect the operation results of the banking system under specific characteristics, while the real banking system has more characteristics. Thus, there are many points needed to be studied in future work. For example, the bank network may not be a random network, and we will consider the scale-free network since relevant research shows that the bank network has obvious scale-free network characteristics [51]. In addition, we will integrate the real bank datasets into the model for empirical research is conducive to improve the model prediction accuracy.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
All authors contributed to the article and approved the submitted version.
Funding
We are grateful for the support from National Natural Science Foundation of China (71971054) and Natural Science Foundation of Shanghai (19ZR1402100).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Jin Y, Zheng ZX. Banking risk and macroeconomic fluctuations. J Bank Finance. (2014) 48:350–60. doi: 10.1016/j.jbankfin.2013.07.039
2. Poledna S, Molina-Borboa JL, Martinez-Jaramillo S, Van Der Leij M, Thurner S. The multi- layer network nature of systemic risk and its implications for the costs of financial crises. J Financ Stabil. (2015) 20:70–81. doi: 10.1016/j.jfs.2015.08.001
3. Neveu AR. A survey of network-based analysis and systemic risk measurement. J Econ Int Coord. (2016) 1:1–41. doi: 10.1007/s11403-016-0182-z
4. Pollak M, Guan Y. Partially overlapping ownership and contagion in financial networks. Complexity. (2017) 2017:1–16. doi: 10.1155/2017/9895632
5. Silva W, Kimura H, Sobreiro VA. An analysis of the literature on systemic financial risk: a survey. J Financial Stab. (2016) 28:91–114. doi: 10.1016/j.jfs.2016.12.004
6. Kanno M. Assessing systemic risk using interbank exposures in the global banking system. J Financial Stab. (2015) 20:105–30. doi: 10.1016/j.jfs.2015.08.006
7. Schuler T, Corrado L. Interbank market failure and macro-prudential policies. J Financial Stab. (2017) 33:133–49. doi: 10.1016/j.jfs.2016.10.007
9. Freixas X, Parigi BM, Rochet JC. Systemic risk, interbank relations, and liquidity provision by the central bank. J Money Credit Bank. (2000) 32:611–38. doi: 10.2307/2601198
10. Ladley D. Contagion and risk-sharing on the inter-bank market. J Econ Dyn Control. (2013) 37:1384–400. doi: 10.1016/j.jedc.2013.03.009
11. Iori G, Jafarey S, Padilla FG. Systemic risk on the interbank market. J Econ Behav Organ. (2006) 61:525–42. doi: 10.1016/j.jebo.2004.07.018
12. Gai P, Kapadia S. Contagion in financial networks. In: Proceedings of Royal Society of London A: Mathematical. Physical and Engineering Sciences. London (2010).
13. Cocco JF, Gomes FJ, Martins NC. Lending relationships in the interbank market. J Financial Intermediat. (2009) 18:24–48. doi: 10.1016/j.jfi.2008.06.003
14. Temizsoy A, Iori G, Montes-Rojas G. The role of bank relationships in the interbank market. J Econ Dyn Control. (2015) 59:118–41. doi: 10.1016/j.jedc.2015.07.008
15. Castiglionesi F. Financial contagion and the role of the central bank. J Bank Finance. (2007) 31:81–101. doi: 10.1016/j.jbankfin.2005.03.025
16. Hasman A, Samartín M. Information acquisition and financial contagion. J Bank Finance. (2008) 32:2136–47. doi: 10.1016/j.jbankfin.2007.12.033
17. Jiang Y, Jiang JC. Understanding social networks from a multiagent perspective. IEEE Trans Parallel Distributed Syst. (2014) 25:2743–59. doi: 10.1109/TPDS.2013.254
18. Madey G, Freeh V, Tynan R, Gao Y, Hoffman C. Agent-based modeling and simulation of collaborative social networks. In: AMCIS 2003 Proceedings. Tampa (2003). p. 1836–42.
19. Abbas SMA. An agent-based model of the development of friendship links within facebook. Comput Math Organ Theory. (2013) 19:232–52. doi: 10.1007/s10588-013-9156-z
20. Lu Q, Korniss G, Szymanski BK. The naming game in social networks: community formation and consensus engineering. J Econ Interact Coord. (2009) 4:221–35. doi: 10.1007/s11403-009-0057-7
21. Cao J, Bu Z, Wang Y, Yang H, Jiang J, Li HJ. Detecting prosumer-community groups in smart grids from the multiagent perspective. IEEE Trans Syst Man Cybernet Syst. (2019) 49:1652–64. doi: 10.1109/TSMC.2019.2899366
22. Bu Z, Wang Y, Li HJ, Jiang J, Wu Z, Cao J. Link prediction in temporal networks: integrating survival analysis and game theory. Inform Sci. (2019) 498:41–61. doi: 10.1016/j.ins.2019.05.050
23. Lenzu S, Tedeschi G. Systemic risk on different interbank network topologies. Phys A Statist Mech Appl. (2012) 391:4331–41. doi: 10.1016/j.physa.2012.03.035
24. Caccioli F, Catanach TA, Farmer JD. Heterogeneity, correlations and financial contagion. Adv Complex Syst. (2012). 15(supp02):1250058 doi: 10.1142/S0219525912500580
25. Georg CP, Poschmann J. Systemic Risk in a Network Model of Interbank Markets with Central Bank Activity. JENA Economic Research Papers. Jena and EconStor (2010).
26. Georg CP. The effect of the interbank network structure on contagion and common shocks. J Bank Finance. (2013) 37:2216–28. doi: 10.1016/j.jbankfin.2013.02.032
27. Lux T. Emergence of a core-periphery structure in a simple dynamic model of the interbank market. J Econ Dyn Control. (2015) 52:A11–23. doi: 10.1016/j.jedc.2014.09.038
28. Nier E, Yang J, Yorulmazer T, Alentorn A. Network models and financial stability. J Econ Dyn Control. (2007) 31:2033–60. doi: 10.1016/j.jedc.2007.01.014
29. Berardi S, Tedeschi G. From banks' strategies to financial (in) stability. Int Rev Econ Finance. (2017) 47:255–72. doi: 10.1016/j.iref.2016.11.001
30. Liu A, Paddrik M, Yang SY, Zhang X. Interbank contagion: an agent-based model approach to endogenously formed networks. J Bank Finance. (2020) 112:105191. doi: 10.2139/ssrn.2888562
32. Financial Stability Board. Global Shadow Banking Monitoring Report 2015. Basel: Financial Stability Board (2015).
33. Adrian T, Ashcraft AB. Shadow Banking: a Review of the Literature. Banking Crises. London: Palgrave Macmillan (2016). p. 282–315. doi: 10.1057/9781137553799_29
34. Pozsar Z, Adrian T, Ashcraft AB, Boesky H. Shadow banking. Staff Rep. (2010) 105:447–57. doi: 10.2139/ssrn.1645337
35. Tucker P. Shadow Banking, Financing Markets and Financial Stability. Remarks at a Bernie Gerald Cantor Partners Seminar. London:Oxford University Press (2010).
36. Wiggers T, Ashcraft AB. Defaults and Losses on Commercial Real Estate Bonds during the Great Depression Era. New York, NY: Federal Reserve Bank of New York Staff Report 544. (2012). doi: 10.2139/ssrn.2002078
39. Gennaioli N, Shleifer A, Vishny RW. A model of shadow banking. J Finance. (2013) 68:1331–63. doi: 10.1111/jofi.12031
40. Colombo E, Onnis L, Tirelli P. Shadow economies at times of banking crises: empirics and theory. J Bank Finance. (2016) 62:180–90. doi: 10.1016/j.jbankfin.2014.09.017
41. Adrian T, Shin HS. The shadow banking system: implications for financial regulation. Banque France Financ Stab Rev. (2009) 13:1–10. doi: 10.2139/ssrn.1441324
42. Loayza NV, Rigolini J. Informal employment: safety net or growth engine. World Dev. (2011) 39:1503–15. doi: 10.1016/j.worlddev.2011.02.003
43. Elias B. Shadow banking and financial stability: European money market funds in the global financial crisis. J Int Money Finance. (2013) 32:579–94. doi: 10.1016/j.jimonfin.2012.05.027
44. Caccioli F, Shrestha M, Moore C, Farmer JD. Stability analysis of financial contagion due to overlapping portfolios. J Bank Finance. (2014) 46:233–45. doi: 10.1016/j.jbankfin.2014.05.021
45. Caccioli F, Farmer JD, Foti N, Rockmore D. Overlapping portfolios, contagion, and financial stability. J Econ Dyn Control. (2015) 51:50–63. doi: 10.1016/j.jedc.2014.09.041
46. Dang TV, Gorton G, Holmstrom B. Opacity and the Optimality of Debt for Liquidity Provision. New Haven, CT: Manuscript Yale University. (2009).
47. Eisenberg L, Noe TH. Systemic risk in financial systems. Manag Sci. (2001) 47:236–49. doi: 10.1287/mnsc.47.2.236.9835
50. Moreira A, Savov A. The macroeconomics of shadow banking. J Finance. (2017) 72:2381–32. doi: 10.1111/jofi.12540
Keywords: macroeconomy fluctuation, shadow banking, interbank network, stability of the banking system, systemic risk
Citation: Pan H and Fan H (2020) Research on the Stability of the Banking System With Shadow Banking Under Macroeconomic Fluctuation. Front. Phys. 8:338. doi: 10.3389/fphy.2020.00338
Received: 17 May 2020; Accepted: 20 July 2020;
Published: 05 November 2020.
Edited by:
Andrea Rapisarda, University of Catania, ItalyReviewed by:
Jiuchuan Jiang, Nanjing University of Finance and Economics, ChinaJie Cao, Nanjing University of Finance and Economics, China
Copyright © 2020 Pan and Fan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hong Fan, aG9uZ2ZhbkBkaHUuZWR1LmNu
 Hongjie Pan
Hongjie Pan Hong Fan
Hong Fan