Shape Evolutions in Fission Dynamics Within Time-Dependent Hartree-Fock Approach

We studied the nuclear shape evolutions in fission process of ²⁴⁰Pu by the time-dependent Hartree-Fock approach with various Skyrme forces. Calculations are performed for the later phase of the fission with large initial deformations toward the scission. We show that calculations with Skyrme forces with large surface energies and large symmetry energies can have extremely long fission evolution time. The symmetry energy plays a role in the evolution of neutron-rich necks. In addition, we also demonstrated the shape oscillations of fission fragments after the fission. We see that particularly the heavy near-spherical fragments have remarkable octupole oscillations.

1. Introduction

Nuclear fission is a very complex and large amplitude collective motion of many-body quantum systems. Although fission was discovered in 1939, the development of a fully self-consistent and predictive microscopic fission theory is still very challenging [1, 2]. The earlier studies [3, 4] of nuclear fission are mainly based on macro-microscopic models, which have gained many insights about the fission mechanism. Thanks to the developments of supercomputing capabilities in recent years, microscopic fission theory has achieved remarkable progresses. The time-dependent Generator-Coordinate Method [5–7] as an adiabatic dynamical fission theory can describe reasonably well the mass distributions of fission yields, based on parallel calculations of complex potential energy surfaces. On the other hand, the time-dependent Hartree-Fock (TDHF) or time-dependent density functional theory [8–16] as a non-adiabatic dynamical theory is helpful for understanding fission mechanisms, particularly in the part of the trajectory close to scission.

There are extensive studies of real-time nuclear dynamics based on the time-dependent Hartree-Fock approach. Indeed, fusion and fission involving transitions between one-body and two-body quantum system are unique non-equilibrium processes. Nuclear dynamics in the TDHF framework provide an opportunity to probe effective nuclear interactions, many-body correlations and transport properties. TDHF has been extended to TDHF+BCS and TD-HFB approaches by including dynamical pairing [9, 17]. The pairing interactions has been demonstrated to increase the fission lifetime by allowing orbital exchanges [9]. On the other hand, the pairing can facilitate the fission at some initial deformations where fission doesn't occur within TDHF [17]. The effective nuclear forces have also been demonstrated to be important in heavy-ion collision reactions [18]. For example, the tensor force is expected to be crucial in nuclear dynamics [19, 20] and in the reproduction of fission barriers [21].

The effective forces are usually obtained by reproducing static nuclear properties. The SkM* force has been widely used for fission studies with good surface properties [22]. However, SkM* is not good at descriptions of global binding energies [23]. The static fission barriers due to different Skyrme forces can lead to significant differences in fission tunneling lifetimes [24–26]. In addition, the symmetry energy has been extensively studied in nuclear collision reactions for transport properties and equation of state [27–29]. It would be interesting to study the role of effective nuclear forces in the evolution of fission dynamics while static fission barriers are not observables in TDHF.

The real-time nuclear fission dynamics can be directly demonstrated by the evolution of nuclear density distributions. The fourier analysis of time-dependent deformations are connected to collective vibrations and damping effects. The non-adiabatic fission studies can only be performed after the saddle of the fission barrier. The nuclear shapes at the scission deformation and after scission are of particular interest. The octupole deformations and shell effects of fission fragments are essential for descriptions of fission yields [13]. The collective oscillations of fission fragments are also an interesting topic [10, 30]. The aim of the present work is to study the role of different Skyrme force in nuclear fission dynamics, as well as the oscillations of fission fragments based on the TDHF framework, which can capture the major features of real-time fission dynamics, at least close to scission. In this work, the studies are about the later phase of the fission with large initial deformations after the tunneling.

2. The TDHF Theory

The TDHF equations can be formally derived from the time-dependent variational method. In the formalism of density matrices, TDHF is the approximation in which the two-body interaction term is approximated by a product of one-body terms [8, 18]. The TDHF equation is written as:

$\begin{array}{ll}i\hslash \frac{\partial {\phi }_k(r,t)}{\partial t}=h(r,t){\phi }_k(r,t)& (1)\end{array}$

where φ_k are the time-dependent single-particle wave functions in coordinate spaces. The single-particle hamiltonian h is also time dependent. The wave functions is always a Slater determinant during the evolution.

We utilize the 3D Skyrme-TDHF solver Sky3D [31, 32] and calculations are performed in the 3D uniform coordinate space. There are no symmetry restrictions on the wavefunctions. For the effective interactions, we adopted the series of SLy5sX [33] forces to study the influences of surface energies. In addition, we adopted the series of SV-sym forces [34] to study the influences of symmetry energies. The pairing has not been included in this work. The grid spacing is set to be 1 fm and the time step of dynamical evolution takes 0.2 fm/c. In Sky3D, the time propagator is evaluated by the Taylor series expansion up to the sixth order [31]. Computations with these settings have been demonstrated to be good enough for descriptions of dynamical properties. The static constrained calculations of ²⁴⁰Pu are firstly carried out to obtain the wave functions by the axial-symmetric Skyrme-Hartree-Fock solver SKYAX [35], which are inputs for time-evolution calculations. The 3D box size in static and dynamical calculations is taken as 50×50×70 fm, along x, y, z-axis respectively. Note that the static wave functions are obtained by the SKYAX solver [35] in axial-symmetric cylindrical coordinate spaces and are transformed into 3D coordinate spaces by interpolations. The interpolation from a 2D grid to a 3D grid can result in small numerical errors, which are around 100 keV in binding energies. In this case, the initial wave functions at any constrained quadrupole and octupole deformations (β₂, β₃) can be obtained efficiently. The energies and density distributions as a function of time are the main outputs of the time-dependent solver.

3. Results and Discussions

3.1. Influences of Surface Energies in Fission Dynamics

The surface energy coefficients of effective nuclear forces are critical properties as the fission is mainly determined by the competition between surface energies and Coulomb energies. To study the influences of surface energies in fission dynamics, we adopted the series of SLy5sX forces [33]. These Skyrme forces are obtained based on the SLy5 force but with varying surface energies in the fit protocol. The properties of equation of state (EoS) of SLy5sX forces are listed in the Table 1. The calculated potential energy curves of SLy5sX forces as a function of quadrupole deformations β₂ are shown in Figure 1. The two-dimensional potential energy surfaces of ²⁴⁰Pu from different calculations can be found in [5, 36, 37]. The SLy5s8 has the largest surface energy and SLy5s1 has the smallest surface energy. Consequently SLy5s8 has the highest fission barriers.

TABLE 1

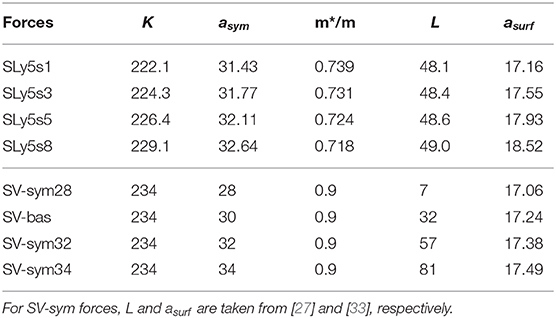
Table 1. The relevant EoS properties of SLy5sX [33] and SV-sym [34] forces are listed, including the incompressibility K (MeV), the symmetry energy a_sym (MeV), the effective mass m^*/m, the slope of the symmetry energy L (MeV), the surface energy coefficient a_surf (MeV).

FIGURE 1

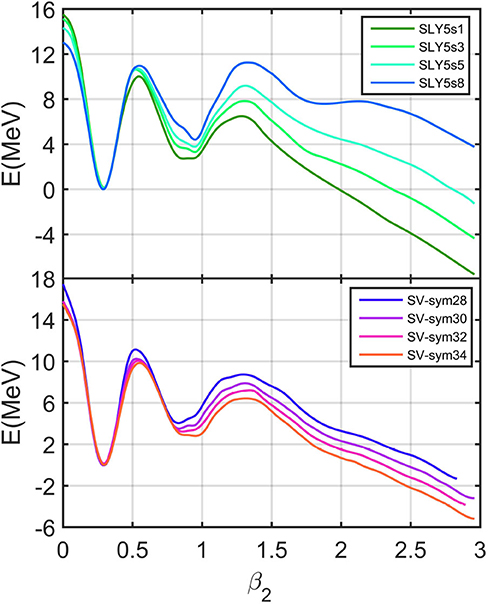
Figure 1. The fission barriers of ²⁴⁰Pu calculated by Skyrme Hartree-Fock+BCS with SLy5sX and SV-sym forces, respectively. Calculations are performed with octupole deformations but without triaxial deformations.

The TDHF calculations of the fission process of ²⁴⁰Pu are performed at the same initial deformations with SLy5s1, SLy5s3, SLy5s5, SLy5s8 forces. Figure 2 shows that the evolutions of quadrupole deformations, in which initial deformations are β₂=2.4 and β₃=0.9 in four calculations. The multipole deformation β_l is defined as [38],

$\begin{array}{ll}{\beta }_l=\frac{4\pi }{3A{R}_0^l}<r^l{Y}_{l0}>& (2)\end{array}$

where $R_0=1.2A^{1/3}$ fm. The quadrupole moment shown in Figure 2 is defined as $<r^2{Y}_{20}>$. We can see that in calculations with SLy5s1, SLy5s3, and SLy5s5, ²⁴⁰Pu goes to fission very quickly at time around 700 fm/c. With increasing surface energies, the fission lifetime increase slightly. However, in calculations with SLy5s8, the fission lifetime is extremely long. We see very slow and large-amplitude oscillations in the quadrupole deformation toward the fission. The results indicate that the fission would be strongly over-damped above a critical surface energy coefficient. This is understandable since the large surface tension would prohibit the fission movement.

FIGURE 2

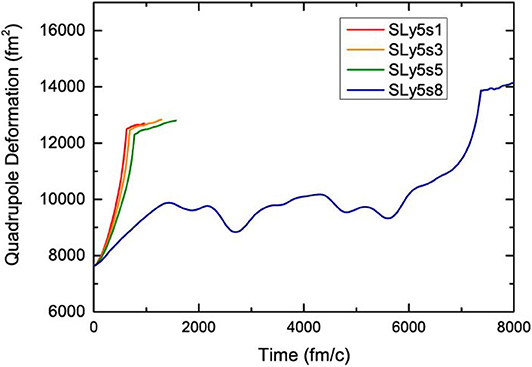
Figure 2. The evolutions of quadrupole deformations in TDHF calculations with the SLy5s1, SLy5s3, SLy5s5, SLy5s8 forces.

3.2. Influences of Symmetry Energies in Fission Dynamics

The symmetry energy is expected to be crucial in the equation of state (EoS) of neutron stars and in exotic neutron-rich nuclei [39]. In Skyrme forces, the symmetry energy is density-dependent and is usually determined according to EoS properties at the saturated density. The larger symmetry energy coefficient indicates that neutron-rich systems are less stable. In the transport model, the large symmetry energy could lead to rapid isospin balance [28]. To study the role of symmetry energy in fission dynamics, we calculate the fission evolutions with Skyrme forces SV-sym28, SV-bas, SV-sym32, SV-sym34 [34], which differ in symmetry energy coefficients, but are otherwise similar. The calculated potential energy curves of SV-sym forces as a function of quadrupole deformations β₂ are shown in Figure 1. The EoS properties of SV-sym forces are listed in the Table 1. The fission barrier of SV-sym34 is slightly lower than that of SV-sym28, although the surface energy coefficient of SV-sym34 is slightly larger than that of SV-sym28. This is consistent with the results of fission barriers in [34]. Note that the surface symmetry energy is important for descriptions of fission barriers [40]. We also noticed that the slopes L of symmetry energies of SV-sym forces are very different, which are difficult to be constrained. The series of SV-sym forces have been used to study the influences of symmetry energies in nuclear fusion processes [27].

Figure 3 shows that the quadrupole deformation evolutions with initial deformations of β₂=2.25 and β₃=0.9 in our calculations. The initial deformation β₂=2.25 used for SV-sym forces is slightly smaller than β₂=2.4 used for SLy5sX forces. This is because ²⁴⁰Pu doesn't fission in calculations with SLy5s8 if the initial deformation is β₂=2.25. We can see that in calculations with SV-sym28, SV-bas, SV-sym32, ²⁴⁰Pu goes to fission quickly. The fission time is longer than that with SLy5s1-3-5 forces (see Figure 2), since the initial deformation used for SLy5sX is slightly larger. The evolutions of SV-sym34 results are similar to three other cases at the beginning. However, just before the scission, the fission with SV-sym34 feels a strong restoring force that delays its fission. Such a restoring force has also subtle influences in SV-sym32 evolutions. The origin of such a restoring force can be understood that the formation of neutron-rich neck is not favored due to a large symmetry energy. Both symmetry energy and surface energy are positive contributions to total binding energies. During the fission process, the kinetic energy and Coulomb energy would decrease while total energies are conserved. Once the kinetic energies are strongly dissipated after several oscillations, the fission would finally occur. This is similar with the case of SLy5s8 with a large surface energy. The fission life times of SV-sym28, SV-bas, SV-sym32 are 1260, 1320, 1530 fm/c respectively. We see that with increased symmetry energies, the fission lifetimes increase non-linearly. This could be related the quantum critical point in dissipation dynamics [41]. Note that the over-damped fission phenomena with SV-sym34 would not appear if the initial deformation is very close to the scission point. The very different slopes of symmetry energies of SV-sym forces could also play a role in fission dynamics. In all cases, the octupole deformations increases very rapidly before 100 fm/c, then varies moderately before scission. At the scission, the octupole deformations increase more rapidly than quadruple deformations. The evolutions of hexadecapole deformations are similar to that of quadruple deformations before the scission.

FIGURE 3

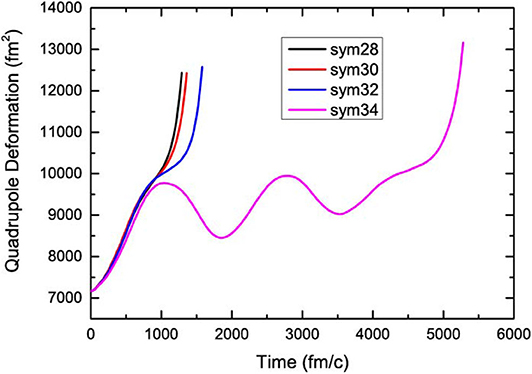
Figure 3. The evolutions of quadrupole deformations in TDHF calculations with the SV-sym28, SV-bas, SV-sym30, SV-sym34 forces.

3.3. The Collective Oscillations of Fission Fragments

The shapes of fission fragments at the scission point are far away from the equilibrium shapes. The octupole deformations of the fragments would strongly impact the fission yields [13]. For example, ¹⁴⁴Ba with favorable octupole shell effects would play a significant role in asymmetric fission yields [13]. In fission dynamics, the oscillations of fission fragments can be connected to the low-lying multipole excitations [30].

Figure 4 shows the multipole deformation oscillations of the heavy fission fragment after the ²⁴⁰Pu fission. The heavy fragment is around ¹³²Sn and is nearly spherical at ground state which is resistant to octupole deformation. However, it can be seen that the oscillation amplitudes of octupole shapes are most significant compared to quadrupole and hexadecapole deformation oscillations. This is understandable since the initial octupole deformation is far from equilibrium. The hexadecapole oscillations are also significant compared to quadrupole oscillations since the initial hexadecapole deformation is very large. It is interesting to see that the large fragments have significant octupole oscillations. The dependence of the octupole oscillation frequencies on different Skyrme forces is not significant.

FIGURE 4

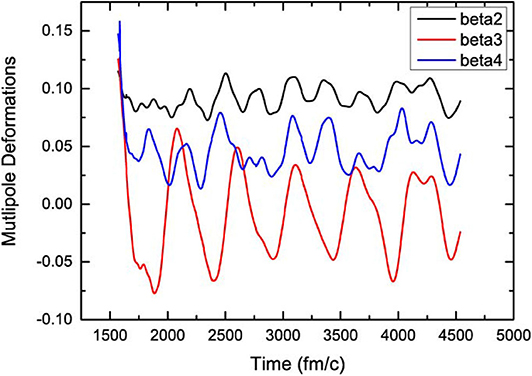
Figure 4. The TDHF evolutions of quadrupole, octupole, and hexadecapole deformations of the heavy fragment after the ²⁴⁰Pu fission with the SV-sym32 force.

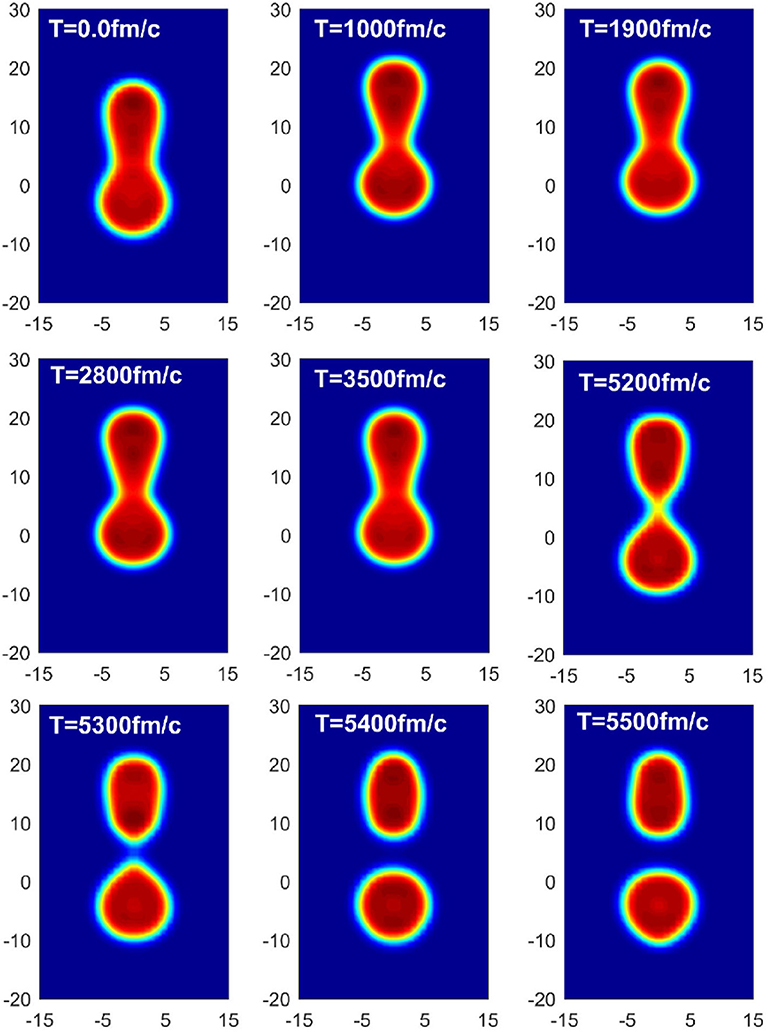
Figure 5 shows the octupole oscillations of both fragments of the ²⁴⁰Pu fission. The corresponding density evolutions are shown in Figure 6. Figure 6 also shows that evolution of fission neck before scission in calculations with SV-sym34. We see that the neck is thin at 1000 fm/c and becomes thick at 1,900 fm/c. The main differences in nuclear shapes are the evolutions of neutron-rich necks, in which the symmetry energy can play a role. The shapes of fragments before scission don't change much. The small fragment around ¹⁰⁷Mo has a significant octupole deformation before scission. The heavy fragment around ¹³³Te which is close to ¹³²Sn is nearly spherical but with an initial octupole deformation before scission. The sizes of the fragments can vary slightly with different Skyrme forces and initial deformations. The amplitudes and frequencies of octupole oscillations of both fragments are comparable. The two fragments are oscillating with opposite octupole deformations. As shown in Figure 6, the small fragment has a significant quadrupole deformation at equilibrium. The heavy fragment has a spherical shape at equilibrium so that the octupole oscillation is very significant. The oscillation frequencies ℏω obtained by Fourier analysis are about 1.3 MeV, which is much lower than the typical experimental energies of the octupole vibration states of the fragments. For descriptions of vibrations of fragments, the finite-temperature QRPA [42] would be appropriate since the fragments are actually thermal excited.

FIGURE 5

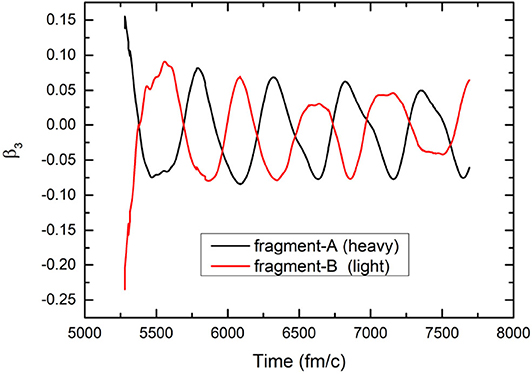
Figure 5. The evolutions of octupole deformations in TDHF calculations of two fission fragments with the SV-sym34 force. The fragment-A is the heavy fragment and fragment-B is the light fragment.

FIGURE 6

Figure 6. The density evolutions of the ²⁴⁰Pu fission in TDHF calculations with the SV-sym34 force.

4. Conclusion

In summary, we studied the shape evolutions in fission process of ²⁴⁰Pu with the TDHF approach. Firstly, the dependence of Skyrme forces in fission dynamics has been investigated. We found that Skyrme forces with large surface energy coefficients and large symmetry energy coefficients can result in extremely long fission times. Before the final scission, in these cases, the fission process would be over-damped with slow and small-amplitude shape oscillations. The symmetry energy can play a role in the evolution of neutron-rich necks before the scission. The evolutions of octupole deformations don't follow that of quadrupole deformations. In addition, we also studied the shape oscillations of the fragments of the ²⁴⁰Pu fission. It is interesting to see that the heavy fragment which is close to spherical at equilibrium has significant octupole oscillations. Both fragments have comparable octupole oscillation amplitudes and frequencies. On the other hand, the quadrupole and hexadecapole oscillations of the fragments are less significant.

Author Contributions

MP did calculations and some figures. JP wrote the manuscript. YQ did part of the coding and figures. PS suggested the topic and worked on the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China under Grant Nos. 11975032, 11790325, 11835001, and 11961141003; the National Key R&D Program of China (Contract No. 2018YFA0404403). It was also supported by UK STFC under grant number ST/P005314/1.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We also acknowledge that computations in this work were performed in Tianhe-1A located in Tianjin.

References

1. Schunck N, Robledo LM. Microscopic theory of nuclear fission: a review. Rep Prog Phys. (2016) 79:116301. doi: 10.1088/0034-4885/79/11/116301

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Bender M, Bernard R, Bertsch G, Chiba S, Dobaczewski J, Dubray N, et al. Future of nuclear fission theory. J Phys G. (2020). doi: 10.1088/1361-6471/abab4f

CrossRef Full Text | Google Scholar

3. Brosa U, Grossmann S, Müller A. Nuclear scission. Phys Rep. (1990) 197:167. doi: 10.1016/0370-1573(90)90114-H

CrossRef Full Text | Google Scholar

4. Nix JR. Summary: our 50-year Odyssey with fission. Nucl Phys A. (1989) 502:609. doi: 10.1016/0375-9474(89)90693-3

CrossRef Full Text | Google Scholar

5. Regnier D, Dubray N, Schunck N, Verriere M. Fission fragment charge and mass distributions in 239Pu(n,f) in the adiabatic nuclear energy density functional theory. Phys Rev C. (2016) 93:054611. doi: 10.1103/PhysRevC.93.054611

CrossRef Full Text | Google Scholar

6. Younes W, Gogny DM, Berger J-F. A microscopic theory of fission dynamics based on the generator coordinate method. In: Lecture Notes on Physics 950. Berlin: Springer (2019). doi: 10.1007/978-3-030-04424-4

CrossRef Full Text | Google Scholar

7. Verriere M, Regnier D. The time-dependent generator coordinate method in nuclear physics. Front Phys. (2020) 8:233. doi: 10.3389/fphy.2020.00233

CrossRef Full Text | Google Scholar

8. Simenel C. Nuclear quantum many-body dynamics: from collective vibrations to heavy-ion collisions. Eur Phys J A. (2012) 48:152. doi: 10.1140/epja/i2012-12152-0

CrossRef Full Text | Google Scholar

9. Bulgac A, Magierski P, Roche KJ, Stetcu I. Induced fission of 240Pu within a real-time microscopic framework. Phys Rev Lett. (2016) 116:122504. doi: 10.1103/PhysRevLett.116.122504

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Goddard P, Stevenson P, Rios A. Fission dynamics within time-dependent Hartree-Fock: deformation-induced fission. Phys Rev C. (2015) 92:054610. doi: 10.1103/PhysRevC.92.054610

CrossRef Full Text | Google Scholar

11. Goddard P, Stevenson P, Rios A. Fission dynamics within time-dependent Hartree-Fock. II. Boost-induced fission. Phys Rev C. (2016) 93:014620. doi: 10.1103/PhysRevC.93.014620

CrossRef Full Text | Google Scholar

12. Simenel C, Umar AS. Heavy-ions collisions and fission dynamics with the time-dependent Hartree-Fock theory and its extensions. Prog Part Nucl Phys. (2018) 103:19. doi: 10.1016/j.ppnp.2018.07.002

CrossRef Full Text | Google Scholar

13. Scamps G, Simenel C. Impact of pear-shaped fission fragments on mass-asymmetric fission in actinides, Nature (2018) 564:382. doi: 10.1038/s41586-018-0780-0

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Negele JW. The mean-field theory of nuclear structure and dynamics. Rev Mod Phys. (1982) 54:9135. doi: 10.1103/RevModPhys.54.913

CrossRef Full Text | Google Scholar

15. Nakatsukasa T, Matsuyanagi K, Matsuo M, Yabana K. Time-dependent density-functional description of nuclear dynamics. Rev Mod Phys. (2016) 88:045004. doi: 10.1103/RevModPhys.88.045004

CrossRef Full Text | Google Scholar

16. Ebata S. Studies on nuclear structure and nuclear dynamics using Cb-TDHFB. Front Phys. (2020) 8:102. doi: 10.3389/fphy.2020.00102

CrossRef Full Text | Google Scholar

17. Scamps G, Simenel C, Lacroix D. Dynamical description of the fission process using the TD-BCS theory. AIP Conf Proc. (2015) 1681:040003. doi: 10.1063/1.4932264

CrossRef Full Text | Google Scholar

18. Stevenson PD, Barton MC. Low-energy heavy-ion reactions and the Skyrme effective interaction. Prog Part Nucl Phys. (2019) 104:142. doi: 10.1016/j.ppnp.2018.09.002

CrossRef Full Text | Google Scholar

19. Stevenson PD, Suckling EB, Fracasso S, Barton MC, Umar AS. Skyrme tensor force in heavy ion collisions. Phys Rev C. (2016) 93:054617. doi: 10.1103/PhysRevC.93.054617

CrossRef Full Text | Google Scholar

20. Guo L, Godbey K, Umar AS. Influence of the tensor force on the microscopic heavy-ion interaction potential. Phys Rev C. (2018) 98:064607. doi: 10.1103/PhysRevC.98.064607

CrossRef Full Text | Google Scholar

21. Bernard RN, Pillet N, Robledo LM, Anguiano M. Description of the asymmetric to symmetric fission transition in the neutron-deficient thorium isotopes: role of the tensor force. Phys Rev C. (2020) 101:044615. doi: 10.1103/PhysRevC.101.044615

CrossRef Full Text | Google Scholar

22. Bartel J, Quentin P, Brack M, Guet C, Håkansson HB. Towards a better parameterisation of Skyrme-like effective forces: a critical study of the SkM force. Nucl Phys A. (1982) 386:79. doi: 10.1016/0375-9474(82)90403-1

CrossRef Full Text | Google Scholar

23. Zuo ZW, Pei JC, Xiong XY, Zhu Y. Global analysis of Skyrme forces with higher-order density dependencies. Chin Phys C. (2018) 42:064106. doi: 10.1088/1674-1137/42/6/064106

CrossRef Full Text | Google Scholar

24. Erler J, Langanke K, Loens HP, Martinez-Pinedo G, Reinhard P-G. Fission properties for r-process nuclei. Phys Rev C. (2012) 85:025802. doi: 10.1103/PhysRevC.85.025802

CrossRef Full Text | Google Scholar

25. Baran A, Kowal M, Reinhard PG, Robledo LM, Staszczak A, Warda M. Fission barriers and probabilities of spontaneous fission for elements with Z ≥ 100. Nucl Phys A. (2015) 944:442. doi: 10.1016/j.nuclphysa.2015.06.002

CrossRef Full Text | Google Scholar

26. Zhu Y, Pei JC. Thermal fission rates with temperature dependent fission barriers. Phys Rev C. (2016) 94:024329. doi: 10.1103/PhysRevC.94.024329

CrossRef Full Text | Google Scholar

27. Reinhard P-G, Umar AS, Stevenson PD, Piekarewicz J, Oberacker VE, Maruhn JA. Sensitivity of the fusion cross section to the density dependence of the symmetry energy. Phys Rev C. (2016) 93:044618. doi: 10.1103/PhysRevC.93.044618

CrossRef Full Text | Google Scholar

28. Zhang Y, Tian J, Cheng W, Guan F, Huang Y, Li H, et al. Long-time drift of the isospin degree of freedom in heavy ion collisions. Phys Rev C. (2017) 95:041602. doi: 10.1103/PhysRevC.95.041602

CrossRef Full Text | Google Scholar

29. Li BA, Chen LW, Ko CM. Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys Rep. (2008) 464:113. doi: 10.1016/j.physrep.2008.04.005

CrossRef Full Text | Google Scholar

30. Simenel C, Umar AS. Formation and dynamics of fission fragments. Phys Rev C. (2014) 89:031601. doi: 10.1103/PhysRevC.89.031601

CrossRef Full Text | Google Scholar

31. Maruhn JA, Reinhard P-G, Stevenson PD, Umar AS. The TDHF code Sky3D. Comp Phys Commun. (2014) 185:2195. doi: 10.1016/j.cpc.2014.04.008

CrossRef Full Text | Google Scholar

32. Schuetrumpf B, Reinhard P-G, Stevenson PD, Umar AS, Maruhn JA. The TDHF code Sky3D version 1.1. Comp Phys Commun. (2018) 229:211. doi: 10.1016/j.cpc.2018.03.012

CrossRef Full Text | Google Scholar

33. Jodon R, Bender M, Bennaceur K, Meyer J. Constraining the surface properties of effective Skyrme interactions. Phys Rev C. (2016) 94:024335. doi: 10.1103/PhysRevC.94.024335

CrossRef Full Text | Google Scholar

34. Klüpfel P, Reinhard P-G, Brvenich TJ, Maruhn JA. Variations on a theme by Skyrme: a systematic study of adjustments of model parameters Phys Rev C. (2009) 79:034310. doi: 10.1103/PhysRevC.79.034310

CrossRef Full Text | Google Scholar

35. Reinhard P-G. Computer Code SKYAX (unpublished).

36. Bulgac, Jin S, Roche KJ, Schunck N, Stetcu I. Fission dynamics of 240Pu from saddle to scission and beyond. Phys Rev C. (2019) 100:034615. doi: 10.1103/PhysRevC.100.034615

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Zhao J, Xiang J, Li ZP, Niksic T, Vretenar D, Zhou SG. Time-dependent generator-coordinate-method study of mass-asymmetric fission of actinides. Phys Rev C. (2019) 99:054613. doi: 10.1103/PhysRevC.99.054613

CrossRef Full Text | Google Scholar

38. Bender M, Heenen PH, Reinhard P-G. Self-consistent mean-field models for nuclear structure. Rev Mod Phys. (2003) 75:121. doi: 10.1103/RevModPhys.75.121

CrossRef Full Text | Google Scholar

39. Steiner AW, Prakash M, Lattimer JM, Ellis PJ. Isospin asymmetry in nuclei and neutron stars. Phys. Rep. (2005) 411:325. doi: 10.1016/j.physrep.2005.02.004

CrossRef Full Text | Google Scholar

40. Nikolov N, Schunck N, Nazarewicz W, Bender M, Pei J. Surface symmetry energy of nuclear energy density functionals. Phys Rev C. (2011) 83:034305. doi: 10.1103/PhysRevC.83.034305

CrossRef Full Text | Google Scholar

41. Tong D, Wong K. Fluctuation and dissipation at a quantum critical point. Phys Rev Lett. (2013) 110:061602. doi: 10.1103/PhysRevLett.110.061602

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Yüksel E, Colò G, Khan E, Niu YF, Bozkurt K. Multipole excitations in hot nuclei within the finite temperature quasiparticle random phase approximation framework. Phys Rev C. (2017) 96:024303. doi: 10.1103/PhysRevC.96.024303

CrossRef Full Text | Google Scholar