Computing Irregularity Indices for Probabilistic Neural Network

Kang, Shunguang; Chu, Yu-Ming; Virk, Abaid ur Rehman; Nazeer, Waqas; Jia, Jia

doi:10.3389/fphy.2020.00359

ORIGINAL RESEARCH article

Front. Phys., 04 September 2020
Sec. Statistical and Computational Physics
Volume 8 - 2020 | https://doi.org/10.3389/fphy.2020.00359

Computing Irregularity Indices for Probabilistic Neural Network

Shunguang Kang¹

Yu-Ming Chu^2,3^*

Abaid ur Rehman Virk⁴

Waqas Nazeer⁵

Jia Jia¹

¹School of Tourism Data, Guilin Tourism University, Guilin, China
²Department of Mathematics, Huzhou University, Huzhou, China
³Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering, Changsha University of Science & Technology, Changsha, China
⁴Department of Mathematics, University of Management and Technology, Lahore, Pakistan
⁵Department of Mathematics, Government College University, Lahore, Pakistan

A topological index (TI) is a quantity expressed as a number that help us to catch symmetry of network. With the help of quantitative structure property relationship (QSPR), we can guess physical and chemical properties of several networks. A neural network is a computer system based on the nerve system. There are numerous uses of these systems in different fields of studies but their most critical use to date is in Neurochemistry. In this paper, we will discuss thirteen irregularity indices for probabilistic neural networks (PNN).

1. Introduction

PNN are likewise Parzen window pdf estimator. In last few years these networks are widely used in different problems. With the help of these networks, we can solve email security problems, also helpful in signature verification. A PNN network contain different sub networks. The input data is from the set of measurements. The Gaussian functions produce the second layer with the help of given set of data points. An average operation is perform by second layer which produce third layer.

Molecular structures can be studied by means of graph. A branch of mathematics thats deals with the study of molecular graphs is know as chemical graph theory. With the help of different tools of mathematics, we are able to identify the features that helps us in QSPR. Contaminate, TIs are arithmetic value link with graph of PNN and has utilization in different fields of study. TIs stay invariant of two isomorphic graphs and helpful to predict many properties of PNN [1–7]. Other growing field is Cheminformatics, in which QSAR and QSPR relationship is used to figure out properties of concerned network. In these investigation, a few Physico-chemical properties and TIs are helpful to examine the behavior of compound structures [8–17].

The other primeval TI is Randić index, introduced by Randić [18] in 1975. Due to huge applications of Randić index, the generalized Randić index was given in [12]. This variant develop intrust for both the mathematicians and chemists [19–24].

After Randić index, the most examined TIs are Zagreb indices [25–27]. The different variants of Zagreb index was studied in [28]. An other important topological invariant is a symmetric division index which is an excellent descriptor of the aggregate surface area for polychlorobiphenyls [29].

2. Topological Indices

A special number, in graph theoretical term, representing a molecular structure, is known as topological descriptor. A topological descriptor when correlates with a molecular property, it can be determine as graph-theoretic index or topological index. The First and second Zagreb indices are the oldest molecular descriptors invented in 1975 by Gutman [18] and their properties are extensively investigated. They are defined as:

M_{1} (G) = \sum_{u v \in E (G)} (d_{u} + d_{v}) .

M_{2} (G) = \sum_{u v \in E (G)} (d_{u} \times d_{v}) .

The first genuine degree based TI was given by Randić in 1975 [18] as:

R (G) = \sum_{u v \in E (G)} \frac{1}{\sqrt{d_{u} . d_{v}}} .

The GRI known as General Randic Index [30] and is defined as:

G R I (G) = \sum_{u v \in E (G)} {(d_{u} . d_{v})}^{α} .

where α is an arbitrary real number.

The TI is known as Irregularity index [31], if TI of graph is greater equal to zero and TI of graph is equal to zero if and only if graph is regular. The Irregularity indices are given below. All these Irregularity indices are belong to degree based topological invariants excluding IRM2(G). A simplified way of expressing the irregularity is a irregularity index.

• $V A R (G) = \sum_{u ϵ V} {(d_{u} - \frac{2 m}{n})}^{2} = \frac{M_{1} (G)}{n} - {(\frac{2 m}{n})}^{2}$

• $A L (G) = \sum_{u v \in E (G)} | d_{u} - d_{v} |$

• $I R 1 (G) = \sum_{u \in V} {(d_{u})}^{3} - \frac{2 m}{n} \sum_{u \in V} {(d_{u})}^{2} = F (G) - \frac{2 m}{n} M_{1} (G)$

• $I R 2 (G) = \sqrt{\frac{\sum_{u v \in E (G)} d_{u} d_{v}}{m}} - \frac{2 m}{n} = \sqrt{\frac{M_{2} (G)}{m}} - \frac{2 m}{n}$

• $I R F (G) = \sum_{u v \in E (G)} {(d_{u} - d_{v})}^{2} = F (G) - 2 M_{2} (G)$

• $I R F W (G) = \frac{I R F (G)}{M_{2} (G)}$

• $I R A (G) = \sum_{u v \in E (G)} {(d_{u}^{- 1 / 2} - d_{v}^{- 1 / 2})}^{2} = n - 2 R (G)$

• $I R B (G) = \sum_{u v \in E (G)} {(d_{u}^{1 / 2} - d_{v}^{1 / 2})}^{2} = M_{1} (G) - 2 R R (G)$

• $I R D I F (G) = \sum_{u v \in E (G)} | \frac{d_{u}}{d_{v}} - \frac{d_{v}}{d_{u}} | = \sum_{i < j} m_{i, j} (\frac{j}{i} - \frac{i}{j})$

• $I R L F (G) = \sum_{u v \in E (G)} \frac{| d_{u} - d_{v} |}{\sqrt{(d_{u} d_{v})}} = \sum_{i < j} m_{i, j} (\frac{j - i}{\sqrt{i j}})$

• $I R L A (G) = 2 \sum_{u v \in E (G)} \frac{| d_{u} - d_{v} |}{(d_{u} + d_{v})} = 2 \sum_{i < j} m_{i, j} (\frac{j - i}{i + j})$

• $I R D 1 (G) = \sum_{u v \in E (G)} l n 1 + | d_{u} - d_{v} | = \sum_{i < j} m_{i, j} l n (i + j - 1)$

• $I R G A (G) \sum_{u v \in E (G)} l n (\frac{d_{u} + d_{v}}{2 \sqrt{d_{u} d_{v}}}) \sum_{i < j} m_{i, j} (\frac{i + j}{2 \sqrt{i j}})$

3. Computations of Probabilistic Neural Network

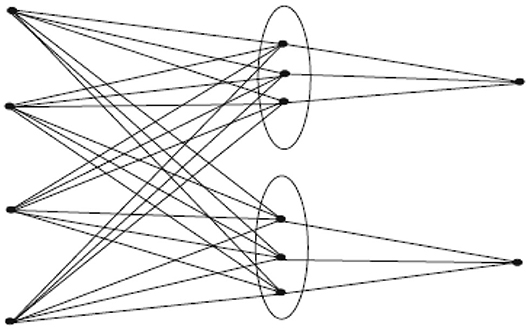
In this section, we will discuss irregularity indices for probabilistic neural network. The molecular graph of PNN(n, k, m) is given in Figure 1. The edge partition of PNN(n, k, m) is given in Table 1. The total vertices in PNN(n, k, m) are n+k(m+1) and number of edges are km(n + 1).

FIGURE 1

Figure 1. PNN(4, 2, 3).

TABLE 1

Table 1. E[PNN(n, k, m)].

Theorem 3.1. Consider G as graph for probabilistic neural network PNN(n, k, m. Then,

1. VAR(G) $= \frac{k m (K^{2} m^{2} - 4 k m n^{2} + k^{2} m + k m^{2} - 5 k m n - k m + 2 k n + m n + 2 n^{2} + 2 k + 2 n)}{{(k m + k + n)}^{2}}$

2. AL(G) = k²m²n − kmn² − km² + 2kmn + km

3. $I R 1 (G) = \frac{1}{k m + k + n} (k m (k^{3} m^{3} + k^{3} m^{2} + k^{2} m^{2} n + 2 k^{2} m n + k m^{3} + 2 k^{2} m + k m^{2} + 2 k n^{2} + m^{2} n + 2 m n^{2} + 2 n^{3} + 4 k n + 2 m n + 4 n^{2} + 2 k + 2 n))$

4. $I R 2 (G) = \frac{1}{k m + k + n} (\sqrt{(k + 1) m} k m - 2 k m n + \sqrt{(k + 1) m} k + \sqrt{(k + 1) m} n - 2 k m)$

Proof:

\begin{array}{l} 1 . V A R (G) = \sum_{u \in V} {(d_{u} - \frac{2 m}{n})}^{2} = \frac{M_{1} (G)}{n} - {(\frac{2 m}{n})}^{2} \\ = \frac{k^{2} m^{2} + k m^{2} + 2 k m n + 2 k m}{k m + k + n} - {(\frac{k m n + k m}{k m + k + n})}^{2} \\ = \frac{1}{{(k m + k + n)}^{2}} (k m (K^{2} m^{2} - 4 k m n^{2} + k^{2} m + k m^{2} \\ - 5 k m n - k m + 2 k n + m n + 2 n^{2} + 2 k + 2 n)) \end{array}

\begin{array}{l} 2 . A L (G) = \sum_{u v \in E (G)} | d_{u} - d_{v} | \\ = | k m - n - 1 | (k m n) + | n + 1 - m | (k m) \\ = k^{2} m^{2} n - k m n^{2} - k m^{2} + 2 k m n + k m . \end{array}

\begin{array}{l} 3 . I R 1 (G) = \sum_{u \in V} d_{u}^{3} - \frac{2 m}{n} \sum_{u \in V} d_{u}^{2} = F (G) - (\frac{2 m}{n}) M_{1} (G) \\ = (k^{3} m^{3} + 2 k^{2} m^{2} n + 2 k^{2} m^{2} + k m^{3} + 2 k m^{2} n \\ + 2 k m n^{2} + 2 k m^{2} + 4 k m n + 2 k m) \\ - \frac{2 (k m n + k m)}{(k m + k + n)} (k^{2} m^{2} + k m^{2} + 2 k m n + 2 k m) \\ = \frac{1}{k m + k + n} (k m (k^{3} m^{3} + k^{3} m^{2} \\ + k^{2} m^{2} n + 2 k^{2} m n + k m^{3} + 2 k^{2} m + k m^{2} + 2 k n^{2} \\ + m^{2} n + 2 m n^{2} + 2 n^{3} + 4 k n + 2 m n \\ + 4 n^{2} + 2 k + 2 n)) . \end{array}

\begin{array}{l} 4 . I R 2 (G) = \sqrt{\frac{\sum_{u v \in E (G)} d_{u} d_{v}}{m}} - \frac{2 m}{n} = \sqrt{\frac{M_{2} (G)}{m}} - \frac{2 m}{n} \\ = \sqrt{\frac{(k m n + k m) k m + k m (m n + m)}{k m n + k m}} \\ - (\frac{2 (k m n + k m)}{k m + k + n}) \\ = \frac{1}{k m + k + n} (\sqrt{(k + 1) m} k m \\ - 2 k m n + \sqrt{(k + 1) m} k \\ + \sqrt{(k + 1) m} n - 2 k m) . \end{array}

□

Theorem 3.2. Consider G as graph for probabilistic neural network PNN(n, k, m. Then,

1. IRF(G) = k³m³ + km³ + 2kmn² + 4kmn + 2km

2. $I R F W (G) = \frac{k^{2} m^{2} + m^{2} + 2 n^{2} + 4 n + 2}{m (k n + k + n + 1)}$

3. $I R A (G) = \frac{1}{\sqrt{k m n + k m} (m n + m)} k m (n \sqrt{m n + m} + \sqrt{k m n + k m})$

4. IRB(G) = (−2k²m²n² − 2k²m²n + k²m² − 2km²n − km² + 2kmn + 2km)

Proof:

\begin{array}{l} 1 . I R F (G) = \sum_{u v \in E (G)} {(d_{u} - d_{v})}^{2} \\ = {(k m - n - 1)}^{2} (k m n) + {(n + 1 - m)}^{2} (k m) \\ = k^{3} m^{3} + k m^{3} + 2 k m n^{2} + 4 k m n + 2 k m . \end{array}

\begin{array}{l} 2 . I R F W (G) = \frac{I R F (G)}{M_{2} (G)} \\ = \frac{k^{2} m^{2} + m^{2} + 2 n^{2} + 4 n + 2}{m (k n + k + n + 1)} . \end{array}

\begin{array}{l} 3 . I R A (G) = \sum_{u v \in E (G)} {(d_{u}^{- 1 / 2} - d_{v}^{- 1 / 2})}^{2} \\ = n - 2 R (G) \\ = \frac{1}{\sqrt{k m n + k m} (m n + m)} \\ k m (n \sqrt{m n + m} + \sqrt{k m n + k m}) . \end{array}

\begin{array}{l} 4 . I R B (G) = \sum_{u v \in E (G)} {(d_{u}^{1 / 2} - d_{v}^{1 / 2})}^{2} \\ = M_{1} (G) - 2 R R (G) \\ = (k m + n + 1) k m + k m (m + n + 1) \\ - 2 k^{2} m^{2} n^{2} - 2 k^{2} m^{2} n - 2 k m^{2} n - 2 k m^{2} \\ = (- 2 k^{2} m^{2} n^{2} - 2 k^{2} m^{2} n \\ + k^{2} m^{2} - 2 k m^{2} n - k m^{2} + 2 k m n + 2 k m) . \end{array}

□

Theorem 3.3. Consider G as graph for probabilistic neural network PNN(n, k, m. Then,

1. $I R D I F (G) = \frac{k^{2} m^{2} n - k m^{2} + k n^{2} - n^{3} + 2 k n - 2 n^{2} + k - n}{n + 1}$

2. $I R L F (G) = \frac{k m n (k m - n - 1)}{\sqrt{k m n + k m}} + \frac{k m (n - m + 1)}{\sqrt{m n + m}}$

3. IRLA(G) = $\frac{k m (k m^{2} n + k m n^{2} - k m^{2} + 2 k m n - m n^{2} - n^{3} + k m - 2 m n - n^{2} - m + n + 1)}{(k m + n + 1) (m + n + 1)}$

4. IRD1(G) = k²m²n − kmn² − km² + km

5. $I R G A (G) = \frac{1}{\sqrt{(k m n + k m) (m n + m)}} (k m (0.71 l n) k m + n + 1) n \sqrt{m n + m} + 0.70 l n (m + n + 1) \sqrt{k m n + k m}$

Proof:

\begin{array}{l} 1 . I R D I F (G) = \sum_{u v \in E (G)} | \frac{d_{u}}{d_{v}} - \frac{d_{v}}{d_{u}} | \\ = (\frac{k m}{n + 1} - \frac{n + 1}{k m}) k m n \\ + (\frac{n + 1}{m} - \frac{n + 1}{m} - \frac{m}{n + 1}) k m \\ = \frac{k^{2} m^{2} n - k m^{2} + k n^{2} - n^{3} + 2 k n - 2 n^{2} + k - n}{n + 1} . \end{array}

\begin{array}{l} 2 . I R L F (G) = \sum_{u v \in E (G)} \frac{| d_{u} - d_{v} |}{\sqrt{d_{u} . d_{v}}} \\ = (\frac{| k m - n - 1 |}{\sqrt{k m n}}) (k m n) + (\frac{| n + 1 - m |}{\sqrt{m n}}) (k m) \\ = \frac{k m n (k m - n - 1)}{\sqrt{k m n + k m}} + \frac{k m (n - m + 1)}{\sqrt{m n + m}} . \end{array}

\begin{array}{l} 3 . I R L A (G) = \sum_{u v \in E (G)} 2 \frac{| d_{u} - d_{v} |}{(d_{u} + d_{v})} \\ = 2 (\frac{| k m - n - 1 |}{k m + n + 1}) (k m n) \\ + 2 (\frac{| n + 1 - m |}{n + 1 + m}) (2 k m) \\ = \frac{1}{(k m + n + 1) (m + n + 1)} (k m (k m^{2} n + k m n^{2} \\ - k m^{2} + 2 k m n - m n^{2} - n^{3} \\ + k m - 2 m n - n^{2} - m + n + 1) . \end{array}

\begin{array}{l} 4 . I R D 1 (G) = \sum_{u v \in E (G)} l n {1 + | d_{u} - d_{v} |} \\ = l n {1 + | k m - n - 1 |} (k m n) \\ + l n {1 + | n + 1 - m |} (k m) \\ = k^{2} m^{2} n - k m n^{2} - k m^{2} + k m . \end{array}

\begin{array}{l} 5 . I R G A (G) = \sum_{u v \in E (G)} l n (\frac{d_{u} + d_{v}}{2 \sqrt{d_{u} d_{v}}}) \\ = l n (\frac{k m + n + 1}{2} \sqrt{k m (n + 1)}) (k m n) \\ + l n (\frac{m + n + 1}{2 \sqrt{m (n + 1)}}) (k m) \\ = \frac{1}{\sqrt{(k m n + k m) (m n + m)}} (k m (0.71 l n) k m + n + 1) \\ n \sqrt{m n + m} + 0.70 l n (m + n + 1) \sqrt{k m n + k m} . \end{array}

□

Conclusion

In this article, we have calculated degree-based irregularity indices of probabilistic neural network. Our outcomes are pertinent in material science and other applied sciences. It is demonstrated certainty that TIs help to anticipate numerous properties without setting off to the wet lab.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

SK revised the introduction section and proofread the paper. Y-MC analyzed the results and arrange funding. AV proved the main results. WN proposed the problem and supervised this work. JJ improved the language and highlight the applications of the results. All authors listed approved it for publication.

Funding

The research was supported by the National Natural Science Foundation of China (Grant Nos. 11971142, 11871202, 61673169, 11701176, 11626101, and 11601485).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Gao W, Younas M, Farooq A, Virk A, Nazeer W. Some reverse degree-based topological indices and polynomials of dendrimers. Mathematics. (2018) 6:214. doi: 10.3390/math6100214

CrossRef Full Text | Google Scholar

2. Gao W, Wang W, Dimitrov D, Wang Y. Nano properties analysis via fourth multiplicative ABC indicator calculating. Arab J Chem. (2018) 11:793–801. doi: 10.1016/j.arabjc.2017.12.024

CrossRef Full Text | Google Scholar

3. Gao W, Wu H, Siddiqui MK, Baig AQ. Study of biological networks using graph theory. Saudi J Biol Sci. (2018) 25:1212–9. doi: 10.1016/j.sjbs.2017.11.022

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Yang K, Yu Z, Luo Y, Yang Y, Zhao L, Zhou X. Spatial and temporal variations in the relationship between lake water surface temperatures and water quality-A case study of Dianchi Lake. Sci Tot Environ. (2018) 624:859–71. doi: 10.1016/j.scitotenv.2017.12.119

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Gao W, Guirao JLG, Abdel-Aty M, Xi W. An independent set degree condition for fractional critical deleted graphs. Discr Contin Dyn Syst. (2018) 12:877–86. doi: 10.3934/dcdss.2019058

CrossRef Full Text | Google Scholar

6. Kang SM, Zahid MA, Virk AR, Nazeer W, Gao W. Calculating the degree-based topological indices of dendrimers. Open Chem. (2018) 16:681–8. doi: 10.1515/chem-2018-0071

CrossRef Full Text | Google Scholar

7. Shao Z, Virk AR, Javed MS, Rehman MA, Farahani MR. Degree based graph invariants for the molecular graph of Bismuth Tri-Iodide. Eng Appl Sci Lett. (2019) 2:1–11. doi: 10.30538/psrp-easl2019.0011

CrossRef Full Text

8. Gao W, Wang W, Farahani MR. Topological indices study of molecular structure in anticancer drugs. J Chem. (2016) 2016. doi: 10.1155/2016/3216327

CrossRef Full Text | Google Scholar

9. Naeem M, Siddiqui MK, Guirao JLG, Gao W. New and modified eccentric indices of octagonal grid omn. Appl Math Nonlin Sci. (2018) 3:209–28. doi: 10.21042/AMNS.2018.1.00016

CrossRef Full Text | Google Scholar

10. Gao W, Farahani MR, Shi L. Forgotten topological index of some drug structures. Acta Med Mediter. (2016) 32:579–85. doi: 10.1155/2016/1053183

CrossRef Full Text | Google Scholar

11. Ghorbani M, Ghazi M. Computing some topological indices of Triangular Benzenoid. Digest J Nanomater Bios. (2010) 5:1107–11.

Google Scholar

12. Amić D, Bešlo D, Lucčić B, Nikolić S, Trinajstic N. The vertex-connectivity index revisited. J Chem Inform Comput Sci. (1998) 38:819–22. doi: 10.1021/ci980039b

CrossRef Full Text | Google Scholar

13. Gutman I. Some properties of the Wiener polynomial. Graph Theory Notes NY. (1993) 125:13–8.

14. Ajmal M, Nazeer W, Munir M, Kang SM, Jung CY. The M-polynomials and topological indices of generalized prism network. Int J Math Anal. (2017) New York, NY 11:293–303. doi: 10.12988/ijma.2017.7118

CrossRef Full Text | Google Scholar

15. Munir M, Nazeer W, Shahzadi Z, Kang S. Some invariants of circulant graphs. Symmetry. (2016) 8:134. doi: 10.3390/sym8110134

CrossRef Full Text | Google Scholar

16. Dobrynin AA, Entringer R, Gutman I. Wiener index of trees: theory and applications. Acta Appl Math. (2001) 66:211–49. doi: 10.1023/A:1010767517079

CrossRef Full Text | Google Scholar

17. Gutman I, Polansky OE. Mathematical Concepts in Organic Chemistry. New York, NY: Springer Science & Business Media (2012).

Google Scholar

18. Randić M. Characterization of molecular branching. J Am Chem Soc. (1975) 97:6609–15. doi: 10.1021/ja00856a001

CrossRef Full Text

19. Hu Y, Li X, Shi Y, Xu T, Gutman I. On molecular graphs with smallest and greatest zeroth-order general Randić index. MATCH Commun Math Comput Chem. (2005) 54:425–34.

Google Scholar

20. Caporossi G, Gutman I, Hansen P, Pavlovic L. Graphs with maximum connectivity index. Comput Biol Chem. (2003) 27:85–90. doi: 10.1016/S0097-8485(02)00016-5

CrossRef Full Text | Google Scholar

21. Li X, Gutman I. Mathematical Chemistry Monographs No. 1. Kragujevac: University of Kragujevac (2006).

22. Li X, Gutman I, Randić M. Mathematical Aspects of Randić-type Molecular Structure Descriptors. Kragujevac: University, Faculty of Science (2006).

Google Scholar

23. Gutman I, Furtula B, Elphick C. Three new/old vertex-degree-based topological indices. MATCH Commun Math Comput Chem. (2014) 72:617–32.

Google Scholar

24. Li X, Shi Y. A survey on the Randić index. MATCH Commun Math Comput Chem. (2008) 59:127–56.

Google Scholar

25. Gutman I, Das KC. The first Zagreb index 30 years after. MATCH Commun Math Comput Chem. (2004) 50:83–92.

Google Scholar

26. Gao W, Wang Y, Wang W, Shi L. The first multiplication atom-bond connectivity index of molecular structures in drugs. Saudi Pharm J. (2017) 25:548–55. doi: 10.1016/j.jsps.2017.04.021

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Vukičević D, Graovac A. Valence connectivity versus Randić, Zagreb and modified Zagreb index: a linear algorithm to check discriminative properties of indices in acyclic molecular graphs. Croat Chem Acta. (2004) 77:501–8.

Google Scholar

28. Miličević A, Nikolić S, Trinajstic N. On reformulated Zagreb indices. Mol Divers. (2004) 8:393–9. doi: 10.1023/B:MODI.0000047504.14261.2a

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Gupta CK, Lokesha V, Shwetha SB, Ranjini PS. On the symmetric division deg index of graph. Southeast Asian Bull Math. (2016) 40:59–80.

Google Scholar

30. Kier L. Molecular Connectivity in Chemistry and Drug Research. Cambridge, MA: Elsevier (1999).

Google Scholar

31. Réti T, Sharafdini R, Dregelyi-Kiss A, Haghbin H. Graph irregularity indices used as molecular descriptors in QSPR studies. MATCH Commun Math Comput Chem. (2018) 79:509–24.

Google Scholar

Keywords: irregularity indices, probabilistic neural network, graph, topological index, Zagreb index

Citation: Kang S, Chu Y-M, Virk AuR, Nazeer W and Jia J (2020) Computing Irregularity Indices for Probabilistic Neural Network. Front. Phys. 8:359. doi: 10.3389/fphy.2020.00359

Received: 25 March 2020; Accepted: 28 July 2020;
Published: 04 September 2020.

Edited by:

Shaohui Wang, Louisiana College, United States

Reviewed by:

Haidar Ali, Government College University, Faisalabad, Pakistan
Darko Dimitrov, Faculty of Information Studies Novo mesto, Slovenia

Copyright © 2020 Kang, Chu, Virk, Nazeer and Jia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Yu-Ming Chu, chuyuming@zjhu.edu.cn

ORIGINAL RESEARCH article

Computing Irregularity Indices for Probabilistic Neural Network

1. Introduction

2. Topological Indices

3. Computations of Probabilistic Neural Network

Conclusion

Data Availability Statement

Author Contributions

Funding

Conflict of Interest

References

This article is part of the Research Topic

People also looked at