Weak Transitions in Light Nuclei

1. Introduction

Nuclei are used for high-precision tests of the Standard Model and for studies of physics beyond the Standard Model. Without a thorough understanding of nuclei, we will not be able to meaningfully interpret the growing body of experimental data nor will be able to disentangle new physics signals from underlying nuclear effects. Current and next generation experimental programs are poised to address open questions within fundamental symmetries and neutrino physics to understand the origin of nonzero neutrino masses, the observed matter, and anti-matter unbalance, and the nature of dark matter. These experimental endeavors often rely on accurate calculations of electroweak structure and reactions in nuclei.

For example, nuclear physics plays a pivotal role in searches for neutrinoless double beta (0νββ) decays, which are the subject of an intense experimental research program [1–14]. In these decays, two neutrons inside the nucleus decay into two protons via the exchange of a neutrino, emitting two electrons. The rates of these decays depend not only on unknown fundamental neutrino parameters but also on nuclear properties. Extracting the neutrino parameters from experiments requires theoretical evaluation of nuclear matrix elements for neutrinoless double beta decay. This decay, if observed, would have tremendous theoretical implications and could give insight into our understanding of the observed matter-antimatter asymmetry in the universe. Calculations for nuclei of experimental interest (A≥ 48) are based on computational methods that inevitably adopt approximations to solve the nuclear many-body problem—e.g., model space truncations and/or omission of many-body effects. As a consequence, estimates of 0νββ matrix elements may vary by a factor of two when computed using different computational models (see [15] and references therein). It is then crucial to understand neutrino–nucleus interactions with great accuracy as well as the role and relevance of many-body dynamics, such as many-nucleon correlations and currents.

Furthermore, intense experimental research activity is currently focused on long-base neutrino oscillation experiments (such as MiniBooNE, T2K, MicroBooNE, Minerνa, and the upcoming DUNE; [16–20]) aimed at profiling neutrinos, whose masses, among other properties, are still not known. Neutrinos signal their presence by interacting with nuclei which are the active material in the detectors. Additionally, in this case, meaningful interpretations of the data require an accurate understanding of the way neutrinos interact with nuclei.

The study of light nuclei, for which the nuclear many-body problem can be solved exactly or within controlled approximations by fully retaining many-nucleon correlations and electroweak currents, offers the possibility of quantifying the contribution from many-body effects and consequently of assessing the robustness of a given approximation. In this work, we report on a recent study of electroweak matrix elements in A ≤ 10 nuclei entering single beta decays and electron captures (or inverse beta decays). Rates of single beta decay—a process in which a proton (neutron) inside the nucleus decays into a neutron (proton) with the emission of a positron (electron) and an electron (anti)neutrino—are, in most cases, experimentally well-known. This provides us with stringent means to validate our theoretical description of nuclear systems and to assess the role of many-body dynamics. In particular, we work within the nuclear microscopic approach in which nuclei are described in terms of non-relativistic nucleons interacting with each other via two- and three-body nuclear potentials and with external probes, such as neutrinos, electrons, and photons, via one- and two-body current operators. We use Quantum Monte Carlo (QMC) computational methods [21–23] to solve the many-body nuclear problem with a nuclear Hamiltonian consisting of high-quality two- and three-body potentials obtained from a chiral effective field theory (χEFT) that retains nucleons, pions, and Δ-isobars as explicit degrees of freedom [24–28]. We base the calculation of the transition matrix elements on one- and two-body axial currents [29] and provide results for one- and two-body weak transition densities. The latter will turn out to be particularly important to understand the role of short-range many-body dynamics.

Ab initio studies in light nuclei allow us to carefully test many-body correlations and electroweak currents and serve as benchmark to approximated many-body methods currently employed to access heavier nuclear systems [30, 31]. A study along these lines has been carried out recently in [32].

This study represents a first step into the validation of our theoretical model. In fact, beta decay processes occur at zero momentum transfer while the energy transfer involved is of the order of a few MeVs. Neutrinos exchanged in 0νββ processes carry a value of momentum transfer of the order of few hundreds of MeV/c [15], while the energy transfer in neutrino oscillation experiments covers a large phase space reaching the GeV scale. It is then essential to validate the theoretical model in a wide range of energy and momentum transfer to have a complete and unified description of neutrino–nucleus interactions. For example, calculations of total and partial muon-capture rates and comparisons with the known experimental data will probe our model at intermediate values of momentum transfer and will be the subject of our future work. At higher energies, neutrino–nucleus cross sections calculations [33, 34] are the main input to interpret the data from long and short baseline neutrino-oscillation experiments, which use nuclei as active material in the detectors. Specifically, current challenges concern the implementation of microscopic models of nuclear dynamics—that fully capture correlation effects—in neutrino event generators [35] used to simulate the neutrino interaction physics.

The paper is structured as follows: In section 2, we briefly summarize the theoretical and computational methods adopted in the present work and refer the interested reader to [36] for further details. In sections 3 and 4, we present our results and conclusions.

2. Theory

2.1. Quantum Monte Carlo Methods

Quantum Monte Carlo methods have been most recently described in several review articles [21–23]. Here, we briefly sketch the employed calculational scheme and refer the reader to [36] for details. We use both Variational Monte Carlo (VMC) and Green's Function Monte Carlo (GFMC) methods to calculate transitions matrix elements. We base our study on the following many-body Hamiltonian:

$\begin{array}{ll}H={\displaystyle \sum _i}{K}_i+{\displaystyle \sum _{i<j}}{v}_{ij}+{\displaystyle \sum _{i<j<k}}{V}_{ijk}& (1)\end{array}$

where K_i is the non-relativistic kinetic energy operator and v_ij and V_ijk are the NV2 and NV3 Norfolk local chiral interactions developed in [24–28]. Together, we denote these interactions as NV2+3.

For a nuclear state with given angular momentum and parity J^π, isospin T, and isospin projection T_Z, the VMC method takes as a starting point a trial wave function ${\Psi }_V(J^{\pi },T,T_z)$, constructed as follows

$\begin{array}{ll}|{\Psi }_V\rangle =S{\displaystyle \prod _{i<j}^A\left[1+U_{ij}+{\displaystyle \sum _{k\ne i,j}^A{\tilde{U}}_{ijk}^{TNI}}\right]}|{\Psi }_J\rangle .& (2)\end{array}$

The Jastrow wave function Ψ_J is fully antisymmetric and has the $(J^{\pi };T,T_z)$ quantum numbers of the state of interest, and U_ij and ${Ũ}_{ijk}^{TNI}$ are two- and three-body correlation operators that reflect the influence of the two- and three-body forces, respectively [37–40]. The state |Ψ_V〉 has embedded variational parameters that one adjusts to minimize the expectation value

$\begin{array}{ll}{E}_V=\frac{\langle {\Psi }_V|H|{\Psi }_V\rangle }{\langle {\Psi }_V|{\Psi }_V\rangle }\ge E_0& (3)\end{array}$

evaluated with Metropolis Monte Carlo integration [41].

The VMC wave function |Ψ_V〉 is further improved using the GFMC method. The variational state is propagated in imaginary time with the operator exp[−(H−E₀)τ]. This is done in small steps in imaginary time, Δτ, and produces the following:

$\begin{array}{ll}\Psi (\tau )=e^{-(H-E_0)\tau }{\Psi }_V={\left[e^{-(H-E_0)\Delta \tau }\right]}^n{\Psi }_V& (4)\end{array}$

One can see that, for τ → ∞, the variational state becomes the desired state Ψ₀. The evaluation of the off-diagonal expectation value of a given operator O is calculated using the following approximation

$\begin{array}{l}\frac{\langle {\Psi }^f(\tau )|O|{\Psi }^i(\tau )\rangle }{\sqrt{\langle {\Psi }^f(\tau )|{\Psi }^f(\tau )\rangle }\sqrt{\langle {\Psi }^i(\tau )|{\Psi }^i(\tau )\rangle }}\\ \approx {\langle O(\tau )\rangle }_{M_i}+{\langle O(\tau )\rangle }_{M_f}-{\langle O\rangle }_V,& (5)\end{array}$

where 〈O〉_V is the variational expectation value and 〈O(τ)〉_M is the mixed estimate defined as the following:

$\begin{array}{llll}{\langle O(\tau )\rangle }_{M_f}& =& \frac{\langle {\Psi }^f(\tau )|O|{\Psi }_V^i\rangle }{\langle {\Psi }^f(\tau )|{\Psi }_V^f\rangle }\sqrt{\frac{\langle {\Psi }_V^f|{\Psi }_V^f\rangle }{\langle {\Psi }_V^i|{\Psi }_V^i\rangle }},& (6)\end{array}$

and 〈O(τ)〉_Mi is defined similarly (see [42] for more details).

2.2. Norfolk Interaction Models

The calculations of weak transitions presented in this work employ the high-quality local NV2+3 interactions developed in [24–27]. The two-nucleon potentials, NV2s, include a strong interaction component derived from a χEFT that involves nucleons, pions, and Δ-isobars as explicit degrees of freedom and an electromagnetic interaction component, including up to terms quadratic in the fine structure constant α. The component induced by the strong interaction is separated into long- and short-range parts, labeled $v_{ij}^L$ and $v_{ij}^S$, respectively. The $v_{ij}^L$ part is mediated via one-pion-exchange (OPE) and two-pion-exchange (TPE) terms up to next-to-next-to-leading order (N2LO) in the chiral expansion. Its strength is determined by the nucleon axial coupling g_A and the nucleon-to-Δ axial coupling h_A, the pion decay amplitude F_π, and LECs c₁, c₂, c₃, c₄, and b₃ + b₈ constrained by fits to πN scattering-data [43]. Values of these LECs are provided in Table 1 of [36].

The pion-range operators are strongly singular at short-range in configuration space and are regularized by a radial function that is characterized by a cutoff R_L as reported in [24–27]. The $v_{ij}^S$ part, however, is described by contact terms up to next-to-next-to-next-to-leading order (N3LO), characterized by 26 unknown LECs. These interactions have been recently constrained to a large set of NN-scattering data, as assembled by the Granada group [44–46], including the deuteron ground-state energy and two-neutron scattering length. For the contact terms, we use a Gaussian representation of the three-dimensional delta function, with R_S being the short-range regulator.

In this work, we focus on one class of NV2 interaction, namely the NV2-Ia. This class fits about 2,700 NN scattering data in the range of 0–125 MeV of laboratory energies with a χ²/datum ≲ 1.1 [24, 25]. The NV2-Ia uses the combination of short- and long-range regulators (R_S, R_L) = (0.8, 1.2) fm.

The NV2 models alone are not enough to provide sufficient attraction in GFMC calculations of the binding energies of light nuclei [25]. For this reason, a consistent three-body interaction up to N2LO in the chiral expansion has been developed [47] to go with the two-body potential. This interaction consists of a long-range part mediated by two-pion exchange and a short-range part parameterized in terms of two contact interactions [48, 49]. The two 3N LECs, namely c_D and c_E, have been obtained either by fitting exclusively strong-interaction observables [47, 50–52] or by relying on a combination of strong- and weak-interaction ones [27, 53, 54]. This last approach is made possible by a relation established in χEFT [55] between c_D and the LECs entering the contact axial current at N3LO [53, 54], [Schiavilla, private communication].

In [47], the values for c_D and c_E were obtained by reproducing both the experimental trinucleon ground-state energies and nd doublet scattering length for each of the NV2 models considered. On the other hand, in [27], these LECs were constrained by fitting, in addition to the trinucleon energies, the empirical value of the Gamow-Teller matrix element in tritium β-decay. The resulting Hamiltonian is denoted as NV2+3-Ia (or Ia for short) in the first case, and as NV2+3-Ia* (or Ia* for short) in the second.

As shown in Table 1, these two different procedures for fixing c_D and c_E produced rather different values for these LECs, particularly for c_E which was found to be relatively large and negative in the unstarred models but quite small, and not consistently negative, in the starred models. This in turn impacts predictions for the spectra of light nuclei [36] and the equation of state of neutron matter, since a negative c_E leads to repulsion in light nuclei but attraction in neutron matter [56].

TABLE 1

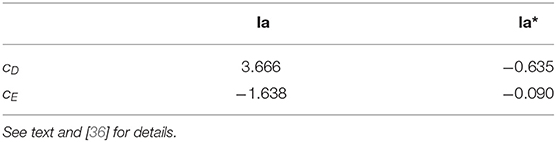
Table 1. c_D and c_E values of the contact terms in the three-nucleon interactions obtained from fits to (i) the nd scattering length and the trinucleon binding energies [27, 47]; and (ii) the central value of the ³H GT matrix element and the trinucleon binding energies (starred values).

The starred and unstarred NV2+3 Norfolk interactions have been implemented in both the VMC and GFMC codes and used to perform calculations of the energy levels [28, 47], charge radii, and longitudinal elastic form factors [23] of A = 4 − 12 nuclei that are found to be in very satisfactory agreement with the experimental data. Furthermore, two of the NV2+3^* models have been also used to perform VMC calculations of the Fermi, Gamow-Teller, and tensor densities for ⁶He → ⁶Be and ¹²Be → ¹²C transitions [57], relevant for studies of 0νββ.

The NV2 models have recently been used in benchmark calculations of the energy per particle of pure neutron matter as a function of the baryon density using three independent many-body methods: Brueckner-Bethe-Goldstone (BBG), Fermi hypernetted chain/single-operator chain (FHNC/SOC), and AFDMC [58]. The inclusion of three-body forces is essential for a realistic description of neutron matter. These types of calculation are particularly relevant for the quantitative assessment of the systematic error of the different many-body approaches and how they depend upon the nuclear interaction of choice.

Preliminary AFDMC calculations of the equation of state of pure neutron matter carried out with the unstarred NV2+3 Norfolk interactions [Piarulli et al., private communication] are not compatible with the existence of two solar masses neutron stars, in conflict with recent observations [59, 60]. However, the smaller values of c_E in the 3N force of the starred NV2+3 potentials might mitigate, if not resolve this problem, while predicting light-nuclei spectra <4% away from the experimental data [36]. Studies along these lines are under way.

2.3. Axial Currents in χEFT

Many-body currents are crucial for providing a quantitatively successful description of many nuclear electroweak observables [61], such as nuclear electromagnetic form factors [62–65], low-energy electroweak transitions [66–73], and electroweak scattering [33]. They have also been used in studies of double beta decay matrix elements [32, 57, 74, 75]. The study of the electroweak matrix elements carried out in this work employs one- and two-body axial currents derived within the same χEFT used for the NV2+3 interactions [27]. We use two-body axial currents at tree-level constructed in [26, 27, 29]. Here, we briefly describe the contributions shown in Figure 1 and refer the reader to [27, 36] for the explicit expressions of the current operators and for the tables reporting the values of the parameters adopted in the present work. We note that χEFT electroweak operators have been also derived in [76–79].

FIGURE 1

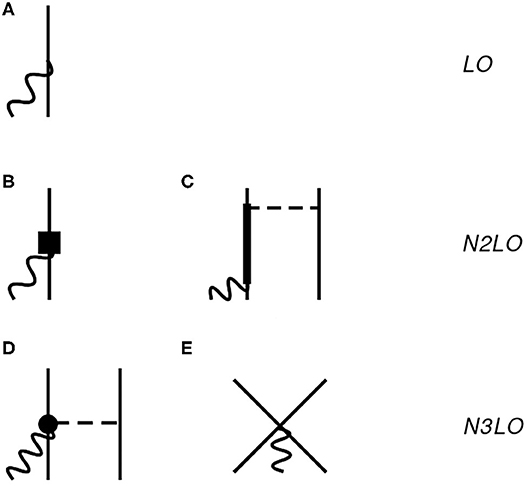
Figure 1. Diagrams illustrating the contributions to the axial current up to N3LO (Q⁰) used in this work. Nucleons, Δ-isobars, pions, and external fields are denoted by solid, thick-solid, dashed, and wavy lines, respectively. The diagrams in (A,B) represent the leading order one-body term and its relativistic correction (denoted by the square vertex), respectively. The remaining diagrams, (C–E) provide two-body corrections to the one-body terms. The dot in (D) denotes a vertex induced by subleading terms in the π-nucleon chiral Lagrangian [26]. Only a single time ordering is shown.

In Figure 1A, the LO term, which scales as Q⁻³ in the power counting (Q denotes generically a low-momentum scale), is given by the standard Gamow-Teller one-body operator

$\begin{array}{ll}{\text{j}}_{5,a}^{\text{LO}}(\text{q})=-\frac{g_A}{2}{\tau }_{i,a}{\sigma }_i{\text{e}}^{i\text{q}·{\text{r}}_i},& (7)\end{array}$

where g_A is the nucleon axial coupling constant (g_A = 1.2723 [80]) σ_i and τ_i are the spin and isospin Pauli matrices of nucleon i, q is the external field momentum, r_i is the spacial coordinate of nucleon i, and a = x, y, z.

We account for an additional one body-operator shown in Figure 1B. This contribution enters at N2LO (or Q⁻¹) in the chiral expansion and represents a relativistic correction to the single-nucleon operator at LO. At N2LO there is the appearance of the leading two-body contribution illustrated in Figure 1C by the tree-level diagram involving the excitation of a Δ-isobar. In the tables and figures below, we label these two contributions as N2LO-RC and N2LO-Δ, respectively. Following the same notation introduced in [27], we write the cumulative N2LO contribution as

$\begin{array}{ll}{\text{j}}_{5,a}^{\text{N}2\text{LO}}(\text{q})={\text{j}}_{5,a}^{\text{N}2\text{LO}}(\text{q};\text{RC})+{\text{j}}_{5,a}^{\text{N}2\text{LO}}(\text{q};\Delta ).& (8)\end{array}$

Finally, the N3LO contributions (scaling as Q⁰) involve a term of one-pion range illustrated in Figure 1D and a contact term shown in Figure 1E, which together give the following N3LO correction

$\begin{array}{ll}{\text{j}}_{5,a}^{\text{N}3\text{LO}}(\text{q})={\text{j}}_{5,a}^{\text{N}3\text{LO}}(\text{q};\text{OPE})+{\text{j}}_{5,a}^{\text{N}3\text{LO}}(\text{q};\text{CT}).& (9)\end{array}$

These terms are denoted with N3LO-OPE and N3LO-CT, respectively, and their expression are reported in Equations (2.7)–(2.10) of [27]. As discussed at length in [36], the N3LO-CT contact current involves the LEC c_D, which also enters the three-nucleon force. The values for the LEC c_D used in this work are reported in Table 1 and are changed consistently in the axial current depending on the nuclear interaction used to construct the wave functions. In this work, we especially focus on the nuclear interactions NV2+3-Ia and NV2+3-Ia*.

3. Results

3.1. VMC Reduced Matrix Elements

In this section, we present the results of calculations of GT reduced matrix elements (RMEs), defined as the following:

$\begin{array}{ll}\text{RME}=\frac{\sqrt{2J_f+1}}{g_A}\frac{\langle J_{f}M|j_{5,\pm }^z|J_{i}M\rangle }{\langle J_{i}M,10|J_{f}M\rangle }& (10)\end{array}$

where $j_{5,\pm }^z$ is the z-component in the limit q → 0 of the charge-raising/lowering current j_5,±= j_5,x ± ij_5,y, and 〈J_iM, 10|J_fM〉 is a Clebsch-Gordan coefficient. Table 2 summarizes the results of the VMC calculation of GT RMEs. These calculations were evaluated with variational wave functions generated using the NV2+3-Ia and NV2+3-Ia* nuclear Hamiltonians. The table breaks the calculations down order-by-order: the LO contribution from the one-body axial current in Figure 1A, the N2LO contributions coming from a one-body relativistic correction to the LO term (Figure 1B) and a two-body contribution involving the excitation of a nucleon into a Δ by pion exchange (Figure 1C), and the contributions at N3LO from the one pion exchange (Figure 1D) and the contact term (Figure 1E). The sum of the two body contributions (Total-LO) and the total RME are given in addition to the breakdown of each contribution. The dominant spatial symmetries [86] of the wave functions in each calculation are listed below the transition in Table 2. Experimental values from [81–85] are listed in the last column of Table 2.

TABLE 2

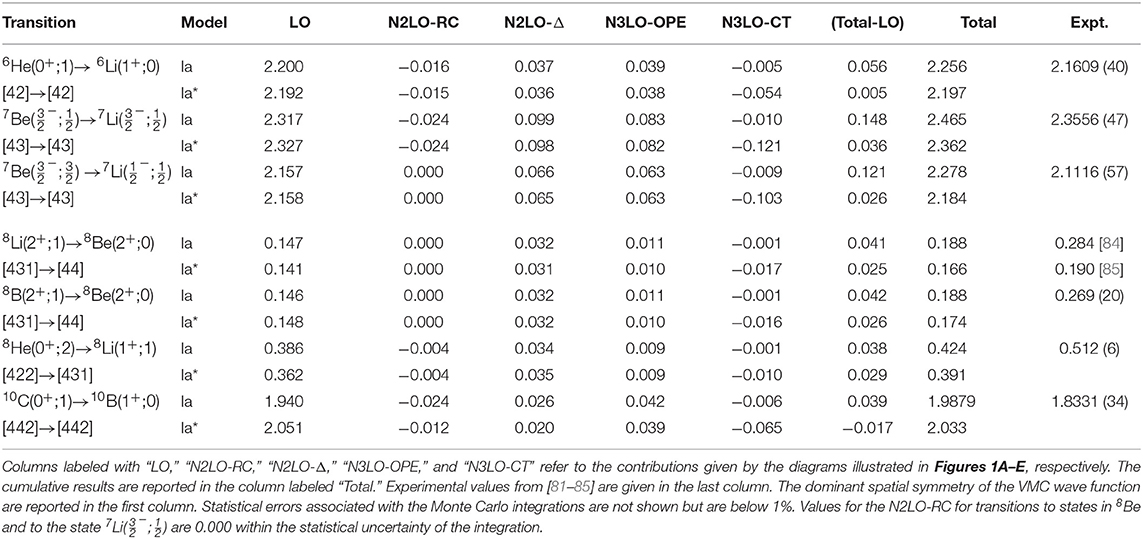
Table 2. Gamow-Teller RMEs in A = 6, 7, 8, and 10 nuclei obtained with chiral axial currents [27] and VMC wave functions corresponding to the NV2+3-Ia/Ia* Hamiltonian models [24, 25, 27, 47].

From these results, we see that in the A = 3, 6, 7, and 10 cases, the LO contribution is ≈ 97% of the total RME in VMC calculations. The other ≃ 3% are made up of beyond leading order contributions. While beyond leading order contributions only make up a small percentage of the total RME for the A = 3, 6, 7, and 10 cases, they are a much larger contribution for A = 8, making up ~ 20–30% of the total RME. This is attributed to a difference in the dominant spatial symmetries between the initial and final states of the A = 8 VMC wave functions, resulting in a smaller overlap between the initial and final wave functions and a consequent suppression of the GT RME at leading order. This indicates that the wave functions are lacking correlations and that an improvement of the theoretical prediction will require further developments of the wave functions, such as the inclusion of more correlations and development of better constrained small components. As similar behavior is also found in the calculations of [87]. The total two-body contribution is typically an enhancement of the total RME, except in the A = 10 case for model NV2+3-Ia*, where the matrix element is reduced. The short-range behavior of the two-body corrections is studied in detail in section 3.2 where we analyze the two-body transition densities.

For ⁸Li → ⁸ Be beta decay, there are two different log(ft) values in the literature that provide very different values for the GT matrix element. In Table 2, we present the RMEs for this decay using the ft values from [84, 85], obtained with the following formula [83]:

$\begin{array}{ll}\text{RME}(\text{EXPT})=\frac{1}{g_A}\sqrt{2J_i+1}\sqrt{\frac{6139\pm 7}{ft}},& (11)\end{array}$

where J_i is the angular momentum of the initial state. Note that the Fermi transition strength is negligible in deriving Equation (11). This formula uses the value g_A = 1.2723. Additionally, we note that in [82, 88], a value of 6,147 is used in place of 6,139. Even with this uncertainty in the experimental value of the RME, our predictions for the A = 8 systems significantly underestimate the data.

3.2. One- and Two-Body Transition Densities

To investigate the behavior of individual contributions to the RMEs, one- and two-body transition densities are calculated. One can define the one-body transition density as a function of the distance of nucleon i from the center of mass:

$\begin{array}{ll}\text{RME}(1\text{b})={\displaystyle \int }\text{d}{r}_{i}4\pi r_i^2{\rho }^{1\text{b}}(r_i).& (12)\end{array}$

In Figures 2, 3, the one-body transition density is found to be consistent between the two cases. Indeed, this is what we expect based on Table 2. The LO contribution is consistent between the two interactions and is not sensitive to how the LECs of the three-body interaction are fit. Looking at the sub-leading order contributions, we find that, with the exception of the N2LO-RC term in the A = 10 transitions, the only term that is model dependent is the N3LO contact term. To better understand this difference, in a fashion similar to what is done in Equation (12) for the one-body case, a two-body transition density as a function of inter-particle spacing r_ij can be defined:

$\begin{array}{ll}\text{RME}(2\text{b})={\displaystyle \int }\text{d}{r}_{ij}4\pi r_{ij}^2{\rho }^{2\text{b}}(r_{ij})& (13)\end{array}$

Two-body transition densities are plotted in Figure 4. For the same transition, the N2LO-Δ and the N3LO-OPE contributions in models NV2+3-Ia and NV2+3-Ia* are nearly identical. This is to be expected, as the two models use the same cutoffs to regularize the interactions and have the two-body interaction fit to the same data. Where the models differ is in the N3LO-CT contribution. Model NV2+3 Ia* has a larger contribution from this term compared to its counterpart. This model-dependence of the contact contribution to the RME makes sense in light of the difference between models NV2+3-Ia and NV2+3-Ia*. The LECs c_D and c_E entering the three-body contact current were fit with two different procedures. In model NV2+3 Ia, the contribution was constrained using only strong interaction data while in model NV2+3 Ia*, both strong and electroweak data were used to constrain it. This results in the two models having different values for these LECs and thus different strengths in the contact term. While there is evidently a model-dependence, it is worth noting that this is a small contribution to the overall RME for the transitions.

FIGURE 2

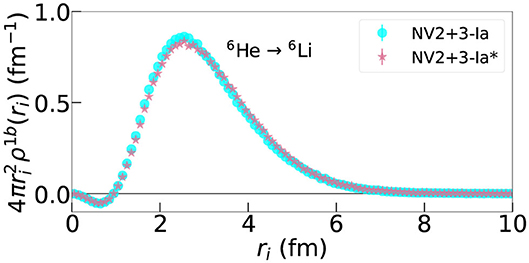
Figure 2. One-body density as defined in Equation (12) for the ⁶He → ⁶Li GT RME obtained using the NV2+3-Ia/Ia* models.

FIGURE 3

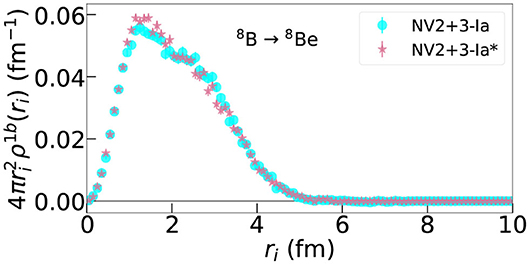
Figure 3. One-body density as defined in Equation (12) for the ⁸B → ⁸Be GT RME obtained using the NV2+3-Ia/Ia* models.

FIGURE 4

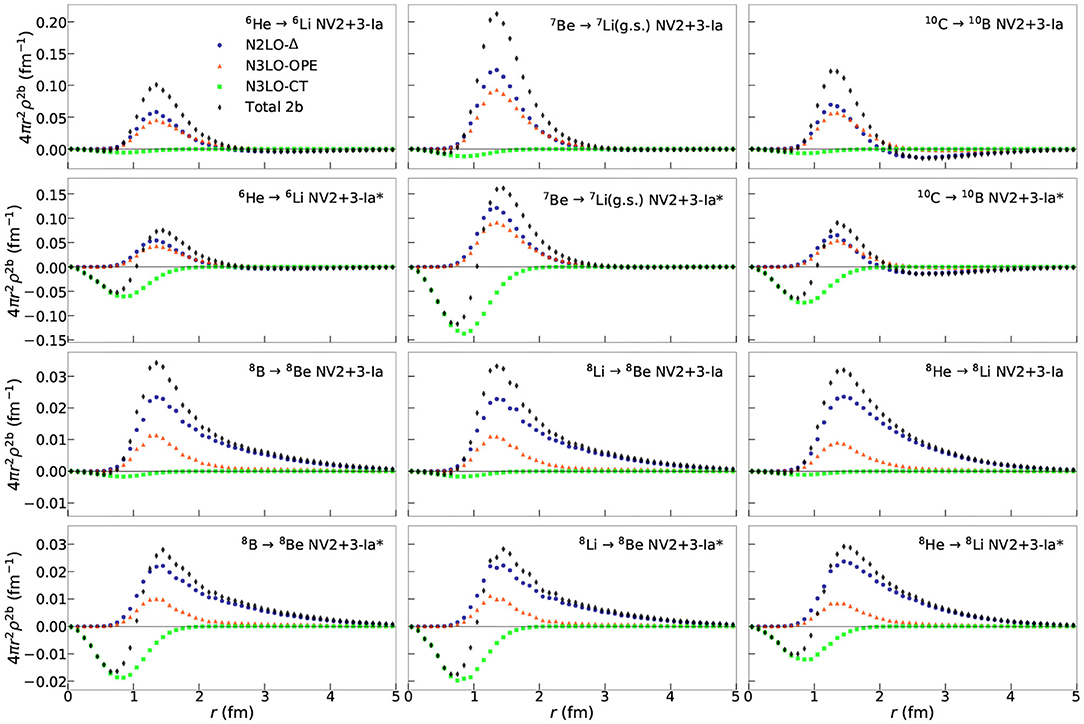
Figure 4. Two-body density as defined in Equation (13) for GT RMEs obtained using the NV2+3-Ia/Ia* models for select nuclei.

Although there is a model dependence in the N3LO-CT term, it is interesting to ask if the behavior of the current is still similar between the two models. For this purpose, in Figure 5, transition densities for the N3LO-CT current selected nuclei are scaled to peak at 1.0 to see if there is a universal behavior in the interactions. The scaling factors to generate Figure 5 are given in Table 3. While there was a difference seen in the size of the contribution of the N3LO-CT term when comparing the un-scaled transition densities, it is seen here that the scaled curve overlaps for not only both models within the same transition but also for all transitions under study. The change in the LECs c_D and c_E results in a re-scaling of the N3LO-CT term. For the A ≤ 7 transitions, the enhancement of the N3LO-CT term relative in NV2+3-Ia* relative to the value given by its counterpart NV2+3-Ia is a factor of ≈ 6.4 for the same transition. For the A ≥ 8 cases, this enhancement is on average a factor of ≈ 2.2.

FIGURE 5

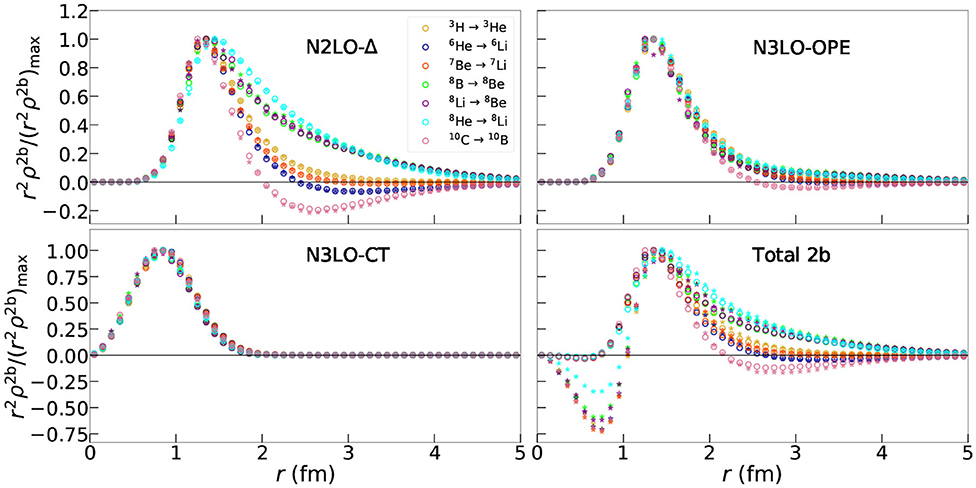
Figure 5. Scaled two-body density as defined in Equation (13) for GT RMEs obtained using the NV2+3-Ia/Ia* models for select nuclei. The distributions are scaled to have a peak value of 1.0 using the factors in Table 3.

TABLE 3

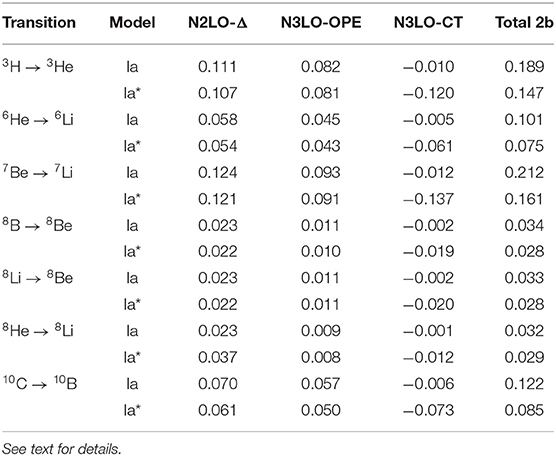
Table 3. The scaling factors ${(r_{ij}^2{\rho }^{\mathrm{\text{2b}}})}_{\mathrm{\text{max}}}$ used to normalize the N2LO-Δ, N3LO-OPE, N3LO-CT, and total two-body transition densities in Figure 5.

Another important feature of the two-body transition densities is the difference in the long-range behavior of the N2LO-Δ and N3LO-OPE terms. In [27], Equations (2.9) and (2.10) give the operator structure of these two currents. In the limit of vanishing momentum transfer, these currents have the same operator structure up to a momentum dependent term that has been verified numerically to provide small contributions. The structures of these operators result in cancelations that are sensitive to the LECs entering into each of these currents, impacting the behavior of the two-body transition density for r_ij ≳ 2 fm. In particular, the N2LO-Δ density is sensitive to the transition under study. In the case of the A = 10 transition, the N2LO-Δ density becomes negative near ≈ 2 fm. When integrating over the whole two-body contribution for the NV2+3-Ia* model, this results in a non-trivial cancelation leading to the quenching of the RME from the inclusion of sub-leading contributions.

3.3. GFMC Extrapolation

In addition to VMC calculations of the RME, we also perform a GFMC extrapolation of the RME. The GFMC wave functions generated with the NV2+3-Ia model in this work produce energies that are in statistical agreement with the results of [47]. For all cases presented below, with the exception of two transitions, GFMC propagation are performed between imaginary time steps τ = 0.2 and 0.82 MeV⁻¹. Typically, an imaginary time evolution of the VMC estimate produces an RME that is reduced by a few percent and stabilizes at τ ≈ 0.2 MeV⁻¹. In the calculations of transitions involving the (J^π; T) = (2⁺; 0) state of ⁸Be and the ground state of ⁸B, the extrapolation must be treated differently. In this two states, as τ increases, the binding energy, magnitude of the quadrupole moment, and point-proton radius all increase monotonically. This is interpreted as the dissolution of ⁸Be into two alpha particles and ⁸B into p+⁷Be. Datar et al. [71], Pastore et al. [72], and Wiringa et al. [89] have previously addressed this issue for ⁸Be. Similar to those references, we perform the extrapolation by noting that the energy drops rapidly in τ, stabilizing at τ ≈ 0.1 MeV⁻¹. We assume that, at this point, spurious contamination in the wave function has been removed by the GFMC procedure and average in a small interval around τ = 0.1 MeV⁻¹, taken to be τ from 0.06 to 0.14 MeV⁻¹. This introduces and additional ≈ 5% systematic uncertainty to these calculations in addition to the statistical uncertainties of QMC.

In all transitions, except for the NV2+3-Ia* model for A = 10, the GFMC extrapolation reduces the VMC RME by a ≲ 4%. Table 4 summarizes results of the LO, total sub-leading order (Total-LO), and total RMEs for the transitions under study. In the A < 10 transitions, the LO contribution is consistent between the two different models under study. In the A = 10 case, this model dependence can be understood by the existence of nearby J^π = 1⁺ excited states in ¹⁰B. The lower state is predominantly ³S₁[442] state and the upper one a ³D₁[442] state. These two states are split by only 1 MeV. The transition from the predominantly ¹S₀[442] ¹⁰C(0⁺) state is large in the S → S components but about five times smaller in the S → D components. This causes the GT matrix element to be particularly sensitive to the exact mixing of the ³S₁ and ³D₁ components in the two ¹⁰B(1⁺) states produced by a given Hamiltonian, as was observed for the calculation of GT matrix elements using the AV18+IL7 interaction [73]. In either case, the NV2+3 interactions overpredict the data.

TABLE 4

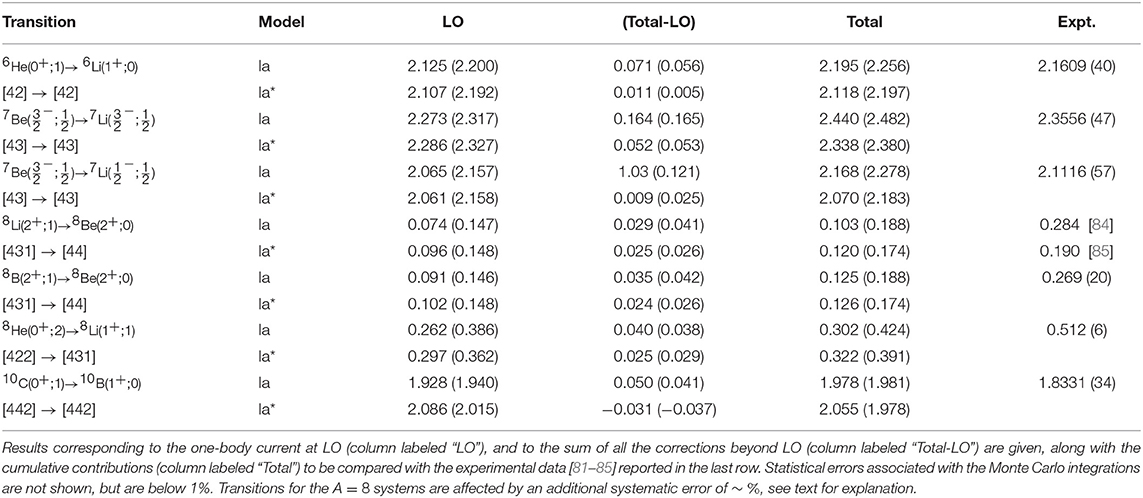
Table 4. Gamow-Teller RMEs in A = 6, 7, 8, and 10 nuclei obtained with chiral axial currents [27] and GFMC (VMC) wave functions corresponding to the NV2+3-Ia/Ia* Hamiltonian models [24, 25, 27, 47].

4. Conclusions

With this work we set the foundations for the development of an accurate and unified understanding of neutrino–nucleus interactions. We are in the process of exploring and validating the QMC approach's description of electroweak processes in a wide range of energy and momentum transfer; in this work, we therefore focused on calculating matrix elements entering beta decay and inverse beta decay in light nuclei. These processes occur at zero momentum transfer and involve energy transferred of the order of a few MeVs.

In our approach, we fully retained two- and three-nucleon correlations induced by the Norfolk potentials, and we described the interaction with the external electroweak probes by means of the associated one- and two-body axial currents at tree-level. This study was focused on the NV2+3-Ia and NV2+3-Ia* models, and was aimed at carefully studying the contributions from two-body axial currents in the two different implementations of the three-nucleon forces. In the unstarred model the LECs c_D and c_E entering the three-nucleon force were fitted to the trinucleon binding energies and the nd scattering length, while the starred model is constrained by the experimental GT value of the triton decay and the trinucleon binding energies. The axial two-body contact current at N3LO, which involves c_D, was taken consistently with the three-nucleon force adopted to generate the nuclear wave functions.

In analogy with previous QMC studies of beta decay in light nuclei [36, 73], we find that corrections from two-body axial currents are at the ~3% level in A = 6, 7 and 10. The A = 8 systems are instead severely underpredicted by the theory, even after the inclusion of large (~ 30−40%) contributions from two-body axial currents. Studies on the electromagnetic transitions in A = 8 nuclei were also found to be problematic [70, 72], which indicates the need of further developments of the A = 8 wave functions.

In this work, we especially focused on the contributions from two-body currents, which, despite the fact that they are in these cases small, can provide us with valuable insights on the composition of these corrections. To this end, we reported studies on two-body transition densities which allow us to understand the relevance of the two-body currents as a function of the interparticle distance. As expected, we find that, for a given interaction model, the transition densities exhibit a universal short-range behavior across the considered nuclei, while they differ in the long-range tails. The starred and unstarred results differ in the contact contribution at N3LO. This is rather visible in the panels of Figure 4 where the starred model leads to a total transition density (black symbols) which presents one or more nodes. The presence of nodes implies non-trivial cancelations when using the starred models.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This research was supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, under the U.S. Department of Energy funds through the FRIB Theory Alliance award DE-SC0013617 (MP and SP). LA and SP have been supported by the U.S. Department of Energy under contract DE-SC0021027.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank our collaborators J. Carlson, S. Gandolfi, R. Schiavilla, and R. B. Wiringa for their contributions to the studies presented in this work. The many-body calculations were performed on the parallel computers of the Laboratory Computing Resource Center, Argonne National Laboratory, the computers of the Argonne Leadership Computing Facility (ALCF) via the ALCC-2019 grant Low energy neutrino-nucleus interactions.

References

1. Gando A, Gando Y, Hachiya T, Hayashi A, Hayashida S, Ikeda H, et al. Publisher's note: search for majorana neutrinos near the inverted mass hierarchy region with KamLAND-Zen [Phys. Rev. Lett. 117, 082503 (2016)]. Phys Rev Lett. (2016) 117:109903. doi: 10.1103/PhysRevLett.117.082503

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Albert JB, Auty DJ, Barbeau P, Beauchamp E. Search for Majorana neutrinos with the first two years of EXO-200 data. Nature. (2014) 510:229–34. doi: 10.1038/nature13432

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Adams C, Alvarez V, Arazi L, Arnquist IJ, Azevedo CDR, Bailey K, et al. Sensitivity of a tonne-scale NEXT detector for neutrinoless double beta decay searches. arXiv [Preprint] arXiv:2005.06467. (2020)

Google Scholar

4. Zsigmond AJ. LEGEND: The future of neutrinoless double-beta decay search with germanium detectors. J Phys Conf Ser. (2020) 1468:012111. doi: 10.1088/1742-6596/1468/1/012143

CrossRef Full Text

5. Cattadori CM. Gerda: results and perspectives. Nucl Part Phys Proc. (2015) 265–6:38–41. doi: 10.1016/j.nuclphysbps.2015.06.010

CrossRef Full Text | Google Scholar

6. Alfonso K, Artusa DR, Avignone FT, Azzolini O, Balata M, Banks TI, et al. Search for neutrinoless double-beta decay of ¹30Te with CUORE-0. Phys Rev Lett. (2015) 115:102502. doi: 10.1103/PhysRevLett.115.102502

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Caden E. Status of the SNO+ experiment. J Phys Conf Ser. (2020) 1342:012022. doi: 10.1088/1742-6596/1342/1/012022

CrossRef Full Text | Google Scholar

8. Blot S. Investigating ββ decay with the NEMO-3 and SuperNEMO experiments. J Phys Conf Ser. (2016) 718:062006. doi: 10.1088/1742-6596/718/6/062006

CrossRef Full Text | Google Scholar

9. Giuliani A. A neutrinoless double-beta-decay search based on ZnMoO₄ and Li₂MoO₄ scintillating bolometers. J Phys Conf Ser. (2017) 888:012239. doi: 10.1088/1742-6596/888/1/012239

CrossRef Full Text | Google Scholar

10. Tetsuno K, Ajimura S, Akutagawa K, Batpurev T, Chan WM, Fushimi K, et al. Status of 48Ca double beta decay search and its future prospect in CANDLES. J Phys Conf Ser. (2020) 1468:012132. doi: 10.1088/1742-6596/1468/1/012132

CrossRef Full Text | Google Scholar

11. Park H. The AMoRE: Search for neutrinoless double beta decay in 100Mo. Nucl Part Phys Proc. (2016) 273–5:2630–2. doi: 10.1016/j.nuclphysbps.2015.10.012

CrossRef Full Text | Google Scholar

12. Ebert J, Fritts M, Gehre D, Gößling C, Göpfert T, Hagner C, et al. The COBRA demonstrator at the LNGS underground laboratory. Nucl Instrum Meth A. (2016) 807:114–20. doi: 10.1016/j.nima.2015.10.079

CrossRef Full Text | Google Scholar

13. Dokania N, Singh V, Ghosh C, Mathimalar S, Garai A, Pal S, et al. Radiation background studies for 0νββ decay in ¹24Sn. In: Topical Research Meeting on Prospects in Neutrino Physics. London, UK (2015).

Google Scholar

14. Fukuda Y. ZICOS - New project for neutrinoless double beta decay experiment using zirconium complex in liquid scintillator. J Phys. (2016) 718:062019. doi: 10.1088/2F1742-6596/2F718/2F6/2F062019

CrossRef Full Text | Google Scholar

15. Engel J, Menndez J. Status and future of nuclear matrix elements for neutrinoless double-beta decay: a review. Rept Prog Phys. (2017) 80:046301. doi: 10.1088/1361-6633/aa5bc5

PubMed Abstract | CrossRef Full Text | Google Scholar

16. [Dataset] The MicroBooNE Experiment. Available online at: http://www-microboone.fnal.gov

Google Scholar

17. [Dataset] The T2K Experiment. Available online at: http://t2k-experiment.org

Google Scholar

18. [Dataset] The Deep Underground Neutrino Experiment. Available online at: http://www.dunescience.org

Google Scholar

19. [Dataset] The NOvA Experiment. Available online at: http://www-nova.fnal.gov

Google Scholar

20. [Dataset] Hyper-Kamiokande. Available online at: http://www.hyperk.org

Google Scholar

21. Carlson J, Gandolfi S, Pederiva F, Pieper SC, Schiavilla R, Schmidt KE, et al. Quantum Monte Carlo methods for nuclear physics. Rev Mod Phys. (2015) 87:1067. doi: 10.1103/RevModPhys.87.1067

CrossRef Full Text | Google Scholar

22. Lynn JE, Tews I, Gandolfi S, Lovato A. Quantum Monte Carlo methods in nuclear physics: recent advances. Ann Rev Nucl Part Sci. (2019) 69:279–305. doi: 10.1146/annurev-nucl-101918-023600

CrossRef Full Text | Google Scholar

23. Gandolfi S, Lonardoni D, Lovato A, Piarulli M. Atomic nuclei from quantum Monte Carlo calculations with chiral EFT interactions. (2020) Front Phys. 8:117. doi: 10.3389/fphy.2020.00117

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Piarulli M, Girlanda L, Schiavilla R, Navarro Pérez R, Amaro JE, Ruiz Arriola E. Minimally nonlocal nucleon-nucleon potentials with chiral two-pion exchange including Δ resonances. Phys Rev C. (2015) 91:024003. doi: 10.1103/PhysRevC.91.024003

CrossRef Full Text | Google Scholar

25. Piarulli M, Girlanda L, Schiavilla R, Kievsky A, Lovato A, Marcucci LE, et al. Local chiral potentials with Δ-intermediate states and the structure of light nuclei. Phys Rev C. (2016) 94:054007. doi: 10.1103/PhysRevC.94.054007

CrossRef Full Text | Google Scholar

26. Baroni A, Girlanda L, Kievsky A, Marcucci LE, Schiavilla R, Viviani M. Tritium β-decay in chiral effective field theory. Phys Rev C. (2016) 94:024003. doi: 10.1103/PhysRevC.94.024003

CrossRef Full Text | Google Scholar

27. Baroni A, Schiavilla R, Marcucci LE, Girlanda L, Kievsky A, Lovato A, et al. Local chiral interactions, the tritium Gamow-Teller matrix element, and the three-nucleon contact term. Phys Rev C. (2018) 98:044003. doi: 10.1103/PhysRevC.98.044003

CrossRef Full Text | Google Scholar

28. Piarulli M, Tews I. Local nucleon-nucleon and three-nucleon interactions within chiral effective field theory. Front Phys. (2020) 7:245. doi: 10.3389/fphy.2019.00245

CrossRef Full Text | Google Scholar

29. Baroni A, Girlanda L, Pastore S, Schiavilla R, Viviani M. Nuclear axial currents in chiral effective field theory. Phys Rev C. (2016) 93:015501. doi: 10.1103/PhysRevC.93.049902

CrossRef Full Text | Google Scholar

30. Coraggio L, Gargano A, Itaco N, Mancino R, Nowacki F. The calculation of the neutrinoless double-beta decay matrix element within the realistic shell model. Phys Rev C. (2020) 101:044315. doi: 10.1103/PhysRevC.101.044315

CrossRef Full Text | Google Scholar

31. Coraggio L, Itaco N, Mancino R. Short-range correlations for neutrinoless double-beta decay and low-momentum NN potentials. In: 27th International Nuclear Physics Conference. Glasgow, UK (2019).

Google Scholar

32. Wang XB, Hayes AC, Carlson J, Dong GX, Mereghetti E, Pastore S, et al. Comparison between variational Monte Carlo and shell model calculations of neutrinoless double beta decay matrix elements in light nuclei. Phys Lett B. (2019) 798:134974. doi: 10.1016/j.physletb.2019.134974

CrossRef Full Text | Google Scholar

33. Pastore S, Carlson J, Gandolfi S, Schiavilla R, Wiringa RB. Quasielastic lepton scattering and back-to-back nucleons in the short-time approximation. Phys Rev C. (2019) 101:044612. doi: 10.1103/PhysRevC.101.044612

CrossRef Full Text | Google Scholar

34. Lovato A, Carlson J, Gandolfi S, Rocco N, Schiavilla R. Ab initio study of $({\nu }_{\ell },{\ell }^{-})$ and $({\overline{\nu }}_{\ell },{\ell }^{+})$ inclusive scattering in ¹2C: confronting the MiniBooNE and T2K CCQE data. Phys Rev X. (2020) 3:031068. doi: 10.1103/PhysRevX.10.031068

CrossRef Full Text | Google Scholar

35. Alvarez-Ruso L, Athar MS, Barbaro MB, Cherdack D, Christy ME, Coloma P, et al. NuSTEC1 1Neutrino scattering theory experiment collaboration http://nustec.fnal.gov. White Paper: Status and challenges of neutrino–nucleus scattering. Prog Part Nucl Phys. (2018) 100:1–68. doi: 10.1016/j.ppnp.2018.01.006

CrossRef Full Text | Google Scholar

36. King GB, Andreoli L, Pastore S, Piarulli M, Schiavilla R, Wiringa RB, et al. Chiral effective field theory calculations of weak transitions in light nuclei. Phys Rev C. (2020) 102:025501. doi: 10.1103/PhysRevC.102.025501

CrossRef Full Text | Google Scholar

37. Wiringa RB. Variational calculations of few-body nuclei. Phys Rev C. (1991) 43:1585–98. doi: 10.1103/PhysRevC.43.1585

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Pudliner BS, Pandharipande VR, Carlson J, Pieper SC, Wiringa RB. Quantum Monte Carlo calculations of nuclei with A < = 7. Phys Rev C. (1997) 56:1720–50. doi: 10.1103/PhysRevC.56.1720

CrossRef Full Text | Google Scholar

39. Nollett KM, Wiringa RB, Schiavilla R. A Six body calculation of the alpha deuteron radiative capture cross-section. Phys Rev C. (2001) 63:024003. doi: 10.1103/PhysRevC.63.024003

CrossRef Full Text | Google Scholar

40. Nollett KM. Radiative alpha capture cross-sections from realistic nucleon-nucleon interactions and variational Monte Carlo wave functions. Phys Rev C. (2001) 63:054002. doi: 10.1103/PhysRevC.63.054002

CrossRef Full Text | Google Scholar

41. Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equation of state calculations by fast computing machines. J Chem Phys. (1953) 21:1087–92. doi: 10.1063/1.1699114

CrossRef Full Text | Google Scholar

42. Pervin M, Pieper SC, Wiringa RB. Quantum Monte Carlo calculations of electroweak transition matrix elements in A = 6,7 nuclei. Phys Rev C. (2007) 76:064319. doi: 10.1103/PhysRevC.76.064319

CrossRef Full Text | Google Scholar

43. Krebs H, Epelbaum E, Meissner UG. Nuclear forces with Delta-excitations up to next-to-next-to-leading order. I. Peripheral nucleon-nucleon waves. Eur Phys J A. (2007) 32:127–37. doi: 10.1140/epja/i2007-10372-y

CrossRef Full Text | Google Scholar

44. Navarro Pérez R, Amaro JE, Ruiz Arriola E. Coarse-grained potential analysis of neutron-proton and proton-proton scattering below the pion production threshold. Phys Rev C. (2013) 88:064002. doi: 10.1103/PhysRevC.88.064002

CrossRef Full Text | Google Scholar

45. Navarro Pérez R, Amaro JE, Ruiz Arriola E. Coarse grained NN potential with chiral two pion exchange. Phys Rev C. (2014) 89:024004. doi: 10.1103/PhysRevC.89.024004

CrossRef Full Text | Google Scholar

46. Navarro Perez R, Amaro JE, Ruiz Arriola E. Statistical error analysis for phenomenological nucleon-nucleon potentials. Phys Rev C. (2014) 89:064006. doi: 10.1103/PhysRevC.89.064006

CrossRef Full Text | Google Scholar

47. Piarulli M, Baroni A, Girlanda L, Kievsky A, Lovato A, Lusk E, et al. Light-nuclei spectra from chiral dynamics. Phys Rev Lett. (2018) 120:052503. doi: 10.1103/PhysRevLett.120.052503

PubMed Abstract | CrossRef Full Text | Google Scholar

48. van Kolck U. Few nucleon forces from chiral Lagrangians. Phys Rev C. (1994) 49:2932–41. doi: 10.1103/PhysRevC.49.2932

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Epelbaum E, Nogga A, Gloeckle W, Kamada H, Meissner UG, Witala H. Three nucleon forces from chiral effective field theory. Phys Rev C. (2002) 66:064001. doi: 10.1103/PhysRevC.66.064001

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Lynn JE, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt KE, et al. Chiral three-nucleon interactions in light nuclei, neutron-α scattering, and neutron matter. Phys Rev Lett. (2016) 116:062501. doi: 10.1103/PhysRevLett.116.062501

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Tews I, Gandolfi S, Gezerlis A, Schwenk A. Quantum Monte Carlo calculations of neutron matter with chiral three-body forces. Phys Rev C. (2016) 93:024305. doi: 10.1103/PhysRevC.93.024305

CrossRef Full Text | Google Scholar

52. Lynn JE, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt KE, et al. Quantum Monte Carlo calculations of light nuclei with local chiral two- and three-nucleon interactions. Phys Rev C. (2017) 96:054007. doi: 10.1103/PhysRevC.96.054007

CrossRef Full Text | Google Scholar

53. Gazit D, Quaglioni S, Navratil P. Three-nucleon low-energy constants from the consistency of interactions and currents in chiral effective field theory. Phys Rev Lett. (2009) 103:102502. doi: 10.1103/PhysRevLett.103.102502

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Marcucci LE, Kievsky A, Rosati S, Schiavilla R, Viviani M. Chiral effective field theory predictions for muon capture on deuteron and ³He. Phys Rev Lett. (2012) 108:052502. doi: 10.1103/PhysRevLett.108.052502

CrossRef Full Text | Google Scholar

55. Gardestig A, Phillips DR. How low-energy weak reactions can constrain three-nucleon forces and the neutron-neutron scattering length. Phys Rev Lett. (2006) 96:232301. doi: 10.1103/PhysRevLett.96.232301

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Lovato A, Benhar O, Fantoni S, Schmidt KE. Comparative study of three-nucleon potentials in nuclear matter. Phys Rev C. (2012) 85:024003. doi: 10.1103/PhysRevC.85.024003

CrossRef Full Text | Google Scholar

57. Cirigliano V, Dekens W, De Vries J, Graesser ML, Mereghetti E, Pastore S, et al. A renormalized approach to neutrinoless double-beta decay. Phys Rev C. (2019) 100:055504. doi: 10.1103/PhysRevC.100.055504

CrossRef Full Text | Google Scholar

58. Piarulli M, Bombaci I, Logoteta D, Lovato A, Wiringa RB. Benchmark calculations of pure neutron matter with realistic nucleon-nucleon interactions. Phys Rev C. (2019) 101:045801. doi: 10.1103/PhysRevC.101.045801

CrossRef Full Text | Google Scholar

59. Demorest P, Pennucci T, Ransom S, Roberts M, Hessels J. Shapiro delay measurement of a two solar mass neutron star. Nature. (2010) 467:1081–3. doi: 10.1038/nature09466

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Antoniadis J, Freire PCC, Wex N, Tauris TM, Lynch RS, van Kerkwijk MH, et al. A massive pulsar in a compact relativistic binary. Science. (2013) 340:6131. doi: 10.1126/science.1233232

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Bacca S, Pastore S. Electromagnetic reactions on light nuclei. J Phys G. (2014) 41:123002. doi: 10.1088/0954-3899/41/12/123002

CrossRef Full Text | Google Scholar

62. Piarulli M, Girlanda L, Marcucci LE, Pastore S, Schiavilla R, Viviani M. Electromagnetic structure of A = 2 and 3 nuclei in chiral effective field theory. Phys Rev C. (2013) 87:014006. doi: 10.1103/PhysRevC.87.014006

CrossRef Full Text | Google Scholar

63. Schiavilla R, Baroni A, Pastore S, Piarulli M, Girlanda L, Kievsky A, et al. Local chiral interactions and magnetic structure of few-nucleon systems. Phys Rev C. (2019) 99:034005. doi: 10.1103/PhysRevC.99.034005

CrossRef Full Text | Google Scholar

64. Nevo Dinur N, Hernandez OJ, Bacca S, Barnea N, Ji C, Pastore S, et al. Zemach moments and radii of ², 3H and ³, 4He. Phys Rev C. (2019) 99:034004. doi: 10.1103/PhysRevC.99.034004

CrossRef Full Text | Google Scholar

65. Marcucci LE, Gross F, Pena MT, Piarulli M, Schiavilla R, Sick I, et al. Electromagnetic structure of few-nucleon ground states. J Phys G. (2016) 43:023002. doi: 10.1088/0954-3899/43/2/023002

CrossRef Full Text | Google Scholar

66. Pastore S, Schiavilla R, Goity JL. Electromagnetic two-body currents of one- and two-pion range. Phys Rev C. (2008) 78:064002. doi: 10.1103/PhysRevC.78.064002

CrossRef Full Text | Google Scholar

67. Pastore S, Girlanda L, Schiavilla R, Viviani M, Wiringa RB. Electromagnetic currents and magnetic moments in (chi)EFT. Phys Rev C. (2009) 80:034004. doi: 10.1103/PhysRevC.80.034004

CrossRef Full Text | Google Scholar

68. Girlanda L, Kievsky A, Marcucci LE, Pastore S, Schiavilla R, Viviani M. Thermal neutron captures on d and ³He. Phys Rev Lett. (2010) 105:232502. doi: 10.1103/PhysRevLett.105.232502

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Pastore S, Girlanda L, Schiavilla R, Viviani M. The two-nucleon electromagnetic charge operator in chiral effective field theory (χEFT) up to one loop. Phys Rev C. (2011) 84:024001. doi: 10.1103/PhysRevC.84.024001

CrossRef Full Text | Google Scholar

70. Pastore S, Pieper SC, Schiavilla R, Wiringa RB. Quantum Monte Carlo calculations of electromagnetic moments and transitions in A ≤ 9 nuclei with meson-exchange currents derived from chiral effective field theory. Phys Rev C. (2013) 87:035503. doi: 10.1103/PhysRevC.87.035503

CrossRef Full Text | Google Scholar

71. Datar VM, Chakrabarty DR, Suresh Kumar, Nanal V, Pastore S, Wiringa RB, et al. Electromagnetic transition from the 4+ to 2+ resonance in Be8 measured via the radiative capture in He4+He4. Phys Rev Lett. (2013) 111:062502. doi: 10.1103/PhysRevLett.111.062502

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Pastore S, Wiringa RB, Pieper SC, Schiavilla R. Quantum Monte Carlo calculations of electromagnetic transitions in ⁸Be with meson-exchange currents derived from chiral effective field theory. Phys Rev C. (2014) 90:024321. doi: 10.1103/PhysRevC.90.024321

CrossRef Full Text | Google Scholar

73. Pastore S, Baroni A, Carlson J, Gandolfi S, Pieper SC, Schiavilla R, et al. Quantum Monte Carlo calculations of weak transitions in A = 6−10 nuclei. Phys Rev C. (2018) 97:022501. doi: 10.1103/PhysRevC.97.022501

CrossRef Full Text | Google Scholar

74. Pastore S, Carlson J, Cirigliano V, Dekens W, Mereghetti E, Wiringa RB. Neutrinoless double-β decay matrix elements in light nuclei. Phys Rev C. (2018) 97:014606. doi: 10.1103/PhysRevC.97.014606

CrossRef Full Text | Google Scholar

75. Cirigliano V, Dekens W, De Vries J, Graesser ML, Mereghetti E, Pastore S, et al. New leading contribution to neutrinoless double-β decay. Phys Rev Lett. (2018) 120:202001. doi: 10.1103/PhysRevLett.120.202001

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Krebs H, Epelbaum E, Meißner UG. Box diagram contribution to the axial two-nucleon current. Phys Rev C. (2020) 101:055502. doi: 10.1103/PhysRevC.101.055502

CrossRef Full Text | Google Scholar

77. Park TS, Min DP, Rho M. Chiral dynamics and heavy fermion formalism in nuclei. 1. Exchange axial currents. Phys Rept. (1993) 233:341–95. doi: 10.1016/0370-1573(93)90099-Y

CrossRef Full Text | Google Scholar

78. Kolling S, Epelbaum E, Krebs H, Meissner UG. Two-pion exchange electromagnetic current in chiral effective field theory using the method of unitary transformation. Phys Rev C. (2009) 80:045502. doi: 10.1103/PhysRevC.80.045502

CrossRef Full Text | Google Scholar

79. Kolling S, Epelbaum E, Krebs H, Meissner UG. Two-nucleon electromagnetic current in chiral effective field theory: one-pion exchange and short-range contributions. Phys Rev C. (2011) 84:054008. doi: 10.1103/PhysRevC.84.054008

CrossRef Full Text | Google Scholar

80. Tanabashi M, Hagiwara K, Hikasa K, Nakamura K, Sumino Y, Takahashi F, et al. Review of particle physics. Phys Rev D. (2018) 98:030001. doi: 10.1103/PhysRevD.98.030001

CrossRef Full Text | Google Scholar

81. Knecht A, Hong R, Zumwalt DW, Delbridge BG, Garcia A. Precision measurement of the He-6 half-life and the weak axial current in nuclei. Phys Rev C. (2012) 86:035506. doi: 10.1103/PhysRevC.86.035506

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Suzuki T, Fujimoto R, Otsuka T. Gamow-Teller transitions and magnetic properties of nuclei and shell evolution. Phys Rev C. (2003) 67:044302. doi: 10.1103/PhysRevC.67.044302

CrossRef Full Text | Google Scholar

83. Chou WT, Warburton EK, Brown BA. Gamow-teller beta-decay rates for A < = 18 nuclei. Phys Rev C. (1993) 47:163–77. doi: 10.1103/PhysRevC.47.163

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Warburton EK. R-matrix analysis of the !!!!-delayed alpha spectra from the decay of !!! and !!!!. Phys Rev C. (1986) 33:303–13. doi: 10.1103/PhysRevC.33.303

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Pritychenko B, BK E, Kellett MA, Singh B, Totans J. The Nuclear Science References (NSR) database and Web Retrieval System. Nucl Instrum Methods Phys Res Sect A. (2011) 640:213–8. doi: 10.1016/j.nima.2011.03.018

CrossRef Full Text | Google Scholar

86. Wiringa RB. Pair counting, pion-exchange forces, and the structure of light nuclei. Phys Rev C. (2006) 73:034317. doi: 10.1103/PhysRevC.73.034317

CrossRef Full Text | Google Scholar

87. Gysbers P, Hagen G, Holt JD, Jansen GR, Morris TD, Navratil P, et al. Discrepancy between experimental and theoretical β-decay rates resolved from first principles. Nat Phys. (2019) 15:428–31. doi: 10.1038/s41567-019-0450-7

CrossRef Full Text | Google Scholar

88. Hardy JC, Towner IS. Superallowed 0⁺ → 0⁺ nuclear decays: 2014 critical survey, with precise results for V_ud and CKM unitarity. Phys Rev C. (2015) 91:025501. doi: 10.1103/PhysRevC.91.025501

CrossRef Full Text | Google Scholar

89. Wiringa RB, Pieper SC, Carlson J, Pandharipande VR. Quantum Monte Carlo calculations of A = 8 nuclei. Phys Rev C. (2000) 62:014001. doi: 10.1103/PhysRevC.62.014001

CrossRef Full Text | Google Scholar