Research on Improved Chaotic Particle Optimization Algorithm Based on Complex Function

Introduction

Complex function optimization is an important research direction of optimization problems. Generally speaking, the solving methods of optimization problems can be divided into analytical method and numerical calculation [1]. The analytical method solves the problem according to the relationship between the derivative of the objective function and the extreme value of the function. This method is only suitable for optimization problems with relatively simple objective function. According to the variation rule of objective function value, In appropriate steps along the direction that optimizes the value of the objective function, An approximate calculation method that approaches the optimal point of the objective function step by step, This method is good at solving continuous differentiated convex optimization problems, With the continuous expansion of engineering optimization problems, most of the objective functions are non-convex optimization problems. The emergence of group intelligent optimization algorithms provides a limited way for complex function optimization problems [2, 3].

Particle Swarm Optimization (PSO) algorithm is a kind of bionic intelligent optimization algorithm based on population, which is proposed by Kennedy et al. [4]. Each particle in the PSO algorithm represents a feasible solution; the location of food source is the global optimal location point. PSO has strong search diversity, simple operation and few adjustment parameters. As soon as it was proposed, it was widely used [5, 6], especially PSO has shown excellent optimization ability in complex optimization problems [7]. In reference [8], Eberhart and Shi found that when the maximum velocity of the particle is not too small (v_max > 3), The inertia weight ω = 0.8 is best. In addition, this conclusion has been confirmed on many subsequent issues. Clert [9] when carefully studying a general PSO system, the change of speed can be controlled by controlling ϕ₁ and ϕ₂. In order to improve the calculation speed of particle motion trajectory, Clert introduced contraction factorχ to improve the basic model of PSO algorithm. PSO algorithm has the following advantages:

First, the algorithm is easy to describe.

Second, there are few parameters to be adjusted in the algorithm.

Third, the number of functions to be evaluated in the algorithm is small.

Fourth, the number of populations required by the algorithm in the process of solving the problem is small.

Fifth, the algorithm converges quickly.

Because there are few parameters in PSO, PSO is easy to Realize, there is also less demand for computing resources, the gradient information of fitness function is not needed, only the value of fitness function is needed. Although PSO algorithm has various advantages, but the PSO algorithm itself also has several limitations, its performance is as follows. First, PSO is a probabilistic algorithm, without systematic and standardized theoretical support, It is still difficult to verify the correctness of PSO algorithm from a mathematical point of view so far. Moreover, based on the theory of random events, it is an extremely difficult task to analyze the particle trajectory quantitatively in the search process of PSO algorithm. However, this is also related to the key issues of convergence and parameter selection of PSO algorithm. Although most scholars are currently verifying the convergence of its improved PSO algorithm, But none of them has produced a set of mature and universal theories. Second, the behavior and characteristics of complex systems are the emergence of behaviors that are continuously superimposed through interaction between individual individuals in the system. Although the control of individual behaviors is relatively simple, however, this does not mean that the control of the whole system is an easy task. Third, as far as the whole algorithm is concerned, due to the lack of balance mechanism, when solving some complex or special problems, the algorithm is easy to lose population diversity and fall into local extreme. The structure and contents of the paper are as follows: (1) Introduce the basic particle swarm optimization algorithm and the algorithm flow; (2) Introduce the quantum chaotic adaptive particle swarm optimization algorithm, explaining the quantum Bloch coordinate coding, chaos optimization method, quantum particle swarm optimization algorithm, adaptive inertia weight and the improved algorithm flow, respectively; (3) Comparing the convergence test through experiments.

Basic PSO

The mathematical description of PSO algorithm is follow that the population with dimension D and scale N can be expressed as X = {X₁, X₂, ..., X_D}, then at time t, the position of the i^th particle is X_i(t) = {X_i1(t), X_i2(t), ..., X_iD(t)} and its velocity is V_i(t) = {V_i1(t), V_i2(t), ..., V_iD(t)}. The algorithm always maintains two optimal positions: evolution process, the individual best position pbest_i(t) of particle i, expressed as p_i(t) = {p_i1(t), p_i1(t), ..., p_iD(t)}, and gbest(t) of population a best location, expressed as p_g(t) = {p_g1(t), p_g1(t), ..., p_gD(t)}. If the optimization model is max f(X), the update formulas of p_i(t) and p_g(t) are as follows:

$\begin{array}{ll}{P}_i^{(t+1)}=\{\begin{array}{c}{X}_i^{(t+1)}\begin{array}{cc}& f(X_i^{(t+1)}>f(P_i^{(t)});\end{array}\\ P_i^{(t)}\begin{array}{cc}& f(X_i^{(t+1)}\le f(P_i^{(t)})\end{array}\end{array}& (1)\end{array}$

$\begin{array}{ll}{p}_g^{(t+1)}=\underset{1\le i\le N}{\max }{p}_i^{(t+1)}& (2)\end{array}$

In the t-th iteration, p_best and g_best represent historical and global optimal positions. Then the calculation formula for particle flight update is expressed as follows:

$\begin{array}{ll}{v}_{i,d}^{t+1}=w{v}_{i,d}^t+c_1{r}_1(pbes{t}_{i,d}^t-x_{i,d}^t)+c_2{r}_2(gbes{t}_d^t-x_{i,d}^t)& (3)\end{array}$

$\begin{array}{ll}{x}_{i,d}^{t+1}=x_{i,d}^t+v_{i,d}^{t+1}& (4)\end{array}$

Where $v_{i,d}^{t+1}$ represents the flight speed of i^th particle iterations t + 1; XID represents the position of i^th particle with iterations t. wrepresents the inertia weight, which is taken here as 0.6; c₁ and c₂ represent learning factors, generally taking c₁ = 2, c₂ = 2; r₁ ∈ [0, 1] r₂ ∈ [0, 1].

The flow of the basic PSO algorithm is as follows:

(1) Set the parameters of PSO algorithm, such as population size, problem dimension, inertia weight, maximum range and maximum speed, etc. Randomly initialize group position and speed.

(2) Judge whether the particle is beyond the search range, and correct the position if it is beyond the range.

(3) According to the state of each particle, calculate the corresponding fitness value.

(4) Update pbest according to the current fitness value.

(5) Update gbest according to the current fitness value.

(6) According to formulas (3) and (4), update the speed and position.

(7) Judge the termination condition, and return to (2) if it is not terminated, otherwise it will end.

Quantum Chaos Adaptive PSO Algorithm

Initial Population of Quantum Bloch Coordinate Coding

In quantum computation, the smallest information unit is expressed by qubits, which are also called qubits. The state of a qubit can be expressed as [10]:

$\begin{array}{ll}|\phi \rangle \text{=}\cos (\theta /2)|0\rangle +e^{i\phi }\text{ sin}(\theta /2)|1\rangle & (5)\end{array}$

In Equation (5), numbers φ and θ define a point, Qubits establish correlation with Bloch spherical points, and the conversion formula is as follows:

$\begin{array}{ll}|\phi \rangle ={\left[\begin{array}{ccc}cos\phi sin\theta & sin\phi sin\theta & cos\theta \end{array}\right]}^T& (6)\end{array}$

Let p_i be the i-th candidate solution in the group, and its coding scheme is as follows:

$\begin{array}{ll}{p}_i={\displaystyle \left|\begin{array}{l}cos{\phi }_{i1}sin{\theta }_{i1}\\ sin{\phi }_{i1}sin{\theta }_{i1}\\ cos{\theta }_{i1}\end{array}\right|}\begin{array}{l}\cdots \\ \cdots \\ \cdots \end{array}{\displaystyle \left|\begin{array}{l}cos{\phi }_{in}sin{\theta }_{id}\\ sin{\phi }_{in}sin{\theta }_{id}\\ cos{\theta }_{id}\end{array}\right|}& (7)\end{array}$

Where φ_ij = 2π × rnd, θ_ij = π × rnd and rnd ∈ [0, 1];Each candidate solution occupies three positions in the space, i.e., represents the following three optimization solutions:

$\begin{array}{ll}\begin{array}{l}{P}_{ix}=(cos{\phi }_{i1}sin{\theta }_{i1},\cdots ,cos{\phi }_{id}sin{\theta }_{id});\\ P_{iy}=(sin{\phi }_{i1}sin{\theta }_{i1},\cdots ,sin{\phi }_{id}sin{\theta }_{id});\\ P_{iz}=(cos{\theta }_{i1},\cdots ,cos{\theta }_{id})\end{array}& (8)\end{array}$

Note that the feasible solutions corresponding to P_ix,P_iy and P_iz are as follows:

$\begin{array}{ll}\begin{array}{l}{x}_{ix}=(x_{i1}^1,x_{i2}^1,\dots ,x_{in}^1);\\ x_{iy}=(x_{i1}^2,x_{i2}^2,\dots ,x_{in}^2);\\ x_{iz}=(x_{i1}^3,x_{i2}^3,\dots ,x_{in}^3)\end{array}& (9)\end{array}$

Transformation of solution space: Bloch coordinates of the i-th qubit on candidate solution p_i are ${\left[x_{ix},x_{iy},x_{iz}\right]}^T$, and the value of solution space is [a_j, b_j], then the transformation formula mapping I^d = [−1, 1]^d is follow:

$\begin{array}{ll}\begin{array}{l}{x}_{ij}^1=\frac{1}{2}\left[b_j(1+x_{ix})+a_j(1-x_{ix})\right];\\ x_{ij}^2=\frac{1}{2}\left[b_j(1+x_{iy})+a_j(1-x_{iy})\right];\\ x_{ij}^3=\frac{1}{2}\left[b_j(1+x_{iz})+a_j(1-x_{iz})\right]\end{array}& (10)\end{array}$

Therefore, individuals with smaller fitness values are selected as the initial population among all candidate solutions. Bloch coding can enhance the ergodicity of the optimization space, improve the population, and further improve the optimization performance.

Chaos Optimization Method

Chaos has the characteristics of randomness, ergodicity and regularity. In the field of optimization design, the ergodicity of chaos phenomenon can be used as an optimization mechanism to avoid falling into local minima in the search process. Chaotic variables are used to search and this method is applied to the optimization of continuous complex objects. The steps of chaos optimization algorithm using Logistic mapping are as follows:

(1) Let k = 0, $x_j^k,j=1,2,...,n$ to chaotic variables $x_j^k\in \left[0,1\right]$.

$\begin{array}{ll}{s}_j^k=\frac{x_j^k-x_{min,j}}{x_{max,j}-x_{min,j}}\begin{array}{c}j=1,2,...,n\end{array}& (11)\end{array}$

In the formula, x_{max, j} is max bounds and x_{min, j} is the search min bounds of the j-dimensional variable, respectively.

(2) Calculate next value $s_j^{k+1}$.

$\begin{array}{ll}{S}_j^{k=1}=4s_j^k(1-s_j^k)& (12)\end{array}$

(3) The chaotic variable $s_j^k$ is transformed into the decision variable $x_j^{k+1}$. Using a certain chaotic mapping structure to generate chaotic sequences, m is the length of chaotic sequences. These sequences are inversely transformed to the original search space through equation (13).

$\begin{array}{ll}{x}_j^{k+1}=x_{min,j}+s_j^{k+1}(x_{max,j}-x_{min,j})& (13)\end{array}$

The new solution is taken as the result of chaotic optimization K = K + 1, otherwise, the new solution is transferred to (2) and the iteration is continued.

(4) Calculate the fitness value F(X_i) of X_i and compare it with the fitness value F(X_i) of X_i to retain the best solution;

(5) Updating Chaotic Search Space $(x_{min,j},x_{max,j})$.

Quantum PSO Algorithm

In 2004, Sun studied the convergence behavior of absorption-related particles and proposed a quantum PSO algorithm based on the model of quantum mechanics. In quantum mechanics, when each particle moves in the search space, there is a DELTA potential well-centered on p. The properties of particles in quantum space satisfying aggregated states are completely different from those in classical mechanics. The particle with quantum behavior has no definite trajectory when moving, i.e., The velocity and position are uncertain, and this uncertainty makes the possible position of the particle “everywhere” (i.e., In the whole feasible solution region) full of possibilities, and the particle has the possibility to get rid of the local optimal value point with large interference. It can ensure the global convergence of the algorithm and has only position vector, no speed vector, few control parameters and strong optimization ability in the optimization model.

Quantum PSO algorithm is described as follows: in D-dimensional space, there are m particles, the individual extreme point is pBest_i = (pBest_i1, pBest_i2, ..., pBest_iD), and the potential center point is p; The current global extreme point searched by the whole particle swarm is gBest = (gBest₁, gBest₂, .., gBest_D). Then, The position update operation for this particle is as follows:

$\begin{array}{ll}p=\frac{rand1()\times pBes{t}_{id}+rand2()\times gBes{t}_d}{rand1()+rand2()}& (14)\end{array}$

$\begin{array}{ll}l=z\times |X_{id}(t)-p|0<z<ln\sqrt{2}& (15)\end{array}$

$\begin{array}{ll}{X}_{id}(t+1)\{\begin{array}{c}p-l\times ln\left[1/rand3()\right]rand3()>0.5;\\ p+l\times ln\left[1/rand3()\right]rand3()\le 0.5\end{array}& (16)\end{array}$

Where i = 1, 2, ..., m and $Z\le ln\sqrt{2}$, usually 0.5–1.0; The range are (0, 1).

Adaptive Inertia Weights

The global exploration ability and local mining ability of PSO algorithm are contradictory to each other, and it is hard to seek a balance point. To balance the global exploration and local development capabilities of PSO algorithm, an improved chaotic particle optimization Algorithm is proposed to further modify the optimization algorithm effect.

Accord to the particle position update formula (3), two adaptive inertia weights w_j and ${w^{\prime }}_j$ are introduced. Among them, w_j is used to control the influence degree of the original particle position on the new particle position, and ${w^{\prime }}_j$ is used to balance the influence weight of the particle flight speed on the new position. The improved particle position update formula is expressed as follows:

$\begin{array}{ll}{x}_{i,d}^{t+1}=w_j{x}_{i,d}^t+{w^{\prime }}_j{v}_{i,d}^{t+1}& (17)\end{array}$

From above formula 17, w_j and ${w^{\prime }}_j$ can keep the fault tolerance of particle population, and enhance robustness of the algorithm to quit the local optimization in the optimization process.

The mathematical expressions for w_jand ${w^{\prime }}_j$ are as follows:

$\begin{array}{ll}{w}_j=1/(1+exp{(-f(j)/u)}^{iter})& (18)\end{array}$

$\begin{array}{ll}{w}_j^{\prime }=1-w_j& (19)\end{array}$

In the formula, f(j) express adaptive value of the j-th particle, u express the best value in the particle population in the first iteration calculation, and iter represents the current iteration number.

Quantum Chaos Adaptive PSO Algorithm Steps

The specific steps of QCPSO algorithm search are as follows:

(1) Initialize all parameters including N, c₁, c₂, M,v,D, t = 0;

(2) The current fitness value of each particle is calculated by the optimization function and compared with the fitness value corresponding to the individual historical optimal solution. If the current fitness value is better than the fitness value corresponding to the individual historical optimal solution, the current solution is replaced by the individual optimal solutionpbest, otherwise it is not replaced.

(3)The optimal solution gbestof the current population is determined by comparing the optimal fitness values of all particles;

(4) Updating the flight speed of particles;

(5) Updating the weights w_j and ${w^{\prime }}_j$;

(6) Updating the position of particles;

(7) If t < M and not converge

t = t + 1

Go to step (3);

Otherwise

Find the global optimal solution and go to step (8);

(8) Output the best value.

Convergence Test Comparisons

The PSO algorithm is improved by parameter adjustment strategy, and the search process is optimized by re-search and reverse learning. In order to embody the effectiveness of the improved PSO algorithm put forward in the research of test case generation, it is relative to other algorithms, and has the best effect. Based on existing problems that need to be studied, this paper uses Matlab 2016a programming to implement the above-mentioned algorithm, and evaluates the advantages and disadvantages through fitness value, average coverage rate and iteration times. To ensure the fairness and scientificity of the performance comparison of all algorithms, each group of experiments is run 100 times to obtain the average value.

The basic parameters of the whole experiment are seen as follows: M = 1,000, N = 30, D = 30, and the range of values is [0.4, 0.9]. To verify the superiority of QCPSO algorithm put forward, four typical test functions Sphere, Rosenbrock, Rastrigrin and Griewank are compared and tested. These four functions include unimodal function, multimodal function and trigonometric function, which are relatively comprehensive. The specific formulas of the test functions are as follows.

$\begin{array}{ll}{f}_1(x)={\displaystyle \sum _{i=1}^n}{x}_i^2\begin{array}{c}x\in \left[-100,100\right]\end{array}& (20)\end{array}$

$\begin{array}{ll}{f}_2(x)={\displaystyle \sum _{i=1}^{n-1}}(100{(x_{i+1}-x_i^2)}^2+{(1-x_i)}^2)x\in \left[-30,30\right]& (21)\end{array}$

$\begin{array}{ll}{f}_3(x)={\displaystyle \sum _{i=1}^n}(x_i^2-10cos(2\pi x_i)+10)x\in \left[-5,5\right]& (22)\end{array}$

$\begin{array}{ll}{f}_4(x)=({\displaystyle \sum _{i=1}^n}{x}_i^2-{\displaystyle \prod _{i=1}^n}cos(x_i/\sqrt{i})+1)/4000x\in \left[-600,600\right]& (23)\end{array}$

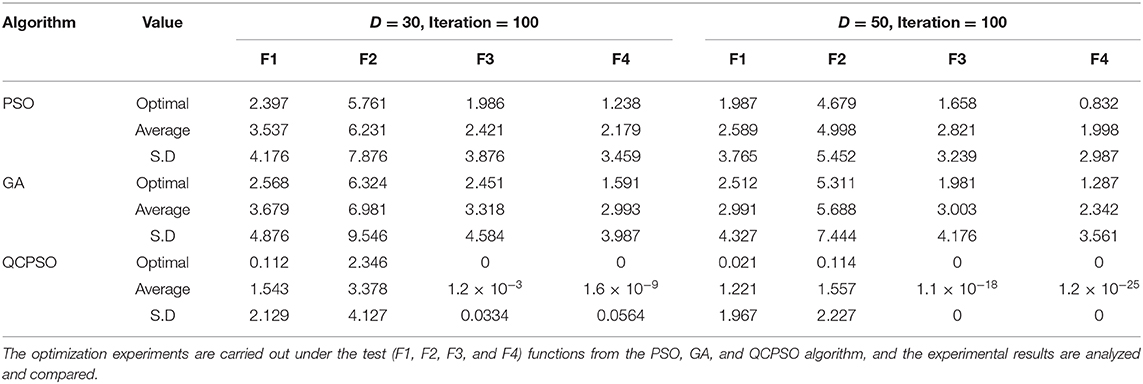
In order to verify the performance advantages of the improved PSO algorithm, it is necessary to judge the fitness values of four typical test functions and compare them with the results of other algorithms. First of all, the inertia weight is used to improve the learning factor. The relationship between the two can be divided into three types: linear, non-linear and trigonometric functions. In this paper, the non-linear relationship is used to carry out the relationship of learning factors, so that the learning factor changes non-linearly and gradually with the inertia weight, and the equation is expressed as c = Aω² + Bω + C; c₂ + c₁ = 2, and the inertia weight adopts the commonly used exponential function decreasing method, taking A = 0.45, B = 0.9, C = 0.45, ω_max = 0.9, ω_min = 0.4. Secondly, the optimal solution and suboptimal solution in the current iteration are searched again, and the particles outside the tabu region are optimized by chaos. The improved algorithm is compared with PSO, GA and QCPSO through four typical test functions. The comparison of four typical test functions in four algorithms is shown in Table 1.

TABLE 1

Table 1. Value for three Algorithms.

For a variable dimension of 20, As can be seen from Table 1: In 20 independent repetitions, For the test functions F3 and F4, QCPSO algorithm result the best value, but for average value and standard deviation of these two test functions, QCPSO is best again, and QCPSO are obviously better than PSO algorithm and GA algorithm. Accord to four functions, QCPSO is significantly better than PSO and GA, accord to the average value, standard deviation and the optimal value.

For the variable dimension of 50, it can be seen from Table 1 that for the test functions F1, F2, F3, and F4, the average value and standard deviation of the optimal value of QCPSO are significantly better than those of PS0 algorithm and GA algorithm, and when the corresponding value ratio dimension is 20, it is smaller as a whole.

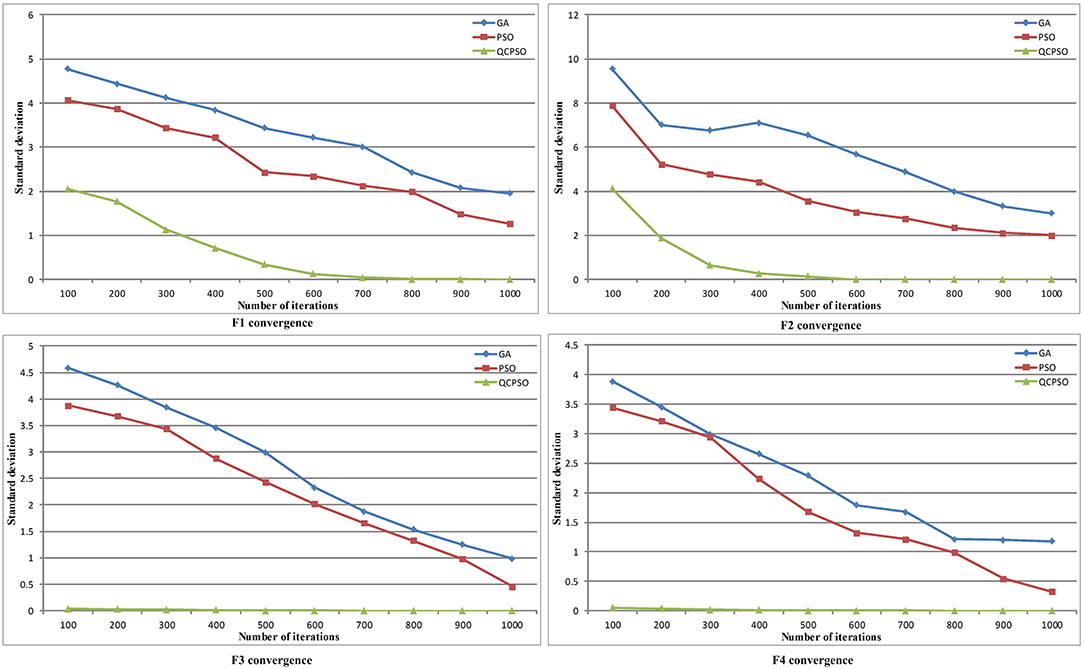
In order to verify the convergence, the following is verified by iterations of the algorithm. The standard deviation value increases with the number of iterations. The specific effect is shown in Figures 1, 2.

FIGURE 1

Figure 1. Convergence Comparison of four Functions (D = 30).

FIGURE 2

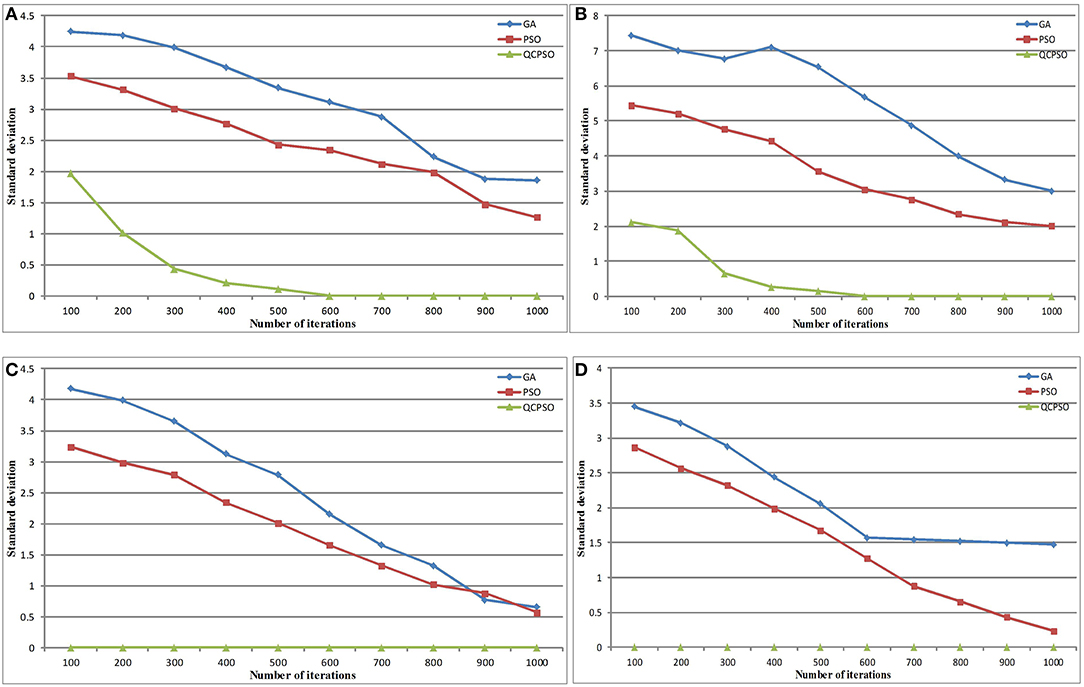
Figure 2. Convergence Comparison of four Functions (D = 50). (A) F1 convergence, (B) F2 convergence, (C) F3 convergence, (D) F4 convergence.

Figures 1, 2 is a 30-dimensional optimization curve of 4 benchmark test functions in QCPSO, PSO, and GA (semi-logarithmic curve, and the optimization curve is drawn by semilogy function). The 30-and 50-dimensional optimization curves obtained in the experiment are similar to those in Figure 2 and will not be given here due to limited space.

As can be seen from Figures 1, 2, when QCPSO algorithm optimizes F2 and F4 functions, there are many inflection points, indicating that QCPSO's ability to jump out of local optimization is enhanced. As can be seen intuitively from Figure 1, QCPSO algorithm is more effective than the PSO and GA algorithms for most of the four functions in Table 1 with dimension 30. Among them, QCPSO algorithm obtains the optimal values in four test functions (F1, F2, F3, F4). The convergence speed of QCPSO is best than other three algorithms. As can be seen from Figures 1, 2, QCPSO quickly searches for satisfactory solutions for most optimization problems.

In short, QCPSO algorithm has greatly improved its optimization capability compared with standard PSO. For most optimization problems, QCPSO algorithm is better than GA and standard PSO algorithms.

Conclusion

In our research, an improved chaotic PSO algorithm based on complex functions are proposed. By comparing the convergence of four complex functions, the proposed QCPSO algorithm has high convergence and stable performance. The convergence of complexity functions is verified to illustrate the advantages of the algorithm, and more complexity functions are used to verify the advantages of the algorithm in the later period. It is proved in different dimensions that the reliability of the algorithm is verified by the population of higher dimensions, and the universality of the algorithm is better explained. In the future research work, the improved particle swarm optimization algorithm for complex functions will be applied in other fields to improve the actual effect of the existing work [11–14]. For example, geographic location prediction, GPS trajectory prediction, flow prediction, etc.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

XX and SL participated in the preparation and presentation of the manuscript.

Funding

This work was supported by the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJQN201902103) and the Open Fund of Chongqing Key Laboratory of Spatial Data Mining and Big Data Integration for Ecology and Environment (No. ZKPT0120193007).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Liu H, Niu P. Enhanced shuffled frog-leaping algorithm for solving numerical function optimization problems. J Intell Manufact. (2015) 29:1133–53. doi: 10.1007/s10845-015-1164-z

CrossRef Full Text | Google Scholar

2. Chen Z, Zhou S, Luo J. A robust ant colony optimization for continuous functions. Exp Syst App. (2017) 81:309–20. doi: 10.1016/j.eswa.2017.03.036

CrossRef Full Text | Google Scholar

3. Li G, Cui L, Fu X, Wen Z, Lu N, Lu J. Artificial bee colony algorithm with gene recombination for numerical function optimization. Appl Soft Comput. (2017) 52:146–59. doi: 10.1016/j.asoc.2016.12.017

CrossRef Full Text | Google Scholar

4. Margreitter C, Oostenbrink C. Correction to optimization of protein backbone dihedral angles by means of hamiltonian reweighting. J Chem Inform Model. (2018) 58:1716–20. doi: 10.1021/acs.jcim.8b00470

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Palma LB, Coito FV, Ferreira BG. PSO based on-line optimization for DC motor speed control. In: 2015 9th International Conference on Compatibility and Power Electronics (CPE). Costa da Caparica (2015).

Google Scholar

6. Sheng-Feng C, Xiao-Hua C, Lu Y. Application of wavelet neural network with improved PSO algorithm in power transformer fault diagnosis. Pow Syst Protect Control. (2014) 42:37–42. Available online at: https://www.researchgate.net/publication/286059512_Application_of_wavelet_neural_network_with_improved_particle_swarm_optimization_algorithm_in_power_transformer_fault_diagnosis

7. Prativa A, Sumitra M. Efficient player selection strategy based diversified PSO algorithm for global optimization. Inform Sci. (2017) 397–8:69–90. doi: 10.1016/j.ins.2017.02.027

CrossRef Full Text | Google Scholar

8. Jiang X, Ling H. A new multi-objective particle swarm optimizer with fuzzy learning sub-swarms and self-adaptive parameters. Adv Sci Lett. (2012) 7:696–9. doi: 10.1166/asl.2012.2720

CrossRef Full Text | Google Scholar

9. Clerc M. The swarm and the queen: towards a deterministic and adaptive PSO.//congress on evolutionary computation-cec. IEEE. (2002) 3:1951–7. doi: 10.1109/cec.1999.785513

CrossRef Full Text | Google Scholar

10. Tsubouchi M, Momose T. Rovibrational wave-packet manipulation using shaped mid-infrared femtosecond pulses toward quantum computation: optimization of pulse shape by a genetic algorithm. Phys Rev A. (2008) 77:052326. doi: 10.1103/PhysRevA.77.052326

CrossRef Full Text | Google Scholar

11. Jiang W, Carter DR, Fu HL, Jacobson MG, Zipp KY, Jin J, et al. The impact of the biomass crop assistance program on the United States forest products market: an application of the global forest products model. Forests. (2019) 10:1–12. doi: 10.3390/f10030215

CrossRef Full Text | Google Scholar

12. Liu JB, Zhao J, Zhu ZX. On the number of spanning trees and normalized laplacian of linear octagonal-quadrilateral networks. Int J Quant Chem. (2019) 119:1–21. doi: 10.1002/qua.25971

CrossRef Full Text | Google Scholar

13. Liu JB, Zhao J, Cai Z. “On the generalized adjacency, laplacian and signless laplacian spectra of the weighted edge corona networks. Phys A. (2020) 540:1–11. doi: 10.1016/j.physa.2019.123073

CrossRef Full Text | Google Scholar

14. Liu W, Li J, Ren L, Xu J, Li C, Li S. Exploring livelihood resilience and its impact on livelihood strategy in rural China. Soc Indicat Res. (2020) 150:977–98. doi: 10.1007/s11205-020-02347-2

CrossRef Full Text | Google Scholar