Research on the Theory of Optical Transmission for Bragg Fiber With High-Index-Core

The paper analyzes the two theories of conducted light signal for Bragg fiber with high-index core, namely total internal reflection and photonic bandgap. From the perspective of the wave equation, the distribution of the electromagnetic field and the conditions for forming the guided mode when the optical signal is transmitted in the core of fiber are explained. The analysis of photonic bandgap adopts the band structure principle of natural crystals for analogy. Then, the formation process of the photonic bandgap is elaborated on.

Introduction

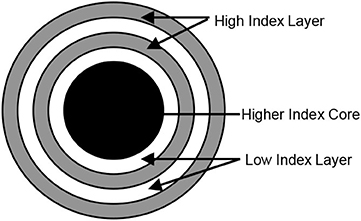
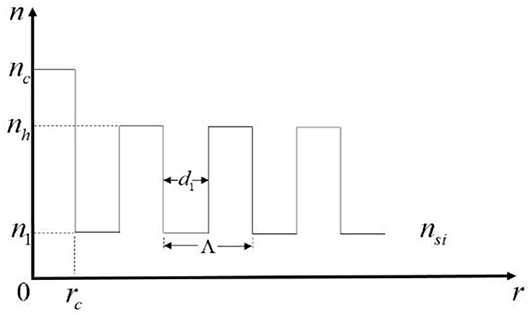
The concept of Bragg fiber has been proposed for a long time. With a periodic refractive index distribution along the radial direction, it belongs to a one-dimensional bandgap photonic crystal fiber. Generally speaking, Bragg fiber is of a cylindrical hollow structure, which is difficult in production and practical application, so the application of this fiber is slow after being proposed for many years. In recent years, it has been proposed to fill the hollow structure of Bragg fiber with a high refractive dielectric material to make it the Bragg fiber with high-index core [1–3]. Figures 1, 2 show the schematic diagram of the sectional drawing and refractive index of Bragg fiber with high-index core, respectively. It combines ordinary hollow Bragg fiber with traditional fiber. In this way, the problem in processing is solved. More importantly, two binding mechanisms for fiber transmission are provided, namely total internal reflection and photonic bandgap effect. Besides, more controllable structural parameters in the design can be obtained, making it free to choose to strengthen or weaken certain non-linear optical effects. Also, dispersion flattened of the specific band, and the extremely high non-linear coefficient can be obtained [2, 4–6].

FIGURE 1

Figure 1. Sectional drawing of Bragg fiber with high-index core.

FIGURE 2

Figure 2. Refractive index of Bragg fiber with high-index core.

Analysis of Wave Theory for Bragg Fiber With High-Index Core

The optical signal should satisfy the wave equation derived from Maxwell's equations [7]

$\begin{array}{ll}{\nabla }^{2}E+{(\frac{n\omega }{c})}^{2}E=0.& (1)\end{array}$

$\begin{array}{ll}{\nabla }^{2}H+{(\frac{n\omega }{c})}^{2}H=0.& (2)\end{array}$

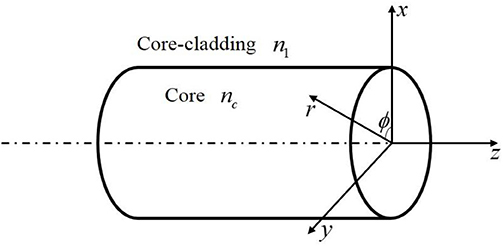
Generally speaking, the vector solution to the earlier mentioned vector wave equation is very complicated. Therefore, the scalar effective index method is adopted for the solution of fiber in most cases [8]. Our concern is the optical power distribution of the optical field in the cross-section of the optical fiber during the transmission of an optical signal in optical fiber. To know the distribution, it is necessary to find the solution for the scalar field of the optical fibers of Equations (1) and (2) that satisfy the core-cladding boundary conditions. In the cylindrical coordinate system (r, ϕ, z) shown in Figure 3, Equation (1) can be expanded into a wave equation [5, 6, 9].

$\begin{array}{ll}\frac{{\partial }^2{E}_Z}{\partial r^2}+\frac{1}{r}\frac{\partial E_Z}{\partial r}+\frac{1}{r^2}\frac{{\partial }^2{E}_Z}{\partial {\varphi }^2}+\frac{{\partial }^2{E}_Z}{\partial z^2}+{(\frac{n\omega }{c})}^2{E}_Z=0& (3)\end{array}$

The following parameters can generally be provided in the field of optical fiber communication k = 2π/λ = 2πf/c = ω/c. λ and f are wavelength and frequency, β is propagation constant. As it is shown in Figure 3, core (0 ≤ r ≤ a) refractive index n(r) = n_c, cladding (r ≥ a) refractive index n(r) = n₁.

FIGURE 3

Figure 3. Schematic diagram of the coordinates of the fiber in the cylindrical coordinate system.

E_z(z) in Equation (3) is set as E_z(r, ϕ, z) = E_z(r)E_z(ϕ)E_z(z) with the method of separation of variables. The optical signal transmitted along the z-axis E_z(z) is of the form of exp(-jβz). As optical fiber is of circular symmetry, E_z(ϕ) is the periodic function for ϕ. As a result, it can be set as exp(jmϕ) in which m is an integer. Because E_z(r) is unknown, it can be expressed as

$\begin{array}{ll}{E}_z(r,\varphi ,z)=E_z(r)e^{j(m\varphi -\beta z)}.& (4)\end{array}$

In the core and cladding, substituting Equation (4) into Equation (3) yields two m-order Bessel equations

$\begin{array}{ll}\frac{d^2{E}_z(r)}{d{r}^2}+\frac{1}{r}\frac{d{E}_Z(r)}{dr}+(\frac{u^2}{a^2}-\frac{m^2}{r^2})E_Z(r)=0(r\le a).& (5)\end{array}$

$\begin{array}{ll}\frac{d^2{E}_z(r)}{d{r}^2}+\frac{1}{r}\frac{d{E}_Z(r)}{dr}-(\frac{w^2}{a^2}-\frac{m^2}{r^2})E_Z(r)=0(r\ge a).& (6)\end{array}$

Among them, u, v, and w are three dimensionless variables namely

$\begin{array}{ll}\begin{array}{l}{u}^2=a^2(n_c^2{k}^2-{\beta }^2).\hfill \\ w^2=a^2({\beta }^2-n_1^2{k}^2).\hfill \\ v^2=u^2+w^2=a^2{k}^2(n_c^2-n_1^2).\hfill \end{array}\}& (7)\end{array}$

Therefore, the specific distribution of the electromagnetic in the fiber can be obtained through analysis of the solution to Equations (5) and (6) [5, 6].

In the core (r ≤ a), the light wave produces total internal reflection, so the transmission of the light wave in the Z direction is slower than the transmission of a plane wave in the medium n_c, namely β < kn_c. Where r = 0, the electromagnetic field should be a finite real number. According to these characteristics, the solution to Equation (5) should be m order Bessel function J_m(ur/a), so the expression of the electric field E_z(r, ϕ, z) and the magnetic field H_z(r, ϕ, z) in the core is as follows

$\begin{array}{ll}\begin{array}{l}{E}_{zc}(r,\varphi ,z)=A\frac{J_m(ur/a)}{J_m(u)}{e}^{j(m\Phi -\beta z)}(0\le r\le a).\hfill \\ H_{zc}(r,\varphi ,z)=B\frac{J_m(ur/a)}{J_m(u)}{e}^{j(m\Phi -\beta z)}(0\le r\le a).\hfill \end{array}\}& (8)\end{array}$

In the cladding (r ≥ a), the light wave decays in the r direction. Where r → ∞, the electromagnetic field should decay to zero, namely β > kn₁. The solution to Equation (6) should take the m-order-corrected Bessel function K_m(ur/a), so the expression of the electric field E_z(r, ϕ, z) and the magnetic field H_z(r, ϕ, z) in the cladding is as follows

$\begin{array}{ll}\begin{array}{l}{E}_{z1}(r,\varphi ,z)=A\frac{K_m(wr/a)}{k_m(w)}{e}^{j(m\Phi -\beta z)}(r\ge a).\hfill \\ H_{z1}(r,\varphi ,z)=B\frac{K_m(wr/a)}{k_m(w)}{e}^{j(m\Phi -\beta z)}(r\ge a).\hfill \end{array}\}& (9)\end{array}$

In the equation, A and B are constants determined by the excitation conditions. It can be concluded from two types of Bessel function curves of the principle of optical fiber communication that J_m(u) is similar to a sine curve with analogous amplitude attenuation, and K_m(w) is similar to an index curve of attenuation. It can be learned from Equation (7) that where such parameters as n_c, n₁, a, and k are determined, u and w are only determined by β. Therefore, deriving the characteristic equation, satisfying β can obtain the value of β and u,w. The boundary condition of the electromagnetic in the core-cladding surface is as follows

$\begin{array}{ll}\begin{array}{l}{E}_{zc}=E_{z1}{H}_{zc}=H_{z1}.\hfill \\ E_{\varphi c}=E_{\varphi 1}{H}_{\varphi c}=H_{\varphi 1}.\hfill \end{array}\}& (10)\end{array}$

It can be learned from Equations (8) and (9) that E_z and H_z satisfy the requirement of the boundary condition. The boundary condition satisfied by E_ϕ and H_ϕ can derive the characteristics equation satisfied by β

$\begin{array}{ll}\begin{array}{c}[\frac{{J^{\prime }}_m(u)}{u{J}_m(u)}+\frac{{K^{\prime }}_m(w)}{w{K}_{{}_m}(w)}][\frac{n_c^2}{n_1^2}\frac{{J^{\prime }}_m(u)}{u{J}_m(u)}+\frac{{K^{\prime }}_m(w)}{wK(w)}]\\ ={(\frac{\beta }{nk})}^2{m}^2(\frac{1}{u^2}+\frac{1}{w^2})(\frac{n_c^2}{n_1^2}\frac{1}{u^2}+\frac{1}{w^2}).\end{array}& (11)\end{array}$

The equation is combined with the characteristic parameters v defined by Equation (7); the value of β can be obtained with the numerical solution and thus determine the electromagnetic field distribution of light wave in the core.

Analysis of Photonic Bandgap Theory for Bragg Fiber With High-Index Core

A photonic crystal is a new type of optical material that emerged in recent years. The regular microstructure is introduced onto ordinary optical material artificially to form the microstructural material with a periodically changing refractive index. Generally speaking, the size of the microstructure is sub-micron and of the same order of magnitude to the wavelength of the light wave. This material with a periodical distribution of refractive index shows the special optical property for selecting different wavelengths of light. In other words, the light of some wavelengths could not exist or be transmitted in the photonic crystal but be reflected. For these wavelengths, photonic crystal is like a mirror to stop and reflect the incident light. This phenomenon is similar to the energy band structure of semiconductor physics [7, 10–12].

According to solid-state physics, the motion of electrons in its periodic potential field satisfies the Schrödinger equation in natural crystal

$\begin{array}{ll}\begin{array}{l}\left[-\frac{{\hslash }^2}{2m}{\nabla }^2+V(\stackrel{\rightharpoonup }{r})\right]\psi =E\psi .\hfill \\ V(\stackrel{\rightharpoonup }{r})=V(\stackrel{\rightharpoonup }{r}+\stackrel{\rightharpoonup }{R}).\hfill \end{array}\}& (12)\end{array}$

In Equation (12), $V(\stackrel{\rightharpoonup }{r})$ represents the potential energy, and $\stackrel{\rightharpoonup }{R}$ represents the lattice constant in the crystal. The electron wave can exhibit the energy band structure in the periodic potential field and form a forbidden band due to the scattering of atoms of the crystal [11]. The formation mechanism of the energy band in the photonic crystal is similar to the earlier mentioned process. The propagation of the electromagnetic wave in medium satisfies Maxwell equation [13–16]

$\begin{array}{ll}\begin{array}{l}\nabla ·\stackrel{\rightharpoonup }{D}=\rho .\hfill \\ \nabla ·\stackrel{\rightharpoonup }{B}=0.\hfill \\ \nabla \times \stackrel{\rightharpoonup }{E}=-\frac{\partial \stackrel{\rightharpoonup }{B}}{\partial t}.\hfill \\ \nabla \times \stackrel{\rightharpoonup }{H}=\stackrel{\rightharpoonup }{J}+\frac{\partial \stackrel{\rightharpoonup }{D}}{\partial t}.\hfill \end{array}\}& (13)\end{array}$

In Equation (13) $\stackrel{\rightharpoonup }{J}=\sigma \stackrel{\rightharpoonup }{E}$ $\stackrel{\rightharpoonup }{D}=\epsilon \stackrel{\rightharpoonup }{E}$ $\stackrel{\rightharpoonup }{B}=\mu \stackrel{\rightharpoonup }{H}$. Among them, σ, ε, andμ represent conductivity, permittivity, and permeability, respectively. If there is no free charge and current while the medium is also a non-magnetic and isotropic material, $\epsilon =\epsilon (\stackrel{\rightharpoonup }{r})$ should be a periodic function considering the periodicity of the photonic crystal [14, 15]. $\epsilon (\stackrel{\rightharpoonup }{r})={\epsilon }_0{\epsilon }_r(\stackrel{\rightharpoonup }{r})$, μ = μ₀, where ${\epsilon }_r(\stackrel{\rightharpoonup }{r})$ is the relative permittivity of the medium. It can be obtained through substituting the discussed parameters into Equation (13)

$\begin{array}{ll}\begin{array}{l}\nabla ·{\epsilon }_0{\epsilon }_r\left(\stackrel{\rightharpoonup }{r}\right)\stackrel{\rightharpoonup }{E}=0.\hfill \\ \nabla ·{\mu }_0\stackrel{\rightharpoonup }{H}=0.\hfill \\ \nabla \times \stackrel{\rightharpoonup }{E}+{\mu }_0\frac{\partial \stackrel{\rightharpoonup }{H}}{\partial t}=0.\hfill \\ \nabla \times \stackrel{\rightharpoonup }{H}-{\epsilon }_0{\epsilon }_r\left(\stackrel{\rightharpoonup }{r}\right)\frac{\partial \stackrel{\rightharpoonup }{E}}{\partial t}=0.\hfill \end{array}\}& (14)\end{array}$

Considering that the incident light signal is a harmonic electromagnetic wave, if $\stackrel{\rightharpoonup }{E}=\stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r})e^{j\omega t}$, $\stackrel{\rightharpoonup }{H}=\stackrel{\rightharpoonup }{H}(\stackrel{\rightharpoonup }{r})e^{j\omega t}$, then it can be obtained through substituting into Equation (14)

$\begin{array}{ll}\begin{array}{l}\nabla ·{\epsilon }_0{\epsilon }_r\left(\stackrel{\rightharpoonup }{r}\right)\stackrel{\rightharpoonup }{E}\left(\stackrel{\rightharpoonup }{r}\right)=0.\hfill \\ \nabla ·{\mu }_0\stackrel{\rightharpoonup }{H}\left(\stackrel{\rightharpoonup }{r}\right)=0.\hfill \\ \nabla \times \stackrel{\rightharpoonup }{E}\left(\stackrel{\rightharpoonup }{r}\right)+j\omega {\mu }_0\stackrel{\rightharpoonup }{H}\left(\stackrel{\rightharpoonup }{r}\right)=0.\hfill \\ \nabla \times \stackrel{\rightharpoonup }{H}\left(\stackrel{\rightharpoonup }{r}\right)-j\omega {\epsilon }_0{\epsilon }_r\left(\stackrel{\rightharpoonup }{r}\right)\stackrel{\rightharpoonup }{E}\left(\stackrel{\rightharpoonup }{r}\right)=0.\hfill \end{array}\}& (15)\end{array}$

After simplifying Equation (15), it can be obtained for TE mode (H_x=H_y=E_z=0) [2, 5, 6]

$\begin{array}{ll}\nabla \times \left[\frac{1}{\epsilon (\stackrel{\rightharpoonup }{r})}\nabla \times \stackrel{\rightharpoonup }{H}(\stackrel{\rightharpoonup }{r})\right]={\left(\frac{\omega }{c}\right)}^2\stackrel{\rightharpoonup }{H}(\stackrel{\rightharpoonup }{r}).& (16)\end{array}$

It can be obtained for TM mode (E_x = E_y = H_z = 0)

$\begin{array}{ll}\nabla \times \nabla \times \stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r})={\left(\frac{\omega }{c}\right)}^2\epsilon (\stackrel{\rightharpoonup }{r})\stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r}).& (17)\end{array}$

In Equations (16) and (17), $c=\frac{1}{\sqrt{{\epsilon }_0{\mu }_0}}$ is the velocity of light in vacuum. Equations (16) and (17) are the Helmholtz equations obtained through Maxwell's equations. The permittivity in photonic crystal shows a periodical change. The permittivity is set as the sum of two parts $\epsilon (\stackrel{\rightharpoonup }{r})\mathrm{\text{=}}{\epsilon }^{\prime }(\stackrel{\rightharpoonup }{r})\mathrm{\text{+}}\bar{\epsilon }$, where ${\epsilon }^{\prime }(\stackrel{\rightharpoonup }{r})$ is the changing permittivity and $\bar{\epsilon }$ is the average permittivity. It can be obtained through substituting the discussed parameter in respect to Equation (17)

$\begin{array}{ll}\begin{array}{l}\left[-{\nabla }^2-{\left(\frac{\omega }{c}\right)}^2{\epsilon }^{\prime }(\stackrel{\rightharpoonup }{r})\right]\stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r})+\nabla \left[\nabla \stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r})\right]\hfill \\ ={\left(\frac{\omega }{c}\right)}^2\overline{\epsilon }\stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r}).\hfill \\ \hfill \\ {\epsilon }^{\prime }(\stackrel{\rightharpoonup }{r})={\epsilon }^{\prime }(\stackrel{\rightharpoonup }{r}+\stackrel{\rightharpoonup }{R}).\hfill \end{array}\}& (18)\end{array}$

Where $\stackrel{\rightharpoonup }{R}$ is the lattice constant of the photonic crystal. If we use Equations (18) and (12) to make the following analogy [17–19]

$\begin{array}{ll}\begin{array}{l}-{\left(\frac{\omega }{c}\right)}^2{\epsilon }^{\prime }(\stackrel{\rightharpoonup }{r})~V(\stackrel{\rightharpoonup }{r}).\hfill \\ {\left(\frac{\omega }{c}\right)}^2\overline{\epsilon }~E.\hfill \end{array}\}& (19)\end{array}$

The two are extremely similar. It is discovered in further comparison that Equation (18) has one more item ∇ [$\nabla \stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r})$] and is a vector, whereas Equation (12) is scalar. However, if vertical incidence or one-dimensional conditions are considered, then∇ [$\nabla \stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r})$] = 0. In this way, there is almost no difference between the two. As a result, Equation (18) can also use the Bloch theorem to calculate the energy band or bandgap. It can be seen from the previous analysis that the movement of a photon in a photonic crystal is similar to the movement of electrons in a periodic potential field, which could cause energy band structure with bandgap. The solution to Equations (16) and (17) show that there is no solution in some frequency bands. It means that photonic crystal stops the transmission of an electromagnetic wave in these frequency bands, resulting in the photonic bandgap. This method to constrain optical transmission is sometimes more efficient than total reflection [6, 20–23]. Because photonic crystal has the special property to control light, researchers introduced this microstructure into the cladding of fiber in the 1990s to form a forbidden band to stop light signal from entering the cladding and constrain it in the core to form a guided mode.

Conclusion

Bragg fiber with high-index core can provide two kinds of light-guiding modes for optical signal transmission, namely full reflection effect and photonic bandgap effect. The specific process of optical signal transmission in optical fiber is analyzed and calculated from the wave equation. The transmission constant is obtained by numerical solution to the equations β, and the distribution of the electromagnetic field and the conditions for forming the guided mode when the optical signal is transmitted in the core of fiber are determined [24, 25]. The photonic bandgap is a kind of special structure obtained by the analogy of photonic crystal and natural crystal, which is similar to the energy band structure of the natural crystal. By analogy with the equation established in the transmission of optical signals in photonic crystal and the Schrodinger equation of solid-state physics, it is learned that the optical signals of certain frequency bands in photonic crystals cannot be transmitted, thus forming the forbidden band, that is, the principle of photonic bandgap effect.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

DL and JZ contributed to the conception and design of the study. JZ organized the literature. DL performed the design of figures and wrote the first draft of the manuscript. All authors contributed to the manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the Natural Science Foundation of Anhui Province of China (Grant Nos. KJ2019A0879 and KJ2018A0588).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to express their sincere gratitude to the reviewers and the editors for their careful reviews and constructive recommendations.

References

1. Zhang WD, Li X, Bai JH, Zhang L, Zhao JL. Generation and application of fiber-based structured light field. Acta Optica Sin. (2019) 39:51–69. doi: 10.3788/AOS201939.0126003

CrossRef Full Text | Google Scholar

2. Niu J. Research on the band-Gap properties of two-dimensional double-layer photonic crystals (M.S. thesis). Dept. Communication, Henan Polytechnic University, Jiaozuo, China (2014).

Google Scholar

3. Zheng Y, Hwa-Yaw T. Industrial and medical applications of fiber Bragg gratings (Invited Paper). Chin Optics Lett. (2016) 14:25–9. doi: 10.3788/COL201614.120007

CrossRef Full Text | Google Scholar

4. Meng Y, Su XM, Pan Y. Characteristics of Fabry-Perot cavity based on dynamic grating in Er-doped fiber and fiber Bragg grating. Acta Optica Sin. (2018) 38:78–86. doi: 10.3788/AOS201838.1006003

CrossRef Full Text | Google Scholar

5. Yue YL. Studies on the band-Gap structures of photonic crystal fiber and properties of directional coupling waveguides (M.S. thesis). Dept. Communication, Nanchang University, Nanchang, China (2008).

Google Scholar

6. Tang C. Research on photonic crystal fibers (M.S. thesis). Dept. Communication, University of Electronic Science and Technology of China, Chengdu, China (2005).

Google Scholar

7. Zhang M, Sun X. Optical Fiber in Principle and System of Optical Fiber Communication. Nanjing: Southeast University Press (2009). p. 24–32.

Google Scholar

8. Xu XN, Chen YJ. Curvature sensing measurement based on seven-core fiber and few-mode fiber splicing structure. Acta Optica Sin. (2019) 39:03060011–7. doi: 10.3788/AOS201939.0306001

CrossRef Full Text | Google Scholar

9. Zhang H, Wu Z, Shum P, Wang R, Dinh X, Fu S, et al. Fiber Bragg gratings in heterogeneous multicore fiber for directional bending sensing. J Optics. (2016) 18:085705–10. doi: 10.1088/2040-8978/18/8/085705

CrossRef Full Text | Google Scholar

10. Ertman S, Lesiak P, Woliński TR. Optofluidic photonic crystal fiber-based sensors. J Lightwave Technol. (2017) 35:3399–405. doi: 10.1109/JLT.2016.2596540

CrossRef Full Text | Google Scholar

11. Li Y, Tian J, Fu Q, Sun Y, Yao Y. A multi-point switchable and self-adaptive ultrasonic sensor using fiber Bragg gratings in a fiber ring laser. J Lightwave Technol. (2019) 37:1160–7. doi: 10.1109/JLT.2018.2888756

CrossRef Full Text | Google Scholar

12. Dong Y, Xiao S, Wu B, Xiao H, Jian S. Refractive index and temperature sensor based on D-shaped fiber combined with a fiber Bragg grating. IEEE Sens J. (2019) 19:1362–7. doi: 10.1109/JSEN.2018.2880305

CrossRef Full Text | Google Scholar

13. Chang M, Li B, Chen N, Lu X, Zhang X, Xu J. A compact and broadband photonic crystal fiber polarization filter based on a plasmonic resonant thin gold film. IEEE Photonics J. (2019) 11:1–12. doi: 10.1109/JPHOT.2019.2899117

CrossRef Full Text | Google Scholar

14. Rifat A, Mahdiraji GA, Ahmed R, Desmond MC, Sua YM, Shee YG, et al. Copper-graphene-based photonic crystal fiber plasmonic biosensor. IEEE Photonics J. (2016) 8:4800408–15. doi: 10.1109/JPHOT.2015.2510632

CrossRef Full Text | Google Scholar

15. Huq Arif MF, Ahmed K, Asaduzzaman S, Azad MAK. Design and optimization of photonic crystal fiber for liquid sensing applications. Photonic Sens. (2016) 6:279–88. doi: 10.1007/s13320-016-0323-y

CrossRef Full Text | Google Scholar

16. Tao C, Wei H, Feng W. Photonic crystal fiber in-line Mach-Zehnder interferometer for explosive detection. Optics Express. (2016) 24:2806–17. doi: 10.1364/OE.24.002806

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Belli F, Abdolvand A, Travers JC, Russell SJ. Control of ultrafast pulses in a hydrogen-filled hollow-core photonic-crystal fiber by Raman coherence. Phys Rev A. (2018) 97:013814–22. doi: 10.1103/PhysRevA.97.013814

CrossRef Full Text | Google Scholar

18. Chen H, Yan H, Shan G. Design of two-dimensional bending vector sensor based on selective infiltration of photonic crystal fiber. Chin J Lasers. (2016) 43:0105003–11. doi: 10.3788/CJL201643.0105003

CrossRef Full Text | Google Scholar

19. Zhang SH, Li JS, Li SG. Surface plasmon resonance sensor based on D-shaped photonic crystal fiber with two micro-openings. Optical Fiber Technol. (2018) 46:311–7. doi: 10.1088/1361-6463/aace72

CrossRef Full Text | Google Scholar

20. Chen X, Xia L, Li C. Surface plasmon resonance sensor based on a novel D-shaped photonic crystal fiber for low refractive index detection. IEEE Photonics J. (2018) 10:1–9. doi: 10.1109/JPHOT.2018.2790424

CrossRef Full Text | Google Scholar

21. Wu T, Shao Y, Wang Y, Cao S, Wang Y. Surface plasmon resonance biosensor based on gold-coated side-polished hexagonal structure photonic crystal fiber. Optics Express. (2017) 25:20313–22. doi: 10.1364/OE.25.020313

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Chen D, Shen L. Ultrahigh Birefringent photonic crystal fiber with ultralow confinement loss. IEEE Photonics Technol Lett. (2014) 4:185–7. doi: 10.1109/LPT.2006.890040

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Xi X, Wong G, Frosz M, Babic F, Ahmed G, Jiang X, et al. Orbital-angular-momentum-preserving helical Bloch modes in twisted photonic crystal fiber. Optica. (2014) 1:00165–9. doi: 10.1364/OPTICA.1.000165

CrossRef Full Text | Google Scholar

24. Morshed M, Imran HM, Roy TK, Uddin MS, Abdur RSM. Microstructure core photonic crystal fiber for gas sensing applications. Appl Opt. (2015) 54:8637–43. doi: 10.1364/AO.54.008637

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Roussel N, Magne S, Martinez C, Ferdinand P. Measurement of index modulation along fiber bragg gratings by side scattering and local heating techniques. Optical Fiber Technol Mater Dev Syst. (2018) 5:119–32. doi: 10.1006/ofte.1998.0277

CrossRef Full Text | Google Scholar