How to Optimize the Supply and Allocation of Medical Emergency Resources During Public Health Emergencies

The solutions to the supply and allocation of medical emergency resources during public health emergencies greatly affect the efficiency of epidemic prevention and control. Currently, the main problem in computational epidemiology is how the allocation scheme should be adjusted in accordance with epidemic trends to satisfy the needs of population coverage, epidemic propagation prevention, and the social allocation balance. More specifically, the metropolitan demand for medical emergency resources varies depending on different local epidemic situations. It is therefore difficult to satisfy all objectives at the same time in real applications. In this paper, a data-driven multi-objective optimization method, called as GA-PSO, is proposed to address such problem. It adopts the one-way crossover and mutation operations to modify the particle updating framework in order to escape the local optimum. Taking the megacity Shenzhen in China as an example, experiments show that GA-PSO effectively balances different objectives and generates a feasible allocation strategy. Such a strategy does not only support the decision-making process of the Shenzhen center in terms of disease control and prevention, but it also enables us to control the potential propagation of COVID-19 and other epidemics.

1. Introduction

In December 2019, a few patients with atypical pneumonia were first diagnosed in Wuhan, China, and this was reported to the World Health Organization (WHO) [1]. Then, its etiology was identified as the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). It is obvious that the disease was spreading continuously from person to person at the end of January 2020 [2]. The confirmed and imported cases in the Hubei province, China, brought about severe coronavirus outbreaks in many cities across China. More seriously, the disease, called COVID-19, has since spread rapidly across China and to the rest of the world [1]. By the end of June 30, 2020, there were 10,185,374 confirmed cases and 503,862 deaths in 210 countries [3].

Currently, vaccines and antiviral medicines for COVID-19 are still under development. Besides, other pharmaceutical treatments (e.g., plasma therapy) are not likely to be implemented on a large scale. Therefore, the use of a personal protective equipment (PPE) (e.g., hand sanitizers, surgical face masks, and protective clothing) becomes one of the major non-pharmaceutical measures to reduce the infectious hazard [4]. The sudden outbreak throughout China has exacerbated an unprecedented PPE shortage, causing austere challenges to epidemic control [5]. Due to the limited stock of a PPE during the early phase of COVID-19 epidemic, the local health organization suffered great challenges. It has been an open problem for us to efficiently allocate a PPE during an epidemic propagation.

Currently, various models (e.g., SIS, SIR, and SVIR) are considered to model the spreading process for the purpose of estimating the affecting scope from the perspective of theoretical analysis [6–10]. It is also possible to introduce evolutionary game theory during the resource allocation process [11]. However, balancing the allocation of a PPE in different regions is still a tough task due to multiple risk factors and high interest. Two key factors are a high-risk population and the severity of infection [12]. As a result, this paper develops an improved particle swarm optimization algorithm to reconcile this decision making problem. It balances the heterogeneity of a high-risk population and the severity of infection by incorporating the one-way crossover and mutation operations into the particle swarm optimization framework and eventually generates a reasonable allocation strategy of a PPE.

We apply this algorithm for balancing the allocation of PPE in Shenzhen, which is one of the largest megacities [with a population of more than 11 million [13]] in Guangdong province, China. During the COVID-19 epidemic in China, Shenzhen reported 195 confirmed COVID-19 cases as of February 1, 2020, which was higher than all other cities except Hebei province at that time. Therefore, improving the medical emergency system has been one of the highest priorities in Shenzhen [14]. More specifically, the supply and allocation of PPE is an urgent matter in Shenzhen.

2. Methods

Shenzhen is divided into ten administrative districts. All parameters are set in Table 1. Let X = (x₁, ..., x₁₀) denote a PPE allocation over 10 districts, and $G=\sum _i{x}_i$ represent the total allocation. The optimization strategy is based on the following assumptions and objectives:

• High-risk population: Due to multiple complications and a high fatality rate of people over 65, we select people over 65 [17]. The ith district with O_i people aged 65 or more is allocated x_i sets of PPE defined in Equation (1), where N_i is the population size in the ith district.

$\begin{array}{ll}{\displaystyle \sum _i}{x}_i\times O_i/N_i& (1)\end{array}$

• The severity of infection: The ith district with I_i confirmed cases is allocated x_i sets of PPE defined in Equation (2). A_i is the number of impacted individuals per confirmed case, which is assumed to be 1,000 for all districts.

$\begin{array}{ll}{\displaystyle \sum _i}{x}_i\times A_i\times I_i/N_i& (2)\end{array}$

Based on the above two objectives, this paper proposes a novel multi-objective optimization algorithm, named as GA-PSO, developed on the basis of MODPSO [18]. More specifically, GA-PSO is partially modified to simultaneously optimize the high-risk population and the severity of infection. The overview of GA-PSO is shown in Figure 1. It adopts one-way crossover and mutation operations to modify MODPSO in order to enhance the quality of solutions and escape the local optimum [19, 20]. Every population is composed of a set of particles which is a feasible solution (i.e., X). Firstly, a random population of particles is initialized. X is a random integer vector by $G=\sum _i{x}_i$. Then, X is evaluated by the high-risk population and the severity of infection. It adopts the roulette method to select the preferable fitness particles. After that, it executes the one-way crossover operation. When a random number is less than the mutation value, it generates random particles. Finally, it iteratively generates new populations using particle status updating rules. During each iteration, the algorithm updates the Pareto solutions. When the number of iterations reaches the set value, the currently obtained Pareto solutions are the final solutions for the optimization problem.

TABLE 1

Table 1. Parameters are used in the experiments of the GA-PSO algorithm.

FIGURE 1

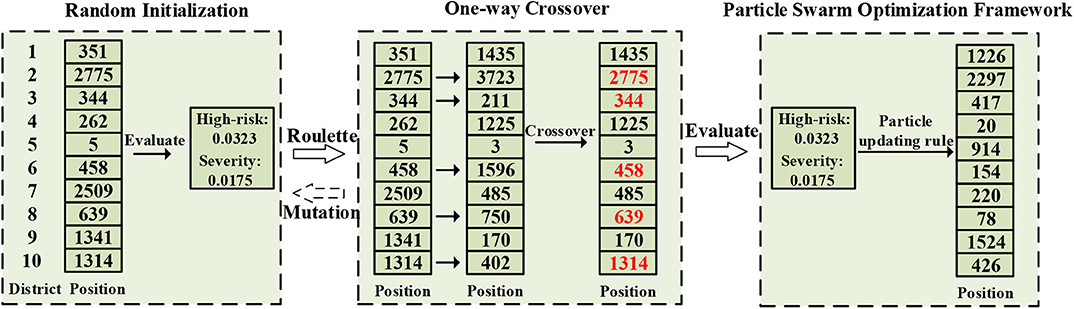
Figure 1. The overview of the GA-PSO algorithm, which comprises three components, i.e., the random initialization, the genetic operations, and the particle swarm optimization framework. The initial particles are selected by the roulette method. When a random number is less than the mutation rate, the particle is executed the initialization operation.

3. Results

The Shenzhen dataset is shown in Table 2 and includes the population size in 2016 [13], the number of people aged 65 or more in 2015 [15], and the cumulative cases on February 1, 2020 [16]. Besides, the PPE optimized allocation is calculated by GA-PSO as shown in Table 2. Figure 2 describes that the GA-PSO detects the Pareto front solutions for the PPE optimized allocation over 10 districts in Shenzhen. Every Pareto front solution indicates a feasible allocation. Different solutions can lead to different objective function values as quantified by the high-risk and severity priorities. The value of high-risk priority has ranged from 4.1% to 5.0%, and the value of the severity priority has ranged from 2.5% to 3.1% in Figure 2.

TABLE 2

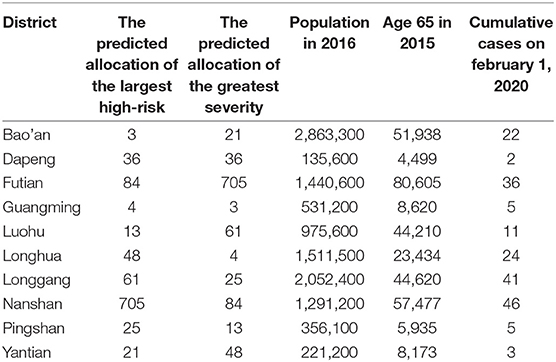
Table 2. The demographic information of 10 districts in Shenzhen and the predicated PPE allocation of the highest risk and the greatest severity objectives.

FIGURE 2

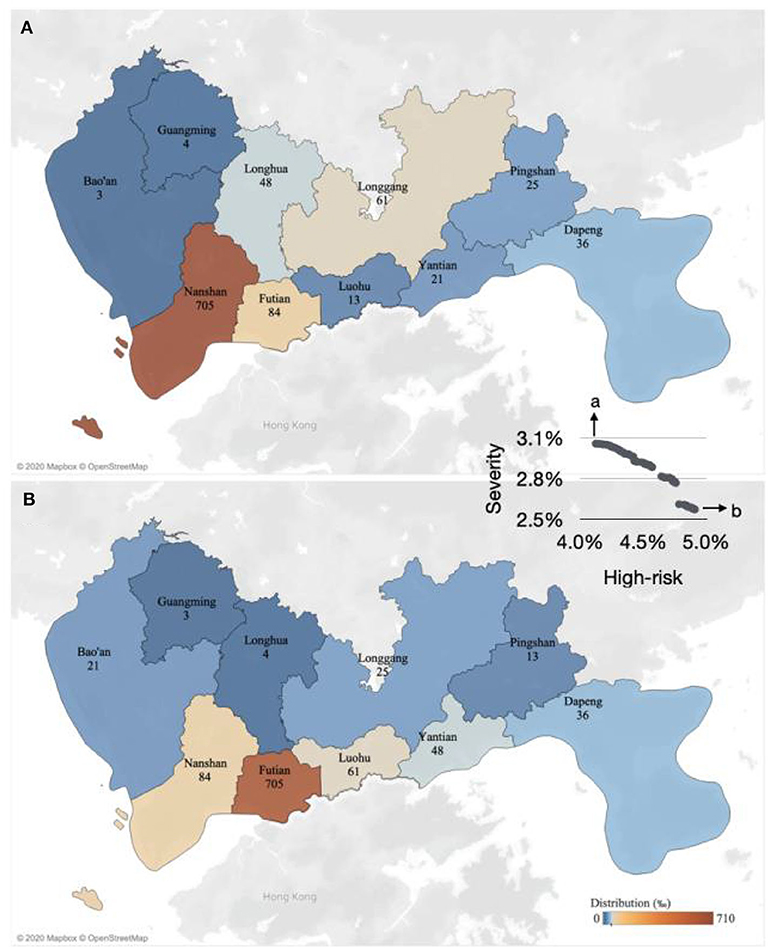
Figure 2. Estimated PPE optimized allocation in the 10 districts of Shenzhen on February 14, 2020. The Pareto frontier uses the two objectives of high-risk and severity priorities in the middle right inset. The predicted allocation of the greatest high-risk priority in (A) and the predicted allocation of the greatest severity priority in (B).

In summary, two objectives (i.e., the high-risk population and the severity of inflection) are added to obtain the PPE accessibility. The maximum value of the PPE accessibility is 7.53% for older or impacted individuals. When only the maximal high-risk population is the objective, the optimized allocation is estimated across 10 districts in Shenzhen, ranging from 3‰in suburban Bao'an to 705‰in central Nanshan. If the severity is the solitary objective, the allocation is from 3‰in suburban Guangming to 705‰in central Futian. The central districts of Futian and Nanshan top the PPE priority because of the maximal older people and confirmed cases.

4. Discussion

Metropols (e.g., New York, London, Paris, and San Paulo) have been experiencing an urgent demand for medical emergency resources since the early phase of the COVID-19 epidemic. The use of a personal protective equipment (PPE) (e.g., hand sanitizers, surgical face masks, and protective clothing) has become one of the major non-pharmaceutical measures with which to reduce the infectious hazard. Due to the limited stock of PPE in particular during the early phase of the COVID-19 epidemic, the local health organization has suffered greatly. It is therefore a challenge to balance the supply and allocation of PPE during the available time. To overcome this challenge for practical applications, the multi-objective optimization is a promising method.

A multi-objective optimization algorithm generates a set of Pareto solutions each of which is a tradeoff between multiple objectives. Consequently, the multi-objective optimization facilitates the decision making problem. In addition to PPE, the pharmaceutical prophylactics (e.g., antibiotics, vaccines, antitoxins, and other critical medical supplies) are also faced with the decision making problem because of the limited supply in the early phase. Our optimization algorithm for PPE can therefore be extended to other pharmaceutical prophylactics to narrow the scope of a disease spread and to avoid catastrophic economic and social consequences.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

CW, CG, YD, ZY, and QC performed the experiments. CW, CG, and FZ analyzed the data. CW, CG, YD, and JK wrote the paper. CW, CG, ZY, CZ, and JK planned the study. All authors contributed to the article and approved the submitted version.

Funding

This work was supported in part by the National Natural Science Foundation of China (No. 61976181), Natural Science Foundation of Chongqing (No. cstc2018jcyjAX0274), the Fundamental Research Funds for the Central Universities (No. XDJK2020D022), the Open Fund of Key Laboratory of Urban Land Resources Monitoring and Simulation (No. MNR KF-2019-04-034), Chongqing Graduate Student Research Innovation Project (No. CYS20116), and the Russian Ministry of Science and Education Agreement (No. 13.1902.21.0026).

Disclaimer

Frontiers Media SA remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Chen S, Yang J, Yang W, Wang C, Barnighausen T. COVID-19 control in China during mass population movements at New Year. Lancet. (2020) 395:764–6. doi: 10.1016/S0140-6736(20)30421-9

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Wu P, Hao X, Lau EHY, Wong JY, Leung KSM, Wu JT, et al. Real-time tentative assessment of the epidemiological characteristics of novel coronavirus infections in Wuhan, China, as at 22 January 2020. Eurosurveillance. (2020) 25:2000044. doi: 10.2807/1560-7917.ES.2020.25.3.2000044

PubMed Abstract | CrossRef Full Text | Google Scholar

3. World Health Organization. Coronavirus Disease 2019 (COVID-19): Situation Report - 162 (2020). Available online at: https://www.who.int/docs/default-source/coronaviruse/20200630-covid-19-sitrep-162.pdf?sfvrsn=e00a5466_2.

Google Scholar

4. Leung NH, Chu DK, Shiu EY, Chan KH, McDevitt JJ, Hau BJ, et al. Respiratory virus shedding in exhaled breath and efficacy of face masks. Nat Med. (2020) 26:676–80. doi: 10.1038/s41591-020-0843-2

CrossRef Full Text | Google Scholar

5. Ranney ML, Griffeth V, Jha AK. Critical supply shortages-the need for ventilators and personal protective equipment during the covid-19 pandemic. N Engl J Med. (2020) 382:e41. doi: 10.1056/NEJMp2006141

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Zhu P, Wang X, Zhi Q, Ma J, Guo Y. Analysis of epidemic spreading process in multi-communities. Chaos Solitons Fractals. (2018) 109:231–7.

PubMed Abstract | Google Scholar

7. Zhu P, Wang X, Li S, Guo Y, Wang Z. Investigation of epidemic spreading process on multiplex networks by incorporating fatal properties. Appl Math Comput. (2019) 359:512–24. doi: 10.1016/j.amc.2019.02.049

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Du Z, Holme P. Coupling the circadian rhythms of population movement and the immune system in infectious disease modeling. PLoS ONE. (2020) 15:e0234619. doi: 10.1371/journal.pone.0234619

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Du Z, Nugent C, Galvani AP, Krug RM, Meyers LA. Modeling mitigation of influenza epidemics by baloxavir. Nat Commun. (2020) 11:1–6. doi: 10.1038/s41467-020-16585-y

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Du Z, Xu X, Wang L, Fox SJ, Cowling BJ, Galvani AP, et al. Proactive social distancing mitigates COVID-19 outbreaks within a month across 58 mainland China cities. Emerg Infect Dis. (2020) 26. doi: 10.1101/2020.04.22.20075762

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Zhu P, Wang X, Jia D, Guo Y, Li S, Chu C. Investigating the co-evolution of node reputation and edge-strategy in prisoners dilemma game. Appl Math Comput. (2020) 386:125474. doi: 10.1016/j.amc.2020.125474

CrossRef Full Text | Google Scholar

12. Bansal S, Pourbohloul B, Meyers LA. A comparative analysis of influenza vaccination programs. PLoS Med. (2006) 3:e387. doi: 10.1371/journal.pmed.0030387

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Yang X, Xie Z. Shenzhen Statistical Yearbook. Shenzhen.

PubMed Abstract

14. Zhang D, Mou J, Cheng J, Griffiths S. Public health services in Shenzhen: a case study. Public Health. (2011) 125:15–19. doi: 10.1016/j.puhe.2010.10.007

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Futian Government. Study on Evaluation of Population Aging in Futian District. Shenzhen (2017). Available online at: http://www.szft.gov.cn/wap/ftzw/tjxx/qttjgb_41536/content/post_3321769.html

PubMed Abstract

16. Shenzhen Health Commission. Distribution of districts in Shenzhen on February 1, 2020. Tencent (2020). Available online at: https://xw.qq.com/cmsid/20200202A04J5Y00

PubMed Abstract

17. The Novel Coronavirus Pneumonia Emergency Response Epidemiology Team. The Epidemiological Characteristics of an Outbreak of 2019 Novel Coronavirus Diseases (COVID-19)–China, 2020 (2020). Available online at: http://weekly.chinacdc.cn//article/id/e53946e2-c6c4-41e9-9a9b-fea8db1a8f51

Google Scholar

18. Cai Q, Gong M, Ruan S, Miao Q, Du H. Network structural balance based on evolutionary multiobjective optimization: a two-step approach. IEEE Trans Evol Comput. (2015) 19:903–16. doi: 10.1109/TEVC.2015.2424081

CrossRef Full Text | Google Scholar

19. Wang C, Deng Y, Li X, Chen J, Gao C. Dynamic community detection based on a label-based swarm intelligence. IEEE Access. (2019) 7:161641–53. doi: 10.1109/ACCESS.2019.2951527

CrossRef Full Text | Google Scholar

20. Wang C, Deng Y, Li X, Xin Y, Gao C. A label-based nature heuristic algorithm for dynamic community detection. In: PRICAI 2019: Trends in Artificial Intelligence. Fiji (2019). p. 621–632.

Google Scholar