Green's Function Techniques for Infinite Nuclear Systems

I review the application of self-consistent Green's function methods to study the properties of infinite nuclear systems. Improvements over the last decade, including the consistent treatment of three-nucleon forces and the development of extrapolation methods from finite to zero temperature, have allowed for realistic predictions of the equation of state of infinite symmetric, asymmetric and neutron matter based on chiral interactions. Microscopic properties, like momentum distributions or spectral functions, are also accessible. Using an indicative set of results based on a subset of chiral interactions, I summarize here the first-principles description of infinite nuclear systems provided by Green's function techniques, in the context of several issues of relevance for nuclear theory including, but not limited to, the role of short-range correlations in nuclear systems, nuclear phase transitions and the isospin dependence of nuclear observables.

1. Introduction

The recent discoveries of neutron-star binaries GW170817 [1] and GW190425 [2] are formidable feats in gravitational-wave (GW) and multimessenger astronomy. These events provide unique insight into a great variety of astrophysical questions, from stellar physics to cosmology. In dense matter physics, the analysis of multimessenger data is providing a unique way forward in our understanding of matter in its most neutron-rich form. Gravitational waves from the inspiral carry imprints of the equation of state (EoS) of neutron-star matter [3]. The initial analysis of the source GW170817 has already provided significant constraints on the masses, radii and EoSs of neutron stars [4]. The expectation is that, as more of these GW sources are detected in the next few years, they will provide more and more accurate observational constraints. Simultaneous developments in X-ray burst observations are also providing equally important and independent constraints on the EoS and the physical properties of neutron stars (NSs) [5]. Soft X-ray waveforms of rotation-powered pulsars also provide promising NS constraints [6, 7].

Theoretical nuclear physics tools provide relevant input for dense matter physics. Among others, there have been several significant efforts trying to put constraints on the symmetry energy [8, 9] or the EoS itself [10]. The data in the new generation of astrophysical observations will tighten these constraints, and may even allow for further relevant conclusions on macroscopic observables, like the EoS [11]. Connecting these bulk observable constraints to the strong interaction among neutrons requires significant efforts on the nuclear theory side. There is a stringent need for the development of realistic predictions with systematic errors based on our understanding of the physics of dense systems. This necessarily requires the use of ab initio nuclear theory techniques that can provide a solid, quantifiable link between macro- and micro-physics [12, 13]. For the case of GW inspirals, this link also demands for an understanding of dense matter properties not only in the zero-temperature domain, but at temperature scales which are significant enough to modify some nuclear properties (e.g., temperatures in the range of tens of MeV) [14–18]. There is a similar need for microphysics inputs in the case of core-collapse supernovae, where the formation process of proto-NSs [19] and the subsequent development of a neutrino-heated shock wave require an understanding of neutrino emission from compact objects [20, 21].

The accuracy of theoretical nuclear physics predictions is hampered by a variety of different factors. First, the strong interaction among nucleons is difficult to pin down. Scattering experiments provide extremely useful insight at the two-body level, but three-neutron forces remain relatively unconstrained [22]. For neutrons, four-body and higher level forces are expected to play a small role for the EoS [23]. Chiral effective field theory (χEFT) [24, 25] and Lattice QCD [26, 27] efforts in the next decade will be crucial to provide clear limits on these terms. As a first approximation, one can estimate the uncertainty in the strong force by considering different input Hamiltonians that fit scattering phase-shifts and few body data [28, 29].

In addition, even if the interaction is perfectly understood, one still needs to solve a many-body multicomponent¹ problem to link the NN force to the macroscopic properties related to the EoS. While several methods have been devised to attack this problem, a clear-cut solution is difficult, if not impossible. The treatment of many-body correlations differs depending on the method that is used to describe dense neutron-rich systems [30, 31]. In particular, the structure of the strong force itself—particularly its short-range core—may preclude low-order perturbative treatments. Self-consistent Green's function (SCGF) techniques can be used to obtain both perturbative and non-perturbative results from these interactions of relevance for nuclear physics [32–34]. This approach offers the promise to simultaneously tackle issues that are relevant for neutron-star astrophysics, while providing insight into problems that are appropriate for nuclear structure (particularly in terms of short-range correlations).

My aim with this review is to provide a summary of the recent advances of the SCGF treatment of infinite nuclear systems. I will only explore the uncertainty associated to the Hamiltonian by looking at calculations performed with three different chiral interactions. This represents a small subset of possible forces, and is by no means representative of the overall uncertainty due to the strong interaction in infinite systems. Even then, these interactions predict relatively different micro- and macroscopic properties below, around and above saturation density. A benchmark analysis with different methods, while necessary to fully understand the limitations of nuclear theory, lies beyond the scope of this contribution. I will instead provide a qualitative, and somewhat limited discussion of the many-body scheme dependence of the results, by providing comparisons to many-body perturbation theory results based on similar Hamiltonians.

I start this review with a brief summary of the formal tools associated to the SCGF formalism in the following section. I note that there are monographs [32, 34] and books [33, 35, 36] that provide many more details, and I refer the interested reader to those. Section 3 is devoted to a discussion of recent numerical results that concern single-particle properties in dense matter. These include spectral functions, self-energies and momentum distributions. In section 4, the discussion turns into the macrophysics of infinite nuclear systems, with a particular emphasis on the EoS. I finally provide some conclusions and an outlook in section 5.

2. Self-Consistent Green's Function Approach

2.1. Formalism

Many-body Green's function are a natural starting point in the discussion of quantum many-body systems [33, 37]. Green's function (or propagators) arise naturally in diagrammatic treatments, and provide a description of several real or virtual excitation processes within the many-body system. Formally, these propagators take the form of time-ordered correlation functions associated to the creation and annihilation of excitations and can be expressed in terms of Feynman diagrams [38, 39]. Broadly speaking, Green's function techniques attempt to sum series of the most physically relevant diagrams to describe the system under consideration. For instance, in the case of thermodynamics of correlated infinite systems, one often resorts to an expansion that involves renormalized interactions treating the short-range core non-perturbatively via infinitely repeated scattering processes [40]. When it comes to the response of finite systems, one instead considers diagrams that describe relevant excitations within the system [32]. This allows SCGF practitioners to look at many-body systems from different perspectives, providing a characterization of the system that includes microscopic and macroscopic properties.

In SCGFs methods, internal propagators of all diagrams are consistently dressed. In other words, renormalization effects are introduced from the onset in the formalism - and hence the monicker “self-consistent.” At a diagrammatic level, this means that only skeleton (or 1-particle-irreducible) diagrams are required for single-particle self-energies. In practice, one pays the price of having to run simulations iteratively for a given system which, in infinite matter, translates into a fixed density (or temperature) [33]. A key advantage of SCGF methods is the direct access to the propagators themselves. These contain relevant information for the system's microphysics, in terms of spectroscopy and strength distributions [32]. Moreover, propagators can also be used to compute bulk properties, including total energies, thermodynamical properties and pressures. Within a single SCGF simulation, one therefore obtains a significantly broad scope in terms of physical information. This goes beyond the reach of other many-body approaches which are mostly tailored to address the energy of the system, either by minimizing it using quantum Monte-Carlo [31, 41] techniques, or addressing it by means of diagrams, like the Brueckner-Hartree-Fock (BHF) approach [30].

Another strategic advantage of the SCGF formalism is its generality. Within the very same formalism, one can tackle both finite and infinite systems—see [42] for a contribution in this volume that specifically discusses recent applications of SCGF techniques to finite nuclei. More importantly in the context of astrophysics, SCGF methods can be formulated consistently at finite temperature [33, 37]. In fact, fully-fledged infinite nuclear matter studies are usually performed at finite temperature [43–45]. For sufficiently large temperatures (typically T ⪆ 2 − 5 MeV), this treatment avoids the complications associated to nuclear superfluidity [43, 46] that plagued early attempts of SCGF calculations in the 1990s [47]. Furthermore, a finite temperature formulation allows for access to astrophysically-relevant temperature dependences of observables [18], and provides insight into liquid-gas, thermally-induced phase transitions in dense systems [48, 49]. It is now possible to use these non-superfluid finite temperature calculations to perform meaningful extrapolations to zero temperatures for both microscopic [50] and bulk properties [51], as we shall see in the following.

A key quantity in the SCGF formalism is the so-called spectral function ${{A}}_k(\omega )$. This characterizes fully the one-body propagator ${G}$, which is generally defined as a time-ordered product of a creation and a destruction operator [33, 36]. Upon a Hilbert transform with a complex energy variable z, the spectral function and the one-body propagator are related via a spectral decomposition,

$\begin{array}{ll}{{G}}_k(z)={\displaystyle \int }\frac{\text{d}\omega }{2\pi }\frac{{{A}}_k(\omega )}{z-\omega }.& (1)\end{array}$

Different time orderings give rise to different components of the propagator, including the retarded and advanced components that can be addressed by taking z = ω ± iη, with η infinitessimal [35]. All time-ordered components can be accessed through the spectral function ${{A}}_k(\omega )$, which also has the advantage of having a probabilistic interpretation. The spectral function provides the probability distribution associated to either extracting or attaching a particle with well-defined momentum k, and energy ω, to the infinite system. In the finite-temperature Matsubara formalism, the Lehmann representation of ${{A}}_k(\omega )$ takes into account not only the thermal excitations on the ground state of the system, but also the presence of excited states that are populated according to a thermal distribution,

$\begin{array}{l}{{A}}_k(\omega )=2\pi {\displaystyle \sum _{n,m}}\frac{e^{-\beta (E_n-\mu N_n)}}{Z}|\langle m|{\widehat{a}}_k^{†}|n\rangle {|}^2\delta \left[\omega -(E_m-E_n)\right]\\ \begin{array}{l}+2\pi {\displaystyle \sum _{n,m}}\frac{e^{-\beta (E_n-\mu N_n)}}{Z}|\langle m|{\widehat{a}}_k|n\rangle {|}^2\delta \left[\omega -(E_n-E_m)\right].\end{array}& (2)\end{array}$

In this equation $\widehat{a}$_k (${\widehat{a}}_k^{†}$) are destruction (creation) operators of single-particle states with well-defined momentum k. A many-body system with N_n particles can have different eigenstates of the many-body Hamiltonian with energy E_n, labeled with quantum number n. $Z=\sum _n{e}^{-\beta (E_n-\mu N_n)}$ is the corresponding partition function and, in the grand-canonical ensemble, the system is described in terms of a given temperature T = 1/β, and a chemical potential μ.

As a well-defined probability distribution, the spectral function is normalized $\int \mathrm{\text{d}}\omega {{A}}_k(\omega )/2\pi =1$. When this integral is weighted by the corresponding thermal population of hole states, one obtains the momentum distribution of the system,

$\begin{array}{ll}{n}_k={\displaystyle \int }\frac{\text{d}\omega }{2\pi }{{A}}_k(\omega )f(\omega ).& (3)\end{array}$

In turn, even though the formulation of the problem is grand-canonical in nature, the momentum distribution can be used to fix the density of the system by requiring that the chemical potential μ in the Fermi-Dirac function f (ω) = [1 + exp[(ω − μ)/T]]⁻¹ is such that the normalization condition

$\begin{array}{ll}\rho =\nu {\displaystyle \int }\frac{{\text{d}}^{3}k}{{(2\pi )}^3}{n}_k& (4)\end{array}$

is fulfilled. Here ν = 2 represents the degeneracy in spin for neutron or asymmetric matter, and ν = 4 is the degeneracy in spin and isospin for symmetric matter.

The Dyson equation $\left[z-k^2/2m-{\Sigma }_k(z)\right]{{G}}_k(z)=1$ provides a connection between the one-body propagator ${G}$ and the self-energy Σ. The latter is traditionally decomposed into a real and an imaginary part, and the spectral function is then connected to the retarded self-energy by the equation:

$\begin{array}{ll}{{A}}_k(\omega )=\frac{-2\text{Im}{\Sigma }_k(\omega )}{[\omega -\frac{k^2}{2m}-\text{Re}{\Sigma }_k(\omega ){]}^2+[\text{Im}{\Sigma }_k(\omega ){]}^2}.& (5)\end{array}$

The real part of the self-energy ReΣ_k(ω), is often interpreted as an energy-dependent mean-field potential [52]. Systems with a well-defined quasi-particle structure have spectral functions with strong peaks around the energy for which the denominator of Equation (5) is smallest. This happens at the so-called quasi-particle energy, which can be accessed from ReΣ_k(ω) by solving the self-consistent equation

$\begin{array}{ll}{\epsilon }_k=\frac{k^2}{2m}+\text{Re}{\Sigma }_k({\epsilon }_k),& (6)\end{array}$

at each momentum k. This on-shell condition provides a one-to-one correspondence between energy and momentum—a dispersion relation that is often used to characterize relevant single-particle properties. Other many-body approaches, like many-body perturbation theory or the BHF diagrammatic method, make use of such on-shell dispersion relations throughout [39]. The SCGF method, in contrast, considers all energy-dependent, offshell components in the self-energy and the spectral function. These effects are relevant to describe the fragmentation of single-particle strength [33].

The imaginary part of the self-energy is usually discussed in terms of quasi-particle lifetimes [33]. For the retarded self-energy, the imaginary component is negative, and is directly related to the available phase space. Indeed, for an energy-independent self-energy, the Fourier transform of Equation (5) to the time domain provides a propagator that decays exponentially in time with a characteristic timescale,

$\begin{array}{ll}{\tau }_k^{-1}={\Gamma }_k=-2\text{ Im}{\Sigma }_k({\epsilon }_k).& (7)\end{array}$

The energy and momentum dependence of the self-energy can be characterized in some domains by a model-independent analysis [33, 52]. According to Luttinger's theorem for normal fermionic systems, at zero temperature the imaginary part of the self-energy should be exactly zero at the Fermi energy and, close to this energy, it should behave quadratically, so that $\text{Im}{\Sigma }_k(\omega =\mu )\approx a_k{(\omega -\mu )}^2$ [53]. When temperature sets in, ImΣ_k at ω = μ grows quadratically with T [37].

Expressions for the self-energy can be derived at different orders in many-body perturbation theory [33, 36]. I will present results here based on the ladder approximation [33]. A summary in terms of diagrams of this approximation is provided in Figure 1. The key ingredient in this approach is the T−matrix shown in diagram (c), which is obtained from a Lippman-Schwinger equation where the intermediate kernel involves a particle-particle and hole-hole two-body propagator at finite temperature. This energy-dependent in-medium interaction describes re-scattering effects in the medium and can therefore capture short-range effects. Three-nucleon forces are included in the ladder approximation by constructing an effective two-body force, diagram (a) of Figure 1. This is the result of adding up the bare two-nucleon force (dashed line), V, and a three-body force (dotted line) that has been appropriately averaged over a third nucleon [54–56].

FIGURE 1

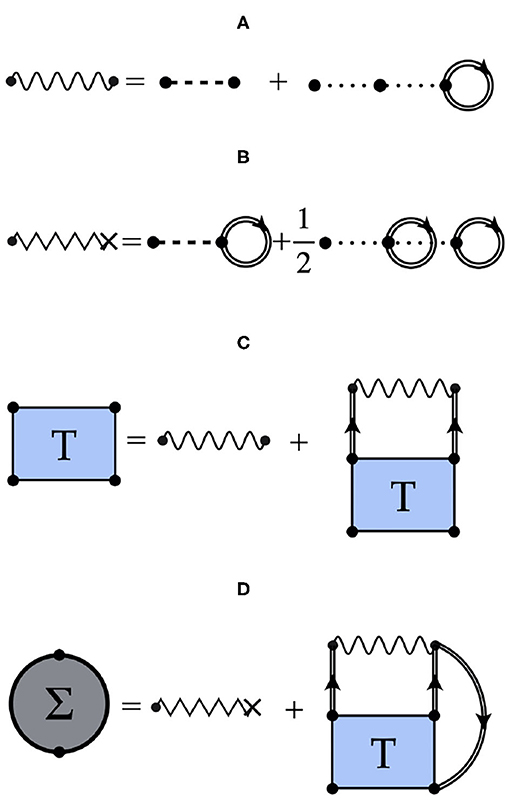
Figure 1. Diagrammatic representation of the ladder approximation to the self-energy, Σ, including three-nucleon interactions. Diagram (A) describes the two-body effective interaction (wiggly line) obtained from the sum of the two-body interaction V (dashed line) and an averaged three-nucleon force W (dotted line). Diagram (B) shows the one-body effective interaction. Diagram (C) provides the self-consistent equation for the T−matrix. Finally, diagram (D) represents the two components of the self-energy: an energy-independent one-body effective interaction, and a dispersive contribution arising from the T−matrix.

In the ladder approximation, the imaginary part of the self-energy is given by the expression:

$\begin{array}{l}\text{Im}{\Sigma }_k(\omega )={\displaystyle \int }\frac{{\text{d}}^3{k}_1}{{(2\pi )}^3}{\displaystyle \int }\frac{\text{d}{\omega }_1}{2\pi }{\langle \text{k}{\text{k}}_1|\text{Im}T(\omega +{\omega }_1)|\text{k}{\text{k}}_1\rangle }_A{{A}}_{k_1}({\omega }_1)\\ \begin{array}{l}\left[f({\omega }_1)+b(\omega +{\omega }_1)\right],\end{array}& (8)\end{array}$

where b(Ω) = [exp[(Ω − 2μ)/T] − 1]⁻¹ is a Bose-Einstein distribution and ImT is the imaginary part of the T−matrix. In SCGF methods, one generally computes the imaginary part first, which tends to be simpler to evaluate thanks to energy and momentum conservation. Whereas explicit expressions for the real part are normally available too, one can avoid a series of complex integrals over momentum and energy phase-space by computing the real part from the dispersion relation,

$\begin{array}{ll}\text{Re}{\Sigma }_k(\omega )={\Sigma }_k^{\infty }-{P}{\displaystyle \int }\frac{\text{d}{\omega }^{\prime }}{\pi }\frac{\text{Im}{\Sigma }_k({\omega }^{\prime })}{\omega -{\omega }^{\prime }},& (9)\end{array}$

where ${P}$ denotes the principal value. The energy-independent (but momentum-dependent) component ${\Sigma }_k^{\infty }$, is akin to a Hartree-Fock self-energy. This effective one-body interaction is built by averaging the two-nucleon and the three-nucleon interaction over the Fermi sea of one or two particles, as depicted in diagram (b) of Figure 1 [54]. This average includes propagator renormalization effects via a correlated momentum distribution,

$\begin{array}{l}{\Sigma }_k^{\infty }=\nu {\displaystyle \int }\frac{{\text{d}}^3{k}_1}{{(2\pi )}^3}{\langle k{k}_1|V|k{k}_1\rangle }_A{n}_{k_1}\\ \begin{array}{l}+\frac{\nu }{2}{\displaystyle \int }\frac{{\text{d}}^3{k}_1}{{(2\pi )}^3}{\displaystyle \int }\frac{{\text{d}}^3{k}_2}{{(2\pi )}^3}{\langle k{k}_1{k}_2|W|k{k}_1{k}_2\rangle }_A{n}_{k_1}{n}_{k_2}.\end{array}& (10)\end{array}$

In this expression, the matrix elements correspond to antisymmetrized two-nucleon (V) and three-nucleon (W) interactions, respectively. The chiral interactions that are used in this work are discussed in more detail in the following section.

The self-energy operator can be defined diagrammatically and encodes different many-body processes depending on the level of approximation [33]. At the lowest order, the so-called mean-field or Hartree-Fock approximation, the self-energy is energy-independent and formally given by the same expression as in Equation (10), but with internal momentum distributions n_k, computed from on-shell Fermi-Dirac distributions n_k = f (ε_k). Second-order self-energies are instead energy-dependent, proportional to V² and have already a non-trivial imaginary part [33, 51]. These account for 2p-1h and 1p-2h excitations within the system. In infinite matter applications, non-perturbative approximations beyond the second order are typically considered. A self-energy arising from a ladder resummation of the in-medium interaction deals effectively with the strong short-range and tensor components of the NN force, and leads to stable numerical results even for hard core interactions—for details see [57, 58].

When a SCGF calculation converges for a given set of external parameters, one typically stores the complex self-energy Σ_k(ω). All other microscopic properties, including spectral functions, can be derived from it according to Equation (5). The energy per particle of the system is then accessed by an energy-weighted integral over the spectral function, the so-called Galitskii-Migdal-Koltun sum-rule [33],

$\begin{array}{ll}\frac{E}{A}=\frac{\nu }{\rho }{\displaystyle \int }\frac{{\text{d}}^3{k}_1}{{(2\pi )}^3}{\displaystyle \int }\frac{\text{d}\omega }{2\pi }\frac{1}{2}\left[\frac{k^2}{2m}+\omega \right]{{A}}_k(\omega )f(\omega )-\frac{1}{2}\langle W\rangle .& (11)\end{array}$

Here, we also incorporate a correction term proportional to the expectation value of the 3NF 〈W〉. This is computed by using an additional integral over momentum of the second term in Equation (10). In other words, we keep the lowest order approximation to the expectation value of the 3NF, in agreement with techniques typically employed in finite nuclei [59]. The formal procedure to go beyond this approximation exists, as discussed in [54], but has not been implemented in infinite systems yet.

At finite temperature, the system is described in terms of thermodynamical potentials like the Helmholtz free energy F = E − TS. This requires an explicit calculation for the entropy S, based on Green's function methods. A proposal to compute S from spectral functions in dense matter was put forward in [58, 60] based on the formal techniques derived by Pethick and Carneiro [61, 62]. With access to the entropy, one can then derive all thermodynamical properties, including the pressure p = ρ(F/A − μ). Formally, the SCGF method is known to give rise to thermodynamically consistent results [33, 63]. For instance, a zero-temperature calculation of the chemical potential μ, from the Fermi energy of the system ε_k=kF, or from the density derivative of the free energy density, provides the same result. This formal agreement has also been demonstrated numerically in the past [45, 60].

In terms of formalism, there is no inconvenience to extend the SCGF method to asymmetric, multicomponent systems. In fact, the SCGF method has already been used to describe isospin asymmetric matter in the past [64, 65]. One can therefore characterize correlations and fragmentation in isospin-imbalanced systems [66, 67]. In asymmetric matter, all quantities become functions of isospin—i.e., the spectral functions for neutrons ${{A}}_k^n(\omega )$ and protons ${{A}}_k^p(\omega )$ are different, as are the self-energies and all other one-body properties. In addition to the isospin splitting, one must also consider changes in the effective interactions, so that neutron-neutron (nn), neutron-proton (np), proton-neutron (pn), and proton-proton (pp) in-medium T-matrices are explicitly different. Extensions of the normal ordering procedure to compute effective one and two-body forces from 3NF matrix elements are also necessary [56], but relatively straightforward [68]. The results for asymmetric matter presented here within the SCGF formalism include explicitly the effect of isospin asymmetry in the normal-ordering of 3NFs and in the extrapolation procedure from finite to zero temperature.

2.2. Interactions

For consistency in the presentation, all the results that follow have been generated with the same set of interactions. I will consider three sets of χEFT-inspired forces. At the NN level, these three interactions have been introduced in [69]: they have been fitted to the same NN scattering data and incorporate different cutoffs in the relative momentum: Λ = 414 MeV, 450 MeV and 500 MeV. These forces also differ slightly in the shape (particularly the sharpness) of the regulator in relative momentum. 3NFs arise naturally in the χEFT formalism [24, 25]. Reference [70] introduced a set of N2LO 3NF forces based on the previous three NN interactions. The associated 3NF low-energy constants c_D and c_E were fitted to the binding energies of A = 3 nuclei and to the ³H-³He Gamow-Teller transition matrix element [70]. Calculations are performed for two-body matrix elements with partial waves up to J = 9.

The 3NFs are included in the SCGF simulations by building effective one- and two-body density-dependent forces using a procedure that is akin to normal ordering [71, 72], but includes a renormalization of occupation probability in n_k. Diagrams (a) and (b) in Figure 1 show the corresponding one- and two-body effective interactions. Diagrams (c) and (d) indicate how these are used in the T−matrix calculation and the corresponding self-energy, respectively. This method is rooted on an extension of the SCGF formalism to multi-body forces [54], and has been implemented in symmetric nuclear matter and neutron matter simulations in [55, 56]. We resort to some numerical approximations in this averaging procedure. First, the normal-ordering procedure ignores the center-of-mass dependence of the 3NF, which is set to P = 0. Second, matrix elements off the diagonal in relative momentum q ≠ q′, are extrapolated from diagonal matrix elements using the prescription $q\to \frac{1}{2}(q^2+{q^{\prime }}^2)$. This procedure also involves a 3NF regulator, which is chosen to be non-local $f(p,q)=exp\left[-{\left(\frac{q^2+p^2/3}{{\Lambda }^2}\right)}^n\right]$, and is based on the two-body relative momentum q and the internal, integrated single-particle momentum p. The exponent n is chosen in accordance to the regulator in the 2NF [70]. Within the P = 0 approximation, the off-shell prescription provides results of very similar quality to many-body perturbation theory calculations that incorporate fully-fledged 3NFs from the outset [73].

2.3. Extrapolation Procedure to Zero Temperature

Finite-temperature calculations are useful on their own, but benchmark comparisons with other methods are typically performed in the zero-temperature limit [30, 31]. A zero-temperature extrapolation procedure for SCGF simulations was developed in the context of beyond-BCS pairing [50, 74]. This procedure is now available generically and can be used to provide zero-temperature data for symmetric and asymmetric systems. For a given fixed density, the extrapolation requires as input a few (typically 4 − 10) finite-temperature simulations. One typically performs simulations from high temperatures of order 20 MeV, and subsequently dials down the temperature to values that are closer to zero. Too close to zero, though, the simulations will not converge as one enters into the superfluid regime - so an intermediate range must be found. It is also important to note that the dependence on temperature typically scales with the dimensionless degeneracy parameter T/ε_F, where ε_F is the Fermi energy. Because ε_F typically increases with density, the expansion is closer to the zero-temperature result (and therefore more accurate) at higher than at lower densities.

The extrapolation from finite temperature to zero temperature works in three independent steps. In a first step, the self-energies from different temperatures are remeshed to the same values of momentum and energy. In the second step, the temperature dependence of the real and imaginary parts of the self-energy (for each value of k and ω) are fitted to a polynomial function in temperature. The third step is to use not one, but different polynomial fits to extrapolate to T = 0. A series of tests are run on these different extrapolations, and a quality measure is built based on a series of consistency checks. For instance, the renormalization factor ${{Z}}_k={\left[1-{\partial }_{\omega }\text{Re}{\Sigma }_k(\omega ){|}_{\omega ={\epsilon }_k}\right]}^{-1}$ is compared to the size of the discontinuity in the momentum distribution at k = k_F. In a consistent theory, the two quantities should provide the same value [33]. The quality measure penalizes fits where these values are significantly different. Importantly, some of these fits have a built-in parabolic energy dependence of ImΣ around ω = μ. Additional details of this extrapolation procedure are discussed in [50].

I provide an example of this extrapolation procedure in Figure 2. This shows the temperature dependence of three properties that are representative of the system's behavior as a function of temperature at a fixed density of ρ = 0.16 fm⁻³. Calculations have been performed with the N3LO Λ = 500 MeV NN force, supplemented with 3NFs at the N2LO level. The averaging procedure for these 3NFs consistently takes into account the density and temperature dependence of the internal propagators. Qualitatively similar results are obtained for the Λ = 450 and 414 MeV interactions.

FIGURE 2

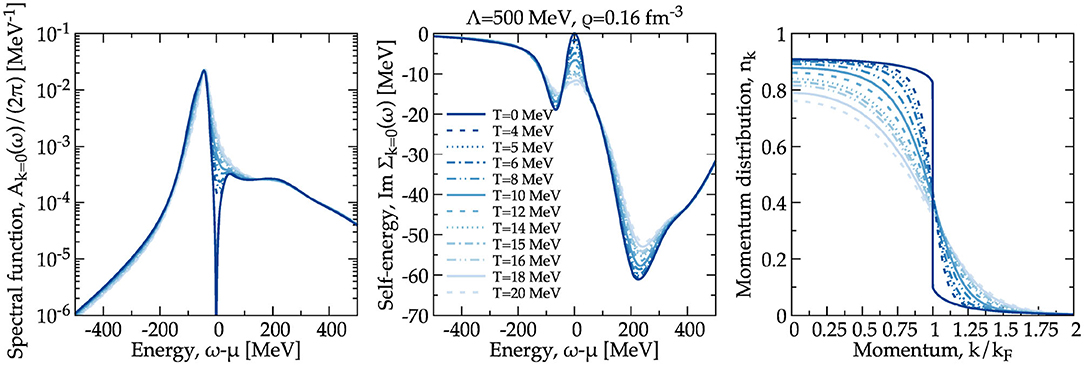
Figure 2. Left: energy dependence of the zero-momentum spectral function ${{A}}_{k=0}(\omega )$ at different temperatures. Central: the same for Im Σ_{k = 0}(ω). Right: momentum distribution as a function of k/k_F. All results have been obtained in symmetric nuclear matter, at a density of ρ = 0.16 fm⁻³ for the Λ = 500 MeV N3LO NN plus N2LO 3NFs forces.

The energy dependence of the spectral function ${{A}}_{k=0}(\omega )$ and the imaginary part of the self-energy Σ_{k = 0}(ω) are displayed in the left and central panels, respectively. I focus on the k = 0 value for simplicity, but the calculation and extrapolation procedure are performed for all available momenta. The effect of temperature in the spectral function is concentrated in the region near ω = μ. The quasi-particle peak and the positive and negative high-energy tails are insensitive to thermal effects. For the self-energy, there is also a relatively strong temperature dependence near ω = μ, which is known to scale with T² [37]. The phase-space dominated peaks in the particle and hole domains at energies about 200 MeV away from μ are also sensitive to the temperature. The extrapolated T = 0 result is able to capture the temperature dependence of these quantities, while providing consistent results.

The right panel of Figure 2 shows the associated momentum distribution n_k, obtained under the same conditions. Thermal effects provide additional depletion at low momenta and populate moderately the vicinity of the Fermi surface. In fact, temperature modulates substantially the momentum distribution around k = k_F even for relatively low values of T ≈ 4 − 5 MeV. The extrapolation procedure, however, captures the energy- and momentum-information sufficiently well to produce a sharp transition at the Fermi surface, as expected from Luttinger's theorem [37]. The size of this discontinuity is also in agreement with the renormalization parameter associated to the self-energy itself. This extrapolation procedure has been implemented not only in the symmetric nuclear matter and pure neutron matter [74], but also in asymmetric infinite matter, as I shall discuss in the following sections.

3. Microscopic Properties

In the following, I provide an overview of the microscopic properties predicted by the SCGF approach for symmetric, asymmetric and pure neutron matter. The aim of this section is to show the broad scope of information that can be generated in SCGF simulations. I focus for simplicity on a single value of the density ρ = 0.16 fm⁻³, which is representative of both nuclear systems and of neutron stars. Note however that the method is customarily used at other densities. The majority of the results are presented in their zero-temperature extrapolated form, although the temperature dependence of most quantities is available and has been used for extrapolation purposes. I leave a full analysis of the density, isospin asymmetry and temperature dependence of these results for future studies.

3.1. Spectral Functions

Figure 3 provides an example of the structure of the zero-temperature spectral function in nuclear systems. The three panels illustrate the energy dependence of the spectral function at three different momenta: k = 0, below the Fermi surface; k = k_F, at the Fermi surface; and k = 2k_F, above the Fermi surface. Results are shown for three interactions: Λ = 414 MeV (red dotted lines); Λ = 450 MeV (yellow dashed lines); and Λ = 500 MeV (blue solid lines).

FIGURE 3

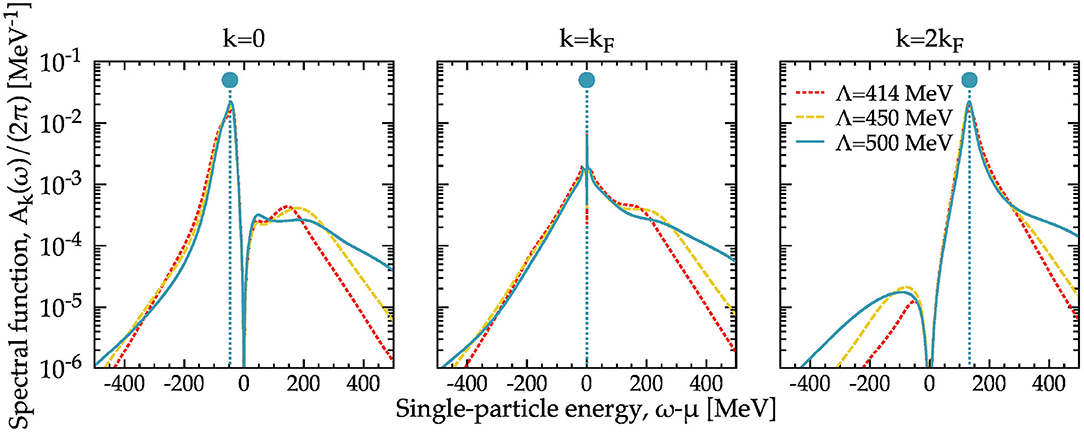
Figure 3. Spectral function ${{A}}_k(\omega )$ as a function of energy for three different momenta: k = 0 (left) k = k_F (central) and k = 2k_F (right). SCGF calculations are performed at a density ρ = 0.16 fm⁻³ and have been extrapolated to zero temperature. Results for N3LO NN plus N2LO 3NFs have been performed with three different cutoffs. The vertical line and solid dot indicate the position of the quasi-particle peak ω = ε_k, for each of these momenta. The height of this peak has been chosen arbitrarily.

The general features of the spectral strength in infinite systems are well-understood [44, 47, 57, 75]. At all momenta other than k_F, the spectral strength has a prominent quasi-particle peak. In infinite nuclear matter, the peak is very close to the quasi-particle energy ω = ε_k obtained from Equation (6). The quasi-particle energy for the Λ = 500 MeV interaction is displayed in the three panels of Figure 3 with vertical lines. The solid dot is shown for illustrative purposes, and its height is chosen arbitrarily. The quasi-particle peak is well-defined in infinite nuclear systems, in the sense that the peak of A_k(ω) and ω = ε_k agree relatively well. At this density, the quasi-particle peak is independent of the interaction under consideration. In fact, the cutoff dependence of the quasi-particle peak is not resolvable on the scale of this graph. I note, however, that while the peaks are well-defined, they are also relatively broad. Typical widths at k = 0 and k = 2k_F are of the order of Γ_k ≈ 40 MeV.

Spectral functions in infinite nuclear matter display slowly decaying high (positive and negative) energy tails. These are particularly prominent at the Fermi surface k = k_F, where the zero-temperature spectral function should be a combination of a broad energy-dependent background and a zero-width δ function centered at ω = ε_kF [33]. In practice, the T = 0 results at k = k_F do show some minor structures around ω = μ as the non-analytical behavior of the δ function is not built in the extrapolation procedure. The results of Figure 3 clearly show a substantial cutoff dependence in these high-energy components. This is relatively unsurprising, since these tails are a direct consequence of the short-range core in the NN force [32]. As expected, the interaction with the largest momentum cutoff (Λ = 500 MeV), and hence the largest resolution in real space, provides the largest high-energy components. These include a shoulder at positive energies in the region 100 − 500 MeV which is characteristic of a relatively strong short-range core. In contrast, the lower cutoff interactions provide much faster (exponential) decaying spectral functions beyond the quasi-particle peak. For positive energies, they provide very little single-particle strength beyond 500 MeV. The Λ = 414 MeV interaction has faster decaying tails than the 450 MeV force, which agrees with intuition. Note that this sharply decaying spectral strength is at odds with calculations employing traditional phenomenological NN forces, which typically populate these offshell regions with higher probabilities [57, 76]. Off-shell high-energy components are observed in electron-scattering experiments [77] and may provide a way to quantify the short-range component of NN forces [78].

The results presented so far concerned symmetric nuclear matter, where by construction one assumes the same fraction of neutrons and protons. Isospin asymmetric systems, however, are interesting on their own. The deep interior of heavy stable and unstable isotopes is expected to be a neutron-rich environment, characterized by an isospin asymmetry parameter,

$\begin{array}{ll}\eta =\frac{{\rho }_n-{\rho }_p}{{\rho }_n+{\rho }_p},& (12)\end{array}$

of order η ≈ 0.2 [79]. In contrast to this relatively mild isospin asymmetry, the core of neutron stars is expected to be extremely asymmetric with η ≈ 0.8 [80]. Finite-temperature SCGF simulations including explicitly isospin asymmetry have been available for over a decade [64]. In these simulations η is an external, tuneable parameter. SCGF calculations then give isospin-dependent self-energies, spectral functions and quasi-particle properties, as well as the corresponding bulk properties. These calculations provided insight into the isospin-asymmetry dependence of the fragmentation of the single-particle strength [66, 67], but were somewhat limited by two factors. First, finite temperature effects have a larger importance in the minority component as asymmetry is turned on, because the corresponding degeneracy parameter $T/{\epsilon }_F^{\tau }$ decreases. Second, the calculations were performed with two-body interactions only and thus missed the effects of 3NFs. None of these factors is particularly critical. Temperature effects can be controlled, and the effect of 3NFs on the spectroscopic strength is small below saturation density for both symmetric nuclear and pure neutron matter [55, 56].

Having said that, recent technical developments have allowed us to overcome these two shortcomings recently. Figure 4 shows the spectral functions of neutrons (top panels) and protons (bottom panels) as a function of energy for different values of the isospin asymmetry η, at a fixed density of ρ = 0.16 fm⁻³. Results are presented for the Λ = 500 MeV N3LO potential supplemented with 3NFs². The results for the isospin dependence of these spectral functions are qualitatively similar to previously obtained results which lacked 3NFs. The evolution of the neutron spectral function from symmetric (η = 0) to neutron (η = 1) matter is relatively mild. The quasi-particle peaks with respect to the corresponding chemical potential μⁿ become slightly more (attractive) repulsive for the (hole) particle components. The high energy tails are relatively insensitive to the isospin asymmetry, and are mostly affected for the negative energy components at momenta above the Fermi surface. All in all, this agrees with the generic picture of a neutron majority component evolving from a symmetric situation, where tensor correlations provide larger correlations, to neutron matter, where only the short-range component is responsible for fragmentation.

FIGURE 4

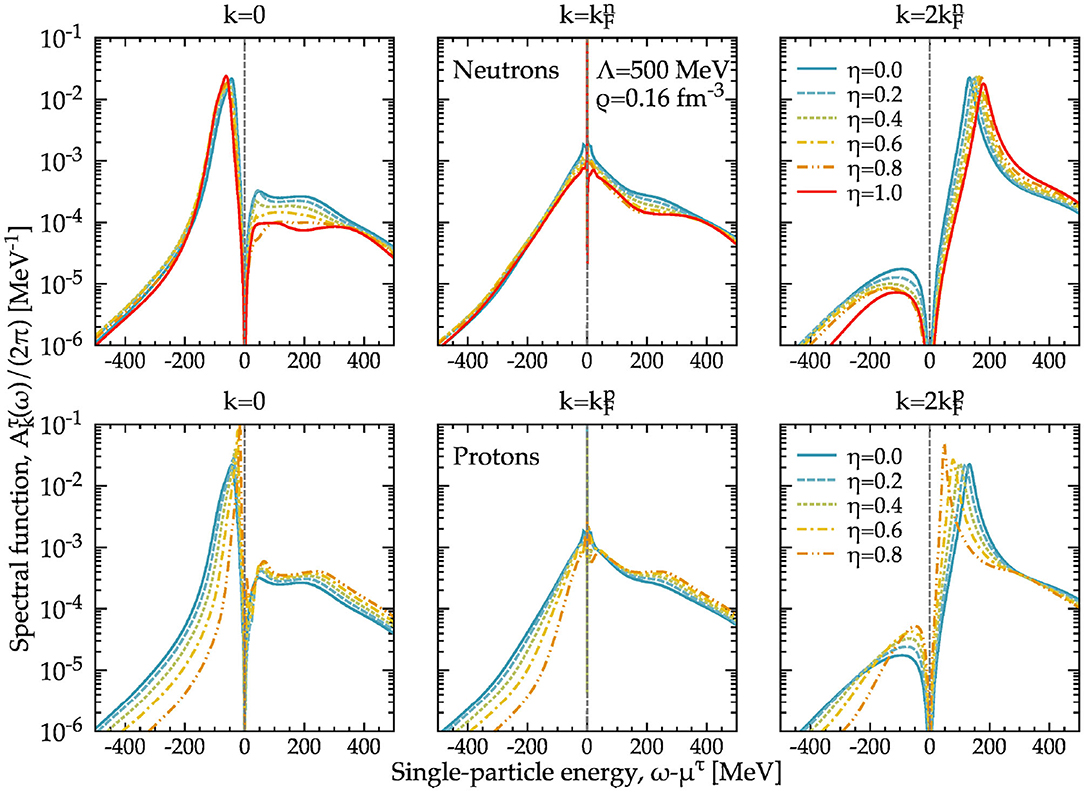
Figure 4. Neutron (top) and proton (bottom) spectral functions ${{A}}_k^{\tau }(\omega )$ as a function of energy for three different momenta: k = 0 (left) $k=k_F^{\tau }$ (central) and $k=2k_F^{\tau }$ (right panels). Calculations with the N3LO Λ = 500 MeV and an N2LO 3NF at a density ρ = 0.16 fm⁻³ have been extrapolated to zero temperature for different isospin asymmetries η. The vertical dashed line is a guide to separate hole (ω < μ^τ) and particle (ω > μ^τ) components.

In contrast, the proton spectral function (bottom panels) is much more affected by isospin asymmetry. In asymmetric conditions, the relative importance of np pairs increases for the minority proton component. Since np interactions are mediated by the tensor component of the NN force, one naively expects enhanced correlation effects for protons in neutron-rich matter. Simultaneously, for neutron-rich conditions the overall proton density decreases, so the proton component should somehow become “less interacting.” SCGF simulations allow us to provide quantitative predictions to distinguish between these scenarios.

As the isospin asymmetry increases, the single-particle peak for protons becomes more repulsive with respect to μ^p. Importantly, the width of the quasi-particle peak for components below the Fermi surface (see k = 0 panel) also decreases substantially. As a consequence, positive high-energy tails increase with isospin. Interestingly, the central panel ($k=k_F^p$), shows a background component that behaves differently for the addition and removal energy components. Whereas for ω < μ^p, the background of the spectral function decreases with isospin asymmetry, at ω > μ^p it increases. Above the Fermi surface ($k>k_F^p$), the quasi-particle peak is more compressed with increasing isospin asymmetry, both in terms of a lower peak and a significantly decreased width. The limit case of a proton impurity in an η = 1 system cannot be tackled with the present set of SCGF technology.

While a full analysis is beyond the scope of this initial presentation of results, the isospin dependence shown here is relevant for both nuclear experiments and astrophysics. Hadronic and electron two-nucleon knock-out reactions from the early 2000s up to the present have shown that np pairs, rather than pp or nn pairs, are more likely to be knocked off isospin symmetric targets [81, 82]. Further electron-scattering results in isospin asymmetric nuclei have provided additional evidence for this neutron-proton dominance [83]. It is likely that the tensor component preferentially acts in relatively high-momentum pairs and provides the physical mechanism behind these strong isophobic correlations [66, 84]. Extending the np dominance picture to isospin imbalanced systems would naively indicate that protons should be more correlated than neutrons in neutron-rich systems, although quantitative statements depends sensitively on the definition of a correlation measure [85–87]. In the astrophysical context, the strong modification of the proton spectral function in isospin asymmetric nuclear matter predicted by SCGF simulations has been explicitly explored at the level of the symmetry energy in [88–90]. The fragmentation of strength in neutron matter has also been used to provide a description of the pairing properties in dense matter [50, 74].

3.2. Self-Energies

Within the SCGF formalism, the spectral strength is directly related to the self-energy. The imaginary part of the retarded self-energy encodes information on both the phase space and the NN interaction, and can even be used to diagnose interactions by means of sum rules [76]. I present a density plot of the zero-temperature extrapolated imaginary part of the self-energy at ρ = 0.16 fm⁻³ in Figure 5. Left, central, and right panels correspond to chiral interactions with cutoffs Λ = 414, 450, and 500 MeV, including in all cases 3NFs. As expected, ImΣ_k is zero at ω = μ throughout all momenta. For energies ω < μ, this function has a hole component with support below k ≈ k_F = 263 MeV. The size and shape of this pocket is relatively interaction-independent. In contrast, the positive energy (ω > μ) components of ImΣ_k show a clearer cutoff dependence. The deep pocket around k = 0 in this component is sensitive to the underlying NN force. Typical phenomenological interactions have deep pockets, and these extend to very high positive energies (into the GeV domain). For this set of chiral interactions, the depth of the pocket is relatively insensitive to the cutoff and of order 50 − 70 MeV. The tails of ImΣ_{k = 0} fall off relatively quickly with energy. In fact, the Λ = 414 and 450 MeV self-energies are almost zero beyond an energy of about 500 MeV. The cutoff also has a clear effect on the momentum dependence of Im Σ_k in the positive energy region. Generally speaking, higher-cutoff forces allow the imaginary part of the self-energy to extend to higher momenta.

FIGURE 5

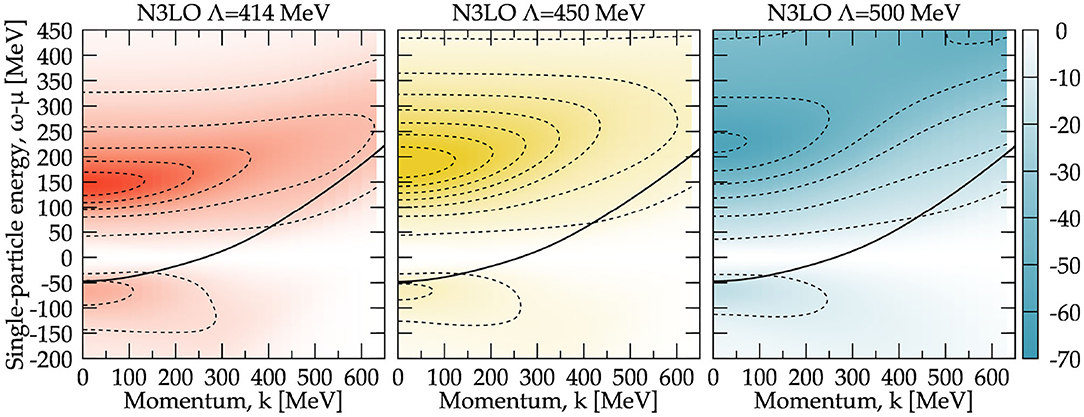
Figure 5. Density plot of the imaginary part of the self-energy ImΣ_k(ω) as a function of momentum and energy. Dashed lines represent contours at constant values spaced by 10 MeV. Extrapolated zero-temperature results for symmetric nuclear matter at a density ρ = 0.16 fm⁻³ are shown for the N3LO NN and N2LO 3NF combinations at cutoffs Λ = 414 MeV (right) 450 MeV (central) and Λ = 500 MeV (right panel). The solid line represents the quasi-particle peak ω = ε_k.

The solid lines in Figure 5 show the trajectory of the quasi-particle peak in the energy-momentum plane. Quasi-particle lifetimes τ_k in Equation (7), are computed along these trajectories. The plot indicates that the lifetimes are relatively insensitive to the differences in self-energies. In other words, largely different offshell self-energies can give rise to relatively similar on-shell properties. On-shell components will be discussed in detail in section 3.4.

The isospin asymmetry dependence of Im${\Sigma }_k^{\tau }(\omega )$ is explored in Figure 6. Results are shown for the Λ = 500 interaction only at a fixed density of ρ = 0.16 fm⁻³, for a variety of isospin asymmetries. The leftmost panel corresponds to the symmetric system (η = 0), and is the same as the right panel of Figure 5. The top panels indicate that the effect of asymmetry in the neutron self-energy is relatively mild. The pocket at negative energies ω < μⁿ, associated to neutron holes, is relatively unchanged as η increases. In contrast, the positive energy (particle) components evolve with isospin in a substantially different way. The pocket that in the symmetric situation decayed relatively quickly with momentum, becomes an almost momentum-independent structure in the most asymmetric case explored here.

FIGURE 6

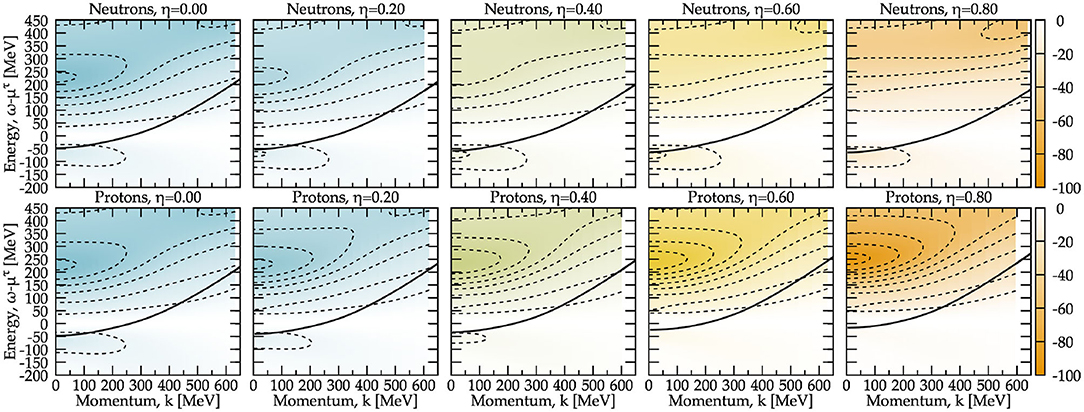
Figure 6. The same as Figure 5 but in isospin asymmetric nuclear matter for the Λ = 500 MeV interaction. Top panels focus on neutrons, and bottom panels on protons. The panels from left to right correspond to different isospin asymmetries, from η = 0 (symmetric nuclear matter, leftmost panel) to the neutron-rich domain with η = 0.8 (rightmost panel).

In contrast, proton self-energies show a strong dependence on isospin asymmetry. As the proton fraction decreases, the negative-energy (hole) components of Im${\Sigma }_k^p$ disappear steadily. This reflects the decrease in density, and hence of available phase space of protons. The corresponding low-momentum ($k<k_F^p$) inverse quasi-particle lifetime is small, which in turn gives rise to an increasingly narrow spectral function. This is clearly in agreement with the results in the bottom left panel of Figure 4. On the positive energy side of the self-energy ω > μ^p, the deep pocket at low momenta becomes noticeably deeper as η increases but, unlike the neutron component, the momentum dependence remains relatively unchanged. The increase in depth of ImΣ_k can be interpreted in terms of an increase in the interaction strength, as expected in the asymmetric case with an increase in the number of np pairs.

In other words, the imaginary component of the self-energy for protons in asymmetric matter shows the competition of the two effects discussed earlier in two different energy regimes. On the one hand, proton holes, associated to the negative energy components, are dominated by phase-space and their self-energy decreases steadily as the proton density decreases. On the other hand, proton particles at positive energies show an increase in interaction strength as expected in a more imbalanced strongly interacting system. The real part of the self-energy is not shown here for brevity. I note, however, that this is connected to Im${\Sigma }_k^{\tau }$ by the dispersion relation in Equation (9).

3.3. Momentum Distributions

A useful characterization of beyond mean-field correlations is obtained with the momentum distribution in Equation (3). For a non-interacting Fermi gas or within the lowest-order Hartree-Fock approximation at zero temperature n_k = 1 (0) for momenta below (above) the Fermi surface. This behavior is illustrated by the double-dotted-dashed line in the left panel of Figure 7. In contrast, the momentum distribution of correlated infinite nuclear matter shows a characteristic depletion below the Fermi surface. This depletion is of the order of 7 − 12%, with small quantitative differences between different interactions.

FIGURE 7

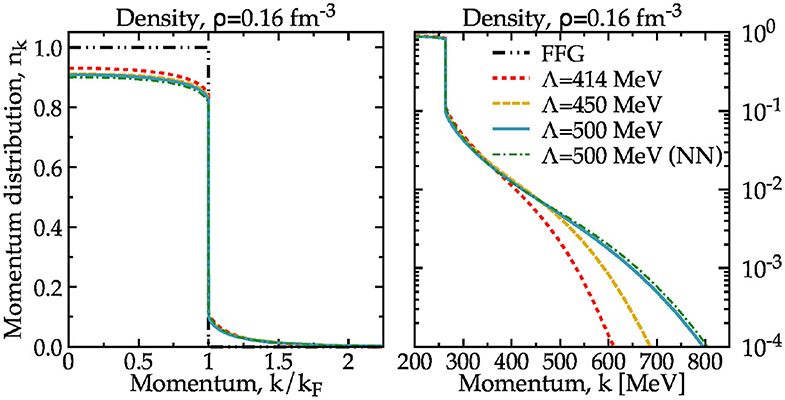
Figure 7. Extrapolated zero-temperature momentum distribution obtained with different NN interactions for symmetric nuclear matter at ρ = 0.16 fm⁻³. The left panel shows the distribution on a linear scale as a function of k/k_F. The right panel shows the same results on a logarithmic scale and as a function of momentum k, in units of MeV. The black dashed-double-dotted line corresponds to the free Fermi gas (FFG). The green dashed-dotted line is obtained from a calculation with the Λ = 500 MeV interaction without 3NFs. Other lines follow the convention of Figure 3.

In turn, a depletion of momentum eigenstates below k_F means that n_k above the Fermi surface must be populated. The logarithmic scale in the right panel of Figure 7 illustrates the effects of such high-momentum components. These components are noticeably different depending on the cutoff. Smaller cutoff interactions give rise to momentum distributions that decay faster and start decaying at lower momenta, than larger cutoff forces. To illustrate the relatively small effect that 3NF have on correlations, I show in Figure 7 the momentum distribution obtained in a SCGF calculation without 3NFs (dashed-dotted line). Remarkably, the difference between the calculation with and without 3NFs is substantially smaller than the cutoff dependence of the interaction. This bodes well with previous observations indicating that the effect of 3NFs on fragmentation properties is quantitatively small, even though they have a substantial influence on the energetics and thermodynamics of the system [55].

The evolution of the momentum distribution with isospin also provides an illustrative understanding of the interplay between short-range and tensor correlations and isospin asymmetry. Figure 8 shows the momentum distribution as a function of momentum for different isospin asymmetries. These results have been obtained with the Λ = 500 MeV interaction, but qualitatively similar plots are found for the other two forces. The left panel shows the results for neutrons. Isospin asymmetry has two main effects on the majority component. On the one hand, the discontinuity in n_k moves to higher momenta, as the Fermi momentum changes from k_F = 263 MeV in symmetric nuclear matter to k_F = 331 MeV in pure neutron matter. This effect would be identical in the free Fermi gas (FFG). In contrast, the distinct increase of n_k below the Fermi surface is specific to correlated systems. The depletion of strength decreases (or gets closer to 1) linearly with the increase of asymmetry. Whereas in symmetric nuclear matter it is around 10%, in pure neutron matter it goes down to a level of around 4 − 5%. In fact, this isospin dependence is rather universal and independent of the NN interaction under consideration [66, 67]. A similar effect is expected for the size of the discontinuity across the Fermi surface, which decreases as isospin asymmetry increases.

FIGURE 8

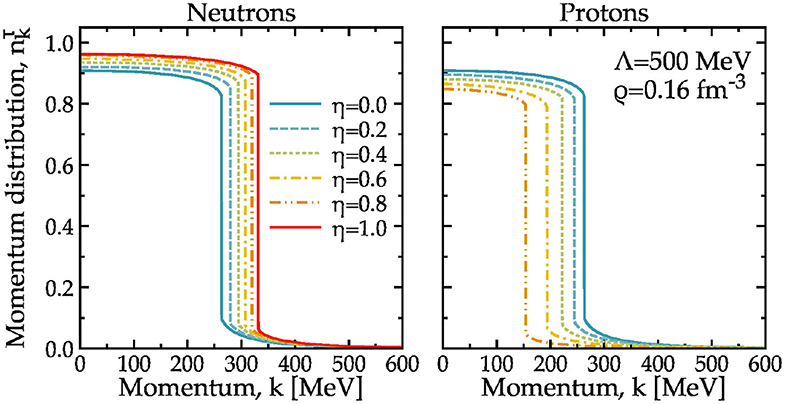
Figure 8. Left: neutron momentum distribution $n_k^n$ as a function of momentum. Extrapolated zero-temperature calculations at different values of isospin asymmetry η are shown at a fixed density of ρ = 0.16 fm⁻³. Results have been obtained for the Λ = 500 MeV interaction including 3NFs. Right: the same for the proton momentum distribution $n_k^p$.

The right panel of Figure 8 provides insight on the asymmetry evolution of the minority component (protons). Mirror effects are obtained in this case. The discontinuity of n_k occurs at smaller and smaller momenta, as expected from FFG considerations. The depletion below the Fermi surface departs further away from 1 as the isospin asymmetry increases. In other words, by this measure, protons (or minority components) become more correlated in a neutron-rich environment. Close to the astrophysically relevant condition at η ≈ 0.8, protons are depleted by about 15% for this specific interaction. This depletion goes in hand with a change of high-momentum components for the proton, which become more important as asymmetry increases [67].

The picture obtained by these complete calculations including zero temperature extrapolations and 3NFs is qualitatively and quantitatively very similar to the one discussed in [66, 67]. Overall, the effect of isospin asymmetry on occupation numbers is relatively small. For the characteristic isospin asymmetry in the interior of nuclei (η = 0.2), the change in occupation below the Fermi surface is of the order of only a few percent. Overall, this shallow asymmetry dependence is at odds with some of the past and recent experimental analysis in both electron- and hadron-induced knock-out reactions [85, 87, 91]. Importantly, however, these calculations at fixed density do not account for the density and isospin-asymmetry dependence within nuclei, which is likely to be relevant for the description of nuclear momentum distributions.

3.4. On-Shell Properties

A unique advantage of SCGF simulations is the access to both off-shell, energy-dependent quantities, as well as the corresponding information on the energy shell—at the quasi-particle energy ω = ε_k. On-shell properties are often used in interpreting the properties of the system and are the input to most astrophysical simulations. In particular, quasi-particle potentials in asymmetric matter at relatively low densities (neutrino-sphere) are important for charged-current neutrino opacities [20, 92]. The quasi-particle spectrum of Equation (6) is a key quantity that allows for a characterization of single-particle excitations in the system. Since the kinetic term in the quasi-particle energy obscures the many-body effects at large momentum, I instead focus on the single-particle potential $U_k^{\tau }=\text{Re}{\Sigma }_k^{\tau }({\epsilon }_k^{\tau })$. This is shown as a function of momentum in Figure 9. Top panels correspond to neutrons, whereas bottom panels correspond to protons. From left to right, the isospin asymmetry of the system changes from symmetric nuclear matter (η = 0) to pure neutron matter (η = 1) at a constant density of ρ = 0.16 fm⁻³. I show results for the Λ = 500 (solid), 450 (dashed) and 414 MeV (dotted lines) interactions.

FIGURE 9

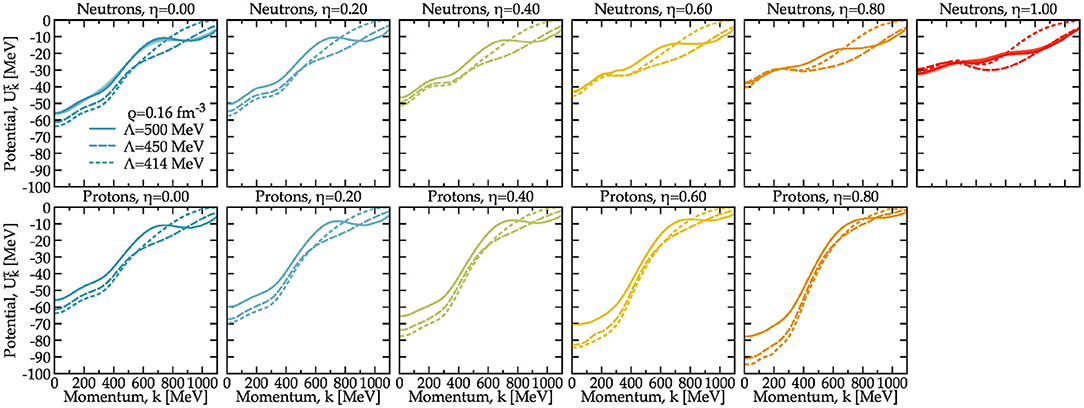
Figure 9. Neutron (top) and proton (bottom) single-particle potentials as a function of the momentum for the three interactions considered in this work. The panels from left to right correspond to different isospin asymmetries, from η = 0 (symmetric nuclear matter, leftmost panel) to neutron matter (rightmost panel). The bands for the η = 0 and η = 1 obtained with the Λ = 500 MeV interaction highlight the temperature dependence from T = 20 to T = 0 MeV.

As discussed previously, these results are obtained from a zero-temperature extrapolation of finite temperature SCGF simulations. As an illustration of the importance of thermal effects, I also show in the top left and top right panels the Λ = 500 MeV results for $U_k^{\tau }$ at temperatures up to T = 20 MeV. The thermal effects are clearly small on the scale of this figure, particularly in comparison to the cutoff and the isospin dependence of the results. I note in passing that the temperature dependence is not monotonous. At momenta below the Fermi surface $U_k^{\tau }$ becomes more attractive as temperature increases. Above the Fermi surface and up to about 500 MeV, the potential instead becomes more repulsive with temperature. This is in agreement with previously reported SCGF results that did not incorporate 3NFs [44].

In terms of isospin dependence, the results also agree with previously reported outcomes in the SCGF approach [64], and in other many-body calculations [93–95]. In symmetric nuclear matter, the single-particle potential has a minimum at low momenta close to U_{k = 0} ≈ −60 MeV, and increases steeply with momenta. At k = 0, the lowest cutoff interaction produces a potential that is about 5 MeV more attractive than the highest cutoff force. This cutoff-dependence is relatively constant as a function of momentum up to k ≈ 600 MeV, where regulator artifacts start to dominate. Above this value of momentum, the results of the 414 MeV and 450 MeV force go to zero relatively quickly, whereas the potential for the 500 MeV interaction shows a characteristic shallow minimum around k = 800 MeV.

As asymmetry increases, the neutron single-particle potential becomes more repulsive and shallower in terms of momentum dependence. In contrast, protons experience a larger attraction when they become the minority species. Their single-particle potentials become significantly more attractive, and in the astrophysically relevant region of η ≈ 0.8, they reach values of 80 − 90 MeV at k = 0. The isospin dependence is to a good approximation linear with isospin asymmetry, as expected on general grounds [94]. I note however that the momentum and isospin dependence of these single-particle potentials is significantly different from those predicted by phenomenological mean-field approaches [96].

Interestingly, the cutoff dependence of the results depends on isospin asymmetry and on the specific nucleon. As neutrons become the predominant species and their single-particle potentials become shallower, the cutoff dependence in the low-momentum single-particle potential below 400 MeV decreases. In neutron matter, the differences between the potentials are of the order of 1 MeV. On the contrary, as the isospin asymmetry increases and the proton spectrum becomes more attractive, the differences between interactions with different cutoffs increase and become of the order of more than 10 MeV.

These differences can be explained by two interrelated factors. One is of a relatively straightforward nature. np interactions play no role in neutron matter, and hence the intrinsic differences in the NN interaction are less likely to appear as several partial waves channels are suppressed. In other words, if the fits to the nn channels have intrinsically smaller differences between forces than the corresponding np channels, neutron-rich systems will show less cutoff dependence. Another factor that plays an important role is the strength (in the sense of “perturbativeness”) in different channels. In terms of χEFT, the small cutoff dependence in neutron matter agrees with the idea that neutron matter is a more perturbative system than symmetric nuclear matter [69, 97, 98], because the strong np components are missing. It is important to emphasize here that the strong cutoff dependence of the impurity spectrum may not be identified in the energetics of the system, but will clearly have an impact on the dynamics of isospin asymmetric systems.

The momentum dependence of $U_k^{\tau }$ is directly related to the concept of the effective mass. SCGF simulations can be used to extract not only the mass associated to the single-particle spectrum, but also to the so-called ω− and k−effective masses. A detailed analysis of these properties within the SCGF approach is ongoing.

The on-shell imaginary part of the self-energy, Equation (7), is interpreted as an inverse quasi-particle lifetime. For a normal correlated many-fermion system at zero temperature Γ_k=kF should be zero, thus signaling an infinite lifetime of quasi-particles at the Fermi surface. The lifetime should be non-zero everywhere else and, as discussed in the context of section 3.2, its magnitude is a combination of phase-space and interaction effects. Figure 10 provides an overview of the momentum dependence of ${\Gamma }_k^{\tau }$ for neutrons (top panels) and protons (bottom panels) as a function of isospin asymmetry. As in the previous figure, extrapolated zero-temperature results are shown.

FIGURE 10

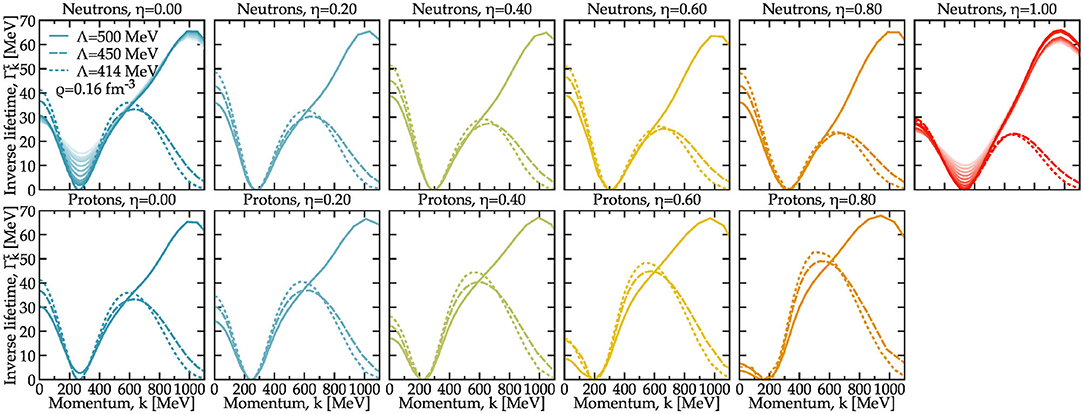
Figure 10. Neutron (top) and proton (bottom) inverse single-particle lifetimes as a function of the momentum. For details, see the caption of Figure 9.

The isospin and cutoff dependence of the results is very different above and below the Fermi surface. Below the Fermi surface, the SCGF simulations predict a non-zero width. Unlike in BHF calculations, intermediate hole states account explicitly for this non-zero width of hole states k < k_F [94]. For neutrons, this hole component is relatively independent of the isospin asymmetry. In fact ${\Gamma }_{k=0}^n$ increases from values around 30 − 40 MeV in symmetric nuclear matter to 40 − 50 MeV around η = 0.6, and decreases again to values around 20 − 30 MeV in neutron matter. In contrast, for protons the hole component decreases steadily with asymmetry. This reflects the decrease in phase space of protons as asymmetry increases. For both neutrons and protons, the cutoff dependence of the hole component is of the order of 10 MeV and relatively independent of isospin asymmetry.

Around the Fermi surface, for all isospin asymmetries, the momentum dependence of ${\Gamma }_k^{\tau }$ is rather universal. In most cases, one cannot distinguish the curves from different interactions within about 100 MeV of the Fermi surface. I demonstrate again the importance of thermal effects for the Λ = 500 MeV interaction at the two extreme asymmetries η = 0 (top left) and η = 1 (top right panel). Whereas regions away from the Fermi surface are temperature independent, these panels show that the temperature dependence in ${\Gamma }_k^{\tau }$ is prominent around $k=k_F^{\tau }$. There, the quasi-particle width switches from zero at T = 0 to a finite (and increasing) value with temperature. This is to be expected, as the behavior around k_F is governed by phase space arguments [33, 53].

The particle component (at $k>k_F^{\tau }$) of ${\Gamma }_k^{\tau }$ is remarkably more cutoff dependent. The momentum dependence immediately above $k_F^{\tau }$ and up to about 500 − 600 MeV is very similar in all cases, and shows an increase from zero up to an isospin-dependent maximum for the Λ = 450 MeV and 414 MeV cases. For neutrons (protons), the peak height decreases (increases) from around 30 MeV in symmetric nuclear matter η = 0, to around 25 MeV (50 MeV) in pure neutron matter η = 1. For these two forces ${\Gamma }_k^{\tau }$ becomes a decreasing function of momentum above k ≈ 500 MeV and eventually vanishes above k ≈ 1 GeV. This is stark contrast to the Λ = 500 MeV interaction, where the peak of the particle component occurs at much higher momenta in the vicinity of k ≈ 1 GeV.

The peak is also relatively independent of the isospin asymmetry, and very similar for neutrons and protons. This peak and, in general, the relatively large values of ${\Gamma }_k^{\tau }$ in this region are indicative of the short lifetime of high-momentum states. The cutoff dependence clearly indicates that this component of ${\Gamma }_k^{\tau }$ depends strongly on the interaction, and the isospin dependence suggests that it is mediated by isoscalar short-range physics independently of the density of the individual components.

These results match with the findings for the spectral functions reported in Figure 4. Whereas the width of the neutron spectral function is qualitatively unaffected by a change in isospin asymmetry, the width of the proton spectral function changes significantly with asymmetry for the hole states $k<k_F^{\tau }$. Single-particle widths provide an alternative way of characterizing beyond mean-field correlations, since in the Hartree-Fock approximation Γ_k = 0. The results in Figure 10 indicate that some of the features of Γ_k are robust against isospin asymmetry changes, whereas others are not. In particular, the relative strong dependence of proton single-particle widths with isospin asymmetry may be related to the isospin dependence of the absorptive component of optical potentials [99].

3.5. Other Microscopic Properties

The microscopic results presented so far provide a very complete picture of the dynamics of infinite nuclear systems. The versatility and wide range of applications is an advantage of SCGF techniques. On-shell and off-shell quantities provide valuable information which, when complemented with modern interactions based on χEFT, can help provide estimates of systematic theoretical errors in simulations. A useful characterization of in-medium nuclear properties can be obtained from energy-weighted moments (or sum-rules) of the spectral function. The first moment is connected to effective single-particle energies [100, 101] and has been studied in the context of both symmetric and asymmetric nuclear mater at zero and finite temperatures [102–104]. The conclusions reached by these studies in the early 2000s indicated that the first moment is sensitive to NN interactions, and provides a useful characterization of correlations. The second moment has only been studied more recently [76]. It measures fluctuations around the single-particle peak, and is a connected to the energy dependence of the imaginary part of the self-energy. Because the latter is also particularly sensitive to the NN force, the second moment can provide a measure of the Hamiltonian properties in both nuclei and infinite nuclear matter.

The SCGF method can be used to study a variety of in-medium quantities which are relevant for nuclear physics experiments. For instance, in the late 1990s, SCGF methods were used to provide a formal redefinition of scattering phaseshifts in the medium [105]. Practical calculations also allowed for predictions of in-medium scattering cross sections in dense matter [106]. The finite lifetime of quasi-particles away from the Fermi surface can be formally translated into an in-medium nucleon mean-free path. This mean-free path is relevant for a variety of nuclear physics considerations, from the validity of the shell model [107] to the characterization of multi-fragmentation reactions [108]. The consistent description of the real and imaginary parts of the self-energy via dispersion relations makes SCGF techniques particularly appealing in this context. In [109], the mean-free path of nucleons in dense infinite matter was computed by means of an extension of the SCGF formalism to the complex plane. Calculations agree well with results obtained with other methods and, most importantly, with a variety of nuclear experiments at intermediate energies [109].

Superfluidity in nuclear systems can be detected by the appearance of in-medium bound states in the two-body scattering matrix, or the two-body propagator. This can be used to characterize the normal-superfluid phase diagram of dense matter. Extensions of the SCGF method to the superfluid domain are possible, by means of the symmetry-breaking Gorkov formalism [43, 46]. Simulations in the normal phase, however, can already provide relevant information for superfluid properties, by extrapolating normal self-energies and spectral functions to zero temperature as discussed above. With this data, one can build effective gap equations that contain the effects associated to the fragmentation of strength [110]. Results with the three chiral interactions presented here indicate that short-range correlations reduce the pairing gap, and provide a gap closure at lower density compared to BCS solutions for both the singlet and the triplet channel [74]. In principle, SCGF calculations at different orders can also be used to estimate systematic uncertainties in this method. This approach may provide a better handle on the role of superfluidity at intermediate and high densities, where the role of long-range correlations is poorly understood [50, 111].

4. Macroscopic Properties

Simulations based on SCGF methods can access the thermodynamics of the system. A wide range of other many-body methods have been extended to the finite temperature domain, including diagrammatic BHF approaches [112], variational methods [113], and many-body perturbation theory techniques [68, 114, 115]. All of these methods share common limitations in terms of the definition of quasi-particles [116]. This can lead to an inconsistency in terms of the chemical potential. On the one hand, the chemical potential is typically obtained from a normalization condition like Equation (4). On the other, one can find μ from the thermodynamical relation

$\begin{array}{ll}\mu =\frac{\partial ϵ}{\partial \rho },& (13)\end{array}$

where ϵ is the energy density. Formally and numerically, these two values may be different depending on the theoretical framework under consideration.

A key advantage of the SCGF formulation at finite temperature is that it guarantees that the two quantities are the same, as long as the self-energy fulfills basic criteria [33]. These criteria are related to the so-called Φ−derivability, and lead to a thermodynamically consistent theory [63]. In practice, this means that in SCGF calculations there is no need to perform numerically the derivative in Equation (13). This is particularly convenient in calculations of the pressure, which can directly be computed from the relation p = ρ(F/A − μ). I note, however, that differences between microscopic and macroscopic chemical potentials may arise at a numerical level, particularly when the approximated treatment of 3NFs is considered [51].

I show the pressure as a function of density for symmetric nuclear matter (left panel) and pure neutron matter (right panel) in Figure 11. These have been computed with the three chiral interactions discussed in this work and include the effect of 3NFs. The results are computed at two finite temperatures T = 20 and 10 MeV, and are also extrapolated to T = 0. Note that the extrapolation uses many more temperatures, which are not displayed here for simplicity. The discussion below is brief, and details of similar calculations can be found in [44, 48, 49].

FIGURE 11

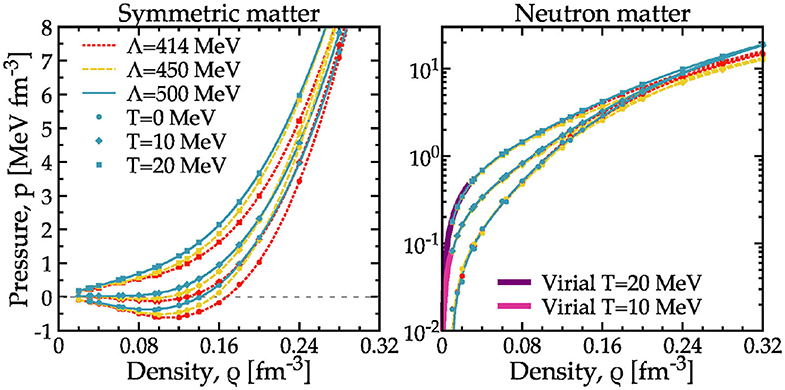
Figure 11. Pressure as a function of density for symmetric nuclear matter (left) and pure neutron matter (right). Results for three NN interactions are shown at three different temperatures: T = 0 10 and 20 MeV. At low density for neutron matter, the two bands display the results from the virial expansion.

For symmetric nuclear matter, the zero-temperature pressure shows a characteristic van der Waals shape, with an area of negative pressure that extends from zero up to the corresponding saturation density of each interaction. This structure signals the existence of a liquid-gas phase transition in nuclear matter [48, 49, 112, 115]. At zero temperature, the pressure vanishes at zero density and at the saturation point. Figure 11 indicates that the three chiral interactions have significantly different saturation densities, in the region ρ₀ = (0.14 − 0.165) fm⁻³. As temperature increases, the spinodal region (where dp/dρ < 0) shrinks, until it disappears. At that stage, the pressure can still have an inflection point, which will smoothen out only at the corresponding critical temperature T_c of the liquid-gas phase transition. Different many-body approaches based on the same NN interaction predict different critical points [48]. Similarly, the same many-body set-up with different interactions can yield different critical points [115].

The recent SCGF analysis presented in [49] suggests that the critical temperature predicted by several different χEFT interactions can range from T_c ≈ 11.0 MeV to T_c ≈ 18 MeV. The cutoff dependence in Figure 11 falls within this rage, and T_c lies between about T_c ≈ 11 MeV for the Λ = 500 MeV interaction and T_c ≈ 16.5 MeV for the Λ = 414 MeV interaction. There is a clear correlation between the saturation energy and the critical temperature, with more attractive saturation energies leading to higher critical temperatures [49]. This intuitive behavior is not supported by the analytical predictions of mean-field models [117]. The relatively wide range of critical temperatures dominates over the uncertainties associated to the many-body approximation. Indeed, in [49], the maximum difference obtained between BHF and SCGF predictions for the critical temperature was about 2 MeV. While further many-body benchmarks may be necessary to understand the full many-body dependence of this result, it is clear that the Hamiltonian uncertainty is relevant for finite temperature predictions [51]. In fact, the cutoff dependence of a sub-saturation density property like T_c can be taken as a sign that finite-temperature many-body correlations are significant in this region.

The temperature dependence of the pressure in neutron matter is relevant for astrophysical considerations, particularly in the context of neutron star mergers [16] and proto-neutron star formation [19]. The right panel of Figure 11 shows the pressure on a semilogarithmic scale as a function of density. The same three temperatures (0, 10 and 20 MeV) are presented. At low densities, the pressure should be well-described in terms of the model-independent virial expansion, which only depends on neutron-neutron scattering phaseshifts [118]. The pressure for fugacities z < 0.5 at T = 10 MeV and 20 MeV is shown with two solid bands at low densities in the figure. Clearly, the low-density SCGF results agree well with virial predictions. The low-density pressure is in fact remarkably cutoff independent, and the first distinguishable cutoff-dependent features only show up above ρ ≈ 0.10 fm⁻³. This is in stark contrast to the case of symmetric nuclear matter. Noticeably, this cutoff independence also holds for the low-density, zero-temperature extrapolated results. All in all, the cutoff and many-body dependence of low-density neutron matter predictions are well under control (independently of temperature), as already discussed elsewhere [23, 28, 29, 69, 97].

The cutoff dependence in neutron matter is only clearly distinguishable above saturation density. There, and toward the high density limit of applicability of chiral interactions, the Λ = 500 MeV interaction is providing more pressure at a given density. This is followed by a decreasing pressure from the Λ = 414 MeV and Λ = 450 MeV forces. It is interesting to note that the last two switch orders with respect to symmetric nuclear matter, where for a given density the Λ = 450 MeV interaction provides more pressure than the Λ = 414 MeV interaction. The cutoff dependence is only one of several systematic uncertainties in these results. SCGF can also provide an estimate of the many-body uncertainties, by performing calculations with self-energies obtained not only at a ladder level, but also at the first- and second-order level. The results of a recent analysis indicate that the many-body uncertainty is smaller than that associated to the underlying NN force by a factor of 2 − 3 at twice saturation density [51].

With respect to the temperature dependence, one can distinguish two distinct regimes. At sub-saturation densities, cutoff independent results dominate. At higher densities, reaching the degenerate supra-saturation regime, the cutoff dependence overtakes temperature effects. A more quantitative analysis of the temperature dependence can be obtained by looking at the so-called thermal index (or adiabatic index) of the equation of state [14]. It characterizes the temperature dependence of the pressure (or energy) of the system. Carbone and Schwenk have recently provided an in-depth analysis of the density, temperature and Hamiltonian dependence of the thermal index obtained in SCGF simulations [18]. They find that some of the assumptions made in previous literature regarding the temperature and density independence of this quantity do not hold. In addition, the effect of 3NFs is important in the high-density regime.

The two extreme limits of isospin asymmetry are interesting on their own, and provide insight into different relevant phenomena. However, both in the study of the liquid-phase transition [119] and in neutron-star astrophysics [73], the actual isospin dependence of the results is relevant. Arbitrary isospin-asymmetric systems can be explored with SCGF simulations, and the results in Figure 12 provide both the energy per particle (top) and the pressure (bottom panels) as a function of density for several asymmetries. Results are presented for the three interactions with different cutoffs.

FIGURE 12

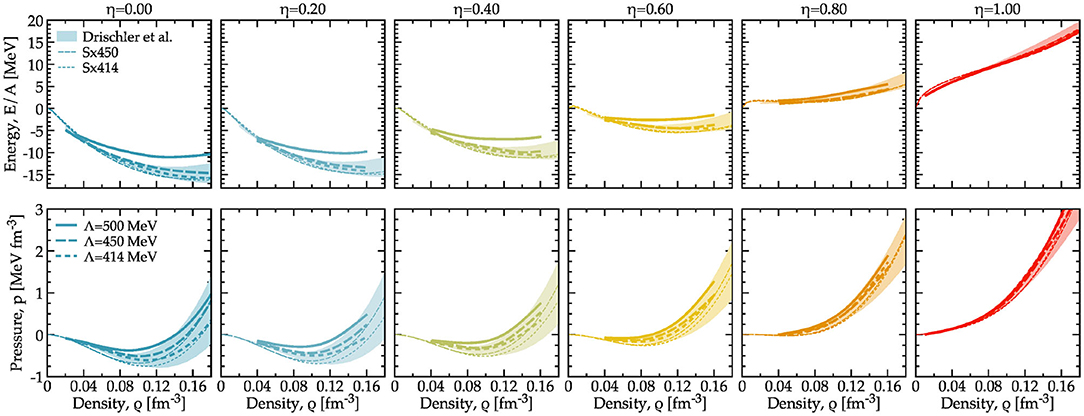
Figure 12. Energy per particle (top) and pressure (bottom) as a function of density for different isospin asymmetries. Results have been extrapolated to zero temperature. The thin lines have been generated from Skyrme functionals fitted to second-order calculations with the same underlying NN forces by Lim and Holt [120]. The bands are obtained from fits to many-body perturbation theory calculations by Drischler et al. [73].

For comparison, I show two different sets of results based on similar ab initio calculations. The narrow lines, labeled Sx450 and Sx414, correspond to Skyrme parametrizations derived in [120]. These density functionals were in turn fit to asymmetric matter calculations performed at second order in many-body perturbation theory for the Λ = 450 MeV and 414 MeV chiral interactions. I do not show the corresponding Sx500 Skyrme results, which were fitted to data with free-particle (rather than self-consistently dressed) intermediate states. The internal dressing of fermion lines is closer in spirit to the SCGF results presented here, and one thus expects to find a better agreement. I note that if non-perturbative effects were small, one would expect an agreement between the fits and the SCGF data.

The bands in the different panels of Figure 12 have been obtained from fits to second-order many-body perturbation theory calculations for seven different chiral interactions in [73]. These fits reproduce the results obtained at second order in perturbation theory with internal Hartree-Fock propagators. These calculations are different to the SCGF approach in that they implement a different averaging procedure for the 3NFs, including an average value of the center-of-mass momentum.

The results from other methods are provided here for reference and only represent a crude estimate of the many-body uncertainties. The discussion below is therefore qualitative, rather than quantitative. The top left panel of Figure 12 clearly indicates that all these interactions and approximations are able to provide saturation for symmetric nuclear matter. The SCGF Λ = 500 MeV results saturate at a too low density and a too high energy per particle. In contrast, the 450 MeV and 414 MeV interactions predict better saturation energies, but are slightly off in terms of density. This may be due to deficiencies of the interactions, the many-body scheme or the implementation of the 3NFs into the SCGF approach [29]. I note however that the saturation energy itself is an extrapolated quantity and a recent reanalysis based on nuclear data suggests it may be a bit more repulsive than anticipated [121].

Comparing the energy per particle to the results of the Sx parametrizations, I find that the SCGF results for the 414 MeV and 450 MeV chiral interactions are qualitatively similar to those obtained in perturbation theory calculations in [70] (for symmetric nuclear matter) and [120] (for asymmetric nuclear matter). The ladder resummation in the SCGF calculations seems to bring in repulsion at intermediate densities for isospin-symmetric systems. This repulsive effect, of the order of a couple of MeV in symmetric nuclear matter, reduces as the isospin asymmetry increases.

As it is well-known, the energy per particle becomes more repulsive as η increases. For pure neutron matter, and in the sub-saturation region shown in the figure, the cutoff dependence of the SCGF results is very small, certainly within 1 MeV. The size of the cutoff dependence is in agreement with the initial findings reported in [69], although the latter were obtained using third-order perturbation-theory calculations. In fact, as the isospin asymmetry of the system increases, the differences in energy between the Sx414 and Sx450 results and the SCGF calculations become much smaller. For densities above 0.06 fm⁻³, all calculations agree in the density dependence of the energy per particle of neutron matter. This is to be expected if one assumes that neutron matter is more perturbative than symmetric nuclear matter. The SCGF and the Sx414 and Sx450 results lie in the lower range of the band provided by [73], which indicates that the cutoff dependence associated to the three chiral interactions presented in this work is not necessarily representative of the systematic uncertainty due to different Hamiltonians.

The reduced cutoff dependence of the results, as the isospin asymmetry evolves from the left to the right panels, has clear implications on the symmetry energy. Because symmetric nuclear matter is more bound for the Λ = 414 MeV and 450 MeV forces, and the neutron matter energy is basically the same, one expects the symmetry energies of these two forces to be relatively larger than that of the 500 MeV interaction. Indeed, computing the symmetry energy as the difference between the two extremes of isospin at ρ = 0.16 fm⁻³, one finds values that range from S₀ = 31.5 MeV for the 414 MeV force up to 29.8 MeV and 25.4 MeV for the 450 MeV and 500 MeV forces. These values are in agreement with those previously reported for these forces in [122], and are somewhat smaller than empirical determinations [8].

The bottom panels of Figure 12 provide a relatively similar picture in terms of the pressure. In symmetric nuclear matter (left panel), the pressure is negative at sub-saturation densities and, other than the Λ = 500 MeV SCGF results, all results agree qualitatively. The picture evolves as isospin asymmetry increases. The spinodal, negative pressure zone decreases as η becomes larger, as expected in general grounds [119]. For most interactions, the critical asymmetry where the spinodal area vanishes is in the range η = 0.6 to 0.8. At these relatively large asymmetries, all the different many-body predictions are contained with the bands obtained by Drischler et al. [73]. Noticeably, the results of the Λ = 500 MeV interaction that were off the band at small asymmetries, fall into the band as isospin asymmetry increases and neutron matter is approached. This indicates that the discrepancies associated to this force with respect to other simulations lie in the isovector component of the interaction.

The cutoff dependence of the SCGF results offers only an initial indication of the size of uncertainties associated to the NN force. In qualitative terms, however, the behavior is similar to that predicted by the bands in [73] which could be explored with non-perturbative methods in the future. At the level of the interaction, there are other sources of uncertainty (like the low-energy constants or the regulator dependence) that are not really considered by these exploratory considerations [51]. The dependence on the many-body method is also relevant as the system becomes more and more isospin symmetric, and quantities like the thermal index or the symmetry energy may be substantially affected by the many-body method under consideration. As such, benchmark comparisons in asymmetric systems would provide an interesting testing ground for newly developed forces.

5. Conclusions

In this work, I have briefly reviewed a set of SCGF techniques that have been used over the last couple of decades to study infinite nuclear systems. SCGF approaches are unique in terms of their flexibility, which allows for both perturbative and non-perturbative studies. The SCGF formalism can be formulated at finite temperature and provide thermodynamically consistent results. The same approach can be used to study the properties of finite nuclei with similar many-body approximations and equivalent interactions [42]. A single SCGF calculation yields not only bulk nuclear properties, including binding energies and thermodynamics, but also a wide range of microphysics information, ranging from predictions associated to the fragmentation of the single-particle strength to the characterization of quasi-particle lifetimes. With an appropriate account of 3NFs, this method can now competitively tackle issues in infinite nuclear matter physics with the same level of predictive power as other many-body approaches. The predictions in terms of the density and isospin dependence of fragmentation strengths are unique and provide an insight that is also relevant for the understanding of the evolution of correlations with isospin.

In this review, I have focused on the properties of symmetric and asymmetric nuclear matter and neutron matter as obtained from a set of three χEFT interactions based on N3LO NN interactions and N2LO 3NFs. This provides a limited but already illustrative set of results that spans a wide range in terms of short-range physics. Of course, one would ideally perform these simulations with the largest possible set of interactions to get a more quantitative estimate of the dependence of the results on the Hamiltonian. A more sophisticated treatment using Bayesian analysis techniques could eventually improve the estimates of systematic uncertainties [9].

The results indicate that the N3LO Λ = 500 MeV interaction produces significantly different strength distributions than the Λ = 450 MeV and 414 MeV forces. As expected, the 500 MeV interaction provides high momentum components in the momentum distribution, and also large additional components in the self-energy. The two softer interactions provide results which are significantly more perturbative. In other words, their momentum distributions die out quicker in momenta and the energy dependence of the associated self-energies is much more limited. These generic results hold independently of the isospin asymmetry. In fact, the results for the 450 MeV and 414 MeV interactions are very similar across a wide range of density, isospin asymmetry and temperatures. In pure neutron matter, the 500 MeV interaction results are also very close to the 450 MeV and 414 MeV interactions. This can be translated into a strong isospin dependence of the overall cutoff dependence. This point has already been discussed in the past in [69, 122], and our SCGF simulations confirm these trends from a different many-body perspective.

SCGF provide access to quasi-particle properties that are relevant in various contexts. Single-particle potentials for neutrons and protons in neutron-rich matter show interesting asymmetry dependences. It is well-known that the single-particle potential for neutrons becomes less attractive with increasing isospin asymmetry. At the same time, it becomes less sensitive to the cutoff. In contrast, the proton potential becomes more attractive in neutron-rich matter and, as the isospin asymmetry increases, the cutoff dependence is enhanced. This behavior should be reflected in the corresponding effective masses. The asymmetry dependence of the single-particle width is also interesting, and again suggests substantial differences in the minority and majority components.

When it comes to bulk properties, I find results that are qualitatively close to those established with many-body perturbation theory methods. Again, the predictions of the Λ = 500 MeV interaction are noticeably different than the lower cutoff results in the isospin symmetric case. In fact, the saturation energy of this interaction is about 4 − 5 MeV more repulsive than empirical estimates, in contrast to the lower cutoff simulations. Results for the 450 MeV-414 MeV forces are more consistent with each other. These also agree well with previous many-body perturbation theory calculations based on these interactions in isospin-symmetric, isospin-asymmetric nuclear matter and pure neutron matter [68].

One can draw several conclusions from this analysis. The isospin dependence of short-range correlations can be predicted with SCGF techniques and appears to be less pronounced in bulk systems than it is in finite nuclei [66, 67, 85, 87]. The cutoff dependence of the results in isospin asymmetric systems affects more the single-particle properties of protons than those of neutrons. In this sense, the simulations of proton impurities in pure neutron matter could provide some insight into the model-dependence of neutron-proton forces. I also note that ab initio simulations of single-particle potentials are significantly different from those predicted by phenomenological approaches [96].

Looking forward, the SCGF method is at an advantage with respect to some other methods in its handling of finite temperature and isospin-asymmetry effects. For supra-saturation densities, this is relevant for neutron star mergers, as well as for neutron-star formation. There, the non-perturbative nature of SCGF methods can handle short-range correlation effects and hence provide meaningful results up to presumably higher densities than perturbative calculations [51]. The effects associated to the fragmentation of strength are also relevant in a variety of high-density astrophysical settings, where they have often been ignored. These include predictions for the equation of state, but also for pairing properties and response functions. Broadly speaking, previous SCGF simulations that have tackled these issues have not relied on systematically improvable chiral interactions that are also helpful in providing estimates of theoretical uncertainties. Interestingly, the low-density high-temperature regime of the neutrinosphere in supernova explosions is also relevant for astrophysical simulations, and it can be tackled with SCGF simulations. There, SCGF methods can provide insight into quantities like single-particle potential shifts [20, 92] and response functions needed for neutrino processes [21]. Our results indicate that these should be interaction-independent, and the dependence on the many-body method will provide a good handle on systematic errors.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author thanks A. Polls, A. Carbone, J. W. Holt, C. Drischler, C. Barbieri, and M. Drissi for fruitful discussion. This work is supported by the UK Science and Technology Facilities Council (STFC) Grant No. ST/P005314/1. Some of the material presented in this paper was available from my contribution to the proceedings of the International Nuclear Physics Conference 2019 [123].

Footnotes

1. ^Multicomponent in the sense that it requires both neutrons and protons.

2. ^I note here for completeness that the η = 0 and η = 1 calculations are performed with independent codes that do not include isospin asymmetry explicitly, and hence provide a good numerical test of the arbitrary isospin simulations.

References

1. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys Rev Lett. (2017) 119:161101. doi: 10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Abbott BP, Abbott R, Abbott TD, Abraham S, Acernese F, Ackley K, et al. GW190425: observation of a compact binary coalescence with total mass ~ 3.4 M ⊙. Astrophys J Lett. (2020) 892:L3. doi: 10.3847/2041-8213/ab75f5

CrossRef Full Text | Google Scholar

3. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. GW170817: measurements of neutron star radii and equation of state. Phys Rev Lett. (2018) 121:161101. doi: 10.1103/PhysRevLett.121.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Abbott BP, Abbott R, Abbott TD, Abraham S, Acernese F, Ackley K, et al. Properties of the binary neutron star merger GW170817. Phys Rev X. (2019) 9:011001. doi: 10.1103/PhysRevX.9.011001

CrossRef Full Text | Google Scholar

5. Raaijmakers G, Greif SK, Riley TE, Hinderer T, Hebeler K, Schwenk A, et al. Constraining the dense matter equation of state with joint analysis of NICER and LIGO/Virgo measurements. Astrophys J Lett. (2020) 893:L21. doi: 10.3847/2041-8213/ab822f

CrossRef Full Text | Google Scholar

6. Miller MC, Lamb FK, Dittmann AJ, Bogdanov S, Arzoumanian Z, Gendreau KC, et al. PSR J0030+0451 mass and radius from NICER data and implications for the properties of neutron star matter. Astrophys J Lett. (2019) 887:L24. doi: 10.3847/2041-8213/ab50c5

CrossRef Full Text | Google Scholar

7. Riley TE, Watts AL, Bogdanov S, Ray PS, Ludlam RM, Guillot S, et al. A NICER View of PSR J0030+0451: millisecond pulsar parameter estimation. Astrophys J Lett. (2019) 887:L21. doi: 10.3847/2041-8213/ab481c

CrossRef Full Text | Google Scholar

8. Tsang MB, Stone JR, Camera F, Danielewicz P, Gandolfi S, Hebeler K, et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys Rev C. (2012) 86:015803. doi: 10.1103/PhysRevC.86.015803

CrossRef Full Text | Google Scholar

9. Drischler C, Furnstahl RJ, Melendez JA, Phillips DR. How well do we know the neutron-matter equation of state at the densities inside neutron stars? A Bayesian approach with correlated uncertainties (2020). arXiv preprint arXiv:2004.07232. Available online at: https://arxiv.org/abs/2004.07232

Google Scholar

10. Danielewicz P, Lacey R, Lynch WG. Determination of the equation of state of dense matter. Science. (2002) 298:1592–96. doi: 10.1126/science.1078070

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Tews I. Quantum Monte Carlo methods for astrophysical applications. Front Phys. (2020) 8:153. doi: 10.3389/fphy.2020.00153

CrossRef Full Text | Google Scholar

12. Baym G, Hatsuda T, Kojo T, Powell PD, Song Y, Takatsuka T. From hadrons to quarks in neutron stars: a review. Rep Prog Phys. (2018) 81:056902. doi: 10.1088/1361-6633/aaae14

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Lim Y, Holt JW. Neutron star tidal deformabilities constrained by nuclear theory and experiment. Phys Rev Lett. (2018) 121:062701. doi: 10.1103/PhysRevLett.121.062701

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Constantinou C, Muccioli B, Prakash M, Lattimer JM. Thermal properties of supernova matter: the bulk homogeneous phase. Phys Rev C. (2014) 89:065802. doi: 10.1103/PhysRevC.89.065802

CrossRef Full Text | Google Scholar

15. Constantinou C, Muccioli B, Prakash M, Lattimer JM. Thermal properties of hot and dense matter with finite range interactions. Phys Rev C. (2015) 92:025801. doi: 10.1103/PhysRevC.92.025801

CrossRef Full Text | Google Scholar

16. Baiotti L, Rezzolla L. Binary neutron star mergers: a review of Einstein's richest laboratory. Rep Prog Phys. (2017) 80:096901. doi: 10.1088/1361-6633/aa67bb

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Duez MD, Zlochower Y. Numerical relativity of compact binaries in the 21st century. Rep Prog Phys. (2018) 82:016902. doi: 10.1088/1361-6633/aadb16

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Carbone A, Schwenk A. Ab initio constraints on thermal effects of the nuclear equation of state. Phys Rev C. (2019) 100:025805. doi: 10.1103/PhysRevC.100.025805

CrossRef Full Text | Google Scholar

19. Pons JA, Reddy S, Prakash M, Lattimer JM, Miralles JA. Evolution of proto-neutron stars. Astrophys J. (1999) 513:780–804. doi: 10.1086/306889

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Martinez-Pinedo G, Fischer T, Lohs A, Huther L. Charged-current weak interaction processes in hot and dense matter and its impact on the spectra of neutrinos emitted from protoneutron star cooling. Phys Rev Lett. (2012) 109:251104. doi: 10.1103/PhysRevLett.109.251104

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Rrapaj E, Holt JW, Bartl A, Reddy S, Schwenk A. Charged-current reactions in the supernova neutrino-sphere. Phys Rev C. (2015) 91:035806. doi: 10.1103/PhysRevC.91.035806

CrossRef Full Text | Google Scholar

22. Gandolfi S, Hammer HW, Klos P, Lynn JE, Schwenk A. Is a trineutron resonance lower in energy than a tetraneutron resonance? Phys Rev Lett. (2017) 118:232501. doi: 10.1103/PhysRevLett.118.232501

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Tews I, Krüger T, Hebeler K, Schwenk A. Neutron matter at next-to-next-to-next-to-leading order in chiral effective field theory. Phys Rev Lett. (2013) 110:032504. doi: 10.1103/PhysRevLett.110.032504

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Epelbaum E, Hammer HW, Meißner UG. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773–825. doi: 10.1103/RevModPhys.81.1773

CrossRef Full Text | Google Scholar

25. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rep. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001

CrossRef Full Text | Google Scholar

26. Ishii N, Aoki S, Hatsuda T. Nuclear force from lattice QCD. Phys Rev Lett. (2007) 99:022001. doi: 10.1103/PhysRevLett.99.022001

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Hatsuda T. Lattice quantum chromodynamics and baryon-baryon interactions. Front Phys. (2018) 13:132105. doi: 10.1007/s11467-018-0829-4

CrossRef Full Text | Google Scholar

28. Drischler C, Hebeler K, Schwenk A. Asymmetric nuclear matter based on chiral two- and three-nucleon interactions. Phys Rev C. (2016) 93:054314. doi: 10.1103/PhysRevC.93.054314

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Drischler C, Hebeler K, Schwenk A. Chiral interactions up to next-to-next-to-next-to-leading order and nuclear saturation. Phys Rev Lett. (2019) 122:042501. doi: 10.1103/PhysRevLett.122.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Baldo M, Polls A, Rios A, Schulze HJ, Vidana I. Comparative study of neutron and nuclear matter with simplified Argonne nucleon-nucleon potentials. Phys Rev C. (2012) 86:064001. doi: 10.1103/PhysRevC.86.064001

CrossRef Full Text | Google Scholar

31. Piarulli M, Bombaci I, Logoteta D, Lovato A, Wiringa RB. Benchmark calculations of pure neutron matter with realistic nucleon-nucleon interactions. Phys Rev C. (2020) 101:045801. doi: 10.1103/PhysRevC.101.045801

CrossRef Full Text | Google Scholar

32. Dickhoff WH, Barbieri C. Self-consistent Green's function method for nuclei and nuclear matter. Prog Part Nucl Phys. (2004) 52:377–496. doi: 10.1016/j.ppnp.2004.02.038

CrossRef Full Text | Google Scholar

33. Dickhoff WH, Van Neck D. Many-Body Theory Exposed! 2nd ed. New Jersey, NJ: World Scientific (2008). doi: 10.1142/6821

CrossRef Full Text | Google Scholar

34. Barbieri C, Carbone A. Self-consistent Green's function approaches. In: Hjorth-Jensen M, Lombardo MP, van Kolck U, editors. An Advanced Course in Computational Nuclear Physics. Springer (2017). p. 571–644. doi: 10.1007/978-3-319-53336-0_11

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Economou EN. Green's Functions in Quantum Physics. Berlin, Heidelberg: Springer (2006). doi: 10.1007/3-540-28841-4

CrossRef Full Text | Google Scholar

36. Stefanucci G, van Leeuwen R. Nonequilibrium Many-Body Theory of Quantum Systems. Cambridge: Cambridge University Press (2013).

Google Scholar

37. Abrikosov AA, Gorkov LP, Dzyaloshinskii IY. Quantum Field Theoretical Methods in Statistical Physics. 2nd ed. Pergamon Press (1965).

38. Mattuck RD. A Guide to Feynman Diagrams in the Many-Body Problem. New York, NY: Dover Publications (1992).

Google Scholar

39. Fetter AL, Walecka JD. Quantum Theory of Many-Particle System. 1st ed. New York, NY: Dover (2003).

Google Scholar

40. Müther H, Polls A. Two-body correlations in nuclear systems. Prog Part Nucl Phys. (2000) 45:243–334. doi: 10.1016/S0146-6410(00)00105-8

CrossRef Full Text | Google Scholar

41. Gandolfi S, Gezerlis A, Carlson J. Neutron matter from low to high density. Annu Rev Nucl Part Sci. (2015) 65:303–28. doi: 10.1146/annurev-nucl-102014-021957

CrossRef Full Text | Google Scholar

42. Somá V. Self-consistent Green's function theory for atomic nuclei (2020).

Google Scholar

43. Bozek P. Superfluidity with dressed nucleons. Phys Lett B. (2003) 551:93. doi: 10.1016/S0370-2693(02)03007-1

CrossRef Full Text | Google Scholar

44. Rios A, Polls A, Vidana I. Hot neutron matter from a self-consistent Green's-functions approach. Phys Rev C. (2009) 79:025802. doi: 10.1103/PhysRevC.79.025802

CrossRef Full Text | Google Scholar

45. Somá V, Bozek P. Thermodynamic properties of nuclear matter with three-body forces. Phys Rev C. (2009) 80:025803. doi: 10.1103/PhysRevC.80.025803

CrossRef Full Text | Google Scholar

46. Bozek P. Superfluid nuclear matter calculations. Nucl Phys A. (1999) 657:187. doi: 10.1016/S0375-9474(99)00325-5

CrossRef Full Text | Google Scholar

47. Polls A, Ramos A, Gearhart CC, Dickhoff WH, Muther H. Short range correlations and spectral functions for nuclear matter and finite nuclei. Prog Part Nucl Phys. (1995) 34:371–380. doi: 10.1016/0146-6410(95)00032-E

CrossRef Full Text | Google Scholar

48. Rios A, Polls A, Ramos A, Müther H. Liquid-gas phase transition in nuclear matter from realistic many-body approaches. Phys Rev C. (2008) 78:044314. doi: 10.1103/PhysRevC.78.044314

CrossRef Full Text | Google Scholar

49. Carbone A, Polls A, Rios A. Microscopic predictions of the nuclear matter liquid-gas phase transition. Phys Rev C. (2018) 98:025804. doi: 10.1103/PhysRevC.98.025804

CrossRef Full Text | Google Scholar

50. Ding D, Rios A, Dussan H, Dickhoff WH, Witte SJ, Carbone A, et al. Pairing in high-density neutron matter including short- and long-range correlations. Phys Rev C. (2016) 94:025802. doi: 10.1103/PhysRevC.94.025802

CrossRef Full Text | Google Scholar

51. Carbone A. Setting nonperturbative uncertainties on finite-temperature properties of neutron matter. Phys Rev Res. (2020) 2:023227. doi: 10.1103/PhysRevResearch.2.023227

CrossRef Full Text | Google Scholar

52. Jeukenne JP, Lejeune A, Mahaux C. Many-body theory of nuclear matter. Phys Rep. (1976) 25:83–174. doi: 10.1016/0370-1573(76)90017-X

CrossRef Full Text | Google Scholar

53. Luttinger JM. Analytic Properties of single-particle propagators for many-Fermion systems. Phys Rev. (1961) 121:942. doi: 10.1103/PhysRev.121.942

CrossRef Full Text | Google Scholar

54. Carbone A, Cipollone A, Barbieri C, Rios A, Polls A. Self-consistent Green's functions formalism with three-body interactions. Phys Rev C. (2013) 88:054326. doi: 10.1103/PhysRevC.88.054326

CrossRef Full Text | Google Scholar

55. Carbone A, Polls A, Rios A. Symmetric nuclear matter with chiral three-nucleon forces in the self-consistent Green's functions approach. Phys Rev C. (2013) 88:044302. doi: 10.1103/PhysRevC.88.044302

CrossRef Full Text | Google Scholar

56. Carbone A, Rios A, Polls A. Correlated density-dependent chiral forces for infinite-matter calculations within the Green's function approach. Phys Rev C. (2014) 90:054322. doi: 10.1103/PhysRevC.90.054322

CrossRef Full Text | Google Scholar

57. Frick T, Müther H. Self-consistent solution to the nuclear many-body problem at finite temperature. Phys Rev C. (2003) 68:034310. doi: 10.1103/PhysRevC.68.034310

CrossRef Full Text | Google Scholar

58. Rios A. Thermodynamical Properties of Nuclear Matter from a Self-Consistent Green's Function Approach. University of Barcelona (2007).

Google Scholar

59. Cipollone A, Barbieri C, Navrátil P. Isotopic chains around oxygen from evolved chiral two- and three-nucleon interactions. Phys Rev Lett. (2013) 111:062501. doi: 10.1103/PhysRevLett.111.062501

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Rios A, Polls A, Ramos A, Müther H. Entropy of a correlated system of nucleons. Phys Rev C. (2006) 74:054317. doi: 10.1103/PhysRevC.74.054317

CrossRef Full Text | Google Scholar

61. Pethick CJ, Carneiro GM. Specific heat of a normal fermi liquid. I. Landau-Theory Approach. Phys Rev A. (1973) 7:304–318. doi: 10.1103/PhysRevA.7.304

CrossRef Full Text | Google Scholar

62. Carneiro GM, Pethick CJ. Specific heat of a normal Fermi liquid. II. Microscopic approach. Phys Rev B. (1975) 11:1106–24. doi: 10.1103/PhysRevB.11.1106

CrossRef Full Text | Google Scholar

63. Kadanoff LP, Baym G. Quantum Statistical Mechanics. New York, NY: W.A. Benjamin (1962).

Google Scholar

64. Frick T, Müther H, Rios A, Polls A, Ramos A. Correlations in hot asymmetric nuclear matter. Phys Rev C. (2005) 71:014313. doi: 10.1103/PhysRevC.71.014313

CrossRef Full Text | Google Scholar

65. Konrad P, Lenske H, Mosel U. Short range correlations and spectral functions in asymmetric nuclear matter. Nucl Phys A. (2005) 756:192–212. doi: 10.1016/j.nuclphysa.2005.03.083

CrossRef Full Text | Google Scholar

66. Rios A, Polls A, Dickhoff WH. Depletion of the nuclear Fermi sea. Phys Rev C. (2009) 79:064308. doi: 10.1103/PhysRevC.79.064308

CrossRef Full Text | Google Scholar

67. Rios A, Polls A, Dickhoff WH. Density and isospin-asymmetry dependence of high-momentum components. Phys Rev C. (2014) 89:044303. doi: 10.1103/PhysRevC.89.044303

CrossRef Full Text | Google Scholar

68. Wellenhofer C, Holt JW, Kaiser N. Thermodynamics of isospin-asymmetric nuclear matter from chiral effective field theory. Phys Rev C. (2015) 92:015801. doi: 10.1103/PhysRevC.92.015801

CrossRef Full Text | Google Scholar

69. Coraggio L, Holt JW, Itaco N, Machleidt R, Sammarruca F. Reduced regulator dependence of neutron-matter predictions with perturbative chiral interactions. Phys Rev C. (2013) 87:014322. doi: 10.1103/PhysRevC.87.014322

CrossRef Full Text | Google Scholar

70. Coraggio L, Holt JW, Itaco N, Machleidt R, Marcucci LE, Sammarruca F. Nuclear-matter equation of state with consistent two- and three-body perturbative chiral interactions. Phys Rev C. (2014) 89:044321. doi: 10.1103/PhysRevC.89.044321

CrossRef Full Text | Google Scholar

71. Holt JW, Kaiser N, Weise W. Density-dependent effective nucleon-nucleon interaction from chiral three-nucleon forces. Phys Rev C. (2010) 81:024002. doi: 10.1103/PhysRevC.81.024002

CrossRef Full Text | Google Scholar

72. Holt JW, Kawaguchi M, Kaiser N. Implementing chiral three-body forces in terms of medium-dependent two-body forces. Front Phys. (2020) 8:100. doi: 10.3389/fphy.2020.00100

CrossRef Full Text | Google Scholar

73. Drischler C, Carbone A, Hebeler K, Schwenk A. Neutron matter from chiral two- and three-nucleon calculations up to N³LO. Phys Rev C. (2016) 94:054307. doi: 10.1103/PhysRevC.94.054307

CrossRef Full Text | Google Scholar

74. Rios A, Polls A, Dickhoff WH. Pairing and short-range correlations in nuclear systems. J Low T Phys. (2017) 189:234–49. doi: 10.1007/s10909-017-1818-7

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Ramos A, Dickhoff WH, Polls A. Binding energy and momentum distribution of nuclear matter using Green's function methods. Phys Rev C. (1991) 43:2239–53. doi: 10.1103/PhysRevC.43.2239

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Rios A, Carbone A, Polls A. Comparison of nuclear Hamiltonians using spectral function sum rules. Phys Rev C. (2017) 96:014003. doi: 10.1103/PhysRevC.96.014003

CrossRef Full Text | Google Scholar

77. Rohe D, Armstrong CS, Asaturyan R, Baker OK, Bueltmann S, Carasco C, et al. Correlated strength in the nuclear spectral function. Phys Rev Lett. (2004) 93:182501. doi: 10.1103/PhysRevLett.93.182501

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Schmidt A, Pybus JR, Weiss R, Segarra EP, Hrnjic A, Denniston A, et al. Probing the core of the strong nuclear interaction. Nature. (2020) 578:540–4. doi: 10.1038/s41586-020-2021-6

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Typel S, Brown BA. Neutron radii and the neutron equation of state in relativistic models. Phys Rev C. (2001) 64:027302. doi: 10.1103/PhysRevC.64.027302

CrossRef Full Text | Google Scholar

80. Haensel P, Potekhin AY, Yakovlev DG. Neutron Stars 1: Equation of State and Structure. New York, NY: Springer (2007). doi: 10.1007/978-0-387-47301-7

CrossRef Full Text | Google Scholar

81. Tang A, Watson JW, Aclander J, Alster J, Asryan G, Averichev Y, et al. n−p short-range correlations from (p, 2p+n) measurements. Phys Rev Lett. (2003) 90:042301. doi: 10.1103/PhysRevLett.90.042301

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Piasetzky E, Sargsian M, Frankfurt L, Strikman M, Watson JW. Evidence for strong dominance of proton-neutron correlations in nuclei. Phys Rev Lett. (2006) 97:162504. doi: 10.1103/PhysRevLett.97.162504

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Hen O, Sargsian M, Weinstein LB, Piasetzky E, Hakobyan H, Higinbotham DW, et al. Nuclear physics. Momentum sharing in imbalanced Fermi systems. Science. (2014) 346:614–7. doi: 10.1126/science.1256785

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Sargsian MM. New properties of the high-momentum distribution of nucleons in asymmetric nuclei. Phys Rev C. (2014) 89:034305. doi: 10.1103/PhysRevC.89.034305

CrossRef Full Text | Google Scholar

85. Duer M, Hen O, Piasetzky E, Hakobyan H, Weinstein LB, Braverman M, et al. Probing high-momentum protons and neutrons in neutron-rich nuclei. Nature. (2018) 560:617–621. doi: 10.1038/s41586-018-0400-z

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Ryckebusch J, Cosyn W, Stevens S, Casert C, Nys J. The isospin and neutron-to-proton excess dependence of short-range correlations. Phys Lett B. (2019) 792:21–8. doi: 10.1016/j.physletb.2019.03.016

CrossRef Full Text | Google Scholar

87. Paschalis S, Petri M, Macchiavelli AO, Hen O, Piasetzky E. Nucleon-nucleon correlations and the single-particle strength in atomic nuclei. Phys Lett B. (2020) 800:135110. doi: 10.1016/j.physletb.2019.135110

CrossRef Full Text | Google Scholar

88. Carbone A, Polls A, Rios A. High-momentum components in the nuclear symmetry energy. Europhys Lett. (2012) 97:22001. doi: 10.1209/0295-5075/97/22001

CrossRef Full Text | Google Scholar

89. Hen O, Li BA, Guo WJ, Weinstein LB, Piasetzky E. Symmetry energy of nucleonic matter with tensor correlations. Phys Rev C. (2015) 91:025803. doi: 10.1103/PhysRevC.91.025803

CrossRef Full Text | Google Scholar

90. Cai BJ, Li BA. Symmetry energy of cold nucleonic matter within a relativistic mean field model encapsulating effects of high-momentum nucleons induced by short-range correlations. Phys Rev C. (2016) 93:014619. doi: 10.1103/PhysRevC.93.014619

CrossRef Full Text | Google Scholar

91. Gade A, Adrich P, Bazin D, Bowen MD, Brown BA, Campbell CM, et al. Reduction of spectroscopic strength: Weakly-bound and strongly-bound single-particle states studied using one-nucleon knockout reactions. Phys Rev C. (2008) 77:044306. doi: 10.1103/PhysRevC.77.044306

CrossRef Full Text | Google Scholar

92. Roberts LF, Reddy S, Shen G. Medium modification of the charged-current neutrino opacity and its implications. Phys Rev C. (2012) 86:065803. doi: 10.1103/PhysRevC.86.065803

CrossRef Full Text | Google Scholar

93. Zuo W, Lejeune A, Lombardo U, Mathiot JF. Microscopic three-body force for asymmetric nuclear matter. Eur Phys J A. (2002) 14:469–75. doi: 10.1140/epja/i2002-10031-y

CrossRef Full Text | Google Scholar

94. Zuo W, Cao LG, Li BA, Lombardo U, Shen CW. Isospin splitting of the nucleon mean field. Phys Rev C. (2005) 72:014005. doi: 10.1103/PhysRevC.72.014005

CrossRef Full Text | Google Scholar

95. Holt JW, Kaiser N, Miller GA. Microscopic optical potential for exotic isotopes from chiral effective field theory. Phys Rev C. (2016) 93:064603. doi: 10.1103/PhysRevC.93.064603

CrossRef Full Text | Google Scholar

96. Sellahewa R, Rios A. Isovector properties of the Gogny interaction. Phys Rev C. (2014) 90:054327. doi: 10.1103/PhysRevC.90.054327

CrossRef Full Text | Google Scholar

97. Hebeler K, Lattimer JM, Pethick CJ, Schwenk A. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys J. (2013) 773:11. doi: 10.1088/0004-637X/773/1/11

CrossRef Full Text | Google Scholar

98. Drischler C, Somá V, Schwenk A. Microscopic calculations and energy expansions for neutron-rich matter. Phys Rev C. (2014) 89:025806. doi: 10.1103/PhysRevC.89.025806

CrossRef Full Text | Google Scholar

99. Charity RJ, Sobotka LG, Dickhoff WH. Asymmetry dependence of proton correlations. Phys Rev Lett. (2006) 97:162503. doi: 10.1103/PhysRevLett.97.162503

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Duguet T, Hagen G. Ab initio approach to effective single-particle energies in doubly closed shell nuclei. Phys Rev C. (2012) 85:034330. doi: 10.1103/PhysRevC.85.034330

CrossRef Full Text | Google Scholar

101. Duguet T, Hergert H, Holt JD, Somá V. Nonobservable nature of the nuclear shell structure: meaning, illustrations, and consequences. Phys Rev C. (2015) 92:034313. doi: 10.1103/PhysRevC.92.034313

CrossRef Full Text | Google Scholar

102. Polls A, Ramos A, Ventura J, Amari S, Dickhoff WH. Energy weighted sum rules for spectral functions in nuclear matter. Phys Rev C. (1994) 49:3050–4. doi: 10.1103/PhysRevC.49.3050

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Frick T, Müther H, Polls A. Sum rules and short-range correlations in nuclear matter at finite temperature. Phys Rev C. (2004) 69:054305. doi: 10.1103/PhysRevC.69.054305

CrossRef Full Text | Google Scholar

104. Rios A, Polls A, Müther H. Sum rules and correlations in asymmetric nuclear matter. Phys Rev C. (2006) 73:024305. doi: 10.1103/PhysRevC.73.024305

CrossRef Full Text | Google Scholar

105. Dickhoff WH. Scattering of dressed nucleons in nuclear matter. Phys Rev C. (1998) 58:2807–20. doi: 10.1103/PhysRevC.58.2807

CrossRef Full Text | Google Scholar

106. Dickhoff WH, Gearhart CC, Roth EP, Polls A, Ramos A. Phase shifts and in-medium cross sections for dressed nucleons in nuclear matter. Phys Rev C. (1999) 60:064319. doi: 10.1103/PhysRevC.60.064319

CrossRef Full Text | Google Scholar

107. Negele J, Yazaki K. Mean free path in a nucleus. Phys Rev Lett. (1981) 47:71–4. doi: 10.1103/PhysRevLett.47.71

CrossRef Full Text | Google Scholar

108. Lopez O, Durand D, Lehaut G, Borderie B, Frankland JD, Rivet MF, et al. In-medium effects for nuclear matter in the Fermi-energy domain. Phys Rev C. (2014) 90:064602. doi: 10.1103/PhysRevC.90.069903

CrossRef Full Text | Google Scholar

109. Somá V. Self-consistent Green's function theory for atomic nuclei. arXiv [Preprint]. (2020) arxiv:2003.11321. URL https://arxiv.org/abs/2003.11321.

Google Scholar

110. Müther H, Dickhoff WH. Pairing properties of nucleonic matter employing dressed nucleons. Phys Rev C. (2005) 72:054313. doi: 10.1103/PhysRevC.72.054313

CrossRef Full Text | Google Scholar

111. Schwenk A, Friman B. Polarization contributions to the spin dependence of the effective interaction in neutron matter. Phys Rev Lett. (2004) 92:082501. doi: 10.1103/PhysRevLett.92.082501

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Baldo M, Ferreira L. Nuclear liquid-gas phase transition. Phys Rev C. (1999) 59:682–703. doi: 10.1103/PhysRevC.59.682

CrossRef Full Text | Google Scholar

113. Mukherjee A, Pandharipande VR. Variational theory of hot nucleon matter. Phys Rev C. (2007) 75:035802. doi: 10.1103/PhysRevC.75.035802

CrossRef Full Text | Google Scholar

114. Tolos L, Friman B, Schwenk A. Neutron matter at finite temperature. Nucl Phys A. (2008) 806:105–16. doi: 10.1016/j.nuclphysa.2008.02.309

CrossRef Full Text | Google Scholar

115. Wellenhofer C, Holt JW, Kaiser N, Weise W. Nuclear thermodynamics from chiral low-momentum interactions. Phys Rev C. (2014) 89:064009. doi: 10.1103/PhysRevC.89.064009

CrossRef Full Text | Google Scholar

116. Wellenhofer C. Zero-temperature limit and statistical quasiparticles in many-body perturbation theory. Phys Rev C. (2019) 99:065811. doi: 10.1103/PhysRevC.99.065811

CrossRef Full Text | Google Scholar

117. Rios A. Effective interaction dependence of the liquid-gas phase transition in symmetric nuclear matter. Nucl Phys A. (2010) 845:58–87. doi: 10.1016/j.nuclphysa.2010.05.057

CrossRef Full Text | Google Scholar

118. Horowitz CJ, Schwenk A. The virial equation of state of low-density neutron matter. Phys Lett B. (2006) 638:153–9. doi: 10.1016/j.physletb.2006.05.055

CrossRef Full Text | Google Scholar

119. Vidana I, Polls A. Spinodal instabilities of asymmetric nuclear matter within the Brueckner–Hartree–Fock approach. Phys Lett B. (2008) 666:232–8. doi: 10.1016/j.physletb.2008.07.066

CrossRef Full Text | Google Scholar

120. Lim Y, Holt JW. Structure of neutron star crusts from new Skyrme effective interactions constrained by chiral effective field theory. Phys Rev C. (2017) 95:065805. doi: 10.1103/PhysRevC.95.065805

CrossRef Full Text | Google Scholar

121. Atkinson MC, Dickhoff WH, Piarulli M, Rios A, Wiringa RB. Revisiting the relation between the binding energy of finite nuclei and the equation of state of infinite nuclear matter (2020). arXiv preprint arXiv:2001.07231. Available online at: https://arxiv.org/abs/2001.07231.

Google Scholar

122. Sammarruca F, Coraggio L, Holt JW, Itaco N, Machleidt R, Marcucci LE. Toward order-by-order calculations of the nuclear and neutron matter equations of state in chiral effective field theory. Phys Rev C. (2015) 91:054311. doi: 10.1103/PhysRevC.91.054311

CrossRef Full Text | Google Scholar

123. Rios A. Short range correlations in nuclei and nuclear matter. In: Proceedings of the International Nuclear Physics Conference. (2019).

Google Scholar