A Novel Robust Strategy for Discontinuous Galerkin Methods in Computational Fluid Mechanics: Why? When? What? Where?

In this paper we will review a recent emerging paradigm shift in the construction and analysis of high order Discontinuous Galerkin methods applied to approximate solutions of hyperbolic or mixed hyperbolic-parabolic partial differential equations (PDEs) in computational physics. There is a long history using DG methods to approximate the solution of partial differential equations in computational physics with successful applications in linear wave propagation, like those governed by Maxwell’s equations, incompressible and compressible fluid and plasma dynamics governed by the Navier-Stokes and the Magnetohydrodynamics equations, or as a solver for ordinary differential equations (ODEs), e.g., in structural mechanics. The DG method amalgamates ideas from several existing methods such as the Finite Element Galerkin method (FEM) and the Finite Volume method (FVM) and is specifically applied to problems with advection dominated properties, such as fast moving fluids or wave propagation. In the numerics community, DG methods are infamous for being computationally complex and, due to their high order nature, as having issues with robustness, i.e., these methods are sometimes prone to crashing easily. In this article we will focus on efficient nodal versions of the DG scheme and present recent ideas to restore its robustness, its connections to and influence by other sectors of the numerical community, such as the finite difference community, and further discuss this young, but rapidly developing research topic by highlighting the main contributions and a closing discussion about possible next lines of research.

1 A Brief Introduction to DG

The first discontinuous Galerkin (DG) type discretisation is either attributed to Reed and Hill in 1973 [1] for an application to steady state scalar hyperbolic linear advection to model neutron transport, or to Nitsche in 1971 [2] who introduced a discontinuous finite element method (FEM) to solve elliptic problems with non-conforming approximation spaces. It was however a series of papers by Cockburn and Shu et al. starting 20 years later [3–6] that introduced the modern form of the so-called Runge-Kutta DG scheme. They applied the method especially to nonlinear hyperbolic problems such as the compressible Euler equations on unstructured simplex grids with slope limiting to capture shocks. Bassi and Rebay were the first that extended the DG method to the compressible Navier-Stokes equations [7]. They used a fully discontinuous ansatz based on a mixed variational formulation, where they rewrote the second order partial differential equation (PDE) into a first order system. The resulting DG formulation requires numerical fluxes for the advective as well as for the diffusive part. Although the methods gave reasonable results for the compressible Navier-Stokes equations, an analysis of the method in Arnold and Brezzi et al. [8, 9] applied to pure elliptic problems revealed how to improve the method in terms of convergence rate, adjoint consistency, and stability. Since the introduction of its modern form, the DG method has been applied and advanced by many researchers across different scientific disciplines around the world. The DG method is used in a wide range of applications such as compressible flows [10–12], electromagnetics and optics [13–16], acoustics [17–21], meteorology [22–25], and geophysics [26, 27]. The first book available on DG was basically a collection of papers [28]. Since then, many different text books on DG are available focusing on theoretical developments as well as specific implementation details, e.g., [29–31].

One of the main applications of DG methods is the discretisation of nonlinear advection-diffusion problems of the form

${\mathbf{u}}_t+{\overrightarrow{\nabla }}_x\cdot \stackrel{⟷}{\mathbf{f}}\left(\mathbf{u}\right)={\overrightarrow{\nabla }}_x\cdot {\stackrel{⟷}{\mathbf{f}}}_v\left(\mathbf{u},{\overrightarrow{\nabla }}_x\mathbf{u}\right)\hspace{0.17em},(1)$

where u is the vector of conserved quantities, e.g., the mass, momentum, or energy. The vector $\overleftrightarrow{\mathbf{f}}\left(\mathbf{u}\right)$ defines the flux functions that in general depend nonlinearly on the solution u, and can be compactly written with the double arrow notation as block vectors

$\stackrel{⟷}{\mathbf{f}}=\left[\begin{array}{c}{\mathbf{f}}_1\\ {\mathbf{f}}_2\\ {\mathbf{f}}_3\end{array}\right]\hspace{0.17em},(2)$

with the fluxes f_i in each spatial direction x_i, i = 1,2,3. The viscous fluxes are denoted by ${\overleftrightarrow{\mathbf{f}}}_v$ and not only depend on the solution, but also on its spatial gradient

${\overrightarrow{\nabla }}_x\mathbf{u}=\left[\begin{array}{c}{\mathbf{u}}_x\\ {\mathbf{u}}_y\\ {\mathbf{u}}_z\end{array}\right]\hspace{0.17em},(3)$

thus modeling parabolic effects, e.g., heat conduction. The problem is typically defined on a given spatial domain $\text{Ω}\subset {\mathcal{R}}^3$, with a final time T, and suitable initial and boundary conditions.

The DG scheme is based on a Galerkin type weak formulation. For the sake of simplicity, we drop the viscous second order terms in what follows and refer to, e.g. [32], for a complete description of the advection-diffusion case. To construct the approximation space of the DG method, the domain is split into non-overlapping elements $E\subset \text{Ω}$. Each component of the solution u is represented as a polynomial function inside each element

$\mathbf{u}\left(\overrightarrow{x},t\right){|}_E\approx \mathbf{U}\left(\overrightarrow{x},t\right)={\displaystyle \sum }_{j=0}^{P\left(N\right)}{\mathbf{U}}_j\left(t\right)\hspace{0.17em}{\varphi }_j\left(\overrightarrow{x}\right),(4)$

where P(N) is the number of polynomial basis functions depending on the polynomial degree N. The time dependent polynomial coefficients are U_j(t), and ${\varphi }_j\left(\overrightarrow{x}\right)$ spans the polynomial basis. The DG approximation space is polynomial inside an element, but discontinuous across element interfaces. For a given element E, we define first the inner product for state vectors

${\langle \mathbf{u},\mathbf{v}\rangle }_E=\underset{E}{{\displaystyle \int }}{\mathbf{u}}^T\mathbf{v}\hspace{0.17em}\text{d}\overrightarrow{x}.(5)$

Similarly, for block vectors,

${\langle \stackrel{⟷}{\mathbf{f}},\stackrel{⟷}{\mathbf{g}}\rangle }_E=\underset{E}{{\displaystyle \int }}{\displaystyle \sum }_{i=1}^3{\mathbf{f}}_i^T{\mathbf{g}}_i\hspace{0.17em}\text{d}\overrightarrow{x}\hspace{0.17em}.(6)$

We obtain the weak formulation by multiplying each equation by a polynomial test function $\varphi \left(\overrightarrow{x}\right)$. Next, we integrate over the element E and use integration-by-parts to move the spatial derivatives off of the physical fluxes onto the test function

${\langle {\mathbf{U}}_t,\varphi \rangle }_E+\underset{\partial E}{{\displaystyle \oint }}{\varphi }^T\stackrel{⟷}{\mathbf{f}}\cdot \overrightarrow{n}\hspace{0.17em}\text{dS}-{\langle \stackrel{⟷}{\mathbf{f}},{\overrightarrow{\nabla }}_x\varphi \rangle }_E=0.(7)$

If we choose the test function $\varphi$ to be all the polynomial basis functions from the solution ansatz space ${\left\{{\varphi }_j\right\}}_{j=0}^P$ it generates P equations in each element for each state variable. This matches exactly the number of unknown polynomial coefficients U_j(t). Due to the discontinuous ansatz, the flux normal $\overleftrightarrow{\mathbf{f}}\cdot \overrightarrow{n}$ at the surface integral is not uniquely defined. Borrowing ideas from the Finite Volume (FV) community, this non-unique normal flux function is replaced and approximated with a so-called numerical surface flux function

$\stackrel{⟷}{\mathbf{f}}\cdot \overrightarrow{n}\approx {\mathbf{f}}^{\text{*}}\left({\mathbf{U}}^{+},\mathbf{U}\right),(8)$

that depends on the two values at the element interface, i.e. on the value inside the element U and outside from the neighbor element U⁺. Typically, the numerical surface fluxes are constructed from (approximate) Riemann solvers, e.g., [33]. With the surface numerical flux, we arrive at the semi-discrete DG formulation of the advection problem in weak form

${\langle {\mathbf{U}}_t,\varphi \rangle }_E+\underset{\partial E}{{\displaystyle \oint }}{\varphi }^T{\mathbf{f}}^{\text{*}}\left({\mathbf{U}}^{+},\mathbf{U}\right)\hspace{0.17em}\text{dS}-{\langle \stackrel{⟷}{\mathbf{f}},{\overrightarrow{\nabla }}_x\varphi \rangle }_E=0,(9)$

or if we apply integration-by-parts once more to the volume terms it becomes the so-called strong DG formulation

${\langle {\mathbf{U}}_t,\varphi \rangle }_E+\underset{\partial E}{{\displaystyle \oint }}{\varphi }^T\left({\mathbf{f}}^{\text{*}}\left({\mathbf{U}}^{+},\mathbf{U}\right)-\overleftrightarrow{\mathbf{f}}\cdot \overrightarrow{n}\right)\hspace{0.17em}\text{dS}+{\langle {\overrightarrow{\nabla }}_x\cdot \stackrel{⟷}{\mathbf{f}},\varphi \rangle }_E=0,(10)$

where the surface contribution is a penalty between the numerical surface flux and the normal flux evaluated from the interior of an element. Note, the weak and strong form DG formulations are equivalent [34].

There are still many critical decisions necessary before the DG formulation produces an algorithm that can be implemented. The type of element shape needs to be decided as well as which polynomial basis. For example, modal polynomial basis functions for tetrahedral elements or nodal tensor product polynomials for hexahedral elements. In addition, the surface integral and the volume integral needs to be discretized. In most cases, the integrals are approximated with numerical quadrature rules, e.g., high order Gauss-Legendre quadrature and cubature. Many variants and detailed descriptions can be found in text books on DG methods and their implementation, e.g., [28–31]. It is important to note that these choices involving the element type, basis functions, and approximation of inner products all have a major impact on the performance of the resulting DG scheme in terms of computational complexity and robustness due, e.g., to the presence of spurious oscillations near discontinuities that result in unphysical solution states (like negative density or pressure) or aliasing instabilities. Many mechanisms exist in the DG community to combat spurious oscillations (i.e., shock capturing) such as slope [3, 5, 35] or WENO [36, 37] limiters, filtering [29, 38, 39], finite volume sub-cells [40–42], MOOD-type limiting [43–47], or artificial viscosity [48, 49]. The issue of shock capturing will not be discussed further. However, aliasing errors, how they arise within the DG method and strategies to remove said errors and increase robustness will be discussed at length in this article.

With the above decisions, we arrive at the generic semi-discrete ordinary differential equation (ODE) form of the DG scheme, which can be integrated in time with an appropriate high order explicit or implicit ODE solver, e.g., [50–54].

The resulting DG method is high order accurate and has excellent dispersion and dissipation behavior, e.g., [55, 56]. Furthermore, due to its compact stencil (only interface neighbor data is needed) the DG scheme is well known for its excellent parallel scaling, e.g., [57, 58], and its ability to handle unstructured and non-conforming grids, e.g., [16, 54, 59–63]. These nice properties of the DG methodology are one reason why more and more researchers apply and extend the DG methodology to many different problem setups in computational physics. However, DG is not the perfect discretisation and there are unfortunately some issues that necessitate detailed analysis and discussion.

The remainder of this review article gives the answers to why we need novel developments, Section 2, when the novel developments started, Section 3, what the key ideas of these novel strategies are, Section 4, and where there are still open questions toward future research directions, Section 5.

2 Why Do We Need a Novel Robust Strategy?

Throughout the analysis and discussions in this manuscript we describe different types of stability for a numerical approximation. Principally, we concentrate on the stability and boundedness of the spatial DG discretization.

2.1 On the L₂-Stability of the DG Method

It is easy to show that the DG scheme is L₂-stable for linear advection problems with constant coefficients due to its Galerkin nature, e.g., as a special case in Ref. 64. As a brief illustrative example let’s consider the one-dimensional scalar linear advection model

$u_t+f{\left(u\right)}_x=0,(11)$

where f(u) = au with constant velocity a. The respective strong form DG scheme reads

${\langle U_t,\varphi \rangle }_E+{\left[\left(f^{\text{*}}\left(U^{+},U\right)-f\right)\varphi \right]}_{\partial E}+{\langle f_x,\varphi \rangle }_E=0.(12)$

We get the discrete evolution of the L₂-norm ${{\displaystyle \int }}^{\text{}}{U}^2\hspace{0.17em}dx$ by inserting $\varphi =U$ for the polynomial test function

${\langle U_t,U\rangle }_E+{\left[\left(f^{\text{*}}\left(U^{+},U\right)-f\right)U\right]}_{\partial E}+{\langle f_x,U\rangle }_E=0.(13)$

Assuming time continuity, the first term reduces to ${\partial }_t\hspace{0.17em}{{\displaystyle \int }}^{\text{}}{U}^2/2\hspace{0.17em}dx$. We observe that in the volume integral f_x = aU_x is a polynomial of degree N−1 and ϕ a polynomial of degree N. Thus, we need the quadrature rule to be exact for polynomials with at least degree 2N−1. This is guaranteed by all Gauss-Legendre type quadrature rules with at least N+1 nodes, such as the Legendre-Gauss-Lobatto (LGL) quadrature.

The volume term contribution is

${\langle a\hspace{0.17em}{U}_x,U\rangle }_E=a\hspace{0.17em}{\langle {\left(\frac{U^2}{2}\right)}_x,1\rangle }_E=\frac{a}{2}\hspace{0.17em}{\left[U^2\right]}_{\partial E},(14)$

which shows that the volume contribution can be lifted to the boundary. In total we have

$\frac{1}{2}\hspace{0.17em}{\partial }_t\hspace{0.17em}\underset{E}{{\displaystyle \int }}{U}^2\hspace{0.17em}\text{d}x+{\left[U\hspace{0.17em}{f}^{\text{*}}\left(U^{+},U\right)-\frac{a}{2}\hspace{0.17em}{U}^2\right]}_{\partial E}=0.(15)$

The discrete evolution of the L₂-norm only depends on the choice of the numerical flux function f^*. A simple choice would be the central flux $f^{\text{*}}=\frac{a}{2}\left(U^{+}+U\right)$. Inserting the central flux into Eq. 15 gives

$\frac{1}{2}\hspace{0.17em}{\partial }_t\hspace{0.17em}\underset{E}{{\displaystyle \int }}{U}^2\hspace{0.17em}\text{d}x+\frac{1}{2}{\left[a\hspace{0.17em}U\hspace{0.17em}{U}^{+}\right]}_{\partial E}=0.(16)$

Summing over all elements E in the domain to get the total L₂-norm and assuming periodic boundary conditions, we get

$\frac{1}{2}{\partial }_t{\Vert \hspace{0.17em}U\Vert }_{L_2}^2=0,(17)$

as $\frac{a}{2}U\hspace{0.17em}{U}^{+}$ is a unique discrete energy flux at every interface and cancels when summing over all elements. Thus, for linear advection, the DG scheme with at least 2N−1 accurate quadrature is L₂-stable, i.e. the discrete L₂-norm is bounded for all times t. Note, that for quadrature rules with less than 2N integration precision, the estimate is not for the exact L₂-norm, but for a discrete L₂-norm corresponding to the quadrature rule chosen.

For linear problems basically all DG variants are stable, but what about nonlinear problems? To address nonlinear problems, there was a crucial contribution by Jiang and Shu in 1994 [65], who demonstrated that for scalar nonlinear hyperbolic problems, the DG method is L₂-stable provided: 1) Exact evaluation of all integrals are used; 2) Entropy stable numerical surfaces fluxes are used at the element interfaces. The L₂-stability result with conditions 1) and 2) also extends to symmetric variable coefficient hyperbolic systems [66]. Again, as a brief example to illustrate the important steps of the analysis, we consider a scalar one-dimensional problem Eq. 11 with a simple quadratic flux function $f\left(u\right)=\frac{1}{2}\hspace{0.17em}{u}^2$, the so-called Burgers’ equation. The DG scheme is, again, given by Eq. 13 and we get the evolution of the discrete L₂-norm by replacing the test function with the DG solution $\varphi =U$. Note, that for this nonlinear problem, the volume integral requires a quadrature rule with higher integration precision to be exact. For the quadratic flux function $f\sim u^2$, the quadrature rule needs 3N−1 integration precision. With the exact evaluation of the volume integral, its contribution is, once again, lifted onto the boundary of the element to give

${\langle \frac{1}{2}\hspace{0.17em}{\left(U^2\right)}_x,U\rangle }_E={\langle {\left(\frac{U^3}{3}\right)}_x,1\rangle }_E=\frac{1}{3}\hspace{0.17em}{\left[U^3\right]}_{\partial E}.(18)$

The resulting discrete evolution of the L₂-norm is

$\frac{1}{2}\hspace{0.17em}{\partial }_t\hspace{0.17em}\underset{E}{{\displaystyle \int }}{U}^2\hspace{0.17em}\text{d}x+{\left[U\hspace{0.17em}{f}^{\text{*}}\left(U^{+},U\right)-\frac{1}{6}\hspace{0.17em}{U}^3\right]}_{\partial E}=0,(19)$

which agin only depends on the choice of the numerical surface flux function f^*. Note, that for the central flux choice $f^{\text{*}}\left(U^{+},U\right)=\frac{1}{2}\left(f\left(U^{+}\right)+f\left(U\right)\right)$ no stability estimate can be derived, as potentially the L₂-norm could grow without bounds. However, for the particular choice

$f^{\text{*}}\left(U^{+},U\right)=\frac{{\left(U^{+}\right)}^2+U^{+}\hspace{0.17em}U+U^2}{6},(20)$

we get

$\frac{1}{2}\hspace{0.17em}{\partial }_t\hspace{0.17em}\underset{E}{{\displaystyle \int }}{U}^2\hspace{0.17em}\text{d}x+\frac{1}{2}{\left[\frac{U\hspace{0.17em}{\left(U^{+}\right)}^2+U^2\hspace{0.17em}{U}^{+}}{3}\right]}_{\partial E}=0.(21)$

Following the same arguments as above for the linear advection problem, we sum over all of the elements in the domain and obtain L₂-stability for the nonlinear scalar hyperbolic problem for quadrature rules with at least 3N−1 integration precision.

Unfortunately, even ignoring the practical issues with the assumption of exact integration for a moment, the results of Jiang and Shu cannot be directly extended to general nonlinear hyperbolic systems, e.g., the compressible Euler equations. A key step in the analysis of Jiang and Shu is that the test functions ϕ in the DG formulation Eq. 10 are replaced with the discrete DG solution

$U\left(\overrightarrow{x},t\right)={\displaystyle \sum }_{j=0}^{P\left(N\right)}{U}_j\left(t\right)\hspace{0.17em}{\varphi }_j\left(\overrightarrow{x}\right),(22)$

which itself is a linear combination of the test functions ${\left\{{\varphi }_j\right\}}_{j=0}^{P\left(N\right)}$ and, hence, an element of the test function space. While this gives an L₂-norm estimate for symmetric systems, this approach does not lead to a proper norm estimate (in the continuous as well as in the discrete case) for general nonlinear systems. This lack of a stability estimate, even when using “exact integration,” is the explanation why the DG method can still crash for complex PDEs, e.g., [67].

2.2 On the Entropy Stability of the DG Method

In the previous section it was shown for a scalar nonlinear conservation law that the DG solution U is bounded in the L₂-norm if a special choice of the numerical surface flux is chosen, such as the one in Eq. 20. We conjecture that an analogous statement of nonlinear stability should be true for systems of nonlinear conservation laws. However, in general, stability in the L₂-norm is insufficient to exclude unphysical phenomena such as expansion shocks [68]. To remove the possibility of such phenomena we generalize the notion of a stability estimate for nonlinear problems.

Before we discuss the mathematics of a general nonlinear hyperbolic system, a detour is taken to examine an important underlying physical principle. In particular, we introduce concepts from thermodynamics, which is a branch of physics relating the heat, temperature, or entropy of a given physical system to energy and work. The laws of thermodynamics are some of the most fundamental laws in all of physics. This is because they play an important role in describing how, and predicting why, physical systems behave and evolve the way that we observe them. Moreover, thermodynamics provides fundamental rules to decide how a physical system cannot behave. That is, what type of solution behavior is physically meaningful and what is not. From a mathematical point of view, we note that satisfying the second law of thermodynamics is not enough to guarantee uniqueness of the PDE solution and that conditions for uniqueness are an active topic of research in the analysis of said PDEs, see for example [69–72].

The first law of thermodynamics concerns the conservation of the total energy in a closed system. The second law of thermodynamics states that the entropy of a closed physical system tends to increase overtime and, importantly, that it cannot shrink. The laws of thermodynamics must be satisfied simultaneously at all times, otherwise a mathematical solution can exhibit strange and obviously incorrect behavior. For example, a fluid that only conserves its total energy but does not take care on the entropy, i.e. satisfying the first law of thermodynamics but not the second law, could transfer all of its internal energy into kinetic energy. The result would be a very fast, but very cold jet of air. Such a flow configuration has never been observed in nature. This discrepancy is removed when incorporating the second law of thermodynamics where the transfer of energies are regulated. For reversible processes the entropy remains constant over time (isentropic) and the time derivative of the total system entropy is zero. For irreversible processes the entropy increases and the time derivative is positive. Solution dynamics where the total system entropy shrinks in time are never observed and deemed unphysical.

To discuss these ideas in a mathematical context consider a system of nonlinear hyperbolic conservations laws

${\mathbf{u}}_t+{\overrightarrow{\nabla }}_x\cdot \overleftrightarrow{\stackrel{⟷}{\mathbf{f}}}\left(\mathbf{u}\right)=0,(23)$

where we take the viscous flux components in Eq. 1 to be zero. Typically, the diffusion terms are dissipative in nature and are mostly uncritical. A prototypical example of a purely hyperbolic system of nonlinear conservation laws is the compressible Euler equations modeling inviscid gas dynamics. A smooth solution that satisfies the system of PDEs Eq. 23 corresponds to a reversible process. One of the difficulties, either analytically or numerically, of nonlinear hyperbolic PDEs is that the solution may develop discontinuities (e.g., shocks) regardless of the continuity of the initial conditions [73]. A discontinuous solution of Eq. 23 corresponds to an irreversible process and dissipates entropy.

To mathematically account for possible discontinuous solutions, system Eq. 23 is considered in its weak form. Just as in the Galerkin discretisation in Section 1, the weak form of the PDE is found by multiplying the governing equations by a smooth test function $\varphi \left(t,\overrightarrow{x}\right)$ with compact support and integrating over ${\mathcal{R}}^{+}\times {\mathcal{R}}^3$. Integration-by-parts is again applied to move the derivatives onto the test function and weaken the smoothness requirements on possible solutions. Hence, weak solutions of system Eq. 23 satisfy

$\underset{{\mathcal{R}}^{+}\times {\mathcal{R}}^3}{{\displaystyle \int }}{\mathbf{u}}^T{\varphi }_t\hspace{0.17em}dt\hspace{0.17em}\text{d}\overrightarrow{x}+\underset{{\mathcal{R}}^{+}\times {\mathcal{R}}^3}{{\displaystyle \int }}{\stackrel{⟷}{\mathbf{f}}}^{\hspace{0.17em}T}{\overrightarrow{\nabla }}_x\varphi \hspace{0.17em}\text{d}t\hspace{0.17em}\text{d}\overrightarrow{x}=\underset{{\mathcal{R}}^3}{{\displaystyle \int }}{\mathbf{u}}_0^T\left(\overrightarrow{x}\right)\varphi \hspace{0.17em}\text{d}\overrightarrow{x}.(24)$

Another form of the conservation law is its integral form that, under the assumption of differentiable fluxes, arises from Gauss’ theorem

$\underset{\text{Ω}}{{\displaystyle \int }}{\mathbf{u}}_t\hspace{0.17em}\text{d}\overrightarrow{x}+\underset{\partial \text{Ω}}{{\displaystyle \oint }}\stackrel{⟷}{\mathbf{f}}\left(\mathbf{u}\right)\cdot \overrightarrow{n}\hspace{0.17em}\text{dS}=0,(25)$

and holds for arbitrary control volumes $\text{Ω}$, e.g., [74]. Unfortunately, weak solutions of a PDE are, in general, not unique and must be supplemented with extra admissibility criteria in order to single out the physically relevant solution [75–77]. This is precisely where the laws of thermodynamics play a pivotal role because, as already discussed, due to their intrinsic ability to select physically relevant solutions. In most applications, e.g., compressible fluid dynamics or astrophysics, the total entropy is not part of the state vector of conservative variables u. However, we know from the discussion above that for reversible (isentropic) processes the total entropy is a conserved quantity. Where is this conservation law “hiding”?

It turns out that there are additional conserved quantities, e.g., the entropy, which are not explicitly built into the nonlinear hyperbolic system Eq. 23 but are still a consequence of the PDE. In order to reveal this auxiliary conservation law we define a convex (mathematical) entropy function s = s(u) that is a scalar function and depends nonlinearly on the conserved variables u. This allows the definition of a new set of entropy variables

$\mathbf{w}=\frac{\partial s}{\partial \mathbf{u}},(26)$

that provides a one-to-one mapping between the conservative variable space and entropy space [78]. If we contract the nonlinear hyperbolic system Eq. 23 from the left with the entropy variables w we have

${\mathbf{w}}^T\left({\mathbf{u}}_t+{\overrightarrow{\nabla }}_x\cdot \stackrel{⟷}{\mathbf{f}}\left(\mathbf{u}\right)\right)=0.(27)$

From the definition of the entropy variables and assuming continuity in time, we know that

${\mathbf{w}}^T{\mathbf{u}}_t=s_t.(28)$

Further, each of the flux vectors in the coordinate directions x_i must satisfy a compatibility condition

${\text{w}}^T{\left({\overleftrightarrow{\mathbf{f}}}_i\right)}_{x_i}={\left(f_i^s\right)}_{x_i},(29)$

where f_i^s, i = 1,2,3 is a corresponding entropy flux [78]. We point out that a chain rule is the linchpin of the manipulations Eqs. 28 and 29 to move from the space of conservative state variables into the space of entropy variables. In the continuous setting this is not an issue under certain continuity assumptions. However, in a numerical setting it is extraordinarily difficult (or even impossible) to recover the chain rule with discrete differentiation, e.g., [79]. We postpone the discussion on this issue and what it means for a high order DG numerical approximation to Section 4.

By definition of a mathematical entropy, contracting the nonlinear hyperbolic system into entropy space, as in Eq. 27, and assuming the solution is smooth (i.e. a reversible process) results in the auxiliary conservation law for the entropy

$s_t+{\overrightarrow{\nabla }}_x\cdot {\overrightarrow{f}}^s=0.(30)$

The corresponding integral form of the entropy conservation is given by

$\underset{\text{Ω}}{{\displaystyle \int }}{s}_t\hspace{0.17em}\text{d}\overrightarrow{x}+\underset{\partial \text{Ω}}{{\displaystyle \oint }}{\overrightarrow{f}}^s\cdot \overrightarrow{n}\hspace{0.17em}\text{dS}=0,(31)$

for an arbitrary volume $\text{Ω}$. For irreversible processes, physical entropy is increasing. In the mathematical community however, entropy is defined as a decaying function and hence the entropy conservation law Eq. 31 becomes the entropy inequality [78]

$\underset{\text{Ω}}{{\displaystyle \int }}{s}_t\hspace{0.17em}\text{d}\overrightarrow{x}+\underset{\partial \text{Ω}}{{\displaystyle \oint }}{\overrightarrow{f}}^s\cdot \overrightarrow{n}\hspace{0.17em}\text{dS}\le 0,(32)$

for discontinuous solutions.

As an illustrative example for the contraction of a nonlinear hyperbolic system of PDEs into entropy space, we consider the compressible Euler equations of gas dynamics in one spatial dimension

${\left[\begin{array}{c}\rho \\ \rho v\\ E\end{array}\right]}_t+{\left[\begin{array}{c}\rho v\\ \rho v^2+p\\ \left(E+p\right)v\end{array}\right]}_x=0,(33)$

with the ideal gas assumption

$p=\left(\gamma -1\right)\left(E-\frac{\rho v^2}{2}\right),(34)$

where γ is the adiabatic constant. The convex entropy function s(u) for the compressible Euler equations is not unique [80]. However, a common choice for the mathematical entropy function is the scaled negative thermodynamic entropy [80–84]

$s\left(\mathbf{u}\right)=-\frac{\rho \varsigma }{\gamma -1},\varsigma =\text{ln}\left(p\right)-\gamma \text{ln}\left(\rho \right),(35)$

with the corresponding entropy flux f^s = v s(u). From this definition of the mathematical entropy function we get the entropy variables

$\mathbf{w}=\frac{\partial s}{\partial \mathbf{u}}={\left[\frac{\gamma -\varsigma }{\gamma -1}-\frac{\rho v^2}{2p}\hspace{0.17em},\hspace{0.17em}\frac{\rho v}{p}\hspace{0.17em},\hspace{0.17em}-\frac{\rho }{p}\right]}^T,(36)$

and see that each component of the entropy variables is a highly nonlinear function of the state vector components. Regardless, the variables Eq. 36 contract the one dimensional compressible Euler equations into entropy space and, when integrated over the domain $\text{Ω}$, become the entropy conservation law Eq. 31 for smooth solutions or the entropy inequality Eq. 32 for discontinuous solutions. It is worth noting that the entropy variables w are further useful in the analysis of the system, as they allow to derive a symmetric form of the PDE [85].

The discrete equivalent of the entropy inequality Eq. 32 is referred to as entropy stability. It is a generalization of the L₂-stability statement to systems of nonlinear hyperbolic PDEs, e.g., [79, 86]. An additional requirement built into the entropy stability condition is that the fluxes $\overleftrightarrow{\mathbf{f}}$ remain bounded [68], which restricts the flow to physically realisable states, e.g., positive density and pressure in gas dynamics. Overall, entropy stability ensures that a numerical approximation obeys the fundamental laws of thermodynamics and is viewed as an important quality to capture [86–88]. But it is an active area of research to investigate the role of entropy stability and how it fits into the question of provable nonlinear stability [82, 89, 90].

At present, we restrict ourselves to one of the key ingredients in the analysis to derive a nonlinear entropy stability estimate for general nonlinear hyperbolic systems, see e.g., [78, 86]. It is natural to develop an entropy stable DG approximation because the continuous and discrete analysis both rely on a weak form of the governing equations. However, for entropy stability the nonlinear system is not multiplied by the solution u as was the case for the L₂-stability analysis. Instead the equation is multiplied with the entropy variables wEq. 26, which are nonlinear functions of the state u, see e.g., the compressible Euler equations in (36). Thus, a direct combination of this approach with the analysis of Jiang and Shu from Section 2.1 is not possible. For a polynomial DG ansatz U, the discrete entropy variables W = W(U) are no longer polynomials of degree N and do not belong to the space of test functions $\varphi$. Hence, it is not allowed to replace the test functions $\varphi$ in the DG formulation Eq. 10 with W. Technically, only a projection of W onto the space of polynomials with degree N can be inserted; however, in this case the analysis does not lead to an entropy stability estimate as the chain rule holds for the full entropy variables and not their projections.

To overcome the issue with the test function space and to enable an entropy stability estimate for the DG method, Hughes et al. [91] as well as Hildebrand and Mishra et al. [92–94] used a space-time DG approach with an ansatz directly written in terms of the entropy variables. The idea is to make the DG ansatz in entropy space, i.e. to approximate the entropy variables

$\mathbf{w}\left(\mathbf{u}\left(\overrightarrow{x},t\right)\right){|}_E\approx \mathbf{W}\left(\overrightarrow{x},t\right)={\displaystyle \sum }_{j=0}^{P\left(N\right)}{\mathbf{W}}_j\left(t\right)\hspace{0.17em}{\varphi }_j\left(\overrightarrow{x}\right),(37)$

with a polynomial of degree N. Ignoring the time discretisation for brevity, the DG formulation changes to

${\langle \mathbf{u}{\left(\mathbf{W}\right)}_t,\varphi \rangle }_E+\underset{\partial E}{{\displaystyle \int }}{\varphi }^T\left({\mathbf{f}}^{\text{*}}\left(\mathbf{u}{\left(\mathbf{W}\right)}^{+},\mathbf{u}\left(\mathbf{W}\right)\right)-\overleftrightarrow{\mathbf{f}}\left(\mathbf{u}\left(\mathbf{W}\right)\right)\cdot \overrightarrow{n}\right)\hspace{0.17em}\text{dS}+{\langle {\overrightarrow{\nabla }}_x\cdot \stackrel{⟷}{\mathbf{f}}\left(\mathbf{u}\left(\mathbf{W}\right)\right),\varphi \rangle }_E=0,(38)$

which shows that the scheme is still formulated in conservative form, however all the conserved variables u now depend implicitly on the polynomial approximation of the entropy variables W. As this approach is naturally implicit, a straightforward and elegant extension of the scheme in time is to use a temporal DG scheme on top of the spatial DG scheme, resulting in a fully implicit space-time DG formulation. Hildebrand and Mishra proved that the resulting discretisation is entropy stable provided: i) Exact evaluation of all integrals; ii) Entropy stable numerical fluxes at the spatial surface integrals and upwind fluxes (due to causality) in the temporal surface integrals are used. These conditions on the space-time DG approximation are very similar to those imposed by Jiang and Shu for the scalar nonlinear hyperbolic case discussed for the nonlinear Burgers’ equation.

Unfortunately, the assumption 1) on exact integration is extremely difficult to guarantee and implement in practical simulations, which we describe in more detail in the next subsection. Without proper exact quadratures of the integral terms, the chain rule does not hold discretely. Such inexact approximations of functions are referred to as aliasing errors. These can occur in realistic simulations and might cause instabilities. Thus, robustness is still an issue and ad hoc dealiasing or stabilization mechanisms, e.g., artificial diffusion [92] are necessary.

2.3 The Unpleasant Role of Numerical Integration, Nonlinearities, Variational Crimes, and Aliasing

As described above it is necessary to discretize the variational formulation and make certain choices in the DG approximation such as the polynomial basis functions and, especially, the discrete integration to approximate the surface and volume integrals. Unfortunately, only in the rarest and simplest cases is it possible to avoid these discretisation steps and use an exact evaluation of the integrals. Hence, the notion of “variational crimes” is introduced to express the steps necessary to turn the formulation into an actual algorithm that can be implemented.

One of the biggest problems when discrediting nonlinear advection-diffusion problems is that in many interesting cases, the nonlinearity is non-polynomial. Our exemplary problem, the compressible Euler equations depend on the mass density u₁, the momentum density in the x direction u₂, and energy density u₃. Often, these are also denoted as $u_1=\rho$ and $u_2=\rho \hspace{0.17em}v$, where v is the velocity. We compute the velocity from the conserved variables as

$v=\frac{u_2}{u_1}.(39)$

This is important in the context of the DG discretisation because if the variables u₁ and u₂ are polynomials of degree N, the velocity v is not a polynomial, but a rational function. This occurs not only for the velocity but also for other quantities that are needed to evaluate the advective fluxes $\overleftrightarrow{\mathbf{f}}$, such as e.g., the pressure p. Hence, the fluxes $\overleftrightarrow{\mathbf{f}}$ are no longer polynomials of degree N, and possibly rational functions, as in case of the compressible Euler equations. When approximating the integrals with high order quadrature formulae, such as the Legendre-Gauss rules, it is important to realize that these numerical integration rules are constructed for polynomial integrands. Hence, in theory, they cannot integrate non-polynomial functions exactly no matter how many quadrature nodes are considered.

If we focus for instance on the strong form DG volume integral from Eq. 38, we see that the core part to evolve the DG solution in time is an L₂ projection of the flux divergence onto the polynomial basis ${\langle {\overrightarrow{\nabla }}_x\cdot \stackrel{⟷}{\mathbf{f}},\varphi \rangle }_E$. If this projection is not evaluated exactly, due to either the aforementioned variational crimes, the nonlinearities of the flux function, or a combination of the two, the exact L₂ projection turns into a discrete projection, most often taking the form of an interpolation at the quadrature nodes. This is a subtle but important observation. In contrast to an exact L₂ projection, which cleanly “cuts out” high order content of the flux divergence with polynomial degrees larger than N, a discrete L₂ projection interprets (i.e. aliases) some of the high order content as part of the projection polynomial. This artificially and unpredictably decreases or increases the polynomial coefficients of the projection. This “incorrect interpretation” of high order content is also well known in Fourier analysis and signal processing. If the sampling rate (in this case the number of Legendre-Gauss quadrature nodes) is not high enough according to the Nyquist theorem, high frequency data (high order content) gets interpreted as low frequency data (onto the polynomial of degree N) and pollutes the result. This analogy to Fourier analysis illustrates the possibility that high frequency information can masquerade as low frequency information when represented on a discrete and unresolved grid. This is the fundamental issue often termed aliasing. As the issue of the discrete projection onto a space of polynomials is similar in spirit, the term aliasing is also often used in the DG community, as well as the spectral and finite difference communities, to give potential consequences of the variational crimes a name. In summary, basically all of the DG algorithms for nonlinear advection dominated problems have the issue of inexact evaluation of the integrals and hence all DG algorithms have aliasing errors.

Unfortunately, these aliasing issues are not simply an abstract and “ugly” theoretical oddity without practical consequences. On the contrary, aliasing plays an important role when using DG methods for realistic complex applications to model nonlinear phenomena. It is worth pointing out that one of the advantages of DG, it’s very low dissipation errors, are in this particular point of view also it’s biggest problem. Due to the inherent low numerical dissipation in a high order DG method, there is no in-built self-defence against the aliasing issues and any instability that they may create. A repercussion of this fact is that it has become naturalized in the numerics community that especially the high order variants of the DG method, with very low dissipation errors, have robustness issues in practical applications. For instance DG approximations of the compressible Euler and Navier-Stokes equations are known to sometimes fail due to aliasing instabilities, e.g., [39]. This instability can manifest itself through the observation that the kinetic energy artificially grows in the simulation, while the inner energy decreases. Note, that the total energy is conserved by construction with the DG method; however, this exchange of kinetic and internal energy is unphysical and violates the second law of thermodynamics and is purely a result of the variational crimes (inexact integration).

An obvious solution to these problematic variational crimes, nonlinearities, and aliasing is to decrease their deleterious effects as much as possible. While technically unavoidable in the strictest mathematical sense, it is possible to increase the amount of Legendre-Gauss quadrature nodes to evaluate all integrals “consistently” such that the inexactness errors are on the order of machine precision, see e.g., Kirby et al. [95]. This approach is quite effective and immediately has a positive stabilizing effect on many applications with nonlinear PDEs, see e.g., [39, 96]. However, it is clear that the computational complexity drastically increases when arbitrarily increasing the number of quadrature nodes. Hence, one often tunes the increased number of Legendre-Gauss quadrature nodes and takes as many as needed to make a simulation stable—which is, of course, unsatisfying and ad hoc, as it highly depends on the particular problem setup. In comparison, another approach is to not directly fight the variational crimes themselves, but the consequences they induce. This is achieved by applying well designed filters to the solution, with the purpose to clip out higher order aliasing content in an effort to decrease its effect, e.g., [39]. It is needless to say that this filtering approach is also very ad hoc and depends on many parameters that need tuning depending on the particular problem one wishes to solve with the high order DG scheme.

While these ad hoc stabilization techniques are reinforced by little to no mathematical analysis or rigor, the prevailing consensus in the DG community has been that, in practice, they work reasonably well. In that, consistent integration (sometimes referred to as over-integration) and filtering increase the robustness of high order DG methods to a level such that they could be applied to model challenging physical problems allowing them to shine with their high order accuracy and low dispersion and dissipation errors. Especially in the turbulence community, many research groups started to apply high order DG methods with stabilization in the context of implicit large eddy simulation with excellent results competitive with others from the broader numerics community, e.g., [97, 98]. However, in Moura et al. [67] it was reported that certain configurations of the DG method for the inviscid Taylor Green vortex problem kept crashing, even when drastically increasing the number of quadrature nodes in the surface and volume integrals. In fact, the amount of quadrature points was increased up to the point where the DG scheme was no longer computationally feasible, but the simulations still crashed. The inviscid Taylor Green vortex setup in this case was used to investigate the case of a very high Reynolds number flow with severe under resolution common in realistic turbulence setups. These findings were also verified by the authors of this review article and have a strong consequence for the DG community. While the ad hoc stabilization techniques were “good enough” in the sense that they helped to make the DG scheme run for a broad range of interesting problems, this approach is apparently not bullet proof. Further, it is impossible to tell a priori for which cases the stabilization will work and for which cases it will not.

This one example, where the high order DG scheme was not stable and could not finish the simulation illustrates, fundamentally, that the removal of aliasing and variational crimes cannot be reliably done in an ad hoc fashion. Instead we need a better understanding of these aliasing errors and how they can be removed from inexact and/or under resolved discretisations. Furthermore, we require a mathematically sound approach to address these aliasing errors in the DG approximation. That is, we need a novel strategy to design robust high order DG methods to approximate the solution of nonlinear advection-diffusion systems.

3 When Did the Novel Development Start?

In 2013, two landmark results completely reshaped the development of the DG method moving forward. First, in his PhD thesis, Fisher extended the work on entropy stable schemes LeFloch and Rhode [99] as well as the high order entropy stable schemes of LeFloch et al. [100] to the summation-by-parts (SBP) finite difference framework with high order boundary closures in Refs. 88 and 101 respectively. LeFloch et al. and Fisher et al. found that the entropy stability estimates for low-order FV methods, developed by Tadmor [78], can be extended to high order accuracy. Whereas the high order reconstruction of LeFloch et al. was for periodic domains (i.e. without considering finite domain boundaries), the SBP finite difference framework includes special boundary closures and are applicable for finite domains. Kreiss et al. [102–105] introduced the SBP finite difference framework to specifically mimic integration-by-parts. Integration-by-parts is a valuable tool for the construction of stability estimates. Further discussion on SBP is given by, e.g., Olsson [106, 107], Strand [108], Nordström [109] and Svärd and Nordström [110].

To briefly introduce the main ideas of the classic SBP finite difference framework, we consider a discretisation in one spatial dimension on a finite interval E = [−1,1]. Within this interval, we consider a set of N+1 regular grid nodes x_j that include the boundaries x₀ = 1 and x_N = 1. On this grid, a continuous function u(x,t) is represented as the grid node values $U_j\left(t\right)=u\left(x_j,t\right)$. In short notation, we collect the nodal values into the vector quantity U. For the approximation of the PDE, we need two discrete operators: One that approximates integration, $ℳ\in {\mathcal{R}}^{\left(N+1\right)\times \left(N+1\right)}$; and one that approximates differentiation, $\mathcal{D}\in {\mathcal{R}}^{\left(N+1\right)\times \left(N+1\right)}$. In this article, we only consider diagonal matrices $ℳ$, sometimes referred to as diagonal norm SBP finite difference operators. With these operators we have

$\underset{E}{{\displaystyle \int }}u\left(x\right)\hspace{0.17em}v\left(x\right)\hspace{0.17em}\text{d}x\approx U^T\hspace{0.17em}ℳ\hspace{0.17em}V\text{ and }\frac{d}{dx}\hspace{0.17em}u\left(x\right){|}_{x_j}\approx {\left(\mathcal{D}\hspace{0.17em}U\right)}_j.(40)$

The discrete integration and differentiation need to be compatible for a SBP operator to satisfy the property

$\left(ℳ\hspace{0.17em}\mathcal{D}\right)+{\left(ℳ\hspace{0.17em}\mathcal{D}\right)}^T=\mathcal{ℬ},(41)$

where $\mathcal{ℬ}$ is the boundary integral evaluation operator with $\mathcal{ℬ}=\text{diag}\left(-\mathrm{1,0},\dots ,\mathrm{0,1}\right)$. Multiplying Eq. 41 by grid values U^T of an arbitrary function u(x) from the left and the approximation V of an arbitrary function v(x) from the right gives

$U^T\left(ℳ\hspace{0.17em}\mathcal{D}\right)\hspace{0.17em}V+U^T{\left(ℳ\hspace{0.17em}\mathcal{D}\right)}^T\hspace{0.17em}V=U^T\mathcal{ℬ}\hspace{0.17em}V=V_N\hspace{0.17em}{U}_N-V_0\hspace{0.17em}{U}_0.(42)$

Grouping terms and using that $ℳ$ is diagonal such that $ℳ={ℳ}^T$ we have

$U^Tℳ\hspace{0.17em}\left(\mathcal{D}\hspace{0.17em}V\right)+{\left(\mathcal{D}\hspace{0.17em}U\right)}^Tℳ\hspace{0.17em}V=V_N\hspace{0.17em}{U}_N-V_0\hspace{0.17em}{U}_0,(43)$

which is a discrete approximation of the integration-by-parts formula for the corresponding functions u and v

$\underset{E}{{\displaystyle \int }}u\hspace{0.17em}\frac{dv}{dx}\hspace{0.17em}\text{d}x+\underset{E}{{\displaystyle \int }}\frac{du}{dx}\hspace{0.17em}v\hspace{0.17em}\text{d}x={[u\hspace{0.17em}v]}_{-1}^1,(44)$

hence the name summation-by-parts.

With the SBP property, it is directly possible to show L₂-stability of the finite difference scheme for constant coefficient linear advection problems. Starting again as an example with the scalar problem Eq. 11 and the linear flux f = au, we get the following SBP finite difference semi-discretisation

${\partial }_{t}U+a\hspace{0.17em}\mathcal{D}\hspace{0.17em}U=0.(45)$

As stated above, one motivation of the SBP framework is to mimic the energy analysis of finite element discretisations like that found in the DG analysis presented above for linear advection. We proceed and first get a corresponding Galerkin type variational form by multiplying with the discrete integration matrix $ℳ$

$ℳ\hspace{0.17em}{\partial }_{t}U+a\hspace{0.17em}ℳ\hspace{0.17em}\mathcal{D}\hspace{0.17em}U=0.(46)$

This form is valid for all grid functions V^T multiplied from the left and hence is a direct approximation of the variational Galerkin form, e.g., Eq. 12. We point out that this finite difference approximation ignores the surface terms that are specific to the discontinuous Galerkin scheme. Here, the arbitrary grid function V^T takes the role of the test function ϕ. Hence, we can mimic the next step in the analysis, i.e. replacing the test function with the DG solution $\varphi =U$, by multiplying Eq. 46 with U^T from the left

$U^Tℳ\hspace{0.17em}{\partial }_{t}U+a\hspace{0.17em}{U}^Tℳ\hspace{0.17em}\mathcal{D}\hspace{0.17em}U=0.(47)$

The volume term can be reformulated with the SBP property to move the discrete derivative onto the test function and generate boundary data

$U^Tℳ\hspace{0.17em}\mathcal{D}\hspace{0.17em}U=U^T\left(\mathcal{ℬ}-{\left(ℳ\hspace{0.17em}\mathcal{D}\right)}^T\right)\hspace{0.17em}U=U^T\mathcal{ℬ}U-U^T{\left(ℳ\hspace{0.17em}\mathcal{D}\right)}^{T}U=U^T\mathcal{ℬ}U-U^T\left(ℳ\hspace{0.17em}\mathcal{D}\right)U.(48)$

From this step we see that the contribution of the volume terms in the SBP finite difference scheme can be again lifted to the interval boundaries

$a\hspace{0.17em}{U}^Tℳ\hspace{0.17em}\mathcal{D}\hspace{0.17em}U=\frac{a}{2}\hspace{0.17em}{U}^T\hspace{0.17em}\mathcal{ℬ}\hspace{0.17em}U,(49)$

but this time without any assumption on a necessary quadrature rule precision. In fact, this is general and holds for all diagonal norm SBP finite difference operators. Again, with the assumption of time continuity and periodic boundary conditions (U_N=U₀), it follows that the discrete L₂-norm of the SBP finite difference solution ${\Vert U\Vert }_{SBP}^2=U^T\hspace{0.17em}ℳ\hspace{0.17em}U$ is bounded for all t.

We emphasize again that neither the reconstruction techniques of LeFloch et al., nor the SBP finite difference framework as a whole, depend on integration or exact evaluation of integrals. Thus, in contrast to the DG stability results discussed above, the stability results obtained for SBP finite differences by Fisher et al. do not assume exact evaluation of any integrals. Thus, such methods yield efficient algorithms with feasible implementations that have provable stability estimates.

The second important result was separately discovered in 2013 by Gassner [111]. He realized that the base operators of the nodal discontinuous Galerkin spectral element method (DGSEM) have the diagonal norm SBP property as long as the collocation nodes ${\left\{x_j\right\}}_{j=0}^N$ and weights ${\left\{{\omega }_j\right\}}_{j=0}^N$ were chosen to be those associated with LGL quadrature. It is interesting to note, that earlier, in 2010, Kopriva and Gassner [34] already found out that for DGSEM with LGL quadrature, the weak DG formulation and the strong DG formulation are discretely equivalent. As shown in Eqs. 9 and 10, the weak form and strong form can be transformed into one another with integration-by-parts. Thus, when both forms are discretely equivalent, it basically means that discrete integration-by-parts, i.e., SBP, holds. We point out that in 1996, in the context of spectral methods with Chebyshev-Lobatto nodes or LGL nodes, Carpenter and Gottlieb [112] showed a similar property as SBP for these spectral operators, however they assumed that integration-by-parts holds for the proof. The results in Refs. 34 and 111 complete their findings as they remove the assumption of exact integration.

In the nodal DGSEM-LGL framework, similar to the finite difference framework, the solution coefficients of the DG polynomial are nodal values $U_j\left(t\right)$ at the location of the LGL nodes x_j. The nodal DG polynomial is represented with Lagrange basis functions ${\left\{{\ell }_j\left(x\right)\right\}}_{j=0}^N$ spanned with the LGL nodes

$u\left(x,t\right){|}_E\approx U\left(x,t\right)={\displaystyle \sum }_{j=0}^N{U}_j\left(t\right)\hspace{0.17em}{\ell }_j\left(x\right),(50)$

which have the Kronecker delta property that ${\ell }_j\left(x_i\right)={\delta }_{ij}$, i.e., 1 if i = j and 0 otherwise. With this choice of basis function and quadrature rule, it is possible to find discrete versions of the corresponding integral operator and the differentiation operator. For the integral we consider

$\underset{E}{{\displaystyle \int }}u\left(x\right)\hspace{0.17em}v\left(x\right)\hspace{0.17em}\text{d}x\approx {\displaystyle \sum }_{j=0}^N{\omega }_{j}u\left(x_j\right)\hspace{0.17em}v\left(x_j\right)=U^T\hspace{0.17em}ℳ\hspace{0.17em}V,(51)$

with $ℳ=\text{diag}\left({\omega }_0,\dots ,{\omega }_N\right)$ and the vector of LGL nodal values U and V. Furthermore, we have for the discrete differentiation

$\frac{d}{dx}u\left(x,t\right){|}_{x_i}\approx U^{\prime }\left(x_i,t\right)={\displaystyle \sum }_{j=0}^N{U}_j\left(t\right)\hspace{0.17em}{\ell }_j^{\prime }\left(x_i\right),(52)$

where we used the short hand notation for the spatial derivative of the Lagrange basis $\frac{d}{dx}\ell \left(x\right)={\ell }^{\prime }\left(x\right)$. Introducing the differentiation matrix as

${\mathcal{D}}_{ij}={\ell }_j^{\prime }\left(x_i\right),i,j=0,\dots ,N,(53)$

we get

$\frac{d}{dx}u\left(x,t\right){|}_{x_i}\approx {\left(\mathcal{D}\hspace{0.17em}U\right)}_j.(54)$

As was shown in Ref. 111, these two discrete operators are again compatible and provide the SBP property

$\left(ℳ\hspace{0.17em}\mathcal{D}\right)+{\left(ℳ\hspace{0.17em}\mathcal{D}\right)}^T=\mathcal{ℬ},(55)$

which means that the DGSEM-LGL operators belong to the class of diagonal norm SBP operators. This simple property of one-dimensional discrete integration-by-parts is the basis for a whole polynomial spectral calculus [113] that includes, for instance, discrete version of Gauss’ law on curvilinear grids in three spatial dimensions.

Returning to the discussion on stability, the LGL quadrature rule with N+1 points has an integration precision of 2N−1. Thus, the DGSEM-LGL is stable for scalar linear advection as shown above. However, the DGSEM-LGL is not stable for nonlinear problems, e.g., for the quadratic flux function discussed in Section 2.1 where an integration precision of 3N−1 is necessary i.e., exact integration of the volume terms. But using the SBP property of the DGSEM-LGL operators, it is possible to apply ideas similar to Fisher et al. and construct a novel DGSEM with LGL quadrature, that is discretely L₂-stable for the nonlinear Burgers’ equation, without the assumption on exact evaluation of the integrals [111]. These first results have been extended and compounded upon for the compressible Euler equations [114–118], the shallow water equations [63, 119–121], the compressible Navier-Stokes equations [32, 122, 124], non-conservative multi-phase problems [124], magnetohydrodynamics [125, 126], relativistic Euler [127], relativistic magnetohydrodynamics [128], the Cahn-Hilliard equations [129], incompressible Navier-Stokes (INS) [130], and coupled Cahn-Hilliard and INS [131] among many other complex PDE models and DG discretization types e.g., [132].

4 What Is the Key Idea?

To recap the discussion, there are several obstacles that make it difficult to obtain entropy stability estimates for high order DG methods in the case of a general nonlinear system of hyperbolic PDEs: 1) The assumption of exact evaluation of integrals is unfeasible in practice; 2) We need to contract with entropy variables w that nonlinearly depend on the conservative quantities u, which means that we need to replace the test functions by a projection (or interpolation) of w(u) ; 3) We need to satisfy a discrete version of the chain rule to contract the flux divergence into entropy space, i.e. a discrete version of ${\mathbf{w}}^T{\left({\mathbf{f}}_i\right)}_{x_i}={\left(f_i^s\right)}_{x_i}$, i = 1,2,3, where now the entropy variables and the flux functions are discrete projections and the derivative is replaced with our discrete derivative operator.

In what follows, the key ideas to resolve all three issues are presented. We focus on issue 1) and consider a scalar nonlinear problem with quadratic fluxes discussed above first. Then we ramp-up the complexity in the second subsection and discuss how to extend the novel approach to general systems and how to resolve all issues (i)-(iii).

4.1 On the Conservative Form, Split Forms and Skew-Symmetry

To illustrate the general idea of a split form and how to incorporate it into a high order DG approximation we examine our simple scalar nonlinear hyperbolic conservation law, the Burgers’ equation. We start with the conservative form

$u_t+{\left(\frac{u^2}{2}\right)}_x=0,(56)$

that can be rewritten into its advective form

$u_t+u\hspace{0.17em}{u}_x=0,(57)$

which is equivalent in the continuous case for smooth solutions. We can also consider an equivalent combination of the two forms

$u_t+\alpha \hspace{0.17em}{\left(\frac{u^2}{2}\right)}_x+\left(1-\alpha \right)\hspace{0.17em}u\hspace{0.17em}{u}_x=0,(58)$

where $\alpha \in \mathcal{R}$ is an arbitrary parameter. This form is called the split form of Burgers’ equation, with α being the split form parameter.

While in the continuous case with smooth solutions all of these forms are equivalent, it is important to note that in the discrete case this is not true. Considering the DGSEM operators with N+1 LGL nodes, the volume terms for the conservative form are given by

${\left(\frac{u^2}{2}\right)}_x\approx \frac{1}{2}\mathcal{D}\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U,(59)$

where U is the vector of values of u at the LGL nodes, $\mathcal{D}$ is the DGSEM-LGL derivative operator and $\underset{¯}{U}=\text{diag}\left(U_0,\dots ,U_N\right)$ is a matrix that has the nodal values U injected onto its diagonal. Analogously, the volume terms for the advective form are

$u\hspace{0.17em}{u}_x\approx \underset{¯}{U}\hspace{0.17em}\mathcal{D}\hspace{0.17em}U.(60)$

Only for polynomial functions u with degree $\le N/2$ and their corresponding nodal values U, do we have

$\frac{1}{2}\mathcal{D}\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U=\underset{¯}{U}\hspace{0.17em}\mathcal{D}\hspace{0.17em}U.(61)$

In all other cases, i.e. in the general case for arbitrary nodal vectors U, we get

$\frac{1}{2}\mathcal{D}\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U\ne \underset{¯}{U}\hspace{0.17em}\mathcal{D}\hspace{0.17em}U.(62)$

The discrete forms are different because of different aliasing errors. Whereas the conservative form computes a discrete derivative of U², the second form computes a “clean” derivative of U, but on the other hand needs to compute the product of two functions U and $\mathcal{D}U$ on a grid with only N+1 nodes. An interesting question is, if we can make use of the different (aliasing) errors in the two forms and find combinations via the split formulation where these errors cancel.

We note that the idea of split formulations was already introduced in the spectral community to develop stable numerical methods for the incompressible Navier-Stokes equations e.g., [133], but is especially prominent in the finite difference fluid dynamics community e.g., [134–139]. Split formulations are used as a built-in dealiasing mechanism to stabilize numerical methods e.g., [140]. Combinations of different forms of the advective terms of the compressible Euler equations yield finite difference approximations that are more robust than the standard conservative ones. In a perfect world, it would be desirable if we could choose the split form parameter α such that the different aliasing errors cancel exactly. Unfortunately, in general, it is not possible to cancel the aliasing errors for each grid node; however, what we will show next is that it is possible to cancel the aliasing errors in a way to get a global L₂-stability estimate similar to the estimates by Jiang and Shu [65], but without the assumption of exact integration.

First, we derive the strong DG formulation of the split form of Burgers’ Eq. 58 by multiplying with a test function ϕ, integrating over a grid cell E, inserting a numerical flux function f^* at the grid cell interface to account for the discontinuous nature of our ansatz, and use integration-by-parts again to arrive at

$\underset{E}{{\displaystyle \int }}{U}_t\hspace{0.17em}\varphi \hspace{0.17em}\text{d}x+\left[\left(f^{\text{*}}\left(U^{+},U\right)-f\left(U\right)\right)\hspace{0.17em}\varphi {]}_{\partial E}+\underset{E}{{\displaystyle \int }}[\alpha \hspace{0.17em}{\left(\frac{U^2}{2}\right)}_x+\left(1-\alpha \right)\hspace{0.17em}U\hspace{0.17em}{U}_x\right]\hspace{0.17em}\varphi \hspace{0.17em}\text{d}x=0,(63)$

where the flux is f(U) = U²/2. We consider specifically the DGSEM-LGL variant to get discrete operators that satisfy the SBP property with diagonal norm (mass matrix) $ℳ$. We arrive at the DGSEM-LGL variant when we replace the integrals by discrete quadrature with N+1 LGL nodes and when using the same N+1 LGL nodes to span the Lagrange basis functions used for our polynomial ansatz. This gives the following discrete DGSEM-LGL split form

${\partial }_{t}U+{ℳ}^{-1}\mathcal{ℬ}\hspace{0.17em}\left[F^{\text{*}}-F\right]+\alpha \frac{1}{2}\mathcal{D}\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U+\left(1-\alpha \right)\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}\mathcal{D}\hspace{0.17em}U=0,(64)$

where $\mathcal{ℬ}$ is the boundary evaluation matrix from the SBP property Eq. 41, F = F(U) is the vector of collocated nodal flux values i.e., $F_j=f\left(U_j\right)\hspace{0.17em}\forall j$, and F^* is a vector that contains the numerical fluxes at the interfaces “left” and “right” in its first and last entry and is zero elsewhere. The value U⁺, again, indicates that the numerical flux functions depends not only on local element values U, but also on the values from the neighbor grid cells. We refer to Gassner [111] for a detailed derivation of this form and its connection to the SBP framework with simultaneous-approximation-terms (SAT).

Next, we follow the standard procedure to derive an L₂-stability estimate by multiplying the scheme with the DG solution and use the quadrature rule to numerically integrate over the element i.e., we multiply by $U^Tℳ$

$U^Tℳ\hspace{0.17em}{\partial }_{t}U+U^T\mathcal{ℬ}\hspace{0.17em}\left[F^{\text{*}}-F\right]+\alpha \frac{1}{2}{U}^Tℳ\mathcal{D}\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U+\left(1-\alpha \right)\hspace{0.17em}{U}^T\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}ℳ\mathcal{D}\hspace{0.17em}U=0,(65)$

where we used the fact that $ℳ\hspace{0.17em}\underset{¯}{U}=\underset{¯}{U}\hspace{0.17em}ℳ$ because both matrices are diagonal. Again, we consider the semi-discrete version and assume continuity in time to have

$U^Tℳ\hspace{0.17em}{\partial }_{t}U=\frac{1}{2}{\partial }_t{U}_{ℳ,E}^2,(66)$

the evolution of the discrete L₂-norm in the grid cell E. Next, we focus on the volume terms. Note, that in the analysis of Jiang and Shu exact integration was assumed to contract the volume contribution to the surface. This is very important, as it allows direct control over the stability of the scheme with the choice of the numerical interface flux F^*. Without the assumption of exact integration however, we look at the influence of the choice of the split form parameter α instead. We realize that the second term in the volume integral can be transposed $U^T\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}ℳ\mathcal{D}\hspace{0.17em}U=U^T{\left(ℳ\mathcal{D}\right)}^T\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U$ and is similar to the first term in the volume integral, except for ${\left(ℳ\hspace{0.17em}\mathcal{D}\right)}^T$ is now transposed. Using the SBP property ${\left(ℳ\mathcal{D}\right)}^T=\mathcal{ℬ}-ℳ\mathcal{D}$ we get

$\begin{array}{c}\alpha \frac{1}{2}{U}^Tℳ\mathcal{D}\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U+\left(1-\alpha \right)\hspace{0.17em}{U}^T\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}ℳ\mathcal{D}\hspace{0.17em}U=\alpha \frac{1}{2}{U}^Tℳ\mathcal{D}\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U+\left(1-\alpha \right)U^T\hspace{0.17em}{\left(ℳ\mathcal{D}\right)}^T\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U,\\ =\left(\alpha \frac{3}{2}-1\right)U^Tℳ\mathcal{D}\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U+\left(1-\alpha \right)U^T\hspace{0.17em}\mathcal{ℬ}\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U.\end{array}(67)$

The term with the boundary evaluation matrix $\mathcal{ℬ}$ is a surface term, however the remainder term is a volume term that can either increase or decrease the L₂-norm. Hence, this term can be potentially critical in cases where it increases the norm, as this is an unstable behavior that could lead to break down of the simulation. We note that this volume term is another expression of the aliasing issues. To guarantee that this term does not affect stability, we need to guarantee that it vanishes. We see that there is a single (unique) choice of the split form parameter $\alpha =2/3$ that cancels the remaining volume term. With this choice, the discrete change of the L₂-norm reads as

$\frac{1}{2}{\partial }_t{U}_{ℳ,E}^2+U^T\mathcal{ℬ}\hspace{0.17em}\left[F^{\text{*}}-F\right]+\frac{2}{3}{U}^T\hspace{0.17em}\mathcal{ℬ}\hspace{0.17em}F=\frac{1}{2}{\partial }_t{\left|\left|U\right|\right|}_{ℳ,E}^2+U^T\mathcal{ℬ}\hspace{0.17em}\left[F^{\text{*}}-\frac{1}{3}F\right]=0.(68)$

This estimate is now analogous to the one with exact integration Eq. 19 and hence, with the same arguments, the choice of the numerical flux functions as

$f^{\text{*},EC}\left(U^{+},U\right)=\frac{1}{6}\left({\left(U^{+}\right)}^2+U^{+}\hspace{0.17em}U+U^2\right),(69)$

gives again a discrete stability estimate

${\partial }_t{\Vert U\Vert }_{ℳ}^2=0,(70)$

for the split form DGSEM-LGL with $\alpha =2/3$ when summing over all grid cells with periodic boundary conditions. It is important to observe that this estimate is discrete in the sense that it did not assume exact integration and that it can be only derived with the particular choice $\alpha =2/3$ to cancel out the volume contribution of the aliasing errors. With this, we have a novel method where we have solved issue i) mentioned in the beginning of the section.

We note that this particular choice of numerical flux function exactly preserves the discrete L₂-norm. If one considers non-smooth solutions this choice would be inappropriate as for e.g., shocks, because the L₂-norm needs to decrease as u² is a mathematical entropy for Burgers’ equation. For scalar equations, s(u) = u²/2 is the square entropy (which leads to an L₂-stability estimate e.g., [99, 141]) that gives the simple entropy variables $w\left(u\right)=\frac{ds}{du}=u$. Hence, the specific choice of numerical flux Eq. 72 is often referred to as an entropy conservative (EC) flux function. For an entropy dissipative flux function, there are many choices available. It can be shown that the class of E-fluxes, e.g., [33], are guaranteed dissipative and lead to the estimate

${\partial }_t{\Vert U\Vert }_{ℳ}^2\le 0.(71)$

As an example, a simple choice of an entropy dissipative numerical flux function is that of Rusanov

$f^{\text{*}}\left(U^{+},U\right)=\frac{1}{2}\left(F\left(U^{+}\right)+F\left(U\right)\right)-\frac{1}{2}\hspace{0.17em}{\lambda }_{max}\left(U^{+}-U\right),{\lambda }_{max}=\underset{U^{+},U}{\text{max}}\left(\frac{\partial f}{\partial u}\right).(72)$

An important question is how we can extend this approach to general nonlinear systems. Following the same ideas, it was possible to derive split forms for the shallow water equations [63, 119, 142], a simplified version of the compressible Euler equations. There are many split forms for compressible Euler that, for instance, give kinetic energy preserving properties e.g., [143, 144]. However, up to now, no split form for the compressible Euler equations is known that gives the desired discrete entropy stability estimate. The problems are issues ii) and iii) mentioned in the beginning of the section, where we need the discrete chain rule property to contract the volume terms to the surface. Concluding this subsection we revisit the derivations of Burgers’ equation and make two important observations.

First, with the proper choice of $\alpha =2/3$, we get the so-called skew-symmetric form

$u_t+\frac{1}{3}\left({\left(u^2\right)}_x+u\hspace{0.17em}{u}_x\right)=0.(73)$

Skew-symmetry is strongly connected to entropy, see e.g., Tadmor [85]. Multiplying the spatial derivative term by u as in the L₂-stability analysis gives

$u\hspace{0.17em}\left({\left(u^2\right)}_x+u\hspace{0.17em}{u}_x\right)=u\hspace{0.17em}{\left(u^2\right)}_x+u^2\hspace{0.17em}{\left(u\right)}_x={\left(u^3\right)}_x,(74)$

which shows that the skew-symmetric form gives a product-rule type form in the stability analysis that can directly be contracted to the divergence form i.e., contracts to the surface when integrating. In fact, for this simple problem, the chain rule needed for contraction reduces to the simpler product rule. Analogously, we get for the discrete skew-symmetric volume terms of the DGSEM-LGL

$U^Tℳ\mathcal{D}\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U+U^T\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}ℳ\mathcal{D}\hspace{0.17em}U=U^T\mathcal{ℬ}\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U.(75)$

Thus, in our derivation, we already used a specific discrete version of the chain rule (product rule) to get our estimate. The question is, how to extend this idea to the general case?

The second important observation pioneered for SBP schemes by Fisher in his PhD thesis [88] (in the spirit of earlier work by LeFloch et al. [100]) is that the particular skew-symmetric volume terms $\frac{1}{3}\left[\mathcal{D}\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U+\underset{¯}{U}\hspace{0.17em}\mathcal{D}\hspace{0.17em}U\right]$ can be rewritten for any diagonal norm SBP operator (hence, also for the DGSEM-LGL case) into

$\begin{array}{c}\frac{1}{3}{[\mathcal{D}\hspace{0.17em}\underset{¯}{U}\hspace{0.17em}U+\underset{¯}{U}\hspace{0.17em}\mathcal{D}\hspace{0.17em}U]}_i=2\hspace{0.17em}\stackrel{N}{{\displaystyle \sum }_{j=0}}{\mathcal{D}}_{ij}\frac{1}{6}\left(U_j^2+U_j\hspace{0.17em}{U}_i+U_i^2\right)\\ =2\hspace{0.17em}\stackrel{N}{{\displaystyle \sum }_{j=0}}{\mathcal{D}}_{ij}{f}^{\text{*},EC}\left(U_j,U_i\right)\\ ={\mathcal{D}}^{EC}f,\end{array}(76)$

with $f^{\text{*},EC}$ being the particular numerical flux Eq. 69 that is symmetric in its arguments and that leads to exact conservation of U². We further introduced the shorthand notation ${\mathcal{D}}^{EC}f$ for the volume term, that indicates that we use a specific derivative operator built on the EC-flux. As a remark, we note that this relation is easy to prove, as the discrete derivative of a constant is zero and then, for instance,

${\displaystyle \sum }_{j=0}^N{\mathcal{D}}_{ij}{U}_i^2=U_i^2\hspace{0.17em}{\displaystyle \sum }_{j=0}^N{\mathcal{D}}_{ij}=0.(77)$

In combination with the first observation we get the property that this new discrete derivative operator (or divergence operator in the multi-dimensional case) satisfies

$U^T\hspace{0.17em}ℳ{\mathcal{D}}^{EC}f=\mathcal{ℬ}\hspace{0.17em}{F}^s,(78)$

where $F^s$ is the collocated nodal vector of the entropy flux $f^s=u^3/3$ for Burgers’ equation with the square entropy s(u) = u²/2. This relation is the important discrete analogue of the chain-rule property $u\hspace{0.17em}{f}_x=f_x^s,$ as it follows with integration that (82) is the discrete analogue of

$\underset{Q}{{\displaystyle \int }}u\hspace{0.17em}{f}_x\hspace{0.17em}\text{d}x={\left[f^s\right]}_{\partial Q}.(79)$

We will see in the next subsection, how these observations guide the path to discrete stability estimates for general hyperbolic PDE systems.

4.2 On the Discrete Entropy Stability of the DGSEM-LGL

We have demonstrated how to build a high order skew-symmetric DG approximation of the scalar nonlinear Burgers’ equation. To do so required a very particular discrete derivative operator Eq. 78 that was the key to restore discrete entropy stability. We now discuss how to extend the split form approach to general systems of nonlinear hyperbolic conservation laws. For general nonlinear systems, it is unclear how to explicitly construct the split form to obtain a discrete chain rule property. In particular, the compatibility condition on the physical fluxes obtained when one contracts into entropy space Eq. 29 that we reproduce here, assuming one spatial dimension, due to their pertinence in the present discussion

${\mathbf{w}}^T{\mathbf{f}}_x=f_x^s.(80)$

As previously indicated, the chain rule is either unfeasible or even impossible to directly recover with discrete differentiation. With this in mind we apply the product rule to this compatibility condition between the physical flux f and the entropy flux f^s to find

${\mathbf{w}}_x^T\mathbf{f}={\left({\mathbf{w}}^T\mathbf{f}\right)}_x-f_x^s={\left({\mathbf{w}}^T\mathbf{f}-f^s\right)}_x.(81)$

A principle motivation for this manipulation is because it is far easier to recover the product rule discretely than it is the chain rule. That is, we already have a particular discrete equivalent for the product rule if the discrete derivative matrix $\mathcal{D}$ is a SBP operator.

Next, we aim to find a discrete version of the new compatibility condition Eq. 81 following the ideas of Tadmor [78]. Tadmor analyzed low order FV schemes and developed conditions on the numerical surface flux to derive a discretely entropy conserving scheme. In the context of the low order FV methodology, our unknowns in the elements are mean values that are naturally discontinuous across grid cell interfaces. As mentioned above, the idea to resolve these discontinuities with numerical flux functions was also used in the construction of the DG approximation. Consider the contribution to the compatibility condition Eq. 81 at an arbitrary interface. It depends on the discrete values in the current cell and the direct neighbor of that cell, denoted again with a “+”. We approximate all derivatives with first order differences and define Tadmor’s entropy conservation condition on the numerical surface flux function

${\left(\frac{\left(\mathbf{w}\left({\mathbf{U}}^{+}\right)\right)-\mathbf{w}\left(\mathbf{U}\right)}{\text{Δ}x}\right)}^T{\mathbf{f}}^{\text{*},EC}\left(U^{+},U\right)=\frac{\left(\mathbf{w}{\left({\mathbf{U}}^{+}\right)}^T\mathbf{f}\left({\mathbf{U}}^{+}\right)-{\mathbf{f}}^s\left({\mathbf{U}}^{+}\right)\right)-\left(\mathbf{w}{\left(\mathbf{U}\right)}^T\mathbf{f}\left(\mathbf{U}\right)-f^s\left(\mathbf{U}\right)\right)}{\text{Δ}x},(82)$

where $\text{Δ}x$ is the size of each grid cell. Equivalently, we arrive at the following general condition on the numerical surface flux for entropy conservation

${\left(\left(\mathbf{w}\left({\mathbf{U}}^{+}\right)\right)-\mathbf{w}\left(\mathbf{U}\right)\right)}^T{\mathbf{f}}^{\text{*},EC}\left({\mathbf{U}}^{+},\mathbf{U}\right)=\left(\mathbf{w}{\left({\mathbf{U}}^{+}\right)}^T\mathbf{f}\left({\mathbf{U}}^{+}\right)-{\mathbf{f}}^s\left({\mathbf{U}}^{+}\right)\right)-\left(\mathbf{w}{\left(\mathbf{U}\right)}^T\mathbf{f}\left(\mathbf{U}\right)-f^s\left(\mathbf{U}\right)\right).(83)$

For scalar nonlinear problems this condition can be solved explicitly [145]. For example, in the case of Burgers’ equation, we have $w\left(u\right)=u$, f(u) = u²/2, and f^s(u) = u³/3 such that solving Eq. 83

$f^{\text{*},EC}\left(U^{+},U\right)=\frac{1}{6}\frac{{\left(U^{+}\right)}^3-U^3}{U^{+}-U}=\frac{1}{6}\left({\left(U^{+}\right)}^2+U^{+}U+U^2\right),(84)$

which matches the particular entropy conservative flux derived in Section 4.1. We note again that the entropy conservative flux is symmetric in its arguments U⁺ and U, and is consistent to the physical flux in the sense that for the same arguments we recover the PDE flux $f^{\text{*},EC}\left(U,U\right)=f\left(U\right)$.

However, for systems of nonlinear hyperbolic conservation laws Eq. 83 is a single algebraic condition for a system vector of unknown flux quantities. Therefore, care must be taken to define an entropy conservative numerical flux function that remains physically consistent. That being said, the entropy conservation condition on the numerical surface flux Eq. 83 is an incredibly powerful statement. Provided we know an explicit form of the entropy variables, the physical flux, and the entropy flux we can define an appropriate numerical flux that ensures entropy consistency for a low order FV numerical approximation. A general form for such a numerical flux was developed by Tadmor [77] defined as a phase integral

${\mathbf{f}}^{\text{*},EC}\left({\mathbf{U}}^{+},\mathbf{U}\right)=\underset{-\frac{1}{2}}{\overset{\frac{1}{2}}{{\displaystyle \int }}}\mathbf{f}\left(\tilde{W}\left(\mathbf{U}\left(\xi \right)\right)\right)\hspace{0.17em}\text{d}\xi ,\tilde{W}\left(\mathbf{U}\left(\xi \right)\right)=\frac{1}{2}\left(\mathbf{W}\left({\mathbf{U}}^{+}\right)+\mathbf{W}\left(\mathbf{U}\right)\right)+\xi \left(\mathbf{W}\left({\mathbf{U}}^{+}\right)-\mathbf{W}\left(\mathbf{U}\right)\right).(85)$

To evaluate the phase integral form of the numerical flux function requires a certain quadrature rule that defines a path through phase space. Though theoretically useful, this phase integral form is computationally prohibitive for practical simulations, even for low order numerical approximations. However, over the past 20 years “affordable” versions of the entropy conservative flux function ${\mathbf{f}}^{\text{*},EC}\left({\mathbf{U}}^{+},\mathbf{U}\right)$ have been developed for a variety of nonlinear systems like the shallow water equations [119, 146], compressible Euler [81, 83], and ideal magnetohydrodynamics [147].

The key to these numerically tractable versions of the entropy conservative numerical flux function is to evaluate the components of the physical flux at various mean states between U⁺ and U. Note that these mean states can take on incredibly complex forms that depend on the arithmetic mean, the product of arithmetic means, or more uncommon quantities like the logarithmic mean. Complete details on the derivation of such numerical flux functions can be found in e.g., [81, 83, 146, 147].

For illustrative purposes we summarize the specific form of an entropy conservative numerical flux for the one dimensional compressible Euler equations with the ideal gas assumption due to Chandrashekar [81]. First, we introduce notation for the arithmetic mean and the logarithmic mean for two quantities a and a⁺:

$\left\{\left\{a\right\}\right\}=\frac{1}{2}\left(a^{+}+a\right),a^{\text{ln}}=\frac{a^{+}-a}{\text{ln}\left(a^{+}\right)-\text{ln}\left(a\right)}.(86)$

Also, we introduce a variable proportional to the inverse of the temperature

$\beta =\frac{p}{2\rho },(87)$

which simplifies the form of the entropy variables Eq. 36 to be

$\mathbf{w}={[\frac{\gamma -s}{\gamma -1}-\beta v^2\hspace{0.17em},\hspace{0.17em}2\beta v\hspace{0.17em},\hspace{0.17em}-2\beta ]}^T.(88)$

Then, applying the entropy conservation condition Eq. 83 and many algebraic manipulations later, we arrive at an analytical expression of an entropy conservative numerical flux for the compressible Euler equations

${\mathbf{f}}^{\text{*},EC}\left({\mathbf{U}}^{+},\mathbf{U}\right)=\left[\begin{array}{c}{\rho }^{\text{ln}}\left\{\left\{v\right\}\right\}\\ {\rho }^{\text{ln}}{\left\{\left\{v\right\}\right\}}^2+\frac{\left\{\left\{\rho \right\}\right\}}{2\left\{\left\{\beta \right\}\right\}}\\ \frac{\left\{\left\{v\right\}\right\}}{2}\left(\frac{{\rho }^{\text{ln}}}{{\beta }^{\text{ln}}\left(\gamma -1\right)}+\frac{\left\{\left\{\rho \right\}\right\}}{\left\{\left\{\beta \right\}\right\}}\right)+\frac{{\rho }^{\text{ln}}\left\{\left\{v\right\}\right\}}{2}\left(2{\left\{\left\{v\right\}\right\}}^2-\left\{\left\{v^2\right\}\right\}\right)\end{array}\right].(89)$

So far, the discussion on entropy conservative numerical approximations has all been in the context of low order finite volume methods. It is possible to create a high order entropy aware scheme with ENO [148] or WENO type reconstructions [149]. However, as mentioned above, a critical and remarkable result of Fisher’s work is that a low order finite volume entropy conservative scheme can be extended to an arbitrarily high order accurate spatial scheme, when it is based on diagonal norm SBP operators [101]. As was described for Burgers’ equation in the last two observations in Section 4.1, the crucial part is to move the contribution to the entropy production from the volume terms to the surface via a discrete version of the chain rule. Once stability is only governed by surface contributions, it is possible to control the stability with a proper choice of numerical interface flux function. In this sense, the analysis of the high order scheme reduces to a similar problem as for the low order finite volume method Eq. 83 and the well-established theoretical analysis tools and results can be reused. It is worth mentioning that ${\mathbf{f}}^{\text{*},EC}$ is not unique and that a particular choice of the entropy conservative flux generates a different split form of the governing equations, e.g., [144, 150, 151].

We return to a strong form DG approximation of a nonlinear hyperbolic system of conservation laws that takes a form identical to Eq. 38 but now only considered in one spatial dimension

${\langle {\mathbf{U}}_t,\varphi \rangle }_E+{\left[{\varphi }^T\left({\mathbf{f}}^{\text{*}}\left({\mathbf{U}}^{+},\mathbf{U}\right)-\mathbf{f}\left(U\right)\right)\right]}_{-1}^1+{\langle {\mathbf{f}}_x,\varphi \rangle }_E=0.(90)$

Here the standard tools of a nodal DG approximation have been applied:

1. The solution and physical fluxes are approximated with polynomials.

2. Any integrals in the variational formulation are approximated with high order LGL quadrature.

3. The interpolation and quadrature nodes are collocated.

Importantly, these steps mean that the discrete DG differentiation matrix is a SBP operator. Furthermore, we use the entropy conservative numerical surface flux at the interface and the particular discrete derivative projection ${\mathcal{D}}^{EC}$ defined in Eq. 76 in the volume contribution to arrive at the entropy conservative DG approximation

${\varphi }^T\left(ℳ{\mathbf{U}}_t+{[{\mathbf{f}}^{\text{*},EC}\left({\mathbf{U}}^{+},\mathbf{U}\right)-\mathbf{f}]}_{-1}^1+ℳ{\mathcal{D}}^{EC}\mathbf{f}\right)=0,\forall \varphi \in {\mathcal{R}}^{N+1}.(91)$

Now, if we take the test function $\varphi =\mathbf{W}$ with ${\mathbf{W}}_j=\mathbf{w}\left({\mathbf{U}}_j\right)$ evaluated at each LGL node x_j, we obtain

${\mathit{W}}^Tℳ{\mathbf{U}}_t={\displaystyle \sum }_{j=0}^N{\omega }_j{\mathbf{W}}_j^T{\left({\mathbf{U}}_t\right)}_j={\displaystyle \sum }_{j=0}^N{\omega }_j{\left(S_t\right)}_j={\langle S_t,1\rangle }_E,(92)$

assuming continuity in time. Also, the discrete differentiation operator ${\mathcal{D}}^{EC}$ moves volume information onto the boundary, see Refs. 32, 101, and 125 for complete details, such that

${\mathit{W}}^Tℳ{\mathcal{D}}^{EC}\mathbf{f}=\mathcal{ℬ}{F}^s.(93)$

We note that this remarkable property holds for general nonlinear systems with available entropy estimate and a corresponding low order entropy conserving flux ${\mathbf{f}}^{\text{*},EC}$. Combining this with the definition of the entropy conservative flux Eq. 83, the discrete entropy evolution of the DGSEM-LGL becomes

${\langle S_t,1\rangle }_E+{\left[F^s\right]}_{-1}^1=0,(94)$

which is the discrete analogue of the integral form of the entropy conservation law discussed in Section 2.2. The resulting DGSEM-LGL is entropy conservative by construction and it is important to note we have assumed no exactness on the integration. From this baseline entropy conservative numerical scheme, that does not dissipate entropy by construction, we can create a high order DGSEM-LGL that enforces the entropy inequality Eq. 32. We do so by introducing dissipation at the element interfaces via the choice of the numerical surface flux function, e.g., the Rusanov flux Eq. 72. More complex dissipation techniques are also available that dissipate solution information according to the different wave strengths with complete details found in, e.g., [152–156]. We finally note that this discussion was restricted to one spatial dimension for the sake of convenience and simplicity. Extensions to general three dimensional curvilinear coordinate systems are available, see e.g., [32, 101, 116, 125, 157, 158] for details.

4.3 Validation of Robustness and Application to Space Physics of the Entropy Stable DGSEM

In this subsection, we demonstrate two exemplary simulation results of a DG scheme based on the key ideas outlined above. The general split form DGSEM with LGL nodes on three dimensional curvilinear hexahedral unstructured meshes is implemented in the open source software FLUXO (project-fluxo/fluxo at github), written in modern Fortran with a special emphasis on massively parallel CPU based hardware. The main focus of the software is on compressible Navier-Stokes and visco-resistive MHD equations. Time integration of the semi-discrete form is done with a fourth order accurate low storage Runge-Kutta method of Carpenter and Kennedy [159].

For the validation of the robustness we revisit an important numerical contribution of Moura et al. [67]. They were the first to report of a test case that the DG scheme with (numerical) exact integration was not able to run, demonstrating, that further improvement on the robustness of the DG methodology was necessary. For this validation test, we consider the compressible Navier-Stokes equations (viscous case) or the compressible Euler equations (inviscid case, basically setting the viscosity parameter to zero). The considered problem is the Taylor-Green vortex in a fully periodic domain, which serves as a test case for a fully periodic turbulent box [0,1]³, that starts with a smooth initial velocity field

$\begin{array}{c}{v}_1=v_0\hspace{0.17em}\text{sin}\left(2\hspace{0.17em}\pi \hspace{0.17em}{x}_1\right)\text{cos}\left(2\hspace{0.17em}\pi \hspace{0.17em}{x}_2\right)\text{cos}\left(2\hspace{0.17em}\pi \hspace{0.17em}{x}_3\right),\\ v_2=-v_0\hspace{0.17em}\text{cos}\left(2\hspace{0.17em}\pi \hspace{0.17em}{x}_1\right)\text{sin}\left(2\hspace{0.17em}\pi \hspace{0.17em}{x}_2\right)\text{cos}\left(2\hspace{0.17em}\pi \hspace{0.17em}{x}_3\right),\\ v_3=0,\end{array}(95)$

and transitions to turbulence during its temporal evolution until it reaches a state similar to homogeneous turbulence. The initial density is uniform $\rho =1$ and the initial pressure is give by $p=p_0+\frac{1}{16}\left(\text{cos}\left(4\hspace{0.17em}\pi \hspace{0.17em}{x}_1\right)+\text{cos}\left(4\hspace{0.17em}\pi \hspace{0.17em}{x}_2\right)\right)\left(\text{cos}\left(4\hspace{0.17em}\pi \hspace{0.17em}{x}_3\right)+2\right)$, where $p_0$ is a background pressure and v₀ the velocity amplitude used to set the initial Mach number. In our case, we choose the Mach number to be Ma = 0.1. Unresolved vortical driven flows are especially prone to the aliasing issues discussed above. The difficulty of this test case lies in its wide range of scales when the Reynolds number increases (i.e., for low viscosities), e.g., [39]. For the DGSEM discretisation, we choose the polynomial degree N and the number of grid cells $N_Q^3$. Thus, the total number of degrees of freedom (DOF) for one conserved quantity is ${\left(N+1\right)}^3\hspace{0.17em}{N}_Q^3$. For the numerical flux function at the surface, we use the Rusanov flux.

For the robustness investigation, we consider an inviscid flow (with the viscosity parameter is zero) and focus on three particular setups, where N = 1,3,7 with number of elements N_Q = 56,28,14 respectively. This ensures that for all three computations the overall number of DOF per conserved quantity is equal, about 1.4 million. There are many more investigations of different configurations presented in Ref. 160, but they all demonstrate the same behavior: while the low order variants N = 1,3 seem to be relatively robust with full integration, the higher the polynomial degree, the less stable the DG method becomes. And for the case N = 7 with N_Q = 14 the simulation crashed at about a simulation time of t_crash = 8.4, even when increasing the quadrature nodes from 8³ up to 32³ = 32768 per element. In contrast, the novel entropy stable DGSEM with standard LGL nodes runs all configurations without crashing.

Furthermore, it is possible to run this challenging test case even without any artificial dissipation, i.e. with the $F^{\text{*},EC}$ numerical flux instead of the Rusanov flux function. This is very interesting, as it allows us to fully observe and control the artificial numerical dissipation generated by the scheme. To demonstrate this, we consider again the Taylor-Green vortex test case, but this time with non-zero viscosity such that the Reynolds number is Re = 1600. In this Navier-Stokes case, it is possible to relate the kinetic energy decay over time with the temporal behavior of the enstrophy to get an estimate for the Reynolds number. In theory, this should be Re = 1600 for the simulation. In practice, the finite resolution causes numerical errors such as dispersion and dissipation, e.g., [55]. We present two results in Figure 1 for the viscous test case with N = 7 and N_Q = 8.

FIGURE 1

FIGURE 1. The estimate of the numerical Reynolds number of an under resolved simulation with polynomial degree N = 7 and eight elements (64³ DOF). The physical Reynolds number of the Taylor-Green vortex setup is Re = 1600. The entropy conservative (EC) scheme retains the physical Reynolds number remarkably well and is virtually dissipation free. The entropy stable (Rusanov) variant clearly introduces stabilizing dissipation as soon as the scales can no longer be resolved starting at about t = 3.

We note, that this test case would crash for the standard DG scheme, however for the presented novel DGSEM-LGL with the proper discrete chain rule, it runs with the dissipative Rusanov numerical flux $F^{\text{*},Rusanov}$ (entropy stable DGSEM-LGL) and even with the non-dissipative numerical flux $F^{\text{*},EC}$ (entropy conservative DGSEM-LGL). After an initial transition zone, the entropy conservative scheme retains the physical Reynolds number remarkably well with Re_numerical = 1600 and the simulation is virtually dissipation free throughout the temporal evolution. The entropy stable variant clearly introduces stabilizing dissipation as soon as the spatial scales can no longer be resolved. It is interesting to note, that these results hint toward the possibility of quantifying and controlling the artificial dissipation of the DGSEM for under resolved turbulence and use this to construct high fidelity turbulence models, see e.g., for a proof of concept [161].

For an exemplary application we consider a complex test case from space physics. We focus on the electrodynamic and plasma interaction of the moon Io with the strong magnetic field of Jupiter. Io is embedded in a dense plasma torus, induced by the magnetosphere of Jupiter, and it exhibits interesting plasma flow characteristics containing steep gradients and discontinuities [162]. The general problem setup is illustrated in Figure 2. Neglecting neutral density, relativistic, viscous, resistive, and Hall effects, this MHD flow within Io's plasma torus can be modeled with the ideal MHD equations. For such magnetohydrodynamic flows, the entropy stable DGSEM solver in FLUXO uses a hyperbolic divergence cleaning mechanism to enforce the divergence-free constraint on the magnetic field variables $\overrightarrow{B}$ [125]. Additionally, the solver must be augmented with a shock capturing technique in order to handle strong discontinuities [163].

FIGURE 2

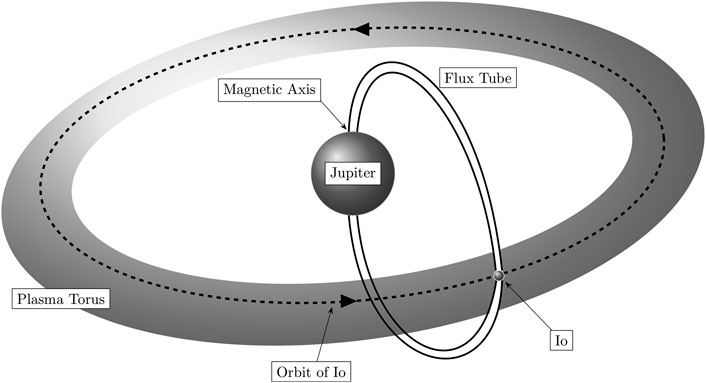
FIGURE 2. Io’s electrodynamic interaction is unique due to its fast rotation and the influence of the strong magnetic field of Jupiter. Plasma interactions with Io’s atmosphere lead to mass loss in the form of ions and neutrons. These neutrons then ionize through radiative effects and accumulate around Io forming a plasma torus. Consequently, this flow of magnetized plasma past the obstacle Io, combined with atmospheric interactions, are the engine behind Io’s plasma interactions with Jupiter’s magnetosphere.

As Io orbits Jupiter, plasma from the torus streams in and forms a local ionosphere that induces polarisation charges and modifies the electric field, thus changing the local Lorentz force and damping electron and ion flow close to Io. The plasma flow is strongly reduced inside Io’s (very weak) atmosphere, which can be modeled by incorporating a neutral collision source term to the ideal MHD system, Saur et al. [162, 164],

${\mathbf{s}}_{\text{collision}}={\left[0\hspace{0.17em},\hspace{0.17em}-\varpi \rho \overrightarrow{v}\hspace{0.17em},\hspace{0.17em}-\frac{1}{2}\varpi \rho \parallel \overrightarrow{v}{\parallel }^2\hspace{0.17em},\hspace{0.17em}\overrightarrow{0}\right]}^T,(96)$

with the collision frequency

$\varpi =\{\begin{array}{ll}{\varpi }_{\text{in}}\hfill & ,\overrightarrow{x}\in \mathfrak{U}\hfill \\ {\varpi }_{\text{in}}\text{exp}\left(\frac{r_{\mathfrak{U}}-r}{d}\right)\hfill & ,\overrightarrow{x}\in \mathfrak{T}\hfill \\ 0\hfill & ,\overrightarrow{x}\notin \mathfrak{U}\cup \mathfrak{T}\hfill \end{array},(101)$

where ${\varpi }_{\text{in}}>0$ is constant. The inner atmosphere of Io is represented as a neutral gas cloud $\mathfrak{U}$. In order to model the ionosphere, we also introduce a smooth transition area $\mathfrak{T}$ by an exponential blending dependent on the radii $r_{\mathfrak{U}},r$ and the dilatation factor d. In this region the neutral atmosphere thins causing ionospheric conductivities to shrink such that they are no longer able to maintain the ionospheric current perpendicular to the magnetic field. Eventually, electric current is continued along the magnetic field lines out of Io’s ionosphere, where it is finally fed into Io’s Alfvén wings as illustrated in Figure 3.

FIGURE 3

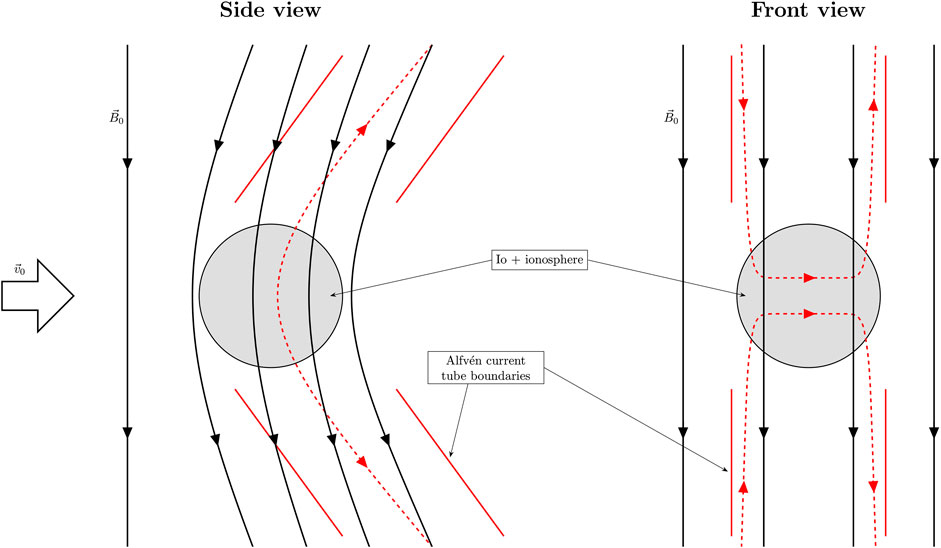
FIGURE 3. Standing Alfvén current tube magneto-spheric disturbances, termed Alfvén wings, that spread and propagate away along field lines in both directions. The development of the Alfvén wings are observable in the regions with decreasing plasma bulk velocity v₁ and perturbed magnetic field B₁ north and south of Io in the xz plane. It is known that the Alfvén current tubes are bent back by a constant angle with respect to the unperturbed background magnetic field. Further, the perturbation of the magnetic field is positively correlated with the perturbation of the velocity field in the northern Alfvén wing and negatively correlated in the southern wing [133].

In the dimensionless computational domain we scale the radius of the atmosphere to take a spherical shape with radius one and locate the center of the sphere at the origin

$\mathfrak{U}=\{\overrightarrow{x}\in \text{Ω}|\parallel \overrightarrow{x}\parallel \le r_{\mathfrak{U}}=1\}.(102)$

The ionospheric processes uses the exponential blending of the collision frequency above with a dilatation factor d = 150/1820. The initial conditions for the flow are taken as

$\rho =1,\overrightarrow{v}={\left(\mathrm{1,0,0}\right)}^T,p=0.148,\overrightarrow{B}={\left(\mathrm{0,0},-3.41\right)}^T,(103)$

that will evolve to a final time T = 5. The gas constant is taken to be $\gamma =5/3$. The boundary states at the left, front and back boundary faces are constant to this reference state, whereas we define outflow boundary conditions at the right, top and bottom of the domain.

In anticipation to capture the relevant physical interactions at the sphere as well as the development of the Alfvén wings best, we exploit the geometric flexibility of the entropy stable DGSEM solver and divide the computational domain into an unstructured, curvilinear mesh presented in Figure 4. Within each element we use a polynomial order of N = 3.

FIGURE 4

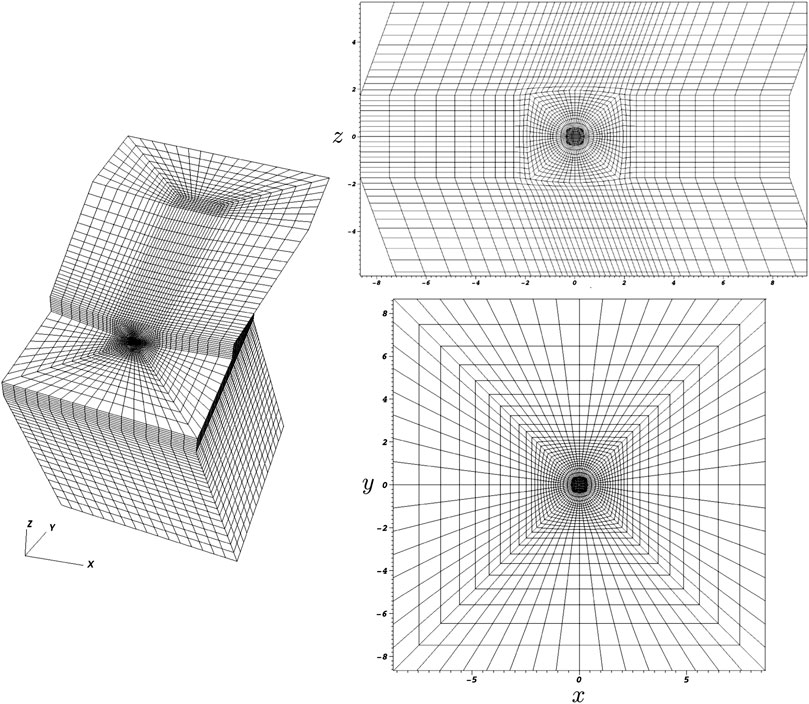
FIGURE 4. Computational mesh for the Alvén wing test problem built from 14,336 curved elements. At the origin the elements are curved to capture the spherical shape of the neutral gas cloud $\mathfrak{U}$. Due to the geometric flexibility of the DGSEM the mesh in the northern and southern regions are titled in order to capture the Alvén wing structures more accurately.

In Figure 5 we show a 2D-slice of the B₁ and v₁ components at y = 0 of the entropy stable approximation at the final time which presents the numerically generated Alfvén wings from the entropy stable DGSEM. It also demonstrates the expected positive correlation of the B₁ variable with the velocity variable v₁ in the northern Alfvén wing and the negative correlation in the southern wing. Moreover, we consider profile slices in these B₁ and v₁ along the line z = 5 and compare the results to a solution computed by the open source software ZEUS (www.astro.princeton.edu/jstone/zeus.html) in Figure 6. ZEUS is a FV solver written in spherical coordinates that uses explicit time integration. For the presented comparison, ZEUS used 10 million grid cells (DOF) in total whereas the entropy stable DGSEM solver used approximately 14,336 elements with N=3 polynomials and a total of about 1 million DOF. The reduction of DOFs also translated in a nearly 10 fold reduction of overall CPU time when both codes were run in parallel using MPI on 100 cores. This increased efficiency of the high order DGSEM-LGL, the increased robustness due to discrete entropy stability, and the geometrical flexibility are several advantages of this novel DG framework.

FIGURE 5

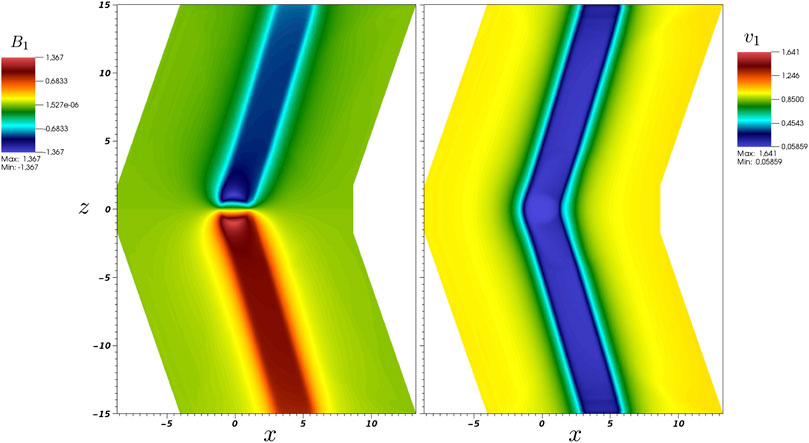
FIGURE 5. Alfvén wings numerically computed with the entropy stable DGSEM for the plasma interaction of a spherical gas cloud. The snapshot is a slice in the xz plane at y = 0 at the final time T = 5. The polynomial order in each spatial direction was N = 3 in each spatial direction. As expected, the Alfvén wings evolve from the northern and southern poles of the neutral gas cloud and are bent back by a constant angle with respect to the background magnetic field. This bending was taken into account in the construction of the curvilinear mesh.

FIGURE 6

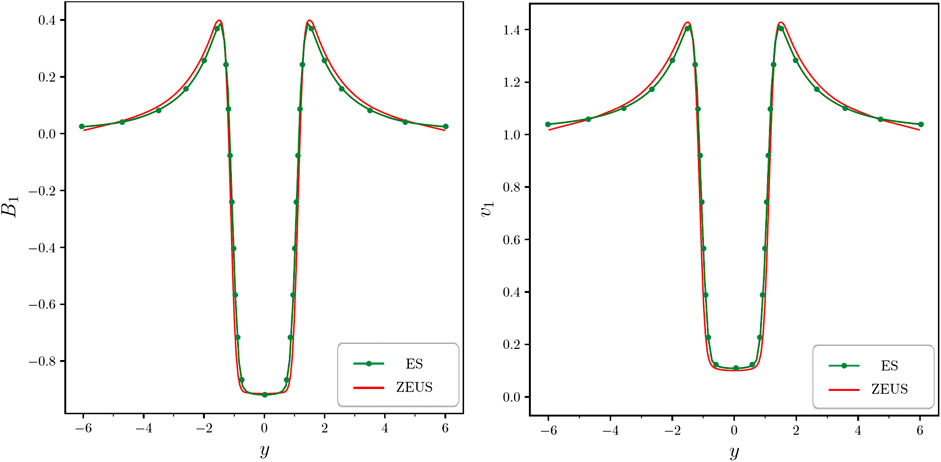
FIGURE 6. One dimensional visualization of the Alfvén wing solution along the line z = 5 from the xz plane slice at y = 0. A comparison is performed between the entropy DG solver with N = 3 in each spatial direction and the first order finite volume solver ZEUS. The entropy stable DG approximation uses 90% fewer DOF compared to the 10 million DOF used for the ZEUS computation. Qualitatively, the solutions are very similar.

5 Where to Go Next?

The response of the DG community to the split form DGSEM with LGL quadrature on tensor-product hexahedra has been astounding. However, naturally, there are still many limitations of this method. Some that have been recently addressed and many others still open. So far, we discussed semi-discrete DGSEM-LGL variants with tensor product expansions on possible curvilinear unstructured hexahedral meshes. Direct extensions of this variant include non-conforming meshes [166, 167], moving meshes [168–170], different related versions such as e.g., the line DG method [171], and a fully discrete space-time approach without the assumption on time continuity [172–175]. An exciting recent development are explicit modified Runge-Kutta methods that retain the semi-discrete entropy stability estimates [176].

A downside of LGL is that in comparison to the Legendre-Gauss (LG) points, the accuracy in dispersion and dissipation is lower, see e.g., [56]. Unfortunately, LG points do not include the boundary nodes, hence they do not directly satisfy the classic SBP property and the presented developments cannot be directly applied to this case. However, there are several developments where the framework was extended to construct entropy stable variants with LG nodes. One is based on a staggered grid approach by Parsani et al. [176]. The authors used the standard LG nodes to span the solution, however to compute the discrete derivative operator, they interpolate onto a higher order staggered LGL grid where they can use the SBP property. Then they ensure that the back-projection is still entropy stable to retain the stability estimate on top of the accuracy of the LG nodes. Another approach is presented by e.g., Ortleb [177] where the author directly constructed a scheme that preserves the kinetic energy with LG nodes. Although SBP could not directly be applied, the difference lies only in the boundary operator $\mathcal{ℬ}$. For classic SBP $\mathcal{ℬ}$ is diagonal, whereas in case of LG nodes $\mathcal{ℬ}$ has some columns filled. Ortleb fixed this by considering special correction terms at the boundary, while using similar ideas as in the LGL case for the volume terms. In his PhD thesis, Fernández [178] extended the classic SBP property to general node sets that do or do not include the boundary nodes, where all grid nodes lie inside or even outside of the considered domain.

A generalization onto multi-dimensional domains is given in e.g., [179], termed multidimensional SBP operators. This is an interesting development, as it resolves another limitation of the classic DGSEM-LGL. In some applications, it is favourable to have more flexibility when generating meshes for geometries with complex shapes. In this case, meshes with simplex element types such as triangles and tetrahedra or even hybrid element types such as prisms and pyramids are desired. We will mention some recent developments and extensions here, but stress that this list is not complete and there are many more. Returning to the multidimensional SBP framework, this approach’s strength is that it can be used to construct stable methods on simplex meshes e.g., by Chan [115, 180], Chen and Shu [132], Hicken et al. [181], and Crean et al. [182]. Another interesting approach to generate DG scheme on general meshes is presented by Chan [115]. He shows that a special projection directly with the entropy variables collocated at the grid nodes can give a SBP type property that can be used to construct stable discretisations.

As stated the response of the DG community has been astonishing with an explosion of developments, extensions, and new insights. However, there are still many unresolved issues that need to be researched in the future to further evolve high order DG methods into a viable tool for computational physics. The most important problem is still robustness. Although entropy stability significantly improves the stability of the scheme in many applications, there are still situations where no significant gain in robustness of the DG scheme can be observed [183, 184]. A possible reason could be, for instance, the incorrect choice of mathematical entropy function. While there is typically only one physical (thermodynamic) entropy, there are many mathematical ones that often lead to a stability estimate in corresponding norms of the solution. So what are the important entropy quantities to consider? What about e.g., kinetic energy, cross helicity and related quantities? For example, in turbulence, the kinetic energy and proper prediction of its behavior seems to play an important role [144, 161, 185, 186]. Besides getting discrete entropy stability estimates, it is possible to use the split form DGSEM-LGL approach from Section 4.1 to construct DG schemes that discretely preserve the kinetic energy and are discretely compatible for the inner and the total energy, e.g., [116]. It could be shown in Refs. 160 and 161 that such kinetic energy preserving DG schemes behave favourably for the simulation of compressible turbulence in comparison to the standard DG, especially in combination with subgrid turbulence models. However, just as in the development of entropy conservative (and in turn entropy stable) numerical flux functions there is nonuniqeuness. There exist many possible solutions to create a numerical flux that is e.g., kinetic energy preserving or entropy conservative or both e.g., [81, 83, 144, 185, 187]. Moreover, the discrete behavior of the kinetic energy as it evolves in time for under-resolved turbulent flows is quite different even between fluxes that are all provably kinetic energy preserving on paper [116, 187, 188]. So, an important question for the future is thus: What are the important quantities not only from a mathematical, but also from a physical point of view?

A fundamental issue in this context are problem setups that involve physical discontinuities e.g., shock waves in the compressible Euler or ideal MHD equations. Discontinuities trigger another instability, inherent in high order methods: the Gibbs phenomenon i.e., numerical oscillations. These oscillations can be devastating as under- or overshoots can cause non-physical state solutions e.g., negative density or pressure. Hence, positivity is a necessary criterion for all numerical methods when simulating such problems. However, up to this date there is still not enough research into the topic of entropy stability and positivity e.g., [40]. It is worth pointing out, that mathematically, the entropy function is only well-defined for positive solutions and, hence, is strongly connected to positivity. Generalizing this discussion, it is evident that entropy stability is “not enough” as a property for the numerical method. We need more properties, such as e.g., positivity. However, this is also where we reach uncharted research territory as even for many continuous problems e.g., the compressible Navier-Stokes equations it is up to this point unclear to show positivity even for the model itself.

The overview in this work focused on the volume contributions and the underlying tools (physical and mathematical) which led to the entropy stable DG method. However, the contributions at the physical boundaries have been ignored. Properly posing the boundary conditions to be entropy stable for a given model, like the compressible Euler or Navier-Stokes equations, has been considered [189–195], but this is remains an active area of research particularly because the treatment and behavior of the solution (whether on the continuous or discrete level) is directly related to the validity of a mathematical PDE model and directly tied into issues of well-posedness.

Concluding, we are currently at an exciting development stage with high order DG methods, where we can mimic important continuous stability estimates by careful construction of discrete operators. However, practical simulations show that these are not enough for the most complex problems that we desire to simulate. Plus, our numerical schemes and their properties are very close to the current analytical knowledge we have about the physical models. It is very hard to progress with the numerical developments further than what is analytically known: Which properties are important? How do you show positivity? Or a more general question: How does one prove physicality of the solutions for a given PDE model? It seems that the answers can only be given in close collaboration of researchers from physics and mathematics.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

GG was supported by the European Research Council (ERC) under the European Union’s Eights Framework Program Horizon 2020 with the research project Extreme, ERC Grant Agreement No. 714487. Support for open access publication was provided by Linköping University.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was partially performed on the Cologne High Efficiency Operating Platform for Sciences (CHEOPS) at the Regionales Rechenzentrum Köln (RRZK) at the University of Cologne. The authors thank Marvin Bohm for his contributions to the space physics discussion.

References

1. Reed WH, Hill TR. Triangular mesh methods for the neutron transport equation (1973) Technical Report LA-UR-73-479. Los Alamos National Laboratory.

Google Scholar

2. Nitsche JA. Über ein Variationsprinzip zur Lösung von Dirichlet-Problemen bei Verwendung von Teilräumen, die keinen Randbedingungen unterworfen sind. Abh Math Sem Univ Hamburg (1971) 36:9–15. doi:10.1007/BF02995904

CrossRef Full Text | Google Scholar

3. Cockburn B, Hou S, Shu C-W. The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. IV: the multidimensional case. Math Comput (1990) 54:545–81. doi:10.2307/2008501

CrossRef Full Text | Google Scholar

4. Cockburn B, Shu CW. The Runge-Kutta local projection -discontinuous Galerkin method for scalar conservation laws. Rairo-Matehmatical Model Num Anal-Modelisation Mathematique et Anale Num (1991) 25:337–61. doi:10.1051/m2an/1991250303371

CrossRef Full Text | Google Scholar

5. Cockburn B, Shu C-W. The Runge-Kutta discontinuous Galerkin method for conservation laws V: multidimensional systems. J Comput Phys (1998) 141:199–224. doi:10.1006/jcph.1998.5892

CrossRef Full Text | Google Scholar

6. Cockburn B, Shu CW. Runge-Kutta discontinuous Galerkin methods for convection-dominated problems. J Sci Comput (2001) 16:173–261. doi:10.1023/A:1012873910884

CrossRef Full Text | Google Scholar

7. Bassi F, Rebay S. A high order accurate discontinuous finite element method for the numerical solution of the compressible Navier-stokes equations. J Comput Phys (1997) 131:267–79. doi:10.1006/jcph.1996.5572Get

CrossRef Full Text | Google Scholar

8. Arnold DN, Brezzi F, Cockburn B, Marini D. Discontinuous Galerkin methods for elliptic problems In Discontinuous Galerkin methods. Berlin, Heidelberg:Springer (3000). p. 89–101.

Google Scholar

9. Arnold DN, Brezzi F, Cockburn B, Marini L. Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J Numer Anal (2002) 39:1749–79. doi:10.1137/S0036142901384162

CrossRef Full Text | Google Scholar

10. Black K. A conservative spectral element method for the approximation of compressible fluid flow. Kybernetika (1999) 35:133–46. doi:10.1006/jcph.1996.5572

CrossRef Full Text | Google Scholar

11. Black K. Spectral element approximation of convection-diffusion type problems. Appl Numer Math (2000) 33:373–9. doi:10.1016/S0168-9274(99)00104-X

CrossRef Full Text | Google Scholar

12. Rasetarinera P, Hussaini M. An efficient implicit discontinuous spectral Galerkin method. J Comput Phys (2001) 172:718–38. doi:10.1006/jcph.2001.6853

CrossRef Full Text | Google Scholar

13. Deng S. Numerical simulation of optical coupling and light propagation in coupled optical resonators with size disorder. Appl Numer Math (2007) 57:475–85. doi:10.1016/j.apnum.2006.07.001

CrossRef Full Text | Google Scholar

14. Deng S, Cai W, Astratov V. Numerical study of light propagation via whispering gallery modes in microcylinder coupled resonator optical waveguides. Optic Express (2004) 12:6468–80. doi:10.1364/opex.12.006468

CrossRef Full Text | Google Scholar

15. Kopriva DA, Woodruff SL, Hussaini MY. Discontinuous spectral element approximation of Maxwell’s Equations In: B Cockburn, G Karniadakis, and C-W Shu, editors. Proceedings of the international symposium on discontinuous Galerkin methods. New York: Springer-Verlag (2000) p. 355–61.

CrossRef Full Text | Google Scholar

16. Kopriva DA, Woodruff SL, Hussaini MY. Computation of electromagnetic scattering with a non-conforming discontinuous spectral element method. Int J Numer Methods Eng (2002) 53:105–22. doi:10.1002/nme.394

CrossRef Full Text | Google Scholar

17. Chan J, Hewett RJ, Warburton T. Weight-adjusted discontinuous Galerkin methods: wave propogation in heterogeneous media. SIAM J Sci Comput (2017) 39:A2935–A2961. doi:10.1002/nme.5720

CrossRef Full Text | Google Scholar

18. Rasetarinera P, Kopriva D, Hussaini M. Discontinuous spectral element solution of acoustic radiation from thin airfoils. AIAA J (2001) 39:2070–5. doi:10.2514/3.14970

CrossRef Full Text | Google Scholar

19. Stanescu D, Farassat F, Hussaini M. Aircraft Engine noise scattering – parallel discontinuous Galerkin spectral element method. AIAA (2002a) doi:10.2514/6.2002-800

CrossRef Full Text | Google Scholar

20. Stanescu D, Xu J, Farassat F, Hussaini M. Computation of engine noise propagation and scattering off an aircraft. Aeroacoustics (2002b) 1:403–20. doi:10.1260/147547202765275989

CrossRef Full Text | Google Scholar

21. Wilcox LC, Stadler G, Burstedde C, Ghattas O. A high-order discontinuous Galerkin method for wave propagation through coupled elastic-acoustic media. J Comput Phys (2010) 229:9373–96. doi:10.1016/j.jcp.2010.09.008

CrossRef Full Text | Google Scholar

22. Bonev B, Hesthaven JS, Giraldo FX, Kopera MA. Discontinuous Galerkin scheme for the spherical shallow water equations with applications to tsunami modeling and prediction. J Comput Phys (2018) 362:425–48. doi:10.1016/j.jcp.2018.02.008

CrossRef Full Text | Google Scholar

23. Giraldo F, Hesthaven J, Warburton T. Nodal high-order discontinuous Galerkin methods for the spherical shallow water equations. J Comput Phys (2002) 181:499–525. doi:10.1006/jcph.2002.7139

CrossRef Full Text | Google Scholar

24. Giraldo F, Restelli M. A study of spectral element and discontinuous Galerkin methods for the Navier–Stokes equations in nonhydrostatic mesoscale atmospheric modeling: equation sets and test cases. J Comput Phys (2008) 227:3849–77. doi:10.1016/j.jcp.2007.12.009

CrossRef Full Text | Google Scholar

25. Restelli M, Giraldo F. A conservative discontinuous Galerkin semi-implicit formulation for the Navier-Stokes equations in nonhydrostatic mesoscale modeling. SIAM J Sci Comput (2009) 31:2231–57. doi:10.1137/070708470

CrossRef Full Text | Google Scholar

26. Fagherazzi S, Furbish D, Rasetarinera P, Hussaini MY. Application of the discontinuous spectral Galerkin method to groundwater flow. Adv Water Res (2004a) 27:129–40. doi:10.1016/j.advwatres.2003.11.001

CrossRef Full Text | Google Scholar

27. Fagherazzi S, Rasetarinera P, Hussaini MY, Furbish DJ. Numerical solution of the dam-break problem with a discontinuous Galerkin method. J Hydraul Eng (2004b) 130:532–9. doi:10.1061/(ASCE)0733

CrossRef Full Text | Google Scholar

28. Cockburn B, Karniadakis G, Shu C-W. The development of discontinuous Galerkin methods. In: B Cockburn, G Karniadakis, and C-W Shu, editors. Proceedings of the inter)national symposium on discontinuous Galerkin methods. New York: Springer-Verlag (2000). p. 3–50.

CrossRef Full Text | Google Scholar

29. Hesthaven J, Warburton T. Nodal discontinuous Galerkin methods: algorithms, analysis, and applications. Verlag New York: Springer (2008)

Google Scholar

30. Karniadakis GE, Sherwin SJ. Spectral/hp element methods for computational fluid dynamics. Oxford:Oxford University Press (2005).

CrossRef Full Text | Google Scholar

31. Kopriva DA. Implementing spectral methods for partial differential equations. Scientific Computation (Netherlands:Springer) (2009).

CrossRef Full Text | Google Scholar

32. Gassner GJ, Winters AR, Hindenlang FJ, Kopriva DA. The BR1 scheme is stable for the compressible Navier-Stokes equations. J Sci Comput (2018) 77:154–200.

CrossRef Full Text | Google Scholar

33. Toro EF. Riemann solvers and numerical methods for fluid dynamics. Springer-Verlag (1999).

CrossRef Full Text | Google Scholar

34. Kopriva DA, Gassner G. On the quadrature and weak form choices in collocation type discontinuous Galerkin spectral element methods. J Sci Comput (2010) 44:136–55.

CrossRef Full Text | Google Scholar

35. Kuzmin D. Entropy stabilization and property-preserving limiters for discontinuous Galerkin discretizations of scalar hyperbolic problems. J Numer Math (2020) 1. doi:10.1515/jnma-2020-0056

CrossRef Full Text | Google Scholar

36. Guo W, Nair RD, Zhong X. An efficient WENO limiter for discontinuous Galerkin transport scheme on the cubed sphere. Int J Numer Methods Fluid (2016) 81:3–21.

CrossRef Full Text | Google Scholar

37. Zhu J, Qiu J. Hermite WENO schemes and their application as limiters for Runge-Kutta discontinuous Galerkin method, III: unstructured meshes. J Sci Comput (2009) 39:293–321.

CrossRef Full Text | Google Scholar

38. Bohm M, Schermeng S, Winters AR, Gassner GJ, Jacobs GB. Multi-element SIAC filter for shock capturing applied to high-order discontinuous Galerkin spectral element methods. J Sci Comput (2019) 81:820–44.

CrossRef Full Text | Google Scholar

39. Gassner GJ, Beck AD. On the accuracy of high-order discretizations for underresolved turbulence simulations. Theor Comput Fluid Dynam (2013) 27:221–37.

CrossRef Full Text | Google Scholar

40. Hennemann S, Rueda-Ramírez AM, Hindenlang FJ, Gassner GJ (2020). A provably entropy stable subcell shock capturing approach for high order split form DG for the compressible Euler equations. J Comput Phys 109935. doi:10.1016/j.jcp.2020.109935

CrossRef Full Text | Google Scholar

41. Markert J, Gassner G, Walch S (2020). A sub-element adaptive shock capturing approach for discontinuous Galerkin methods. arXiv:2011.03338.

Google Scholar

42. Sonntag M, Munz C-D. Efficient parallelization of a shock capturing for discontinuous Galerkin methods using finite volume sub-cells. J Sci Comput (2017) 70:1262–89. doi:10.1007/s10915-016-0287-5

CrossRef Full Text | Google Scholar

43. Dumbser M, Loubère R. A simple robust and accurate a posteriori sub-cell finite volume limiter for the discontinuous Galerkin method on unstructured meshes. J Comput Phys (2016) 319:163–99. doi:10.1016/j.jcp.2016.05.002

CrossRef Full Text | Google Scholar

44. Dumbser M, Zanotti O, Loubère R, Diot S. A posteriori subcell limiting of the discontinuous Galerkin finite element method for hyperbolic conservation laws. J Comput Phys (2014) 278:47–75. doi:10.1016/j.jcp.2014.08.009

CrossRef Full Text | Google Scholar

45. Fambri F. Discontinuous Galerkin methods for compressible and incompressible flows on space–time adaptive meshes: toward a novel family of efficient numerical methods for fluid dynamics. Arch Comput Methods Eng (2020) 27:199–283. doi:10.1007/S11831-018-09308-6

CrossRef Full Text | Google Scholar

46. Giri P, Qiu J. A high-order Runge-Kutta discontinuous Galerkin method with a subcell limiter on adaptive unstructured grids for two-dimensional compressible inviscid flows. Int J Numer Methods Fluid (2019) 91:367–94. doi:10.1002/fld.4757

CrossRef Full Text | Google Scholar

47. Zanotti O, Fambri F, Dumbser M, Hidalgo A. Space–time adaptive ADER discontinuous Galerkin finite element schemes with a posteriori sub-cell finite volume limiting. Comput. Fluids (2015) 118:204–24. doi:10.1016/j.compfluid.2015.06.020

CrossRef Full Text | Google Scholar

48. Ching EJ, Lv Y, Gnoffo P, Barnhardt M, Ihme M. Shock capturing for discontinuous Galerkin methods with application to predicting heat transfer in hypersonic flows. J Comput Phys (2019) 376:54–75. doi:10.1016/j.jcp.2018.09.016

CrossRef Full Text | Google Scholar

49. Persson P-O, Peraire J. Sub-cell shock capturing for discontinuous Galerkin methods. In 44th AIAA aerospace sciences meeting and exhibit (2006). p. 112.

Google Scholar

50. Beskok A, Warburton TC. An unstructured finite-element scheme for fluid flow and heat transfer in moving domains. J Comput Phys (2001) 174:492–509. doi:10.1006/jcph.2001.6885

CrossRef Full Text | Google Scholar

51. Carpenter M, Kennedy C, Bijl H, Viken S, Vatsa V. Fourth-order Runge-Kutta schemes for fluid mechanics applications. J Sci Comput (2005) 25:157–94. doi:10.1007/s10915-004-4637-3

CrossRef Full Text | Google Scholar

52. Constantinescu E, Sandu A. Multirate explicit adams methods for time integration of conservation laws. J Sci Comput (2009) 38:229–49. doi:10.1007/s10915-008-9235-3

CrossRef Full Text | Google Scholar

53. Gassner G, Haas M. An explicit high order accurate predictor-corrector time integration method with consistent local time-stepping for discontinuous Galerkin schemes. AIP Conf Proceed (2009) 1168:1188–91. doi:10.1063/1.3241276

CrossRef Full Text | Google Scholar

54. Kopera MA, Giraldo FX. Analysis of adaptive mesh refinement for IMEX discontinuous Galerkin solutions of the compressible Euler equations with application to atmospheric simulations. J Comput Phys (2014) 275:92–117. doi:10.1016/j.jcp.2014.06.026

CrossRef Full Text | Google Scholar

55. Gassner G, Kopriva DA. A comparison of the dispersion and dissipation errors of Gauss and Gauss-Lobatto discontinuous Galerkin spectral element methods. SIAM J Sci Comput (2010) 33:2560–79. doi:10.1137/100807211

CrossRef Full Text | Google Scholar

56. Stanescu D, Kopriva D, Hussaini M. Dispersion analysis for discontinuous spectral element methods. J Sci Comput (2001) 15:149–71. doi:10.1023/A:1007629609576

CrossRef Full Text | Google Scholar

57. Altmann C, Beck AD, Hindenlang F, Staudenmaier M, Gassner GJ, Munz C-D. An efficient high performance parallelization of a discontinuous Galerkin spectral element method. In: R Keller, D Kramer, and J-P Weiss, editors Facing the multicore-challenge IIIof lecture notes in computer science. Springer Berlin Heidelberg (2013), Vol. 7686, p. 37–47.

CrossRef Full Text | Google Scholar

58. Hindenlang F, Gassner GJ, Altmann C, Beck A, Staudenmaier M, Munz C-D. Explicit discontinuous Galerkin methods for unsteady problems. Comput Fluids (2012) 61:86–93. doi:10.1016/j.compfluid.2012.03.006

CrossRef Full Text | Google Scholar

59. Dumbser M, Käser M, Toro EF. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes–V. local time stepping and p-adaptivity. Geophys J Int (2007) 171:695–717. doi:10.1111/j.1365-246X.2007.03427.x

CrossRef Full Text | Google Scholar

60. Frank HM, Munz C-D. Direct aeroacoustic simulation of acoustic feedback phenomena on a side-view mirror. J Sound Vib (2016) 371:132–49. doi:10.1016/j.jsv.2016.02.014

CrossRef Full Text | Google Scholar

61. Persson P-O. A sparse and high-order accurate line-based discontinuous Galerkin method for unstructured meshes. J Comput Phys (2013) 233:414–29. doi:10.1016/j.jcp.2012.09.008

CrossRef Full Text | Google Scholar

62. Warburton T. Application of the discontinuous Galerkin method to Maxwell’s equations using unstructured polymorphic -finite elements. In: B Cockburn, G Karniadakis, and C-W Shu, editors. Proceedings of the international symposium on discontinuous Galerkin methods. New York: Springer-Verlag (2000). p. 451–8.

CrossRef Full Text | Google Scholar

63. Wintermeyer N, Winters AR, Gassner GJ, Kopriva DA. An entropy stable nodal discontinuous Galerkin method for the two dimensional shallow water equations on unstructured curvilinear meshes with discontinuous bathymetry. J Comput Phys (2017) 340:200–42. doi:10.1016/j.jcp.2017.03.036

CrossRef Full Text | Google Scholar

64. Kopriva DA, Gassner GJ. An energy stable discontinuous Galerkin spectral element discretization for variable coefficient advection problems. SIAM J Sci Comput (2014) 34:A2076–A2099. doi:10.1137/130928650

CrossRef Full Text | Google Scholar

65. Jiang G, Shu C-W. On a cell entropy inequality for discontinuous Galerkin methods. Math Comput (1994) 62:531–8. doi:10.2307/2153521

CrossRef Full Text | Google Scholar

66. Kopriva DA. Stability of overintegration methods for nodal discontinuous Galerkin spectral element methods. J Sci Comput (2017b) 76:426–42. doi:10.1007/s10915-017-0626-1

CrossRef Full Text | Google Scholar

67. Moura R, Sherwin S, Peiro J. On DG-based iLES approaches at very high Reynolds numbers. Research Gate: Report (2015).

Google Scholar

68. Merriam ML. Smoothing and the second law. Comput Methods Appl Mech Eng (1987) 64:177–93. doi:10.1016/0045-7825(87)90039-9

CrossRef Full Text | Google Scholar

69. Chiodaroli E. A counterexample to well-posedness of entropy solutions to the compressible Euler system. J Hyperbolic Differ Equ (2014) 11:493–519. doi:10.1142/S0219891614500143

CrossRef Full Text | Google Scholar

70. Klingenberg C, Markfelder S. Non-uniqueness of entropy-conserving solutions to the ideal compressible MHD equations. In: A Bressan, M Lewicka, D Wang, and Y Zheng, editors. Hyperbolic problems: theory, numerics, applications. AIMS on Applied Mathematics (2020), Vol. 10, p. 491–8.

Google Scholar

71. LeFloch PG, Novotny J. Hyperbolic systems of conservation laws: the theory of classical and nonclassical shock waves. Appl Mech Rev (2003) 56:B53–4. doi:10.1007/978-3-0348-8150-0

CrossRef Full Text | Google Scholar

72. Terracina A. Non-uniqueness results for entropy two-phase solutions of forward–backward parabolic problems with unstable phase. J Math Anal Appl (2014) 413:963–75. doi:10.1016/j.jmaa.2013.12.045

CrossRef Full Text | Google Scholar

73. Evans LC. Partial differential equations. Providence, Rhode Island:American Mathematical Society (2012).

Google Scholar

74. LeVeque RJ. Finite volume methods for hyperbolic problems. Cambridge:Cambridge University Press (2002).

Google Scholar

75. Lax PD. Weak solutions of nonlinear hyperbolic conservation equations and their numerical computation. Commun Pure Appl Math (1954) 7:159–93. 10.1002/cpa.3160070112

CrossRef Full Text | Google Scholar

76. Lax PD. Hyperbolic difference equations: a review of the Courant-Friedrichs-Lewy paper in the light of recent developments. IBM J Res Develop (1967) 11:235–8. doi:10.1147/rd.112.0235

CrossRef Full Text | Google Scholar

77. Tadmor E. Entropy functions for symmetric systems of conservation laws. J Math Anal Appl (1987) 122:355–9. doi:10.1016/0022-247X(87)90265-4

CrossRef Full Text | Google Scholar

78. Tadmor E. Entropy stability theory for difference approximations of nonlinear conservation laws and related time-dependent problems. Acta Numer (2003) 12:451–512. doi:10.1017/S0962492902000156

CrossRef Full Text | Google Scholar

79. Ranocha H. Mimetic properties of difference operators: product and chain rules as for functions of bounded variation and entropy stability of second derivatives. BIT Num Math (2019) 59:547–63. doi:10.1007/s10543-018-0736-7

CrossRef Full Text | Google Scholar

80. Harten A. On the symmetric form of systems of conservation laws with entropy. J Comput Phys (1983) 49:151–64. doi:10.1016/0021-9991(83)90118-3

CrossRef Full Text | Google Scholar

81. Chandrashekar P. Kinetic energy preserving and entropy stable finite volume schemes for compressible Euler and Navier-Stokes equations. Commun Comput Phys (2013) 14:1252–86. doi:10.4208/cicp.170712.010313a

CrossRef Full Text | Google Scholar

82. Dutt P. Stable boundary conditions and difference schemes for Navier-Stokes equations. SIAM J Numer Anal (1988) 25:245–67. doi:10.1137/0725018

CrossRef Full Text | Google Scholar

83. Ismail F, Roe PL. Affordable, entropy-consistent Euler flux functions II: entropy production at shocks. J Comput Phys (2009) 228:5410–36. doi:10.1016/j.jcp.2009.04.021

CrossRef Full Text | Google Scholar

84. Mock MS. Systems of conservation laws of mixed type. J Differ Equ (1980) 37:70–88. doi:10.1016/0022-0396(80)90089-3

CrossRef Full Text | Google Scholar

85. Tadmor E. Skew-selfadjoint form for systems of conservation laws. J Math Anal Appl (1984) 103:428–42. doi:10.1016/0022-247X(84)90139-2

CrossRef Full Text | Google Scholar

86. Merriam ML. An entropy-based approach to nonlinear stability. NASA Tech Memo (1989) 101086:1–154.

Google Scholar

87. Derigs D, Gassner GJ, Walch S, Winters AR. Entropy stable finite volume approximations for ideal magnetohydrodynamics. Jahresber Dtsch Math Ver (2018) 120:153–219. doi:10.1365/s13291-018-0178-9

CrossRef Full Text | Google Scholar

88. Fisher T. High-order stable multi-domain finite difference method for compressible flows. [PhD thesis]. West Lafayette, Indiana:Purdue University (2012).

Google Scholar

89. Evans LC. Entropy and partial differential equations. Lecture Notes at Berkeley, California:University of California, Berkeley (2004).

Google Scholar

90. Svärd M. Entropy solutions of the compressible Euler equations. BIT Num Math (2016) 56:1479–96. doi:10.1007/s10543-016-0611-3

CrossRef Full Text | Google Scholar

91. Hughes TJ, Franca L, Mallet M. A new finite element formulation for computational fluid dynamics: I. Symmetric forms of the compressible Euler and Navier-Stokes equations and the second law of thermodynamics. Comput Methods Appl Mech Eng (1986) 54:223–34. doi:10.1016/0045-7825(86)90127-1

CrossRef Full Text | Google Scholar

92. Hiltebrand A, Mishra S. Entropy stable shock capturing space–time discontinuous Galerkin schemes for systems of conservation laws. Numer Math (2013) 126:103–51. doi:10.1007/s00211-013-0558-0

CrossRef Full Text | Google Scholar

93. Hiltebrand A, Mishra S. Entropy stability and well-balancedness of space-time DG for the shallow water equations with bottom topography. Netw Heterogeneous Media (2016) 11:145–62. doi:10.3934/nhm.2016.11.145

CrossRef Full Text | Google Scholar

94. Hiltebrand A, Mishra S, Parés C. Entropy-stable space–time DG schemes for non-conservative hyperbolic systems. ESAIM Math Model Numer Anal (2018) 52:995–1022. doi:10.1051/m2an/2017056

CrossRef Full Text | Google Scholar

95. Kirby RM, Karniadakis G. De-aliasing on non-uniform grids: algorithms and applications. J Comput Phys (2003) 191:249–64. doi:10.1016/S0021-9991(03)00314-0

CrossRef Full Text | Google Scholar

96. Mengaldo G, Grazia DD, Moxey D, Vincent PE, Sherwin SJ. Dealiasing techniques for high-order spectral element methods on regular and irregular grids. J Comput Phys (2015) 299:56–81. doi:10.1016/j.jcp.2015.06.032

CrossRef Full Text | Google Scholar

97. Beck AD, Bolemann T, Flad D, Frank H, Gassner GJ, Hindenlang F, et al. High-order discontinuous Galerkin spectral element methods for transitional and turbulent flow simulations. Int J Numer Methods Fluid (2014) 76:522–48. doi:10.1002/fld.3943

CrossRef Full Text | Google Scholar

98. Persson P-O, Bonet J, Peraire J. Discontinuous Galerkin solution of the Navier-Stokes equations on deformable domains. Comput Methods Appl Mech Eng (2009) 198:1585–95. doi:10.1016/j.cma.2009.01.012

CrossRef Full Text | Google Scholar

99. LeFloch P, Rohde C. High-order schemes, entropy inequalities, and nonclassical shocks. SIAM J Numer Anal (2000) 37:2023–60. doi:10.1137/S0036142998345256

CrossRef Full Text | Google Scholar

100. LeFloch PG, Mercier J-M, Rohde C. Fully discrete, entropy conservative schemes of arbitrary order. SIAM J Numer Anal (2002) 40:1968–92. doi:10.1137/S003614290240069X

CrossRef Full Text | Google Scholar

101. Fisher T, Carpenter M. High-order entropy stable finite difference schemes for nonlinear conservation laws: finite domains. J Comput Phys (2013) 252:518–57. doi:10.1016/j.jcp.2013.06.014

CrossRef Full Text | Google Scholar

102. Kreiss H-O, Oliger J. Methods for the approximate solution of time-dependent problems (1973). GARP Report No.:10. Geneva: World Meteorological Organization.

Google Scholar

103. Kreiss H-O, Olliger J. Comparison of accurate methods for the integration of hyperbolic equations. Tellus (1972) 24:199–215. doi:10.3402/tellusa.v24i3.10634

CrossRef Full Text | Google Scholar

104. Kreiss H-O, Scherer G. Finite element and finite difference methods for hyperbolic partial differential equations. Math Aspect Finite Elem Part Diff Equat (Elsevier) (1974) 195–212. doi:10.1016/B978-0-12-208350-1.50012-1

CrossRef Full Text | Google Scholar

105. Kreiss H-O, Scherer G. On the existence of energy estimates for difference approximations for hyperbolic systems (1977). Tech. Rep. Uppsala:Department of Scientific Computing. Uppsala University.

Google Scholar

106. Olsson P. Summation by parts, projections, and stability. I. Math Comput (1995a) 64:1035–65. doi:10.2307/2153482

CrossRef Full Text | Google Scholar

107. Olsson P. Summation by parts, projections, and stability. II. Math Comput (1995b) 64:1473–93. doi:10.2307/2153366

CrossRef Full Text | Google Scholar

108. Strand B. Summation by parts for finite difference approximations for d/dx. J Comput Phys (1994) 110:47–67. doi:10.1006/jcph.1994.1005

CrossRef Full Text | Google Scholar

109. Nordström J. Conservative finite difference formulations, variable coefficients, energy estimates and artificial dissipation. J Sci Comput (2006) 29:375–404. doi:10.1007/s10915-005-9013-4

CrossRef Full Text | Google Scholar

110. Svärd M, Nordström J. Review of summation-by-parts schemes for initial-boundary-value problems. J Comput Phys (2014) 268:17–38. doi:10.1016/j.jcp.2014.02.031

CrossRef Full Text | Google Scholar

111. Gassner G. A skew-symmetric discontinuous Galerkin spectral element discretization and its relation to SBP-SAT finite difference methods. SIAM J Sci Comput (2013) 35:A1233–A1253. doi:10.1137/120890144

CrossRef Full Text | Google Scholar

112. Carpenter MH, Gottlieb D. Spectral methods on arbitrary grids. J Comput Phys (1996) 129:74–86. doi:10.1006/jcph.1996.0234

CrossRef Full Text | Google Scholar

113. Kopriva DA. A polynomial spectral calculus for analysis of DG spectral element methods. In Bittencourt ML, Dumont NA, and Hesthaven, JS, editors. Spectral and high order methods for partial differential equations ICOSAHOM 2016. Cham:Springer International Publishing (2017) p. 21–40.

CrossRef Full Text | Google Scholar

114. Carpenter M, Fisher T, Nielsen E, Frankel S. Entropy stable spectral collocation schemes for the Navier-Stokes equations: discontinuous interfaces. SIAM J Sci Comput (2014) 36:B835–B867. doi:10.1137/130932193

CrossRef Full Text | Google Scholar

115. Chan J. On discretely entropy conservative and entropy stable discontinuous Galerkin methods. J Comput Phys (2018) 362:346–74. doi:10.1016/j.jcp.2018.02.033

CrossRef Full Text | Google Scholar

116. Gassner G, Winters A, Kopriva DA. Split form nodal discontinuous Galerkin schemes with summation-by-parts property for the compressible Euler equations. J Comput Phys (2016a) 327:39–66. doi:10.1016/j.jcp.2016.09.013

CrossRef Full Text | Google Scholar

117. Gassner GJ. A kinetic energy preserving nodal discontinuous Galerkin spectral element method. Int J Numer Methods Fluid (2014) 76:28–50. doi:10.1002/fld.3923

CrossRef Full Text | Google Scholar

118. Gouasmi A, Duraisamy K, Murman SM. Formulation of entropy-stable schemes for the multicomponent compressible Euler equations. Comput Methods Appl Mech Eng (2020) 363:112912. doi:10.1016/j.cma.2020.112912

CrossRef Full Text | Google Scholar

119. Gassner GJ, Winters AR, Kopriva DA. A well balanced and entropy conservative discontinuous Galerkin spectral element method for the shallow water equations. Appl Math Comput (2016b) 272(2):291–308. doi:10.1016/j.amc.2015.07.014

CrossRef Full Text | Google Scholar

120. Wu X, Chan J (2020). Entropy stable discontinuous Galerkin methods for nonlinear conservation laws on networks and multi-dimensional domains. arXiv:2010.09994.

Google Scholar

121. Wu X, Chan J, Kubatko E (2020). High-order entropy stable discontinuous Galerkin methods for the shallow water equations: curved triangular meshes and GPU acceleration. arXiv:2005.02516.

CrossRef Full Text | Google Scholar

122. Parsani M, Carpenter M, Nielsen E. Entropy stable discontinuous interfaces coupling for the three-dimensional compressible Navier-Stokes equations. J Comput Phys (2015a) 290:132–8. doi:10.1016/j.jcp.2015.02.042

CrossRef Full Text | Google Scholar

123. Parsani M, Carpenter M, Nielsen E. Entropy stable wall boundary conditions for the three-dimensional compressible Navier-Stokes equations. J Comput Phys (2015b) 292:88–113. doi:10.1016/j.jcp.2015.03.026

CrossRef Full Text | Google Scholar

124. Renac F. Entropy stable DGSEM for nonlinear hyperbolic systems in nonconservative form with application to two-phase flows. J Comput Phys (2019) 382:1–26. doi:10.1016/j.jcp.2018.12.035

CrossRef Full Text | Google Scholar

125. Bohm M, Winters AR, Gassner GJ, Derigs D, Hindenlang F, Saur J. An entropy stable nodal discontinuous Galerkin method for the resistive MHD equations. Part I: theory and numerical verification. J Comput Phys (2018) 422:108076. doi:10.1016/j.jcp.2018.06.027

CrossRef Full Text | Google Scholar

126. Liu Y, Shu C-W, Zhang M. Entropy stable high order discontinuous Galerkin methods for ideal compressible MHD on structured meshes. J Comput Phys (2018) 354:163–78. doi:10.1016/j.jcp.2017.10.043

CrossRef Full Text | Google Scholar

127. Biswas B, Kumar H (2019). Entropy stable discontinuous Galerkin approximation for the relativistic hydrodynamic equations. arXiv:1911.07488.

Google Scholar

128. Wu K, Shu C-W (2019). Entropy symmetrization and high-order accurate entropy stable numerical schemes for relativistic MHD equations. arXiv:1907.07467.

Google Scholar

129. Manzanero J, Rubio G, Kopriva DA, Ferrer E, Valero E. A free–energy stable nodal discontinuous Galerkin approximation with summation–by–parts property for the Cahn–Hilliard equation. J Comput Phys (2020c) 403:109072. doi:10.1016/j.jcp.2019.109072

CrossRef Full Text | Google Scholar

130. Manzanero J, Rubio G, Kopriva DA, Ferrer E, Valero E. An entropy–stable discontinuous Galerkin approximation for the incompressible Navier–Stokes equations with variable density and artificial compressibility. J Comput Phys (2020a) 408:109241. doi:10.1016/j.jcp.2020.109241

CrossRef Full Text | Google Scholar

131. Manzanero J, Rubio G, Kopriva DA, Ferrer E, Valero E. Entropy–stable discontinuous Galerkin approximation with summation–by–parts property for the incompressible Navier–Stokes/Cahn–Hilliard system. J Comput Phys (2020b) 408:109363. doi:10.1016/j.jcp.2020.109363

CrossRef Full Text | Google Scholar

132. Chen T, Shu C-W. Entropy stable high order discontinuous Galerkin methods with suitable quadrature rules for hyperbolic conservation laws. J Comput Phys (2017) 345:427–61. doi:10.1016/j.jcp.2017.05.025

CrossRef Full Text | Google Scholar

133. Zang TA. On the rotation and skew-symmetric forms for incompressible flow simulations. Appl Numer Math (1991) 7:27–40. doi:10.1016/0168-9274(91)90102-6

CrossRef Full Text | Google Scholar

134. Ducros F, Laporte F, Soulères T, Guinot V, Moinat P, Caruelle B. High-order fluxes for conservative skew-symmetric-like schemes in structured meshes: application to compressible flows. J Comput Phys (2000) 161:114–39. doi:10.1006/jcph.2000.6492

CrossRef Full Text | Google Scholar

135. Honein AE, Moin P. Higher entropy conservation and numerical stability of compressible turbulence simulations. J Comput Phys (2004) 201:531–45. doi:10.1016/j.jcp.2004.06.006

CrossRef Full Text | Google Scholar

136. Kennedy CA, Gruber A. Reduced aliasing formulations of the convective terms within the Navier–Stokes equations for a compressible fluid. J Comput Phys (2008) 227:1676–700. doi:10.1016/j.jcp.2007.09.020

CrossRef Full Text | Google Scholar

137. Pirozzoli S. Generalized conservative approximations of split convective derivative operators. J Comput Phys (2010) 229:7180–90. doi:10.1016/j.jcp.2010.06.006

CrossRef Full Text | Google Scholar

138. Sandham ND, Li Q, Yee HC. Entropy splitting for high-order numerical simulation of compressible turbulence. J Comput Phys (2002) 178:307–22. doi:10.1006/jcph.2002.7022

CrossRef Full Text | Google Scholar

139. Sjögreen B, Yee HC, Kotov D. Skew-symmetric splitting and stability of high order central schemes. J Phys Conf (2017) 837:012019. doi:10.1007/s00193-019-00925-z

CrossRef Full Text | Google Scholar

140. Blaisdell GA, Spyropoulos ET, Qin JH. The effect of the formulation of nonlinear terms on aliasing errors in spectral methods. Appl Numer Math (1996) 21:207–19. doi:10.1016/0168-9274(96)00005-0

CrossRef Full Text | Google Scholar

141. LeFloch PG, Mohammadian M. Why many theories of shock waves are necessary: kinetic functions, equivalent equations, and fourth-order models. J Comput Phys (2008) 227:4162–89. doi:10.1016/j.jcp.2007.12.026

CrossRef Full Text | Google Scholar

142. Winters AR, Gassner GJ. A comparison of two entropy stable discontinuous Galerkin spectral element approximations for the shallow water equations with non-constant topography. J Comput Phys (2015) 301:357–76. doi:10.1016/j.jcp.2015.08.034

CrossRef Full Text | Google Scholar

143. Coppola G, Capuno F, Pirozzoli S, de Luce L. Numerically stable formulations of convective terms for turbulent compressible flows. J Comput Phys (2019) 382:86–104. doi:10.1016/j.jcp.2019.01.007

CrossRef Full Text | Google Scholar

144. Kuya Y, Totani K, Kawai S. Kinetic energy and entropy preserving schemes for compressible flows by split convective forms. J Comput Phys (2018) 375:823–53. doi:10.1016/j.jcp.2018.08.058

CrossRef Full Text | Google Scholar

145. Tadmor E. Perfect derivatives, conservative differences and entropy stable computation of hyperbolic conservation laws. Disc Contin Dyn Syst-A (2016) 36:4579–98. 10.3934/dcds.2016.36.4579

CrossRef Full Text | Google Scholar

146. Fjordholm US, Mishra S, Tadmor E. Well-balanced and energy stable schemes for the shallow water equations with discontiuous topography. J Comput Phys (2011) 230:5587–609. doi:10.1016/j.jcp.2011.03.042

CrossRef Full Text | Google Scholar

147. Winters A, Gassner G. Affordable, entropy conserving and entropy stable flux functions for the ideal MHD equations. J Comput Phys (2016) 301:72–108. doi:10.1016/j.jcp.2015.09.055

CrossRef Full Text | Google Scholar

148. Fjordholm US, Mishra S, Tadmor E. Arbitrarily high-order accurate entropy stable essentially nonoscillatory schemes for systems of conservation laws. SIAM J Numer Anal (2012) 50:544–73. doi:10.1137/110836961

CrossRef Full Text | Google Scholar

149. Fjordholm US, Ray D. A sign preserving WENO reconstruction method. J Sci Comput (2016) 68:42–63. doi:10.1007/s10915-015-0128-y

CrossRef Full Text | Google Scholar

150. Ranocha H. Shallow water equations: split-form, entropy stable, well-balanced, and positivity preserving numerical methods. GEM-International Journal on Geomathematics (2017) 8:85–133. doi:10.1007/s13137-016-0089-9

CrossRef Full Text | Google Scholar

151. Ranocha H. Comparison of some entropy conservative numerical fluxes for the Euler equations. J Sci Comput (2018) 76:216–42. doi:10.1007/s10915-017-0618-1

CrossRef Full Text | Google Scholar

152. Barth TJ. Numerical methods for gasdynamic systems on unstructured meshes. In: D Kröner, M Ohlberger, and C Rohde, editors An introduction to recent developments in theory and numerics for conservation laws of lecture notes in computational science and engineering. Springer Berlin Heidelberg (1999), Vol. 5, p. 195–285.

CrossRef Full Text | Google Scholar

153. Derigs D, Winters AR, Gassner GJ, Walch S. A novel averaging technique for discrete entropy-stable dissipation operators for ideal MHD. J Comput Phys (2017) 330:624–32. doi:10.1016/j.jcp.2016.10.055

CrossRef Full Text | Google Scholar

154.Fjordholm US. High-order accurate entropy stable numercial schemes for hyperbolic conservation laws. [Ph.D. thesis]. ETH Zurich (2013).

Google Scholar

155. Ray D, Chandrashekar P. An entropy stable finite volume scheme for the two dimensional Navier–Stokes equations on triangular grids. Appl Math Comput (2017) 314:257–86. doi:10.1016/j.amc.2017.07.020

CrossRef Full Text | Google Scholar

156. Winters AR, Derigs D, Gassner GJ, Walch S. A uniquely defined entropy stable matrix dissipation operator for high Mach number ideal MHD and compressible Euler simulations. J Comput Phys (2017) 332:274–89. doi:10.1016/j.jcp.2016.12.006

CrossRef Full Text | Google Scholar

157. Chan J, Wilcox LC. On discretely entropy stable weight-adjusted discontinuous Galerkin methods: curvilinear meshes. J Comput Phys (2019) 378:366–93. doi:10.1016/j.jcp.2018.11.010

CrossRef Full Text | Google Scholar

158. Rojas D, Boukharfane R, Dalcin L, Fernández DCDR, Ranocha H, Keyes DE, et al. On the robustness and performance of entropy stable collocated discontinuous Galerkin methods. J Comput Phys (2020) 109891. doi:10.1016/j.jcp.2020.109891

CrossRef Full Text | Google Scholar

159. Carpenter M, Kennedy C. Fourth-order -storage Runge-Kutta schemes (1994). Tech. Rep. NASA TM 109111. Hampton, Virginia:NASA Langley Research Center.

Google Scholar

160. Winters AR, Moura RC, Mengaldo G, Gassner GJ, Walch S, Peiro J, et al. A comparative study on polynomial dealiasing and split form discontinuous Galerkin schemes for under-resolved turbulence computations. J Comput Phys (2018) 372:1–21. doi:10.1016/j.jcp.2018.06.016

CrossRef Full Text | Google Scholar

161. Flad D, Gassner G. On the use of kinetic energy preservaing DG-scheme for large eddy simulation. J Comput Phys (2017) 350:782–95. doi:10.1016/j.jcp.2020.109891

CrossRef Full Text | Google Scholar

162. Saur J, Neubauer FM, Strobel DF, Summers ME. Three-dimensional plasma simulation of Io’s interaction with the Io plasma torus: asymmetric plasma flow. J Geophys Res: Space Physics (1999) 104:25105–26. doi:10.1029/1999JA900304

CrossRef Full Text | Google Scholar

163. Bohm M. An entropy stable nodal discontinuous Galerkin method for the resistive MHD equations. [PhD thesis]. Universität zu Köln (2018).

Google Scholar

164. Saur J, Neubauer FM, Connerney J, Zarka P, Kivelson MG. Plasma interaction of Io with its plasma torus. In: Bagenal F, Dowling, TE, and McKinnon, WB, editors. Jupiter. The Planet, Satellites and Magnetosphere. vol. 1. Cambridge: Cambridge University Press (2004). p. 537–60.

Google Scholar

165. Chan J, Bencomo M, Fernández DCDR (2020). Mortar-based entropy-stable discontinuous Galerkin methods on non-conforming quadrilateral and hexahedral meshes. arXiv:2005.03237.

Google Scholar

166. Friedrich L, Winters AR, Fernández DCDR, Gassner GJ, Parsani M, Carpenter MH. An entropy stable non-conforming discontinuous Galerkin method with the summation-by-parts property. J Sci Comput (2018) 77:689–725. doi:10.1007/s10915-018-0733-7

CrossRef Full Text | Google Scholar

167. Kopriva DA, Winters AR, Bohm M, Gassner GJ. A provably stable discontinuous Galerkin spectral element approximation for moving hexahedral meshes. Comput Fluids (2016) 139:148–60. doi:10.1016/j.compfluid.2016.05.023

CrossRef Full Text | Google Scholar

168. Schnücke G, Krais N, Bolemann T, Gassner GJ. Entropy stable discontinuous Galerkin schemes on moving meshes for hyperbolic conservation laws. J Sci Comput (2020) 82:1–42. doi:10.1007/s10915-020-01171-7

CrossRef Full Text | Google Scholar

169. Yamaleev NK, Fernandez DCDR, Lou J, Carpenter MH. Entropy stable spectral collocation schemes for the 3-D Navier-Stokes equations on dynamic unstructured grids. J Comput Phys (2019) 399:108897. doi:10.1016/j.jcp.2019.108897

CrossRef Full Text | Google Scholar

170. Pazner W, Persson P-O. Analysis and entropy stability of the line-based discontinuous Galerkin method. J Sci Comput (2019) 80:376–402. doi:10.1007/s10915-019-00942-1

CrossRef Full Text | Google Scholar

171. Friedrich L, Schnücke G, Winters AR, Fernández DCDR, Gassner GJ, Carpenter MH. Entropy stable space–time discontinuous Galerkin schemes with summation-by-parts property for hyperbolic conservation laws. J Sci Comput (2019) 80:175–222. doi:10.1007/s10915-019-00933-2

CrossRef Full Text | Google Scholar

172. Gouasmi A, Duraisamy K, Murman S (2018). On entropy stable temporal fluxes. arXiv:1807.03483.

Google Scholar

173. Gouasmi A, Murman SM, Duraisamy K. Entropy conservative schemes and the receding flow problem. J Sci Comput (2019) 78:971–94. doi:10.1007/s10915-018-0793-8

CrossRef Full Text | Google Scholar

174. Parsani M, Boukharfane R, Nolasco IR, Fernández DCDR, Zampini S, Hadri B, et al. High-order accurate entropy-stable discontinuous collocated Galerkin methods with the summation-by-parts property for compressible CFD frameworks: scalable SSDC algorithms and flow solver. J Comput Phys (2020) 424:109844. doi:10.1016/j.jcp.2020.109844

CrossRef Full Text | Google Scholar

175. Ranocha H, Sayyari M, Dalcin L, Parsani M, Ketcheson DI. Relaxation Runge–Kutta methods: fully discrete explicit entropy-stable schemes for the compressible Euler and Navier–Stokes equations. SIAM J Sci Comput (2020) 42:A612–A638. doi:10.1137/19M1263480

CrossRef Full Text | Google Scholar

176. Parsani M, Carpenter MH, Fisher TC, Nielsen EJ. Entropy stable staggered grid discontinuous spectral collocation methods of any order for the compressible Navier–Stokes equations. SIAM J Sci Comput (2016) 38:A3129–A3162. doi:10.1137/15m1043510

CrossRef Full Text | Google Scholar

177. Ortleb S. A kinetic energy preserving DG scheme based on Gauss–Legendre points. J Sci Comput (2016) 71:1135–68. doi:10.1007/s10915-016-0334-2

CrossRef Full Text | Google Scholar

178. Fernández DCDR. Generalized summation-by-parts operators for first and second derivatives. [PhD thesis]. University of Toronto (2015).

Google Scholar

179. Fernández DCDR, Hicken JE, Zingg DW. Simultaneous approximation terms for multi-dimensional summation-by-parts operators. J Sci Comput (2017) 75:83–110. doi:10.1007/s10915-017-0523-7

CrossRef Full Text | Google Scholar

180. Chan J. Entropy stable reduced order modeling of nonlinear conservation laws. J Comput Phys (2020) 423:109789. doi:10.1016/j.jcp.2020.109789

CrossRef Full Text | Google Scholar

181. Hicken JE, Fernández DCDR, Zingg DW. Multidimensional summation-by-parts operators: general theory and application to simplex elements. SIAM J Sci Comput (2016) 38:A1935–A1958. doi:10.1137/15m1038360

CrossRef Full Text | Google Scholar

182. Crean J, Hicken JE, Fernández DCDR, Zingg DW, Carpenter MH. Entropy-stable summation-by-parts discretization of the Euler equations on general curved elements. J Comput Phys (2018) 356:410–38. doi:10.1016/j.jcp.2017.12.015

CrossRef Full Text | Google Scholar

183. Gassner GJ, Svärd M, Hindenlang FJ (2020).Stability issues of entropy-stable and/or split-form high-order schemes. arXiv:2007.09026

Google Scholar

184. Ranocha H, Gassner GJ (2020). Preventing pressure oscillations does not fix local linear stability issues of entropy-based split-form high-order schemes. arXiv:2009.13139.

Google Scholar

185. Jameson A. Formulation of kinetic energy preserving conservative schemes for gas dynamics and direct numerical simulation of one-dimensional viscous compressible flow in a shock tube using entropy and kinetic energy preserving schemes. J Sci Comput (2008) 34:188–208. doi:10.1007/s10915-007-9172-6

CrossRef Full Text | Google Scholar

186. Kuya Y, Kawai S. A stable and non-dissipative kinetic energy and entropy preserving (KEEP) scheme for non-conforming block boundaries on Cartesian grids. Comput Fluids (2020) 200:104427. doi:10.1016/j.compfluid.2020.104427

CrossRef Full Text | Google Scholar

187. Ranocha H. Entropy conserving and kinetic energy preserving numerical methods for the Euler equations using summation-by-parts operators. In: SJ Sherwin, D Moxey, J Peiró, PE Vincent, and C Schwab, editors Spectral and high order methods for partial differential equations ICOSAHOM 2018. Cham: Springer International Publishing (2020). p. 525–35.

CrossRef Full Text | Google Scholar

188. Pirozzoli S. Numerical methods for high-speed flows. Annu Rev Fluid Mech (2011) 43:163–94. doi:10.1146/annurev-fluid-122109-160718

CrossRef Full Text | Google Scholar

189. Dalcin L, Rojas D, Zampini S, Fernández DCDR, Carpenter MH, Parsani M. Conservative and entropy stable solid wall boundary conditions for the compressible Navier–Stokes equations: adiabatic wall and heat entropy transfer. J Comput Phys (2019) 397:108775. doi:10.1016/j.jcp.2019.06.051

CrossRef Full Text | Google Scholar

190. Dubois F, LeFloch P. Boundary conditions for nonlinear hyperbolic systems of conservation laws. J Differ Equ (1988) 71:93–122. doi:10.1016/0022-0396(88)90040-X

CrossRef Full Text | Google Scholar

191. Hindenlang FJ, Gassner GJ, Kopriva DA. Stability of wall boundary condition procedures for discontinuous Galerkin spectral element approximations of the compressible Euler equations. In: SJ Sherwin, D Moxey, J Peiró, PE Vincent, and C Schwab, editors. Spectral and high order methods for partial differential equations ICOSAHOM 2018. Springer International Publishing (2020). p. 3–19.

CrossRef Full Text | Google Scholar

192. Parsani M, Carpenter MH, Nielsen EJ. Entropy stable wall boundary conditions for the three-dimensional compressible Navier–Stokes equations. J Comput Phys (2015c) 292:88–113. doi:10.1016/j.jcp.2015.03.026

CrossRef Full Text | Google Scholar

193. Svärd M. Entropy stable boundary conditions for the Euler equations. J Comput Phys (2020) 109947. doi:10.1016/j.jcp.2020.109947

CrossRef Full Text | Google Scholar

194. Svärd M, Mishra S. Entropy stable schemes for initial-boundary-value conservation laws. Z Angew Math Phys (2012) 63:985–1003. doi:10.1007/s00033-012-0216-x

CrossRef Full Text | Google Scholar

195. Svärd M, Özcan H. Entropy-stable schemes for the Euler equations with far-field and wall boundary conditions. J Sci Comput (2014) 58:61–89. doi:10.1007/s10915-013-9727-7

CrossRef Full Text | Google Scholar