- 1School of Information and Control Engineering, China University of Mining and Technology, Xuzhou, China
- 2School of Computer Engineering, Jiangsu University of Technology, Changzhou, China
- 3Department of Mathematics and Science Education, Faculty of Education, Harran University, Sanliurfa, Turkey
- 4School of Information Science and Technology, Yunnan Normal University, Kunming, China
Ontology is one of the oldest terminologies in physics and is used to describe the origin and most essential attributes of all things in the world. With the development of contemporary science, ontology was given a specific definition and then introduced into the computer science as a conceptual model to describe the relationship between objects. In the past decade, the algorithms and applications in the ontology-related field have attracted the attention of many scholars. In this work, a support vector machines based multi-dividing ontology learning algorithm is proposed. We pay attention to the similarity of topological indices in chemical graph theory, and apply SVM-based multi-dividing ontology learning algorithms to give some calculation results of similarity between topological indices.
Introduction
The term “ontology” first appeared in philosophy and physics, and was used to describe the most original appearance and most essential characteristics of things. In early 1990's ontology was introduced into the field of artificial intelligence. Being a model for conceptual semantic storage, analysis and management, it has drawn great attention from the fields of computer science and information technology. When it comes to twenty-first century, scholars from various disciplines use ontology tools to deal with various engineering problems, making ontology popular in multidisciplinary research, such as biology, pharmacy, education systems, psychology, medicine, neuroscience, and nanotechnology.
Recently, ontology methods have been utilized to various ontology projects. In biology and medicine, from the genetic and human protein chains of each gene to the probability and symptoms of disease, it is widely used in the development of various gene ontology tools. Based on the semantic similarity of disease, an ontology-based fixed genome sequencing and gene sequencing algorithm was proposed by Cannataro et al. [1]. Duong et al. [2] respectively gave two kinds of GO ontology conceptual similarity calculation methods under the condition of GO tree and independent of GO tree. Wei et al. [3] developed NaviGO for the visualizations and analysis of functional similarities and associations between GO terms and genes. Wan and Freitas [4] used gene ontology to test four hierarchical feature selection algorithms. Yang and Tang [5] proposed an approach to combine the faction-based prediction method and GO gene ontology annotation to overcome the interference of false positive and false negative interactions in PPI network to predict results and improve the prediction accuracy. In terms of different GO correction rules, two predicted interaction sets are generated to ensure the quality and quantity of the predicted protein interactions. Cheng et al. [6] studied the OAHG database, which deals with the ontology of gene ontology (GO), disease ontology (DO) and human phenotype ontology, and establishes comprehensive functions for human protein-coding genes (PCG), miRNAs and lncRNAs. Annotate resources. Now OAHG has 1,434,694 entries containing 16,929 PCGs, 637 miRNAs, 193 lncRNAs, and 24,894 ontology terms. Cozzetto et al. [7] proposed FFPred 3 to map gene ontology terms to human protein chains, providing help if homology to characteristic proteins. By predicting the input sequence for the support vector machine array, each support vector machine examines the protein function and describes the biophysical properties of the secondary structure, the relationship between the transmembrane helix, the inherently disordered region, the signal peptide and other motifs. Saha et al. [8] proposed to use gene ontology-based neighborhood analysis and physicochemical features to predict protein function. Al-Mubaid [9] proposed a method for calculating gene versatility scores in terms of functional annotation of target genes from gene ontology. The trick is on the basis of identification of GO annotation pairs that state semantically various biological functions. Any gene annotated with two annotations in a pair is seen multifunctional. GO annotations can be used for the identifications of multifunctional genes in the entire human genome.
In particular, the GO ontology receives a lot of attention. Ochs et al. [10] introduced a heuristic approach based on the identification of anomalous groups of items with certain classification definitions. If these potential problem areas are automatically identified in the ontology, time and electronics will be preserved in manual review of the gene ontology GO content. Vitali et al. [11] developed the Nutrition Research Ontology ONS by aligning the selected pre-existing facts with new health and nutrition terminology, thereby facilitating the description and specification of complex nutrition research. Pomaznoy et al. [12] produced the open source GOnet web application (http://tools.dice-database.org/GOnet/), which obtains a list of gene or protein entries from human or mouse data to generate analyzable data format, while achieving interactive visualization of GO analysis results. The interactive results permit the exploration of gene and GO ontology terms as a diagram which describes the natural hierarchy of terms and preserves the relationship between terms and genes/proteins. Hassan and Shanak [13] proposed a tool GOTrapper which can move up or down to the bottom of the GO hierarchy. The tool acquires shared ontology terms through a set of input genes required by Homo sapiens. Passi et al. [14] proposed a gene ontology-based network involving 26,404 edges, 6,630 drugs, and 4,083 target nodes, while using network-based reasoning (NBI) to analyze networks with molecular functional ontology. The degree of functional diversity (DoFD), a gene ontology-based quantitative index was put forward by Paul and Maji [15] proposed to make the functional diversity of a set of genes selected by any gene selection algorithm quantified. In addition, a new gene selection algorithm was proposed, which combines the advantages of DoFD and RSMRMS to select those related and important genes with diverse functions. Peng et al. [16] attempted to reconstruct a gene ontology (GO)-based neural network to reduce the dimensionality of scRNA-seq data. Connecting GO to unsupervised and supervised models, two new methods were raised, called GOAE (Gene Ontology AutoEncoder) and GONN (Gene Ontology Neural Network). Lamurias et al. [17] raised up a novel model for detecting and classifying the relation BO-LSTM in text, which uses a domain-specific ontology describing every entity as an order of its ancestors in ontology. BO-LSTM is carried on as a recurring neural network with long and short-term memory units, and uses open biomedical ontology, especially biological interest chemical entities (ChEBI), human phenotypes and gene ontology. When domain-specific ontology other than word embedding and WordNet is used, BO-LSTM improves the F1 score for drug-drug interaction detection and classification, especially in document sets with a limited number of annotations. The existing DDI extraction model was modified using the ontology-based method, and a higher F1 score than the original model was obtained. In addition, the authors developed and provided a corpus of 228 abstracts annotating the relationship between genes and phenotypes and showing the process of BO-LSTM applications to other types of relationships. Mortensen et al. [18] used the same population-based approach and a panel of experts to validate a subset of gene ontology GOs (200 relationships), pointing out that the Google search results for the gene ontology concept were significantly less than the SNOMED CT concept. This difference can lead to performance differences - the fewer search results indicates the harder the task of the staff will be. And the number of Internet search results can be used to measure suitable tasks for the population. Milano et al. [19] used Gene Ontology (GO) for the storage and organization of information about biomolecular function through a controlled vocabulary (GO terminology), whose term refers to biological concepts through an annotation process. The authors used a number of different annotation processes to make every term with a distinguished specificity which was formally assessed by information content (IC). Kuznetsova et al. [20] proposed an open source CirGO (cyclic gene ontology) software that visualizes non-redundant two-level hierarchical ontology terms from gene expression data in 2D space.
Lots of machine learning methods are also utilized for ontology similarity calculation and ontology engineering applications. Gao et al. [21] raised the ontology sparse vector learning algorithm for ontology similarity measurement and ontology mapping via ADAL trick. Gao et al. [22] confirmed the strong and weak stability of k-partite ranking based ontology learning algorithm. Considering eigenpair computation, Gao et al. [23] borrowed the ranking based ontology scheming. Based on singular value decomposition and applied it in multidisciplinary, Gao et al. [24] put forward the novel ontology algorithm. Gao et al. [25] put forward margin based ontology sparse vector learning algorithm and took it in biology application. Considering linear programming, Gao et al. [26] deduced the distance learning techniques for ontology similarity measurement and ontology mapping.
This paper mainly raises new multi-dividing ontology learning algorithm based on support vector machines. The organizational structure of the rest paper is as follows: initially, the specific SVM-based multi-dividing ontology algorithms and detailed techniques are presented; then, the feasibility of the SVM based algorithm is illustrated by experiment on similarity measuring between chemical topological index.
Multi-Dividing Ontology Algorithm Based on Support Vector Machines
Multi-dividing ontology learning algorithms have a wide range of applications in the background of acyclic ontology graphs, as most of the ontology graphs possess a tree structure. The primary thought of the algorithm is using the structural features of the ontology graph itself to determine the class of vertex division according to the number of branches, and then the domain experts determine the prior order relationships of various types. Through the learning of ontology samples, the optimal ontology function is finally obtained. The information of every ontology vertex is sewn with a vector of fixed dimension p. Let k be the number of classifications, f:ℝp → ℝ be the ontology function. For each ontology sample (v, y), y ∈ {1, ⋯ , k} is used to mark the rate of ontology vertex v. The ontology sample in multi-dividing setting can be expressed by S = (S1, S2, ⋯ , Sk), where for any a ∈ {1, 2, ⋯ , k}, we have . Let |Sa| = na, and Da = DV|Y = a be conditional distribution for a ∈ {1, 2, ⋯ , k}. In the learning process of the ontology samples, the multi-dividing algorithm follows the following rules: For 1 ≤ a < b ≤ k, under the action of the ontology function f, the value which corresponds to the vertex in the rate α is bigger than that corresponding to the vertex in the rate b, that is f(v) > f(v′), if v ∈ Sa and . The entire learning process is to find the optimal ontology function f that actually meets this rule as much as possible.
The paper aims to give a multi-dividing ontology learning algorithm based on Support Vector Machine (SVM).
Multi-Dividing Ontology Learning Model Under Sparse Vector Expression Setting
The AUC [area under ROC (operating characteristic curve)] ontology learning model under the multi-dividing framework can be stated as:
where f is an ontology function, I(·) is the truth function: equal to 1 if and 0 else wise. The optimal ontology function is obtained by maximizing AUC(f).
Let S = (S1, S2, ⋯ , Sk) be ontology sample. In the vector representation frame, the ontology function can be denoted by
where β ∈ ℝp is ontology vector, ε ∈ ℝ is a offset. The AUC maximization ontology optimization model under the multi-dividing framework is expressed as
The above ontology model can be improved from the following two aspects:
(1) Under the background of big data, the information contained in the ontology concept is huge, including not only the information of the concept itself, but also the structural characteristics of the concept and the entire ontology graph, as well as information representing instances and attributes. However, under a specific background in the actual engineering field, we only focus on a small amount of key information, and the information contained in most of the components of the ontology vertex corresponding vector will only play a role in other related application backgrounds. That is, the same ontology has different labeled ontology samples for different applications. Even with the same ontology vertex, different label information will appear in different application backgrounds. Furthermore, due to different ontology sample information, even the same supervised learning algorithm execution steps will get completely different ontology functions. This is one of the essential differences between ontology learning and general learning algorithms.
The reason why ontology learning algorithms have such characteristics is determined by the characteristics of the ontology itself: ontology is used as a tool in various fields. Compared with the single use of other data, ontology data has the characteristics of multi-purpose. For example, the genetic “GO” ontology and the botanical “PO” ontology can be regarded as dictionaries or query databases, which belong to public resources. Scholars in different fields use these ontology as a tool to assist them from different perspectives to achieve their own research goals. This is why there are thousands of research papers related to these two ontology every year.
Back to the framework of multi-dividing ontology learning algorithms. In this setting, in addition to the fixed p-dimensional vector corresponding to each ontology vertex (this vector has already contained all the information of the corresponding concept of the ontology vertex and the information of the ontology vertex in the ontology graph), there is only one special attachment. Mark to indicate the rate of the vertex of the ontology. Therefore, compared with other ontology learning algorithms, the label information is a real number and changes with the application background. In the multi-dividing ontology learning algorithm, the value of the additional label of the vector band corresponding to the ontology vertex is only in the range of the set {1, ⋯ , k}, which only represents the ontology vertex subordinate class. On the other hand, once the ontology graph structure is fixed, the value of k will be determined immediately, and the specific class of a vertex will be determined according to the structure of the ontology graph itself. From this perspective, the multi-dividing ontology learning algorithm is relatively less affected by specific engineering applications. It is closer to the classification algorithm of k classes than the regression algorithm, although the ontology function maps the vertex of the ontology to real number. Essentially, there is a huge difference between the multi-dividing ontology learning algorithm and the traditional regression algorithm, which lies between the classification and clustering algorithms with k classes. From the perspective of geometric structure, it requires that the entire real number axis is divided into disjoint k segments, and these k segments are sequentially assigned to the vertices of k branches on the ontology graph in a certain order of the k classes. Hence, the ontology vertices in the same branch of is finally mapped into the same interval segment in the real number axis by the ontology function.
While, due to the needs of the ontology learning algorithm itself, we still hope that the ontology vector β is sparse, that is, most of the components have a value of 0, or they can be small or negligible. In order to achieve this goal, our method is to add an additional term to represent sparsity of β, which is usually a 1-norm or a 2-norm term.
(2) Since the multi-dividing ontology learning algorithm involves k classes and the vertices of two of them are taken each time for a pairwise comparison, thus in the actual comparison process, it is difficult to satisfy every pair (a, b) with 1 ≤ a < b ≤ k, and all i ∈ {1, ⋯ , na} and j ∈ {1, ⋯ , nb} have . Therefore, in the learning model, we need to soften this hard condition to allow a certain degree of error. The commonly used method is to set the parameter as a range that allows errors.
Combining the above two points, we give a modified multi-dividing ontology learning model as follows:
s.t. , ∀1 ≤ a < b ≤ k, i ∈ {1, ⋯ , na}, j ∈ {1, ⋯ , nb}
where ρa, b > 0 is the softening parameter, and C > 0 is the equilibrium parameter.
The above multi-division ontology optimization model can be solved using the traditional Lagrangian multiplier method. The corresponding Lagrangian function of the original ontology optimization problem can be expressed as
The calculation shows that the Lagrangian partial derivative of the primal variable is
and for any (a, b) with 1 ≤ a < b ≤ k, and any i ∈ {1, ⋯ , na} and j ∈ {1, ⋯ , nb}, we have
It can be seen that the dual problem of the primal ontology optimization problem (1) can be stated as
From the perspective of operational research, this is a secondary optimization problem that can be solved using classic algorithms (such as interior points or active constraint methods). Similar to the classical support vector machine, the expression of β indicates that the ontology function depends only on the ontology data. In this particular case, the multi-dividing ontology function depends on the difference between the ontology vertices of each class. Thus, it can be stated as
where is the solution obtained by maximizing the ontology dual optimization problem (2).
The value of Lagrangian multiplier represents to some extent the difficulty of meeting the constraints of the constraint optimization problem. Therefore, as long as these variables are analyzed well, the above ontology optimization problem can be better understood. Through simple derivation, we can know that the above-mentioned multi-dividing ontology algorithm has the characteristics below.
Property 1. For every pair (a, b) satisfying 1 ≤ a < b ≤ k, f:ℝp → ℝ is the ontology function. By the ontology original problem and the dual problem under the multi-dividing framework described in (1) and (2), all ontology vertex pairs , where i ∈ {1, ⋯ , na}, j ∈ {1, ⋯ , nb}, the ontology optimization constraints on Lagrange multipliers can be expressed as follows:
Let's briefly explain Property 1. For any (a, b) satisfy 1 ≤ a < b ≤ k, according to the ontology optimization model (1), we know that:
• If , then , and thus . By bringing it into the constraints of the original ontology optimization problem (1), we know that hold;
• If , then , and thus . By bringing it into the constraints of the original ontology optimization problem (1), we know that hold;
• Finally, if , then . On the other hand, also hold, thus we get .
In the following, we will explain that the above-mentioned sparse vector multi-dividing ontology learning algorithm can be transformed into a multi-dividing ontology learning algorithm based on support vector machine, and then it is essentially an ontology learning algorithm based on support vector machine.
Multi-Dividing Ontology Learning Algorithm Based on Support Vector Machine
It can be said that support vector machine is one of the earliest machine learning algorithms. It originated from the generalized portrait algorithm in pattern recognition. The earliest work was completed by former Soviet scientists and published in 1963. In the 1970's and 1980's, with the introduction of the VC dimension (Vapnik-Chervonenkis dimension), the breakthrough of the solution method for the relaxation variable programming problem, and the deepening of the research on the maximum boundary theory, the support vector machine was theoreticalized and became a classic algorithm in statistical learning theory. Since the 1990's, various methods based on support vector machines have emerged, such as kernel-based support vector machines, non-linear support vector machines, and so on. The successful application of support vector machines to handwritten symbol recognition systems has allowed scholars to see the huge potential of support vector machines.
Below we explain that the multi-dividing ontology learning algorithm given in the previous subsection is essentially an ontology learning algorithm on the basis of support vector machines.
Support Vector Machine Based Multi-Dividing Ontology Learning Algorithm
Formally, the sparse vector multi-dividing ontology learning framework in the previous subsection is very similar to the traditional support vector machine based optimization algorithm. In fact, the ontology algorithms (1) and (2) can be regarded as a transformation of the classical support vector machine algorithm. Although there are huge differences in the feasible region, the final solutions are consistent in a certain sense.
According to the support vector machine model, the ontology optimization framework can be expressed as
For every pair (a, b) satisfies 1 ≤ a < b ≤ k. In classic support vector machine classification algorithms, linearly separable means
That is, for each class a (here a ∈ {1, ⋯ , k}), under the action of the ontology function f, the real numbers corresponding to the vertices of the ontology of this class are within the interval . When k = 2, and , then the boundary returned to the case of the binary problem. Let βSVM be the ontology vector obtained by the multi-dividing learning algorithm based on support vector machine, we verify
Thus,
holds for ∀1 ≤ a < b ≤ k, i ∈ {1, ⋯ , na}, j ∈ {1, ⋯ , nb}.
Now let's return to the multi-segmenting ontology learning algorithm under the condition of sparse vectors in the previous section. Let βSparse be the ontology sparse vector obtained in the previous section. For each pair (a, b) with 1 ≤ a < b ≤ k, we set
Set
We can easily check that
and
Therefore, for each 1 ≤ a < b ≤ k, we yield
It implies that we can get the appropriate ε such that βSVM = ρβSparse, where the parameter ρ is a complex parameter related to , and its value depends on the structural characteristics of the ontology itself and the ontology sample.
Finally, for non-linear situations, the kernel function method can be used to obtain the ontology learning model under the multi-dividing framework. Let K(·, ·) be a kernel function and the corresponding feature space is F, then the ontology function is expressed as
where is the optimal solution for the following ontology optimization problem
Experiments
In this section, our main aim is to measure the similarity of chemical topological indices in terms of SVM based multi-dividing ontology learning algorithm which is stated in section multi-dividing ontology algorithm based on support vector machines. First, we introduce chemical graph theory and topological indices. Then, we present the similarity computing results by means of multi-dividing ontology learning algorithm.
Introduce of Chemical Graph Theory and Topological Index
In the chemical experiments in 1960's and 1970's, scientists realized that there was an inevitable connection between the physico-chemical properties of a compound and its molecular structure. That is, what kind of molecular structure possesses what kind of chemical properties. This discovery was gradually confirmed in later experimental science, and a new field was born from this point of view, which uses chemical structure to infer the properties of compounds. According to this idea, scientists use graphs to represent molecular structures: vertices represent atoms, and edges between vertices represent chemical bonds between atoms. The graph is regarded a molecular graph, and the properties of chemicals are studied by defining the topological index on the graph. Early topological indexes include Wiener index, PI index, Szeged index, etc., which can well reflect simple physical properties such as the melting point and boiling point of compounds.
Experimental Design and Results
We analyzed in detail the existing topological indexes and polynomials and divided them into two classes: (1) degree-based topological index and polynomial (for example: Zagreb index, Sum connectivity index, Katayama index, ect.), and the other is a distance-based topological index (for example: Wiener index, PI index, Ediz eccentric connectivity index, ect.). We take 430 degree-based topological indexes and polynomials, 380 distance-based topological indexes and polynomials from more than 2,000 existing topological indexes and polynomials, and thus construct the first and second classes corresponding to two branches of ontology graph respectively. In order to form a tree structure, we specially construct 30 virtual vertices as a connecting bracket for connecting vertices. Thus, our new ontology graph has totally 840 vertices and two branches. Using SVM based multi-dividing ontology learning algorithm, take k = 2.
For a given ontology vertex (except the virtual vertices), we utilize a multi-dimensional vector to represent all the information for its corresponding topological index or polynomial. This vector not only contains the concept, structure, attributes, instance information. We also numerically extract the formula of the topological index or polynomial integrate into the vector.
We use P@N criterion to research the equality of the experiment result. The specific implementation process is as follows: first, for each ontology vertex v, the domain expert gives the N vertices which are most similar to v, and denote it as ; second, N vertices which are most similar to each vertex v are obtained in light of our multi-dividing ontology learning algorithm and marked as ; third, the accuracy of each vertex v is calculated by ; finally the average accuracy of the vertices in entire ontology graph is calculated by . In the learning process, we take 200 vertices respectively from the first and second class as ontology samples, i.e., S = (S1, S2), |S1| = |S2| = n1 = n2 = 200 and n = n1 + n2 = 400. Moreover, we claim the followings facts:
(1) The 30 virtual vertices are not considered into ontology sample data;
(2) We didn't compute Acc(v) for virtual vertices, and these vertices corresponding to fake ontology concepts (topological indices or polynomials) are not computed into Acc(G) as well, which implies |V(G)| = 810.
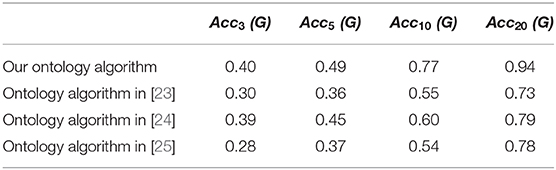
For the purpose of comparison of the result data, ontology learning tricks borrowed in Gao et al. [23–25] are carried out on our new ontology, and the precision ratios deduced from these ontology learning frameworks are manifested in Table 1.
By means of compared data depicted in Table 1, it's verified that our SVM based multi-dividing ontology algorithm is much more efficient than ontology learning tricks introduced in Gao et al. [23–25] especially as N becoming large. The purpose of the topological index collation is to eliminate those topological indices which have no practical value to chemical science introduced by only formula transformation or parameter replacement. However, the high similarity does not mean that some of the topological indexes are redundant and useless. Our calculation results will give chemists some data references, but cannot work as direct evidence that judging a chemical index is useless.
Conclusions
Our main ontology learning algorithm is designed in the multi-dividing setting based on support vector machines trick. We focus on the chemical topological data and the experiment result shows the effective of our introduced algorithm.
Constructing an ontology for more than 2,000 topological indices is a heavy task, and we need to give specific vectors for each index or polynomial. So far, this work has been completed in less than half. At the same time, we note that new topological indexes are constantly being artificially defined, that is, the total number of indexes is still increasing. We hope in the future, we can show an ontology with more than 2,000 indices, which can promote further the development of chemical experiments and theoretical chemical science.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This work was supported in part by the National Natural Science Foundation of China (51574232), the Open Research Fund by Jiangsu Key Laboratory of Recycling and Reuse Technology for Mechanical and Electronic Products (RRMEKF1612), the Industry-Academia Cooperation Innovation Fund Project of Jiangsu Province (BY2016030-06), and Six Talent Peaks Project in Jiangsu Province (2016-XYDXXJS-020).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Thanks to the reviewers for their constructive comments on the revision of this article.
References
1. Cannataro M, Guzzi PH, Milano M. GoD: an R-package based on ontologies for prioritization of genes with respect to diseases. Comput Sci. (2015) 9:7–13. doi: 10.1016/j.jocs.2015.04.017
2. Duong D, Ahmad WU, Eskin E, Chang KW, Li JJ. Word and sentence embedding tools to measure semantic similarity of gene ontology terms by their definitions. J Comput Biol. (2019) 26:38–52. doi: 10.1089/cmb.2018.0093
3. Wei Q, Khan IK, Ding ZY, Yerneni S, Kihara D. NaviGO: interactive tool for visualization and functional similarity and coherence analysis with gene ontology. BMC Bioinformatics. (2017) 18:177. doi: 10.1186/s12859-017-1600-5
4. Wan C, Freitas AA. An empirical evaluation of hierarchical feature selection methods for classification in bioinformatics datasets with gene ontology-based features. Artif Intell Rev. (2018) 50:201–40. doi: 10.1007/s10462-017-9541-y
5. Yang L, Tang XL. Protein-protein interactions prediction based on iterative clique extension with gene ontology filtering. Sci World J. (2014) 2014:523634. doi: 10.1155/2014/523634
6. Cheng L, Sun J, Xu WY, Dong LX, Hu Y, Zhou M. OAHG: an integrated resource for annotating human genes with multi-level ontologies. Sci Rep. (2016) 6:34820. doi: 10.1038/srep34820
7. Cozzetto D, Minneci F, Currant H, Jones DT. FFPred 3: feature-based function prediction for all gene ontology domains. Sci Rep. (2016) 6:31865. doi: 10.1038/srep31865
8. Saha S, Prasad A, Chatterjee P, Basu S, Nasipuri M. Protein function prediction from protein–protein interaction network using gene ontology based neighborhood analysis and physico-chemical features. J Bioinform Comput Biol. (2018) 16:1850025. doi: 10.1142/S0219720018500257
9. Al-Mubaid H. Gene multifunctionality scoring using gene ontology. J Bioinform Comput Biol. (2018) 16:1840018. doi: 10.1142/S0219720018400188
10. Ochs C, Perl Y, Halper M, Geller J, Lomax J. Quality assurance of the gene ontology using abstraction networks. J Bioinform Comput Biol. (2016) 14:1642001. doi: 10.1142/S0219720016420014
11. Vitali F, Lombardo R, Rivero D, Mattivi F, Franceschi P, Bordoni A, et al. ONS: an ontology for a standardized description of interventions and observational studies in nutrition. Genes Nutr. (2018) 13:12. doi: 10.1186/s12263-018-0601-y
12. Pomaznoy M, Ha B, Peters B. GOnet: a tool for interactive Gene Ontology analysis. BMC Bioinform. (2018) 19:470. doi: 10.1186/s12859-018-2533-3
13. Hassan H, Shanak S. GOTrapper: a tool to navigate through branches of gene ontology hierarchy. BMC Bioinform. (2019) 20:20. doi: 10.1186/s12859-018-2581-8
14. Passi A, Rajput NK, Wild DJ, Bhardwaj A. RepTB: a gene ontology based drug repurposing approach for tuberculosis. J Cheminform. (2018) 10:24. doi: 10.1186/s13321-018-0276-9
15. Paul S, Maji P. Gene ontology based quantitative index to select functionally diverse genes. Int J Mach Learn Cybernet. (2014) 5:245–62. doi: 10.1007/s13042-012-0133-5
16. Peng JJ, Wang XY, Shang XQ. Combining gene ontology with deep neural networks to enhance the clustering of single cell RNA-Seq data. BMC Bioinform. (2019) 20(Suppl.8):284. doi: 10.1186/s12859-019-2769-6
17. Lamurias A, Sousa D, Clarke LA, Couto FM. BO-LSTM: classifying relations via long short-term memory networks along biomedical ontologies. BMC Bioinform. (2019) 20:10. doi: 10.1186/s12859-018-2584-5
18. Mortensen JM, Telis N, Hughey JJ, Fan-Minogue H, Van Auken K, Dumontier M, et al. Is the crowd better as an assistant or a replacement in ontology engineering? an exploration through the lens of the gene ontology. J Biomed Inform. (2016) 60:199–209. doi: 10.1016/j.jbi.2016.02.005
19. Milano M, Agapito G, Guzzi PH, Cannataro M. An experimental study of information content measurement of gene ontology terms. Int J Mach Learn Cybernet. (2018) 9:427–39. doi: 10.1007/s13042-015-0482-y
20. Kuznetsova I, Lugmayr A, Siira SJ, Rackham O, Filipovska A. CirGO: an alternative circular way of visualising gene ontology terms. BMC Bioinform. (2019) 20:84. doi: 10.1186/s12859-019-2671-2
21. Gao W, Zhu LL, Wang KY. Ontology sparse vector learning algorithm for ontology similarity measuring and ontology mapping via ADAL technology. Internat J Bifur Chaos. (2015) 25:1540034. doi: 10.1142/S0218127415400349
22. Gao W, Gao Y, Zhang YG. Strong and weak stability of k-partite ranking algorithm. Information. (2012) 15:4585–90.
23. Gao W, Zhu LL, Wang KY. Ranking based ontology scheming using eigenpair computation. J Intell Fuzzy Syst. (2016) 31:2411–9. doi: 10.3233/JIFS-169082
24. Gao W, Guo Y, Wang KY. Ontology algorithm using singular value decomposition and applied in multidisciplinary. Cluster Comput. (2016) 19:2201–10. doi: 10.1007/s10586-016-0651-0
25. Gao W, Baig AQ, Ali H, Sajjad W, Farahani MR. Margin based ontology sparse vector learning algorithm and applied in biology science. Saud J Biol Sci. (2017) 24:132–8. doi: 10.1016/j.sjbs.2016.09.001
Keywords: ontology, restricted boltzmann machine, deep learning, back propagation, topological index
Citation: Zhu L, Hua G, Baskonus HM and Gao W (2020) SVM-Based Multi-Dividing Ontology Learning Algorithm and Similarity Measuring on Topological Indices. Front. Phys. 8:547963. doi: 10.3389/fphy.2020.547963
Received: 02 April 2020; Accepted: 25 August 2020;
Published: 23 October 2020.
Edited by:
Jinjin Li, Shanghai Jiao Tong University, ChinaReviewed by:
Waqas Nazeer, University of Education, Winneba, GhanaYongqun Oliver He, University of Michigan, United States
Copyright © 2020 Zhu, Hua, Baskonus and Gao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gang Hua, Z2h1YUBjdW10LmVkdS5jbg==
 Linli Zhu
Linli Zhu Gang Hua1*
Gang Hua1* Haci Mehmet Baskonus
Haci Mehmet Baskonus Wei Gao
Wei Gao