- Institute of Mathematics, Czestochowa University of Technology, Czestochowa, Poland
A rich variety of multicomponent systems operating under parallel loading may be mapped on and then examined by employing a family of the Fiber Bundle Models. As an example, we consider a system composed of N immobile units located in nodes of a network
Introduction
Numerous systems, encountered in nature as well as in different areas of science and technology, are multicomponent, i.e., they are composed of a great number of functionally identical units. When loaded, the units process a given task in a fully parallel manner. It happens, however, that a unit becomes overloaded and fails. Its load has to be undertaken by other units, which in turn may trigger subsequent overloading followed by resulting failures. Such a chain of failures gradually degrades the system performance and leads to an avalanche of failures. It may even happen that the avalanche becomes self-sustained giving rise to a catastrophe which overwhelms all the units. Different factors characterize a given system. This is important to identify those working together that push the system toward the catastrophic avalanche.
The Fiber Bundle Model (FBM) is a particular case of a wide class of cascading processes on networks [1]. It offers a flexible approach to study how multicomponent systems evolve under varying load [2–8]. The flexibility refers to such aspects as: a) range and symmetry of interactions among units [9], b) rate of load’s variation, c) heterogeneity/uniformity of units [10, 11]), or d) varying quality of units [12, 13], to name a few. The aspects a) and b) especially refer to ingredients of the FBM that play a major role when a given system is mapped onto a bundle of interacting fibers [14]. Exemplary problems, from an ample set of systems expressed in the FBM framework, cover research fields that span from geophysics including earthquakes, snow or landslides, to technology with electrical and mechanical engineering systems.
In this context, we consider a toy model of failures spreading in a set of interconnected units. Our model consists of N units that reside at nodes of an undirected simple graph
This group, identified by nodes of
Within this work we are interested in questions like: how small a group of units can be and/or to what extent we can apply the external load while still preventing the extinction of reliable units. Subsequently, we apply the FBM to study evolving failure on “small-world” networks that are omnipresent in life and technology. Specifically, we will focus on a family of random graphs generated by the Watts-Strogatz model [15]. The reason is that such graphs reveal short average path lengths and high clustering that are key features of social networks [16].
Model Description
Take a locally overloaded system which detects a failure of a unit. In the first instance the system attempts to solve the problem locally by distributing the load among nearest neighbors of the failed unit. If such a neighborhood does not exist, the entire set of reliable units is engaged into sharing the load from the unit being lost. Such a mode of load transfer yields a significant impact on the system’s strength. Whenever an island of reliable units emerges during the evolution, its terminal load is shared globally by the system. This means that the net load transferred to reliable units that are located on the outer island’s perimeter is lower than it would be if the local load sharing (LLS) rule has been in operation. In consequence, the switching Local-Global-Sharing (sLGS) mitigates the expansion of a dominantly large cluster (DLC) of failed units and thus, the strength of the system becomes higher than that one corresponding to the LLS rule [5].
In the following, we consider an ensemble of units assigned to nodes of a graph
Watts-Strogatz Model and Small-World Networks
There exists an ample set of papers that discuss the Watts-Strogatz model in details [17]. Hence, for the purpose of our model, it is sufficient to present the simplest exemplary graph and sketch how its modifications enable a smooth passage from an ordered network to disordered ones through a multitude of “small-world” graphs. One such passage is shown in Figure 1. The presented graphs are generated in two steps:
• a ring over N nodes is created and each node is connected with its k nearest neighbors, k is even.
• for every node with uniform independent probability p, each edge is rewired to a node that is selected uniformly at random while avoiding loops and edge duplication.
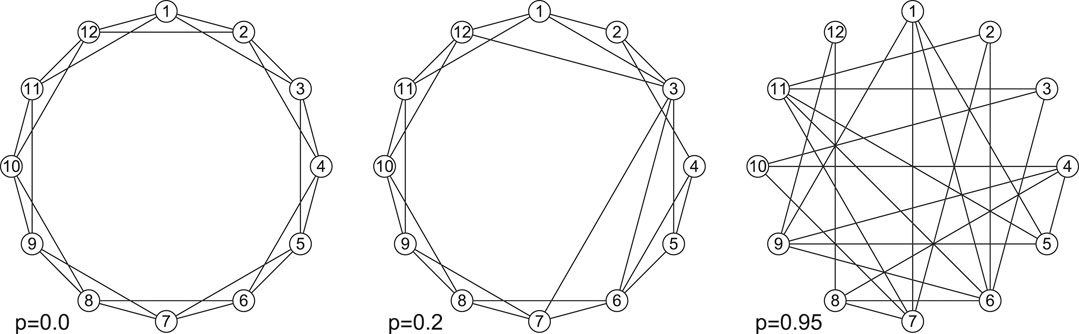
FIGURE 1. Exemplary “small-world” networks generated by the Watts-Strogatz model with mean node degree
These steps are illustrated in Figure 1, e.g., the first step corresponds to the graph with
Among the different characteristics of a network, one is particularly important in the view of our study, namely the global clustering coefficient C defined as:
where nodes of a triangle form a 3-clique, and a connected triple is a tree.
Applying External Load
We have assumed the external load F is distributed identically on all reliable units. Consider a load
We consider a configuration
In order to identify
From this, we derive the stopping rule:
where
Load Sharing Rule
The load transfer requires a rule that indicates how a load released by a failure is shared by other reliable units. We define our rule in a following way: the reliable network neighbors are obliged to equally share the load if they are accessible and all the reliable units acquire the load in the contrary case.
From this definition’s point of view, our rule “dynamically” switches between two rules, which are known in the FBM framework as global load sharing (GLS) and LLS. These rules correspond to two extremal ranges of load transfer. In the GLS rule, a load originating from a failed unit is transferred equally to all the reliable units and thus, the range of transfer is maximal. The LLS rule, in turn, engages only the nearest neighbors of a node that fails, so the range of load transfer is minimal. As a consequence, the load distributed according to the GLS rule is the least harmful for the system, whereas the LLS represents the most damaging method of the load distribution.
In simulations, we call this rule the sLGS and assume that the load transfer is an almost instantaneous process that happens simultaneously. We can mathematically express the sLGS in a framework for cascading processes on networks [18]. For this purpose, let
where
Equation 4 has a structure that resembles schemes of load transfer known from the literature. Namely the mixed-mode load sharing (MMLS) [19] and the heterogeneous load sharing (HLS) [20] merge together the LLS and the GLS in order to study a crossover behavior in FBM on regular lattices. The MMLS employs a constant quota q to split each transferred load into two streams: a portion q of the load goes to nearest neighbors under the LLS rule and the remaining portion is transferred according to the GLS rule. Thereby, the MMLS folds the LLS and the GLS in a manner that both rules are simultaneously activated in each failure. This is in contrast to the HLS, which in turn assigns units to two groups in order to discriminate between units located in “rigid nodes” and those residing in a “flexible” fraction of the support. If the “rigid” unit fails then the GLS transfers its load whereas the LLS governs the transfer from the “flexible” unit. The MMLS and the HLS are static, i.e., the corresponding values of q and sets of nodes at which q-weighted sharing rules operate are chosen and fixed prior to loadings. We also want to mention the modified LLS rule [21]. By employing the scheme
It is worth noting that rules, similar to the sLGS have been applied recently in such contexts as a strategy for stopping failure cascades [22] or clogging in multichannel supply systems [23].
A Range of Possible Applications
The above-described load sharing rule operating among units interconnected through a small world network may serve as a toy model of cascading failures in economy or technology. A general scenario we have in mind concerns a default initiated by an unsupported on-site demand that spreads through the system in a form of a contagion from the defaulter, either to units which are closely associated or to other ones. Clearly, when a unit switches into default this affects other units. Depending on the context, units could be: a) institutions, as, e.g., banks belonging to an interbank network, b) workers with beneficial loans from a company, borrowers in micro financial markets or c) elements of power grids, especially of small scale smart grids. With this same spirit a load could be seen as a demand, e.g., for liquidity or electric power. Below we list some basic facts that are relevant to our model.
Interbank Market
Undirected graphs are suitable to modeling interbank networks, especially in the context of a financial contagion [24, 25]. Among representations which are convenient and applied in studies, a possible one connects a pair of banks by an undirected edge whenever there exists an interbank liability or claim [25]. When an ensemble of interdependent banks is mapped onto a graph, one can analyze its static and dynamic properties. A class of small world graphs certainly is relevant in this context. It was shown, e.g., that the interbank market of
Microeconomy
Many companies offer beneficial loans to its employees. Specifically, to those suffering financial troubles. These employees-debtors, being colleagues and friends, are frequently mutual guarantors and can thus be considered as members of a resulting social network.
Power Grids
The small world topology is frequently reported as present in power grid networks [26–28]. This is equally true for large scale installations involving nationwide power systems in the US or Europe as well as for medium or small power grids [29, 30]. Particularly, in smart grids of renewable energy sources, such as small-scale photovoltaic systems or small-wind turbines [31, 32], the small world topology is beneficial. For example, networks with small world connectivity can significantly enhance their robustness against different attack by simultaneous increase of the rewiring probability and average degree [33].
Results and Discussion
In order to acquire data necessary to build reliable empirical distributions, we have adopted two computational schemes that correspond to small and large numbers of units. In the first scheme, for each N, an ensemble of
We use both computational schemes for uniformly distributed load thresholds. In simulations with the Weibull distribution we consider
Subsequently, when averaging a quantity Y over either
Maximal Supported Load and Minimal Number of Reliable Units
Following the described computational schemes, we have collected large data sets containing detailed information about how the maximal load, together with the minimal number of units, vary when we pass through all pairs
The gathered data turn out to be skewed independently of what distribution governs
where μ, σ and α are the location, scale and shape parameters, respectively.
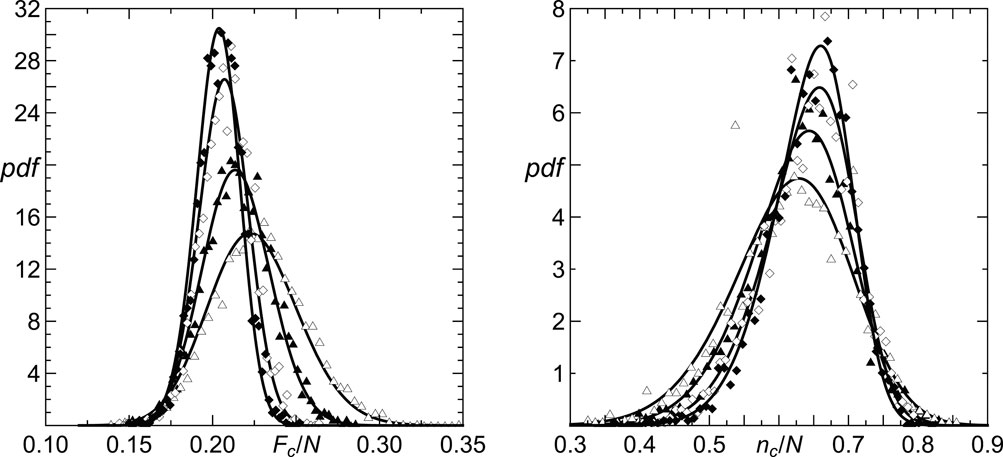
FIGURE 2. Calculated distributions of
We have rigorously examined the data sets employing a number of goodness of fit tests, including the Cramer-von Mises and Anderson-Darling tests [35] and have accepted
We have also estimated values of the parameters μ, σ and α. The gathered data yield estimate functional dependences of μ, σ and α on model parameters
We have directly written that
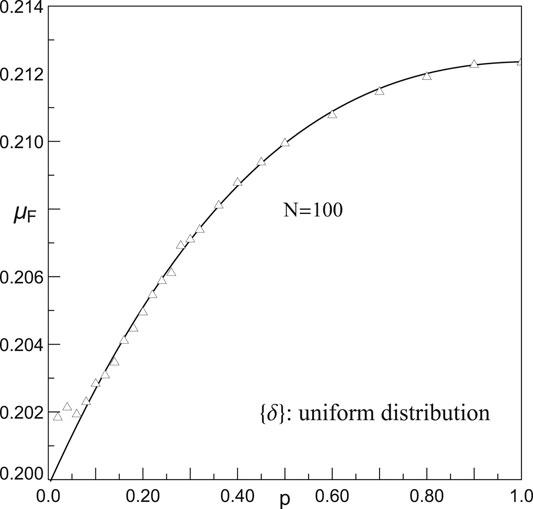
FIGURE 3. Estimated functional dependence of
Since the location parameter
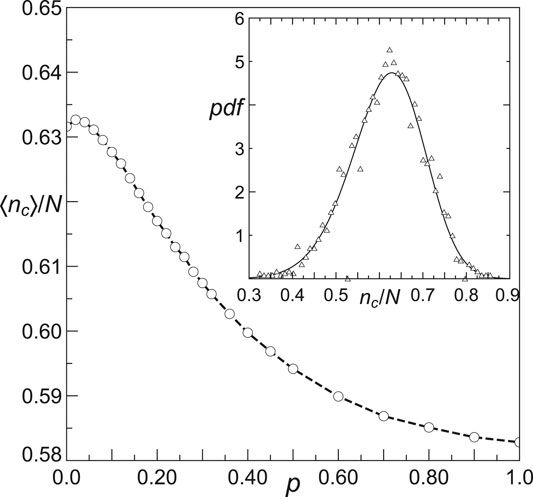
FIGURE 4. Scaled mean critical number of reliable units
It should be pointed out that when p is growing, the resulting networks become more and more disordered and the probability that a given node has a low degree increases. Hence, the sLSG activates all the reliable units more frequently than it happens in networks generated with a small value of p.
Large N Limit
Even though the applications mentioned in Section 2.4 refer to networks composed of about
It is known that the LLS model on a complex network behaves similarly to the GLS model giving rise to a non-vanishing critical strength
Based on results of simulations of large-N systems, we have found that: i)
while for the Weibull p.d. the best fit reads
where the subscripts u and w stand for the uniform and Weibull distributions, respectively. The estimated system’s strength
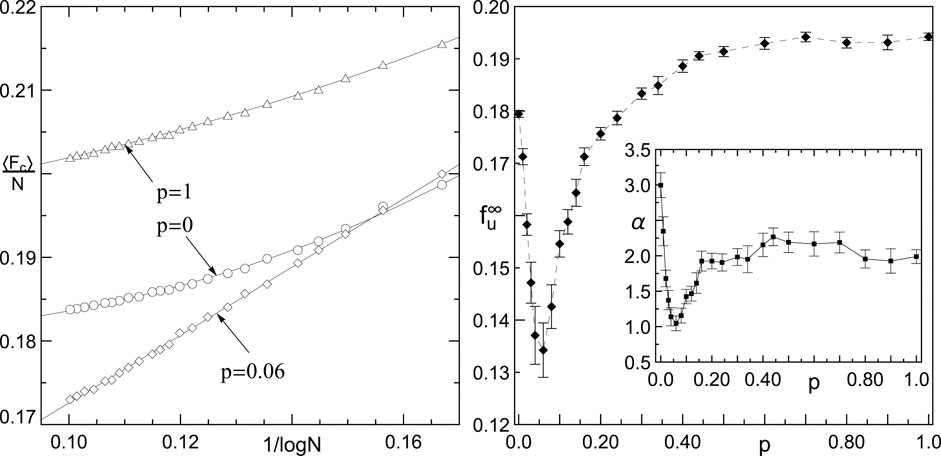
FIGURE 5. Left panel: The logarithmic size dependence of system strength for networks that: are ordered (
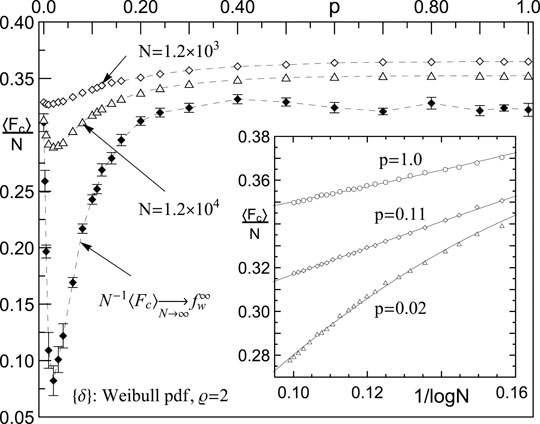
FIGURE 6. The system’s strength scaled by size in the large N limit. Inset: the logarithmic dependence of scaled system strength for:
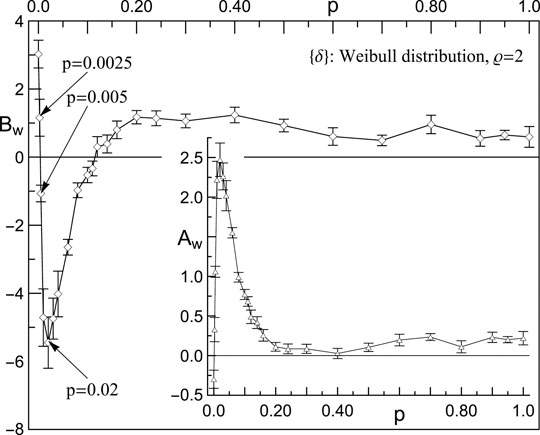
FIGURE 7. Amplitudes
These plots illustrate a variety of ways in which
A deep minimum of
Within our numerical approach, it is difficult to precisely estimate
Internal vs. External Load From a Reliable-Unit’s Point of View
When considering its future reliability, a prospective unit behaves as an outer observer whose forecast is limited to the external load F. When entering the system, the unit is confronted with an internal-load impact. It is thus worth discussing to what extent these two points of view differ.
We have assumed that during the evolution, the external load F is distributed identically on reliable units and is growing stepwise along the rule that was discussed in SubSection 2.3.
Having initially
if
This iterative chain involves successive patterns of local load
Now, consider
It is important to make a distinction between impacts of external and internal loads on units. To obtain a closer look at these different impacts, we compare
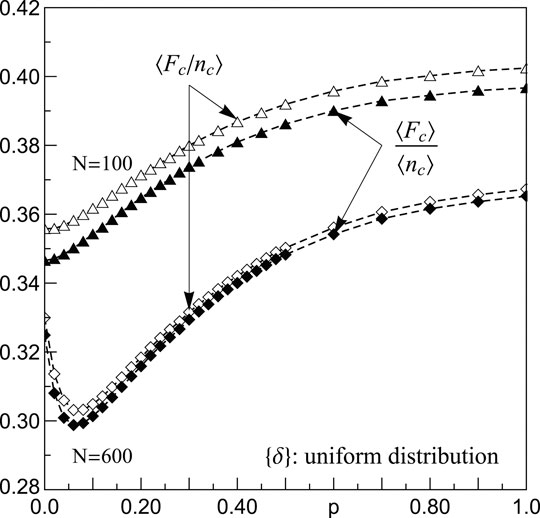
FIGURE 8. Mean critical load per reliable unit: white plot marks - internal load
Analyzing computed values, we detect that the mean internal load prevails over the mean external one for all values of p. In networks with
Small-World Properties at Critical Configuration
When the sLGS rule is in operation, a load is assigned according to accessibility of reliable units, i.e., either locally or globally. If the hosting network reveals a relatively strong local connectivity, then the sLGS looks like the LLS.
A lasting presence of reliable nearest-neighbours depends on a connectivity of an underlying network. Independently of the value of rewiring probability p, random graphs generated by the Watts-Strogatz model preserve the number of edges and mean-node degree. This means that when p grows, we pass from ordered to disordered networks, keeping the numbers of nodes and edges unchanged. For intermediate values of p, the resulting networks turn out to be locally clustered, whereas randomly rewired edges reduce the mean path lengths. Thus, there exists a range of p, where networks belonging to
We thus expect that the “small-world” properties would mark their presence in data sets related to
best fits the quantity
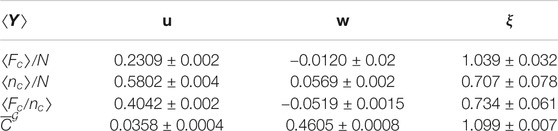
TABLE 1. Estimated coefficients in Eq. 9:
Figure 9 displays respective relations for systems with uniformly distributed
with
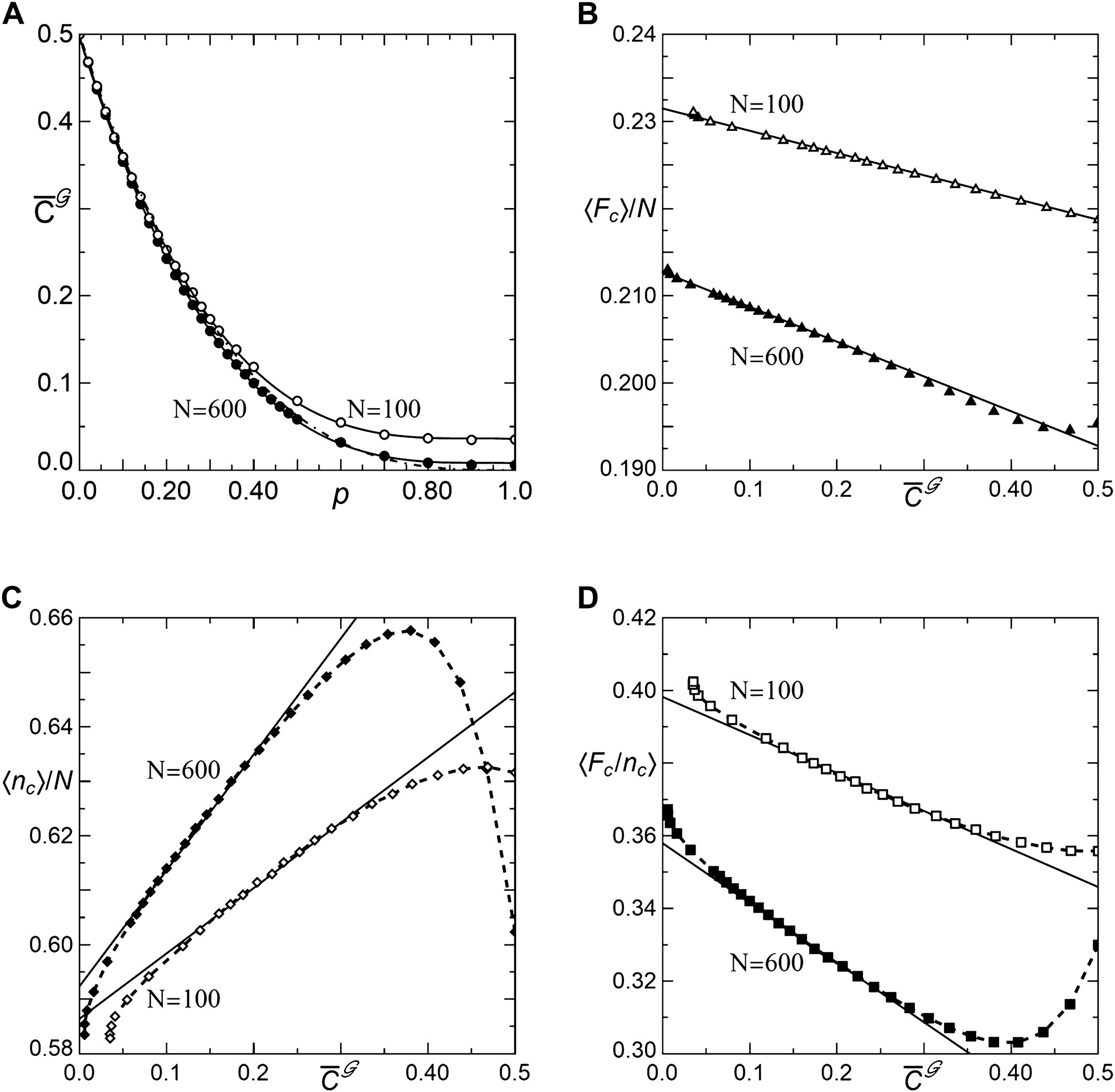
FIGURE 9. (A) Calculated mean empirical global clustering coefficient

TABLE 2. Estimated coefficients in Eq. 10:
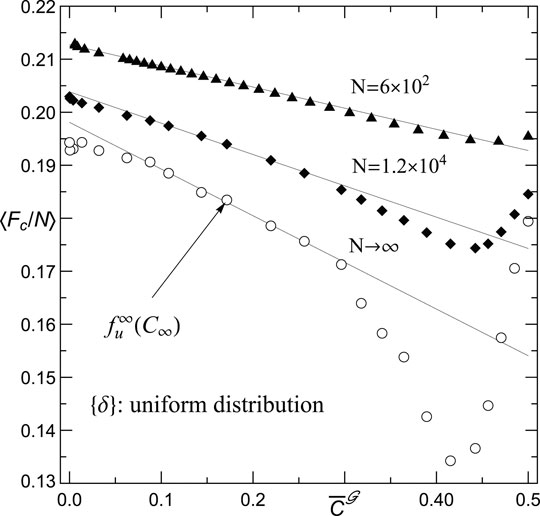
FIGURE 10. Mean strength of the system vs. mean global clustering coefficient for growing number of units. The linear scaling (11) between the ultimate strength
When sets
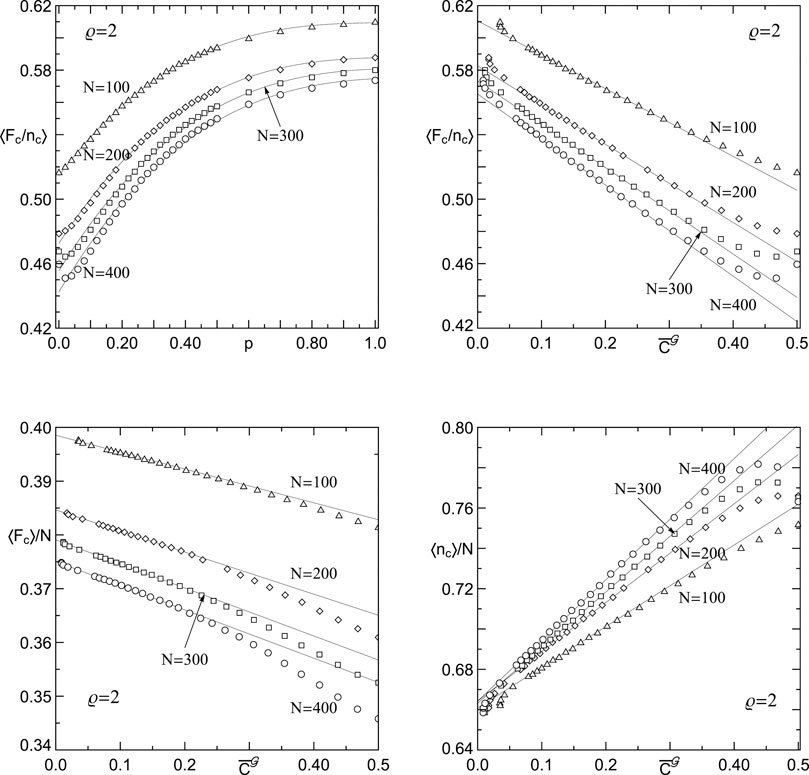
FIGURE 11. Upper panels: Mean system’s strength per reliable unit at critical configuration: (left) as function of p with solid lines drawn according to 9 and (right) on a linear scale for the respective mean
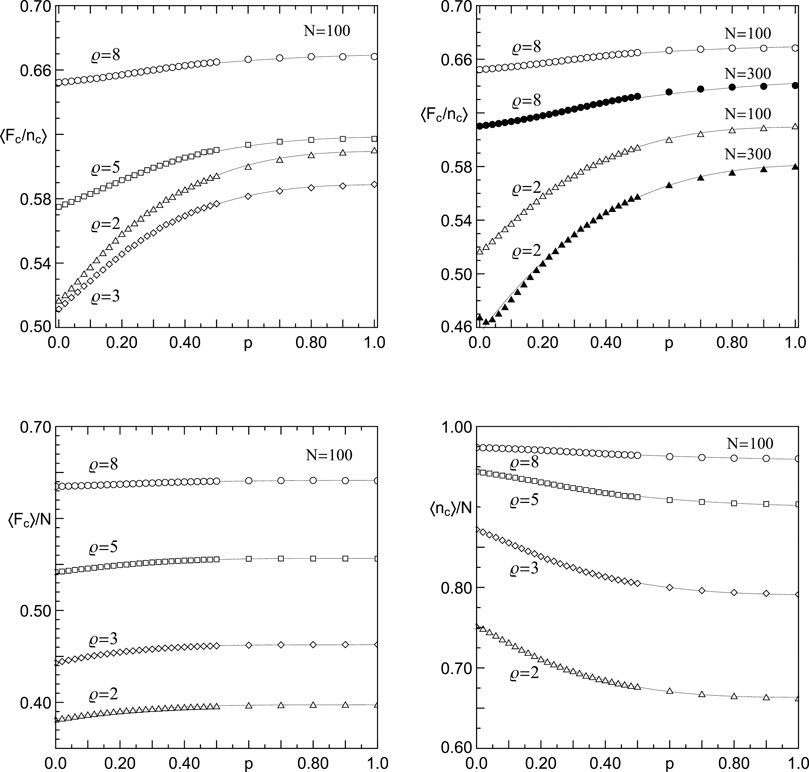
FIGURE 12. Scaled mean critical quantities:
It should be noticed that the expressibility of
Summary
We have investigated the evolution of failure among units that live at nodes of “small-world” networks and are exposed to a growing load. By introducing the sLGS rule of load transfer, which switches between the LLS and GLS rules depending on the accessibility of local interdependent nodes, we were able to mimic unit failures, and thus follow the evolution of the system toward the limit of its functionality. In particular, by employing the Watts-Strogatz random graphs to simulate the networks, we have collected data sufficient to form empirical distributions of the maximal load
The simulations show that if p is within the range of values given in Table 2 then
We are conscious of the fact that our simplified model of failure evolution involves some less realistic assumptions. Among the most serious is that we have considered each link between a pair of units as a reciprocally profitable relation. The other less strict assumption is that we allow the load thresholds be identically distributed. Our model can be tailored to fit a particular realistic scenario, e.g., by employing directed graphs, we would prevent some less reliable units from being interdependent.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the author, without undue reservation.
Author Contributions
ZD performed the research and wrote the manuscript.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Lorenz J, Battiston S, Schweitzer F. Systemic risk in a unifying framework for cascading processes on networks. Eur Phys J B (2009) 71:441. doi:10.1140/epjb/e2009-00347-4
2. Capelli A, Reiweger I, Lehmann P, Schweizer J. Fiber-bundle model with time-dependent healing mechanisms to simulate progressive failure of snow. Phys Rev E (2018) 98:023002. doi:10.1103/PhysRevE.98.023002
3. Domanski Z. Damage statistics in progressively compressed arrays of nano-pillars. Eng Lett (2019a) 27:18–23.
4. Hemmer PC, Pradhan S. Failure avalanches in fiber bundles for discrete load increase. Phys Rev E (2007) 75:046101. doi:10.1103/PhysRevE.75.046101
5. Kim D-H, Kim BJ, Jeong H. Universality class of the fiber bundle model on complex networks. Phys Rev Lett (2005) 94:025501. doi:10.1103/PhysRevLett.94.025501
6. Kun F, Raischel F, Hidalgo R, Herrmann H. Extensions of fibre bundle models. In: P Bhattacharyya BK Chakrabarti, editors Modelling critical and catastrophic phenomena in geoscience. Berlin, Heidelberg: Springer (2006) p 57–92.
7. Pradhan S, Hansen A, Chakrabarti BK. Failure processes in elastic fiber bundles. Rev Mod Phys (2010) 82:499–555. doi:10.1103/RevModPhys.82.499
8. Pugno NM, Bosia F, Abdalrahman T. Hierarchical fiber bundle model to investigate the complex architectures of biological materials. Phys Rev E (2012) 85:011903. doi:10.1103/PhysRevE.85.011903
9. Hidalgo RC, Zapperi S, Herrmann HJ. Discrete fracture model with anisotropic load sharing. J Stat Mech Theor Exp (2008b) 2008:P01004. doi:10.1088/1742-5468/2008/01/P01004
10. Hidalgo RC, Kovács K, Pagonabarraga I, Kun F. Universality class of fiber bundles with strong heterogeneities. EPL (2008a) 81:54005. doi:10.1209/0295-5075/81/54005
11. Sbiaai H, Hader A, Boufass S, Achik I, Bakir R, Boughaleb Y. The effect of the substitution on the failure process in heterogeneous materials: fiber bundle model study. Eur Phys J Plus (2019) 134:148. doi:10.1140/epjp/i2019-12475-7
12. Wang D, Jiang C, Park C. Reliability analysis of load-sharing systems with memory. Lifetime Data Anal (2017) 25:341–60. doi:10.1007s10985-018-9425-8
13. Zhao X, Liu B, Liu Y. Reliability modeling and analysis of load-sharing systems with continuously degrading components. IEEE Trans Reliab (2018) 67:1096–110. doi:10.1109/TR.2018.2846649
14. Hansen A, Hemmer P, Pradhan S. The fiber bundle model: modeling failure in materials. Weinheim, Germany: Viley-VCH (2015)
15. Watts D, Strogatz S. Collective dynamics of ‘small-world’ networks. Nature (1998) 393:440–2. doi:10.1038/30918
16. Jackson MO. An overview of social networks and economic applications. In: Benhabib J, Bisin A, Jackson M, editors. Handbook of social economics. Vol. 1A. North Holland, Netherlands: Elsevier (2012) p. 511–85.
17. Newman M. The structure and function of complex networks. SIAM Rev (2003) 45:167–256. doi:10.1137/S003614450342480
18. Burkholz R, Schweitzer F. Framework for cascade size calculations on random networks. Phys Rev E (2018) 97:042312. doi:10.1103/PhysRevE.97.042312
19. Pradhan S, Chakrabarti BK, Hansen A. Crossover behavior in a mixed-mode fiber bundle model. Phys Rev E (2005) 71:036149. doi:10.1103/PhysRevE.71.036149
20. Biswas S, Chakrabarti BK. Crossover behaviors in one and two dimensional heterogeneous load sharing fiber bundle models. Eur Phys J B (2013) 86:160. doi:10.1140/epjb/e2013-40017-4
21. Kim BJ. Phase transition in the modified fiber bundle model. Europhys Lett (2004) 66:819–25. doi:10.1209/epl/i2004-10038-4
22. La Rocca CE, Stanley HE, Braunstein LA. Strategy for stopping failure cascades in interdependent networks. Phys Stat Mech Appl (2018) 508:577–83. doi:10.1016/j.physa.2018.05.154
23. Domanski Z. Statistics of flow through a multichannel supply system with random channel capacitances. IAENG J Appl Math (2019b) 43:18–23.
25. Boss M, Elsinger H, Summer M, Thurner S. Network topology of the interbank market. Quant Finance (2004) 4, 677–84. doi:10.1080/14697680400020325
26. Cuadra L, Salcedo-Sanz S, Del Ser J, Jiménez-Fernández S, Geem Z. A critical review of robustness in power grids using complex networks concepts. Energies (2015) 8:9211–65. doi:10.3390/en8099211
27. Pagani GA, Aiello M. The power grid as a complex network: a survey. Phys Stat Mech Appl (2013) 392:2688–700. doi:10.1016/j.physa.2013.01.023
28. Rosas-Casals M, Valverde S, Solé RV. Topological vulnerability of the european power grid under errors and attacks. Int J Bifurc Chaos (2007) 17:2465–75. doi:10.1142/S0218127407018531
29. Pagani GA, Aiello M. Towards decentralization: a topological investigation of the medium and low voltage grids. IEEE Trans Smart Grid (2011) 2:538–47. doi:10.1109/TSG.2011.2147810
30. Saniee Monfared MA, Jalili M, Alipour Z. Topology and vulnerability of the iranian power grid. Phys Stat Mech Appl (2014) 406:24–33. doi:10.1016/j.physa.2014.03.031
31. Cuadra L, Pino M, Nieto-Borge J, Salcedo-Sanz S. Optimizing the structure of distribution smart grids with renewable generation against abnormal conditions: a complex networks approach with evolutionary algorithms. Energies (2017) 10:1097. doi:10.3390/en10081097
32. Sun Y, Tang X, Zhang G, Miao F, Wang P. Dynamic power flow cascading failure analysis of wind power integration with complex network theory. Energies (2017) 11:63. doi:10.3390/en11010063
33. Zhang Z-Z, Xu W-J, Zeng S-Y, Lin J-R. An effective method to improve the robustness of small-world networks under attack. Chin Phys B (2014) 23:088902. doi:10.1088/1674-1056/23/8/088902
34. Azzalini A. The skew-normal and related families. Cambridge, UK: Institute of Mathematical Statistics Monographs (Cambridge University Press) (2013)
35. Arnold T, Emerson J. Nonparametric goodness-of-fit tests for discrete null distributions. R J (2011) 3:34–9. doi:10.32614/RJ-2011-016
36. Wasserman L, Ramdas A, Balakrishnan S. Universal inference. Proc Natl Acad Sci USA (2020) 117:16880–90. doi:10.1073/pnas.1922664117
Keywords: failure evolution, fiber bundle model, switchable load sharing, simulations, small-world network, statistics
Citation: Domanski Z (2020) Spreading of Failures in Small-World Networks: A Connectivity-Dependent Load Sharing Fibre Bundle Model. Front. Phys. 8:552550. doi: .3389/fphy.2020.552550
Received: 16 April 2020; Accepted: 18 September 2020;
Published: 13 October 2020.
Edited by:
Ferenc Kun, University of Debrecen, HungaryReviewed by:
Soumyajyoti Biswas, SRM University, IndiaBikas K. Chakrabarti, Saha Institute of Nuclear Physics (SINP), India
Zoltan Neda, Babes-Bolyai University, Romania
Copyright © 2020 Domanski. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zbigniew Domanski, emJpZ25pZXcuZG9tYW5za2lAaW0ucGN6LnBs
 Zbigniew Domanski
Zbigniew Domanski