- 1Anhui Province Key Laboratory of Animal Nutritional Regulation and Health, Anhui Science and Technology University, Fengyang, China
- 2School of Mathematical Sciences, Anhui University, Hefei, China
- 3Mathematics and Applied Mathematics, Reading Academy Nanjing University of Information Science and Technology, Nanjing, China
- 4Department of Applied Mathematics, Northwestern Polytechnical University, Xi’an, China
- 5Institute of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu, China
The Wiener polarity index
1. Introduction
Graph theory is one of the most special and unique branches of mathematics. Recently, it has attained much attention among researchers because of its wide range of applications in computer science, electrical networks, interconnected networks, biological networks, chemistry, etc.
The chemical graph theory (CGT) is a fast-growing area among researchers. It helps in understanding the structural properties of a molecular graph. There are many chemical compounds that possess a variety of applications in the fields of commercial, industrial, and pharmaceutical chemistry and daily life and in the laboratory.
In a chemical graph, the vertices represent atoms and edges refer to the chemical bonds in the underlying chemical structure. A topological index is a numerical value that is computed mathematically from the molecular graph. It is associated with the chemical constitution indicating the correlation of the chemical structure with many physical and chemical properties and biological activities [1–3].
Let G be a simple and connected graph with
A unicyclic graph of order n is a connected graph with n vertices and m edges. It is well-known that every unicyclic graph has exactly one cycle. Let
Let
There is another important graph-based structure descriptor, called Wiener index, based on distances in a graph. The
The name Wiener polarity index is introduced by Harold Wiener [4] in 1947. In Ref. [4], Wiener used a linear formula of
where
If
In 1998, Lukovits and Linert [5] demonstrated quantitative structure-property relationships in a series of acyclic and cycle-containing hydrocarbons by using the Wiener polarity index. In 2002, Hosoya [6] found a physicochemical interpretation of
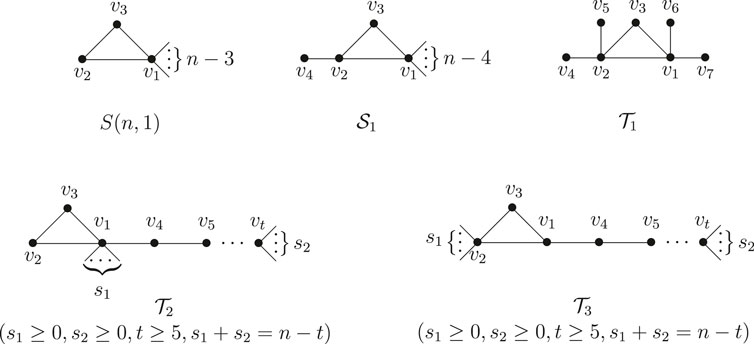
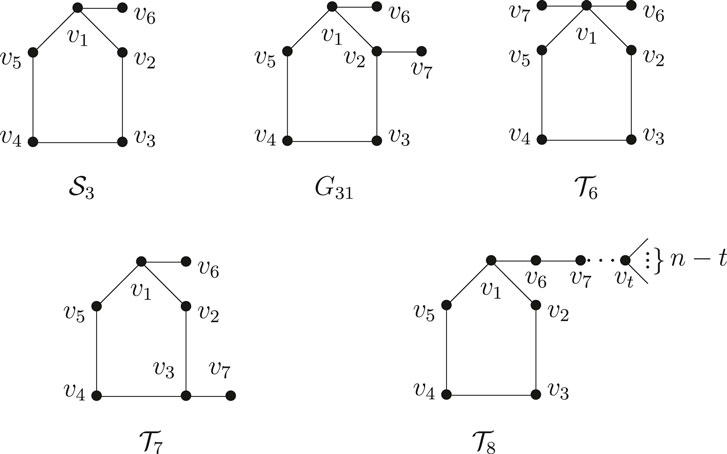
2. The Third Smallest Wiener Polarity Index of Unicyclic Graphs
The girth
A
Lemma 2.1. [10] Let
Lemma 2.2. Let
Proof. Since
Lemma 2.3 [10]. Suppose
Lemma 2.4. Let
Proof. Let
Case 1.
This implies that U is a unicyclic graph obtained by attaching
Obviously,
Case 2.
the equality holds if and only if
By combining the above arguments, the result follows.
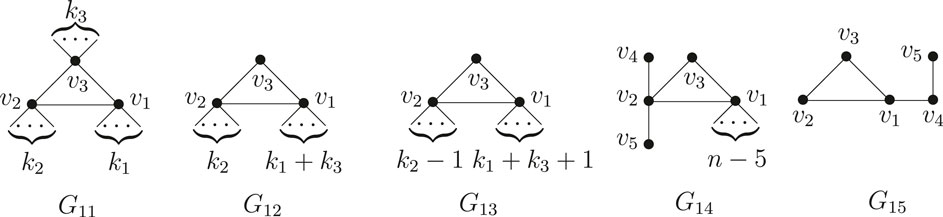
Lemma 2.5 Let
Proof. Let
Case 1.
This implies that U is a unicyclic graph obtained by attaching
Obviously,
Case 2.
the equality holds if and only if
the equality holds if and only if
By combining the above arguments, the result follows.
Lemma 2.6 Let
Proof. Let
Case 1.
This implies that U is a unicyclic graph obtained by attaching
If
If
If
If
Case 2.
By combining the above arguments, the result follows.
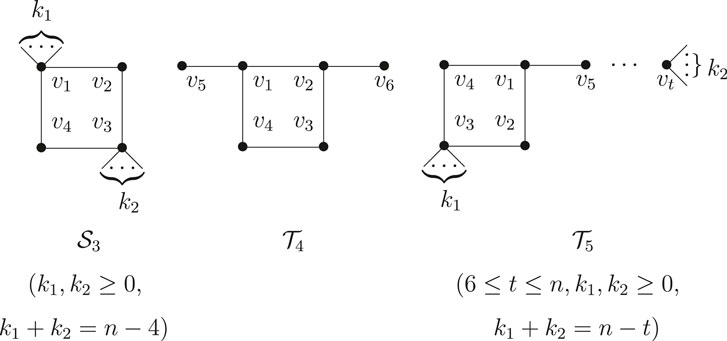
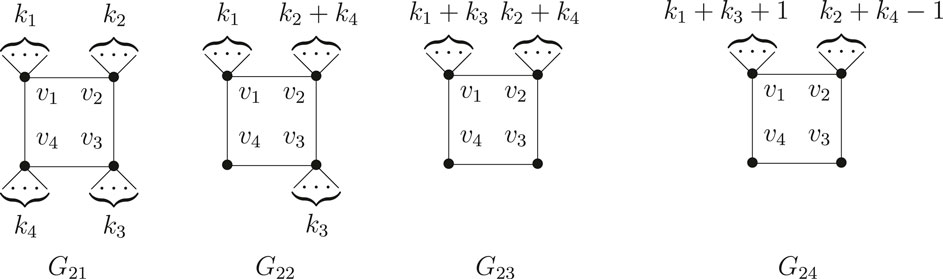
Lemma 2.7 Let
Proof. When
When
Lemma 2.8 Let
Proof. If
If
By combining the above arguments, the result follows.
Theorem 2.9. Let
Proof. By Lemma 2.4–2.8, the result follows.
3. Conclusions
Chemical graph theory is an important area of research in mathematical chemistry which deals with topology of molecular structure such as the mathematical study of isomerism and the development of topological descriptors or indices. In this paper, we first introduce some useful graph transformations and determine the third smallest Wiener polarity index of unicyclic graphs. In addition, all the corresponding extremal graphs are characterized.
Data Availability Statement
All datasets presented in this study are included in the article.
Author Contributions
WF performed conceptualization. FC and HD were responsible for methodology. WF and MM wrote the original manuscript. WF and FC reviewed and edited the article.
Funding
This work was supported by open project of Anhui University (No. KF2019A01), Natural Science Research Foundation of Department of Education of Anhui Province (No. KJ2019A0817, No. KJ2020A0061), and National Science Foundation of China under grant (No. 11601001).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Liu J-B, Wang C, Wang S, Wei B. Zagreb indices and multiplicative zagreb indices of eulerian graphs. Bull. Malays. Math. Sci. Soc (2019) 42:67–78. doi:10.1007/s40840-017-0463-2
2. Liu J-B, Pan X-F, Hu F-T, Hu F-F. Asymptotic Laplacian-energy-like invariant of lattices. Appl Math Comput (2015) 253:205–14. doi:10.1016/j.amc.2014.12.035
3. Liu J-B, Pan X-F. Minimizing Kirchhoff index among graphs with a given vertex bipartiteness. Appl Math Comput (2016) 291:84–8. doi:10.1016/j.amc.2016.06.017
4. Wiener H. Structural determination of paraffin boiling points. J Am Chem Soc (1947) 69:17–20. doi:10.1021/ja01193a005
5. Lukovits I, Linert W. Polarity-numbers of cycle-containing structures. J Chem Inf Comput Sci (1998) 38:715–9. doi:10.1021/ci970122j
6. Hosoya H. Mathematical and chemical analysis of Wieners polarity number. In: Rouvray DH, King RB, editors Topology in chemistry-discrete mathematics of molecules. Vol. 57. Chichester: Horwood (2002).
7. Du W, Li X, Shi Y. Algorithms and extremal problem on Wiener polarity index. MATCH Commun. Math. Comput. Chem (2009) 62:235–44.
8. Lei H, Li T, Shi Y, Wang H. Wiener polarity index and its generalization in trees. MATCH Commun. Math. Comput. Chem (2017) 78:199–212.
9. Hou H, Liu B, Huang Y. The maximum Wiener polarity index of unicyclic graphs. Appl Math Comput (2011) 218:10149–57. doi:10.1016/j.amc.2012.03.090
Keywords: wiener polarity index, minimum, unicyclic graph, extremal graph, electrical networks
Citation: Fang W, Ma M, Chen F and Dong H (2020) Third Smallest Wiener Polarity Index of Unicyclic Graphs. Front. Phys. 8:553261. doi: 10.3389/fphy.2020.553261
Received: 18 April 2020; Accepted: 09 September 2020;
Published: 27 October 2020.
Edited by:
Muhammad Javaid, University of Management and Technology, PakistanReviewed by:
YaJing Wang, North University of China, ChinaAkbar Ali, University of Hail, Saudi Arabia
Copyright © 2020 Fang, Ma, Chen and Dong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fuyuan Chen, Y2hlbl9mdXl1YW5Ac2luYS5jb20=
 Wei Fang
Wei Fang Muhan Ma3
Muhan Ma3