Diagnostic Methodologies of Laser-Initiated 11B(p,α)2α Fusion Reactions

Introduction

Nuclear fusion is a promising mechanism for future electric plants. Fusion reactors will help to resolve global energetic problem and, at the same time to decrease the worldwide pollution of air, water, and soil significantly.

Deuterium-tritium (DT) reaction is the best-known candidate for future reactors, due to the lowest energy needed to initiate the fusion process. The total cross-section of the reaction versus the center of mass is plotted in Figure 1A [1–3, 6]. This reaction requires the use of radioactive combustible (tritium), and generates neutrons, besides other products. Neutrons may be used to produce tritium by opportune reactions with lithium targets. Moreover, depending on the method the fusion reactors are built, neutrons may be used in hybrid fusion-fission reactors [7, 8]. On the other hand, neutrons induce activation on the materials they come in contact with, which is an essential issue in the setting and the maintenance of the fusion reactors. Moreover, the energy conversion efficiency of neutrons is low.

FIGURE 1

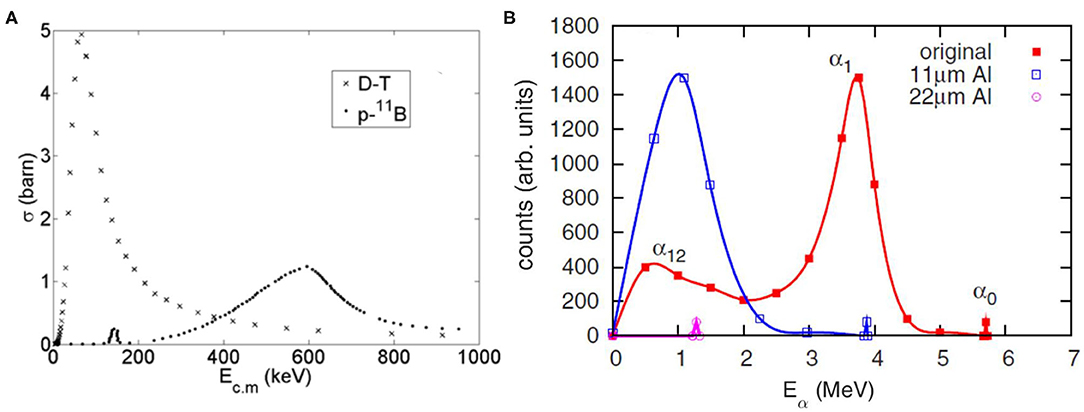
Figure 1. (A) Total fusion cross-section vs. center-of-mass energy for D–T and p–¹¹B fusion reactions [1–3]. Reprinted with permission from Ref. [1]. (B) Alpha energy spectrum in the reaction ¹¹B(p,α)2α at 660 keV incident proton beam energy achieved from Ref. [4], given by full squares joined by a red thick line. The shifts of the energy spectrum due to screening by 11- and 22-μm-thick aluminum foils are also shown. The small α₀ sharp peak at 5.7 MeV in the original spectrum is broadened and shifted to 1.27 MeV by the 22-μm-thick Al foil. Reprinted with permission from [5].

Promising nuclear fusion reactions which do not produce neutrons are the p+¹¹B → 3α + 8.7 MeV [1–6, 9, 10] and the D+³He → p + α + 18.34 MeV [6, 10, 11] which, in addition, do not require radioactive reagents. Indeed, in D+³He, some neutrons are produced by D-D reactions. The p+¹¹B reaction is considered for the third-generation fusion reactors, while D+³He for the second generation [12], although one major problem is the scarcity of available ³He in nature [10, 13]. The higher energy required to achieve fusions from these reactions, with respect to the D-T makes them more difficult to be realized under laboratory conditions. In Figure 1A, the comparison of the cross-sections between the D-T and the p+¹¹B reactions is shown as an example.

Indeed, it has been demonstrated in many experiments that these nuclear reactions can be obtained by specific laser-plasma interactions [1, 5, 10, 14–26]. In particular, effective experimental investigations for the D+³He reaction were performed in laser-generated exploding plasmas with the Texas PW laser at petawatt regimes [14–18]. Moreover, several experiments around the world have demonstrated the possibility to initiate p+¹¹B fusion reactions by means of tailored laser-plasma interaction schemes [1, 5, 19–26]. A significant yield for p+¹¹B fusion was achieved in this way, and this might lead to the future employment of laser-plasma interactions as powerful alpha-particle references [21–24]. In this case, there is abundance in nature of both the two reagents, and there are many prominent future applications of this reaction apart from inertial fusion energy plants, for example, to medical treatments [27–29]. The careful study of low-rate nuclear reactions in plasmas is also an important topic for astrophysical research [16, 17, 20, 30, 31]. For example, p+¹¹B is the primary pathway for depleting ¹¹B in stellar interiors, and the abundance of ¹¹B observed in stellar atmospheres can be used to determine the depth of stellar convection when studied in comparison with the abundances of Li and Be [30, 32]. Indeed, in general, the cross-sections of these reactions in plasmas are still unknown at low energies and usually derived by those at higher energy. The classical methods to determine cross-sections in beam-target schemes are actually not accurate for low energies because they suffer from the effect of electron screening [30]. The measurement of these quantities directly in plasmas is therefore still an open question that can be approached successfully by tailored laser-matter experiments.

So far, two main approaches have been proposed and verified to obtain p+¹¹B reactions from laser-matter experiments.

∘ Scheme 1. Generating a H and B plasma by means of energetic laser pulses on composite targets, such as doped-boron plastic or Si enriched with hydrogen and boron, for example [10, 19, 20, 22–24] (see Figure 2A). This was proved for both picosecond [10, 19] and energetic nanosecond pulses [20, 22–24]. In this plasma, the ion and hot-electron components are capable of giving some number of fusions. The use of specific targets may increase this number considerably [22– 24], and this is thought to be due to resonance phenomena [33–36].

∘ Scheme 2. Producing a laser-plasma accelerated proton beam to be sent to a B target or to a laser-generated boron plasma (Figure 2B). This was studied for both picosecond regime lasers [1, 21] and femtosecond high-repetition rate lasers [25, 26, 37].

FIGURE 2

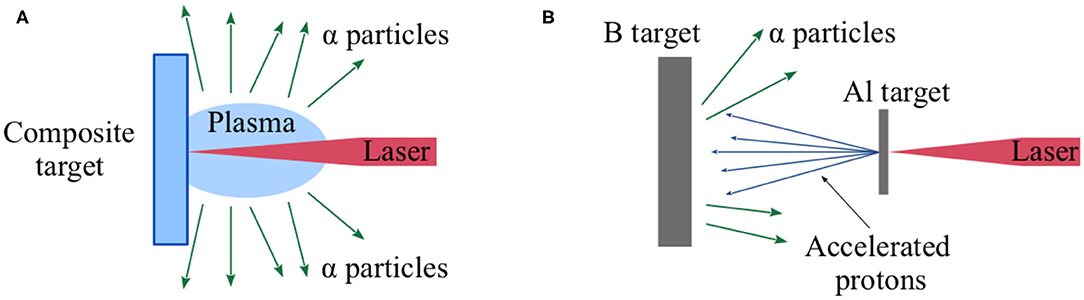
Figure 2. Schematic drawings of “scheme 1” (A) and “scheme 2” (B) for producing fusion reactions described in the text. The α particles indicated in the two pictures are only those that are suitable to detection, but of course in the two schemes there are also α particles that are directed toward the target (scheme 1) and that are not capable to exit it (scheme 2).

Details on the expected α spectrum in the different schemes are given in section Characterization of Fusion Rates in Proton-Boron Reactions.

Besides the full knowledge of the interaction conditions, the actual principal issue on experiments involving p+¹¹B low-rate fusion reactions is the accurate detection of the fusion products. As explained in the following sections, alpha particles are intrinsically challenging to be detected in high-power laser-plasma experiments, and this is a notable drawback in the schemes where the number of generated particles is intrinsically low. An example is a campaign performed at the ABC laser facility [38] with scheme 1 of Figure 2A, where laser pulses at 1054 nm, 2.5 ns duration, energy of several tens of joules, and intensity higher than 10¹⁵ W cm⁻², were directed on boron-doped plastic targets leading to the observation of fewer than 10⁵ alphas [20].

Another type of experiment with an intrinsically low number of fusion yield is described in references [25, 26, 37]. In this case, the 110-mJ femtosecond ECLIPSE laser was used at ~2 × 10¹⁸ W cm⁻² intensity, according to scheme 2 of Figure 2B, to accelerate protons to energy sufficient to initiate the p+¹¹B reaction toward a massive boron target. Here, the high repetition rate of interaction was the key to accumulating a reasonably high fusion yield in a short time. Other experiments where the produced alphas are intrinsically low are those for determining the reaction cross-sections in plasmas at low temperatures for studies of astrophysical interest, where the problem of the accurate alpha detection becomes thus more demanding.

As mentioned, recent experiments have demonstrated that a significant number of laser-generated p+¹¹B fusion reactions can occur [22–24]. This would, in principle, simplify the difficult task of the alpha detection. Nevertheless, experiments of intense laser-matter interaction produce a wide spectrum of ionizing electromagnetic (UV, X, γ) and particle radiation (electrons, ions), together with radiofrequency-microwave emissions. The simultaneous production of such a wide and multifaceted emission is one of the main reasons making the diagnostics of the produced plasma and of the emitted radiation a task that has to be always managed with great care. In many situations, the associated background present in any diagnostic method can be a significant obstacle, even in case of high-rate reactions. In some cases, this radiation can even induce failure and damage on the diagnostics. This is not only an issue for the detection of fusion products but, in general, also for the detailed characterization of the experimental conditions of the interaction. For this reason, details for the different diagnostic methods are given in the related section Diagnostic Methods.

Characteristics of ¹¹B(p,α)2α Reactions

As shown in Figure 1A, the ¹¹B(p,α)2α reaction has a cross-section with two main resonances, one at energy E_R1 = 148 keV and one at energy E_R2 = 620 keV in the center-of-mass frame, where the latest has higher cross-section [2, 3, 9]. The reaction induces three-particle decay [2, 3, 5, 9], and the predominant channels are described hereafter. It can occur through the ⁸Be ground state, which subsequently decays into 2α (Q = 91.8 keV):

$\begin{array}{ll}\text{p}{+}^{11}\text{B}\to {\text{α}}_0{+}^8\text{Be},& (1)\end{array}$

with the reaction Q = 8.59 MeV or through the ⁸Be excited state:

$\begin{array}{ll}\text{p}{+}^{11}\text{B}\to {\text{α}}_1{+}^8\text{B}{\text{e}}^{*},& (2)\end{array}$

with Q = 5.65 MeV and a large width of 1.5 MeV. The decay of the excited beryllium follows this

$\begin{array}{ll}{}^8\text{B}{\text{e}}^{*}\to 2{\text{α}}_{12},& (3)\end{array}$

with Q = 3.028 MeV. The energy distribution of the generated α particles can be observed in Figure 1B. In the laser-induced plasmas, the α₀ and α₁ are estimated to have energies of 5.7 and 3.76 MeV, respectively, in the exit channel [5]. However, as mentioned, the energy spectrum of α₁ has a large width; consequently, the α₁₂ spectra spread from 0 to higher than 5 MeV. These considerations are resumed in the α spectrum shown in Figure 1B, where the contributions coming from the different channels are briefly indicated with the respective symbols.

In both channels (1) and (2), there is the formation of a nucleus of ¹²C^* followed by sequential α decays via an unbound ⁸Be in its fundamental (1) or first-excited state (2). A further channel exists, with a very low cross-section, that produces a ¹²C^* compound nucleus that decays by γ emission, releasing ~15.9 MeV [1, 9].

Characterization of Fusion Rates in Proton-Boron Reactions

As mentioned, this is one of the key issues in experiments of this type, due to the low alpha yield. Here, we will show that it is challenging to discriminate them with respect to the background that may be at comparable levels. Several methodologies can be applied to this purpose, and they will be discussed in the next sections. An effective method to estimate the background ion emission due to the interaction, consists on the repetition of the same experiment with the same laser regimes and with similar targets, where the ¹¹B ions are not present and instead substituted with ¹⁰B or C ones, which have similar mass but do not generate the expected alpha spectrum [21–23].

It is important to point out that the actual spectrum of the expected alpha particles to be detected in each of the two schemes of Figure 2 may differ from the ideal one shown in Figure 1B because, before reaching the detector, the produced alphas interact with the solid target and the surrounding plasma.

These interactions may modify the spectrum of the detected alpha particles. First, we consider the simplified conditions of scheme 2, where protons entering normally to the surface of a solid B target will produce fusions, with a probability depending on their energy. Figures 3A,B shows the ranges of several elements in B and in Al materials. They are reported from tables supplied by the SRIM package and based on methods and data from references [39, 40]. Let us consider the two resonances at 148 and 620 keV of the p+¹¹B reaction in the center-of-mass frame [2] depicted in Figure 1A; this will mean protons with energies ~160 and ~675 keV in the laboratory frame.

FIGURE 3

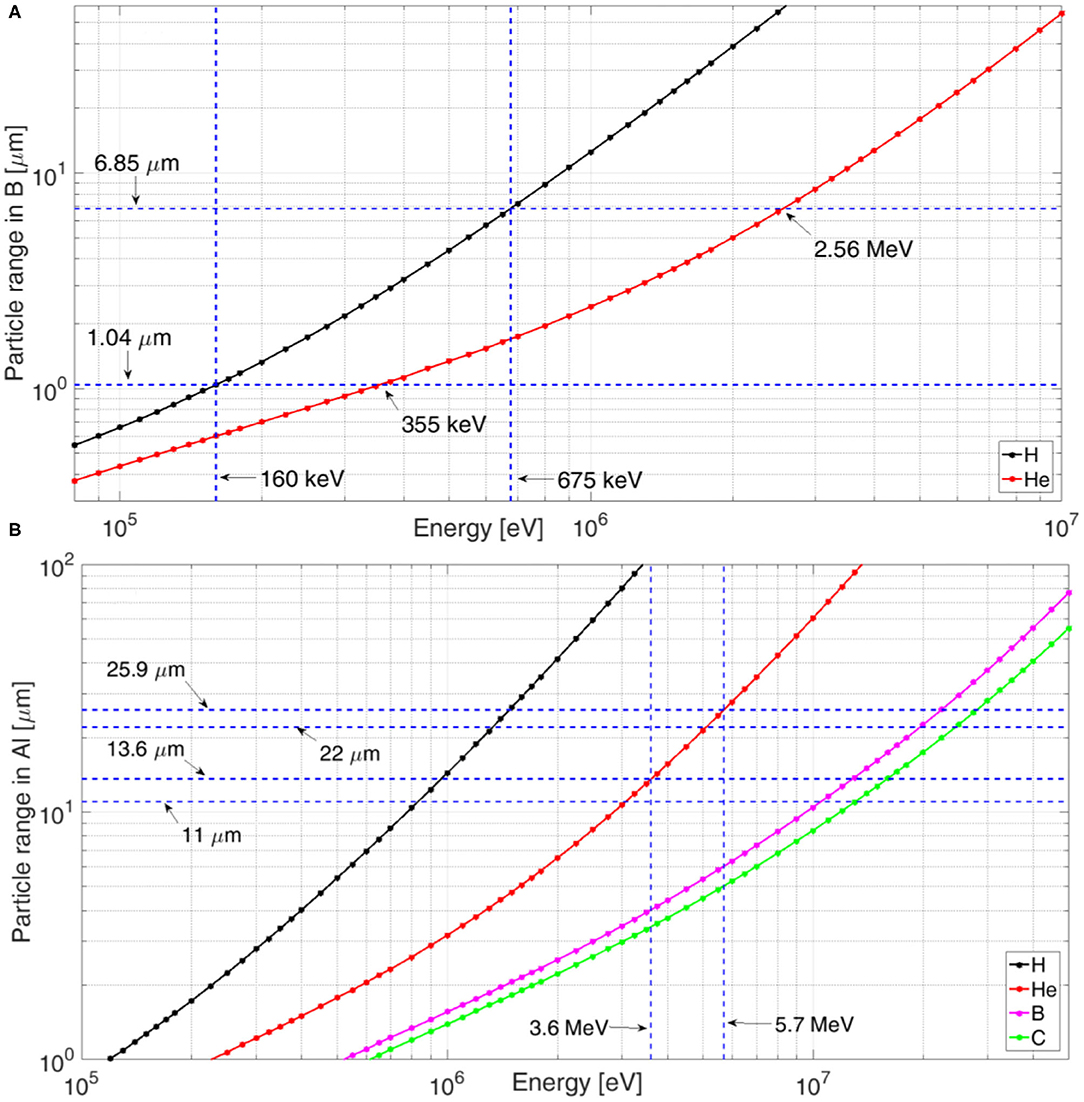
Figure 3. (A) Ranges of H and He in B and (B) ranges of several elements in Al. They are reported from tables supplied by the SRIM package and based on methods and data from Ref. [39, 40].

From Figure 3A, the ranges in B for incoming protons with the mentioned energies are ~1.04 and ~6.85 μm, respectively. In these cases, alphas are mostly produced in these respective locations. They have spectrum shown in Figure 1B, but they must exit the target to be detected. Therefore, their initial energies will be degraded and alphas having them lower than a given threshold value may even come to rest before of exiting the target. This threshold depends on the specific α actual exit path within B, and so on its direction with respect to the B surface. For instance, let us consider the simple case of alphas directed normally with respect to the B surface. They will have to cross the same path (in B) of the incoming protons, but to escape B, they need to have energies higher than protons, to compensate for their higher Coulomb charge. Figure 3A shows that in these two cases, only alphas with energies higher than 355 and 2.56 MeV, respectively, will exit the B target; instead, those with lower energies will be trapped in it. This will also decrease the energies of alphas escaping the B, and the initial alpha spectrum shown in Figure 1B will be modified. Certainly, alphas emitted toward a direction different from the normal to the B surface will have a longer path within B, and thus will undergo an increased energy loss. This will cause an enhanced effect both on the spectrum and on the overall number of exiting particles. Thus, the actual spectrum will be dependent on the angle of detection with respect to the target normal, because of the different angular-dependent thickness of the particle path in B [2, 3, 32, 41].

In Figure 4, the number of alpha particles detected in an experiment at CEDAD Laboratory (Lecce, Italy) is shown [41]. A proton beam of 675 keV and 2 nA current was accelerated from a Tandetron and impinged in the normal direction of the surface of a solid boron target for a total of 900 s, corresponding to a total number of protons N_p ~ 10¹³. This produced a localized source (diameter ~ 1 mm) of alpha particles [42], common data for CEDAD accelerator. A set of CR39 track detectors (see more details in section Use of Track Detectors) was deployed along the vacuum chamber at different angles with respect to the target normal, and the tracks were read after standard etching. Figure 4 reports an example of the angular dependence of the overall number of detected alphas achieved by the CR39 detectors, confirmed by results obtained on the same campaign by a Passivated Implanted Planar Silicon (PIPS) detector CANBERRA PD100-13-100AM.

FIGURE 4

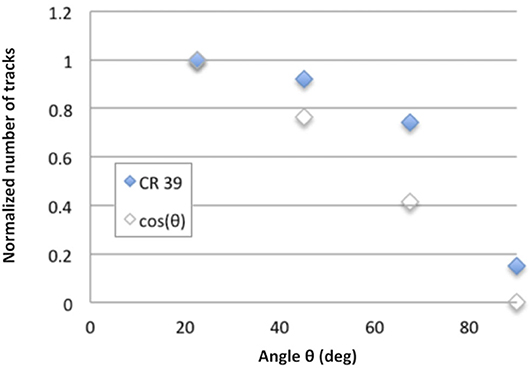
Figure 4. Normalized α particle yield vs. detection angle, obtained by CR39 exposition and compared with the cos(θ) law, being θ the angle with respect to the target normal. The numbers were normalized to the value at 20°. Reprinted with permission from Ref. [41].

The considerations here discussed in the case of scheme 2 for solid B targets can be applied only at some extent to the case when the fusion reactions occur in a plasma, both in schemes 1 and 2. Certainly, alphas will interact with the plasma before being detected, and this will produce modifications and energy reduction on the expected α spectrum to detect. Detailed discussions on this topic require tailored calculations and measurements according to the specific conditions of the plasma generated in each situation, that we believe are far from the purposes of this paper.

Diagnostic Methods

Use of Track Detectors

The fundamental method of detection for alpha products in this type of experiments is to use Solid-State Nuclear Track Detectors (SSNTD) [5, 10, 19–24, 26, 43–54]. They are solid materials where exposition to ionizing radiation generates local damaging to the detector. In the polymer types of SSNTD, damages are caused by the breaking of the long polymer chains due to incoming radiation. A typical example is the well-known CR39 plastic polymer, or allyl diglycol carbonate (ADC) [1, 19–21, 43–54], but the PM-355 plastic is also commonly used [22, 23, 43, 44, 51, 52]. Along these damaged regions, the material is more susceptible to chemical attack, and thus has a much faster velocity of etching compared with undamaged material. In this way, tracks can be created in the damaged regions. Track detectors are widely used in different fields. They are fundamental in environments heavily affected by transient electromagnetic pulses (EMPs) of high intensity, typical in high-power laser-matter interactions [55], where active electronic detectors will not be usable and even often damaged by the high EMP levels.

As mentioned, to detect the latent tracks after exposure to ionizing radiation, the plastic SSNTDs are typically immersed in a NaOH solution with specific concentration and temperature, for a certain amount of time. This causes bulk etching of plastic, and because of the enhanced etching properties of the regions exposed to radiation, tracks become visible and with sizes increasing with the duration of the bath. When the etching procedure is executed for several hours, tracks of micrometer dimension are achieved and can be characterized by confocal microscopes generating high-resolution images [43–50]. Software for analysis of these images is freely available, such as the well-known ImageJ program [56]. Information on particle energy can be inferred by track dimension and etching rate, compared with that of the detector bulk [10, 19, 26, 43–54]. In some cases, information on the particle type may also be achieved.

The problem is that, besides alphas, the detector is also reached by all the other radiations produced in the experiment. Electrons, X-rays, and γ-rays do not produce a remarkable effect on the detector but change its average solubility [43, 44, 48–50]. The issue is about the other ions generated in the reaction. In particular, in experiments with energetic nanosecond-regime pulses using scheme 1, it was proved that protons and ions up to the MeV range could be produced [22–24]. The ion energies are usually increased in the case of picosecond pulses in schemes 1 and 2 [1, 10, 19, 21, 57, 58] or femtosecond pulses in scheme 2 [57, 58]. Because of the low rate of these reactions, the number of alpha products reaching a given detector is usually much lower than the number of H, B, C, etc. ions reaching the same detector. Thus, it is necessary to find an effective way to discriminate between alphas and other particle species. Some methods are discussed in the following subsections.

Application of Foil Filters

It is possible to use plastic or metal foils, acting as filters, that are capable of stopping low-energy and heavy particles and leave high-energy alphas to pass through them [1, 23, 24]. This is quite an easy task for incoming B, C, or heavier ions and can show many limitations for protons. Figure 3B shows the range of different ions in aluminum [39]. According to Figure 1B, the ideal alpha spectrum extends up to E₁ = 5.7 MeVs, although the main peak is placed at around E₂ = 3.6 MeV. In the case of pure Al foils, results show that (see Figure 3B) the t₁ = 25.9 μm and t₂ = 13.6 μm thicknesses are capable of stopping alphas with energies up to E₁ and E₂, respectively, and at the same time they will just stop protons with energies E_1p = 1460 keV and E_2p = 950 keV, respectively. So, it is much more difficult to stop protons than alpha particles. This leads to some considerations.

• When using filters, it is necessary that the spectrum of protons that are produced in the reaction and, in particular, of those reaching the detector, is accurately known. This will enable to understand if unique alpha selection by the filtering method can be obtained.

• The use of filters decreases the energy of alphas reaching the detector and may cut most of the alpha spectrum. The spectra of alphas passing through 11 and 22 μm Al foils are shown in Figure 1B. Since, in the 22-μm case, very few alphas will pass through the foil, it is reasonable to use Al filters with thickness about 11 μm, at most, that will stop up to about 800 keV protons. This is roughly the operative limit for the use of this technique, which may still be used in some experiments using scheme 1 with nanosecond regime lasers. Experiments with higher-energy protons will give residual contaminants on the detector—and still in a large number, considering the expected low number of alphas—and will profoundly affect the signal-to-noise ratio of the measurement.

• With scheme 1 at ps or fs regime, and in general with scheme 2, this approach is rarely usable, because protons of several MeVs are commonly generated in these contexts [57, 58]. Alternative techniques are thus necessary.

Particle Identification Due to Track Dimension

As mentioned, it is possible to have some discrimination of particles impinging on a detector by studying the dimensions of the produced tracks and their evolution with respect to etching time bulk [10, 19, 22–24, 43–54]. Certainly, this requires a prior exposition of the same detector to reference particle beams, produced by classical accelerators [19, 22–24, 41, 44–51] or laser-plasma accelerators [53, 54], and the study of the produced tracks with respect to different conditions of the etching solution, temperature, and immersion time. A typical example of obtained results is shown in Figures 5A–C for the CR39 detector [53]. In this case, the etching was performed in a NaOH solution (6N, 70°C) for several hours.

FIGURE 5

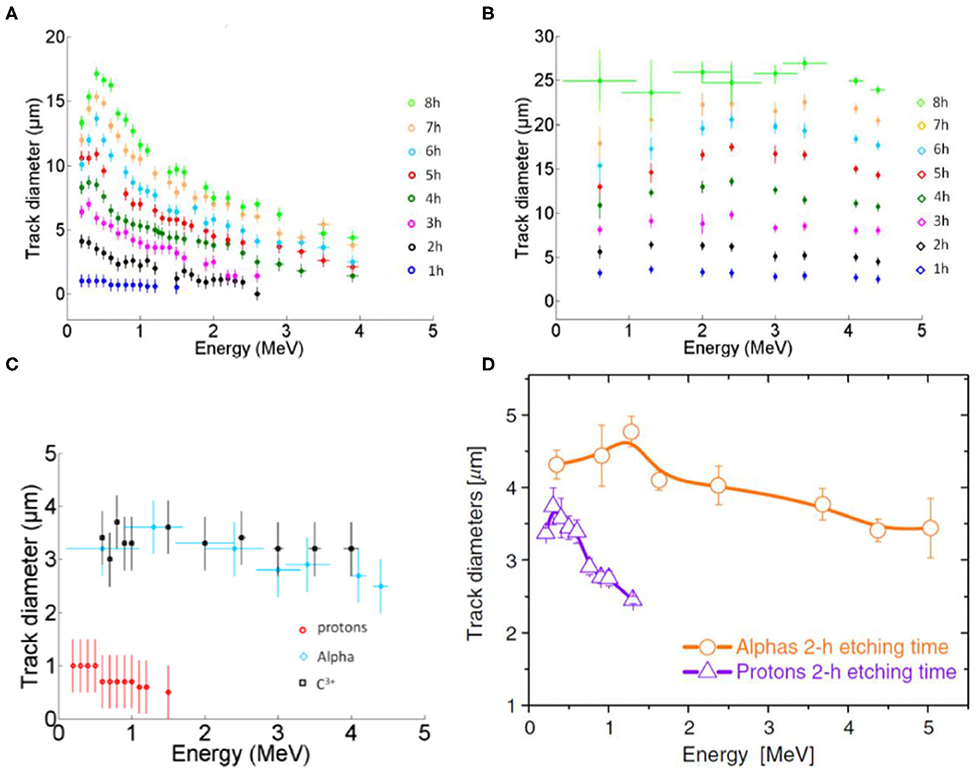
Figure 5. (A) Proton track diameters and (B) alpha particle track diameters on CR-39 track detector vs. particle energy for different etching times. For (B), the energy error bars presented for the case of 8 h etching time apply to all the other etching times. (C) Comparison of proton, alpha particle, and C³⁺ ion track diameters vs. energy for 1 h etching time. Reprinted with permission from Ref. [53]. (D) The PM-355 calibration curve for alpha particles and protons after 2 h etching time. Reprinted with permission from Ref. [22].

In Figure 5A, it is shown that, for a pure proton beam, track diameters are always monotonically decreasing versus the energy of the incoming protons for etching times up to 2 h. Anyway, the decreasing remains within the diameter tolerance of detection at the lowest etching times and thus not very useful for getting proton energy discrimination. Larger times should be thus needed but, in these cases, the diameters first increase for energies below 500 keV, and then again decrease monotonically. So the relation is no more univocal in the whole energy range but still usable for the higher energies. In Figure 5B, the track evolution of alphas with respect to the etching time is shown. Tracks of dimension larger than for protons are usually achieved for equal etching times. In Figure 5C, it is noted that there is indeed a small gap difference between the maximum of the proton curve and the minimum of the alpha one at 1 h etching time, if compared with the measurement tolerance. More favorable situations can be obtained for larger times, but always with small gaps between maximum for protons and minimum for alphas, and this makes the discrimination not always reliable when using only the track-diameter criteria. This is also shown in Figure 5D for the case of PM355 detector at 2 h etching time, where alphas with energy higher than 4 MeV have tracks with the same dimension of protons at around 0.5 MeV.

Therefore, more complex methods have to also be used in this case. But, in particular, the combined application of this technique to the use of filters might give some help in some situations. When a filter is used with an incoming wideband particle beam, the low-energy component will be cut, and the remaining one will undergo an energy attenuation. In Figure 1B, the original α spectrum from proton boron reaction is shown, together with those achieved after filtering due to 11- and 22-μm-thick aluminum foils. In particular, for the 11-μm case, the alpha spectrum has only ~2.5 MeV maximum energy. From Figure 5D, α tracks with diameters lower than ~4 μm will be absent. The careful selection of the filter material and thickness may thus lead to some improvement on the discrimination of α tracks from proton tracks.

Particle Identification by Track Shape

Track shapes on SSNTDs are affected by several parameters, some associated with the etching conditions and others to the geometry of the particle collision [26, 43–52, 54]. In general, tracks with circular shape are generated if particles enter the surface at normal incidence and, in the other cases, the shape of the etched track can be described as an ellipse with the major axis along the direction of particle propagation. It is possible to use ellipticity and orientation to discriminate tracks actually due to the nuclear reactions of interest from those associated with the detector background [26, 43, 44]. Environmental radioactivity, in fact, causes the presence of some tracks on the SSNDTs. This background constantly increases after the production of the detector. The process of discriminating tracks according to their orientation can be used to decrease the latent background tracks on the detectors, allowing the improved diagnosis of fusion products also for very low yield, where the number of events is comparable with the detector background, thus increasing the detector sensitivity effectively. The drawback of this technique is the necessity that fusion products have some preferential direction with respect to the detector place, which complicates the analysis.

This methodology can be used to separate the contribution given by the alphas emerging from p+¹¹B in the experiments with respect to the other ions generated and accelerated by the same laser-matter interaction. In Figure 6A, an example of a successful application of this technique is shown by using a specific setup which allowed useful direction of some alpha products [25, 26]. In that scheme, protons where accelerated by means of the TNSA mechanisms given by the interaction of the ECLIPSE laser (110 mJ, 2 × 10¹⁸ W cm⁻², 35 fs), on the Al foil target placed on the left, and then sent to a B target (schematically represented in Figure 6A with an ellipsoid) through two concentric holes, one on 1 mm-thick Al screen and one on the CR39. The proton beam then interacted with the B, and the alpha products, emitted roughly isotropically, were detected on the CR39.

FIGURE 6

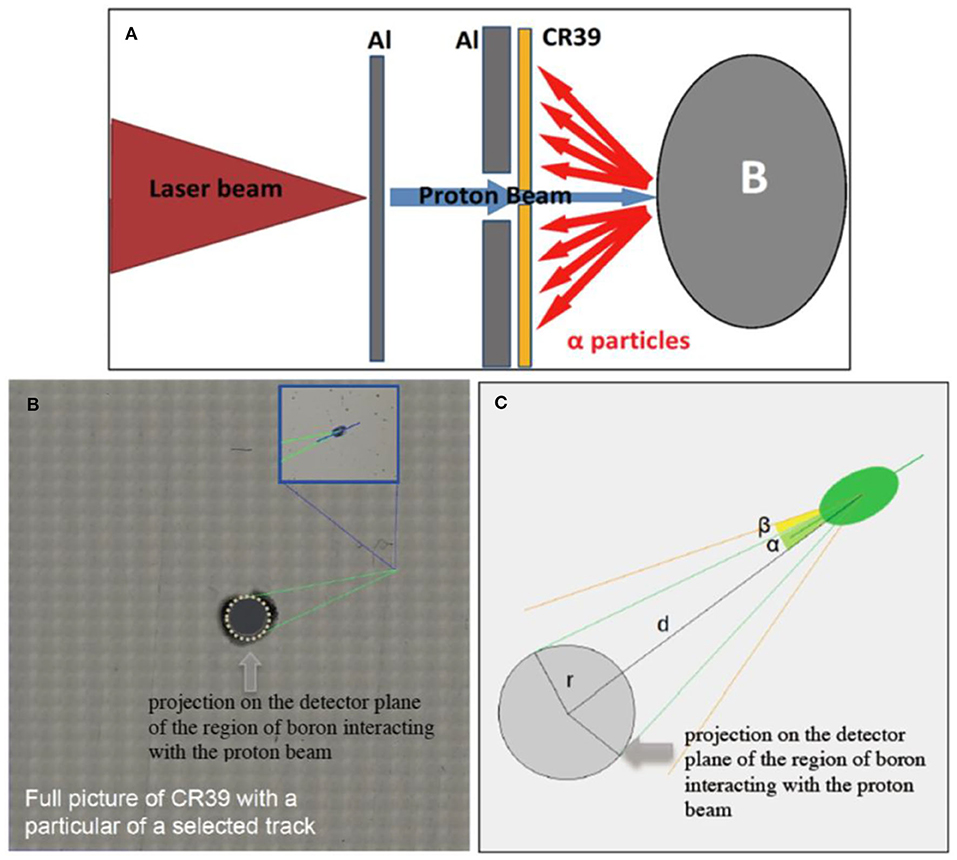
Figure 6. (A) Scheme where the technique of “directional selection” was successfully applied to particles reaching the detector. Here, the B target is schematically represented with the ellipsoid on the right; this was not its actual shape. The alpha particles indicated in the scheme are only those directed toward the CR39; the actual alphas produced in the experiment are of course omnidirectional. (B) Complete image of the etched CR39 obtained as an array of multiple scans by a confocal microscope. The central hole on the CR39 is evident. In the inset, a detail of this image is enlarged, and a detected track is shown. (C) Basic scheme for illustrating the parameters for the track selection method. The gray circle with radius r in this picture is the projection on the detector plane of the region of boron interacting with the proton beam. Reprinted with permission from Ref. [26].

Figure 6B shows the image produced by confocal imaging for the whole etched CR39 used in the scheme of Figure 6A; the central hole is evident. In the inset, a detail of this image is enlarged and a detected track is shown. To get a useful reference for the Directional Track Selection (DTS) method, as a first step the actual particle source was “projected” on the detector plane, as indicated in Figure 6C. The gray circle in that picture is the projection on the detector plane of the region of boron interacting with the proton beam, as shown in Figure 6A. Thus, the reference system was set at the center of this circle. Here, the expected particle direction is given by the segment of length d connecting the origin of the reference system to the center of the track image and is individuated by the associated θ angle to the horizontal axis. The overall acceptance angle γ = α+β = arcsin(r/d)+β includes the possible provenience of particles from a generic point on the source (α), the tolerances on the track ellipsoid drawn by the imaging program and the tolerances in assessing both the source dimension and the center position (β).

Among all the observed tracks present on the detector, the process of track discrimination was thus applied only to those with dimension compatible with alpha particles for that given etching time. This gave a first reduction of the number of samples to examine. As a second step, for each remaining track, the φ angle between the major ellipse axis and the x-axis was obtained. Thus, only the tracks fulfilling the condition |φ−θ| ≤ γ were validated, and the others were discarded. In ref. [26], this technique was capable of reducing the background noise level of about one order of magnitude in experiments performed with the low-energy ECLIPSE laser, where the number of expected fusion reactions was predicted to be very low.

Use of Thomson Spectrometers

Thomson spectrometers [59] are well-known effective devices used for discriminating particles with a different charge-mass ratio in high-power laser experiments. Figure 7A shows their principle operation. An electrostatic and a magnetostatic field, both orthogonal to the main horizontal direction of propagation of the incoming charged particles, determine a vertical (the electric field) and a horizontal (the magnetic field) deflection of the particles, leading to parabolic traces, each univocally associated with different charge-over-mass ratios. From the trace profile and the use of calibrated detectors, as imaging plates [60–63] or scintillators [64], for example, it is possible to retrieve the absolute particle spectrum [60, 65, 66].

FIGURE 7

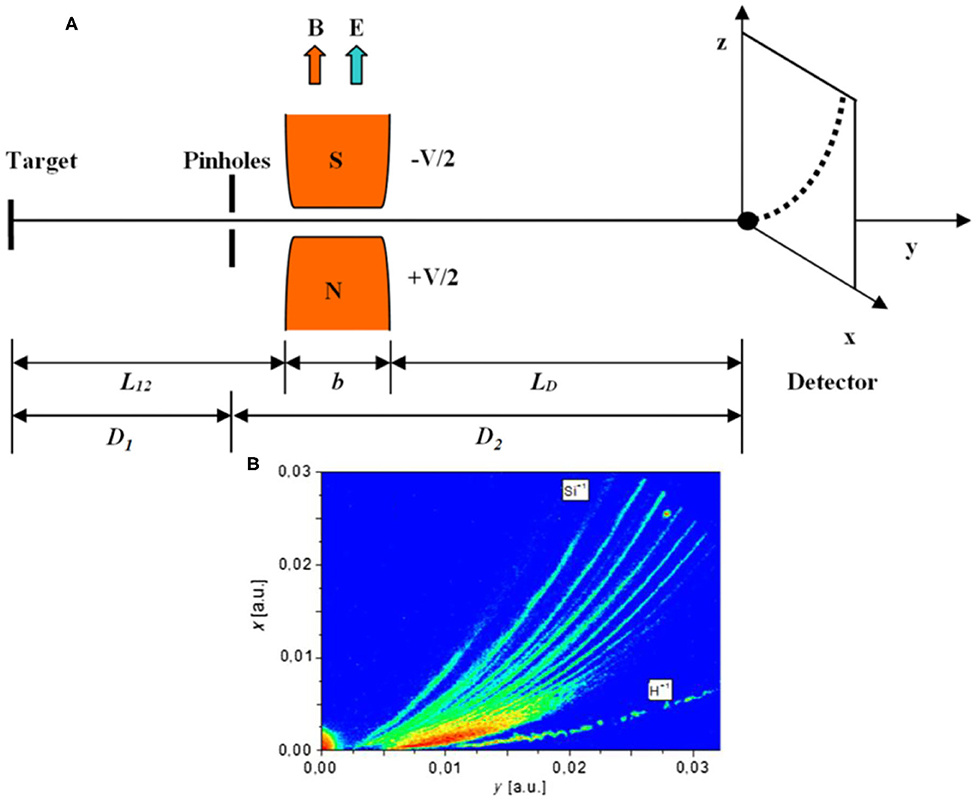
Figure 7. (A) Scheme of the Thomson spectrometer configuration, with an indication of the magnetostatic and electrostatic deflector, drift, detector and parabolic trace. Reprinted with permission from Ref. [60]. (B) Typical spectrometer traces in case of interaction on scheme 1 with PALS laser on Si-H-B target. Protons and Si ions are visible. Reprinted with permission from Ref. [22].

This can only be performed with the necessary accuracy if the incoming beam is selected by a pinhole, to limit its transversal profile. It is an important issue, because extensively-large pinholes enhance the spectrometer sensitivity but, on the other hand, determine larger trace sizes on the detector plane, and more intense electric and magnetic fields would be required to separate them at the higher energies of the ion spectra.

Examples of trace superimposed in p+¹¹B laser-plasma experiments are reported in refs. [22–24] and shown in Figure 7B. Typical pinholes used in these experiments have diameters from a few tenths of mm to 1–2 mm, at most. Sensitivity is, certainly, of primary importance for the detection of fusion products in these low-rate reactions. Indeed, the detection capability of the device depends on the actual solid angle covered, and then also on the target-pinhole distance. According to the scheme of Figure 7A, under the simplified hypothesis of point emission of particles from the laser-matter interaction, the traces will have size [67]

$\begin{array}{ll}{S}_t~2(D_1+D_2)\sqrt{\Omega /\pi }& (4)\end{array}$

where $\Omega =\frac{\pi }{4}{\left(\frac{{\phi }_p}{D_1}\right)}^2$ the solid angle of detection, φ_p the pinhole diameter, and D₁ and D₂ the target-pinhole and the pinhole-detector distances, respectively. So, for a given maximum acceptable S_t, caused by the spectrometer maximum electric and magnetic field, the maximization of the solid angle of detection will require the use of large φ_p and small D₁. On the other hand, the enhancement of the solid angle implies larger background noise that can be potentially coupled with the spectrometer. This can come from different contributions.

• Ionizing electromagnetic radiation. This contribution scales with the square of the distance from the laser-target interaction point. UV and X-rays are commonly stopped by the pinhole frame, and also low-energy γ-rays up to a few tens of keV, depending on the pinhole material and thickness. γ-Rays of higher energy will be capable of overcoming the shielding and interacting with the detector, actually increasing the background. Anyway, radiation of such high energy is normally emitted by laser-matter interactions with energetic fs or ps laser pulses, so it is mostly a problem for scheme 2, and only in some cases also for scheme 1. The pinhole is usually the most delicate part in this case, because pinholes of small diameter often require thin substrates. For this reason, a couple of concentric pinholes are often used: the internal pinhole with lower diameter and the external one instead with larger diameter and thickness. The discussed requirement of higher solid angle will thus give larger pinhole images and associated background. This may not be a serious issue, provided that suitable thick and high-Z shielding is used to protect the detector plate of the spectrometer, according to the specific regime of laser-matter interaction. It is a common practice to place also suitable thick and high-Z bricks between the laser-interaction point and the spectrometer. In this way, low-noise detection of particles was demonstrated for an optimized Thomson spectrometer placed at ~50 cm distance from the laser interaction point, in recent experiments at GSI laser (100 J, ~10¹⁹ W cm⁻², 750 fs pulses) [67].

• Electrons. Considerations similar to what was discussed in the previous paragraph apply also to electrons. For those of lower energy (up to several tens of keV), a permanent magnet can be placed in front of the spectrometer pinhole. This will cause low-energy electrons to be deflected in the region between the two concentric pinholes, and then to not enter the spectrometer [60]. This will decrease the background noise caused by their bremsstrahlung when stopped by the internal spectrometer surfaces.

• EMPs. In high-energy and high-intensity laser-matter interaction, it is well-known that radiofrequency-microwave EMPs are produced, that their intensity can be very high, and that it increases strongly by approaching the target [55]. This is the main reason why Thomson spectrometers used in these experiments often present traces that appear to be sinusoidally modulated parabolas, as it is possible to observe in ref. [24]. This usually makes the different traces to superimpose in the detector plate, especially at the higher energies. This problem is usually much bigger in those experiments where the expected number of fusions is low, and thus the spectrometers should be placed as close as possible to the target, as in the cases described in refs. [20, 25, 26]. Careful design of such spectrometers is thus required in order to minimize at most the EMP coupling to the deflecting region of the device and its drift unit. Thick conductive walls for the spectrometer and filtering and double shielding for any cable reaching the device are common issues. Examples of this for low-rate fusion reactions are shown in refs. [60, 68].

Generally speaking, shorter distances to the target mean larger angular spread of the incoming beam, which requires improved design and calibration of the spectrometers [60, 63, 65, 69], since the particle propagation will no longer be ideally normal to the fields [70].

Magnetic fields of about 1 T or less are commonly used in laser-matter experiments and easily achieved either with permanent magnets or with electromagnets. With common vacuums in high-power laser systems (~10⁻⁵ mbar), the electric fields are limited to a few tens of kV/cm to avoid breakdowns, which can produce serious permanent damages to the electrode structure. According to these values for the B and the E fields, whenever larger deflections are required to have good trace separation, longer electrodes are needed. This implies large dimensions of the device that can be a problem for the spectrometer positioning close to the target.

From these considerations, it follows that Thomson spectrometers suitable to detect products of low-rate fusion reactions should have the following features:

• high electric and magnetic fields, for a suitable trace separation at high energies;

• large pinholes, for improved solid angle of detection;

• positioning as close as possible to the interaction point;

• careful shielding for ionizing electromagnetic radiation and electrons;

• careful EMP shielding and particle trajectory characterization.

Certainly, Thomson or even simple magnetostatic or electrostatic spectrometers are useful to give a description of the emitted alpha spectrum and provide a suitable spectrum of protons and heavier ions involved in the interaction, for the detailed characterization of the reaction conditions [1, 21, 22, 24]. The pumping system in the vacuum chambers is well-known to induce the deposition of hydrocarbon impurities to the target surfaces. This means that in any laser-matter experiment H and C ions are to be expected and, in intense interactions, fully stripped C ions are commonly produced [57, 58]. This is an important issue, because they have the same charge-over-mass ratio of the alpha particles, and then they will be superimposed on the same trace. Alphas will have on this trace the same position of ¹²C⁶⁺ ions having three times their energy, according to the ratio of their charge states [60]. Figure 1B shows that the maximum α contribution is for energies higher than ~2.5 MeV. Thus, a significant superimposition with C ions will be achieved only if the latter have energies higher than ~7.5 MeV. This may be not an issue in nanosecond laser-matter interactions, where such energetic C ions are may be not present, but in some conditions such energies may be reached for energetic ps or fs laser interactions. In such cases, a discrimination between these two contributions may be performed, for example, by using CR39 track detectors, since the respective traces have diameters in ranges that are fairly distant, as shown in Figure 5 [53]. Anyway, this is possible only if the trace is not saturated, i.e., if there are not too many particles, so that the different tracks are clearly separated. This is not very common, especially if the detection is at an angle close to the target normal. Similar considerations apply also for fully stripped B ions, since their trace will be very close to that of alphas.

Use of Time-Of-Flight Detection

Time-of-flight schemes may be applied to the detection of fusion products in p+¹¹B reaction [22, 23, 63], with some intrinsic limitations. In this technique, information on particle velocity is sensed by the detection of the time of arrival at some distance from the target. This must be detected together with the reference of the time of laser-matter interaction. This information is commonly achieved on the same measurement because detectors commonly used in these schemes are sensitive also to the emitted UV–X-rays. The velocity resolution is given by the overall time resolution of the detection scheme divided by the target-detector distance, where the overall time resolution accounts for that of the detector (usually in the nanosecond order in classical Diamond or SiC Detectors), and that of the employed hardware (oscilloscopes, long cables used for connections) [37, 71–73]. To overcome the limitations due to the time resolution, one needs to place the detector at some distance from the interaction point. However, this, in turn, reduces the covered solid angle, and thus the sensitivity.

The main issue is that, whenever using TOF schemes in laser-matter interactions, in general there is no discrimination on particles but only on their velocities. For this reason, the difficulties on application of TOF methodologies to the detection of low-rate fusion products in the p+¹¹B reaction are due to the possible simultaneous arrival of alphas and other ions (mainly protons) to the detector. According to the energy spectrum shown in Figure 1B, the generated alpha particles have E₁ = 5.7 MeV maximum energy. Thus, they can be simultaneously detected with protons having energy up to E_max−p = E₁^*m_p/m_α = 1.425 MeV, where m_p and m_α are the proton and alpha masses, respectively. The application of suitable filters (such as Al foils, for example) can definitely be beneficial to minimize the simultaneous contribution of B and C ions but will be not effective for protons, unfortunately. In fact, Figure 3B shows that, to some extent, the range of protons in Al is roughly that of alphas multiplied by the same m_p/m_α term. So, a filter cutting up to 1.425 MeV protons will also cut the whole alpha spectrum. Moreover, the number of alphas produced will be usually much lower than protons, due to the low-cross section of the reaction, and any possible modulation on the proton signal due to the alpha contribution is expected to be very small and thus barely visible and not recognizable.

One possible way to use the TOF technique effectively is to couple it to a suitable Thomson spectrometer with electric and magnetic fields high enough to give the proton trace not superimposed to that of He²⁺ ions, at least up to 1.425 MeV proton energy. In this way, a clear spectrum of the incoming protons, and of their maximum energy E_max−p, will be achieved. According to the spectrum of Figure 2B, a clear discrimination of alphas by TOF can occur, for example, if the main alpha peak, starting in Figure 2B at E_α ~ 3 MeV, will have no time superimposition with protons, and this means E_max−p ≤ 750 keV. In this or in similar cases, alphas will be the fastest particles and will clearly be detected by the TOF technique [22]. But this sets limits on the type of laser-matter interaction where this approach can be used and/or on the direction of detection. It will hardly be applicable to scheme 2, and in general, it may be used in experiments of scheme 1 where the maximum proton energy will be lower than ~750 keV, so for not very high laser intensities [20, 22, 23].

In these few conditions, there is still the drawback of the small solid angle covered. It is possible to deal with it somehow by placing the TOF detector as close as possible to the target, at some expenses of the energy resolution, and provided that the detector is very well-shielded against intense EMPs, as discussed in section Use of Thomson Spectrometers, which is not an easy issue [72]. Moreover, it is possible to develop large-area detectors such as those based on fast scintillators, which can lead to improved sensitivity of the technique and to a suitable compromise with resolution [74].

Besides the detection of alpha products, the TOF technique is certainly useful in this type of experiments to give important information on the maximum energies of generated protons [25, 37].

Indirect Estimation of the ¹¹B(p,α)2α Reaction by Detecting Products of Different Simultaneous Reactions

One of the important and appealing features of reactions such as p+¹¹B is that they release only alpha products. On the other hand, as discussed, there are many difficulties in directly detecting them. In some cases, it is indeed possible to obtain information on them from the study of other reactions occurring in the same experiment and generating products different from alphas, that can be detected more easily.

Moreover, in principle, it might be possible to get a link between the number of products from these side reactions and the number of p+¹¹B → α reactions which were simultaneously obtained, and so a possible estimation of the yield.

¹¹B is present in about 80% of natural B, the remaining being ¹⁰B. Thus, if in the experiment where the p+¹¹B reaction is meant to occur, natural B is used instead of ¹¹B, according to the laser-matter parameters there is some probability that the reaction ¹⁰B(p, α)⁷Be may take place simultaneously to the expected ¹¹B(p, α)2α one, with a cross-section smaller than ¹¹B(p, α)2α. The released radioactive ⁷Be has a half-life of 53.22 days [75]. By electron capture, the nucleus of ⁷Be decays to the 3/2⁻ ground state of ⁷Li directly with a branching ratio of 89.5% and to its first excited state with a 10.5% ratio, which decays subsequently to its ground state by emitting 478 keV gamma rays [76]. So, the important difference and the great advantage of this reaction is that the associated gamma signature from ⁷Be, collected from the residues of the target and its stalk after the interaction, can be detected more easily than alphas, for example by classical high sensitivity gamma detectors. From these measurements, it can be possible to obtain information firstly on the correct operation of the designed scheme. As an example of this technique, ~478 keV γ-rays were detected by means of a high purity germanium semiconductor detector on samples collected after a certain number of laser shots at the ABC laser facility, in scheme 1 of Figure 2A, on natural-boron-doped plastic targets at ~3 × 10¹⁵ W cm⁻² laser intensity [20].

Another possible option is, for instance, to dope pB targets in scheme 1 with deuterium at a known concentration. In the plasma, D-D fusions will be achieved, and the corresponding neutron yield will be measured more effectively than alphas. This information will put constraints on the number of fusion reactions occurring in the simultaneous p+¹¹B processes.

An interesting feature of the mentioned p+¹¹B and p+¹⁰B simultaneous reactions, when using natural boron targets, is that in case the alpha products of the p+¹¹B and the gamma emission due to p+¹⁰B are both determined with good accuracy, the ratio of the yield coming from the two of them can give estimation of the effective temperature of the plasma where the reactions took place. Figure 8 shows the reaction-rate ratio corrected for concentration for the reactions p+¹⁰B and p+¹¹B, with rates taken from the NACRE compilation [77]. A similar method was successfully applied to determine the plasma temperature in a laser-cluster fusion experiment at the Texas Petawatt laser from the ratio of the rates of two different nuclear reactions occurring in the plasma at the same time: D(d,³He)n and ³He(d, p)⁴He [14].

FIGURE 8

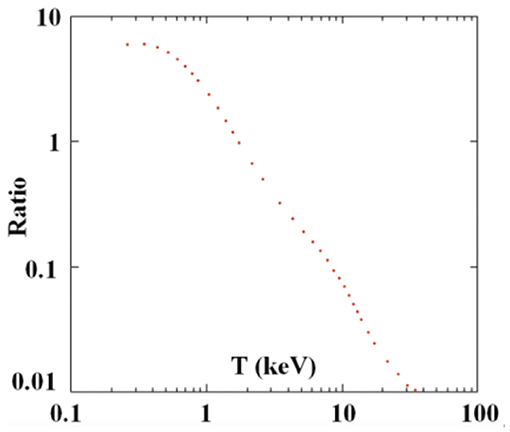
Figure 8. Reaction-rate ratio for the reactions p+¹⁰B and p+¹¹B, corrected for the concentrations. The reaction rates are taken from the NACRE compilation [77].

Another useful reaction is ¹⁰B(p,γ)¹¹C, releasing the radioactive ¹¹C, with a half-life of 20.364 min. The decay is normally due to positron emission, ¹¹C → ¹¹B + e⁺ + ν_e + 0.96 MeV [78, 79]. Also in this case the gamma emission can be an important observable.

Moreover, it is interesting to note that the interaction of protons and ¹¹B can generate ¹¹C through the nuclear reaction: p + ¹¹B → n + ¹¹C – 2.9 MeV [9]. This was used in ref. [21] to estimate the number of protons with energy higher than 5 MeV reaching the target in scheme 2 of Figure 2B after laser-plasma acceleration.

Discussion

Several methods that can be used for the possible detection of p+¹¹B fusion-reaction products were here discussed, outlining their actual application to this purpose and the limitations with respect to the different scenarios. The difficulties of this task and the actual uncertainties on the use of one method or the other have been highlighted. The result is that the unique detection of the alpha particle products given by the reaction is not accomplished normally using a single detection technique, but the simultaneous use of different techniques is required. The actual number and type of diagnostics and their configuration may differ, also of a large extent, for each of the different possible experiments included in schemes 1 and 2.

The considerations here developed apply not only to the p+¹¹B reaction, but, in general, to all the low-rate nuclear reactions producing ions that need to be detected in the context of laser-matter interactions, such as p+⁶Li and p+⁷Li [6, 30], to name a few examples. This paper is intended as a general reference for researchers who would like to start getting involved with the difficult issue of experiments with low-rate fusion reactions in intense and energetic laser-matter interactions in different scenarios. The research activity on methodologies that can be more sensitive, accurate, and can give more precise identification of the low-number of products of these nuclear fusion reactions is still very open and is the actual key for enabling the important possible use of these laser-initiated reactions as localized sources of alpha particles, for example, for medical applications [27–29] or for studies of astrophysical interest [16, 17, 20, 30, 31], besides of course the possible future applications in new-generation inertial fusion energy plants [6, 12, 13].

Author Contributions

All the authors contributed to the work. FC wrote the paper with the collaboration of RDA and MC. AB and DG contributed in writing some sections and gave valuable advices on the overall text. All the authors contributed to the preparations and to the discussions on different sections of the paper and reviewed and approved the manuscript.

Funding

This work has been carried out within the framework of the EUROfusion Consortium and funded from the Euratom research and training programme 2014–2018 and 2019–2020 under grant agreement no. 633053.

Disclaimer

The views and opinions expressed herein do not necessarily reflect those of the European Commission.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Baccou C, Depierreux S, Yahia V, Neuville C, Goyon C, De Angelis R, et al. New scheme to produce aneutronic fusion reactions by laser-accelerated ions. Laser Part Beams. (2015) 33:117–22. doi: 10.1017/S0263034615000178

CrossRef Full Text | Google Scholar

2. Becker HW, Rolfs C, Trautvetter HP. Low-energy cross sections for ¹¹B(p, 3α). Z Physik A Atomic Nuclei. (1987) 327:341–55. doi: 10.1007/BF01284459

CrossRef Full Text | Google Scholar

3. Nevins WM, Swain R. The thermonuclear fusion rate coefficient for p- ¹¹ B reactions. Nucl Fusion. (2000) 40:865–72. doi: 10.1088/0029-5515/40/4/310

CrossRef Full Text | Google Scholar

4. Liu J, Lu X, Wang X, Chu W-K. Cross-sections of B(p,α)⁸Be reaction for boron analysis. Nucl Instrum Methods Phys Res B. (2002) 190:107–11. doi: 10.1016/S0168-583X(01)01272-1

CrossRef Full Text | Google Scholar

5. Kimura S, Anzalone A, Bonasera A. Comment on “Observation of neutronless fusion reactions in picosecond laser plasmas.” Phys Rev E. (2009) 79:038401. doi: 10.1103/PhysRevE.79.038401

CrossRef Full Text | Google Scholar

6. Atzeni S, Meyer-Ter-Vehn J. The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter. Oxford: Oxford University Press (2004). doi: 10.1093/acprof:oso/9780198562641.003.0010

CrossRef Full Text | Google Scholar

7. Brandenburg JE. The hybrid fusion-fission reactor as the solution to the energy crisis. J Space Expl. (2014) 3:7. Available online at: https://www.tsijournals.com/abstract/the-hybrid-fusionfission-reactor-as-the-solution-to-the-energy-crisis-7023.html

Google Scholar

8. Freidberg JP, Kadak AC. Fusion–fission hybrids revisited. Nature Phys. (2009) 5:370–2. doi: 10.1038/nphys1288

CrossRef Full Text | Google Scholar

9. Ajzenberg-Selove F. Energy levels of light nuclei A = 11–12. Nucl Phys A. (1990) 506:1–158. doi: 10.1016/0375-9474(90)90271-M

CrossRef Full Text | Google Scholar

10. Belyaev VS, Vinogradov VI, Matafonov AP, Rybakov SM, Krainov VP, Lisitsa VS, et al. Excitation of promising nuclear fusion reactions in picosecond laser plasmas. Phys Atom Nuclei. (2009) 72:1077–98. doi: 10.1134/S1063778809070011

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wielunska B, Mayer M, Schwarz-Selinger T, von Toussaint U, Bauer J. Cross section data for the D(³ He,p)⁴ He nuclear reaction from 0.25 to 6 MeV. Nucl Instrum Methods Phys Res B. (2016) 371:41–5. doi: 10.1016/j.nimb.2015.09.049

CrossRef Full Text | Google Scholar

12. Kulcinski GL, Santarius JF. Advanced fuels under debate. Nature. (1998) 396:724–5. doi: 10.1038/25456

CrossRef Full Text | Google Scholar

13. Bonasera A. Quale energia per il futuro?: Tutela ambientale e risorse. Milano: Springer Milan (2010). doi: 10.1007/978-88-470-1418-3

CrossRef Full Text | Google Scholar

14. Bang W, Barbui M, Bonasera A, Dyer G, Quevedo HJ, Hagel K, et al. Temperature measurements of fusion plasmas produced by Petawatt-laser-irradiated D₂ – He³ or CD₄- He³ clustering gases. Phys Rev Lett. (2013) 111:055002. doi: 10.1103/PhysRevLett.111.055002

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Bang W, Barbui M, Bonasera A, Quevedo HJ, Dyer G, Bernstein AC, et al. Experimental study of fusion neutron and proton yields produced by petawatt-laser-irradiated D₂-³He or CD₄-³He clustering gases. Phys Rev E. (2013) 88:033108. doi: 10.1103/PhysRevE.88.033108

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Barbui M, Bang W, Bonasera A, Hagel K, Schmidt K, Natowitz JB, et al. Measurement of the plasma astrophysical S factor for the He³(d, p)He⁴ reaction in exploding molecular clusters. Phys Rev Lett. (2013) 111:082502. doi: 10.1103/PhysRevLett.111.082502

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Lattuada D, Barbarino M, Bonasera A, Bang W, Quevedo HJ, Warren M, et al. Model-independent determination of the astrophysical S factor in laser-induced fusion plasmas. Phys Rev C. (2016) 93:045808. doi: 10.1103/PhysRevC.93.045808

CrossRef Full Text | Google Scholar

18. Barbui M, Bang W, Bonasera A, Hagel K, Schmidt K, Natowitz J, et al. Study of the yield of D-D, D-³He fusion reactions produced by the interaction of intense ultrafast laser pulses with molecular clusters. J Phys Conf Ser. (2013) 420:012060. doi: 10.1088/1742-6596/420/1/012060

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Belyaev VS, Matafonov AP, Vinogradov VI, Krainov VP, Lisitsa VS, Roussetski AS, et al. Observation of neutronless fusion reactions in picosecond laser plasmas. Phys Rev E. (2005) 72:026406. doi: 10.1103/PhysRevE.72.026406

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Bonasera A, Caruso A, Strangio C, Aglione M, Anzalone A, Kimura S, et al. Measuring the astrophysical S-factor in plasmas. In: Hamilton JH, editor. Fission and Properties of Neutron-Rich Nuclei. Sanibel Island, FL: World Scientific (2013). p. 503–7.

Google Scholar

21. Labaune C, Baccou C, Depierreux S, Goyon C, Loisel G, Yahia V, et al. Fusion reactions initiated by laser-accelerated particle beams in a laser-produced plasma. Nat Commun. (2013) 4:2506. doi: 10.1038/ncomms3506

CrossRef Full Text | Google Scholar

22. Picciotto A, Margarone D, Velyhan A, Bellutti P, Krasa J, Szydlowsky A, et al. Boron-proton nuclear-fusion enhancement induced in boron-doped silicon targets by low-contrast pulsed laser. Phys Rev X. (2014) 4:031030. doi: 10.1103/PhysRevX.4.031030

CrossRef Full Text | Google Scholar

23. Margarone D, Picciotto A, Velyhan A, Krasa J, Kucharik M, Mangione A, et al. Advanced scheme for high-yield laser driven nuclear reactions. Plasma Phys Control Fusion. (2015) 57:014030. doi: 10.1088/0741-3335/57/1/014030

CrossRef Full Text | Google Scholar

24. Giuffrida L, Belloni F, Margarone D, Petringa G, Milluzzo G, Scuderi V, et al. High-current stream of energetic α particles from laser-driven proton-boron fusion. Phys Rev E. (2020) 101:013204. doi: 10.1103/PhysRevE.101.013204

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Giulietti D, Andreoli P, Batani D, Bonasera A, Boutoux G, Burgy F, et al. Laser-plasma energetic particle production for aneutronic nuclear fusion experiments. Nucl Instrum Methods Phys Res B. (2017) 402:373–5. doi: 10.1016/j.nimb.2017.03.076

CrossRef Full Text | Google Scholar

26. Ingenito F, Andreoli P, Batani D, Bonasera A, Boutoux G, Burgy F, et al. Directional track selection technique in CR39 SSNTD for lowyield reaction experiments. EPJ Web Conf . (2018) 167:05006. doi: 10.1051/epjconf/201816705006

CrossRef Full Text | Google Scholar

27. Cirrone GAP, Manti L, Margarone D, Petringa G, Giuffrida L, Minopoli A, et al. First experimental proof of Proton Boron Capture Therapy (PBCT) to enhance protontherapy effectiveness. Sci Rep. (2018) 8:1141. doi: 10.1038/s41598-018-19258-5

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Giuffrida L, Margarone D, Cirrone GAP, Picciotto A, Cuttone G, Korn G. Prompt gamma ray diagnostics and enhanced hadron-therapy using neutron-free nuclear reactions. AIP Adv. (2016) 6:105204. doi: 10.1063/1.4965254

CrossRef Full Text | Google Scholar

29. Giuffrida L, Margarone D, Korn G, Cirrone GAP, Picciotto A. Device and Method for Imaging and Enhanced Proton-Therapy Treatment Using Nuclear Reactions. European Patent 3266470A1 (2016)

Google Scholar

30. Clayton DC. Principles of Stellar Evolution and Nucleosyntesis. Chicago: The University of Chicago Press (1983).

Google Scholar

31. Barbui M, Bang W, Bonasera A, Hagel K, Schmidt K, Zheng H, et al. A laser application to nuclear astrophysics. In: AIP Conference Proceedings. Sicily (2014). p. 168–172.

Google Scholar

32. Spraker MC, Ahmed MW, Blackston MA, Brown N, France RH, Henshaw SS, et al. The ¹¹B(p,α)⁸Be → α + α and the ¹¹B(α,α)¹¹B reactions at energies below 5.4 MeV. J Fusion Energ. (2012) 31:357–67. doi: 10.1007/s10894-011-9473-5

CrossRef Full Text | Google Scholar

33. Eliezer S, Hora H, Korn G, Nissim N, Martinez Val JM. Avalanche proton-boron fusion based on elastic nuclear collisions. Phys Plasmas. (2016) 23:050704. doi: 10.1063/1.4950824

CrossRef Full Text | Google Scholar

34. Hora H, Eliezer S, Kirchhoff GJ, Nissim N, Wang JX, Lalousis P, et al. Road map to clean energy using laser beam ignition of boron-hydrogen fusion. Laser Part Beams. (2017) 35:730–40. doi: 10.1017/S0263034617000799

CrossRef Full Text | Google Scholar

35. Hora H, Korn G, Eliezer S, Nissim N, Lalousis P, Giuffrida L, et al. Avalanche boron fusion by laser picosecond block ignition with magnetic trapping for clean and economic reactor. High Pow Laser Sci Eng. (2016) 4:e35. doi: 10.1017/hpl.2016.29

CrossRef Full Text | Google Scholar

36. Belloni F, Margarone D, Picciotto A, Schillaci F, Giuffrida L. On the enhancement of p- ¹¹B fusion reaction rate in laser-driven plasma by α → p collisional energy transfer. Phys Plasmas. (2018) 25:020701. doi: 10.1063/1.5007923

CrossRef Full Text | Google Scholar

37. Cipriani M, Consoli F, Andreoli PL, Batani D, Bonasera A, Boutoux G, et al. Spectral characterization by CVD diamond detectors of energetic protons from high-repetition rate laser for aneutronic nuclear fusion experiments. J Inst. (2019) 14:C01027. doi: 10.1088/1748-0221/14/01/C01027

CrossRef Full Text | Google Scholar

38. Caruso A, Strangio C. Inertial Confinement Physics and Technology Progress Report (1994–1995). Available online at: http://www.iaea.org/inis/collection/NCLCollectionStore/_Public/29/067/29067556.pdf (accessed October 19, 2020).

Google Scholar

39. Littmark U, Ziegler JF. Handbook of Range Distributions for Energetic Ions in All Elements. New York, NY: Pergamon Press Incorporated (1980). doi: 10.1016/B978-0-08-021607-2.50001-5

CrossRef Full Text | Google Scholar

40. Ziegler JF, Biersack JP, Littmark U. The Stopping and Range of Ions in Matter. New York, NY: Pergamon Press (1985). doi: 10.1007/978-1-4615-8103-1_3

CrossRef Full Text | Google Scholar

41. De Angelis R, Giulietti D, Calcagnile L, Quarta G, Andreoli P, Cipriani M, et al. α particle space distribution from fusion reactions in Boron irradiated bymono-energetic protons. EPJ Web Conf . (2018) 167:05005. doi: 10.1051/epjconf/201816705005

CrossRef Full Text | Google Scholar

42. Calcagnile L, Quarta G, D'Elia M, Muscogiuri D, Maruccio L, Butalag K, et al. Instrumental developments at the IBA-AMS dating facility at the University of Lecce. Nucl Instrum Methods Phys Res B. (2005) 240:22–5. doi: 10.1016/j.nimb.2005.06.081

CrossRef Full Text | Google Scholar

43. Durrani SA, Bull RK. Solid State Nuclear Track Detection: Principles, Methods, and Applications. 1st ed. Oxford, NY: Pergamon Press (1987). doi: 10.1016/B978-0-08-020605-9.50005-8

CrossRef Full Text | Google Scholar

44. Nikezic D, Yu K. Formation and growth of tracks in nuclear track materials. Mater Sci Eng R Rep. (2004) 46:51–123. doi: 10.1016/j.mser.2004.07.003

CrossRef Full Text | Google Scholar

45. Nikezic D, Yu KN. Computer program TRACK_TEST for calculating parameters and plotting profiles for etch pits in nuclear track materials. Comput Phys Commun. (2006) 174:160–5. doi: 10.1016/j.cpc.2005.09.011

CrossRef Full Text | Google Scholar

46. Nikezic D, Yu KN. Computer program TRACK_VISION for simulating optical appearance of etched tracks in CR-39 nuclear track detectors. Comput Phys Commun. (2008) 178:591–5. doi: 10.1016/j.cpc.2007.11.011

CrossRef Full Text | Google Scholar

47. Nikezic D, Yu KN. Analyses of light scattered from etched alpha-particle tracks in PADC. Radiat Meas. (2008) 43:1417–22. doi: 10.1016/j.radmeas.2008.02.003

CrossRef Full Text | Google Scholar

48. Nikezic D, Yu KN. Light scattering from an assembly of tracks in a PADC film. Nucl Instrum Methods Phys Res B. (2009) 602:545–51. doi: 10.1016/j.nima.2009.01.204

CrossRef Full Text | Google Scholar

49. Law YL, Nikezic D, Yu KN. Optical appearance of alpha-particle tracks in CR-39 SSNTDs. Radiat Meas. (2008) 43:128–31. doi: 10.1016/j.radmeas.2008.03.030

CrossRef Full Text | Google Scholar

50. Yu KN, Lee HHW, Wong AWT, Law YL, Cheung SFL, Nikezic D, et al. Optical appearance of alpha particle tracks in CR-39 SSNTD. Nucl Instrum Methods Phys Res B. (2007) 263:271–8. doi: 10.1016/j.nimb.2007.04.306

CrossRef Full Text | Google Scholar

51. Szydlowski A, Czyzewski T, Jaskola M, Sadowski M, Korman A, Kedzierski J, et al. Investigation of response of CR-39, PM-355 and PM-500 types of nuclear track detectors to energetic carbon ions. Radiat Meas. (1999) 31:257–60. doi: 10.1016/S1350-4487(99)00125-0

CrossRef Full Text | Google Scholar

52. Malinowska A, Szydłowski A, Jaskóła M, Korman A, Malinowski K, Kuk M. Calibration of new batches and a study of applications of nuclear track detectors under the harsh conditions of nuclear fusion experiments. Nucl Instrum Methods Phys Res B. (2012) 281:56–63. doi: 10.1016/j.nimb.2012.03.023

CrossRef Full Text | Google Scholar

53. Baccou C, Yahia V, Depierreux S, Neuville C, Goyon C, Consoli F, et al. CR-39 track detector calibration for H, He, and C ions from 0.1-0.5 MeV up to 5 MeV for laser-induced nuclear fusion product identification. Rev Sci Instrum. (2015) 86:083307. doi: 10.1063/1.4927684

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Jeong TW, Singh PK, Scullion C, Ahmed H, Hadjisolomou P, Jeon C, et al. CR-39 track detector for multi-MeV ion spectroscopy. Sci Rep. (2017) 7:2152. doi: 10.1038/s41598-017-02331-w

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Consoli F, Tikhonchuk VT, Bardon M, Bradford P, Carroll DC, Cikhardt J, et al. Laser produced electromagnetic pulses: generation, detection and mitigation. High Pow Laser Sci Eng. (2020) 8:e22. doi: 10.1017/hpl.2020.13

CrossRef Full Text | Google Scholar

56. Image-J. Available online at: https://imagej.nih.gov/ij/index.html (accessed May 5, 2020).

Google Scholar

57. Macchi A, Borghesi M, Passoni M. Ion acceleration by superintense laser-plasma interaction. Rev Mod Phys. (2013) 85:751–93. doi: 10.1103/RevModPhys.85.751

CrossRef Full Text | Google Scholar

58. Gibbon P. Short Pulse Laser Interactions with Matter: An Introduction. London: Imperial College Press (2005). doi: 10.1142/p116

CrossRef Full Text | Google Scholar

59. Thomson JJ. Rays of positive electricity. Proc R Soc Lond A. (1913) 89:1–20. doi: 10.1098/rspa.1913.0057

CrossRef Full Text | Google Scholar

60. Consoli F, Angelis RD, Bonasera A, Sura J, Andreoli P, Cristofari G, Cipriani M, et al. Study on a compact and adaptable Thomson Spectrometer for laser-initiated ¹¹ B(p,α) ⁸ Be reactions and low-medium energy particle detection. J Inst. (2016) 11:C05010. doi: 10.1088/1748-0221/11/05/C05010

CrossRef Full Text | Google Scholar

61. Bonnet T, Comet M, Denis-Petit D, Gobet F, Hannachi F, Tarisien M, et al. Response functions of imaging plates to photons, electrons and ⁴ He particles. Rev Sci Instrum. (2013) 84:103510. doi: 10.1063/1.4826084

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Boutoux G, Batani D, Burgy F, Ducret J-E, Forestier-Colleoni P, Hulin S, et al. Validation of modelled imaging plates sensitivity to 1-100 keV x-rays and spatial resolution characterisation for diagnostics for the “PETawatt Aquitaine Laser.” Rev Sci Instrum. (2016) 87:043108. doi: 10.1063/1.4944863

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Consoli F, De Angelis R, Andreoli P, Cristofari G, Di Giorgio G, Bonasera A, et al. Diagnostics improvement in the ABC facility and preliminary tests on laser interaction with light-atom clusters and p+¹¹B targets. Nucl Instrum Methods Phys Res A. (2013) 720:149–52. doi: 10.1016/j.nima.2012.12.013

CrossRef Full Text | Google Scholar

64. Treffert F, Ji Q, Seidl PA, Persaud A, Ludewigt B, Barnard JJ, et al. Design and implementation of a Thomson parabola for fluence dependent energy-loss measurements at the Neutralized Drift Compression eXperiment. Rev Sci Instrum. (2018) 89:103302. doi: 10.1063/1.5030541

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Morrison JT, Willis C, Freeman RR, Van Woerkom L. Design of and data reduction from compact Thomson parabola spectrometers. Rev Sci Instrum. (2011) 82:033506. doi: 10.1063/1.3556444

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Alejo A, Kar S, Ahmed H, Krygier AG, Doria D, Clarke R, et al. Characterisation of deuterium spectra from laser driven multi-species sources by employing differentially filtered image plate detectors in Thomson spectrometers. Rev Sci Instrum. (2014) 85:093303. doi: 10.1063/1.4893780

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Scisciò M. In preparation.

PubMed Abstract | Google Scholar

68. Di Giorgio G, Consoli F, Andreoli P, Cipriani M, Cristofari G, Salvadori M, et al. Development of advanced Thomson spectrometers for nuclear fusion experiments initiated by laser. J Inst. (2020). doi: 10.1088/1748-0221/15/10/C10013

CrossRef Full Text | Google Scholar

69. Schillaci F, Maggiore M, Velyhan A, Cirrone GAP, Cuttone G, Margarone D, et al. Calibration and energy resolution study of a high dispersive power Thomson Parabola Spectrometer with monochromatic proton beams. J Inst. (2014) 9:T10003. doi: 10.1088/1748-0221/9/10/T10003

CrossRef Full Text | Google Scholar

70. Wiedemann H. Particle Accelerator Physics. 1st ed. Berlin Heidelberg: Springer-Verlag (2007). Available online at: http://dx.doi.org/10.1007/978-3-540-49045-6 (accessed May 11, 2020). doi: 10.1007/978-3-540-49045-6

CrossRef Full Text | Google Scholar

71. De Angelis R, Consoli F, Verona C, Di Giorgio G, Andreoli P, Cristofari G, et al. High performance diagnostics for Time-Of-Flight and X ray measurements in laser produced plasmas, based on fast diamond detectors. J Inst. (2016) 11:C12048. doi: 10.1088/1748-0221/11/12/C12048

CrossRef Full Text | Google Scholar

72. Salvadori M, Consoli F, Verona C, Cipriani M, Anania MP, Andreoli P, et al. Accurate spectra for high energy ions by advanced time-of-flight diamond-detector schemes in experiments with high energy and intensity lasers. Sci. Rep. (2020)

Google Scholar

73. Milluzzo G, Scuderi V, Alejo A, Amico AG, Booth N, Borghesi M, et al. A new energy spectrum reconstruction method for time-of-flight diagnostics of high-energy laser-driven protons. Rev. Sci. Instrum. (2019) 90:083303. doi: 10.1063/1.5082746

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Consoli F, De Angelis R, Andreoli P, Cipriani M, Cristofari G, Di Giorgio G, et al. Research activity in the laboratory for inertial confinement fusion in ENEA – Centro Ricerche Frascati. In: LIMS 2018, Luce, Imaging, Microscopia, Spettri di applicazione. Frascati (2018).

Google Scholar

75. Lombardo I, Dell'Aquila D, Conte F, Francalanza L, La Cognata M, Lamia L, et al. New measurement of the ¹⁰ B(p, α ₀) ⁷ Be reaction cross section at low energies and the structure of ¹¹ C. EPJ Web Conf . (2016) 117:09009. doi: 10.1051/epjconf/201611709009

CrossRef Full Text | Google Scholar

76. Firestone RB. 1999 Table of Isotopes Update with CD-ROM. 8th ed. New York, NY: Wiley (1999).

Google Scholar

77. Xu Y, Takahashi K, Goriely S, Arnould M, Ohta M, Utsunomiya H. NACRE II: an update of the NACRE compilation of charged-particle-induced thermonuclear reaction rates for nuclei with mass number A <16. Nucl Phys A. (2013) 918:61–169. doi: 10.1142/9789814383646_0089

CrossRef Full Text | Google Scholar

78. Tonchev AP, Nelson SO, Sabourov K, Crowley BT, Joshi K, Weller HR, et al. The ¹⁰B(p, γ)¹¹C reaction at astrophysically relevant energies. Phys Rev C. (2003) 68:045803. doi: 10.1103/PhysRevC.68.045803

CrossRef Full Text | Google Scholar

79. Kafkarkou A, Ahmed MW, Kendellen DP, Mazumdar I, Mueller JM, Myers LS, et al. Cross section measurements of the ¹⁰B(p, γ) ¹¹C reaction between 2.0 and 6.0 MeV. Phys Rev C. (2014) 89:014601. doi: 10.1103/PhysRevC.89.014601

CrossRef Full Text | Google Scholar