Trend Analysis of COVID-19 Based on Network Topology Description

In this study, the trend of the epidemic situation of COVID-19 is analyzed based on the analysis method for network topology. Combining with the sliding window method, the dynamic networks with different topologies for each window are built to reflect the relationship of the data on different days. Then, the static statistical features on network topologies at different times are extracted during the dynamic evolution of complex networks. A new trend function defined on the average degree and clustering coefficient of the network is tailored to measure the characteristics of the trend. Through the value of the trend function, we can analyze the trend of the epidemic situation in real time. It is found that if the value of the trend function tends to decrease, it means that the epidemic will have to be effectively controlled. Finally, we put forward some suggestions for early control of the epidemic.

1. Introduction

Since December 2019, patients with pneumonia of unknown cause have appeared in some medical institutions. By now, the number of cases caused by coronavirus (COVID-19) has increased. The World Health Organization (WHO) declared the COVID-19 disease a pandemic on March 11, 2020. The cumulative confirmed cases have reached almost 3,220,000 as of May 1, 2020 worldwide. For new outbreaks, it is significant to understand the transmission dynamics of infection, which can help governments take effective measures to contain them and reduce the number of spread. In the survey of other two pandemics caused by coronavirus severe acute respiratory syndrome coronavirus (SARS-CoV) and Middle East respiratory syndrome coronavirus (MERS-CoV), scientists have put forward many effective measures to build the transmission models, such as the transmission analysis based on genome research (Qin et al., 2003) and the mathematical model of infection kinetics (Liang, 2020).

Since the outbreak of COVID-19, scholars have conducted relevant research through different models. Zhu and Chen give a statistical analysis of COVID-19 with early transmission model (Zhu and Chen, 2020). A data-based iterative prediction method is proposed to find growth rates under which the situation will be in control (Perc et al., 2020). Robust time series are used to complete statistical forecasts for the confirmed cases of COVID-19 by Fotios and Spyros (Petropoulos and Makridakis, 2020). In (Chen and Zhou, 2020), a Monte Carlo method is proposed to quantify the control efficacy, which is completed by calculating the mean number of secondary cases infected by a case with symptom onset every day. Moreover, a segmented Poisson model is adopted in Zhang et al. (2020) to analyze the new cases, which takes the governments’ regulations into consideration. An extended SIR model is employed by Jia and Han to compare the epidemics trend in Italy and Hunan, China (Jia et al., 2020).

With the development of complex networks, the spread analysis of epidemics on complex networks has attracted wide attention in the literature. Based on the SIR model in complex networks, Xia et al. have investigated the effects of delaying the time to recovery and of nonuniform transmission on the propagation of diseases on structured populations (Xia et al., 2012; Xia et al., 2013). In (Small and Tse, 2005), Small and Tse propose a new four state model based on the transmission of SARS, where community is modeled as a small-world network of interconnected nodes. Wang et al. point out the spread of epidemics in small-world networks (Wang and Li, 2016). The prevalence of infectious diseases in the population, the spread of viruses on computer networks, and the spread of rumors in human society can all be regarded as the problem of information dissemination on the network, which belongs to the dynamic process of the network and can be dealt with machine learning (Silva and Zhao, 2016).

In the study of complex network diseases (Wang et al., 2019; Wu and Hadzibeganovic, 2020), individuals in the population are regarded as nodes in the network, and the connections between individuals are regarded as edges in the network, which establishes the topology of the network. Since the real network is usually small scale and scale-free, it is generally that the network under study is a Watts–Strogatz (WS) or Barabási-Albert (BA) scale-free network (Wu et al., 2019). After the establishment of network topology, a mathematical model that can reflect the dynamic characteristics of infectious diseases is able to be built according to the transmission characteristics and infectious diseases between individuals (Huang, 2008; Liu and Li, 2019; Lu and Liu, 2019; Zhou and Wu, 2019; Aadil et al., 2020). In this paper, we attempt to make use of empirical data and combine the characteristics of COVID-19 transmission to analyze the trend of COVID-19. We mainly use the knowledge of network topology to give the trend analysis of COVID-19, which networks are established based on the data from COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (https://github.com/CSSEGISandData/COVID-19).

The article is organized as follows. Section 1 introduces the process of relevant research. In Section 2, which is also the most significant part of the article, we present the construction of the networks and the topological features extracted from the networks. Section 3 displays the networks we built and analyzes the epidemic situation in the four regions through the topological characteristics of the networks. We summarize the method we used and give some suggestions in Section 4.

2. Methodology

This section introduces the construction of the networks and the topological features extracted from the networks.

2.1. Networks Constructing

Here, we select four regions for the analysis, including Wuhan, South Korea, Russia, and Germany. The total number of confirmed cases is extracted for every day in each region. We get a time series $R_1=\left\{x_1,x_2,\dots ,x_n\right\}$, where $x_i$ is the number of diagnoses in the ith day, and n is the total days from the virus outbreak. Then, the growth rate of the number of diagnoses $y_i$ in the ith day is described as follows:

$y_i=\{\begin{array}{ll}\frac{x_{i+1}-x_i}{x_i},\hfill & x_i\ne 0\hfill \\ 0,\hfill & x_i=0\hfill \end{array}(1)$

From this treatment, the change in the daily diagnostic number can be seen more clearly. At the same time, the impact of the total local population on the growth rate of the number of confirmed cases can also be ignored. Then, we get a new time series on the growth rate of daily diagnoses $R_2=\left\{y_1,y_2,\dots ,y_{n-1}\right\}$.

The dynamic evolution analysis method is an important way for data analysis based on the features of network topology. In dynamic evolution, the feature measurement of networks is a function of time. In the same evolution mode, two subnetworks obtained at different times have different features. Therefore, it is a very important and effective way to analyze and classify the network by using static statistical features at different times during the dynamic evolution of networks (Backes et al., 2009). Here, the sliding window method is used to extract the features of network topology for further observation. The key to selecting sliding windows is how to effectively maintain the quality and quantity of the original time series information, while minimizing the calculation complexity to the most extent (Li and Zhang, 2004; Li and Xiao, 2009). In this study, we apply the sliding window with the length of 9 days and the step size of 1 day. Figure 1 shows the process of sliding windows for the time series data. Next, we will use the daily growth rate to build the networks.

FIGURE 1

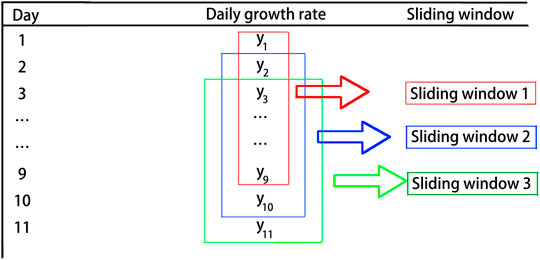
FIGURE 1. Sliding windows are used to form the time series. The length of sliding windows is chosen as 9 days, and the step size is 1 day. The figure shows the process of constructing time series.

For one of the sliding window $R_i=\left\{y_i,y_{i+1},\dots ,y_{i+8}\right\}$, using the nine-day growth rates as nodes, we calculate the Euclidean distance between any two nodes to get the $9\times 9$ distance matrix D with

$d_{ij}=\left|y_i-y_j\right|,(2)$

where $d_{ij}$ is the element of D in row i and column j. The growth rate defined in (1) formulates the difference between the different nodes, so the connections in the network give a relevance description for the data in the 9 days. Set the average value of the distance as the threshold denoted by δ. When $d_{ij}<\delta$, there is a connection between nodes i and j, that is, $a_{ij}=1$ in the connection matrix A of the network. Otherwise, we stipulate a) if one of $y_i$ and $y_j$ is 0, $a_{ij}=0$; b) if $d_{ij}<0.0002$, $a_{ij}=0$. Here, a) is to exclude the relationship between the current day and the remaining days if a certain growth rate is 0, and b) is an adjustment for the following consideration: at the time of the definition of the growth rate, the number of diagnoses per day on the previous day is increasing, and the growth rate is changing even if the number of growth is invariant. The construction of connection matrix is described as follows:

$a_{ij}=\{\begin{array}{ll}1,\hfill & \text{if}0.0002<d_{ij}<\delta \text{and}\min \left\{y_i,y_j\right\}\ne 0\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}(3)$

2.2. Topological Features of Networks

The degree $k_i$ of the node i is defined as the number of sides connected to the node. In an undirected and unauthorized network, the mathematical formula for degree can be expressed as follows:

$k_i={\displaystyle \sum }_{j=1}^N{a}_{ij},(4)$

where $a_{ij}$ is the element of connection matrix A and N is the total number of nodes. Then, we can get the average degree k of the whole network as follows:

$k=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{k}_i(5)$

The clustering coefficient is a coefficient that measures the degree of network aggregation, which can be formulated as follows:

$C=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\frac{2\left|e_i\right|}{k_i\left(k_i-1\right)},(6)$

where $\left|e_i\right|$ represents the number of connected edges between nodes in the neighborhood of node i (i.e., the number of triangles formed by node i and other two nodes in its neighborhoods) and $k_i$ is the degree of node i. In general, the clustering coefficient of the network quantifies the connection between nodes in the network with $C\in \left[\mathrm{0,1}\right]$. If $C=1$, all points in the network are connected. If the value of C is relatively small, the network connection is loose.

3. Experimental Results

In this section, we combine the daily number of confirmed cases in Wuhan, South Korea, Russia, and Germany to build the networks and analyze the epidemic situation in the four regions through the topological characteristics of the networks.

3.1. Data Processing

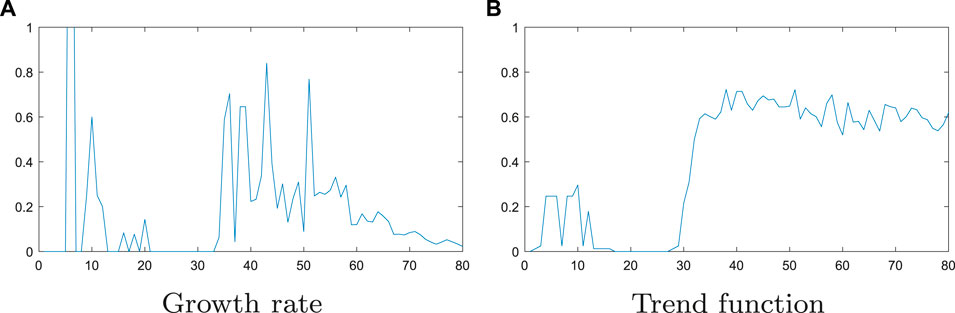
We use the daily number of diagnoses from January 22, 2020 to May 16, 2020 as the data set. So, for each region, we can get the total number of diagnoses per day for 116 days. First, from (1), the data are processed to calculate the 115-day daily diagnosis growth rate for each region. Then, using a sliding window of 9 days and a step size of 1 day, the time series data are divided into 107 periods, and 107 networks are constructed with nine nodes in each period. Figure 2 shows the networks at the 43rd day of the four regions. The more connections the network has, the greater the change is of the 9-day growth rate. It should be emphasized that few connections cannot only indicate the control period of the disease but also the period of early outbreak.

FIGURE 2

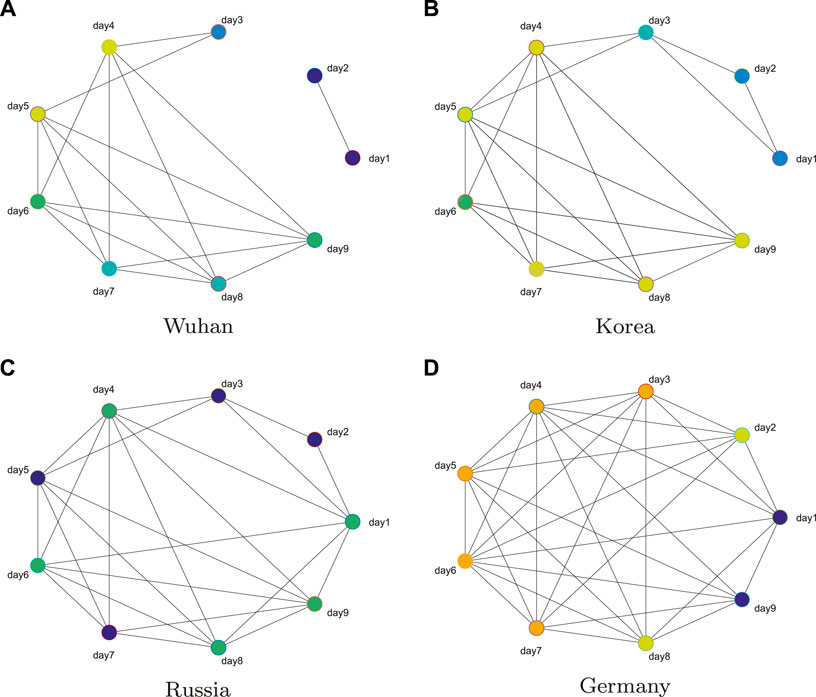
FIGURE 2. Networks at the 43rd day of the four regions. The number of connections in the network reflects the change degree of nine-day growth rate.

3.2. Analysis of Network Topological Characteristics

We use the equations in Eqs (5) and (6) to calculate the average degree and clustering coefficient of each network, and the trend function is defined as $I=0.5C+0.5k$ combining the average degree and clustering coefficient. Taking Germany for example, Figure 3A shows the growth rate change chart of Germany in the first 80 days, and Figure 3B depicts the evolution of trend function. It can be seen from Figure 3A that the daily growth rate in the first 80 days has changed greatly, and it is difficult to find the regular pattern of epidemic development. However, it can be seen from Figure 3B that when the value of trend function is relatively large and stable, the epidemic situation has not been completely controlled. This situation can be seen from the data in the next few days. It shows that the network topology method proposed in this article is efficient for the analysis of epidemic situation.

FIGURE 3

FIGURE 3. Growth rate and the evolution of trend function of Germany.

The evolution of the trend function in the four regions is shown in Figure 4. In the figure, the value of the abscissa is the number of days passed from January 22, 2020, and the ordinate is the value of the trend function I. The larger the I value, the larger is the clustering coefficient and mean sum. The larger the clustering coefficient, the difference of growth rate of any 3 days is less than the threshold in 9 days, and the larger the average degree, the difference of the growth rate in 9 days is less than the threshold number of days. Therefore, when the daily diagnostic growth rate of 9 days becomes relatively small, the clustering coefficient and average degree will be relatively small. If the growth rate changes greatly in 1 day in the 9 days, the average threshold will become larger, and the number of connections will increase in the remaining 8 days, then the value of trend function will also increase.

FIGURE 4

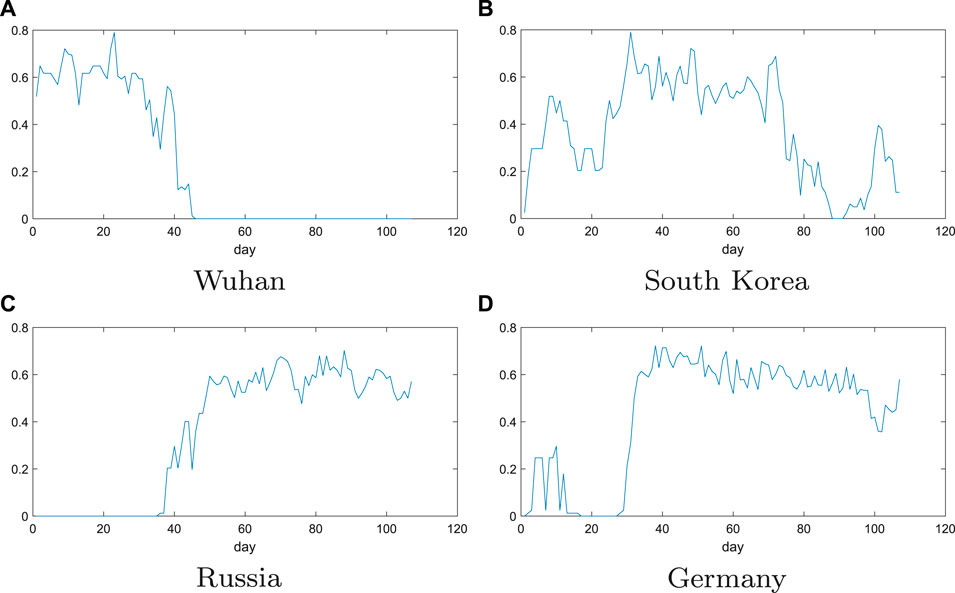
FIGURE 4. Evolution of trend function for the four regions: Wuhan, South Korea, Russia, and Germany. The value of the abscissa is the number of days passed from January 22, 2020, and the ordinate is the value of the trend function I. The larger the I value, the larger is the clustering coefficient and mean sum.

From Figure 4A in Wuhan, there is a clear downward trend in the values of the trend function around March 2. The growth rate of the number of confirmed patients in the next 9 days has also dropped to $0.1\text{\%}$ for the first time, and the growth rate is also declining in the next few days, gradually turning to 0. This indicates that the change trend is related to the change of the daily growth rate. Furthermore, if the values of trend function show a downward trend, it can be inferred that the growth rate of the region has dropped to a smaller value, and it can be considered that the epidemic situation in the region has been effectively controlled.

In Figure 4D, the values of trend function change in Germany can be seen that it has a small wave peak at first, and then suddenly increases until it stabilizes around 0.6. So, it can be speculated that there was a small outbreak in Germany between January 22 and February 2, and then it was effectively controlled, resulting in a growth rate of almost zero. But since February 22, there has been a second outbreak in Germany. The values of trend function have been fluctuating around 0.6, indicating that Germany’s growth rate still remains high and the epidemic has not been effectively controlled. The above results are consistent with the local epidemic data in Germany, which proves that the method is effective.

From above analysis, we can analyze and predict the epidemic situation in South Korea and Russia. From Figure 4, it can be seen that the figure of South Korea has shown a clear downward trend since April 2, indicating that the epidemic situation in South Korea has been effectively controlled. However, there was a small upward trend at the 100th day. This indicates that the daily growth rate in South Korea has increased by a small margin recently. But, it can be controlled quickly. For Russia, where the values of trend function is still fluctuating around 0.6, which indicates a certain fluctuation in the growth rate of the daily confirmed population in Russia during April. We can also see that the growth rate is still relatively high, which shows that the Russian epidemic has not been effectively controlled, and the growth rate will not be significantly reduced in the near future, and more stringent measures are needed to control the development of the epidemic.

Note that the effective control of the epidemic in this article refers to the fact that the daily growth rate is almost zero, that is, there is almost no new infection, rather than the change in the daily growth rate of 0, or in other words, the next day is approximately equal to the daily growth rate of the previous day, as mentioned in some articles. For example, for the platform period mentioned in Perc et al. (2020), we understand it as the epidemic situation has been preliminarily controlled, and only when there is no new infection can it be considered to be effectively controlled.

4. Discussions and Conclusions

In this article, we proposed a trend analysis method based on network construction with sliding windows to extract the characteristics of network dynamic evolution over time and analyzed the epidemic trend in four typical regions. In the analysis, we found that some regions had better control of the epidemic, while others were still in the process of outbreak. So, we put forward some suggestions and hope that the epidemic situation in various countries can be effectively controlled as soon as possible.

The proposed method in this article is easy but efficient for the trend analysis of COVID-19. In general, since COVID-19 patients’ mid-term course of disease develops rapidly, it is hard to accurately judge the cycle from mild to severe. Moreover, the issue of infectivity in the incubation period and the infectious power of those infected patients during the recovery period remains to be studied, which may be the cause of second outbreak in Germany. The intensity of different infection generation and the difference of infection are still unknown. The question of whether the virus will disappear or persist in the population remains to be resolved.

Many countries have taken effective measures to the epidemic, such as closing churches, bars, and gymnasiums. In severe cases, some countries such as China seal off the city from all outside contact to stop the spread of the plague. We can learn from the above analysis that Wuhan has got the epidemic under control in a relatively short time. In order to block the transmission chain of the virus, it is a very effective method to trace the confirmed patient’s activity route and contacts. For countries like Russia where the epidemic is still serious, which can be observed from the trend in Figure 4, they should consider to strengthen the isolation measures.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here https://github.com/CSSEGISandData/COVID-19.

Author Contributions

JZ and QL designed and performed the research. JZ, YJ, TL, and HL wrote the manuscript.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant 61876036.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Aadil L., Adel S., Hamza E. M., Mustapha E. J., Mohamed E. F. (2020). Global dynamics of an epidemic model with incomplete recovery in a complex network. J. Franklin Inst. 357, 4414–4436. doi:10.1016/j.jfranklin.2020.03.010

CrossRef Full Text | Google Scholar

Backes A. R., Casanova D., Bruno O. M. (2009). A complex network-based approach for boundary shape analysis. Pattern Recogn. 42, 54–67. doi:10.1016/j.patcog.2008.07.006

CrossRef Full Text | Google Scholar

Chen D., Zhou T. (2020). Control efficacy on COVID-19. Populations and evolution. arXiv:2003.00305.

Google Scholar

Huang S.-Z. (2008). A new SEIR epidemic model with applications to the theory of eradication and control of diseases, and to the calculation of. Math. Biosci. 215, 84–104. doi:10.1016/j.mbs.2008.06.005

CrossRef Full Text | Google Scholar

Jia W., Han K., Song Y., Cao W., Wang S., Yang S., et al. (2020). Extended SIR prediction of the epidemics trend of COVID-19 in Italy and compared with Hunan, China. Front. Med. 7, 169. doi:10.3389/fmed.2020.00169

CrossRef Full Text | Google Scholar

Li F., Xiao J. (2009). How to get effective slide-window size in time series similarity search. J. Front. Comput. Sci. Tech. 3, 105–112. [in Chinese]. doi:1673-9418/2009/03(01)-0105-08

Google Scholar

Li J., Zhang D. (2004). Algorithms for dynamically adjusting the sizes of sliding windows. J. Softw. 15, 1800–1814. [in Chinese]. doi:1000-9825/2004/15(12)1800

Google Scholar

Liang K. (2020). Mathematical model of infection kinetics and its analysis for COVID-19, SARS and MERS. Infect. Genet. Evol. 82, 104306. doi:10.1016/j.meegid.2020.104306

CrossRef Full Text | Google Scholar

Liu Q., Li H. (2019). Global dynamics analysis of an seir epidemic model with discrete delay on complex network. Phys. Stat. Mech. Appl. 524, 289–296. doi:10.1016/j.physa.2019.04.258

CrossRef Full Text | Google Scholar

Lu Y., Liu J. (2019). The impact of information dissemination strategies to epidemic spreading on complex networks. Phys. Stat. Mech. Appl. 536, 120920. doi:10.1016/j.physa.2019.04.156

CrossRef Full Text | Google Scholar

Perc M., Gorišek Miksić N., Slavinec M., Stožerr A. (2020). Forecasting COVID-19. Front. Phys. 8, 127. doi:10.3389/fphy.2020.00127

CrossRef Full Text | Google Scholar

Petropoulos F., Makridakis S. (2020). Forecasting the novel coronavirus COVID-19. PLoS One 15, e0231236. doi:10.1371/journal.pone.0231236

CrossRef Full Text | Google Scholar

Qin E. d., He X., Tian W., Liu Y., Li W., Wen J, et al. (2003). A genome sequence of novel SARS-CoV isolates: the genotype, gd-ins29, leads to a hypothesis of viral transmission in south China. Dev. Reprod. Biol. 1, 101–107. doi:10.1016/s1672-0229(03)01014-3.

CrossRef Full Text | Google Scholar

Silva T. C., Zhao L. (2016). “Case study of network-based semi-supervised learning: stochastic competitive-cooperative learning in networks.” in Machine learning in complex networks (Cham, Switzerland: Springer International Publishing), 291–321.

Google Scholar

Small M., Tse C. K. (2005). Clustering model for transmission of the SARS virus: application to epidemic control and risk assessment. Phys. Stat. Mech. Appl. 351, 499–511. doi:10.1016/j.physa.2005.01.009

CrossRef Full Text | Google Scholar

Wang B., Li P. (2016). Introduction of small world network. Mod. Phys. 28, 51–55. [in Chinese]. doi:10.13405/j.cnki.xdwz.2016.03.018

Google Scholar

Wang Y., Yuan G., Fan C., Hu Y., Yang Y. (2019). Disease spreading model considering the activity of individuals on complex networks. Phys. Stat. Mech. Appl. 530, 121393. doi:10.1016/j.physa.2019.121393

CrossRef Full Text | Google Scholar

Wu Q., Hadzibeganovic T. (2020). An individual-based modeling framework for infectious disease spreading in clustered complex networks. Appl. Math. Model. 83, 1–12. doi:10.1016/j.apm.2020.02.012

CrossRef Full Text | Google Scholar

Wu Y., Gao L., Zhang Y., Xiong X. (2019). Structural balance and dynamics over signed BA scale-free network. Phys. Stat. Mech. Appl. 525, 866–877. doi:10.1016/j.physa.2019.04.038

CrossRef Full Text | Google Scholar

Xia C., Wang L., Sun S., Wang J. (2012). An sir model with infection delay and propagation vector in complex networks. Nonlinear. Dynam. 69, 927–934. doi:10.1007/s11071-011-0313-y

CrossRef Full Text | Google Scholar

Xia C.-Y., Wang Z., Sanz J., Meloni S., Moreno Y. (2013). Effects of delayed recovery and nonuniform transmission on the spreading of diseases in complex networks. Phys. Stat. Mech. Appl. 392, 1577–1585. doi:10.1016/j.physa.2012.11.043

CrossRef Full Text | Google Scholar

Zhang X., Ma R., Wang L. (2020). Predicting turning point, duration and attack rate of COVID-19 outbreaks in major western countries. Chaos Solit. Fractals 135, 109829. doi:10.1016/j.chaos.2020.109829

CrossRef Full Text | Google Scholar

Zhou R., Wu Q. (2019). Epidemic spreading dynamics on complex networks with adaptive social-support. Phys. Stat. Mech. Appl. 525, 778–787. doi:10.1016/j.physa.2019.03.107

CrossRef Full Text | Google Scholar

Zhu Y., Chen Y. Q. (2020). On a statistical transmission model in analysis of the early phase of COVID-19 outbreak. Stat Biosci. 1–17. doi:10.1007/s12561-020-09277-0

CrossRef Full Text | Google Scholar