Microscopic Theory for Spontaneous Fission

Nuclear fission is a fascinating field of research that involves large-amplitude collective dynamics of a microscopic many-body system. Specifically, the process of spontaneous-fission decay can only be explained within the quantum tunneling phenomenon. The present review discusses recent advancements in the theoretical understanding of spontaneous fission. These concern precise prediction of the spontaneous fission observables like fission lifetime and distribution of fragment yields. The theoretical developments presented here are based on a coherent coupling between the adiabatic collective dynamics and the static inputs obtained from the nuclear energy density functional formalism.

1. Introduction

Nuclear spontaneous fission (SF) is a unique decay mechanism that has crucial applications in both basic and applied sciences [1–3]. Particularly, the stability of very heavy and superheavy nuclei strongly depends on the SF probability [4–6]. Although superheavy nuclei predominantly decay via α-emission at the beginning of a decay chain, SF leads to terminate the chain. This type of decay sequences are experimentally observed for isotopes of Fl and Ts [7, 8]. Moreover, in comparison to α-emission, SF is predicted to be the preferred decay mode for neutron-rich superheavy nuclei [5, 9, 10]. In the case of nuclear astrophysics, SF strongly impacts the abundances of heavy elements in stars by participating in the r-process recycling mechanism [11–13]. Specifically, distributions of fission-fragment yields from different fission modes (SF, beta-delayed fission, and neutron-induced fission) are essential components of the r-process abundances [9, 14–19] and, therefore, very accurate prediction of these yields is required to improve the r-process network calculations. Further, as suggested in a recent study [20], the precise estimation of fission yields is indispensable for a better understanding of the chemical evolution of r-process elements produced in binary neutron-star mergers. In the application frontier, SF data are important to calibrate the nuclear material counting techniques relevant to power generation and international safeguards [21, 22]. However, measurements in actinide nuclei are restricted due to safety issues. Therefore, for both basic science and applications, predictive modeling of SF observables is of utmost interest. The present scenario and the prospects of fission theory are described in a recent review [23].

In the SF process, a fissioning nucleus undergoes quantum tunneling through a single or multiple potential barriers generated by the coherent motion of strongly interacting nucleons. Ideally, the time-dependent density functional theory (TDDFT) provides the most realistic microscopic framework to deal with such large amplitude collective dynamics [24–27]. Specifically, in the characterization of fission yields, nuclear dissipation plays a crucial role near the scission configuration and would be best accounted for by TDDFT. Albeit very promising, TDDFT poses several limitations in its application to SF. Primarily, the quantum tunneling is energetically forbidden within this semiclassical approach. Besides, current implementations of TDDFT simulate only a single fission path for a given initial condition; reconstruction of a full yield distribution requires large-scale Monte Carlo sampling, which is beyond the current computational capabilities. The exascale computing platforms may open up the avenues to overcome such restrictions [23].

In general, the collective dynamics of a nucleus is believed to be a much slower process than the random motion of the constituent nucleons. Consequently, majority of the fission models are implemented within the adiabatic approximation that segregates the collective degrees of freedom from the intrinsic coordinates. The same approach is adopted in a static nuclear density functional theory (DFT) based model [28], where the collective motion is simulated by incorporating the DFT inputs within an appropriate equation of motion. Specifically, in case of SF, the dynamics of a fissioning system can be divided into two successive steps as depicted in Figure 1 [29]. In the first step, the system tunnels through a multidimensional space of collective coordinates. This process is mainly governed by the potential energy profile and the collective inertia, which is often calculated within the adiabatic time-dependent Hartree-Fock-Bogoliubov (ATDHFB) formalism [30, 31]. The region beyond the outer turning point (“out” in Figure 1) is energetically accessible and the time-evolution in this space can be followed with a simple classical prescription, e.g., the Langevin dynamical model. Finally, the system breaks into two fragments at the scission configuration. The dynamics in the second phase involves the collective inertia and the dissipative forces as well. The SF half-life is primarily decided by the tunneling phase as, for most of the relevant nuclei, it is significantly slower than the subsequent propagation outside the barrier. The second dynamical phase controls the fission fragment properties like yield and total kinetic energy (TKE) distributions.

FIGURE 1

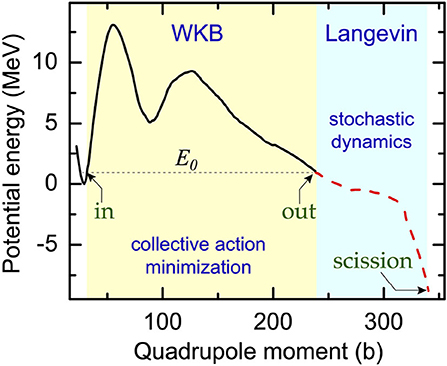
Figure 1. Variation in potential energy calculated along the most-probable fission path of ²⁴⁰Pu. The region marked as WKB is classically forbidden as the fission excitation energy E₀ is less than the potential energy. Shape evolution: the collective action is minimized between the turning points “in” and “out” by using the WKB method and, from “out” to scission, dynamics is governed by Langevin dynamics. The figure is adapted from Sadhukhan et al. [29].

Apart from the standard inputs discussed in the previous paragraph, paring correlations play a critical role in controlling the SF lifetime and the connected fission pathway. The individual nucleonic motion leads to shell structures that guide both the nuclear shape and the potential energy along a fission path. Moreover, crossings of single-particle levels can modify the collective inertia through associated changes in the single-particle configurations [32–34]. The residual interaction among these crossing configurations is strongly influenced by the pairing force. Precisely, a larger pairing gap Δ helps the collective motion to be more adiabatic [35–40]. The enhancement of pairing fluctuations along the fission path was first postulated in Moretto and Babinet [41] by using a simple parabolic potential. In fact, the collective inertia and potential energy show opposite trends as Δ changes. The potential energy increases as Δ deviates from the static value Δ_s, obtained from the self-consistent energy minimization procedure. In contrast, the collective inertia varies as Δ⁻² [35, 42–45] and, therefore, the dynamic Δ, corresponding to the minimum collective action, may differ from Δ_s. This suggests that the parameter Δ should be implemented as an independent dynamical variable to determine the least action trajectory. Indeed, a reduction in the collective action due to pairing fluctuations is observed in many macroscopic-microscopic studies [46–49]. In addition, the pairing fluctuations are recently treated as dynamical variables in microscopic models based on the DFT formalism [50, 51].

2. A Model for Spontaneous Fission Half-Life

2.1. Fission Half-Life

The SF mechanism involves a very wide range of timescales depending on the choice of the fissioning nucleus. For example, the observed SF half-life for actinides varies from a few ms to 10²⁰ yrs. Therefore, it is impractical to develop a SF model based on the real-time quantum dynamics. The most common approach for the calculation of SF half-life is rooted in the one-dimensional WKB approximation to the quantum tunneling process. The corresponding half-life can be expressed as [52, 53], T_1/2 = ln2/(nP), where n is the rate of collision on the fission barrier and P is the barrier penetration probability given by

$\begin{array}{ll}P={\left(1+exp\left[2S\left(L\right)\right]\right)}^{-1}.& (1)\end{array}$

In the above equation, S(L) is the action integral calculated along a predefined fission path L(s) in the multidimensional collective space. The expression for S(L) is given by,

$\begin{array}{ll}S\left(L\right)={\displaystyle {\int }_{s_{\text{in}}}^{s_{\text{out}}}}\frac{1}{\hslash }\sqrt{2{{M}}_{\text{eff}}\left(s\right)\left(V\left(s\right)-E_0\right)}ds,& (2)\end{array}$

where V(s) and ${{M}}_{\mathrm{\text{eff}}}(s)$ are the potential energy and collective inertia, respectively, along the path L(s). Here, s_in and s_out indicate the classical turning points defined by V(s) = E₀; E₀ being the zero-point energy at the ground state configuration. We can define different fission paths [L(s)] by choosing different values of q_i(s) along the path's length s. The minimum of S(L) corresponds to the most probable fission path [35, 54]. The ${{M}}_{\mathrm{\text{eff}}}$ can be expressed in terms of the multidimensional collective inertia tensor ${{M}}_{ij}(q_1,q_2,...)$ as [52, 53, 55]:

$\begin{array}{ll}{{M}}_{\text{eff}}\left(s\right)={\displaystyle \sum _{ij}}{{M}}_{ij}\left(q_1,q_2,...\right)\frac{d{q}_i}{ds}\frac{d{q}_j}{ds}.& (3)\end{array}$

Generalization of the WKB method to several dimensions is recently recommended as a future goal [23].

The potential energy V is obtained by subtracting the vibrational zero-point energy E_ZPE [56] from the Hartree-Fock-Bogoliubov (HFB) energy E_HFB(= 〈Ĥ_HFB〉). In the DFT formalism, E_HFB can be computed self-consistently by solving the constrained HFB equations for the Routhian:

$\begin{array}{ll}{Ĥ}^{\prime }={Ĥ}_{\text{HFB}}-{\displaystyle \sum _{ij}}{\lambda }_{ij}{\widehat{Q}}_{ij}-{\displaystyle \sum _{\tau =n,p}}\left({\lambda }_{\tau }{\widehat{N}}_{\tau }-{\lambda }_{2\tau }\Delta {\widehat{N}}_{\tau }^2\right),& (4)\end{array}$

where Ĥ_HFB, ${\widehat{Q}}_{ij}$, and ${\widehat{N}}_{\tau }$ represent the HFB hamiltonian, the mass multipole moment operators, and particle-number operators for neutrons (τ = n) and protons (τ = p), respectively. The Lagrange multipliers λ_2τ can be used to control the particle-number fluctuation terms: $\Delta {\widehat{N}}_{\tau }^2={\widehat{N}}_{\tau }^2-{\langle {\widehat{N}}_{\tau }\rangle }^2$. Pairing correlations in nucleons are interconnected to the particle-number fluctuations [57, 58] and, hence, expected to be stronger for λ_2τ > 0, compared to its static value obtained with λ_2τ = 0. Further, the overall magnitude of pairing correlations is linked to the average pairing gap [31, 59]. Therefore, λ_2n and λ_2p can be utilized as dynamical coordinates [50] to scan the configuration space over a wide range of Δ. It is indeed more physical to select the isoscalar (λ_2n + λ_2p) and the isovector (λ_2n − λ_2p) variations as independent coordinates. Consequently, a one-dimensional path L(s) can be identified with the collective variables {q_i} ≡ {Q₂₀, Q₂₂, Q₃₀, …, λ_2n + λ_2p, λ_2n − λ_2p} as functions of path's length s. In a recent study [50], the role of dynamical isovector pairing is found to be negligible and, therefore, the associated coordinate λ_2n − λ_2p can be set to zero. I denote λ_2n + λ_2p as λ₂ in the subsequent discussions. Also, I should mention that an appropriate normalization scheme for all the coordinates must be adopted to make ds dimensionless in Equation (2) [50].

Minimum-action paths can be simulated by using two different techniques named as the dynamic-programming method (DPM) [52, 56] and the Ritz method (RM) [53, 56]. In DPM, the dynamical space is first discretized into a multi-dimensional mesh. Then, at any intermediate step, minimum action paths are calculated for all the mesh points on a hypersurface perpendicular to the elongation coordinate (Q₂₀). Calculation is propagated along the Q₂₀ direction and finally the hypersurface of the desired outer-turning point is reached. In this method, path lengths are further divided into smaller segments whenever the distance between two adjacent mesh points is large. This is essential to ensure numerical accuracy as the collective inertia may vary quite sharply in certain regions of the collective space. In the case of RM, trial paths are defined in terms of Fourier series of dynamical coordinates and the coefficients of different Fourier components are obtained by minimizing the action. Although RM is easier to implement numerically, efficiency of this method depends on the number of Fourier components needed to reproduce the actual fission path. On the other hand, DPM is free of such limitations.

The HFB energy E_HFB can be calculated by employing either covariant or non-relativistic energy density functionals (EDFs). In the case of non-relativistic EDFs, the SkM* parametrization [60] of the zero range Skyrme functionals is commonly used in fission studies together with the density-dependent mixed pairing interaction [61], where the pairing strengths are calculated locally by reproducing the odd-even mass differences around ²⁴⁰Pu [62]. The parameters of this parametrization are benchmarked for large deformations relevant to fission. Recent optimizations of the Skyrme functionals are performed within the UNEDF project [63] and one of its variants, UNEDF1_HFB, Schunck et al. [64] is successfully applied to fission works [65–67]. Apart from these, other microscopic interactions like the finite-range Gogny interaction [68–70] and the Barcelona-Catania-Paris-Madrid EDFs [9, 69, 71, 72] are widely used in the SF calculations. Despite different groups of EDFs exist, appropriate benchmarking with the experimental data are performed to ensure the consistency of model predictions. For example, it is recently shown that the SF yields of the superheavy ²⁹⁴Og nucleus are robust against different choices of EDFs [66]. Covariant EDFs [51, 73–78] based frameworks for large-amplitude collective dynamics are becoming more accessible with the increasing computational resources. Interestingly, SF pathways, calculated within covariant EDFs [51, 74], are found to be in close agreement with the non-relativistic results.

2.2. Calculation of Fission-Fragment Yields

It is desirable to use the TDDFT framework to study the evolution of a fissioning system in the collective space beyond the outer-turning point (Figure 1: region in-between “out” and “scission”). However, as pointed out in a recent study [79], the dynamics near scission is strongly dissipative and existing versions of TDDFT are not adequate since they are lacking fluctuations in collective coordinates. Also, an advanced TDDFT framework is recently proposed that incorporates fluctuations to generate TKE and yield distributions of fission fragments. In this approach, density fluctuations are assumed to prepare an ensemble of different configurations outside the barrier region and the subsequent propagation is followed with the standard TDDFT [80]. However, the fluctuations are considered in a somewhat restricted configuration space and a more exhaustive calculation may require huge computations. A feasible alternative to TDDFT is the time-dependent generator coordinate method (TDGCM) [77, 81–84]. However, in this approach, the Gaussian overlap approximation [81, 85] is additionally assumed to derive simple expressions for the parameters of the collective Hamiltonian. As a result, structural details like large fluctuations in the collective inertia are diluted [86]. It is also pointed out in the recent proposal [23] by Bender et al. that a stochastic mean-field approach with large fluctuations is more suitable for calculating fragment yields. Furthermore, the requirement of strongly dissipative dynamics for yield distributions of excited nuclei is well-established [87].

The stochastic Langevin dynamical model is a plausible option to avoid all the above-mentioned difficulties. It is quite straightforward to implement this model even in a complicated multidimensional collective space. In Langevin dynamics, the intrinsic motion of the nucleons is assumed to form a heat bath. The collective coordinates interact with the heat bath through random and dissipative forces. This decoupling of the collective coordinates from the internal degrees of freedom is performed under the adiabatic approximation. Fluctuations (random forces) introduce stochasticity in the collective dynamics and dissipation hinders the motion by transferring collective energy to the heat bath. Also, the collective motion experiences the standard conservative force exerted by potential energy. First, a family of SF probabilities P(s_out) is obtained on the hypersurface of outer turning points s_out. The hypersurface should contain mass octupole moment Q₃₀ as one of the coordinates since this variable defines different realizations of the fragment mass and charge. Subsequently, fission paths are computed for all the s_outs by solving the Langevin equations [88, 89]:

$\begin{array}{l}\frac{d{p}_i}{dt}=-\frac{p_j{p}_k}{2}\frac{\partial }{\partial q_i}{\left({{M}}^{-1}\right)}_{jk}-\frac{\partial V}{\partial q_i}-{\eta }_{ij}{\left({{M}}^{-1}\right)}_{jk}{p}_k+g_{ij}{\Gamma }_j\left(t\right),\\ \frac{d{q}_i}{dt}={\left({{M}}^{-1}\right)}_{ij}{p}_j,& (5)\end{array}$

where p_i is the momentum conjugate to q_i. η_ij and g_ij represent the dissipation tensor and the strength of the random force, respectively, and these two quantities are connected through Einstein's fluctuation-dissipation theorem: $\sum _k{g}_{ik}{g}_{jk}={\eta }_{ij}{k}_{\text{B}}T$. Here, T is the temperature of the nucleus. It is calculated at each instant of the Langevin evolution by assuming the nucleus as a non-interacting Fermi gas and the resulting formula is $T=\sqrt{E^{*}/a}$ (T in MeV); a being the level density parameter and $E^{*}=V(s_{\text{out}})-V(s)-\frac{1}{2}\sum {({{M}}^{-1})}_{ij}{p}_i{p}_j$. In the case of SF studies, a can be approximated as a shape independent constant given by a = A/10 MeV⁻¹ [29, 66]. The stochastic variable Γ_j(t) signifies the Markovian nature of the random force with the time correlation property: $\langle {\Gamma }_k(t){\Gamma }_l(t^{\prime })\rangle =2{\delta }_{kl}\delta (t-t^{\prime })$. The excitation energy E^* increase as the system slides down to lower potential resulting stronger effects from fluctuations. The scission configuration is defined with the condition that the number of neck-particles (N_q) in the fissioning system is less than a critical value [28]. Each point on the scission hypersurface uniquely identifies the particle numbers of two fission fragments and these numbers can be calculated by integrating the nucleonic density distributions [62]. Owing to the random force, an ensemble of Langevin events with the same initial configuration (i.e., same s_out) yields different fission pathways. Finally, the charge and mass distributions of the yields can be extracted by counting the number of events terminating at a given fragmentation. The numbers are weighted with P(s_out) to account for the tunneling phase. Further, to incorporate the uncertainties in N_q, Langevin yields are convoluted with Gaussian functions [90].

Although the Langevin model does not explicitly simulate the time evolution of nucleonic degrees of freedom, it incorporates all the essential microscopic effects through the input quantities like PES and collective inertia which are obtained from effective nucleon-nucleon interactions. A special characteristic of the Langevin formalism is the presence of fluctuating and dissipative forces. In the case of induced fission, the importance of fluctuations and dissipation is well-established [87, 91] as the compound system is produced at least with a reasonable amount of excitation energy. In SF, the ground-state zero-point vibration is the initial source of excitation energy and it is inadequate to trigger any noticeable randomness in the collective motion. However, for all the relevant nuclei, potential energy drops rapidly below its ground state value as the deformation grows beyond the tunneling region. Consequently, nuclei acquire sufficient excitation energy that enhances fluctuations to a considerable level. In the following section, I have demonstrated the impact of the random force in Equation (5) on SF pathways.

2.3. Nucleonic Localization Function and Pre-fragments

For a better understanding of the structural evolution in a fissioning nucleus, nucleonic localization functions (NLF) are calculated [25, 92, 93]. NLF measures the probability of finding two nucleons with the same spin σ and isospin q at the same spatial localization. It is computed as described in references [93, 94]:

$\begin{array}{ll}{C}_{q\sigma }={\left[1+{\left(\frac{{\tau }_{q\sigma }{\rho }_{q\sigma }-\frac{1}{4}|\nabla {\rho }_{q\sigma }{|}^2-j_{q\sigma }^2}{{\rho }_{q\sigma }{\tau }_{q\sigma }^{\text{TF}}}\right)}^2\right]}^{-1},& (6)\end{array}$

where ρ_qσ, τ_qσ, j_qσ and ∇ρ_qσ are the particle density, kinetic energy density, current density, and density gradient, respectively. The Thomas-Fermi kinetic energy density ${\tau }_{q\sigma }^{\mathrm{\text{TF}}}=\frac{3}{5}{(6{\pi }^2)}^{2/3}{\rho }_{q\sigma }^{5/3}$ is introduced as a normalization parameter. A value of C ~ 1 indicates a large nucleon's localization, i.e., a low probability of finding two nucleons with the same quantum numbers at the same spatial location. On the other hand, C = 1/2 corresponds to the limit of a homogeneous Fermi gas. The concept of NLF was originally applied to characterize chemical bonds in electronic systems. In nuclear physics, it is first used to visualize the cluster structures in light nuclei [94]. As illustrated in references [93, 94], the clustering of nucleons inside a nucleus can be predicted more precisely by NLFs in comparison to the scalar density distributions given by ρ_qσ. This is because the spatial distributions of NLFs exhibit pattern of concentric rings that reflect the underlying shell structure, but such patterns are averaged out in the density distributions. Recent studies [66, 67, 92, 93] suggest that NLFs can be utilized to identify prefragments in a fissioning nucleus. The method is described in Sadhukhan et al. [92] for a typical case of elongated ²⁴⁰Pu. The corresponding NLFs are shown in Figure 2. Evidently, the parts of NLFs for z ≥ z_L and z ≤ z_H contain ring-like patterns delineating the presence of localized nucleons inside the deformed ²⁴⁰Pu. This finding is further extended to define prefragments by integrating the densities of the localized portions and doubling the result to account for reflection symmetry. As replicated in Figure 2, the compound nuclear NLFs were found to be in remarkable agreement with the ground-state NLFs of the predicted prefragments (¹²⁸Sn and ⁸⁰Ge) [92]. Similarly, prefragments are predicted successfully by comparing the scalar densities [95, 96]. Here, I should mention that the notion of prefragments is a purely theoretical concept as it cannot be measured experimentally. Moreover, other definitions of pre-fragment exist [25, 97]. Therefore, the validity of a pre-fragment based description depends on its ability to reproduce the experimental observables.

FIGURE 2

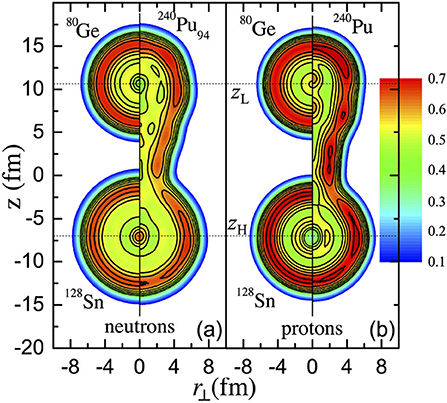
Figure 2. Right of each panel: neutron (a) and proton (b) localization functions in a deformed configuration on the fission path of ²⁴⁰Pu. Left of each panel: NLFs of the localized prefragments, ⁸⁰Ge and ¹²⁸Sn, as indicated. Vertical lines are symmetry axes. Maximum extensions of the NLFs along the radial coordinate r_⊥(z) are marked with horizontal dotted lines: z = z_L and z = z_H. The figure is adapted from Sadhukhan et al. [92].

3. Results on Different Aspects of Spontaneous Fission

Calculation of SF observables is a very active field of research as the theoretical capability is increasing. In parallel, appropriate sets of fission observables are required to benchmark theoretical models [98]. In the rest of this review, I will discuss selected results from the recent theoretical achievements pertinent to both of these aspects.

3.1. Effect of Collective Inertia in Fission Pathway

In recent studies [56, 74], it is demonstrated that the SF pathways are strongly influenced by the characteristics of the collective inertia. The microscopic collective inertia is usually calculated within the ATDHFB formalism [30, 31] and it is commonly known as the cranking inertia ${{M}}^C$ [86]. An exact calculation of ${{M}}^C$ requires derivatives of the particle and pairing densities with respect to the dynamical coordinates. These can be achieved by employing the three-point or a higher-order Lagrange formula [99, 100]. On the other hand, in case of the commonly used perturbative cranking inertia ${{M}}^{C^p}$ [86], these derivatives are reduced to matrix elements of mass multipole moments (Q_ij). Figure 3 demonstrates the variations of square-root-determinants of both ${{M}}^C$ and ${{M}}^{C^p}$ calculated for ²⁶⁴Fm in a two-dimensional collective space of (Q₂₀, Q₂₂). As discussed in 1, $|{{M}}^C{|}^{1/2}$ shows large fluctuations as an outcome of crossings in single-particle levels at the Fermi energy [39]. To affirm this, single-particle energies for ²⁶⁴Fm are displayed in Figure 4 along two straight lines defined by Q₂₂ = 0 and Q₂₀ = 61 b. Multiple level crossings near the Fermi energy are clearly visible at deformations where ${{M}}^C$ changes sharply. Similar features of the inertia tensor are observed within the covariant EDF formalism [74].

FIGURE 3

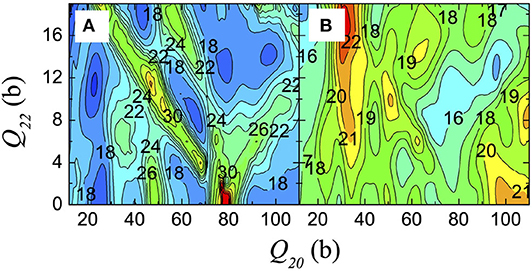
Figure 3. Square-root-determinant of inertia tensors (A) $|{{M}}^C{|}^{1/2}$ and (B) $|{{M}}^{C^{\text{p}}}{|}^{1/2}$ (both in ℏ² MeV⁻¹ b⁻²/1,000) calculated for ²⁶⁴Fm. The figure is modified from Sadhukhan et al. [56].

FIGURE 4

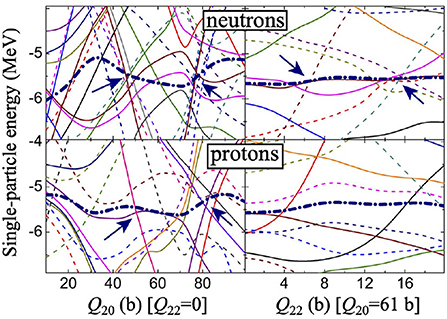
Figure 4. Variation in single-particle energies of neutron (top) and proton (bottom) calculated for ²⁶⁴Fm along Q₂₀ (left, at Q₂₂ = 0) and Q₂₂ (right, at Q₂₀ = 61 b). The Fermi energies are marked with thick dash-dotted lines. The arrows indicate regions of level-crossings near Fermi energy. The figure is adapted from Sadhukhan et al. [56].

The dynamical minimum-action paths (or equivalently most probable paths), obtained with ${{M}}^C$ and ${{M}}^{C^p}$, are drawn in Figure 5. The same figure also shows the static path that traverses the minimized collective potential [56]. Due to strong dynamical hindrance by the perturbative inertia the corresponding minimum-action path avoids large triaxial shapes. ${{M}}^{C^{\text{p}}}$ varies rather smoothly along both the deformation coordinates and, therefore, the minimum in the action integral in Equation (2) is achieved by minimizing the path-length. This weaker dependency on the triaxial shapes, imposed by collective inertia, is also observed in older fission studies [101–105]. On the other hand, due to localized large variations in ${{M}}^C$, the non-perturbative path passes through the triaxial shapes that are fairly close to the static pathway. Apparently, both the non-perturbative and static trajectories always adhere to a configuration that tries to minimize the density of single-particle levels on the Fermi energy by avoiding level crossings. In short, the underestimation of structural details in ${{M}}^{C^p}$ results in an artificial restoration of axial symmetry, which is broken in both static and non-perturbative approaches. This conclusion is also verified within the relativistic mean-field formalism [74]. Although the inertia strongly influences the topology of the minimum action path near the first fission barrier in actinides, it is rather simple in the space outside the fission isomer. Here, the SF path usually follows the minimum distance from a mass-symmetric configuration to the nearest outer turning point [29] (shown in the following figure, Figure 8).

FIGURE 5

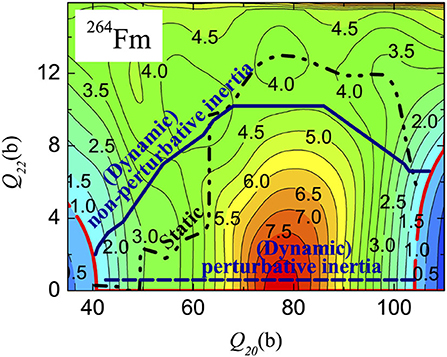
Figure 5. Minimum-action (or most-probable) fission paths of ²⁶⁴Fm [56], calculated for ${{M}}^C$ (solid line) and ${{M}}^{C^{\text{p}}}$ (dashed line) using the DPM technique. cranking inertia using DMP technique. The static pathway is shown by the dash-dotted line. The loci of turning points are marked by thick solid lines. The PES (in MeV) is plotted for reference. The figure is modified from Sadhukhan et al. [56].

Most importantly, apart from modifying the fission pathways, collective inertia strongly impacts the fission lifetime. The SF half-life changes by orders of magnitude depending on the choice of collective inertia, even for the same fission trajectory [56]. For example, values of T_1/2 and S(L) corresponding to different selections of the fission path and inertia are given in Table 1.

TABLE 1

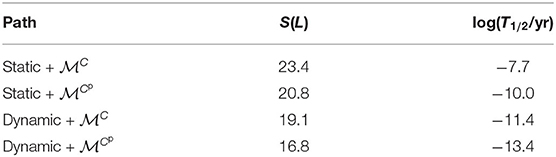
Table 1. Values of the action integral (2) and half-lives for different spontaneous fission pathways shown in Figure 5.

3.2. Role of Pairing Correlations

In the previous subsection, I demonstrated that a fissioning system tries to always follow single-particle configurations with comparatively lower level density. This can be fulfilled by avoiding the regions of level-crossing. In contrast, pairing correlations increases with the single-particle level density and, as I have discussed in 1, it affects the potential and collective inertia in the opposite way. The potential energy use to increase with pairing fluctuations, while the collective inertia diminishes as the pairing correlations become stronger than self-consistent values. The least-action path is determined dynamically by the interplay between these two inverse effects. Typical nature of a PES and ${{M}}^C$ along the pairing coordinate is shown in Figure 6 [50]. It portrays clear evidence of the opposite tendencies discussed above. Minimum action paths for two different nuclei are calculated in Sadhukhan et al. [50] by including the pairing degrees of freedom. Corresponding projections onto the (Q₂₀, Q₂₂) and (Q₂₀, λ₂) planes are shown in Figure 7. Also, two-dimensional (2D) fission paths calculated without pairing fluctuations are compared in this figure. In the case of ²⁶⁴Fm, the three-dimensional (3D) pathway, calculated with pairing fluctuations, closely follows triaxial configurations of the corresponding 2D path. However, this scenario changes for ²⁴⁰Pu, where the difference between the axial and triaxial barrier-heights is small and, as a result, pairing correlations could enforce the axial symmetry of the path in the region between the ground state configuration and superdeformed fission isomer. Nevertheless, irrespective of this system dependence, the pairing fluctuations are substantially enhanced in both the cases. Therefore, the dynamic coupling between pairing and deformation coordinates can produce dramatic changes in the SF process. Relativistic mean-field calculation [51] for Fm isotopes also shows a similar behavior of the fission pathway under the influence of dynamic paring fluctuations. Moreover, owing to the associated reduction in the action integral, the calculated SF half-life decreases by as much as three decades. These strong dynamical effects, predicted for SF, are however expected to disappear at higher excitation energies of the compound system. The subsection is concluded by demonstrating the average pairing gaps (Δ_n and Δ_p), in Figure 8, along the SF path of ²⁴⁰Pu [29]. Although the dynamic (3D) path overlaps with the static pathway in the (Q₂₀, Q₃₀) space, average pairing gaps are always higher in case of the 3D path except near the outer turning line where pairing correlations are quenched.

FIGURE 6

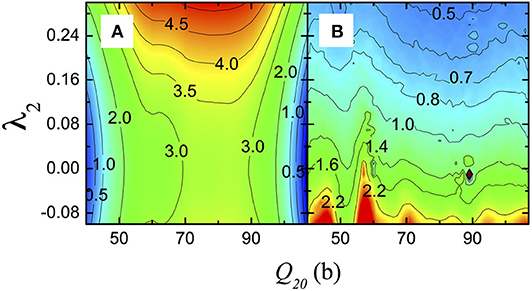
Figure 6. Projections of (A) potential energy (in MeV) after subtracting the ground state value, and (B) $|{{M}}^C{|}^{1/3}$ (in ℏ² MeV⁻¹/1,000). Both are calculated for ²⁶⁴Fm in the three-dimensional space of (Q₂₀, Q₂₂, λ₂) and then projected on the Q₂₂ = 0 plane. The figure is modified from Sadhukhan et al. [50].

FIGURE 7

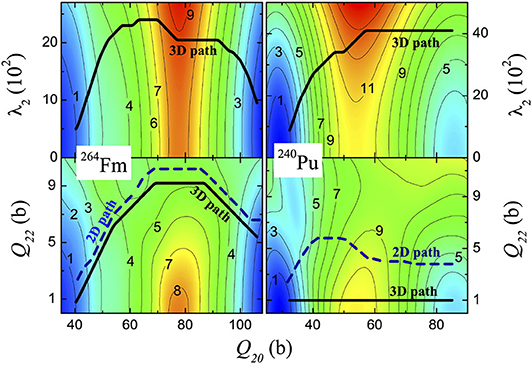
Figure 7. Thick solid lines: projections of the three-dimensional (3D) minimum-action paths for ²⁶⁴Fm (left) and ²⁴⁰Pu (right) on the (Q₂₀, λ₂; Q₂₂ = 0) (top) and (Q₂₀, Q₂₂; λ₂ = 0) (bottom) planes. Thick dashed lines: two-dimensional (2D) paths computed without pairing fluctuations. The PES corresponding to Q₂₂ = 0 (top) and static pairing, i.e., λ₂ = 0, (bottom) are shown for reference. The figure is modified from Sadhukhan et al. [50].

FIGURE 8

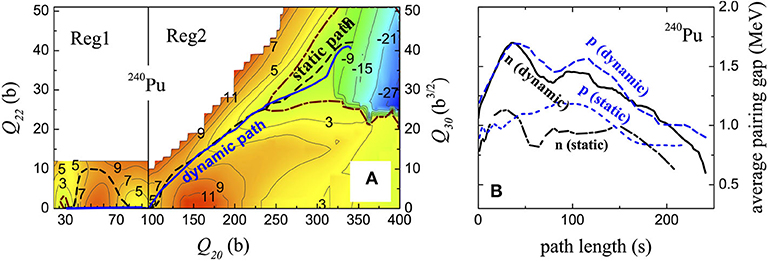
Figure 8. (A) The 3D dynamic path (solid line), projected on the λ₂ = 0 surface, and the 2D static path (dashed line) in the two considered regions (Reg1: (Q₂₀, Q₂₂, λ₂), Reg2: (Q₂₀, Q₃₀, λ₂)) of the collective space. The reason for this choice of 3D-3D configuration space is explained in Sadhukhan et al. [29]. The contours of inner and outer turning points are shown by dash-dotted lines. (B) Average pairing gaps, for neutrons (n) and protons (p), along the 3D dynamic (with pairing fluctuations) and 2D static (λ₂ = 0) pathways shown in (A). The figure is modified from Sadhukhan et al. [29].

3.3. Fission-Fragment Yield Distributions

Stochastic Langevin dynamics is widely used to study fission fragment yield distributions of excited compound systems [89, 91, 106, 107]. Only recently, it is successfully applied to calculate SF yields [29]. The detailed formalism is described in 1. Since the dynamics is stochastic in nature, it is difficult to understand the time evolution from a single fission event. Therefore, the concept of effective fission path (EFP) is devised in Sadhukhan et al. [92] for a better realization of the post-tunneling dynamics. First, for a given initial configuration, the local density of Langevin trajectories [108] is computed by counting the number of tracks in a small volume element of the collective space. Such distributions for two initial configurations are presented in Figure 9. Evidently, these two distributions are quite distinct in nature. The spreading of distribution is mainly governed by the interplay between the conservative and fluctuating forces. As I explained in 1, fluctuations become dominant near the scission and it leads to broader trajectory distributions.

FIGURE 9

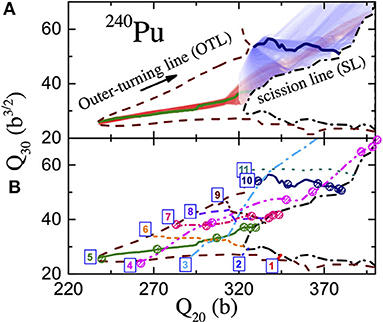
Figure 9. (A) The density of Langevin trajectories for two different initial configurations and the corresponding EFPs in the (Q₂₀, Q₃₀) plane. The loci of outer turning-points land scission configurations are shown by dashed and dash-dotted lines, respectively. (B) Eleven EFPs marked according to their initial coordinates. The figure is adapted from Sadhukhan et al. [92].

Next, the EFP is calculated by tracing the maxima in a trajectory-density distribution. Effectively, an EFP guides to the most probable fragmentation for the associated initial configuration. Eleven distinct EFPs are calculated in Sadhukhan et al. [92] for the representative system ²⁴⁰Pu, and these are further shown in Figure 9. Also, the partial contribution of each EFP to the total mass distribution is extracted by weighing the corresponding distribution with the appropriate tunneling probability. All the eleven partial mass distributions are plotted in Figure 10 along with the overall distribution. Due to higher tunneling probability, the peak region of the cumulative distribution is mostly contributed by EFPs close to the most probable path (EFP 5). On the other hand, contributions are negligible from those EFPs which originate far away from the most-probable outer turning point. For example, EFP 1 and EFP 11 hardly alters the total mass distribution. Most interestingly, certain EFPs (e.g., EFP 3 and EFP 4), associated with high tunneling probability, end up at large mass asymmetries and these constitute the tail part of the yield distribution. Such fission trajectories can only appear due to the presence of the random force in the Langevin dynamics.

FIGURE 10

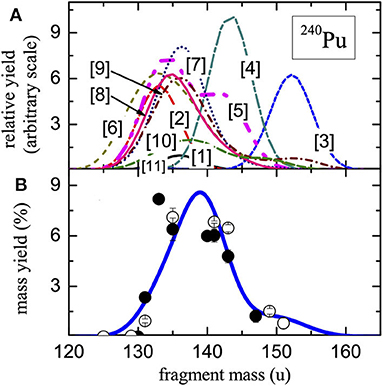
Figure 10. (A) Partial mass distributions for different EFPs of Figure 9B as indicated. The distribution corresponding to the most-probable fission path, i.e., EFP 5, is shown by a thick line. (B) The mass distribution for the SF of ²⁴⁰Pu obtained by counting contributions from all the Langevin trajectories, in addition to the eleven selected EFPs. The experimental data [109, 110] are shown by circles that include mirror points (open circles). Only the heavy-fragment parts are plotted in both (A,B). The figure is partially adapted from Sadhukhan et al. [92].

In addition to the isolated yield distributions corresponding to either mass or charge of the fission fragments, DFT inputs enable the Langevin model to predict the correlation between mass and charge numbers of the fragments. In a recent study [66], it is calculated for the heaviest discovered element ${}_{118}^{294}$Og. Three different EDFs are used for this purpose and, as shown in Figure 11, all of them predict a strongly asymmetric fission, or cluster emission, to be the dominant decay mode for this nucleus.

FIGURE 11

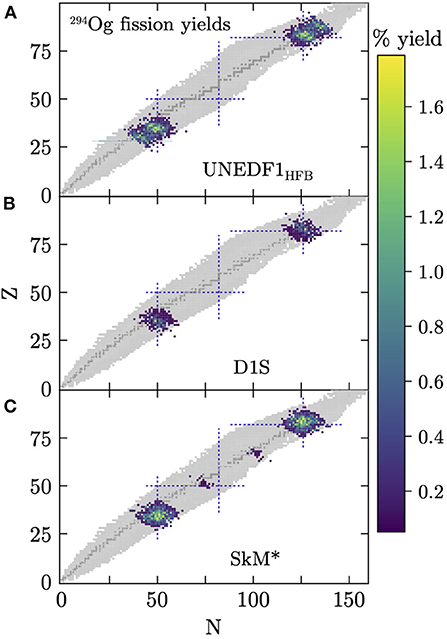
Figure 11. Fission fragment distributions for ${}_{118}^{294}$Og₁₇₆ obtained in UNEDF1_HFB (A), D1S (B), and SkM* (C) EDFs using the non-perturbative cranking ATDHFB inertia and a standard value of dissipation strength [66]. Known isotopes are marked in gray [111]. Dotted lines indicate the magic numbers: 50, 82, and 126. The figure is adapted from Matheson et al. [66].

3.4. Uncertainties in Yield Distributions

It is necessary to estimate the uncertainties due to different model parameters [112]. In case of SF yield distributions, predicted within the hybrid WKB + Langevin method, uncertainties are primarily associated to the three input quantities: ground state zero-point energy E₀, dissipation tensor η_ij in Equation (5), and scission configuration which is defined with the neck-particle number N_q. Moreover, the use of a particular EDF may induce additional bias in the results. In practice, the SF half-life is reproduced by tuning the free parameter E₀ [5, 29] that effectively shifts the location of the inner and outer turning-points. As a result, both P(s_out) and fission paths are modified. Secondly, the fragment properties are expected to strongly depend on the scission configuration. However, no method exists that defines the scission configuration uniquely within the static adiabatic description of fission. Usually, different values of N_q are used to identify the scission hypersurface in a multidimensional space. In the case of η_ij, a microscopic theory is still missing and it is considered as an adjustable parameter in the SF model [29, 66]. Considering all these limitations, a sensitivity analysis of the yield distributions with respect to all the model parameters is essential. Calculations are performed in Sadhukhan et al. [29] to illustrate the uncertainties in the yield distributions produced by E₀, N_q, and η_ij. As demonstrated in Figure 12, the mass and charge distributions of ²⁴⁰Pu are found to be robust against wide variations of all these input quantities. A similar response to the dissipation tensor is observed for the yield distributions of ${}_{118}^{294}$Og [66]. Further, as plotted in Figure 13, both mass and charge distributions show weak dependency on the choice of the EDF and also on the dimensionality of the configuration space. Therefore, the hybrid model, with reasonable values of the input parameters, can be used for a reliable prediction of the SF yields. Of course, theoretical progresses toward a more precise calculation of input parameters is required [23].

FIGURE 12

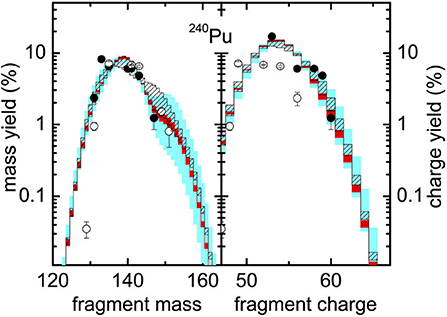
Figure 12. Mass (left) and charge (right) distributions of heavier fragment in the SF of ²⁴⁰Pu. The symbols are experimental values as shown in Figure 10. The shaded regions describe uncertainties in the yield distributions corresponding to different values of the model parameters: E₀ (narrow red band), dissipation tensor (wider cyan band), and scission configuration (linear hatch pattern). See Sadhukhan et al. [29] for details. The figure is adapted from Sadhukhan et al. [29].

FIGURE 13

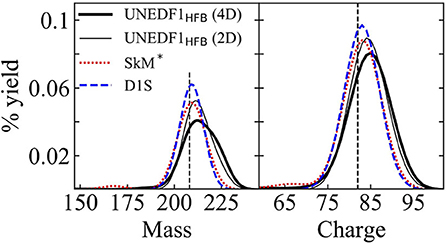
Figure 13. Predicted heavy-fragment mass and charge yields of ²⁹⁴Og obtained by employing UNEDF1_HFB functional in the 4D (Q₂₀, Q₂₂, Q₃₀, λ₂) and the 2D (Q₂₀, Q₃₀) spaces, and in the 2D (Q₂₀, Q₃₀) space for other functionals (SkM^* and D1S). The figure is adapted from Matheson et al. [66].

3.5. Prediction of Fragments From Localized Pre-fragment

I have already argued how a pre-fragment can be defined from NLFs (see section 1). Properties of such prefragments are needed to be scrutinized very carefully to validate their applicability in predicting the fission fragments. To this end, the particle numbers of the prefragments are extracted along the EFPs shown in Figure 9 [92]. The results are reiterated here in Figure 14 and it displays that the pre-fragment particle-numbers remain remarkably stable as the deformation increases toward scission. Moreover, variations in these numbers, indicated by the bands in Figure 14, become fairly narrow (< ±2 particles) at large deformations. This suggests that the prefragments formed in an initial configuration of the fissioning nucleus hardly change. This early development of the prefragments is a manifestation of the freeze-out of single-particle energies along the fission pathway [25, 39, 56, 113], since the system tries to retain its microscopic configuration by escaping the level crossings. The concept is further extended to predict the particle numbers of the fission fragments. This is accomplished by distributing the neck nucleons to each pre-fragments following a statistical prescription. The predicted yield distributions are found to agree well with the experimental data [67].

FIGURE 14

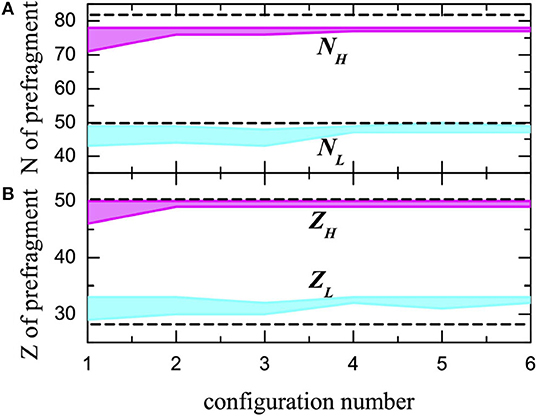
Figure 14. The ranges for the number of localized neutrons (A) and protons (B) for heavier (N_H, Z_H) and lighter (N_L, Z_L) prefragments as a function of the configurations along the EFPs marked in Figure 9B by circles. The magic numbers are marked by horizontal dotted lines.

This fast and efficient method of fission-fragment identification will be very useful in the r-process network calculations that predict the astrophysical abundances of more than half of the elements heavier than iron. In a very neutron-rich environment, such at those exists in the ejecta of neutron-star mergers, neutron-induced and β-delayed fission are highly probable. It is speculated that nuclear fission terminates the r-process paths near A ~ 300. The location of the r-process endpoint can significantly influence the final yield distribution [114]. Since these superheavy nuclei can not be studied with a standard laboratory procedure, reliable theoretical predictions are of utmost interest. Hence, the density functional formalism, which is deeply rooted in the underlying nucleon-nucleon interactions, provides an ideal platform. Moreover, there can be multiple fission cycles along the r-process path and these cycles involve a wide variety of fissioning nuclei. Therefore, the theoretical method needs to be very time-efficient. The model prescribed in Sadhukhan et al. [67] fulfills both the requirements. In parallel, precise measurements of fission fragment yield distributions of neutron rich actinides and heavier elements may help to minimize the theoretical uncertainties associated with model parameters.

4. Conclusion

In this review, I have elaborated on a successful theoretical model for the spontaneous fission yields and lifetime. It is developed in a hybrid manner by combining the WKB approximation for quantum tunneling with the stochastic Langevin dynamics. Several recent advancements to enhance the predictive capabilities of this hybrid model are presented. In particular, I elucidated the intricate role of collective inertia and pairing correlations in guiding the dynamics during the tunneling phase. The inevitable presence of fluctuation and dissipation in the final stage of the fission dynamics is explained in connection with the calculation of fragment yields. This approach could be a prospective candidate for large-scale applications to a wide range of fissioning nuclei. In parallel, further improvements in different aspects of the model are in queue [23].

Although an accurate prediction of the fission observables is the foremost priority for a fission model, global calculations of fragment properties related to stellar nucleosynthesis processes additionally demand a faster and more reliable technique compared to existing models. This is because such calculations involve a large variety of fissioning nuclei most of which are outside the valley of nuclear stability. For this purpose, a quicker method [67] is recently proposed that utilizes the idea of shell-stabilized/localized prefragments. This model enables the identification of fragments by performing self-consistent calculations within a very localized domain of the configuration space. Clearly, theoretical investigation of the fission process is a diverse field of research with a broad perspective.

Author Contributions

The author confirms being the sole contributor of this review work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author acknowledges useful discussions with Witold widows.

References

1. Krappe HJ, Pomorski K. Theory of Nuclear Fission: A Textbook. New York, NY: Springer (2012).

Google Scholar

2. Shultis JK, Faw RE. Fundamentals of Nuclear Science and Engineering. 2nd ed. Boca Raton, FL: CRC Press (2007).

Google Scholar

3. Wagemans C. The Nuclear Fission Process. Boca Raton, FL: CRC Press (1991).

Google Scholar

4. Oganessian YT. Heaviest nuclei from ⁴⁸Ca-induced reactions. J Phys G. (2007) 34:R165. doi: 10.1088/0954-3899/34/4/R01

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Staszczak A, Baran A, Nazarewicz W. Spontaneous fission modes and lifetimes of superheavy elements in the nuclear density functional theory. Phys Rev C. (2013) 87:024320. doi: 10.1103/PhysRevC.87.024320

CrossRef Full Text | Google Scholar

6. Giuliani SA, Matheson Z, Nazarewicz W, Olsen E, Reinhard PG, Sadhukhan J, et al. Colloquium: superheavy elements: Oganesson and beyond. Rev Mod Phys. (2019) 91:011001. doi: 10.1103/RevModPhys.91.011001

CrossRef Full Text | Google Scholar

7. Khuyagbaatar J, Yakushev A, Düllmann CE, Ackermann D, Andersson LL, Asai M, et al. ⁴⁸Ca+²⁴⁹Bk fusion reaction leading to element Z = 117: long-lived α-decaying ²⁷⁰Db and discovery of ²⁶⁶Lr. Phys Rev Lett. (2014) 112:172501. doi: 10.1103/PhysRevLett.112.172501

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Utyonkov VK, Brewer NT, Oganessian YT, Rykaczewski KP, Abdullin FS, Dmitriev SN, et al. Neutron-deficient superheavy nuclei obtained in the ²⁴⁰Pu+⁴⁸Ca reaction. Phys Rev C. (2018) 97:014320. doi: 10.1103/PhysRevC.97.014320

CrossRef Full Text | Google Scholar

9. Giuliani SA, Martínez-Pinedo G, Robledo LM. Fission properties of superheavy nuclei for r-process calculations. Phys Rev C. (2018) 97:034323. doi: 10.1103/PhysRevC.97.034323

CrossRef Full Text | Google Scholar

10. Afanasjev AV, Agbemava SE, Gyawali A. Hyperheavy nuclei: existence and stability. Phys Lett B. (2018) 782:533. doi: 10.1016/j.physletb.2018.05.070

CrossRef Full Text | Google Scholar

11. Arnould M, Goriely S, Takahashi K. The r-process of stellar nucleosynthesis: Astrophysics and nuclear physics achievements and mysteries. Phys Rep. (2007) 450:97. doi: 10.1016/j.physrep.2007.06.002

CrossRef Full Text | Google Scholar

12. Panov IV, Korneev IY, Rauscher T, Martínez-Pinedo G, Kelic-Heil A, Zinner NT, et al. Neutron-induced astrophysical reaction rates for translead nuclei. Astron Astrophys. (2010) 513:A61. doi: 10.1051/0004-6361/200911967

CrossRef Full Text | Google Scholar

13. Erler J, Langanke K, Loens HP, Martinez-Pinedo G, Reinhard PG. Fission properties for r-process nuclei. Phys Rev C. (2012) 85:025802. doi: 10.1103/PhysRevC.85.025802

CrossRef Full Text | Google Scholar

14. Horowitz CJ, Arcones A, Côté B, Dillmann I, Nazarewicz W, Roederer IU, et al. r-process nucleosynthesis: connecting rare-isotope beam facilities with the cosmos. J Phys G. (2019) 46:083001. doi: 10.1088/1361-6471/ab0849

CrossRef Full Text | Google Scholar

15. Goriely S, Sida JL, Lemaître JF, Panebianco S, Dubray N, Hilaire S, et al. New fission fragment distributions and r-process origin of the rare-earth elements. Phys Rev Lett. (2013) 111:242502. doi: 10.1103/PhysRevLett.111.242502

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Eichler M, Arcones A, Kelic A, Korobkin O, Langanke K, Marketin T, et al. The role of fission in neutron star mergers and its impact on the r-process peaks. Astrophys J. (2015) 808:30. doi: 10.1088/0004-637X/808/1/30

CrossRef Full Text | Google Scholar

17. Goriely S. The fundamental role of fission during r-process nucleosynthesis in neutron star mergers. Eur Phys J A. (2015) 51:22. doi: 10.1140/epja/i2015-15022-3

CrossRef Full Text | Google Scholar

18. Vassh N, Vogt R, Surman R, Randrup J, Sprouse TM, Mumpower MR, et al. Using excitation-energy dependent fission yields to identify key fissioning nuclei in r-process nucleosynthesis. J Phys G. (2019) 46:065202. doi: 10.1088/1361-6471/ab0bea

CrossRef Full Text | Google Scholar

19. Vassh N, Mumpower MR, McLaughlin GC, Sprouse TM, Surman R. Co-production of light and heavy r-process elements via fission deposition. Astrophys J. (2019) 896:28. doi: 10.3847/1538-4357/ab91a9

CrossRef Full Text | Google Scholar

20. Côté B, Fryer CL, Belczynski K, Korobkin O, Chruślińska M, Vassh N, et al. The origin of r-process elements in the milky way. Astrophys J. (2017) 855:99. doi: 10.3847/1538-4357/aaad67

CrossRef Full Text | Google Scholar

21. Nichols A, Aldama D, Verpelli M. Handbook for Nuclear Data for Safeguards: Database Extensions, August 2008. INDC(NDS)-0534. Vienna: International Atomic Energy Agency (2008).

Google Scholar

22. Murray R, Holbert KE. Nuclear Energy: An Introduction to the Concepts, Systems, and Applications of Nuclear Processes. Elsevier (2014).

Google Scholar

23. Bender M, Bernard R, Bertsch G, Chiba S, Dobaczewski JJ, Dubray N, et al. Future of nuclear fission theory. J Phys G. (2020) arXiv:2005.10216. doi: 10.1088/1361-6471/abab4f

CrossRef Full Text | Google Scholar

24. Nakatsukasa T, Matsuyanagi K, Matsuo M, Yabana K. Time-dependent density-functional description of nuclear dynamics. Rev Mod Phys. (2016) 88:045004. doi: 10.1103/RevModPhys.88.045004

CrossRef Full Text | Google Scholar

25. Scamps G, Simenel C. Impact of pear-shaped fission fragments on mass-asymmetric fission in actinides. Natute. (2018) 564:382. doi: 10.1038/s41586-018-0780-0

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Simenel C, Umar AS. Formation and dynamics of fission fragments. Phys Rev C. (2014) 89:031601. doi: 10.1103/PhysRevC.89.031601

CrossRef Full Text | Google Scholar

27. Scamps G, Simenel C, Lacroix D. Superfluid dynamics of $^258\mathrmFm$ fission. Phys Rev C. (2015) 92:011602. doi: 10.1103/PhysRevC.92.011602

CrossRef Full Text

28. Schunck N, Robledo LM. Microscopic theory of nuclear fission: a review. Rep Prog Phys. (2016) 79:116301. doi: 10.1088/0034-4885/79/11/116301

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Sadhukhan J, Nazarewicz W, Schunck N. Microscopic modeling of mass and charge distributions in the spontaneous fission of ²⁴⁰Pu. Phys Rev C. (2016) 93:011304. doi: 10.1103/PhysRevC.93.011304

CrossRef Full Text | Google Scholar

30. Baranger M, Vénéroni M. An adiabatic time-dependent Hartree-Fock theory of collective motion in finite systems. Ann Phys. (1978) 114:123. doi: 10.1016/0003-4916(78)90265-8

CrossRef Full Text | Google Scholar

31. Dobaczewski J, Flocard H, Treiner J. Hartree-Fock-Bogoliubov description of nuclei near the neutron-drip line. Nucl Phys A. (1984) 422:103–39. doi: 10.1016/0375-9474(84)90433-0

CrossRef Full Text | Google Scholar

32. Hill DL, Wheeler JA. Nuclear constitution and the interpretation of fission phenomena. Phys Rev. (1953) 89:1102. doi: 10.1103/PhysRev.89.1102

CrossRef Full Text | Google Scholar

33. Wilets L. Surface coupling mechanism for approaching statistical equilibrium in compound nucleus formation, with application to fission. Phys Rev. (1959) 116:372. doi: 10.1103/PhysRev.116.372

CrossRef Full Text | Google Scholar

34. Hasse RW. Approaches to nuclear friction. Rep Prog Phys. (1978) 41:1027. doi: 10.1088/0034-4885/41/7/002

CrossRef Full Text | Google Scholar

35. Brack M, Damgaard J, Jensen AS, Pauli HC, Strutinsky VM, Wong CY. Funny Hills: the shell-correction approach to nuclear shell effects and its applications to the fission process. Rev Mod Phys. (1972) 44:320. doi: 10.1103/RevModPhys.44.320

CrossRef Full Text | Google Scholar

36. Schütte G, Wilets L. Dynamics and non-adiabaticity in the fission process. Nucl Phys A. (1975) 252:21. doi: 10.1016/0375-9474(75)90598-9

CrossRef Full Text | Google Scholar

37. Schütte G, Wilets L. Excitation during collective deformation: how simple it is. Z Phys A. (1978) 286:313. doi: 10.1007/BF01408263

CrossRef Full Text | Google Scholar

38. Strutinsky VM. Collective motion at large amplitudes and finite velocities. Z Phys A. (1977) 280:99. doi: 10.1007/BF01438114

CrossRef Full Text | Google Scholar

39. Nazarewicz W. Diabaticity of nuclear motion: problems and perspectives. Nucl Phys A. (1993) 557:489. doi: 10.1016/0375-9474(93)90565-F

CrossRef Full Text | Google Scholar

40. Nakatsukasa T, Walet NR. Diabatic and adiabatic collective motion in a model pairing system. Phys Rev C. (1998) 57:1192. doi: 10.1103/PhysRevC.57.1192

CrossRef Full Text | Google Scholar

41. Moretto LG, Babinet RP. Large superfluidity enhancement in the penetration of the fission barrier. Phys Lett B. (1974) 49:147. doi: 10.1016/0370-2693(74)90494-8

CrossRef Full Text | Google Scholar

42. Urin MG, Zaretsky DF. On the spontaneous fission of nuclei. Nucl Phys. (1966) 75:101. doi: 10.1016/0029-5582(66)90749-8

CrossRef Full Text | Google Scholar

43. Ledergerber T, Pauli HC. On the dynamics of fission: the role of reflection asymmetry in the nuclear shape. Nucl Phys A. (1973) 207:1–32. doi: 10.1016/0375-9474(73)90022-5

CrossRef Full Text | Google Scholar

44. Lazarev YA. Influence of pairing correlations on the probability and dynamics of tunnelling through the barrier in fission and fusion of complex nuclei. Phys Scr. (1987) 35:255. doi: 10.1088/0031-8949/35/3/007

CrossRef Full Text | Google Scholar

45. Pomorski K. Pairing as a collective mode. Int J Mod Phys E. (2007) 16:237. doi: 10.1142/S0218301307005685

CrossRef Full Text | Google Scholar

46. Staszczak A, Baran A, Pomorski K, Böning K. Coupling of the pairing vibrations with the fission mode. Phys Lett B. (1985) 161:227. doi: 10.1016/0370-2693(85)90750-6

CrossRef Full Text | Google Scholar

47. Staszczak A, Piłat S, Pomorski K. Influence of the pairing vibrations on spontaneous fission probability. Nucl Phys A. (1989) 504:589. doi: 10.1016/0375-9474(89)90559-9

CrossRef Full Text | Google Scholar

48. Łojewski Z, Staszczak A. Role of pairing degrees of freedom and higher multipolarity deformations in spontaneous fission process. Nucl Phys A. (1999) 657:134. doi: 10.1016/S0375-9474(99)00328-0

CrossRef Full Text | Google Scholar

49. Mirea M, Bobulescu RC. Cranking mass parameters for fission. J Phys G. (2010) 37:055106. doi: 10.1088/0954-3899/37/5/055106

CrossRef Full Text | Google Scholar

50. Sadhukhan J, Dobaczewski J, Nazarewicz W, Sheikh JA, Baran A. Pairing-induced speedup of nuclear spontaneous fission. Phys Rev C. (2014) 90:061304. doi: 10.1103/PhysRevC.90.061304

CrossRef Full Text | Google Scholar

51. Zhao J, Lu BN, Niksic T, Vretenar D, Zhou SG. Multidimensionally-constrained relativistic mean-field study of spontaneous fission: coupling between shape and pairing degrees of freedom. Phys Rev C. (2016) 93:044315. doi: 10.1103/PhysRevC.93.044315

CrossRef Full Text | Google Scholar

52. Baran A, Pomorski K, Lukasiak A, Sobiczewski A. A dynamic analysis of spontaneous-fission half-lives. Nucl Phys A. (1981) 361:83. doi: 10.1016/0375-9474(81)90471-1

CrossRef Full Text | Google Scholar

53. Baran A. Some dynamical aspects of the fission process. Phys Lett B. (1978) 76:8. doi: 10.1016/0370-2693(78)90085-0

CrossRef Full Text | Google Scholar

54. Skalski J. Nuclear fission with mean-field instantons. Phys Rev C. (2008) 77:064610. doi: 10.1103/PhysRevC.77.064610

CrossRef Full Text | Google Scholar

55. Baran A, Łojewski Z, Sieja K, Kowal M. Global properties of even-even superheavy nuclei in macroscopic-microscopic models. Phys Rev C. (2005) 72:044310. doi: 10.1103/PhysRevC.72.044310

CrossRef Full Text | Google Scholar

56. Sadhukhan J, Mazurek K, Baran A, Dobaczewski J, Nazarewicz W, Sheikh JA. Spontaneous fission lifetimes from the minimization of self-consistent collective action. Phys Rev C. (2013) 88:064314. doi: 10.1103/PhysRevC.88.064314

CrossRef Full Text | Google Scholar

57. Vaquero NL, Rodríguez TR, Egido JL. On the impact of large amplitude pairing fluctuations on nuclear spectra. Phys Lett B. (2011) 704:520. doi: 10.1016/j.physletb.2011.09.073

CrossRef Full Text | Google Scholar

58. Vaquero NL, Egido JL, Rodríguez TR. Large-amplitude pairing fluctuations in atomic nuclei. Phys Rev C. (2013) 88:064311. doi: 10.1103/PhysRevC.88.064311

CrossRef Full Text | Google Scholar

59. Dobaczewski J, Nazarewicz W, Werner TR. Closed shells at drip-line nuclei. Phys Scr. (1995) 1995:15. doi: 10.1088/0031-8949/1995/T56/002

CrossRef Full Text | Google Scholar

60. Bartel J, Quentin P, Brack M, Guet C, Håkansson HB. Towards a better parametrisation of Skyrme-like effective forces: a critical study of the SkM force. Nucl Phys A. (1982) 386:79. doi: 10.1016/0375-9474(82)90403-1

CrossRef Full Text | Google Scholar

61. Dobaczewski J, Nazarewicz W, Stoitsov MV. Nuclear ground-state properties from mean-field calculations. Eur Phys J A. (2002) 15:21. doi: 10.1140/epja/i2001-10218-8

CrossRef Full Text | Google Scholar

62. Schunck N, Duke D, Carr H, Knoll A. Description of induced nuclear fission with Skyrme energy functionals: static potential energy surfaces and fission fragment properties. Phys Rev C. (2014) 90:054305. doi: 10.1103/PhysRevC.90.054305

CrossRef Full Text | Google Scholar

63. Nam H, Stoitsov M, Nazarewicz W, Bulgac A, Hagen G, Kortelainen M, et al. UNEDF: advanced scientific computing collaboration transforms the low-energy nuclear many-body problem. J Phys Conf Ser. (2012) 402:012033. doi: 10.1088/1742-6596/402/1/012033

CrossRef Full Text | Google Scholar

64. Schunck N, McDonnell JD, Sarich J, Wild SM, Higdon D. Error analysis in nuclear density functional theory. J Phys G. (2015) 42:034024. doi: 10.1088/0954-3899/42/3/034024

CrossRef Full Text | Google Scholar

65. Tsekhanovich I, Andreyev AN, Nishio K, Denis-Petit D, Hirose K, Makii H, et al. Observation of the competing fission modes in 178Pt. Phys Lett B. (2019) 790:583. doi: 10.1016/j.physletb.2019.02.006

CrossRef Full Text | Google Scholar

66. Matheson Z, Giuliani SA, Nazarewicz W, Sadhukhan J, Schunck N. Cluster radioactivity of ${}_{118}^{294}\text{O}{\text{g}}_{176}$. Phys Rev C. (2019) 99:041304. doi: 10.1103/PhysRevC.99.041304

CrossRef Full Text | Google Scholar

67. Sadhukhan J, Giuliani SA, Matheson Z, Nazarewicz W. Efficient method for estimation of fission fragment yields of r-process nuclei. Phys Rev C. (2020) 101:065803. doi: 10.1103/PhysRevC.101.065803

CrossRef Full Text | Google Scholar

68. Rodríguez-Guzmán R, Robledo LM. Microscopic description of fission in uranium isotopes with the Gogny energy density functional. Phys Rev C. (2014) 89:054310. doi: 10.1103/PhysRevC.89.054310

CrossRef Full Text | Google Scholar

69. Giuliani SA, Robledo LM, Rodríguez-Guzmán R. Dynamic versus static fission paths with realistic interactions. Phys Rev C. (2014) 90:054311. doi: 10.1103/PhysRevC.90.054311

CrossRef Full Text | Google Scholar

70. Bernard RN, Pillet N, Robledo LM, Anguiano M. Description of the asymmetric to symmetric fission transition in the neutron-deficient thorium isotopes: role of the tensor force. Phys Rev C. (2020) 101:044615. doi: 10.1103/PhysRevC.101.044615

CrossRef Full Text | Google Scholar

71. Baldo M, Robledo LM, Schuck P, Viñas X. New Kohn-Sham density functional based on microscopic nuclear and neutron matter equations of state. Phys Rev C. (2013) 87:064305. doi: 10.1103/PhysRevC.87.064305

CrossRef Full Text | Google Scholar

72. Giuliani SA, Robledo LM. Fission properties of the BCPM functional. Phys Rev C. (2013) 88:054325. doi: 10.1103/PhysRevC.88.054325

CrossRef Full Text

73. Abusara H, Afanasjev AV, Ring P. Fission barriers in covariant density functional theory: extrapolation to superheavy nuclei. Phys Rev C. (2012) 85:024314. doi: 10.1103/PhysRevC.85.024314

CrossRef Full Text | Google Scholar

74. Zhao J, Lu BN, Niksic T, Vretenar D. Multidimensionally constrained relativistic Hartree-Bogoliubov study of spontaneous nuclear fission. Phys Rev C. (2015) 92:064315. doi: 10.1103/PhysRevC.92.064315

CrossRef Full Text | Google Scholar

75. Agbemava SE, Afanasjev AV, Ray D, Ring P. Assessing theoretical uncertainties in fission barriers of superheavy nuclei. Phys Rev C. (2017) 95:054324. doi: 10.1103/PhysRevC.95.054324

CrossRef Full Text | Google Scholar

76. Zhao J, Niksic, Vretenar D, Zhou SG. Microscopic self-consistent description of induced fission dynamics: finite-temperature effects. Phys Rev C. (2019) 99:014618. doi: 10.1103/PhysRevC.99.014618

CrossRef Full Text | Google Scholar

77. Zhao J, Xiang J, Li ZP, Niksic T, Vretenar D, Zhou SG. Time-dependent generator-coordinate-method study of mass-asymmetric fission of actinides. Phys Rev C. (2019) 99:054613. doi: 10.1103/PhysRevC.99.054613

CrossRef Full Text | Google Scholar

78. Shi Z, Afanasjev AV, Li ZP, Meng J. Superheavy nuclei in a microscopic collective Hamiltonian approach: the impact of beyond-mean-field correlations on ground state and fission properties. Phys Rev C. (2019) 99:064316. doi: 10.1103/PhysRevC.99.064316

CrossRef Full Text | Google Scholar

79. Bulgac A, Jin S, Roche KJ, Schunck N, Stetcu I. Fission dynamics of ²⁴⁰Pu from saddle to scission and beyond. Phys Rev C. (2019) 100:034615. doi: 10.1103/PhysRevC.100.034615

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Tanimura Y, Lacroix D, Ayik S. Microscopic phase-space exploration modeling of ²⁵⁸Fm spontaneous fission. Phys Rev Lett. (2017) 118:152501. doi: 10.1103/PhysRevLett.118.152501

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Reinhard PG, Goeke K. The generator coordinate method and quantised collective motion in nuclear systems. Rep Prog Phys. (1987) 50:1. doi: 10.1088/0034-4885/50/1/001

CrossRef Full Text | Google Scholar

82. Goutte H, Berger JF, Casoli P, Gogny D. Microscopic approach of fission dynamics applied to fragment kinetic energy and mass distributions in ²³⁸U. Phys Rev C. (2005) 71:024316. doi: 10.1103/PhysRevC.71.024316

CrossRef Full Text | Google Scholar

83. Regnier D, Dubray N, Schunck N, Verriére M. Fission fragment charge and mass distributions in ²³⁹Pu(n, f) in the adiabatic nuclear energy density functional theory. Phys Rev C. (2016) 93:054611. doi: 10.1103/PhysRevC.93.054611

CrossRef Full Text | Google Scholar

84. Regnier D, Dubray N, Schunck N. From asymmetric to symmetric fission in the fermium isotopes within the time-dependent generator-coordinate-method formalism. Phys Rev C. (2019) 99:024611. doi: 10.1103/PhysRevC.99.024611

CrossRef Full Text | Google Scholar

85. Ring P, Schuck P. The Nuclear Many-Body Problem. Berlin; Heidelberg: Springer-Verlag (2000).

Google Scholar

86. Baran A, Sheikh JA, Dobaczewski J, Nazarewicz W, Staszczak A. Quadrupole collective inertia in nuclear fission: cranking approximation. Phys Rev C. (2011) 84:054321. doi: 10.1103/PhysRevC.84.054321

CrossRef Full Text | Google Scholar

87. Randrup J, Möller P. Brownian shape motion on five-dimensional potential-energy surfaces: nuclear fission-fragment mass distributions. Phys Rev Lett. (2011) 106:132503. doi: 10.1103/PhysRevLett.106.132503

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Abe Y, Ayik S, Reinhard PG, Suraud E. On stochastic approaches of nuclear dynamics. Phys Rep. (1996) 275:49. doi: 10.1016/0370-1573(96)00003-8

CrossRef Full Text | Google Scholar

89. Fröbrich P, Gontchar II. Langevin description of fusion, deep-inelastic collisions and heavy-ion-induced fission. Phys Rep. (1998) 292:131. doi: 10.1016/S0370-1573(97)00042-2

CrossRef Full Text | Google Scholar

90. Younes W, Gogny D. Fragment Yields Calculated in a Time-Dependent Microscopic Theory of Fission. LLNL-TR-586678. Livermore, CA: Lawrence Livermore National Laboratory (LLNL) (2012).

Google Scholar

91. Sierk AJ. Langevin model of low-energy fission. Phys Rev C. (2017) 96:034603. doi: 10.1103/PhysRevC.96.034603

CrossRef Full Text | Google Scholar

92. Sadhukhan J, Zhang C, Nazarewicz W, Schunck N. Formation and distribution of fragments in the spontaneous fission of ²⁴⁰Pu. Phys Rev C. (2017) 96:061301. doi: 10.1103/PhysRevC.96.061301

CrossRef Full Text | Google Scholar

93. Zhang CL, Schuetrumpf B, Nazarewicz W. Nucleon localization and fragment formation in nuclear fission. Phys Rev C. (2016) 94:064323. doi: 10.1103/PhysRevC.94.064323

CrossRef Full Text | Google Scholar

94. Reinhard PG, Maruhn JA, Umar AS, Oberacker VE. Localization in light nuclei. Phys Rev C. (2011) 83:034312. doi: 10.1103/PhysRevC.83.034312

CrossRef Full Text | Google Scholar

95. Warda M, Staszczak A, Nazarewicz W. Fission modes of mercury isotopes. Phys Rev C. (2012) 86:024601. doi: 10.1103/PhysRevC.86.024601

CrossRef Full Text | Google Scholar

96. Warda M, Zdeb A. Fission fragment mass yield deduced from density distribution in the pre-scission configuration. Phys Scr. (2015) 90:114003. doi: 10.1088/0031-8949/90/11/114003

CrossRef Full Text | Google Scholar

97. Scamps G, Simenel C. Effect of shell structure on the fission of sub-lead nuclei. Phys Rev C. (2019) 100:041602. doi: 10.1103/PhysRevC.100.041602

CrossRef Full Text | Google Scholar

98. Bertsch GF, Loveland W, Nazarewicz W, Talou P. Benchmarking nuclear fission theory. J Phys G. (2015) 42:077001. doi: 10.1088/0954-3899/42/7/077001

CrossRef Full Text | Google Scholar

99. Giannoni MJ, Quentin P. Mass parameters in the adiabatic time-dependent Hartree-Fock approximation. II. Results for the isoscalar quadrupole mode. Phys Rev C. (1980) 21:2076. doi: 10.1103/PhysRevC.21.2076

CrossRef Full Text | Google Scholar

100. Yuldashbaeva EK, Libert J, Quentin P, Girod M. Mass parameters for large amplitude collective motion: a perturbative microscopic approach. Phys Lett B. (1999) 461:1. doi: 10.1016/S0370-2693(99)00836-9

CrossRef Full Text | Google Scholar

101. Smolańczuk R, Klapdor-Kleingrothaus HV, Sobiczewski A. Role of the deformation space admitted in the analysis of spontaneous fission. Acta Phys Pol B. (1993) 24:685.

102. Smolańczuk R, Skalski J, Sobiczewski A. Spontaneous-fission half-lives of deformed superheavy nuclei. Phys Rev C. (1995) 52:1871. doi: 10.1103/PhysRevC.52.1871

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Gherghescu RA, Skalski J, Patyk Z, Sobiczewski A. Non-axial shapes in spontaneous fission of superheavy nuclei. Nucl Phys A. (1999) 651:237. doi: 10.1016/S0375-9474(99)00126-8

CrossRef Full Text | Google Scholar

104. Warda M, Egido JL. Fission half-lives of superheavy nuclei in a microscopic approach. Phys Rev C. (2012) 86:014322. doi: 10.1103/PhysRevC.86.014322

CrossRef Full Text | Google Scholar

105. Delaroche JP, Girod M, Goutte H, Libert J. Structure properties of even-even actinides at normal and super deformed shapes analysed using the Gogny force. Nucl Phys A. (2006) 771:103. doi: 10.1016/j.nuclphysa.2006.03.004

CrossRef Full Text | Google Scholar

106. Karpov AV, Nadtochy PN, Vanin DV, Adeev GD. Three-dimensional Langevin calculations of fission fragment mass-energy distribution from excited compound nuclei. Phys Rev C. (2001) 63:054610. doi: 10.1103/PhysRevC.63.054610

CrossRef Full Text | Google Scholar

107. Nadtochy PN, Ryabov EG, Gegechkori AE, Anischenko YA, Adeev GD. Four-dimensional Langevin dynamics of heavy-ion-induced fission. Phys Rev C. (2012) 85:064619. doi: 10.1103/PhysRevC.85.064619

CrossRef Full Text | Google Scholar

108. Pal S, Chaudhuri G, Sadhukhan J. The role of neck degree of freedom in nuclear fission. Nucl Phys A. (2008) 808:1. doi: 10.1016/j.nuclphysa.2008.05.001

CrossRef Full Text | Google Scholar

109. Laidler JB, Brown F. Mass distribution in the spontaneous fission of 240Pu. J Inorg Nucl Chem. (1962) 24:1485. doi: 10.1016/0022-1902(62)80001-3

CrossRef Full Text | Google Scholar

110. Thierens H, De Clercq A, Jacobs E, De Frenne D, D'hondt P, De Gelder P, et al. Kinetic energy and fragment mass distributions for ²⁴⁰Pu(s.f.), ${}^{239}\text{P}\text{u}(n_{\text{t}\text{h}},f)$, and ²⁴⁰Pu(γ, f). Phys Rev C. (1981) 23:2104. doi: 10.1103/PhysRevC.23.2104

CrossRef Full Text | Google Scholar

111. Interactive Chart of Nuclides. NuDat 2.7. Available online at: https://www.nndc.bnl.gov/nudat2/

Google Scholar

112. Dobaczewski J, Nazarewicz W, Reinhard PG. Error estimates of theoretical models: a guide. J Phys G. (2014) 41:074001. doi: 10.1088/0954-3899/41/7/074001

CrossRef Full Text | Google Scholar

113. Negele JW. Microscopic theory of fission dynamics. Nucl Phys A. (1989) 502:371. doi: 10.1016/0375-9474(89)90676-3

CrossRef Full Text | Google Scholar

114. Kajino T, Aoki W, Balantekin AB, Diehl R, Famiano MA, Mathews GJ. Current status of r-process nucleosynthesis. Prog Part Nucl Phys. (2019) 107:109. doi: 10.1016/j.ppnp.2019.02.008

CrossRef Full Text | Google Scholar