Monte Carlo Modeling of DNA Lesions and Chromosomal Aberrations Induced by Mixed Beams of Alpha Particles and X-Rays

Introduction

Correct processing of DNA damage is crucial for maintaining the genomic stability of cells. Among the most important sources of DNA damage in humans is ionizing radiation, both of natural and man-made origin [1, 2]. Radiation is a potent inducer of DNA double-strand breaks (DSB), many of which are complex in nature and pose serious problem in the DNA repair machinery [3, 4]. Per unit radiation dose, the level of complex DSB increases with ionization density, which is described as the linear energy transfer (LET) [5, 6].

Biological effects of radiations characterized by various LETs have been analyzed in numerous studies. The majority of studies focused on analyzing effects induced by radiation of a single quality. However, environmental, occupational, and medical exposures are often mixed, showing simultaneous action of radiations with different LETs. Examples include gamma radiation plus alpha particles in high natural background radiation areas [1], gamma radiation and neutrons plus charged particles during aircraft or space flight operation [7], and gamma radiation and neutrons plus protons during some forms of radiotherapy [8, 9].

The interesting question behind mixed beam exposure is whether the radiations interact, resulting in effects that are higher than that expected based on an additive action of the single beam components. Using a dedicated mixed beam exposure facility [10], we could demonstrate in several studies that this is indeed the case [11–16].

Two radiation types may interact via various mechanisms leading to a synergistic effect. First, it is possible that the action of both radiation types in a target volume will lead to an increased density of ionization events and an increase in LET. Such effect could lead to an augmented level of single-strand breaks (SSB) and DSB and higher DNA damage complexity. Second, it is possible that exposure to one type of radiation transforms the DNA damage response machinery in such a degree that the additional damage induced by the other radiation type will not be signaled and/or repaired properly [13]. Results published so far suggest that mixed beam exposure overwhelms the DNA repair machinery [14, 15]. Up to this time, we have not been able to study the question whether mixed beam exposure leads to higher than expected yield of SSB and DSB, resulting in higher DSB complexity.

The distribution of hits inside a nucleus can be calculated with great precision by Monte Carlo (MC) simulation methods [6, 17, 18]. Methods are used to precisely calculate the number of hits within a certain volume in a certain time and per a certain dose. The track structure analyses rely on an “event-by-event” description of the physical and chemical processes following irradiation. Each type of interaction for an ingoing particle is described by the deposited energy and the position where the interaction takes place. This information allows studying spatial correlations of lesions within the DNA molecule and between different chromosomes within a cell nucleus. The PARTRAC codes [19] combine track structure calculations with a multilevel cellular DNA model; moreover, cellular repair processes and the formation of chromosomal aberrations (CA) can also be simulated [20].

The aim of the present study was to simulate, using PARTRAC codes, the formation of SSB, DSB, and CA in human peripheral blood lymphocytes exposed to mixed beams as described in the study by Staaf et al. [10, 11]. The computed chromosomal aberration frequencies were compared with the published experimental results [12].

Materials and Methods

Experimental Data

Experimental data were generated using the mixed beam exposure facility MAX [10] available at the Stockholm University that allows exposure of cells to two different types of ionizing radiation: alpha particles and X-rays. The source of alpha particles was Am-241 with a energy of 5.49 MeV, yielding a dose rate of 0.21 Gy/min. The source of X-rays was an X-ray tube operating at 190 kV and 4 mA, yielding a dose rate of 0.07 Gy/min. The X-ray energy spectrum had a single peak at 80 keV and is described in the study by Brehwens et al. [21].

Staaf et al. [12] analyzed translocations and complex aberrations in human peripheral blood lymphocytes (from a single male donor) exposed to mixed beams. A complex aberration was defined as an exchange resulting from at least three primary breaks in two or more chromosomes [22]. Chromosomal aberrations were analyzed in chromosomes 2, 8, and 14 using fluorescence in situ hybridization for combined doses of 0.20, 0.40, and 0.80 Gy X-rays (X); 0.13, 0.27, and 0.54 Gy alpha particles (α); and 0.20X + 0.07α, 0.40X + 0.13α, and 0.40X + 0.27α Gy mixed beams. A linear-quadratic, dose–response curve for complex aberrations was observed after X-rays, and a linear dose–response curve was observed after alpha particles. Higher than expected from additivity frequencies of complex aberrations were observed at chromosomal aberration levels of 1.3 and 1.6 aberrations per cell. The uncertainties were not included in the publication, so they were calculated based on Poisson distribution and used for comparison with MC simulations. To expand the dose range, the fitted dose–response curves for experimental data were used.

Staaf et al. [12] presented aberration frequencies scored in chromosomes 2, 8, and 14. For comparing the observed frequencies with those generated by MC simulations, whole-genome frequencies of aberrations were calculated as described by Lucas et al. [23], assuming that the fraction of the male human whole-genome DNA represented by chromosomes 2, 8, and 14 is 0.0803, 0.0488, and 0.0338, respectively [24]. The envelopes of additivity [25] were constructed based on dose–response curves for CA induced by X-rays and alpha radiation.

The edges of the envelopes of additivity correspond to two isobolograms created for heteroadditive and isoadditive forms of interaction between these two types of radiation. Isoaddition is calculated based on assumption that two agents have the same mechanism of action, so that the combined effect is superadditive. Heteroaddition is calculated based on assumption that when the two agents have different mechanism of action, the combined effect is additive. The mixed beam data inside the envelope of the additivity mean the additive mixed beam effect, if they are outside, that the effect is either synergistic (to the left) or antagonistic (to the right).

MC Simulations

PARTRAC codes were used to model the frequencies of SSB, DSB, and CA. MC simulations were performed for the three types of ionizing radiations used by Staaf et al. [12]. Simulations were carried out for 1,000 cell nuclei of cells with a spherical shape and a diameter of 10 μm, being an approximation of published data [26]. It was assumed that each cell nucleus contains a total genomic length of 6.6 Gbp. Details of the model of chromatin structure inside the nucleus are described in the study by Friedland et al. [19].

Photon irradiation was simulated with PARTRAC by implementation of the spectrum of X-rays generated by a 190 kVp machine. Photons were generated randomly from the surface of the cytoplasm, and the simulations were performed until the dose values are achieved. The doses delivered to a cell nucleus were calculated based on energy deposition of X-rays passing through the cell nucleus. The energy limit for photon and electron scattering was 20 and 10 eV, respectively. The simulated dose range (0.2–2.43 Gy) for X-ray irradiation was wider than that used in the experiment. In case of alpha particle exposure, the simulated dose range started from 0.3 Gy, which is more than the dose of 0.13 Gy obtained experimentally, but it contains higher values till 2.33 Gy. Alpha particles with the energy spectra of Am-241 were generated based on Poisson distribution, and the dose was determined as division of the deposited energy by the mass of the target. The increased dose ranges for both types of radiation resulted in wide dose range of 0.44–4.76 Gy for mixed beam simulations. The physical and chemical interactions were generated separately for X-rays and alpha particles, and the combined information about track structures was used to calculate the DSB and SSB induced by mixed beams.

PARTRAC allows studying complex DNA damage and repair processes at each elementary stage: starting from the physical interaction with the DNA, through the indirect interactions coming from the water radiolysis products (chemical module), until the response at the level of chromosomal aberrations due to misrepair of DNA damage. Details of the physical, chemical, and biological modules that were used to model the level of chromosomal aberrations are described elsewhere [19, 27]. The parameters of the CA model were taken from Friedland et al. [28] but disregarding the special DNA structure of the hybrid cell type in that study. The DSB was considered when two DNA breaks were separated by no more than 10 bp. The DSB cluster was defined by two or more DSB occurred within a genomic distance of 25 bp.

The CA induction model starts from radiation-induced DNA damage assessed by overlapping radiation track structures with the DNA molecule as described above. The repair of DNA DSB via nonhomologous end joining is considered. The use of nonhomologous end joining and not of homologous recombination repair is considered because the simulations were carried out for unstimulated peripheral blood lymphocytes that are in the G₀ phase of the cell cycle. Additionally, to the initial spatial distribution and complexity, the simulation includes diffusive motion, enzymatic processing, synapsis, and ligation of individual DSB ends. Improper joining of DNA fragments results in different chromosome aberration types simulated with the PARTRAC repair module by tracking the chromosome origin of the ligated fragments and the positions of centromeres. The motion of DNA ends is modeled considering chromatin mobility within time scales of a few hours. For a model validation, the number of dicentrics per cell was calculated with PARTRAC and compared with published results [27, 28].

Results

The physical interactions of X-rays and alpha particles with the DNA molecule and the chemical reactions were simulated to calculate the DNA damage and its location in the nucleus using the appropriate modules of PARTRAC. High-energy helium nuclei ionize densely along their tracks when they pass the cell nucleus, giving rise to highly clustered and complex DNA lesions. High-energy photons and the energetic electrons liberated via photoelectric and Compton effect interact sparsely with electrons of atoms and can travel long distances inside a cell nucleus before they interact. Examples of simulated ionization events for X-rays and alpha particles are shown in Figure 1 (the simulations of early DNA damage take also into account excitation of the water medium, but they are not shown in the figure).

FIGURE 1

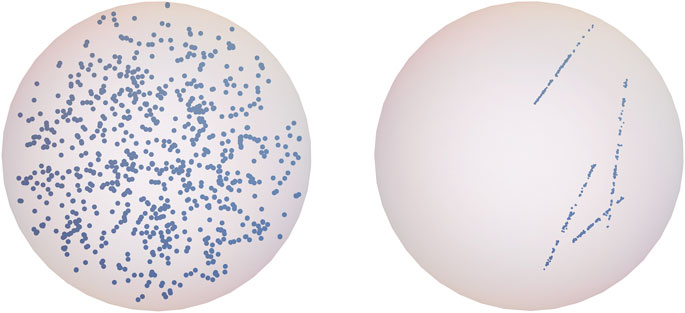
FIGURE 1. The simulated spatial ionization distribution within an exemplary lymphocyte nucleus after X-ray (left panel) and alpha irradiation (right panel) with the dose equal 1 Gy.

Verification of the Simulation Model Using Single-Strand Breaks and Double-Strand Breaks

In PARTRAC, DNA molecule structure includes the double helix, nucleosomes, chromatin fibers, chromatin fiber loops, chromatin domains, and chromosomes, which are represented by more than 6 billion DNA base pairs. The geometrical information about the interactions with the DNA can be translated into genomic distances given as numbers of base pairs from the end of the hit chromosomes and thus used to define the DNA damage size and position. The configuration of the damage can be retrieved as the number and position of individual SSB and DSB. The linear dependence of the dose of X-rays and alpha particles and the amount of SSB and DSB formation after physical and chemical stages are shown in Figure 2. For 1 Gy of X-rays (1,299 ± 40) SSB and (56 ± 7) DSB were induced per nucleus. According to theoretical predictions, 1 Gy of X-rays causes about 1000 SSB [29] and 50 DSB [30] per nucleus. Experimental data indicate that radiation causes about 923 SSB [31], and the ratio between SSB and DSB is equal to 25 [32]. Taking into account the uncertainties of performed simulations, it can be assumed that the simulated mean values of SSB and DSB are in line with experimental data and calculations performed with independent MC tools. The total SSB (110 ± 10) and DSB (21 ± 4) yields per 1 Gy and 1 Gbp calculated for alpha irradiation emitted from Am-241 source are comparable to simulated values (72 and 16, respectively) with Geant4-DNA published in the study by de la Fuente Rosales et al. [33].

FIGURE 2

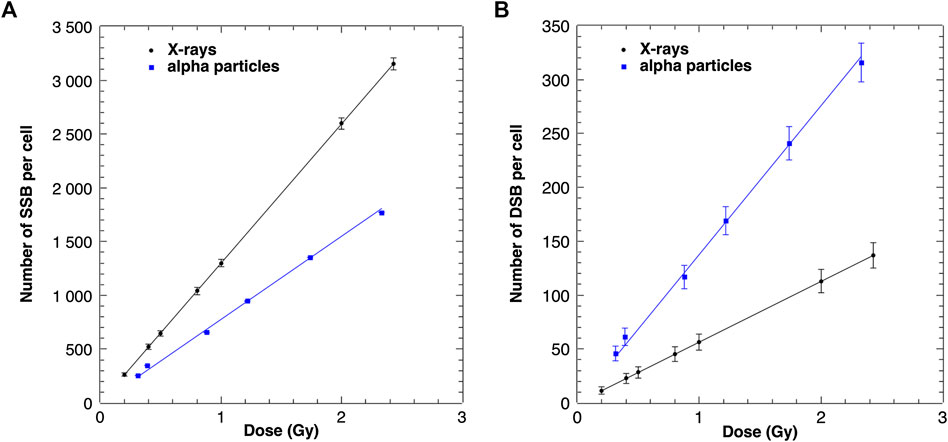
FIGURE 2. Modeled numbers of SSB (A) and DSB (B) induced in a cell nucleus after X-ray and alpha particle irradiation as a function of the absorbed dose. The uncertainties are given as standard deviations.

Additionally, the SSB and DSB numbers were simulated for a simultaneous exposure of cells to alpha particles and X-rays. Because the linear function given by the equation y = Ax + B was fitted to all performed simulations (presented in Table 1), the expected numbers of SSB and DSB calculations based on additivity assumption could be generated. Both sets of results are shown in Figure 3. The simulated SSB and DSB induced by mixed beams are in agreement with calculated sums of SSB and DSB of alpha particles and X-rays simulated independently.

TABLE 1

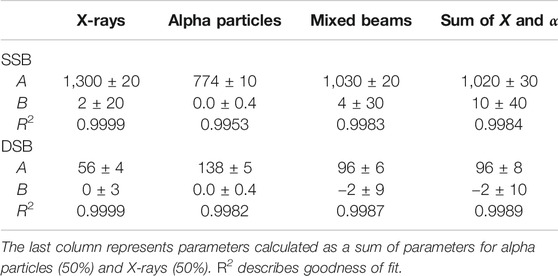
TABLE 1. Dose–response fitting parameters for simulated SSB and DSB induced by X-rays, alpha particles, and mixed beams.

FIGURE 3

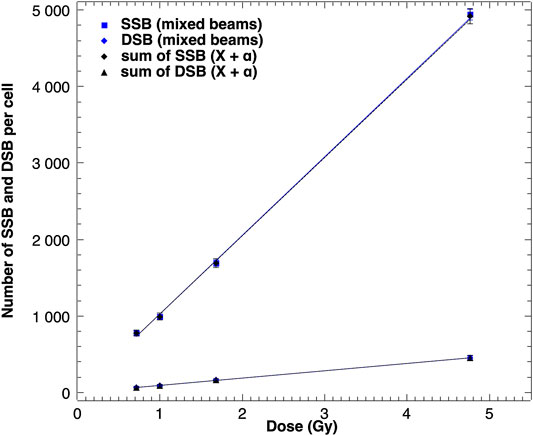
FIGURE 3. Modeled numbers of SSB and DSB induced in a cell nucleus by mixed beams of alpha particles and X-rays and sums of SSB and DSB induced by both radiation types given independently. Error bars indicate standard deviations.

The equality of linear regression coefficients was tested with the Student’s t-test. The aim was to verify that the two Pearson’s linear correlation coefficients in tested samples are equal. The determined p value was 0.007 for SSB and 0.03 for DSB, indicating that the correlation coefficients do not differ.

The difference between low- and high-LET radiation interactions within cells is described by spatial distributions of ionization acts inside a nucleus. As shown in Figure 4, DSB clusters appear more often for densely ionizing alpha particles as compared with X-ray irradiation. However, PARTRAC calculations for mixed beams containing 50% of alpha particles and 50% of X-rays gives the total number of DSB clusters as the sum of DSB clusters induced by alpha particles and X-rays independently.

FIGURE 4

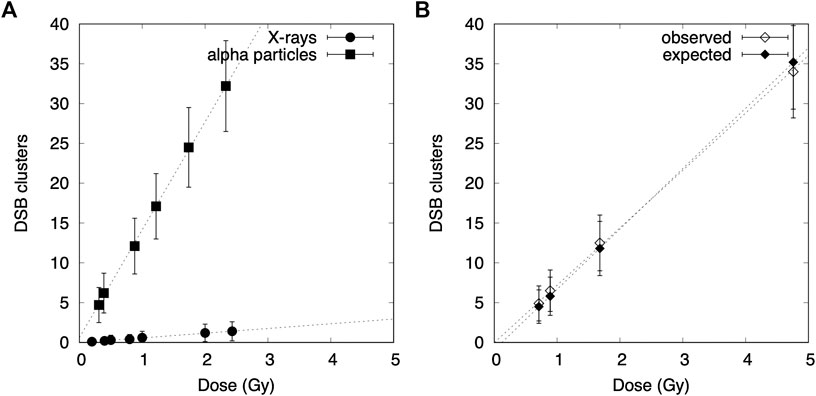
FIGURE 4. Dose–response curves for simulated DSB clusters in lymphocytes exposed to X-rays, alpha particles, and mixed beams: (A) comparison between alpha particles and X-rays, (B) calculated values for a mixed beam simulation compared with expected values if additivity is preserved.

Cellular Response in the Form of Chromosomal Aberrations

The calculated total numbers of CA formation in spherical cells (human peripheral blood lymphocytes) were compared with experimental data [12] collected previously in our laboratory for cells exposed to X-rays, alpha particles, and mixed beams. The results are shown in Figures 5 and 6. The uncertainties of data points scored during the experiment were calculated as square roots of variations based on Poisson distribution.

FIGURE 5

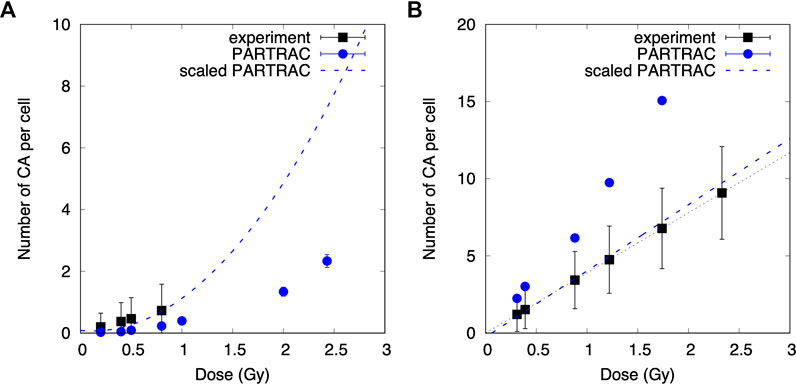
FIGURE 5. Comparison of modeled and experimental results. Linear quadratic and linear relationships between the number of chromosomal aberrations (CA) scored for a cell induced by X-rays (A) and alpha particles (B) and the dose for experimental data and MC simulations. The blue dashed lines represent PARTRAC calculations including scaling factors.

FIGURE 6

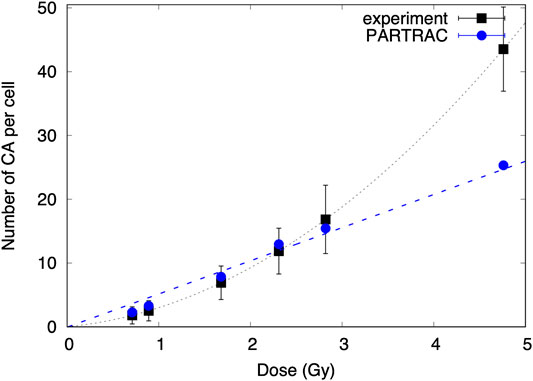
FIGURE 6. The number of chromosomal aberrations scored for a cell induced by mixed beams as a function of the dose for experimental data and MC simulations.

Although the calculated numbers of CA per cell for X-ray irradiation are described by linear quadratic function: CA = (0.08 ± 0.05) − (0.3 ± 0.2)D + (1.3 ± 0.1)D², the dose response for alpha exposure is given by the formulae: CA = (−0.3 ± 0.2) + (4.3 ± 0.2)D.

Comparison of CA dose responses of cells irradiated with X-rays shows different trends obtained with experimental data and MC simulations. The experimental data were described by linear function in contrast to PARTRAC calculations, showing linear quadratic relationship. However, CA was scored experimentally only up to 0.8 Gy, where the quadratic element has smaller impact than the linear one. The scaling factor equal to 3.3 for simulations of CA induced by X-rays was introduced. The number of CA induced by alpha irradiation modeled with PARTRAC is higher than that induced by the experimental data (CA_exp = (0.0002 ± 0.0001) + (3.90 ± 0.01)D) and needed to be divided by a factor 2. According to Student’s t-test, both linear functions are in agreement (p < 0.05).

Number of chromosomal aberrations induced by mixed beam radiation and modeled with PARTRAC was comparable to the experimental data, and no scaling factor was needed. The simulated dose response is described by the linear function: CA = −(0.01 ± 0.01) + (5.2 ± 0.3)D and differs from linear quadratic function describing experimental data. However, simulated data points are in agreement with the experimental data because the experimental uncertainties are large with respect to error bars of simulations.

Synergism or Additivity

Analogous to the approach taken by Staaf et al. [12], envelopes of additivity were prepared and compared with simulations of mixed beams consisting of equal contributions of both radiation qualities. In the experimental study [12], exposure to alpha particles and X-rays always started simultaneously, with X-ray irradiation source remaining on for a few minutes after the alpha exposure was stopped. There is no dose-rate model implemented in the PARTRAC codes, so simulations of X-ray and alpha particle irradiation were performed separately and combined for mixed beam calculations. It is assumed that cells need 48 h to repair the damage before they reach the first posttreatment mitosis. The results are shown in Figure 7.

FIGURE 7

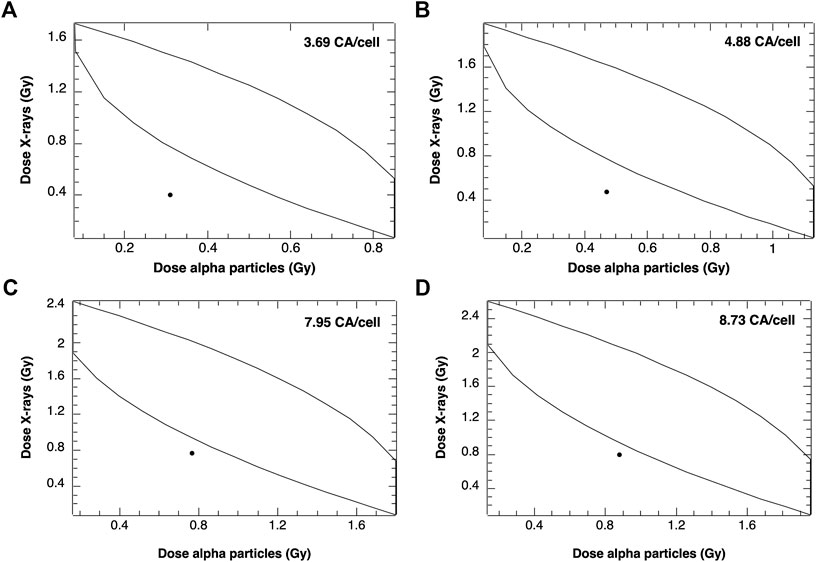
FIGURE 7. Envelopes of additivity calculated for 4 selected frequencies of chromosomal aberrations (CA), from mixed beams composed of 50:50 alpha particles and X-rays: A: 3.69 CA/cell, B: 4.88 CA/cell, C: 7.95 CA/cell and D: 8.73 CA/cell. The mixed beam doses were 0.71 Gy (A), 0.94 Gy (B), 1.53 Gy (C), and 1.68 Gy (D).

Data points showing simulated numbers of CA induced by mixed beam radiation are located outside of the left envelope borders, indicating an interaction of alpha particles and X-rays leading to CA frequencies higher than predicted based on assuming additivity.

The same procedures were performed for two different composition of mixed beams: containing 80% X rays (and remaining 20% of alpha particles) and 80% alpha particles (and 20% of X rays). The results are shown in Figure 8.

FIGURE 8

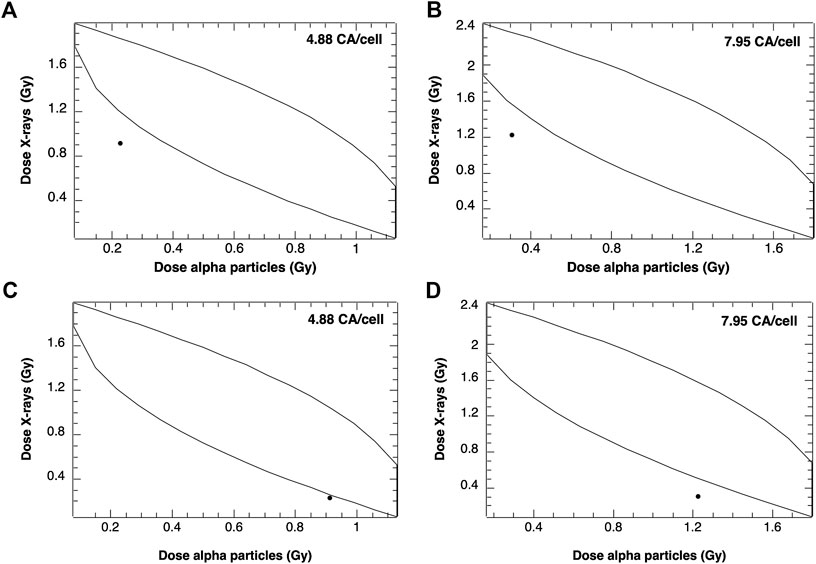
FIGURE 8. Envelopes of additivity calculated for 2 selected frequencies of CA for mixed beams composed of 20% alpha particles and 80% X-rays (A), (B) and 80% alpha particles and 20% X-rays (C), (D). The mixed beam doses for 4.88 CA/cell and 7.95 CA/cell were 0.94 and 1.53 Gy, respectively.

The data points representing mixed beam-induced CA were again outside the left envelope borders, indicating synergism. However, a stronger synergistic effect was observed following exposure of cells to 20% alpha particles and 80% X-rays as compared to 80% alpha particles and 20% X-rays.

Discussion

The characteristics of the physical features of the interaction of ionizing radiations with living matter and accompanying chemical reactions are a major determinant of their final biological consequences. The complexity of DNA damage increases with ionization density, poses serious problems for the DNA repair machinery, and increases the probability of misrepair. A combined action of alpha particles and X-rays results in an interaction of lesions leading to increased damage complexity and impaired damage repair. An interaction of the two types of radiations leads to an increase in biological effectiveness of mixed beam, beyond the level expected from additivity dependent on contribution of beam component with high LET.

There are differences between PARTRAC calculations and experimental number of chromosomal aberrations induced by radiation from X-ray tube and Am-241. Discrepancy in the number of dicentrics was previously observed and discussed for alpha and photon irradiation [27]. The scaling factors obtained from these adaptations were implemented in PARTRAC codes and used to model CA within this analysis. Nevertheless, the cellular response varies depending on the cell system, giving different number and different type of chromosomal aberrations (including dicentrics). CA overestimation by a factor of 2 in the alpha irradiation simulations may result from those aberrations that are not experimentally detectable. Underestimation of the number of CA induced by X-rays may come from the scaling factor introduced from dicentric analysis.

Synergistic effect in CA induction is observed for PARTRAC calculations, which were adapted using the experimental data collected at the Stockholm University. There are no signs of synergism observed after the physicochemical phase of interaction between ionizing radiation and cells. Spatial distributions of ionizations acts within a nucleus lead to spatial distributions of DNA damage, which can be classified as DSB or SSB of DNA. Alpha radiation, which densely ionizes the cell, gives more DSB, whereas X-rays damage DNA sparsely creating more SSB. The number of DSB and SSB from alpha and X-ray radiations given together is just a sum of DSB and SSB coming from single exposures. Complexity of the DNA damage is described not by absolute values of induced DNA breaks, but it depends on their relative position in a small volume of nuclear matter. Mixed beams produce clusters including DNA strand breaks, which are more difficult to be repaired. The complexity of DNA damage and focus induction for mixed beams consisting of different LET radiations was also modeled with PARTRAC codes [34].

The deviations from additive approach appeared in the last interaction phase, which is the biological response of the irradiated cells. Based on the calculated envelopes of additivity, the synergistic effect of CA induction using MC simulations was confirmed. MC modeling allowed us to perform different compositions of mixed beams to study the impact of high-LET radiation contribution. When the cells were irradiated with mixed beams containing 50% of both types of radiations or X-rays with small addition of alpha particles (20%), the stronger synergistic effect was seen for a given CA number per cell. Using mixed beams with large contribution of high-LET radiation, the effect becomes less significant.

The synergistic effect results from joining of broken DNA ends due to DSB from alpha particle irradiation with those from photon irradiation. In X-ray irradiated cells, the broken DNA ends are spread over the whole cell nucleus. They rarely undergo misrejoining with DNA ends from other chromosomes as long as the dose is relatively low. Alpha particle tracks typically cross the territories of a few chromosomes so that DNA ends from adjacent chromosome territories may misrejoin and form CA. The linear increase with dose or the number of alpha tracks per nucleus shows that the intertrack contribution (joining of DSB ends from different alpha particle tracks) is small under the conditions studied here. However, the presence of DSB ends in many chromosomes due to X-ray irradiation under mixed beam condition is supposed to considerably enhance the misrejoining probability for alpha particle–induced DNA ends aligned along the particle tracks.

In a recent study, Pantelias et al. [35] demonstrated that exposure to high-LET radiation induces chromosome shattering, which may give rise to chromothripsis. The scale of chromosomal rearrangements leading to chromothripsis is in excess of 1,000 bp, corresponding to a distance of 50–100 nm. The PARTRAC code does not consider such large-scale chromosomal rearrangements. On the other hand, despite applying the technique of chemically induced premature chromosome condensation, chromothripsis was not observed by Staaf et al. [12], suggesting that human peripheral blood lymphocytes with such extensive damage do not reach the G2 phase of the cell cycle or the mitosis, possibly by undergoing interphase death. In this respect, the results obtained by MC simulation with the PARTRAC codes are compatible with the reference experimental results.

Conclusions

Mathematical modeling, like PARTRAC codes, allows testing the mechanisms of cellular response to ionizing radiation, which are proposed based on experimental data. It can be done for different experimental scenarios taking into account different cell lines, radiation qualities, and experimental setups. The only price of doing it is computing power, which is not an issue nowadays. Using temporal and spatial evolution of particle track structure, the DNA damage in form of DSB and SSB induced by radiations with low- and high-LET was simulated. It was used to investigate morphological changes of chromosomes in cells after simultaneous exposure to alpha particles and X-rays. Although the PARTRAC simulation code allows the calculations of early DNA damage and has been validated based on numerous irradiation scenarios, the biophysical model of chromosomal aberration induction is still fragile. Modeling the DNA repair mechanism is very sophisticated, and it should always takes into account the reproducibility of the experimental data. The synergism observed in series of experiments performed at the Stockholm University was confirmed using adapted Monte Carlo simulations of chromosomal aberrations.

The action of mixed beams is interesting from the perspective of how cells cope with different forms of DNA damage. This is an important question in the area of genome stability, which is relevant both for basic cell research and for a deeper understanding of processes leading to radiation-induced transformation of cells. It is relevant for the assessment of cancer risk due to exposure to mixed beams as encountered during modern external beam radiotherapy with high-energy photons or with protons.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

BW: conceptualization, methodology, writing of original draft preparation; AT: data curation and writing of original draft preparation; AW: conceptualization, writing, reviewing, and editing.

Funding

BW was supported in part by a grant from NCN, Poland (2016/23/D/ST7/03544). AT was supported by the Polish Funds for Science. AW is supported by grants from the Swedish Radiation Safety Authority (SSM).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank Werner Friedland for providing the PARTRAC codes, valuable discussions, and helpful comments.

References

1. Hendry JH, Simon SL, Wojcik A, Sohrabi M, Burkart W, Cardis E, et al. Human exposure to high natural background radiation: what can it teach us about radiation risks? J Radiol Prot. (2009). 29(2A):A29–42. doi:10.1088/0952-4746/29/2a/s03

CrossRef Full Text | Google Scholar

2. Sodickson A, Baeyens PF, Andriole KP, Prevedello LM, Nawfel RD, Hanson R, et al. Recurrent CT, cumulative radiation exposure, and associated radiation-induced cancer risks from CT of adults. Radiology. (2009). 251(1):175–84. doi:10.1148/radiol.2511081296

CrossRef Full Text | Google Scholar

3. Lomax ME, Folkes LK, O’Neill P. Biological consequences of radiation-induced DNA damage: relevance to radiotherapy. Clin Oncol. (2013). 25(10):578–85. doi:10.1016/j.clon.2013.06.007

CrossRef Full Text | Google Scholar

4. Mavragani IV, Nikitaki Z, Souli MP, Aziz A, Nowsheen S, Aziz K, et al. Complex DNA damage: a route to radiation-induced genomic instability and carcinogenesis. Cancers. (2017). 9(7):91. doi:10.3390/cancers9070091

CrossRef Full Text | Google Scholar

5. Goodhead DT. Energy deposition stochastics and track structure: what about the target? Radiat Protect Dosim. (2006). 122:3–15. doi:10.1093/rpd/ncl498

CrossRef Full Text | Google Scholar

6. Nikjoo H, O’Neill P, Wilson WE, Goodhead DT. Computational approach for determining the spectrum of DNA damage induced by ionizing radiation. Radiat Res. (2001). 156:577–83. doi:10.1667/0033-7587(2001)156[0577:cafdts]2.0.co;2

CrossRef Full Text | Google Scholar

7. Durante M, Cucinotta FA. Heavy ion carcinogenesis and human space exploration. Nat Rev Cancer. (2008). 8:465–72. doi:10.1038/nrc2391

CrossRef Full Text | Google Scholar

8. Takam R, Bezak E, Marcu LG, Yeoh E. Out-of-field neutron and leakage photon exposures and the associated risk of second cancers in high-energy photon radiotherapy: current status. Radiat Res. (2011). 176:508–20. doi:10.1667/rr2606.1

CrossRef Full Text | Google Scholar

9. Yonai S, Furukawa T, Inaniwa T. Measurement of neutron ambient dose equivalent in carbon-ion radiotherapy with an active scanned delivery system. Radiat Protect Dosim. (2014). 161 (1–4):433–6. doi:10.1093/rpd/nct251

CrossRef Full Text | Google Scholar

10. Staaf E, Brehwens K, Haghdoost S, Pachnerova-Brabcova K, Czub J, Braziewicz J, et al. Characterization of a setup for mixed beams exposure of cells to 241Am alpha particles and X-rays. Radiat Protect Dosim. (2012). 151:570–9. doi:10.1093/rpd/ncs024

CrossRef Full Text | Google Scholar

11. Staaf E, Brehwens K, Haghdoost S, Nievaart S, Pachnerova-Brabcova K, Czub J, et al. Micronuclei in human peripheral blood lymphocytes exposed to mixed beams of X-rays and alpha particles. Radiat Environ Biophys. (2012). 51:283–93. doi:10.1007/s00411-012-0417-x

CrossRef Full Text | Google Scholar

12. Staaf E, Deperas-Kaminska M, Brehwens K, Haghdoost S, Czub J, Wojcik A. Complex aberrations in lymphocytes exposed to mixed beams of 241Am alpha particles and X-rays. Mutat Res. (2013). 756:95–100. doi:10.1016/j.mrgentox.2013.05.001

CrossRef Full Text | Google Scholar

13. Sollazzo A, Brzozowska B, Cheng L, Lundholm L, Haghdoost S, Scherthan H, et al. Alpha particles and X-rays interact in inducing DNA damage in U2OS cells. Radiat Res. (2017). 188:400–11. doi:10.1667/rr14803.1

CrossRef Full Text | Google Scholar

14. Sollazzo A, Brzozowska B, Cheng L, Lundholm L, Scherthan H, Wojcik A. Live dynamics of 53BP1 Foci following simultaneous induction of clustered and dispersed DNA damage in U2OS cells. Int J Mol Sci. (2018). 19:519. doi:10.3390/ijms19020519

CrossRef Full Text | Google Scholar

15. Cheng L, Brzozowska B, Sollazzo A, Lundholm L, Lisowska L, Haghdoost S, et al. Simultaneous induction of dispersed and clustered DNA lesions compromises DNA damage response in human peripheral blood lymphocytes. PLoS One. (2018). 13(10):e0204068. doi:10.1371/journal.pone.0204068

CrossRef Full Text | Google Scholar

16. Cheng L, Brzozowska-Wardecka B, Lisowska H, Wojcik A, Lundholm L. Impact of ATM and DNA-PK inhibition on gene expression and individual response of human lymphocytes to mixed beams of alpha particles and X-rays. Cancers. (2019). 11(12):2013. doi:10.3390/cancers11122013

CrossRef Full Text | Google Scholar

17. Friedland W, Kundrat P. “Modeling of radiation effects in cells and tissues.” In: Brahme, A, editor. Comprehensive biomedical physics. Vol. 9. Amsterdam, Netherlands: Elsevier (2014). p. 105–42.

Google Scholar

18. Nikjoo H, Girard P. A model of the cell nucleus for DNA damage calculations. Int J Radiat Biol. (2012). 88:87–97. doi:10.3109/09553002.2011.640860

CrossRef Full Text | Google Scholar

19. Friedland W, Dingfelder M, Kundrat P, Jacob P. Track structures, DNA targets and radiation effects in the biophysical Monte Carlo simulation code PARTRAC. Mutat Res. (2011). 711:28–40. doi:10.1016/j.mrfmmm.2011.01.003

CrossRef Full Text | Google Scholar

20. Friedland W, Kundrat P. Track structure based modelling of chromosome aberrations after photon and alpha-particle irradiation. Mutat Res. (2013). 756:213–23. doi:10.1016/j.mrgentox.2013.06.013

CrossRef Full Text | Google Scholar

21. Brehwens K, Bajinskis A, Staaf E, Haghdoost S, Cederwall B, Wojcik A. A new device to expose cells to changing dose rates of ionising radiation. Radiat Protect Dosim. (2012). 148(3):366–71. doi:10.1093/rpd/ncr092

CrossRef Full Text | Google Scholar

22. Savage JRK, Simpson PJ. FISH “painting” patterns resulting from complex exchanges. Mutat Res. (1994). 312:51–60. doi:10.1016/0165-1161(94)90008-6

CrossRef Full Text | Google Scholar

23. Lucas JN, Poggensee M, Straume T. Translocations between two specific human chromosomes detected by three-color “chromosome painting”. Cytogenet Cell Genet. (1993). 62:11–2. doi:10.1159/000133434

CrossRef Full Text | Google Scholar

24. Deperas-Kaminska M, Zaytseva EM, Deperas-Standylo J, Mitsyn GV, Molokanov AG, Timoshenko GN, et al. Inter-chromosomal variation in aberration frequencies in human lymphocytes exposed to charged particles of LET between 0.5 and 55 keV/μm. Int J Radiat Biol. (2010). 86:975–85. doi:10.3109/09553002.2010.496028

CrossRef Full Text | Google Scholar

25. Steel GG, Peckham MJ. Exploitable mechanisms in combined radiotherapy–chemotherapy: the concept of additivity. Int J Radiat Oncol Biol Phys. (1979). 5:85–91. doi:10.1016/0360-3016(79)90044-0

CrossRef Full Text | Google Scholar

26. Sharma S, Cabana R, Shariatmadar S, Krishan A. Cellular volume and marker expression in human peripheral blood apheresis stem cells. Cytometry. (2008). 73A:160–7. doi:10.1002/cyto.a.20524

CrossRef Full Text | Google Scholar

27. Friedland W, Kundrat P. Chromosome aberration model combining radiation tracks, chromatin structure, DSB repair and chromatin mobility, Radiat Protect Dosim. (2015). 166(1–4):71–4. doi:10.1093/rpd/ncv174

CrossRef Full Text | Google Scholar

28. Friedland W, Kundrát P, Schmitt E, Becker J, Ilicic K, Greubel C, et al. Modeling studies on dicentrics induction after sub-micrometer focused ion beam grid irradiation. Radiat Protect Dosim. (2019). 183(1–2):40–4. doi:10.1093/rpd/ncy266

CrossRef Full Text | Google Scholar

29. Hill MA, O’Neill P, McKenna WG. Comments on potential health effects of MRI induced DNA lesions: quality is more important to consider than quantity. Eur Heart J Cardiovasc Imaging. (2016). 17(11):1230–8. doi:10.1093/ehjci/jew163

CrossRef Full Text | Google Scholar

30. Newman HC, Prise KM, Folkard M, Michael BD. DNA double-strand break distributions in X-ray and a-particle irradiated V79 cells: evidence for non-random breakage, Int J Radiat Biol. (1997). 71(4):347–63. doi:10.1080/095530097143978

CrossRef Full Text | Google Scholar

31. Milian FM, Gouveia AN, Gual MR, Echeimberg JO, Arruda-Neto JDT, Garcia F, et al. In vitro effects of gamma radiation from 60Co and 137Cs on plasmid DNA. J Biol Phys. (2007). 33(2):155–60. doi:10.1007/s10867-007-9050-3

CrossRef Full Text | Google Scholar

32. Fulford J, Nikjoo H, Goodhead DT, O’Neill P. Yields of SSB and DSB induced in DNA by AlK ultrasoft X-rays and a-particles: comparison of experimental and simulated yields, Int J Radiat Biol. (2001). 77(10):1053–66. doi:10.1080/09553000110069308

CrossRef Full Text | Google Scholar

33. de la Fuente Rosales L, Incerti S, Francis Z, Bernal MA. Accounting for radiation-induced indirect damage on DNA with the Geant 4-DNA code. Phys Med. (2018). 51:108–16. doi:10.1016/j.ejmp.2018.06.006

CrossRef Full Text | Google Scholar

34. Brzozowska B, Galecki M, Tartas A, Friedland W, Wojcik A. Modeling of radiation-induced foci features in cell exposed to alpha and X-ray radiation using particle track structures. manuscript in preparation.

Google Scholar

35. Pantelias A, Zafiropoulos D, Cherubini R, Sarchiapone L, De Nadal V, Pantelias GE, et al. Interphase cytogenetic analysis of G0 lymphocytes exposed to α-particles, C-ions, and protons reveals their enhanced effectiveness for localized chromosome shattering—a critical risk for chromothripsis. Cancers. (2020). 12:2336. doi:10.3390/cancers12092336

CrossRef Full Text | Google Scholar