Measuring the Impact of Nuclear Interaction in Particle Therapy and in Radio Protection in Space: the FOOT Experiment

Introduction

In the last decade a continuous increase in the number of cancer patients treated with charged Particle Therapy (PT) [1] has been registered, as a consequence of its effectiveness in the treatment of deep-seated solid tumors [2]. While protons and carbon ions are, nowadays, used in PT clinical routines, an interest also in helium and oxygen ions as therapeutic beams is growing [3, 4].

The use of light ion beams to treat tumors in PT is mainly motivated by the depth-dose profile of charged particles. This is characterized by an entrance channel where a low amount of dose is released, followed by a narrow region, the Bragg Peak (BP), where the maximum of the dose is deposited that is used to cover the cancer region, allowing to spare the surrounding healthy tissues. Furthermore the increase in the radiation Linear Energy Transfer (LET) in the BP region enhances its Relative Biological Effectiveness (RBE) in cell killing when comparing with conventional radio therapy using photons. Even though the track structure also plays a role, as a general approximation, high LET corresponds to high RBE, so the effect is particularly important for ions like ¹²C or ¹⁶O, where the LET increases significantly near the BP region. The RBE increase as a function of LET stops around 100–200 keV/µm, where the RBE peaks, depending on the ion specie, and than drops down for further LET increases [5, 6].

The increase in the RBE of ¹²C or ¹⁶O beams comes at the price of an increased difficulty in planning the treatment to properly account for the beam fragmentation. In the interaction with the atomic nuclei inside the patient body, the beam particles can fragment producing secondary particles with lower atomic number Z. Such fragments have a longer range that results in an energy loss tail beyond the BP region. Moreover the lightest fragments, especially protons and neutrons, can be emitted with large angle with respect to the beam direction. Fragmentation processes modify the delivered dose map with respect to the one that can be computed only accounting for the primary ions contribution [7]. This effect strongly depends on the mass and the energy of the ion beam and on the target involved in the interaction. Treatment plans, generally based on deterministic codes [8], and benchmarked against MC simulations [9–12], are not yet able to include the fragmentation contribution with the accuracy (3%) required for radiotherapy applications [13, 14]. This is due to the lack of experimental data, and in particular of double differential cross section measurements with respect to the angle and the kinetic energy of the fragment. In recent years some experiments have been dedicated to the measurement of the ¹²C ions fragmentation cross sections, however this program was carried out only for a few, energies-target combinations [15–17] and the completion of the experimental data inputs collected using thin targets is still eagerly needed. The targets of main interest for the study of fragmentation cross sections for PT applications are the ¹⁶O, ¹²C and ¹H nuclei, being the most abundant elements in the human tissues, while, as for the beams, together to ¹²C and ¹⁶O, ⁴He is of great interest due to the low fragmentation yield and to the good compromise between LET and RBE [18, 19].

The landscape is quite different for proton treatments: no beam fragmentation is expected and due to the low and slowly varying LET a constant RBE value equal to 1.1 is currently adopted in clinical practice. However, recent radiobiological measurements provided indications of a significant increase in the RBE above 1.1 [20]. In particular the such increase could lead to a biological range extension after the BP or to an enhancement of the biological damage in the entrance channel (plateau region in the Bragg curve before the BP), i.e. in the region where the beam crosses the healthy tissues [21, 22]. The increase could be connected to the nuclear interactions occurring between the beam and the patient tissues. In the case of proton beams, only target fragmentation occurs, generating a spectrum of low energy fragments whose recoil depends on the beam energy and target materials. These secondary charged particles have an extremely short range (e.g. order of 10-100 µm), and are characterized by very high LET and, hence, high RBE. Particles produced in target fragmentation interactions [21] could be one of the causes of the proton RBE increase [23]. In proton therapy this process can have an impact in particular in the entrance channel, where the contribution to the dose deposition from the primary beam ionization processes is smaller with respect to the one occurring in the Bragg Peak region.

Unfortunately at present this effect is difficult to explore due to the missing cross sections measurements related to the production of heavy fragments induced by the proton irradiation with energies in the range of interest for PT (≤200 MeV). The process of target fragmentation so far has been almost completely neglected. The only available measurements cover the light fragment (Z < 3) production, with a total lack of data for the heavier fragments. In order to improve the modeling of the RBE, including the contribution from target fragmentation, the study of protons interactions with O and C targets are of fundamental importance.

The fragmentation of light ions on light targets is of interest also in the field of radioprotection in space. ESA, NASA and other space agencies have started, since several years, the astronauts risk assessment studies in view of long duration space missions (E.g. the travel to Mars). An efficient spacecraft shielding system from space radiation is mandatory to ensure the astronauts safety [24, 25]. There are three main sources of energetic particles in space: Solar Particle Events (SPEs), Galactic Cosmic Rays (GCR) and the geomagnetically trapped particles. SPEs are mainly composed of protons emitted from the sun during coronal mass ejections and solar flares. Their energy spectrum can reach the GeV region and, being unpredictable, they can fluctuate and become so intense as to inflict a lethal dose to the astronauts. GCRs are originated from supernovae within the Milky Way Galaxy and consist mainly of high energy protons (≃86%), helium (≃12%) and heavier nuclei (≃1%) up to ⁵⁶Fe, called HZE - high (H) energetic (E) charged (Z) nuclei. GCRs energy spectrum ranges from MeV to TeV, peaking around 100–800 MeV/nucleon. The geomagnetically trapped particles consist of protons and electrons confined by the Earth magnetic field in two regions named Van Allen belts. Protons reach energies up to a few hundreds MeV in the inner belt and electrons up to 100 keV in the outer belt.

When the incident radiation, and in particular ⁴He and HZE ions from GCRs, interacts with the spacecraft hull and internal materials, the nuclear fragmentation modifies the space radiation spectra, producing of secondary fragments that contribute to the dose release. This process has to be taken into account when designing the proper shield to reduce the dose delivered to astronauts and to prevent damages to the electronic systems and instrumentations [24]. Dose estimates can be obtained, with a limited precision, through direct measurements, but the main tools available for the planning task are calculations with deterministic and Monte Carlo transport codes [26]. An essential ingredient for validating and benchmarking the simulation results is the comparison with the measured nuclear fragmentation cross sections for the interaction of the space primary ion components on different types of shielding [27]. Light materials, rich in hydrogen, are now considered as best shielding candidates and are preferred to aluminium, the material currently used to build most spacecraft structures. While the mass stopping power (depending on $Z/A$) is maximized for light elements, the nuclear interaction cross section (proportional to $\sigma /A$) is minimized, reducing to a minimum the yield of neutrons produced in the interaction with the shield [24, 25]. Low Z, and especially liquid hydrogen, are hence among the most effective materials to be used to build shielding structures for space applications [28]. While liquid hydrogen is not a suitable practical choice, being a low temperature liquid, shielding structures can be built using hydrogen stored in graphite nanofibers or lithium hydride compounds (⁶LiH). So far, polyethylene has been extensively studied and is regarded as a good compromise between the achieved performance and easiness of practical integration with the spacecraft structure.

Summarizing, there is a common ground between protecting the astronauts from the harmful effects of space radiation and improving the tumor therapy planning of patients treated with protons and ions. The particle species currently available in PT (protons and ¹²C) or considered as promising alternative candidates (⁴He, ¹⁶O) are among the most abundant in space. The overlap is also in terms of targets (H and C) and energy, especially in the region of interest for tumor therapy applications that is the same of solar flare protons and Van Allen trapped protons and is placed near the peak of the GCR spectrum.

In this landscape the FOOT (FragmentatiOn Of Target) collaboration has the purpose of performing precise measurements of differential fragmentation cross sections, with respect to the emitted fragment kinetic energy and production angle [29, 30]. The FOOT measurements campaign foresees an extensive program focused on the nuclear fragmentation of ⁴He, ¹²C and ¹⁶O beams impinging on thin C and H rich targets, like polyethylene C₂H₄, in the energy range 100-800 MeV/nucleon, of interest for PT and radioprotection in space (RPS) applications.

The FOOT Experiment

The FOOT experiment, funded by INFN (Istituto Nazionale di Fisica Nucleare, Italy), has been designed to detect, track and identify all the charged fragments produced in ion collisions with different targets, with the aim of measuring both projectile and target fragmentation. The latter, which is of interest for applications in the proton-Nucleus (p-N) collisions field, is an exceptionally challenging task because of the very short range of the produced fragments that results in a very low probability of escaping the target. Their range is limited to tens of microns and even a very thin solid target would stop them or badly spoil their energy measurement.

Target fragmentation cross sections will be hence measured using an inverse kinematic approach, studying the interactions of different ion beams (like ¹²C and ¹⁶O) impinging on hydrogen enriched targets, such as C₂H₄, with an energy in the 50-200 MeV/nucleon range. The p-N cross sections will be therefore computed using the data collected using C₂H₄ and C targets by means of a subtraction method whose feasibility has been already shown by the authors of refs. [31, 32].

When the projectile nucleus (¹²C or ¹⁶O) collides with a H nucleus of the target, the projectile fragments in the laboratory frame can be seen (applying a suitable Lorentz boost) as the products of a process where a p collides onto a C or O target nucleus, but can be more easily measured. While the process of boosting the fragments in the reference frame in which the patient is at rest is a procedure that implies some additional uncertainties (related to the limited precision achievable on the physical quantities used to perform the Lorentz boost), the proposed method allows to perform the differential cross section measurements that would have been impossible otherwise.

A detector capable of performing the target fragmentation measurement using the inverse kinematic approach can as well perform the direct measurement of projectile fragmentation cross sections induced by C, He and O beams. The targets are the same (graphite and polyethylene) both for PT applications and to explore the higher incoming beam energy range for RPS in deep space applications. Using additional target materials, like polymethyl methacrylate (PMMA, C₅O₂H₈), also other nuclei of interest for biological effects, like oxygen, can be studied. A summary of the physics program of FOOT is reported in Table 1.

TABLE 1

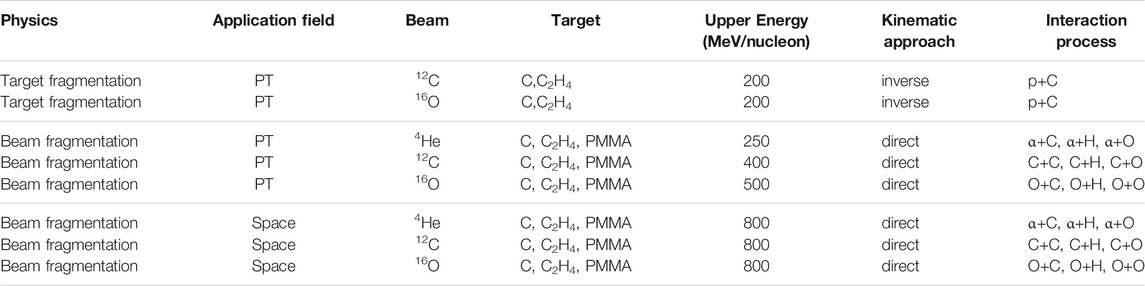
TABLE 1. FOOT physics program: in the last column the interaction processes to be studied for a given combination of beam, target, energy and kinematic approach are shown.

The most stringent requirements on the precision that FOOT has to reach are driven by the study of the target fragmentation process.

The final goal of the FOOT experiment is to measure differential cross sections with respect to the kinetic energy (dσ/dE_kin) for the target fragmentation process with an accuracy better than 10% and double differential cross sections (d²σ/dΩ·dE_kin) for the projectile fragmentation process with an accuracy better than 5% on the determination of the fragment yields in angle and in kinetic energy.

To achieve these performances the charge and isotopic identification capability of the fragments should reach the level of 2–3% and 5% precision respectively, in order to have a clear separation of all the isotopes under study. Such requirements become particularly difficult to match in the inverse kinematic approach, translating in a needed resolution on reconstructed momentum and kinetic energy of the order of few percent and a resolution on the emission angle with respect to the beam direction of the order of few mrad. To minimize the multiple scattering impact and the probability of secondary fragmentation inside the target, its overall density weighted thickness has to be of the order of 2-4 g/cm², limiting the fragmentation probability to ∼10⁻².

A MC simulation of a ¹⁶O beam of 200 MeV/nucleon kinetic energy impinging on a C₂H₄ target has been implemented using the FLUKA code [33, 34] to design and optimize the detector. The results of such simulation in terms of fragments yields in angle (Figure 1 (Left)) and in kinetic energy (Figure 1 (Right)) show that heavier fragments (Z > 2) are forward peaked within a polar angle of ≃10° and with a kinetic energy per nucleon peaked around the corresponding primary beam value. The light fragments, instead, have wider angular and kinetic energy distributions. Such distribution have been considered when designing the experimental setup, as they have a strong impact on the detector geometrical acceptance.

FIGURE 1

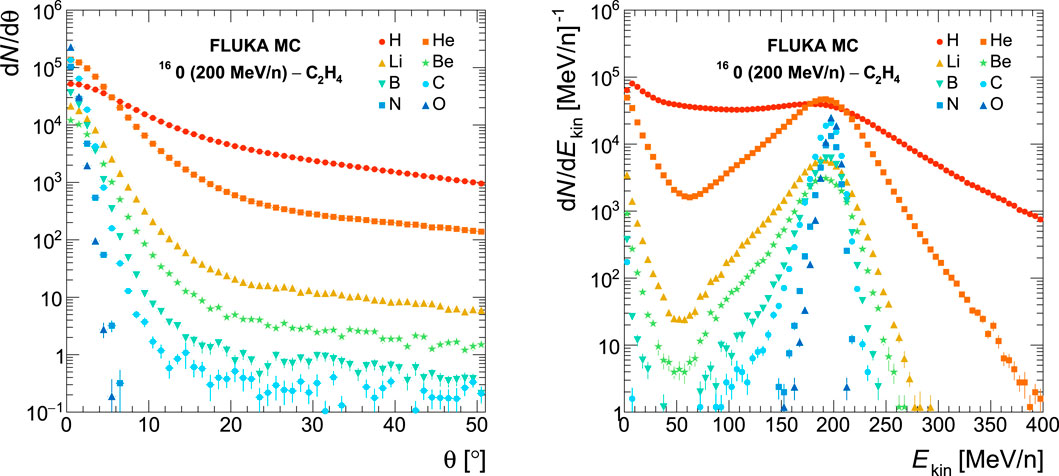
FIGURE 1. MC calculation [33, 34] of the angular (Left) and kinetic energy (Right) distributions of different fragments produced by a 200 MeV/nucleon ¹⁶O beam impinging on a C₂H₄ target.

Another constraint for the FOOT experiment comes from the request to have a “movable” detector capable of fitting the space limitations set by the different experimental rooms where ion beams of therapeutic energies are available. The standard choice, for a fixed target experiment like FOOT, would be a magnetic spectrometer composed by a dipolar magnet and high precision tracking detectors, together with some detector for particle identification.

However as seen in Figure 1 low mass fragments (Z < 3) are emitted with a wide angular aperture and the necessary cost, size, and weight of a magnetic apparatus capable of tracking them with the required precision would become impracticable in view of a “table top” setup design.

The FOOT experiment will implement an “upstream region” composed by the pre-target detectors, that will be used to monitor the impinging beam, and a region, including the target, for the tracking and the identification of the fragments that foresee two alternative and complementary setups:

1. a setup that implements a magnetic spectrometer, coupled with detectors for tracking and detectors optimized for the identification of fragments heavier than ⁴He. Such setup covers an angular acceptance up to a polar angle of about 10° with respect to the beam axis;

2. a setup based on an emulsion spectrometer, optimized for low Z fragments identification emitted at large polar angles that will extend the angular acceptance of FOOT up to about 70°.

The construction of the FOOT detector has started in 2018 and will be completed by the end of 2020, allowing to take data in the following years. Most of the upstream region and of the magnetic spectrometer detectors have already been built and tested in different calibration campaigns at CNAO (Pavia, Italy), TIFPA (Trento, Italy) and GSI (Darmstadt, Germany), with different ion beams of different energies. In the following sections a general description of these detectors will be provided. A detailed review of the technologies employed by the detectors and their measured performances will be reported in dedicated papers, whereas some of them have been already published [35].

Fragmentation cross section measurements using carbon beams impinging on different thin targets in the energy range 115–353 MeV/nucleon have been performed studying fragments emitted at large angles. Such preliminary studies [36] have been performed with an experimental setup very far from the final, optimised, one.

Tests carried out at LNS of the FOOT emulsion chambers have already proved their capability in achieving the required FOOT performances in charge separation [37]. Measurements with the full emulsion chamber setup have been already performed at GSI in 2019 and 2020 using ¹⁶O beams of 200 and 400 MeV/nucleon kinetic energy and a ¹²C beam of 700 MeV/nucleon kinetic energy impinging on C and C₂H₄ thin targets. The ongoing analysis will be the subject of a dedicated paper.

The Upstream Region

The upstream region is composed of pre-target detectors that will be used to monitor the beam, providing its direction and the interaction point on the target, and to count the number of impinging ions. The overall material budget, crossed by the beam, has to be minimised to reduce the out-of-target fragmentation, as well as the multiple scattering of the beam. The chosen configuration foresees two detectors: the Start Counter, a thin plastic scintillator read out by SiPMs, followed by the Beam Monitor, a drift chamber, placed upstream of the target.

The Start Counter

The Start Counter (SC) consists of a thin squared foil of EJ-228 plastic scintillator 250 µm thick. The foil has an active surface with a 5 cm side that is sufficient to cover the typical beam transverse size (see Figure 2 (Left)) and is held by means of an aluminum frame enclosed in a black 3D printed box to provide the light tightness needed for the detector operation. In the black box, two squared windows are placed in correspondence of the scintillator field of view and closed with a thin layer of 4 µm aluminized mylar.

FIGURE 2

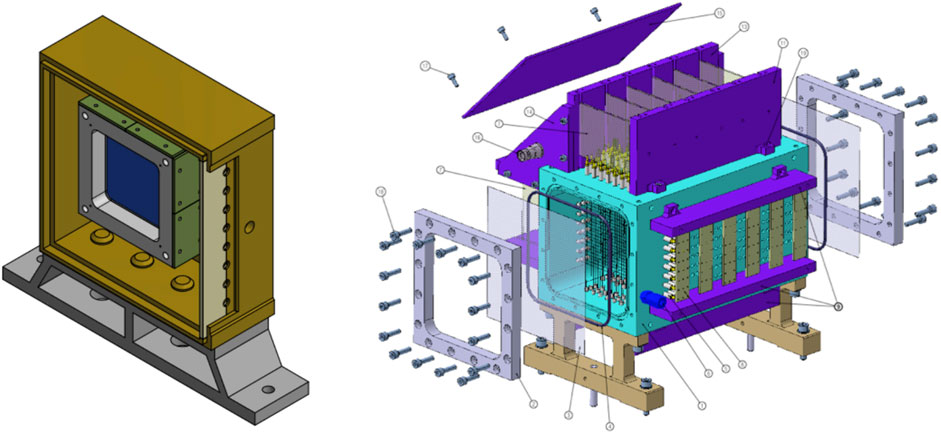
FIGURE 2. Left: Start Counter detector inside the plastic box. The aluminum mechanical structure holds the EJ-228 plastic scintillator foil (in dark blue). Right: Technical drawing of the Beam Monitor drift chamber. The two orthogonal views x–y of the wires are clearly visible. Two enclosing mylar windows held by aluminum frames are shown as well.

The light produced in the scintillator is collected laterally by 48 (AdvanSiD ASD-NUV3S¹) 3 × 3 mm² SiPMs, 12 per side, bundled in eight electronic channels, each reading a chain of 6 SiPMs. The readout and powering of the SiPMs is handled by the WaveDAQ system [38], capable of sampling signals at rates up to 5 Gsamples/s in a dynamic range of 1 V. A gain between 0.5 and 100 can be applied to the incoming signal before digitization allowing to optimise the detector response in case of different beam types or energies. In this way it is possible to maximise the detector efficiency compensating for the low light signal released due to the scintillator thinness.

The acquired waveforms are analyzed offline with a constant fraction discriminator technique to extract the event time t₀.

The SC, placed upstream of the BM and of the target, fulfills four main tasks: it provides the Minimum Bias trigger of the experiment, measures the incoming ion flux (with an efficiency >99%), provides the reference time for all the other detectors and it is used to perform the Time-Of-Flight (TOF) measurement in combination with the TOF-detector (called Tof Wall, TW, see Tof Wall Detector). A time resolution of the order of σ_t ≃ 60 ps has been measured using a ¹²C beam of 700 MeV/nucleon kinetic energy at GSI. Different thicknesses (ranging from 250 µm to 1 mm) can be used to monitor different beam projectiles and energy range combinations, in order to preserve the SC high performances in terms of efficiency and time resolution. A different Start Counter, developed within the FIRST experiment [17, 39], made with the same plastic scintillator, 250 µm thick, but read by PMT, has been used for the Emulsion chamber setup characterization so far as time performances were not requested (see Section The Emulsion Spectrometer, Figure 10 (Left)) and the detector was only used to count the incoming ions.

The Beam Monitor

The Beam Monitor (BM), already used in the FIRST experiment [17], is a drift chamber consisting of twelve wire layers, with three drift cells per layer (see Figure 2 (Right)). Planes with wires oriented along the x and y axes are alternated allowing the beam profile reconstruction in both views. The cell shape is rectangular (16 mm × 10 mm). In each view, two consecutive layers are staggered by half a cell to solve left-right ambiguities in track reconstruction [39]. New studies of BM working operations and achievable performances have been done in the context of the FOOT experiment. The BM operates at ≃0.9 bar with a 80/20% gas mixture of Ar/CO₂, at a working point ranging between 1850 and 2200 V, depending on the primary beam. A BM efficiency of ≃90% has been measured, at the working point, for different combinations of ion beam and energies. A lower limit on the spatial resolution of 100 µm, in the central part of the BM cell, has been achieved [40]. The BM detector will be placed between the SC and the target and will be used to measure the direction and impinging point of the beam ions on the target, a crucial information needed to address the pile-up ambiguity in the tracking devices downstream the target and to discard events in which the beam has fragmented in the SC producing one or more deviated tracks. In order to reject pile-up vertices, an high precision alignment is required between the BM and the devices downstream the target. The BM high spatial resolution is fundamental to measure the direction of the fragments with respect to the beam with an accuracy of few mrad, needed to measure the kinetic energy of the fragments in inverse kinematic with the required resolution. Finally, the BM information about the beam spot size is essential, particularly in the case of the emulsion spectrometer, to monitor the very low intensity beams used for the FOOT acquisitions (see Section Trigger and Data Acquisition System), whereas the monitoring performed with the standard facilities devices, especially in centers for patients treatment, usually cannot provide the required accuracy and resolution at such low rates.

The Magnetic Spectrometer

The driving criterion of the FOOT detector design is the need for an accurate charge and isotopic identification of the produced fragments. To achieve the experimental goals a redundancy in measuring the different kinematic variables is needed, exploiting different particle identification (PID) techniques. For this reason the FOOT setup includes a Time-Of-Flight (TOF) system and a calorimeter for the fragments energy measurement, that, combined with the measurement of the energy released in thin detectors and with the information provided by the magnetic spectrometer, allows the isotope mass identification. The charge Z of fragments reaching the TW can be identified from the energy loss $\text{Δ}E$ and the TOF information, exploiting the Bethe-Bloch formula. The tracking through the magnetic field provides the fragment rigidity ($p/Z$) and its path L that coupled with the measurement of TOF and Z provides the momentum p and the velocity $\beta \cdot c = L/\text{TOF}$ of the particle. Finally the fragment mass identification can be achieved by momentum p, velocity β and kinetic energy $E_{\text{kin}}$ measurements using the following relationships:

$p=mc\beta \gamma ,E_{\text{kin}}=m{c}^2\left(\gamma -1\right),E_{\text{kin}}=\sqrt{p^2{c}^2+m^2{c}^4}-m{c}^2(1)$

where γ is the Lorentz factor. Once the mass and the charge Z are measured the fragment is uniquely identified.

In order to match the precision requirements stated before on the final cross section measurements, it will be necessary to achieve the following experimental resolutions:

$\sigma \left(p\right)/p$ at level of 4-5%;

$\sigma \left(TOF\right)$ at level of 100 ps;

$\sigma \left(E_{\text{kin}}\right)/E_{\text{kin}}$ at level of 1-2%;

$\sigma \left(\text{Δ}E\right)/\text{Δ}E$ at level of 5%.

The detector design has to keep the fragmentation contribution due to the detector material as low as possible and should result in a full apparatus sufficiently compact to be transported and installed in the different facilities where ⁴He, ¹²C and ¹⁶O beams are available. The overall detector size should lie within the 2–3 m range. The actual length of the setup will change according with the β of the beam to allow an almost constant resolution on the fragment TOF. Extensive FLUKA simulations (Figure 1) have been used to optimise the transverse dimension of the detectors in order to fit the required angular acceptance, and their granularity studying the minimum separation angle between the emitted fragments.

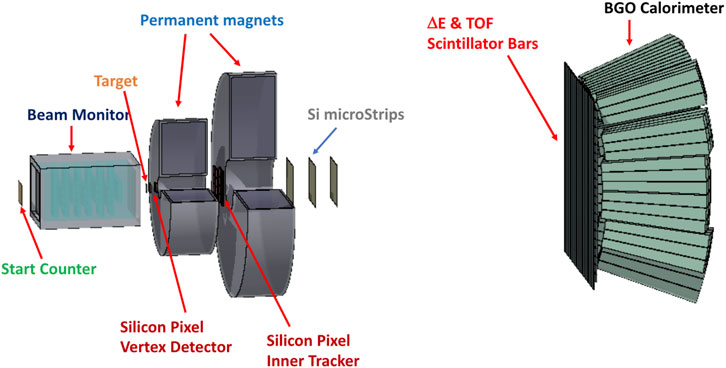
A schematic view of the final choice for the Magnetic Spectrometer setup, together with the upstream region, is shown in Figure 3. Three main regions can be identified in the experimental setup:

1. The upstream region, composed of the Start Counter and the Beam Monitor (see Section The Upstream Region).

2. The interaction and tracking region, composed of the target followed by three stations of pixel and strip detectors placed upstream, between and downstream of two permanent magnets providing the fragments production vertex and momentum measurement through the tracking in the magnetic field.

3. The PID region, in the distal part of the detector located at least 1 m away from the target. It is composed of two orthogonal planes of thin plastic scintillator bars, providing the stop of the TOF and the measurement of the energy loss $\text{Δ}E$. A BGO calorimeter, placed immediately after the TW, provides the fragment kinetic energy measurement.

FIGURE 3

FIGURE 3. Schematic view of the upstream region and the Magnetic Spectrometer setup.

Interaction and Tracking Region

The overall tracking system of the FOOT experiment is conceived as three measuring stations allocated upstream, between and downstream of two permanent magnets, as shown in Figure 4 (Left). The first tracking station is coupled to the target acting as vertex detector (VTX) of the experiment. The needs in terms of momentum resolution and global acceptance together with the minimization of multiple scattering and re-fragmentation in both the sensors and the mechanical structures themselves suggest the use of monolithic pixel sensors in the two upstream stations, the VTX and the inner tracker (ITR), while a telescope of silicon microstrip detectors (MSD) is envisaged for the downstream station. In between the three stations two permanent magnets, in Halbach configuration, provide the required magnetic field.

FIGURE 4

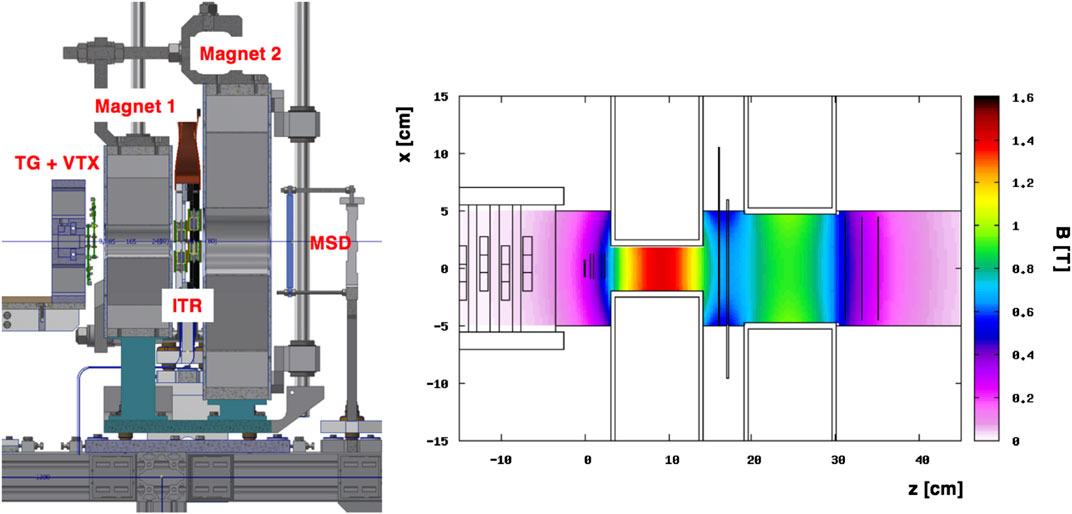
FIGURE 4. (Left) Technical design of the interaction and tracking regions: the vertical axis is the y axis, while the horizontal axis is the z axis. The beam coming from the left, along the z-axis, cross sequentially the target (TG), the vertex detector (VTX), moves into the magnets region and crosses the Inner Tracker (ITR) and, immediately after the second magnet, passes through the Micro Strip Detetor (MSD). (Right) Computed magnetic field map produced by the FOOT magnets in Halbach configuration. The magnetic field intensity B, shown in the palette, is referred to its y-axis component.

Target and Vertex Detector

The target and the Vertex detector (VTX) are hosted in a mechanical structure designed to hold up to five different targets in a sliding tray that can eventually be moved by a remote controlled actuator [17, 41]. The Vertex detector is organized in 4 different pixel sensor layers of 2 × 2cm² transverse dimension, placed along the z axis, respectively at 0.6-0.9-2.1–2.4 cm from the target center guaranteeing a geometrical acceptance of about 40° for the emitted fragments. In order to fulfill the requirements of low material budget and high precision and efficiency, the technology of the MIMOSA-28 (M28) Monolithic Active Pixel Sensors (MAPS) has been adopted for each layer of the VTX. The M28 sensor, developed by the Strasbourg CNRS PICSEL group [42] for the upgrade of the vertex detector inner layer of the STAR experiment at RHIC [43, 44], consists of a matrix with 928 (rows) × 960 (columns) pixels of 20.7 µm pitch. The chip total size is 20.22 mm × 22.71 mm. The M28 sensor is implemented in the AMS-C35B4/OPTO design process that uses 4 metal- and 2 poly- layers. The thickness of the epitaxial layer is 15 µm on a high resistivity substrate of the order of 400 Ω·cm. All four M28 sensors are thinned to 50 µm, resulting in an overall material budget for the entire Vertex tracker of 200 µm. The architecture of the M28 integrates a binary readout and a zero suppression in-chip logic to reduce the amount of data transferred. Each pixel includes an amplification and a Correlated Double Sampling (CDS) circuitry. The sensor employs a rolling shutter readout technique with a 185.6 µs frame readout time: all the pixels CDS output of one row are read out in parallel row by row at the end of the column where 960 discriminators are placed, one per column, each with a configurable threshold level. The VTX readout has been implemented by means of a DE10 board system housing an Intel System-on-Chip (SoC) FPGA (Cyclon V) with a dual-core Cortex-A9 CPU. The FPGA is interfaced with the sensors and with the DAQ control (trigger, time-stamping and busy signals) and the CPU is used to send data to the central DAQ via a 1 GbE connection. The kinematic inverse approach requires the beam particles direction before the target and the fragment emission angle after the target to be tracked with an angular accuracy at the mrad level. The high spatial resolution of 5 µm achieved [45] with the VTX, matched with the information from the BM, can provide such angular resolution while minimizing the multiple scattering thanks to the reduced material budget of both BM and VTX.

The magnetic System

A key element for the FOOT spectrometer is the magnetic system used to bend the fragments produced in the target. The portability of the system, when matched with the needed momentum resolution, forces the choice in the direction of having permanent magnets generating the needed ($B\times L$) in a limited sizes and weight, where $B=B\left(z\right)$ is the magnetic field intensity, strongly dependent on the fragment z-position, while L is the length along the z-axis of the magnetic field region where the particles experience the magnetic field effect and that can be roughly assumed to be placed between the VTX and the MSD trackers. A magnetic dipole in vacuum with two tracking stations placed upstream and downstream would ensure as well that the needed momentum resolution is achieved, but is not a viable solution to be implemented in a ‘portable’ table top experiment. The final choice is hence to have a magnetic system kept in air composed of two magnets, in Halbach configuration, which allow an additional tracking station in between the two needed to match the required momentum resolution. In the Halbach configuration an approximately dipolar magnetic field is obtained in the internal hole of a cylindrical permanent magnet. The magnetic field increases with the external cylinder radius while decreases with the gap radius. So in order to match the final momentum resolution producing the needed ($B\times L$) and at the same time have an angular acceptance of 10° for the emitted fragments, two different magnet dimensions have been chosen. The first magnet has a gap diameter of 5 cm while the second one of 10.6 cm. They can provide respectively a maximum intensity of 1.4 T and 0.9 T along the y axis in the internal cylindrical hole. The magnetic field intensity along the cylinder z axis exhibits a gaussian shape for each magnet, according to the computed magnetic map shown in Figure 4 (Right): the inner tracker, sitting in-between the two magnets, will experience a field with an intensity of ∼0.6 T. Each magnet will be made of twelve single units of Samarium-Cobalt, which maintains its magnetic properties also in a high radiation environments. The two magnets will be assembled in a single mechanical structure sufficiently robust to withstand the magnetic forces produced and to provide a high precision in the alignment with the tracking stations. Thanks to a detailed field map, it will be possible to reach the intrinsic achievable accuracy of about 10 µm. The capability of vertically displacing, of about 40 cm, the magnets with respect to the beam line, will give the opportunity to inter-align the tracking stations in specific runs without the magnets, to adapt the setup to different experimental rooms and will ease the tracking detectors access and cabling once the setup will be finally assembled.

Inner Tracker

The FOOT Inner Tracking (ITR) station foresees two planes of pixel sensors to track the fragments in the magnetic region. In order to fit the required acceptance, granularity and tracking performances each plane will cover a sensitive area of about 8 × 8 cm², with 16 M28 sensors per layer. The main reasons for such choice are again the quest for the material budget reduction together with the need of high tracking performances. Furthermore the tracking performances of M28 sensors are not expected to be significantly affected by the foreseen residual magnetic field in between the permanent magnets [46]. In addition, by using the same technology implemented by the VTX the architecture of the DAQ system will be simplified. Differently with respect to the VTX, the large detector area implies the use of a mechanical support, that results in an increase of the overall material budget.

The ITR will be built using ladders similar to the ones implemented in the PLUME project [47]. The ITR ladder will implement a double-sided layout, which consist of two modules of M28-sensor layers glued on the opposite sides of a support structure, 2 mm thick, made of low density silicon carbide (SiC) foam. Each module is composed of 4 M28 sensors glued and bonded on a kapton-metal flex cable. The flex cables provide all the communications and services of the sensors from and to the outside world. The overall material budget of an ITR ladder is $x/X_0\simeq 0.3\%$, where x and $X_0$ are respectively the overall thickness and radiation length of the ITR ladder. The ITR will be composed of four ladders, two for each plane, supported by a metallic frame to hold the entire tracker. While the described design is the final one, the detector still has to be fully assembled and tested.

Micro Strip Detector

The fragments tracking downstream the magnetic region is essential for the measurement of momentum and for the matching of the reconstructed tracks with the hits in the TW and in the calorimeter. This task is entrusted to a microstrip silicon detector (MSD), that, operating with an analogue readout, can also provide a redundant measurement of dE/dx [48–50], for fragments charge Z identification, complementary to the one performed by the TW. A tracking station of three MSD x-y planes with an active area of 9.6 × 9.3 cm², separated by a 2 cm gap along the beam direction and positioned right after the second magnet, ensure the needed angular acceptance to measure ions with Z > 2, as expected from the FLUKA simulation. In order to reduce the amount of material and to provide the x-y coordinate readout, a solution exploiting two perpendicular Single-Sided Silicon Detector (SSSD) sensors thinned down to 150 µm has been adopted for each MSD x-y plane. Each sensor is glued on a hybrid Printed Circuit Board (PCB) that provides the needed mechanical support and the interface with the MSD readout. Light tightness of each plane is ensured using the metallized sensors backplane. A strip pitch size of 50 µm has been chosen in order to minimize the fragment pile-up in the same strip. Each SSSD is readout by 10 VA1140 chips, with a readout pitch of 150 µm, bonded and glued on the PCB, for a total of 640 channels. The front-end hybrids, hosting the readout chips, is glued at one side of each silicon module minimizing the dead space in the beam region. A digital readout of the strips with pitch of 150 µm would provide a spatial resolution of ≃40 µm, while with the selected analog readout a further factor 3 can be gained, as shown in [51, 52], with the additional advantage to measure also the dE/dx, for each x-y view of each layer independently. The analog signals provided by the VA1140 readout chips are digitized by 1 MHz 12-bits ADC and their data are sent to a TERASIC DE10 nano board for data collection and event shipping to the general FOOT DAQ.

Fragment Identification Region

The fragment identification region is the distal part of the detector, located at least 1 m away from the target. It is composed of two orthogonal planes of plastic scintillator bars (Tof-Wall detector), providing the stop of the TOF and the measurement of the energy loss, followed by a BGO calorimeter used to measure the fragment kinetic energy (see Figure 5).

FIGURE 5

FIGURE 5. Schematic view of the fragment identification region. The two orthogonal layers of 20 plastic scintillator bars are shown in front of the matrix of BGO crystals used to build the calorimeter.

Tof Wall Detector

The Tof-Wall detector (TW) is composed of two layers of 20 plastic scintillator bars (EJ-200 by Eljen Technology), arranged orthogonally and wrapped with reflective aluminum and darkening black tape [35, 53]. Each bar is 0.3 cm thick, 2 cm wide and 44 cm long. The two orthogonal x-y layers form a 40 × 40 cm² active area detector that provides the measurements of the energy deposited $\text{Δ}E$, the needed information to compute the TOF (using as input the t₀ from SC), and the hit position. The simultaneous measurement of $\text{Δ}E$ and TOF allows to identify the charge Z of the impinging ions [54, 55]. The Z-identification plays a fundamental role in determining the fragment mass and is used, together with the x-y hit position, as a seed for the fragments tracking through the magnetic field. The TW transverse dimensions have been chosen to match the angular aperture of the heavy fragments at the distance of the detector from the target (1–2 m) set by the experimental room conditions. The chosen granularity keeps the pile-up of multiple fragments in the same bar below ≃1%. The thickness of the bar has been chosen as a trade-off between a higher scintillation signal (reflecting in better timing and energy resolution) and a lower secondary fragmentation probability in the bars, that would spoil the particle identification and tracking.

Each of the two edges of the TW bars is coupled to 4 SiPM (MPPC S13360-3025PE²) with a 3 × 3 mm² active area and 25 µm microcell pitch. The signals of each channel (two channels per bar) are digitized at rates of 3–4 Gsamples/s depending on the trigger scheme adopted (see Section Trigger and Data Acquisition System) by the WaveDAQ system [38] as described in Section The Start Counter. A total of 1024 samples are collected for each signal allowing to record the whole waveform, and to extract offline the time and the charge information. The thickness of the bars and the selected readout chain, have been chosen to meet the FOOT requirements of a TOF resolution better than 100 ps and an energy loss resolution $\text{σ}\left(\text{Δ}E\right)/\text{Δ}E\simeq 5\%$, for the heavier fragments [35]. Thanks to the high number (4 × 14400) of pixels per channel of the SiPM, this setup is able to guarantee a dynamic range spanning over two orders of magnitude and allow the identification of fragments with significantly different energy release (from proton to oxygen with different kinetic energies). Finally, the high precision time measurement can be used to reconstruct the hit position along the bar [35] with a precision σ_pos < 8 mm, better than the one achievable only exploiting the information about the bars crossing, an important information used to reduce the combinatorial association of multiple fragments in the front and rear side of the TW in the offline reconstruction.

Calorimeter

The FOOT calorimeter is the most downstream detector and it is designed to measure the fragments kinetic energy needed to compute their mass A. Depending on the energy of the incoming fragment, different phenomena can take place in the calorimeter in the energy range of interest for the FOOT experiment. At the highest energies, ≃700–800 MeV/nucleon, that will be explored in the context of space radiation protection studies, the pion production threshold is exceeded and hadronic showering takes place. In these conditions a full containment cannot be achieved with affordable calorimeter dimensions, and this results in a worsening of the achievable resolution at these energies. On the other hand, the highest resolution is needed for the case of target fragmentation studies, that involves ¹²C and ¹⁶O up to 200 MeV/nucleon. In this energy range, the main mechanism of energy loss is by far through electromagnetic interaction with the target electrons and nuclei. In that case a proper containment of the fragments can be achieved allowing to maximise the energy resolution. In all cases, however, it shuold be noted that for a fraction of the events neutron production takes place and part of the fragment energy escapes the detector, causing a systematic error that spoils the energy resolution. The impact of such effect can be minimised exploiting the redundant information coming from the other detectors. Since FOOT will work at a relatively low beam intensity, the ideal material for a calorimeter is a dense crystal, with high light yield, without strict requirements on the response speed: BGO was identified as the best candidate providing the needed performance, on one side, while easing the matching with the mechanical constraints and the overall cost on the other. The high density of this material (ρ = 7.13 g/cm³) guarantees a high stopping power, that, coupled to a light yield of ≃10 photon/keV, meets the requirements on the energy resolution. The FOOT calorimeter will be composed of 320 Bi₄Ge₃O₁₂ (BGO) crystals positioned with an approximately disk-like arrangement (≃20 cm radius) and mechanically divided in modules of 3 × 3 crystals, in order to best handle their weight and positioning. The crystals have a truncated pyramid shape with a front (back) face of about 2 × 2 cm² (3 × 3 cm²) and a length of 24 cm. The BGO crystal transverse size is similar to the TW granularity. The probability of pile-up in the same crystal due to multi-fragmentation events is kept below ≃1–2%, depending on the beam energy/experimental room setup configuration. The crystal depth has been chosen in order to minimize the energy leakage mainly due to neutrons escaping the calorimeter. Each BGO crystal is coupled to a 25 SiPMs matrix with an active surface of 2 × 2 cm², where each microcell has a pitch of 15 µm, small enough to have a linear response in the energy range up to about 10 GeV. Each SiPM matrix is coupled to a readout board specifically designed to match the dimensions of the SiPMs, ensuring a very compact design of the overall detector. The Front-end board will be interfaced with the WaveDAQ system, the same readout system used for SC and TW detectors [38], that will sample the signal at 1 Gsample/s, allowing a measurement based on both the signal amplitude and its integral, as well as a shape analysis. The same board is used to readout the SiPM temperature sensor, useful to compensate the variation of the system response caused by temperature variations and to equalize the calorimeter response offline. Several beam tests have been performed in a wide energy range (from 70 MeV protons to 400 MeV/nucleon ¹²C), in order to choose the optimal combination of SiPM array, readout configuration and BGO wrappings. A very good linearity response is achieved in the whole investigated energy range and the measured energy resolution $\text{σ}\left(E_{\text{kin}}\right)/E_{\text{kin}}$ below 2% meets the experiment requirements for the heavier fragments [56, 57].

Trigger and Data Acquisition System

The FOOT detector will be equipped with a DAQ system designed to acquire the data with high accuracy in a controlled and online-monitored environment.

The main experiment trigger (Minimum Bias) will be based on signals provided by the SC and will be fired whenever the multiplicity of the channels above thresholds exceeds a programmable value (majority trigger). This choice minimise the source of systematic uncertainties on the cross section measurements due to the events trigger selection. A fragmentation trigger asking for activity outside the central bars of the TW in a logical OR can also be used, in addition to a prescaled Minimum Bias trigger, to enhance the fraction of recorded fragmentation events. The technology that will be used to implement the trigger is provided by a CAEN V2495 board³, whose FPGA and internal logic is fully programmable. The maximum acquisition rate affordable when operating with a Minimum Bias trigger would depend on the slowest detectors in the experiment. These are the MIMOSA 28 chips used in the pixel trackers (VTX and ITR), which have a frame readout time of 185.6 µs, needed to read about 10⁶ pixels per chip. The overall maximum readout rate would be hence of about R_max = 5 kHz. The system will be designed to handle a maximum DAQ rate of R_daq = R_max, but in order to reduce pile-up effects in the MIMOSA chips the actual trigger rate will be of the order of R_trigger = 1 kHz. With this rate, considering a duty cycle of $f_{\text{dc}}$ = 30%, during stable running conditions, up to N_day ≃ 86400·1k·0.3 = 26 M events per day can be collected with a Minimum Bias trigger.

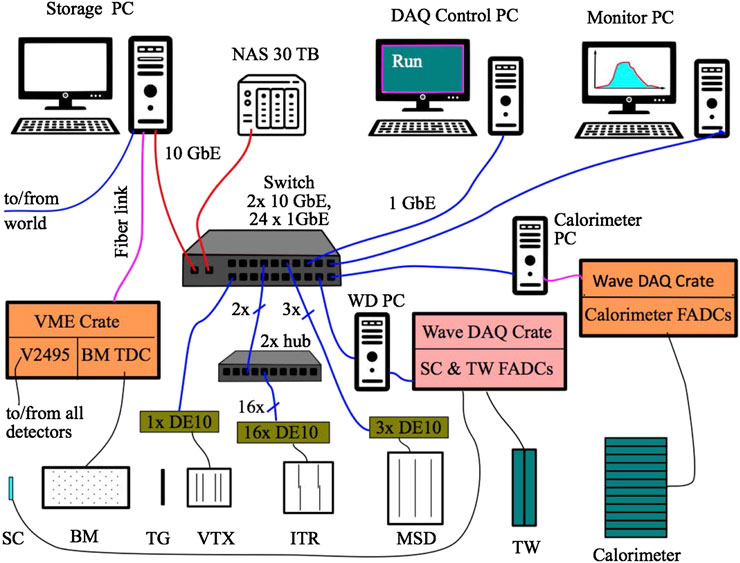
The DAQ system that will be implemented for the whole apparatus is a flexible hierarchical distributed system based on linux PCs, VME crates and boards, detector integrated readout systems and standard communication links like ethernet, USB and optical fibers, schematized in Figure 6.

FIGURE 6

FIGURE 6. DAQ logical scheme.

The system control will be hosted on a controller PC used to run the DAQ GUI interface to start/stop a single run, to control and to configure other nodes in the system. Another PC (Storage PC) will be used to collect the information coming from the different detectors, to perform an event building and to store on disk the acquired data. On the same PC, a MYSQL DataBase (DB) will have the role to store the configuration data (structured DB tables or in form of retrievable text files) and to store the DAQ process information (start/stop DAQ time, events collected, other global DAQ information). An electronic logbook interfaced with the DAQ system will be installed on the same machine.

The steering of the acquisition process and the reading of the other nodes will be managed through an ethernet switch connected via a 10 GbE cable and a CAEN V2718⁴ VME to PCI Optical Link Bridge. The switch is used to collect all the data from the detectors via 1Gbps ethernet connections: the whole tracking system (VTX, ITR and MSD), based on 20 DE10-nano or DE10 Terasic boards, the time of flight system (SC and TW) and the calorimeter based on the WaveDAQ system. The DE10-nano boards have an FPGA for detector reading and a dual core ARM cortex 9 processor for event formatting, zero suppression and data shipping via ethernet. The WaveDAQ boards for the TOF system and for the calorimeter send its data to intermediate PCs providing data calibration, compression and data shipping. The VME to PCI Optical Link Bridge in the storage PC is connected to a VME crate holding the trigger board V2495 and the Beam Monitor discriminators and TDC board CAEN V1190B. The expected typical event size is of the order of 30 kB, but can be increased if needed up to 100 kB. The availability of RAM memories along the data collection paths (in the FPGAs, in the DE10, in the PCs, in the switch and in the CAEN boards) allows an almost complete decoupling of the trigger signal time from the event building time in the storage PC that can happen several seconds apart, while still keeping an average DAQ rate of 1 kHz (with rate peaks of 5 kHz). The whole system is designed to store data on a SSD disk (max rate 400 MB/s) during data taking and to transfer the data to a dedicated (>20 TB) NAS system during idle times. The DAQ system will be equipped with a set of online monitoring tools. The DAQ running related information can be easily collected from each VME board or data provider at a rate ∼Hz, depending on the specific sub-detector system, and provided to a network of PCs connected to the experiment. Typical online monitoring histograms based either on local or distributed data will show detector occupancy, particle arrival times, particle energies, collected charges and so on. The online monitoring foresee also a fast online event reconstruction performed, on the fly, on a fraction of the events. Performing a complete event reconstruction it will be possible to monitor the fragments momentum spectra, TOF, reconstructed charges and masses.

MC Simulation and Fragment Identification Performances

Detailed MC simulations with the FLUKA software [33, 34] have been developed for different combinations of ion beams, beam kinetic energy and targets, in order to optimize the detector design and evaluate its expected performances taking into account the constraints set by the different experimental rooms where FOOT will acquire data. The full detector geometry and materials, already described in Section The Magnetic Spectrometer, have been implemented in the MC simulation to properly evaluate the interactions in all the active detectors and the production of secondary particles in out-of-target fragmentation processes. Care has been taken in detailing at the highest possible degree the different detector subsystems to evaluate with high accuracy the acceptances, efficiencies and resolutions needed for the cross-section measurement.

In the following, the results of a FLUKA simulation of a ¹⁶O beam of 200 MeV/nucleon kinetic energy impinging on a 2 mm thick C₂H₄ target are shown to document the expected performances of the magnetic spectrometer setup in terms of fragment identification [58, 59].

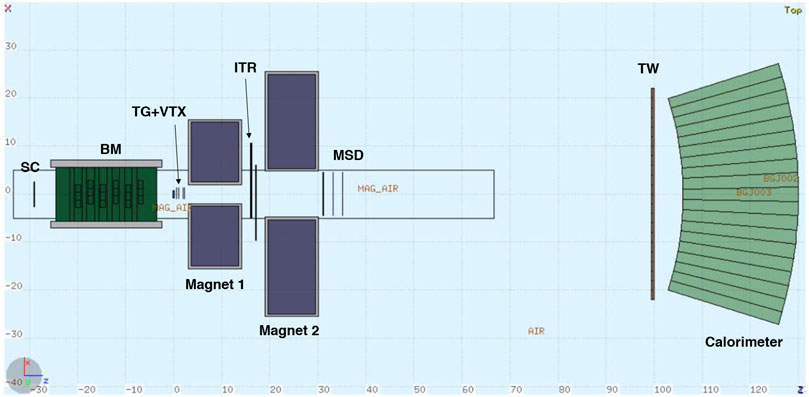
The 2-D top view of the full FOOT detector setup is shown in Figure 7, in a geometrical configuration in which the distance between TG and TW is 1 m, compatible with most of the experimental rooms where FOOT experiment is expected to collect data.

FIGURE 7

FIGURE 7. 2-D top view of the full FOOT setup geometry implemented in the FLUKA MC simulation.

The MC scoring provides the fundamental quantities related to each FOOT detector sub-system: times in SC, fired cells in BM, fired pixels in VTX and ITR detectors, energy released in MSD strips, and time and energy released in TW bars and calorimeter crystals. The reconstruction of the quantities of interest, like clusters, tracks, TOF, fragment charge Z and kinetic energy, is performed locally for each detector. To estimate the detector capability in identifying the fragments in terms of charge and mass, the experimental resolutions of the fundamental quantities necessary for particle identification, when available, have been included in the MC simulation, by means of a Gaussian smearing. No signal digitization has been performed.

The Time Of Flight (TOF), energy loss ($\text{Δ}E$) and kinetic energy ($E_{\text{kin}}$) resolutions implemented in the simulation have been extracted from the results obtained during specific test beams for SC (Section The Start Counter), TW (Section Tof Wall Detector) and for calorimeter (Section Calorimeter). The momentum (p) resolution, not yet measurable due to the absence of the magnets and downstream tracking stations, has been evaluated by means of dedicated MC simulations using a standard Kalman tracking algorithm. The resolutions of the quantities of interest included in the simulation are ranging in the following intervals:

$\sigma \left(p\right)/p$ ≃ 3–5%;

$\sigma \left(TOF\right)$ ≃ 70–250 ps;

$\sigma \left(E_{\text{kin}}\right)/E_{\text{kin}}$ ≃ 1.5–2.5%;

$\sigma \left(\text{Δ}E\right)/\text{Δ}E$ ≃ 3–10%

where the best performances are always referred to the ones expected for the highest fragment charges.

A nuclear fragment is uniquely identified when its charge and mass number are correctly measured. The charge Z of the fragment is measured by means of the TW detector. As shown in Figure 8 (Left) the TW resolution allows the discrimination of eight regions in the $\text{Δ}E$-TOF plane, related to different fragment charges. For each region a Bethe-Bloch curve, parametrized as a function of TOF, has been used to fit the MC simulation results to describe the average energy loss of fragments of the same charge Z impinging on TW with different angles, kinetic energies, TOF and path lenghts L. For each fragment the charge corresponding to the closest Bethe-Bloch curve in the $\text{Δ}E$-TOF plane is assigned. The identification capability depends mainly on the $\text{Δ}E$ resolution, that, with the aforementioned values, implies a fragment charge mis-identification <4%. The fragments pile-up in the same TW bar can partially spoil this value. The MSD information can be exploited to improve the charge identification capabilities partially reducing this latter background source.

FIGURE 8

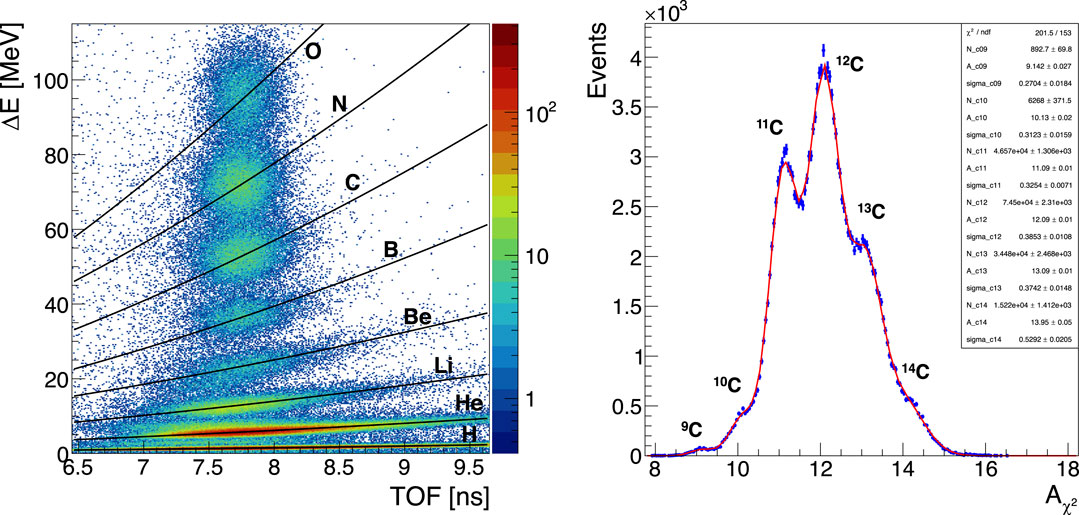
FIGURE 8. (Left) Fragments charge identification in TW using the energy release in the scintillators $\text{Δ}E$ and the TOF calculation performed together to the SC. For each region a Bethe-Bloch curve (shown as a different black curve), parametrized as a function of TOF, has been used to fit the MC simulation results to describe the average energy loss of fragments of the same charge Z impinging on TW with different angles, kinetic energies, TOF and path lenghts L. (Right) An example of mass number determination obtained with the ${\chi }^2$ fit for the carbon fragments for the case of $\sigma \left(\text{TOF}\right)$ ≃ 70 ps, $\sigma \left(p\right)/p\simeq 3.7\%$ and $\sigma \left(E_{\text{kin}}\right)/E_{\text{kin}}\simeq 1.5\%$. The ¹¹C, ¹²C and ¹³C isotopes are clearly visible.

The fragments charge measurement, when coupled to the rigidity ($p/Z$) one provided by the fragment tracking inside the magnetic field, allows to compute the momentum p. As discussed in Section TheFOOT Experiment, by using the measurement of p, TOF and $E_{\text{kin}}$ and inverting the set of Eq. 1, it is possible to have three different, correlated, measurements of the fragment mass. The mass identification resolution is directly related to the precision achieved on p, TOF and $E_{\text{kin}}$. These have to be maximised to match the final cross section precision requirements. In order to get the best mass estimation, taking advantage of the measurement redundancy, a standard ${\chi }^2$ minimization approach or an Augmented Lagrangian Method (ALM) [60] approach can be pursued, performing a fit to the mass values. The two fit procedures lead to compatible results, centering the mass of the selected fragments always around the expected values. The final mass resolution ranges between 3% for ¹²C to 6% for protons. Additionally, the ${\chi }^2$ of the selected fit procedure can be used to exclude the events with a worse mass determination. Once the mass and Z of each fragment are determined the isotopic identification of each fragment is completed. In addition, the fit provides as output better evaluations of the TOF, p and $E_{\text{kin}}$ observables.

An example of mass number determination obtained with the ${\chi }^2$ minimization fit after applying a ${\chi }^2 <5$ cut in the case of carbon ions fragmentation studies is shown in Figure 8 (Right). These results have been obtained with the following parameters: $\sigma \left(\text{TOF}\right)\simeq 70\text{ps}$, $\sigma \left(p\right)/p\simeq 3.7\%$ and $\sigma \left(E_{\text{kin}}\right)/E_{\text{kin}}\simeq 1.5\%$.

To understand which detectors mostly affect the precision achievable on the mass determination, a systematic study varying the TOF, p and $E_{\text{kin}}$ resolutions has been performed. The carbon isotopes mass resolution dependence on each of the three parameters (TOF, p, $E_{\text{kin}}$) is shown in Figure 9. A major influence of the TOF resolution value is evident as shown in Figure 9.

FIGURE 9

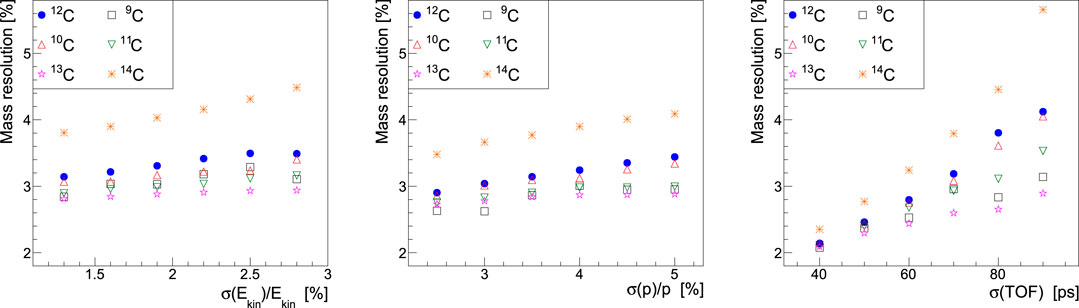
FIGURE 9. Mass resolution of the identified isotopes of carbon ions (⁹C, ¹⁰C, ¹¹C, ¹²C , ¹³C, ¹⁴C) as a function of: A) kinetic energy resolution ($\sigma \left(\text{TOF}\right)=70\text{ps}$ and $\sigma \left(p\right)/p=3.7\%$) B) momentum resolution ($\sigma \left(\text{TOF}\right)=70\text{ps}$ and $\sigma \left(E_{\text{kin}}\right)/E_{\text{kin}}=1.5\%$) C) carbon ions TOF ($\sigma \left(p\right)/p=3.7\%$ and $\sigma \left(E_{\text{kin}}\right)/E_{\text{kin}}=1.5\%$).

The Emulsion Spectrometer

To characterize the production of low Z fragments, an emulsion spectrometer (ES) has been included in the FOOT setup as described in Section TheFOOT Experiment. In Figure 10 (Left) the arrangement of the emulsion chambers inside the FOOT detector is shown: the ES is placed after the SC and the BM, with the beam incoming from the left. The SC and BM are used only for beam monitoring purposes and their DAQ (see Section Trigger and Data Acquisition System) is completely decoupled from the ES that acts as a complete, self standing, experiment. The SC and BM have been used to perform an on-line control of the beam flux on the active ES surface, to avoid spatial pile-up of events in the ES.

FIGURE 10

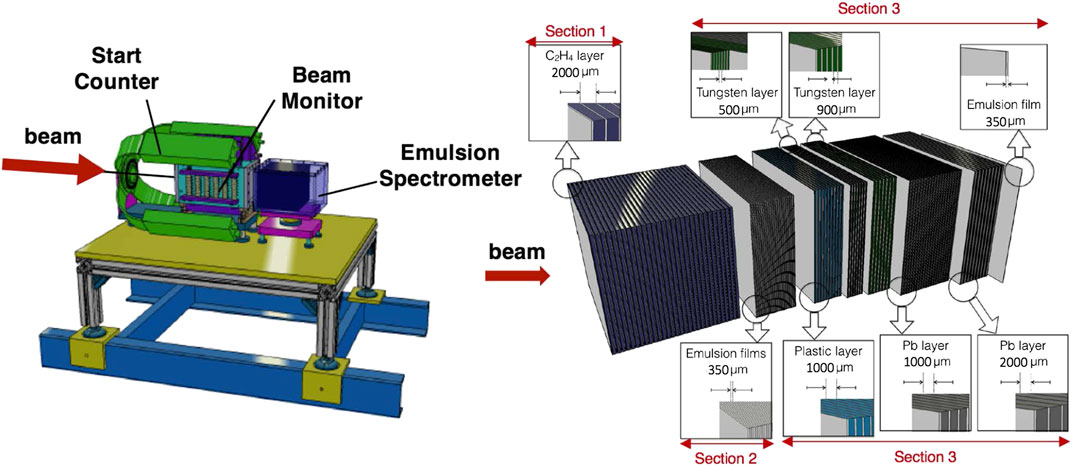
FIGURE 10. (Left) Emulsion spectrometer setup placed downstream the SC and the BM. (Right) Scheme of the emulsion spectrometer composition with the C2H4 target.

Among all tracking devices used in particle physics, nuclear emulsion detectors achieve the highest spatial resolution (sub-micrometric) for tracking ionizing particles. Emulsion chambers integrate target and detector in a very compact setup and provide a very accurate reconstruction of the interactions occurring inside the target. Moreover, no power supply or any readout electronics is required and this helps to keep the emulsion setup compact maximising its active area. The use of emulsions is coupled to the continuous development in the field of automated scanning system techniques: last generation microscopes [61–64] allow very fast scanning with wide angular acceptances of huge data sets. Furthermore, it was demonstrated that a controlled fading of the emulsions in terms of different thermal treatments extends their dynamical range when crossed by different ions, providing charge identification capabilities [37, 65, 66]. The possibility to measure particles emitted with an angular acceptance above 70° with respect to the incident angle, coupled to the very high spatial resolution and charge identification capability, made the nuclear emulsion technology an ideal choice for new generation of measurements of differential fragmentation cross sections. For this reason, emulsion detectors have been already adopted in different measurements campaigns to study fragments produced at large angles by ¹²C ions impinging on thin targets in the energy range of interest for PT [67, 68], showing their capability in the charge identification of the produced fragments [65, 66]. The nuclear emulsion films, used for the FOOT experiment, consist of two 70 µm thick sensitive layers deposited on both sides of a 210 µm plastic base, resulting in a total thickness of 350 µm. The sensitive regions are made of AgBr crystals of 0.2 µm diameter scattered in a gelatine binder, able to detect charged particles. The charged particle trajectory is recorded by a series of sensitised AgBr crystals along its path acting as latent image centres. A chemical process, known as development, enhances latent images, inducing the growth of silver clusters (grains) with a diameter of 0.6 µm which can be seen with an optical microscope. The density of grains is proportional to the charge particle ionization within the detector dynamical range. After the development, the emulsions are scanned by an automated system. The acquired image is then analyzed by a dedicated software to recognize clusters of dark pixels aligned, which represent the track produced by the penetrating particle. A straight sequence of pixels in one emulsion layer defines a “micro-track”. Two aligned micro-tracks belonging to the top and bottom layers of an emulsion film form a “base-track”. The reconstructed base-track has a micrometer accuracy of 1.0 µm in position and 3 mrad in angle [64]. Base-tracks belonging to a straight line along different films, are connected to form “volume-tracks”. The sum of the pixels of the grains belonging to the volume-track is a variable sensitive to the specific ionization, hence to the particle charge. This variable is called track volume (see Section Charge Identification Region).

The Emulsion Spectrometer for the FOOT experiment has been designed with passive materials alternated to nuclear emulsions films acting both as high-resolution tracking devices and ionization detectors. It is composed of three sections with different purposes, as shown in Figure 10 (Right):

1. Interaction and vertexing region (ES Section 1)

2. Charge identification region (ES Section 2)

3. Momentum measurement region (ES Section 3)

The imprinting process due to the passage of a particle in the emulsion film and the following development process makes the emulsion spectrometer a one-shot detector: for each data taking with a fixed combination of ion beam, energy and target, a different emulsion spectrometer has to be assembled, exposed and lately scanned and analyzed.

Interaction and Vertexing Region

The ES Section 1 is made of several elementary cells composed of layers of target element, Carbon or C₂H₄, alternated with emulsion films, as shown in Figure 10 (Right). Whenever the ion beam interacts within the cells of this section, secondary fragments will be emitted and detected by the following regions of the spectrometer. The detector emulsion structure will track the fragments and reconstruct the interaction vertex position. The length of this section will be optimized for each different data taking, to achieve a statistically significant number of reactions accordingly to the combination of ion beam, energy and target. In the GSI 2019 data taking, four emulsion spectrometer setups have been used: for each of the two ¹⁶O beam configurations, at 200 and 400 MeV/nucleon, two different stacks of 30 cells have been used. Each cell was composed of an emulsion film and a target layer of 1 mm of Carbon in one case and of 2 mm of C₂H₄ in the other case. According to MC simulation, based on FLUKA code, about 32% and 30% of ¹⁶O ions at 200 MeV/n are expected to interact within 60 mm of C₂H₄ and within 30 mm of Carbon, respectively.

Charge Identification Region

The particles at the minimum of their ionizing power (MIPs) generate in nuclear emulsion thin tracks whose grain density ranges from 30 to 50 grains/100 µm, according to the emulsions sensitivity. Highly ionizing particles cause a saturation effect suppressing the charge identification. Nevertheless, by keeping the emulsions for an appropriate time (about 24 h) at a relatively high temperature (above 28°C) and a high relative humidity (around 95%), a fading is induced which partially or totally erases the particles tracks. Thus, for instance, films may be made insensitive to MIPs and suited for highly ionizing particles. The combination of several films, having undergone different thermal treatments after exposure, allows overcoming saturation effects for particles with largely different ionizations. This technique has already been used in previous works [37, 65, 66] to enlarge the dynamical range of emulsions. The ES Section 2 aimed to the charge identification for low Z fragments (H, He, Li), is made by elementary cells composed of four emulsion films. After the exposure and before the chemical development, four different thermal treatments were applied to the emulsions, hereafter denoted as R0 (not thermally treated), R1 (28°C), R2 (34°C) and R3 (36°C). For each thermal condition, each track is characterized by four track volume variables, VR0, VR1, VR2 and VR3, respectively, that are proportional to the silver grain density along the trajectory. In the not thermally treated emulsions (R0), all the tracks are visible and the saturation effect makes not possible the charge separation. The R1 thermal process produces the complete erasing of all tracks due to MIPs. The fragments charge separation is obtained by looking at correlations between appropriate pairs of track volume variables, or by a linear combination of them. In the GSI 2019 data taking, a set of nine quadruplets of emulsion films refreshed as explained before has been used.

Momentum Measurement Region

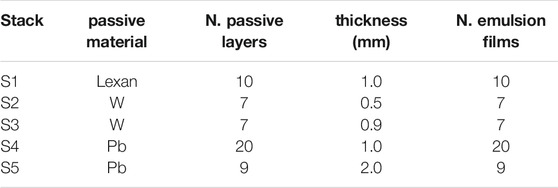
The ES Section 3, dedicated to the momentum measurement, is made of emulsion films interleaved with layers of passive material, as shown in Figure 10 (Right). The section length, the number of passive layers and their thicknesses are set according to the incident beam energy. The materials used as passive layers are Lexan, W and Pb. As an example, the composition of the ES Section 3 used in the GSI 2019 data taking is shown in Table 2, where five different stacks of different combination of passive layer material/thickness have been used. The momentum will be evaluated with the range technique. Measuring the length of the whole particle track, its momentum will be estimated on the basis of the correlation between range and kinetic energy, using data supplied by NIST [69]. The accuracy of this method strongly depends on the segmentation of the ES Section 3 in passive layers and on their thickness and material, chosen in order to stop the crossing fragments, as in a calorimeter. As shown in Table 2, the lower Z passive layers are placed at the beginning of the stack, while the higher Z layers at the end, in order to increase the dynamical range of the momentum measurement. The particle trajectory measurements provide also an estimate of the charged particles momentum through the Multiple Coulomb Scattering (MCS) method [70, 71]. For each particle track, the x-y spatial coordinates and the slope (${\theta }_x$, ${\theta }_y$) are estimated with high accuracy. Thanks to the measurements along a track of the particle direction, provided by the high segmentation of the ES, the particle momentum can be estimated by the MCS method according to the formula:

$p\left(\text{MeV}/\text{c}\right)=\frac{13.6}{\beta \cdot \delta \theta \left(\text{mrad}\right)}\cdot Z\cdot \sqrt{\frac{x}{X_0}}(2)$

where p is the fragment momentum, β its velocity, Z its charge, x the traversed distance, $X_0$ the radiation length in the material and $\delta \theta$ the deviation of the track slope along its path. By using two independent methods for the energy and momentum estimation (i.e the range and multiple Coulomb scattering), combined to the charge measurement performed by the ES Section 2, the fragments mass for the isotopic identification can be assessed. According to FLUKA MC simulation, 77% and 72% of the fragments produced by the interaction of the ¹⁶O (400 MeV/nucleon) beam on C and C₂H₄ targets, respectively, is contained inside the ES.

TABLE 2

TABLE 2. ES Section 3 composition in the GSI 2019 data taking.

Conclusion

The FOOT (FragmentatiOn Of Target) experiment, funded by INFN (Istituto Nazionale di Fisica Nucleare, Italy), has been designed to perform measurements of differential cross sections for the production of charged fragments in the nuclear interaction between ion beams (p, ⁴He, ¹²C, ¹⁶O) and targets (H, C, O) of interest for charged Particle Therapy and space radioprotection applications. The experiment has been designed with the main goal of investigating target fragmentation in proton therapy by means of an inverse kinematic approach, using beams of ¹²C, ¹⁶O impinging on graphite and polyethylene targets, to extract cross sections for the production of charged fragments in p+C and p+O collisions in the energy range of 50–200 MeV/nucleon. The same apparatus will be used to investigate the double differential cross sections of the projectile fragmentation process for beams of ⁴He, ¹²C and ¹⁶O impinging on graphite, polyethylene and PMMA targets up to 500 MeV/nucleon for charged PT and up to 800 Mev/nucleon for space radioprotection. The FOOT detector exploits two alternative complementary setups, a magnetic spectrometer and an emulsion spectrometer, for the tracking and the identification of the fragments in order to provide high acceptance, efficiency and identification capability in a wide dynamical range that spreads from protons to heavier ions up to ¹⁶O. The construction of the detector is being finalized and several beam tests have already been performed for calibration purposes. The experiment started its scientific program using the Emulsion setup at GSI, in 2019 with ¹⁶O ions of 200 and 400 MeV/nucleon kinetic energy on C and C₂H₄ targets, and in 2020 with ¹²C ions of 700 MeV/nucleon kinetic energy, on the same targets. Data analysis is still in progress. The magnetic spectrometer setup is under construction and a first data taking in this configuration is being scheduled at CNAO, using ¹²C ions of 200 MeV/nucleon kinetic energy. An application for beam time in 2021/2022 at GSI is in preparation, having as one of the main priorities the request of a ⁴He ion beam of 700 MeV/nucleon kinetic energy. In future, an upgrade of the FOOT detector is being considered: the evaluation of the neutron production together with the charged fragments can constrain even more strongly MC nuclear production models that are relevant both for PT and RPS. Different strategies for providing neutron detection capability to the FOOT experiment are currently under study.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

The FOOT Collaboration

A. Alexandrov, INFN Section of Napoli, Napoli, Italy, Department of Physics “E. Pancini”, University of Napoli, Napoli, Italy, National University of Science and Technology, MISIS, RUS-119049 Moscow, Russia, and Lebedev Physical Institute of the Russian Academy of Sciences, RUS-119991 Moscow, Russia; B. Alpat, INFN section of Perugia, Perugia, Italy; G. Ambrosi, INFN section of Perugia, Perugia, Italy; S. Argirò, INFN Section of Torino, Torino, Italy and Department of Physics, University of Torino, Torino, Italy; R. Arteche Diaz, Ceaden, Centro de Aplicaciones Tecnologicas y Desarrollo Nuclear, Havana, Cuba; N. Bartosik, INFN Section of Torino, Torino, Italy; G. Battistoni, INFN Section of Milano, Milano, Italy; N. Belcari, INFN section of Pisa, Pisa, Italy and Department of Physics, University of Pisa, Pisa, Italy; E. Bellinzona, Trento Institute for Fundamental physics and applications, Istituto Nazionale di Fisica Nucleare (TIFPA-INFN), Trento, Italy; S. Biondi, INFN section of Bologna, Bologna, Italy and Department of Physics and Astronomy, University of Bologna, Bologna, Italy; M. G. Bisogni, INFN section of Pisa, Pisa, Italy and Department of Physics, University of Pisa, Pisa, Italy; G. Bruni, INFN section of Bologna, Bologna, Italy; P. Carra, INFN section of Pisa, Pisa, Italy and Department of Physics, University of Pisa, Pisa, Italy; P. Cerello, INFN Section of Torino, Torino, Italy; E. Ciarrocchi, INFN section of Pisa, Pisa, Italy and Department of Physics, University of Pisa, Pisa, Italy; A. Clozza, INFN Laboratori Nazionali di Frascati, Frascati, Italy; S. Colombi, Trento Institute for Fundamental physics and applications, Istituto Nazionale di Fisica Nucleare (TIFPA-INFN), Trento, Italy and Department of Physics, University of Trento, Trento, Italy; G. De Lellis, INFN Section of Napoli, Napoli, Italy and Department of Physics “E. Pancini”, University of Napoli, Napoli, Italy; A. Del Guerra, INFN section of Pisa, Pisa, Italy and Department of Physics, University of Pisa, Pisa, Italy; M. De Simoni, INFN section of Roma 1, Rome, Italy and Department of Physics, University of Rome La Sapienza, Rome, Italy; A. Di Crescenzo, INFN Section of Napoli, Napoli, Italy and Department of Physics “E. Pancini”, University of Napoli, Napoli, Italy; B. Di Ruzza, Trento Institute for Fundamental physics and applications, Istituto Nazionale di Fisica Nucleare (TIFPA-INFN), Trento, Italy; M. Donetti, Centro Nazionale di Adroterapia Oncologica (CNAO), Pavia, Italy amd INFN Section of Torino, Torino, Italy; Y. Dong, INFN Section of Milano, Milano, Italy and Department of Physics, University of Milano, Milano, Italy; M. Durante, Biophysics Department, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany and Technische Universität Darmstadt Institut für Festkörperphysik, Darmstadt, Germany; R. Faccini, INFN section of Roma 1, Rome, Italy and Department of Physics, Rome, University of Rome La Sapienza, Italy; V. Ferrero, INFN Section of Torino, Torino, Italy; E. Fiandrini, INFN section of Perugia, Perugia, Italy and Department of Physics and Geology, University of Perugia, Perugia, Italy; Ch. Finck, CNRS, IPHC UMR 7871, F-67000, Université de Strasbourg, Strasbourg, France; E. Fiorina, INFN Section of Torino, Torino, Italy; M. Fischetti, INFN section of Roma 1, Rome, Italy and Department of Scienze di Base e Applicate per l’Ingegneria (SBAI), University of Rome La Sapienza, Rome, Italy; M. Francesconi, INFN section of Pisa, Pisa, Italy and Department of Physics, University of Pisa, Pisa, Italy; M. Franchini, INFN section of Bologna, Bologna, Italy and Department of Physics and Astronomy, University of Bologna, Bologna, Italy; G. Franciosini, INFN section of Roma 1, Rome, Italy and Department of Physics, University of Rome La Sapienza, Rome, Italy; G. Galati, INFN Section of Napoli, Napoli, Italy; L. Galli, INFN section of Pisa, Pisa, Italy; V. Gentile, INFN Section of Napoli, Napoli, Italy and National University of Science and Technology, MISIS, RUS-119049 Moscow, Russia; G. Giraudo, INFN Section of Torino, Torino, Italy; R. Hetzel, RWTH Aachen University, Physics Institute III B, Aachen, Germany; E. Iarocci, INFN Laboratori Nazionali di Frascati, Frascati, Italy; M. Ionica, INFN section of Perugia, Perugia, Italy; A. Iuliano, INFN Section of Napoli, Napoli, Italy and Department of Physics “E. Pancini”, University of Napoli, Napoli, Italy; K. Kanxheri, INFN section of Perugia, Perugia, Italy; A. C. Kraan, INFN section of Pisa, Pisa, Italy; V. Lante, Centro Nazionale di Adroterapia Oncologica (CNAO), Pavia, Italy; C. La Tessa, Trento Institute for Fundamental physics and applications, Istituto Nazionale di Fisica Nucleare (TIFPA-INFN), Trento, Italy and Department of Physics, University of Trento, Trento, Italy; M. Laurenza, INFN Laboratori Nazionali di Frascati, Frascati, Italy; A. Lauria; INFN Section of Napoli, Napoli, Italy and Department of Physics “E. Pancini”, University of Napoli, Napoli, Italy; E. Lopez Torres, INFN Section of Torino, Torino, Italy; Ceaden, Centro de Aplicaciones Tecnologicas y Desarrollo Nuclear, Havana, Cuba; M. Marafini, INFN section of Roma 1, Rome, Italy; Museo Storico della Fisica e Centro Studi e Ricerche Enrico Fermi, Rome, Italy; C. Massimi, Department of Physics and Astronomy, University of Bologna, Bologna, Italy; I. Mattei, INFN Section of Milano, Milano, Italy; A. Mengarelli, INFN section of Bologna, Bologna, Italy; A. Moggi, INFN section of Pisa, Pisa, Italy; M. C. Montesi, INFN Section of Napoli, Napoli, Italy; Department of Chemistry, University of Napoli, Napoli, Italy; M. C. Morone, Department of Physics, University of Rome Tor Vergata, Rome, Italy; INFN section of Roma tor Vergata, Rome, Italy; M. Morrocchi, INFN section of Pisa, Pisa, Italy and Department of Physics, University of Pisa, Pisa, Italy; S. Muraro, INFN Section of Milano, Milano, Italy; F. Murtas, Department of Physics, University of Rome La Sapienza, Rome, Italy; L. Narici, Department of Physics, University of Rome Tor Vergata, Rome, Italy and INFN section of Roma tor Vergata, Rome, Italy; A. Pastore, INFN section of Bari, Bari, Italy; N. Pastrone, INFN Section of Torino, Torino, Italy; V. Patera, INFN section of Roma 1, Rome, Italy and Department of Scienze di Base e Applicate per l’Ingegneria (SBAI), University of Rome La Sapienza, Rome, Italy; F. Pennazio, INFN Section of Torino, Torino, Italy; P. Placidi, INFN section of Perugia, Perugia, Italy and Department of Engineering, University of Perugia, Perugia, Italy; M. Pullia, Centro Nazionale di Adroterapia Oncologica (CNAO), Pavia, Italy; F. Raffaelli, INFN section of Pisa, Pisa, Italy; L. Ramello, INFN Section of Torino, Torino, Italy and Department of Science and Technological Innovation, University of Piemonte Orientale, Alessandria, Italy; R. Ridolfi, Department of Physics and Astronomy, University of Bologna, Bologna, Italy; V. Rosso, INFN section of Pisa, Pisa, Italy and Department of Physics, University of Pisa, Pisa, Italy; C. Sanelli, INFN Laboratori Nazionali di Frascati, Frascati, Italy; A. Sarti, INFN section of Roma 1, Rome, Italy and Department of Scienze di Base e Applicate per l’Ingegneria (SBAI), University of Rome La Sapienza, Rome, Italy; G. Sartorelli, INFN section of Bologna, Bologna, Italy and Department of Physics and Astronomy, University of Bologna, Bologna, Italy; O. Sato, Department of Physics, Nagoya University, Nagoya, Japan; S. Savazzi, Centro Nazionale di Adroterapia Oncologica (CNAO), Pavia, Italy; L. Scavarda, INFN Section of Torino, Torino, Italy and Department of Physics, University of Torino, Torino, Italy; A. Schiavi, INFN section of Roma 1, Rome, Italy and Department of Scienze di Base e Applicate per l’Ingegneria (SBAI), University of Rome La Sapienza, Rome, Italy; C. Schuy, Biophysics Department, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany, E. Scifoni, Trento Institute for Fundamental physics and applications, Istituto Nazionale di Fisica Nucleare (TIFPA-INFN), Trento, Italy; A. Sciubba, INFN Laboratori Nazionali di Frascati, Frascati, Italy and Department of Scienze di Base e Applicate per l’Ingegneria (SBAI), University of Rome La Sapienza, Rome, Italy; A. Sécher, Université de Strasbourg, CNRS, IPHC UMR 7871, F-67000 Strasbourg, France; M. Selvi, INFN section of Bologna, Bologna, Italy; L. Servoli, INFN section of Perugia, Perugia, Italy; G. Silvestre, INFN section of Perugia, Perugia, Italy and Department of Physics and Geology, University of Perugia, Perugia, Italy; M. Sitta, INFN Section of Torino, Torino, Italy; Department of Science and Technological Innovation, University of Piemonte Orientale, Alessandria, Italy; R. Spighi, INFN section of Bologna, Bologna, Italy; E. Spiriti, INFN Laboratori Nazionali di Frascati, Frascati, Italy; G. Sportelli, INFN section of Pisa, Pisa, Italy and Department of Physics, University of Pisa, Pisa, Italy; A. Stahl, RWTH Aachen University, Physics Institute III B, Aachen, Germany; V. Tioukov, INFN Section of Napoli, Napoli, Italy; S. Tomassini, INFN Laboratori Nazionali di Frascati, Frascati, Italy; F. Tommasino, Trento Institute for Fundamental physics and applications, Istituto Nazionale di Fisica Nucleare (TIFPA-INFN), Trento, Italy and Department of Physics, University of Trento, Trento, Italy; M. Toppi, INFN Laboratori Nazionali di Frascati, Frascati, Italy; University of Rome La Sapienza, Department of Scienze di Base e Applicate per l’Ingegneria (SBAI), Rome, Italy; G. Traini, INFN section of Roma 1, Rome, Italy and Department of Physics, University of Rome La Sapienza, Rome, Italy; S. M. Valle, INFN Section of Milano, Milano, Italy; M. Vanstalle, Université de Strasbourg, CNRS, IPHC UMR 7871, F-67000 Strasbourg, France; M. Villa, INFN section of Bologna, Bologna, Italy and Department of Physics and Astronomy, University of Bologna, Bologna, Italy; U. Weber, Biophysics Department, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany; R. Zarrella, INFN section of Pisa, Pisa, Italy and Department of Physics, University of Pisa, Pisa, Italy; A. Zoccoli, INFN section of Bologna, Bologna, Italy and Department of Physics and Astronomy, University of Bologna, Bologna, Italy.

Author Contributions

All authors of the FOOT collaboration have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The FOOT Collaboration acknowledges the INFN for its support in building and running the detector. We would like to acknowledge all the personnel of the CNAO and APSS-Trento centres that provided us support during the operational tests performed using carbon and proton beams at their facilities. The GSI data were taken in the IBER_006 experiment, supported by European Space Agency (ESA) -IBER17 project, in the frame of FAIR Phase-0.

Footnotes

¹http://advansid.com/products/product-detail/asd-rgb-nuv-3s-p.

²https://www.hamamatsu.com/resources/pdf/ssd/s13360_series_kapd1052e.pdf.

³https://www.caen.it/products/v2495/

⁴https://www.caen.it/products/v2718/

References

1. Jermann M. Particle therapy statistics in 2014. International Journal of Particle Therapy (2015) 2(1):50–4. doi:10.14338/IJPT-15-00013

CrossRef Full Text | Google Scholar

2. Durante M, Loeffler JS. Charged particles in radiation oncology. Nat Rev Clin Oncol (2010) 7(1):37–43. doi:10.1038/nrclinonc.2009.183

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Tommasino F, Scifoni E, Durante M. New Ions for therapy. Int J Part Therapy (2016) 2(3):428–38. doi:10.14338/IJPT-15-00027.1

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Krämer M, Scifoni E, Schuy C, Rovituso M, Tinganelli W, Maier A, et al. Helium ions for radiotherapy? Physical and biological verifications of a novel treatment modality. Med Phys (2016) 43(4):1995. doi:10.1118/1.4944593

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Durante M, Paganetti H. Nuclear physics in particle therapy: a review, Reports on Progress in Physics (2016) 79: 096702. doi:10.1088/0034-4885/79/9/096702

CrossRef Full Text

6. Schardt D, Elsasser T, Schulz-Ertner D. Heavy-ion tumor therapy: physical and radiobiological benefits. Rev Mod Phys (2010) 82(1):383–425. doi:10.1103/RevModPhys.82.383

CrossRef Full Text | Google Scholar

7. Schardt D, Schall I, Geissel H, Irnich H, Kraft G, Magel A, et al. Nuclear fragmentation of high-energy heavy-ion beams in water. Adv Space Res (1996) 17(2):87–94. doi:10.1016/0273-1177(95)00516-H

CrossRef Full Text | Google Scholar

8. Krämer M, Durante M. Ion beam transport calculations and treatment plans in particle therapy. Eur Phys J D (2010) 60:195–202. doi:10.1140/epjd/e2010-00077-8

CrossRef Full Text | Google Scholar

9. Sommerer F, Parodi K, Ferrari A, Poljanc K, Enghardt W, Aiginger H. Investigating the accuracy of the FLUKA code for transport of therapeutic ion beams in matter. Phys Med Biol (2006) 51:4385. doi:10.1088/0031-9155/51/17/017

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Sato T, Kase Y, Watanabe R, Niita K, Sihver L. Biological dose estimation for charged-particle therapy using an improved PHITS code coupled with a microdosimetric kinetic model. Radiat Res (2009) 171(1):107–17. doi:10.1667/RR1510.1

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Böhlen TT, Cerutti F, Dosanjh M, Ferrari A, Gudowska I, Mairani A, et al. Benchmarking nuclear models of FLUKA and GEANT4 for carbon ion therapy. Phys Med Biol (2010) 55(19):5833–47. doi:10.1088/0031-9155/55/19/014

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Bolst D, Cirrone G, Cuttone G, Folger G, Incerti S, Ivanchenko V, et al. Validation of Geant4 fragmentation for heavy ion therapy. Nucl Instrum Meth A (2017) 869:68–75. doi:10.1016/j.nima.2017.06.046

CrossRef Full Text | Google Scholar

13. Pleskac R, Abou-Haidar Z, Agodi C, Alvarez MAG, Aumann T, Battistoni G, et al. The FIRST experiment at GSI. Nucl Instrum Meth A (2012) 678:130–8. doi:10.1016/j.nima.2012.02.020

CrossRef Full Text | Google Scholar

14. Thwaites D. Accuracy required and achievable in radiotherapy dosimetry: have modern technology and techniques changed our views? J Phys Conf (2013) 444:012006. doi:10.1088/1742-6596/444/1/012006

CrossRef Full Text | Google Scholar

15. De Napoli M, Agodi C, Battistoni G, Blancato AA, Cirrone GA, Cuttone G, et al. Carbon fragmentation measurements and validation of the GEANT4 nuclear reaction models for hadrontherapy. Phys Med Biol (2012) 57:7651–71. doi:10.1088/0031-9155/57/22/7651

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Dudouet J, Labalme M, Cussol D, Finck C, Rescigno R, Rousseau M, et al. Zero-degree measurements of ¹²C fragmentation at 95 MeV/nucleon on thin targets. Phys Rev C (2014) 89:064615. doi:10.1103/PhysRevC.89.064615

CrossRef Full Text | Google Scholar

17. Toppi M, Abou-Haidar Z, Agodi C, Alvarez MAG, Aumann T, Balestra F, et al. Measurement of fragmentation cross sections of ¹²C ions on a thin gold target with the FIRST apparatus. Phys Rev C (2016) 93:064601. doi:10.1103/PhysRevC.93.064601

CrossRef Full Text | Google Scholar

18. Marafini M, Paramatti R, Pinci D, Battistoni G, Collamati F, De Lucia E, et al. Secondary radiation measurements for particle therapy applications: nuclear fragmentation produced by ⁴He ion beams in a PMMA target. Phys Med Biol (2017) 62:1291–309. doi:10.1088/1361-6560/aa5307

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Rovituso M, Schuy C, Weber U, Brons S, Cortés-Giraldo MA, La Tessa C, et al. Fragmentation of 120 and 200 MeV/u ⁴He ions in water and PMMA targets. Phys Med Biol (2017) 62:1310–26. doi:10.1088/1361-6560/aa5302

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Tang JT, Inoue T, Inoue T, Yamazaki H, Fukushima S, Fournier-Bidoz N, et al. Comparison of radiobiological effective depths in 65-MeV modulated proton beams. Br J Cancer (1997) 76:220–5. doi:10.1038/bjc.1997.365

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Tommasino F, Durante M. Proton radiobiology. Cancers (Basel) (2015) 7(1):353–81. doi:10.3390/cancers7010353

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Carabe A, Moteabbed M, Depauw N, Schuemann J, Paganetti H. Range uncertainty in proton therapy due to variable biological effectiveness. Phys Med Biol (2012) 57(5):1159–72. doi:10.1088/0031-9155/57/5/1159

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Mairani A, Dokic I, Magro G, Tessonnier T, Bauer J, Böhlen TT, et al. A phenomenological relative biological effectiveness approach for proton therapy based on an improved description of the mixed radiation field. Phys Med Biol (2017) 62:1378–95. doi:10.1088/1361-6560/aa51f7

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Durante M, Cucinotta FA. Physical basis of radiation protection in space travel. Rev Mod Phys (2011) 83:1245. doi:10.1103/RevModPhys.83.1245

CrossRef Full Text | Google Scholar

25. Durante M. Space radiation protection: destination mars. Life Sci Space Res (Amst) (2014) 1:2–9. doi:10.1016/j.lssr.2014.01.002

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Durante JH, Slaba TC, Blattnig SR, Tripathi RK, Townsend LW, Handler T, et al. Comparison of the transport codes HZETRN, HETC and FLUKA for a solar particle event. Adv Space Res (2011) 47:1079–88. doi:10.1016/j.asr.2010.11.012

CrossRef Full Text | Google Scholar

27. Norbury JW, Miller J, Adamczyk AM, Heilbronn LH, Townsend LW, Blattnig SR, et al. Review of nuclear physics experimental data for space radiation. Health Phys (2012) 103(5):640–2. doi:10.1016/j.radmeas.2012.03.00410.1097/HP.0b013e318261fb7f

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Wilson JW, Miller J, Konradi A, Cucinotta FA. Shielding strategies for human space exploration. NASA Conference Publication 3370 (1997)

Google Scholar

29. Patera V, Argiró S, Barbosa D, Battistoni G, Belcari N, Bruni G, et al. The foot (fragmentation of target) experiment, PoS INPC (2016) 128.

Google Scholar

30. Battistoni G, Alexandrov A, Argiró S, Barbosa D, Belcari N, Bisognic MG, et al. The foot (fragmentation of target) experiment, PoS BORMIO (2017) 23.

Google Scholar

31. Webber WR, Kish JC, Schrier DA. Total charge and mass changing cross sections of relativistic nuclei in hydrogen, helium, and carbon targets. Phys Rev C Nucl Phys (1990) 41(2):520. doi:10.1103/PhysRevC.41.52.0

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Dudouet J, Juliani D, Labalme M, Cussol D, Angelíque JC, Braunn B, et al. Double-differential fragmentation cross-section measurements of 95 MeV/nucleon ¹²C beams on thin targets for hadron therapy. Phys Rev C (2013) 88(2):064615. doi:10.1103/PhysRevC.88.024606

CrossRef Full Text | Google Scholar

33. Ferrari A, Sala P, Fassó A, Ranft J. FLUKA: a multi-particle transport code. (2005). Technical Report No.: CERN-2005-10, INFN/TC-05/11, SLAC-R-773, CERN, INFN, SLAC.

CrossRef Full Text

34. Böhlen TT, Cerutti F, Chin M, Fassó A, Ferrari A, Ortega P, et al. FLUKA code: developments and challenges for high energy and medical applications. Nucl Data Sheets (2014) 120:211–4. doi:10.1016/j.nds.2014.07.049

CrossRef Full Text | Google Scholar

35. Morrocchi M, Ciarrocchi E, Alexandrov A, Alpat B, Ambrosi G, Argiró S, et al. Development and characterization of a ΔE-TOF detector prototype for the FOOT experiment. Nucl Instrum Meth A (2019) 916:116–24. doi:10.1016/j.nima.2018.09.086

CrossRef Full Text | Google Scholar

36. Mattei I, Alexandrov A, Solestizi LA, Ambrosi G, Argiró S, Bartosik N, et al. Measurement of ¹²C Fragmentation cross sections on C, O and H in the energy range of interest for particle therapy applications. IEEE TRANSACTIONS ON RADIATION AND PLASMA MEDICAL SCIENCES (2020) 4:269–82. doi:10.1109/TRPMS.2020.2972197

CrossRef Full Text | Google Scholar

37. Montesi MC, Lauria A, Alexandrov A, Solestizi LA, Ambrosi G, Argiró S, et al. Ion charge separation with new generation of nuclear emulsion films. Open Phys (2019) 17:233–40. doi:10.1515/phys-2019-0024

CrossRef Full Text | Google Scholar

38. Galli L, Baldini AM, Cei A, Chiappini M, Francesconi M, Grassi M, et al. WaveDAQ: an highly integrated trigger and data acquisition system. Nucl Instrum Meth A (2019) 936:399–400. doi:10.1016/j.nima.2018.07.067

CrossRef Full Text | Google Scholar

39. Abou-Haidar Z, Agodi C, Alvarez MAG, Anelli A, Aumann T, Battistoni G, et al. Performance of upstream interaction region detectors for the FIRST experiment at GSI. J Inst Met (2012) 7:P02006. doi:10.1088/1748-0221/7/02/P02006

CrossRef Full Text | Google Scholar

40. Dong Y, Gianluigi S, Sofia C, Andrey A, Behcet A, Giovanni A, et al. The Drift Chamber detector of the FOOT experiment: performance analysis and external calibration. Nucl Instrum Meth A (2021) 986:164756. doi:10.1016/j.nima.2020.164756

CrossRef Full Text | Google Scholar

41. Rescigno R, Finck C, Juliani D, Spiriti E, Baudot J, Abou-Haidar Z, et al. Performance of the reconstruction algorithms of the FIRST experiment pixel sensors vertex detector. Nucl Instrum Meth A (2014) 767:34–40. doi:10.1016/j.nima.2014.08.024

CrossRef Full Text | Google Scholar

42.Strasbourg In2p3 PICSEL group. Available at: www.iphc.cnrs.fr/PICSEL.html

43. Greiner L, Anderssen E, Matis HW, Ritter HG, Schambach J, Silber J, et al. A MAPS based vertex detector for the STAR experiment at RHIC. Nucl Instrum Meth A (2011) 650:68–72. doi:10.1016/j.nima.2010.12.006

CrossRef Full Text | Google Scholar

44. Valin I, Hu-Guo C, Baudot J, Bertolone G, Besson A, Colledani C, et al. A reticle size CMOS pixel sensor dedicated to the STAR HFT. J Inst Met (2012) 7:C01102. doi:10.1088/1748-0221/7/01/C01102

CrossRef Full Text | Google Scholar

45. Spiriti E, Finck C, Baudot J, Divay C, Juliani D, Labalme M, et al. CMOS active pixel sensors response to low energy light ions. Nucl Instrum Meth A (2017) 875:35–40. doi:10.1016/j.nima.2017.08.058

CrossRef Full Text | Google Scholar

46. de Boer W, Bartsch V, Bol J, Dierlamm A, Grigoriev E, Hauler F, et al. Measurements with a CMOS pixel sensor in magnetic fields. Nucl Instrum Meth A (2002) 487:163–9. doi:10.1016/S0168-9002(02)00960-9

CrossRef Full Text | Google Scholar

47.PLUME web site. Available at: www.iphc.cnrs.fr/PLUME.html

48. Meroli S, Passeri D, Servoli L. Energy loss measurement for charged particles in very thin silicon layers. J Inst Met (2011) 6:P06013. doi:10.1088/1748-0221/6/06/P06013

CrossRef Full Text | Google Scholar

49. Alpat B, Ambrosi G, Balboni C, Battiston R, Biland A, Bourquin M, et al. High-precision tracking and charge selection with silicon strip detectors for relativistic ions. Nucl Instrum Meth A (2000) 446:522–35. doi:10.1016/S0168-9002(99)01184-5

CrossRef Full Text | Google Scholar

50. Zuccon P. On behalf of the AMS Tracker collaboration. The AMS silicon tracker: construction and performance. Nucl Instrum Meth A(2008) 596:74–8. doi:10.1016/j.nima.2008.07.116

CrossRef Full Text | Google Scholar

51. Adriani O, Babucci E, Bacchetta N, Bagliesi G, Bartalini P, Basti A, et al. Beam test results for single- and double-sided silicon detector prototypes of the CMS central detector. Nucl Instrum Meth A (1997) 396:76–92. doi:10.1016/S0168-9002(97)00750-X

CrossRef Full Text | Google Scholar

52. Alpat B, Ambrosi G, Azzarello P, Battiston R, Bertucci B, Bourquin M, et al. The internal alignment and position resolution of the AMS-02 silicon tracker determined with cosmic-ray muons. Nucl Instrum Meth A (2010) 613:207–17. doi:10.1016/j.nima.2009.11.065

CrossRef Full Text | Google Scholar

53. Ciarrocchi E, Belcari N, Camarlinghi N, Carra P, Del Guerra A, Francesconi M, et al. The ΔE-TOF detector of the FOOT experiment: experimental tests and Monte Carlo simulations. Nucl Instrum Meth A (2019) 936:78–9. doi:10.1016/j.nima.2018.08.117

CrossRef Full Text | Google Scholar

54. Kraan AC, Battistoni G, Belcari N, Camarlinghi N, Carra P, Ciarrocchi E, et al. Charge identification performance of a ΔE-TOF detector prototype for the FOOT experiment. Nucl Instrum Meth A (2020) 958:162422. doi:10.1016/j.nima.2019.162422

CrossRef Full Text | Google Scholar

55. Galli L, Kraan AC, Ciarrocchi E, Battistoni G, Belcari N, Camarlinghi N, et al. Fragment charge identification technique with a plastic scintillator detector using clinical carbon beams. Nucl Intrum Meth A (2020) 953:163146. doi:10.1016/j.nima.2019.163146

CrossRef Full Text | Google Scholar

56. Scavarda L. On behalf of the FOOT collaboration. Design and performance of the Calorimeter for the FOOT experiment. Il Nuovo Cimento 43 C (2020)123:1–7. doi:10.1393/ncc/i2020-20123-3

CrossRef Full Text | Google Scholar

57. Scavarda L. On behalf of the FOOT collaboration. The foot experiment: measuring proton and light nuclei fragmentation cross sections up to 700 MeV/A. Bull Russ Acad Sci Phys (2020) 84:480–484. doi:10.3103/S1062873820040267

CrossRef Full Text | Google Scholar

58. Spighi R, Alexandrov A, Alpat B, Ambrosi G, Argiró S, Battistoni G, et al. FOOT: FragmentatiOn of target experiment. Il Nuovo Cimento C (2019) 42:134. doi:10.1393/ncc/i2019-19134-6

CrossRef Full Text | Google Scholar

59. Valle SM, Alexandrov A, Alpat B, Ambrosi G, Argiró S, Battistoni G, et al. FOOT: a new experiment to measure nuclear fragmentation at intermediate energies. Perspectives in Science (2019) 12:100415. doi:10.1016/j.pisc.2019.100415

CrossRef Full Text | Google Scholar

60. Cho WS, Gainer JS, Kim D, Lim SH, Matchev KT, Moortgat F, et al. OPTIMASS: a package for the minimization of kinematic mass functions with constraints. JHEP (2016) 01:26. doi:10.1007/JHEP01(2016)026

CrossRef Full Text | Google Scholar

61. Alexandrov A, Tioukov V, Vladymyrov M. Further progress for a fast scanning of nuclear emulsions with large angle scanning system. J Inst Met (2014) 9:C02034. doi:10.1088/1748-0221/9/02/C02034

CrossRef Full Text | Google Scholar

62. Alexandrov A, Buonaura A, Consiglio L, D’Ambrosio N, De Lellis G, Di Crescenzo A, et al. A new fast scanning system for the measurement of large angle tracks in nuclear emulsions. J Inst Met (2015) 11:P11006. doi:10.1088/1748-0221/10/11/P11006

CrossRef Full Text | Google Scholar

63. Alexandrov A, Buonaura A, Consiglio L, D’Ambrosio N, De Lellis G, Di Crescenzo A, et al. A new generation scanning system for the high-speed analysis of nuclear emulsions. J Inst Met (2016) 11:P06002. doi:10.1088/1748-0221/11/06/P06002

CrossRef Full Text | Google Scholar

64. Alexandrov A, Buonaura A, Consiglio L, D'Ambrosio N, Lellis G, Crescenzo AD, et al. The continuous motion technique for a new generation of scanning systems. Sci Rep (2017) 7:7310. doi:10.1038/s41598-017-07869-3

PubMed Abstract | CrossRef Full Text | Google Scholar

65. De Lellis G, Buontempo S, Di Capua F, Marotta F, Migliozzi P, Petukhov Y, et al. Emulsion Cloud Chamber technique to measure the fragmentation of high-energy carbon beam. J Inst Met (2007) 2:P06004. doi:10.1088/1748-0221/2/06/P06004

CrossRef Full Text | Google Scholar

66. De Lellis G, Buontempo S, Di Capua F, Di Crescenzo A, Migliozzi P, Petukhov Y, et al. Measurements of the fragmentation of Carbon nuclei used in hadron therapy. Nucl Phys (2015) 853(1):124–34. doi:10.1016/j.nuclphysa.2011.01.019

CrossRef Full Text | Google Scholar

67. Alexandrov A, Consiglio L, De Lellis G, Di Crescenzo A, Lauria A, Montesi MC, et al. Measurement of large angle fragments induced by 400 MeV/n carbon ion beams. Meas Sci Technol (2015) 26:094001. doi:10.1088/0957-0233/26/9/094001

CrossRef Full Text | Google Scholar

68. Alexandrov A, De Lellis G, Di Crescenzo A, Lauria A, Montesi MC, Pastore A, et al. Measurements of ¹²C ions beam fragmentation at large angle with an Emulsion cloud chamber. J Inst Met (2017) 12:P08013. doi:10.1088/1748-0221/12/08/P08013

CrossRef Full Text | Google Scholar

69.National Institute of Standards and Technology, Gaithersburg, MD. Available at: https://www.nist.gov.

70. Agafonova N, Aleksandrov A, Altinok O, Anokhina A, Aoki S, Ariga A, et al. Momentum measuremets by the multiple coulomb scattering method in the OPERA lead-emulsion target. New J Phys (2012) 14:013026. doi:10.1088/1367-2630/14/1/013026

CrossRef Full Text | Google Scholar

71. De Serio M, Ieva M, Simone S, Giorgini M, Sioli M, Sirri G, et al. Momentum measurement by the angular method in the emulsion cloud chamber. Nucl Instrum Meth A (2003) 512(3):539–45. doi:10.1016/S0168-9002(03)02016-3

CrossRef Full Text | Google Scholar