- 1Department of Physics, Indian Institute of Technology Madras, Chennai, India
- 2Department of Physics, Indian Institute of Science Education and Research, Punjab, India
- 3Department of Nuclear Physics, University of Madras, Chennai, India
Upconverting nanoparticles typically absorb low frequency radiation and emit at higher frequencies relying upon multiphoton processes. One such type of particle is NaYF4:Yb,Er, which absorbs at 975 nm while emitting in visible radiation. Such particles have routinely been optically trapped. However, we find that trapping at the absorption maximum induces non-equilibrium features to the system. When we ascertain the Mean Square Displacement (MSD) of the axial motion, we find features that resemble Hot Brownian Motion (HBM) in active particles. We characterize the HBM observed here and find that the effective translational velocity of the system is 36 nm/s, small enough to be compensated by the optical tweezers. Thus, we have a system which is optically confined and stationary but in non-equilibrium, which we can also use to study non-equilibrium fluctuations.
1. Introduction
The study of non-equilibrium system thermodynamics and active matter as emerged as a topic of intense interest in the recent decades [1–3], necessiated by the need to study the physics of microscopic systems where athermal fluctuations pay a crucial role [4, 5] and of living matter which is inherently far from equilibrium [6, 7]. Active matter, comprised of active agents, has the ability to transform energy to motion. Such study is important keeping in mind that biological systems are active in nature. In this context a key question is to use thermodynamic parameters to explain active systems [8–10].
One of the first active systems used an active Brownian particle moving at a constant speed in a medium with a direction determined by rotational diffusion [11]. Earlier, Boltzmann distribution was used to model the position of an active swimmer while in motion, with the effective temperature being higher than the ambient temperature. However, recent research showed that such assumptions fail when such a system is considered in confinement [12, 13]. Further, Argun et al. also showed that when a set of tracer particles is placed in a bacterial bath, the motion of the tracers show deviation from the mean field theory [8]. When and how the Boltzmann statistics fails for the active swimmers is an open question [7].
Here, we present a new system of an Upconverting Nanoparticle (UCNP) optically trapped [14, 15] on the absorption resonance that generates a thermal gradient across the particle due to preferential absorption of 975 nm light and emission of visible light on one side that propels the particle into a HBM [16]. We find that the MSD of the axial motion of the particle bears a signature that deviates from the effective temperature picture and instead follows HBM. The experimental system is much simpler than what has previously been attempted to generate an optically trapped active system, not to mention, there being an equilibrated directed motion inside the trap as opposed to being half the time along one direction and other half another direction [17]. The position distribution function is also simpler to analyse here than in the earlier case because of a clear preference for direction. There have been reports of estimation of instantaneous ballistic velocity [18] of such UCNP but active motion never reported.
2. The Experiment
The experiment was performed on a setup made from the optical tweezers kit OTKB/M (Thorlabs) in the inverted configuration [19–21]. A linearly polarized 400 mW, 975 nm butterfly laser (Thorlabs) is inserted into the set-up to trap the upconverting particles. The objective used was an Olympus 100X, 1.3 NA oil immersion objective with the illumination aperture being overfilled and the condenser being a 10x, 0.25 NA Nikon air-immersion one. The power at the sample plane was about 30 mW, with the schematic being shown in Figure 1. There are a set of two dichroic mirrors, one at the input while one is at the output. An LED lamp illuminates the sample from the top via the output dichroic and passes through the bottom dichroic into a CMOS camera (Thorlabs). The 975 nm laser passes through the sample chamber and the forward scattered light is selected using the top dichroic into the Quadrant Photodiode (QPD). Only the 975 nm infra-red trapping light is used to infer positional information from the set-up.
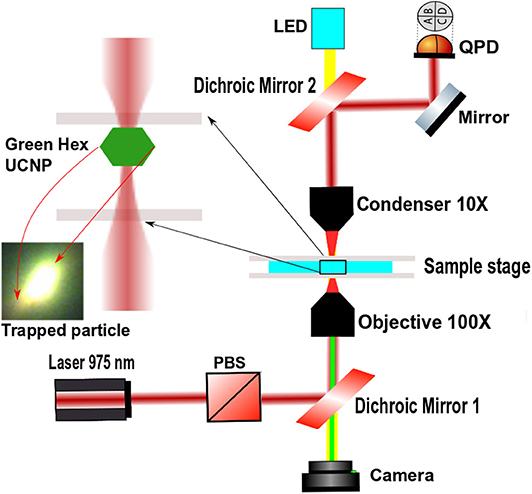
Figure 1. This figure represents the schematic diagram of the experiment. The inset shows a hexagonal shaped UCNP trapped in the optical trap and aligned in the side-on orientation.
The hexagonal upconversion disks (NaYF4:Yb,Er) were prepared using a modified hydrothermal method [22]. 1.26 g of yttrium nitrate and 1.23 g of sodium citrate were dissolved in 14 ml of deionized water and stirred for 10 min. Then, 0.38 g of Yb(NO3)3 and 0.037 g of Er(NO3)3 were added in 21 ml of aqueous solution and mixed into the above solution. The white solution converted into a clear solution by adding 1.411 g of NaF (67 ml aqueous solution). The transparent solution was heated to 200 C for 12 h using a 200 ml teflon lined autoclave. The white colored powders were collected after washing with ethanol/water, followed by drying at 100 C about 12 h.
Such powder was suspended in double distilled de-ionized water and used for the experiment by placing in the sample chamber. The sample chamber consisted of a glass slide at the top (Blue Star, 75 mm length, 25 mm width, and a thickness of 1.1 mm) and a cover slip at bottom (Blue Star, number 1 size, English glass). For the air-water interface experiment, we used a long cover slip (Blue Star, number 1 size, English glass) over which the suspension was directly dropped, as reported in [21]. The system is room temperature controlled by the air-conditioner of the room, set at 25 C.
3. The Theory
An UCNP that absorbs in 975 nm and emits in visible typically has the light incident from one side of the particle [23]. It is on that backscattered direction itself that a large amount of visible light is also emitted. There is some light escaping in the forward scattered direction too but is much lower in intensity. This kind of configuration generates a temperature differential across the UCNP with the bottom part being hotter than the top. Such a configuration typically pushes the particle forward along the direction of propagation of the trapping beam.
In order to derive the MSD, lets consider the Langevin equation (Equation 1).
Here, the k is the trap stiffness, γ is the drag coefficient, is the unit vector along the activity direction, v0 is the velocity with which the particle is moving and η the Gaussian distributed random noise due to Brownian motion. From here, the MSD is derived to be
In 2-dimensions,
and the correlation function between the normal vectors assuming Dr is the rotational diffusion coefficient of the particle in 2 dimensions,
Thus the MSD, in the presence of the confining potential with trapping stiffness k is given by the expression
This simplifies to the expression, in the limit of very small k and Dr replaced as ,
where, v0 is the velocity with which the particle is moving, τr is the timescale associated with the rotational motion of the particle, D is the diffusion coefficient and Δt is the elapsed time. This MSD expression corresponds to Hot Brownian Motion (HBM) [16, 24] and comprises a normal translational diffusion term with an extra term giving the rotational diffusion.
When Δt is much smaller than τr, the Equation (6) reduces to
In order to calibrate the motion of the UCNP particle, we can use the PSD of the motion of the particle in the axial direction. The fit to the PSD is a lorentzian of the form (Equation 8).
The calibration factor can then be ascertained using the expression [25].
Here, γ is the drag coefficient for an oblate spheroid, T is the ambient room temperature and kB is the Boltzmann constant. The drag coefficient is assumed for that of an oblate spheroid, given as [26],
For a typical UCNP which has a 5 μm major axis and 1 μm minor axis, the e = 0.2. Then the drag coefficient become γ = γ0. Here γ0 is the drag coefficient of a sphere with the same radius as the semimajor axis as the spheroid, for the particle placed away from any other surfaces in water.
4. Results and Discussions
The UCNP used in this experiment is the hexagonal one which has an absorption resonance at 975 nm and emits in red and green bands [27]. The scanning electron microscopy image for the particles is shown in Figure 2A. The particles are hexagonal in shape with diagonals about 5 μm and a thickness of about 1 μm. The Figure 2B represents the Power Spectral Density (PSD) for such a hexagonal shaped particle trapped using optical tweezers. The particle tends to align side-on preferentially [28] and the motion along the axial direction is recorded using the QPD in the forward scattered direction. The PSD is for a laser power of 20 mW and fits well to a Lorentzian in the high frequency limit. However, at lower frequencies, there is a deviation from the Lorentzian which may indicate the HBM characteristics. The local temperature of the UCNP surface can be probed with the spectrum of emission [29]. The spatial distribution of the particles are reported in Figure 2C.
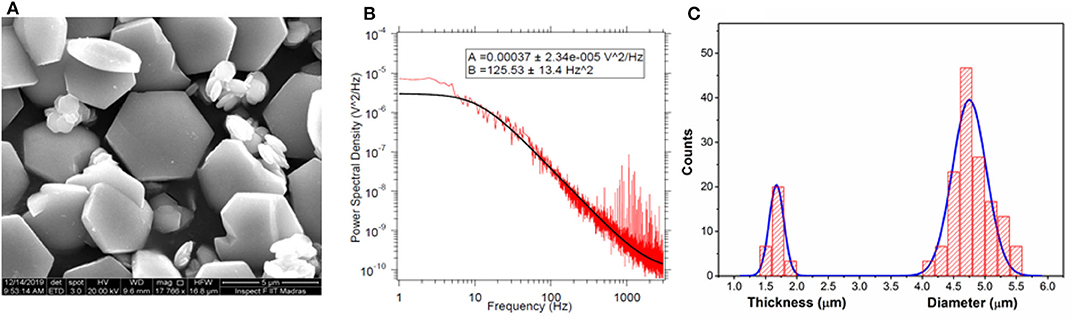
Figure 2. (A) This figure represents the SEM image of the hexagonal UCNP particles. (B) This represents the power spectral density of the axial motion of a hexagonal UCNP particle trapped on absorption resonance at 975 nm. (C) This represents the size of the hexagonal shaped particles, both in thickness and in width.
Optical trapping of such individual particles is routinely performed and can easily be visualized in a 100x objective. We have shown one such trapped particle in Figure 1 with the visible glow when the trapping is performed at 975 nm.
Using the lorentzian parameters, we get β = 20 nm/V.
We go on to carefully study the MSD characteristics of the axial motion and find that the conventional Fluctuation-Dissipation theorem holds good to yield a exponent of 1 for the relation between MSD and lag time, as indicated by the green curve in Figure 3, which is taken at a trapping wavelength of 1064 nm. However, as soon as the trapping wavelength is changed to 975 nm, there are major variations from the exponent of 1. Here, a fit of the form Equation (6) fits better, thereby indicating HBM.
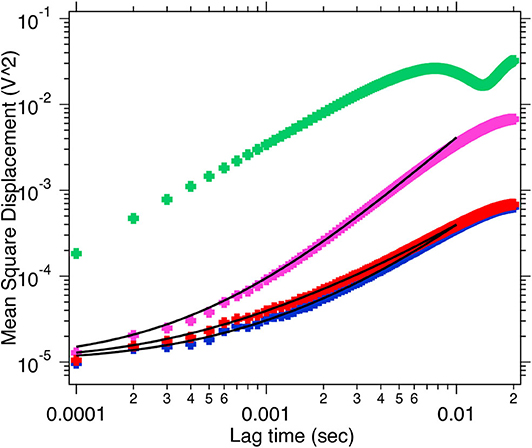
Figure 3. This figure represents the MSD as a function of lag time for the axial motion of the hexagonal shaped UCNP performed with lasers of two different wavelengths, 1,064 nm (green) and 975 nm (pink, red, and blue). The power at the sample plane for the pink curve is 20 mW, for red curve 40 mW and blue curve 50 mW, while the 1,064 nm has 40 mW power in the sample plane. The data have been fitted with an equation of the form Equation (6) representing HBM.
We go on to plot the histograms for the time series at three different 975 nm laser powers of 20, 40, and 50 mW, shown in Figure 4, and find a gradual skewing of the histogram to one side. This indicates that the particle is getting pushed axially and spends more time on the far side than the near side. The effect is more pronounced at higher powers. The histograms have been calibrated for the different powers of the laser and normalized to have the total area under the curve as 1.
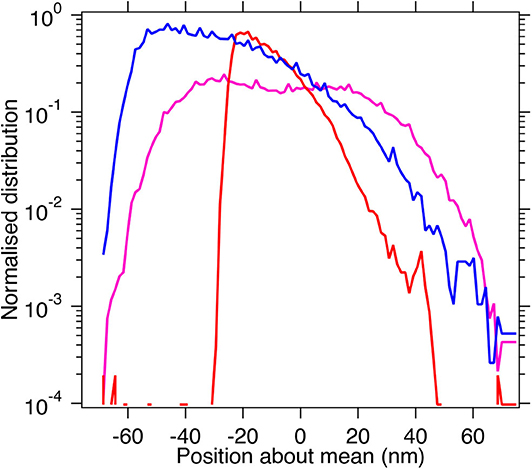
Figure 4. This figure represents the calibrated and normalized histogram for the time series data for axial motion of a hexagonal UCNP trapped with 975 nm light at three different powers, namely, 20 mW (pink), 40 mW (red), and 50 mW (blue). Here, the negative side is the far side in the axial direction for the laser injected from the bottom.
We can also note that the maximum probability of the peak of the distribution becomes higher at higher values of power due to increased trap stiffness.
We also calibrate the MSD for a particle trapped at 20 mW laser power at 975 nm and find the curve in Figure 5, fitted to Equation (6). The relaxation time and velocity calculated from the fit parameters are 2.76 s and 36 nm/s, respectively.
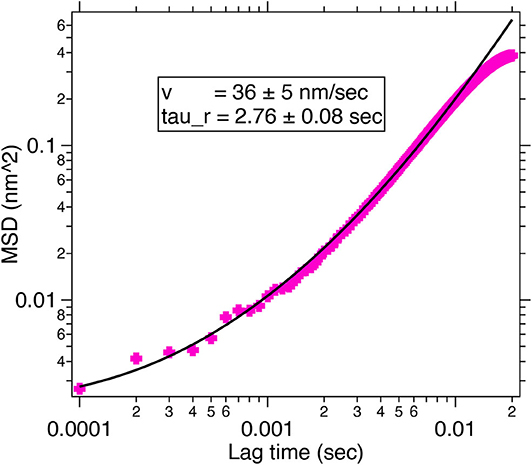
Figure 5. A typical MSD of the hexagonal UCNP trapped on optical resonance at 975 nm with a power of 20 mW at the sample plane. The MSD fits well to the Equation (6), providing a velocity of 36 nm/s and τr = 2.76 s.
The corresponding drag force encountered by the 5 μm diameter hexagonal shaped UCNP particle moving with an effective velocity of 36 nm/s is about 1 fN, which can be easily compensated by the optical tweezers.
In order to confirm heating effects, we place such a particle on the side edge of an air-water interface. When the 975 nm light is illuminated on the edge, there i.e., no effect, as reported in Figure 6a. However as soon as the particle is illuminated with 975 nm light, there is water vapor bubble formation on the interface, shown in Figure 6b. That confirms local heating due to the particle. This is also the proof that heating is performed when the particle is illuminated by 975 nm light, and not directly by absorption of the laser by water. Thus trapping of the particle at other wavelengths like 800 nm is not required. Thermometry using the spectrum emitted by the particle has been proven to be problematic [30], and thus has not been used.
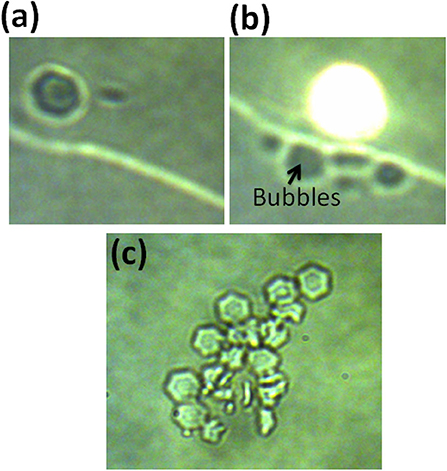
Figure 6. This figure indicates the effect of 975 nm light incident on UCNP. (a) Here, the UCNP is away from the light and the interface does not form water vapor bubbles. (b) Here, the UCNP is illuminated by 975 nm light with subsequent formation of water vapor bubbles at the air-water interface. This indicates local heating of the sample. (c) This indicates an UCNP cluster being illuminated from the reverse direction by 975 nm light so that the forward scattered light is captured by high numerical aperture lens and eventually by the camera. There is no visible glow here indicating less emission in forward direction.
Further, the confirmation of directional heating required a more imaginative configuration where the 975 laser was inserted just in front of QPD (reported in Figure 1), to propagate in the backward direction. When the light was illuminated on a cluster of UCNP placed on the surface, there was no visible glow, shown in Figure 6c. This indicates that very little visible light is radiated in the forward scattered direction. Nonetheless, the accessibility of the forward scattered light in our configuration is harder as the camera is located in the backscattered direction while the condenser is just 10 X and will lose much of the light in the forward scattered direction.
5. Conclusions
Thus, we describe a new kind of active motion where the particle is trapped in optical tweezers while exhibiting what we believe is HBM, simultaneously. An UCNP trapped optically at the absorption resonance absorbs more light at the near end from the trapping light while also emitting preferentially in the backscattered direction. This generates a higher temperature at the near end than the far end, thereby creating a temperature differential that leads to the HBM. The MSD of the axial motion bears signature of the HBM. A typical velocity due to the HBM was found to be 36 nm/s with a force exerted of 1 fN which can be easily compensated by optical tweezers. Such a system can be used to study controlled interactions of active particles while confined in optical tweezers.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
This project was designed by BR and JS while the UCNP particles were made by MG and JS. The experiments performed by AK, RV, and SK. The theory was done by DC. The manuscript was written by BR, AK, and SK.
Funding
We thank the Indian Institute of Technology Madras, India for their Seed and Initiation grants.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Jarzynski C. Equalities and inequalities: irreversibility and the second law of thermodynamics at the nanoscale. Annu Rev Condens Matter Phys. (2011) 2:329. doi: 10.1146/annurev-conmatphys-062910-140506
2. Seifert U. Stochastic thermodynamics, fluctuation theorems, and molecular machines. Rep Prog Phys. (2012) 75:126001. doi: 10.1088/0034-4885/75/12/126001
3. Cates ME. Diffusive transport without detailed balance in motile bacteria: does microbiology need statistical physics. Rep Prog Phys. (2012) 75:042601. doi: 10.1088/0034-4885/75/4/042601
4. Evans DJ, Cohen EGD, Morriss GP. Probability of second law violations in nonequilibrium steady states. Phys Rev Lett. (1993) 71:2401. doi: 10.1103/PhysRevLett.71.2401
5. Wang GM, Sevick EM, Mittag E, Searles DJ, Evans DJ. Experimental demonstration of violations of the second law of thermodynamics for small systems and short time scales. Phys Rev Lett. (2002) 89:050601. doi: 10.1103/PhysRevLett.89.050601
6. Barkai E, Garini Y, Metzler R. Strange kinetics of single molecules in living cells. Phys Today. (2012) 65:29. doi: 10.1063/PT.3.1677
7. Bechinger C, Leonardo RD, Lowen H, Reichhardt C, Volpe G, Volpe G. Active particles in complex and crowded environments. Rev Mod Phys. (2016) 88:045006. doi: 10.1103/RevModPhys.88.045006
8. Argun A, Moradi AR, Pince E, Bagci GB, Imparato A, Volpe G. Non-Boltzmann stationary distributions and nonequilibrium relations in active baths. Phys Rev E. (2016) 94:062150. doi: 10.1103/PhysRevE.94.062150
9. Takatori SC, Brady JF. Towards a thermodynamics of active matter. Phys Rev E. (2015) 91:032117. doi: 10.1103/PhysRevE.91.032117
10. Fodor E, Nardini C, Cates ME, Tailleur J, Visco P, van Wijland F. How far from equilibrium is active matter? Phys Rev Lett. (2016) 117:038108. doi: 10.1103/PhysRevLett.117.038103
11. Basu U, Majumdar SN, Rosso A, Schehr G. Active Brownian motion in two dimensions. Phys Rev E. (2018) 98:062121. doi: 10.1103/PhysRevE.98.062121
12. Uspal WE, Popescu MN, Dietrich S, Tasinkevych M. Self-propulsion of a catalytically active particle near a planar wall: from reflection to sliding and hovering. Phys Rev E. (2015) 11:434. doi: 10.1039/C4SM02317J
13. Ray D, Reichhardt C, Reichhardt CJO. Casimir effect in active matter systems. Phys Rev E. (2014) 90:013019. doi: 10.1103/PhysRevE.90.013019
14. Haro-Gonzalez P, del Rosal B, Maestro L, Rodriguez EM, Naccache R, Capobianco JA, et al. Optical trapping of NAYF4:ER3+,YB3+ upconverting fluorescent nano-particles. Nanoscale. (2013) 5:12192. doi: 10.1039/c3nr03644h
15. Anbharasi L, Rekha EAB, Rahul VR, Roy B, Gunaseelan M, Yamini S, et al. Tunable emission and optical trapping of upconverting LiYF4:Yb,Er nanocrystal. Opt Lightwave Tech. (2020) 126:106109. doi: 10.1016/j.optlastec.2020.106109
16. Schachoff R, Selmke M, Bregulla A, Cichos F, Rings D, Chakraborty D, et al. Hot Brownian motion and photophoretic self-propulsion. Diffus Fundam. (2015) 23:1–19. Available online at: https://diffusion.uni-leipzig.de/pdf/volume23/TP1_SFG-Abschlussbericht.pdf
17. Shen C, Ou-Yang HD. The far-from- equilibrium fluctuation of an active Brownian particle in an optical trap. Proc SPIE 11083, Optical Trapping Optical Micromanipulation XVI. San Diego, CA (2019). p. 110831Q. doi: 10.1117/12.2531434
18. Brites CDS, Xie X, Debasu ML, Qin X, Chen R, Huang W, et al. Instantaneous ballistic velocity of suspended Brownian nanocrystals measured by upconversion nanothermometry. Nat Nanotech. (2016) 11:851–6. doi: 10.1038/nnano.2016.111
19. Vaippully R, Bhatt D, Ranjan AD, Roy B. Study of adhesivity of surfaces using rotational optical tweezers. Phys Scr. (2019) 94:105008. doi: 10.1088/1402-4896/ab292d
20. Vaippully R, Ramanujan V, Bajpai S, Roy B. Measurement of viscoelastic properties of the cellular cytoplasm using optically trapped Brownian probes. J Phys Cond Mat. (2020) 32:235101. doi: 10.1088/1361-648X/ab76ac
21. Bhatt D, Vaippully R, Kharbanda B, Ranjan AD, Sulochana R, Dharod V, et al. Detection of self-generated nanowaves on the interface of an evaporating sessile water droplet. Opt Exp. (2019) 27:31900–31912. doi: 10.1364/OE.27.031900
22. Ortiz-Rivero E, Prorok K, Skowickl M, Lu D, Bednarkiewicz A, Jaque D, et al. Single-cell biodetection by upconverting microspinners. Small. (2019) 15:1904154. doi: 10.1002/smll.201904154
23. Gunaseelan M, Yamini S, Kumar GA, Senthilselvan J. Highly efficient upconversion luminescence in hexagonal NaYF4:Yb3+, Er3+ nanocrystals synthesized by a novel reverse microemulsion method. Opt Mater. (2018) 75:174–86. doi: 10.1016/j.optmat.2017.10.012
24. Howse JR, Jones RAL, Ryan AJ, Gough T, Vafabakhsh R, Golestanian R. Self-motile colloidal particles: from directed propulsion to random walk. Phys Rev Lett. (2007) 99:048102. doi: 10.1103/PhysRevLett.99.048102
25. Schaffer E, Norrelykke SF, Howard J. Surface forces and drag coefficients of microspheres near a plane surface measured with optical tweezers. Langmuir. (2007) 23:3654–3665. doi: 10.1021/la0622368
26. Datta S, Srivastava DK. Stokes drag on axially symmetric bodies: a new approach. Proc Indian Acad Sci. (1999) 109:441–52. doi: 10.1007/BF02838005
27. Gunaseelan M, Yamini S, Kumar GA, Santhosh C, Senthilselvan J. Photon upconversion characteristics of intense green emitting BaYF5:Yb3+,Er3+ nanoclusters prepared by reverse microemulsion. Mater Res Bull. (2018) 107:366–78. doi: 10.1016/j.materresbull.2018.08.010
28. Rodriguez-Sevilla P, Zhang Y, de Sousa N, Marques MI, Sanz-Rodriguez F, Jaque D, et al. Optical torques on upconverting particles for intracellular microrheometry. Nano Lett. (2016) 16:8005–14. doi: 10.1021/acs.nanolett.6b04583
29. Balabhadra S, Debasu ML, Brites CDS, Fereira RAS, Carlos LD. Upconverting nanoparticles working as primary thermometers in different media. J Phys Chem C. (2017) 121:13962–8. doi: 10.1021/acs.jpcc.7b04827
Keywords: optical tweezers, hot Brownian motion, upconverting nanoparticles, active matter, nanophotonics
Citation: Kumar S, Kumar A, Gunaseelan M, Vaippully R, Chakraborty D, Senthilselvan J and Roy B (2020) Trapped in Out-of-Equilibrium Stationary State: Hot Brownian Motion in Optically Trapped Upconverting Nanoparticles. Front. Phys. 8:570842. doi: 10.3389/fphy.2020.570842
Received: 09 June 2020; Accepted: 28 August 2020;
Published: 08 October 2020.
Edited by:
Ayan Banerjee, Indian Institute of Science Education and Research Kolkata, IndiaReviewed by:
Patricia Haro González, Autonomous University of Madrid, SpainFrancisco J. Sevilla, Universidad Nacional Autónoma de México, Mexico
Copyright © 2020 Kumar, Kumar, Gunaseelan, Vaippully, Chakraborty, Senthilselvan and Roy. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Basudev Roy, YmFzdWRldkBpaXRtLmFjLmlu
 Sumeet Kumar1
Sumeet Kumar1 M. Gunaseelan
M. Gunaseelan Dipanjan Chakraborty
Dipanjan Chakraborty Basudev Roy
Basudev Roy