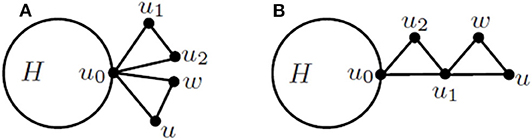- 1School of Computer, Qinghai Normal University, Xining, China
- 2Department of Mathematics, West Virginia University, Morgantown, WV, United States
For a given network, the number of spanning trees is a key parameter to measure its reliability in edge failure cases, while the number of subtrees is a key parameter to measure its reliability in both vertex and edge failures cases. Zhang et al. investigated the entropy of spanning trees, spanning forests and connected spanning subgraphs of Koch networks. In this paper, we extend Koch networks to 3–cactus networks, and study the entropy of subtrees of 3–cactus networks. We present a linear algorithm to count the number of subtrees in a 3–cactus network, determine the upper and lower bounds of the entropy of subtrees of these networks and characterize those attaining the extremal values. As an application, a linear algorithm is developed to count the number of subtrees in Koch networks, with complexity O(g), where g is the number of iterations. Finally, we determine the entropy of subtrees of Koch networks.
1. Introduction
The number of subtrees of a connected network is well-studied, as an important parameter to measure the reliability of a network for both vertex and edge failures. For a network G, let p be the probability of failure of a vertex in G, and q be the probability of failure of an edge in G. The reliability of the network G, denoted by R(G; p, q), is the probability that the remaining vertices can communicate with each other. Zhao [1] showed that for given numbers m and n, among the networks with n vertices and m edges, if p → 0 and q → 1 with p and 1 − q are equivalent infinitesimals, then networks with more subtrees are more reliable. Therefore, it is of interest to develop efficient algorithms to count the number of subtrees in a network and, in a given family of networks, characterize the networks with extremal number of subtrees. Denote by η(G) the number of subtrees of G. For a vertex v ∈ V(G), let ηv(G) denote the number of subtrees containing v in G. Székely and Wang [2] determined the maximum and minimum values of η(G) and characterized all extremal networks among all trees G with given number of vertices. Yan and Yeh [3] developed a linear algorithm to count the number of subtrees of a tree. In the same paper, they also characterized all trees having diameter at least d with maximum number of subtrees, as well as all trees having maximum degree at least Δ with minimum number of subtrees. On the other hand, Kirk and Wang [4] characterized all trees with a given maximum degree that have the maximum number of subtrees. Zhang and Zhang [5] and Zhang et al. [6, 7] characterized the trees attaining the maximum and minimum numbers of subtrees among all trees with the given degree sequence. Xiao et al. [8] showed that 5 + n + 2n−3 ≤ η(T) ≤ 2n−1 + n − 1 for any tree T with n vertices. Yang et al. [9, 10] studied the number of subtrees in spiro and polyphenyl hexagonal chains and hexagonal and phenylene chains, respectively. For more results on this topic, we refer the readers to references [11–17].
Koch networks, introduced by Zhang et al. [18], are typical fractal networks. Zhang et al. showed that Koch networks have some important properties in real life networks, such as a power law degree distribution with exponent between 2 and 3, a large clustering coefficient and a small average path length. However, the number of subtrees in Koch networks has not been determined. In this paper, we investigate the entropy and enumeration of subtrees in 3–cactus networks, which is a generalization of Koch networks. We first establish a linear algorithm to count the number of subtrees in an arbitrary 3–cactus network. Then we characterize the 3–cactus networks with upper and lower bounds of the entropy of subtrees. Finally, as an application, we obtain the entropy of subtrees in Koch networks.
2. Preliminaries
We first introduce some general notation and definitions that will be used throughout the paper. Undefined notation and terminology will follow Bondy and Murty [19].
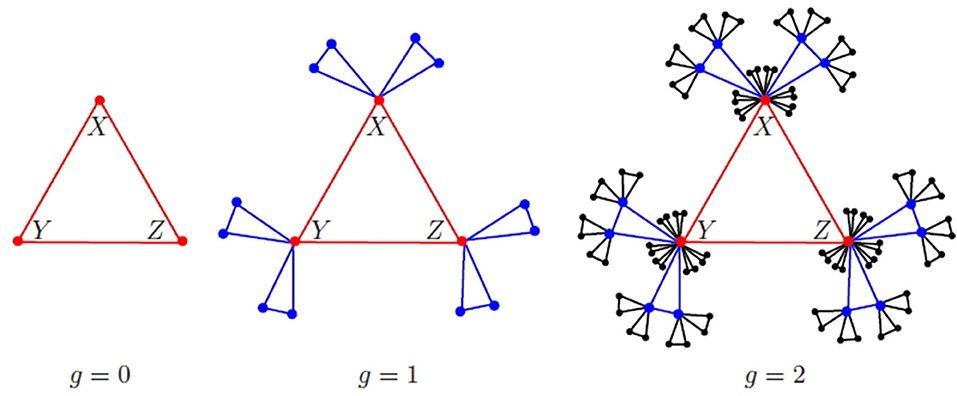
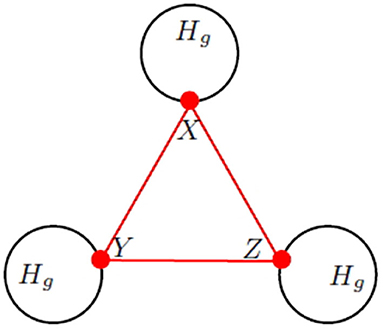
We follow Zhang et al. [18] and Wu et al. [20] to define Koch networks. Denote by Gm,g the Koch network after g iterations, which has Ng vertices, Eg edges and Lg triangles. At g = 0, Gm, 0 is a triangle with three vertices labeled by X, Y, and Z, respectively. This triangle is called the initial triangle, and its three vertices are called hub vertices. For g ≥ 1, Gm,g is obtained from Gm,g−1 by attaching m triangles to each of the three vertices in each triangle in Gm,g−1. The Koch networks for m = 2 are shown in Figure 1.
By definition, L0 = 1 and for g ≥ 1, Lg = (3m + 1)Lg−1. This implies that . Likewise, it is routine to derive that and . More properties of Koch networks can be found in Zhang et al. [18].
To extend the notion of Koch networks, we introduce 3–cactus networks.
Definition 1. Let (t) be the set of all 3–cactus networks with t triangles. We define a 3–cactus network Gt ∈ (t) by the following recursive iterations.
Step 1: When t = 0, G0 is isomorphic to K1, the graph with one vertex and no edges. The only vertex in G0 is called the initial vertex of Gt.
Step 2: Assume that t ≥ 1 and a 3–cactus network Gt−1 is already generated by (t−1) iterations. Then, a 3–cactus network Gt can be obtained from Gt−1 and a new triangle by identifying a vertex of the new triangle and a vertex of the Gt−1.
Let G be a subnetwork of G′. If the vertex set (or edge set) of G is a proper subset of the vertex set (or edge set) of G′, G is called a proper subnetwork of G′. Let dG(u) denote the degree of vertex u in G, and (v1, v2, v3) denote the triangle with vertices v1, v2, and v3. A triangle (v1, v2, v3) in G is called a d-pendant triangle if two of the vertices v1, v2, v3 have degree 2 in G and the third vertex has degree equals d in G for some integer d ≥ 3. A d-pendant triangle is also called a pendant triangle.
By Definition 1, a network Gt ∈ (t) will contain a pendant triangle with a vertex of degree at least 4. Define a 3–cactus networks Gt ∈ (t) to be in Class I if Gt contains a 4-pendant triangle, and in Class II if Gt does not contain a 4-pendant triangle. The following observations follow from Definition 1.
Observation 1. Let t ≥ 0 be an integer, and let Gt ∈ (t) be a network formed by Definition 1 using t iterations. Each of the following holds.
(i) The 3–cactus networks is a generalization of Koch networks, as building a Koch network Gm,g using g iterations amounts to (3m + 1)g iterations in building a 3–cactus network.
(ii) Gt has t triangles, 2t + 1 vertices and 3t edges.
(iii) If (u0, u1, u2) is a pendant triangle of Gt with dGt(u1) = dGt(u2) = 2, then t ≥ 2 and u0 is a cut vertex of Gt.
(iv) Every Class II 3–cactus network G contains two pendant triangles (u0, u1, u2) and (u0, v1, v2) sharing a common vertex u0.
Proof: It suffices to justify (iv) as all others are direct consequences from Definition 1. Let G be a Class II 3–cactus network. By Definition 1, G ∈ (t) for some t ≥ 3, and if G ∈ (3), then G has a vertex of degree 6 and all other vertices of degree 2, and so (iv) holds. Assume that t ≥ 4 and (iv) holds for smaller values of t. By Definition 1, G contains a pendant triangle (x, z1, z2) with dG(z1) = dG(z2) = 2. Since G is of Class II, dG(x) > 4. Let . Then G′ ∈ (t − 1). If G′ is of Class II, then by induction, G′ has two pendant triangles (u0, u1, u2) and (u0, v1, v2) sharing a common vertex u0. But as G is of Class II, u0 cannot be a vertex of degree 4 in a 4-pendant triangle in G. If x ∉ {u0, u1, u2, v1, v2}, then (u0, u1, u2) and (u0, v1, v2) are two pendant triangles in G, and so (iv) holds and we are done. Hence we assume that x ∉ {u0, u1, u2, v1, v2}. If x = u0, then (u0, u1, u2), (u0, v1, v2), and (u0, z1, z2) are three pendant triangles with a common vertex u0, implying (iv) also. Hence we must have x ∈ {u1, u2, v1, v2}. By symmetry, we assume that x = u1. Then the two triangles (u0, u1, u2) and (u1, z1, z2) sharing a common vertex x = u1 with dG(u1) = 4, and so (u1, z1, z2) is a 4-pendant triangle. This implies that G is of Class I, a contradiction. Therefore, we assume that G′ is of Class I, and so G′ has a 4-pendant triangle with . Since G is of Class II, we may assume that . Thus either , whence G has two pendant triangles and (x, z1, z2) satisfying (iv); or , whence G is of Class I, contrary to the assumption that G is of Class II. □
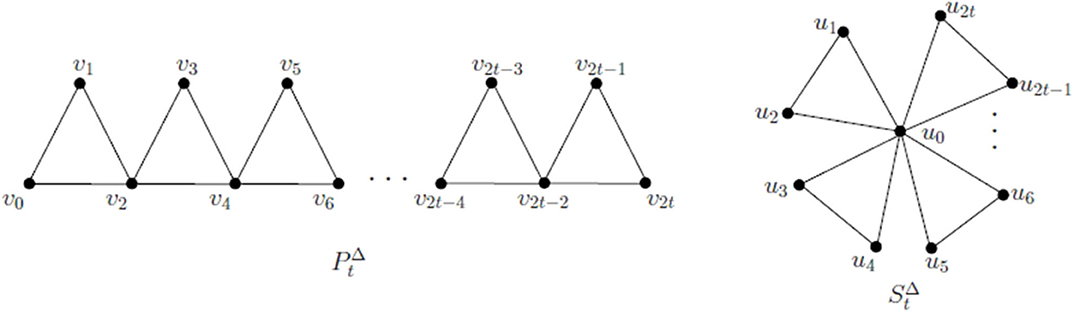
Thus every Koch network is a 3–cactus network. However, there exist 3–cactus networks that are not Koch networks, as shown by the triangle–path and the triangle–star are two special classes of 3–cactus networks with t triangles. Examples of these 3–cactus networks are depicted in Figure 2.
3. Algorithm for Counting the Number of Subtrees
In this section, we present a linear algorithm to count the number of subtrees in a 3–cactus network and its proof of the correctness.
Algorithm A: Initial condition: Let Gt = (V, E) be a 3–cactus network with t triangles with the vertex set V = {u0, u1, v1, u2, v2, …, ut, vt} and the edge set E = {e1, e2, …, e3t}, where ui and vi are the vertices added at the i-th iteration, for each i = 1, 2, …, t. Let η(Gt) be the number of subtrees of Gt. For every v, we assign an ordered pair of real numbers (1, 0) as the initial weight of the vertex.
Step 1. Set k = t.
Step 2. Let (a1, b1), (a2, b2), and (a3, b3) denote the weights of uk, vk and the common neighbor of uk and vk, respectively. Delete the vertices uk and vk, and reset the value of (a3, b3) by the following:
Step 3. If k = 1, then stop, output η(Gt) = a3 + b3. Otherwise, set k: = k − 1 and go to Step 2.
As there will be t iterations using Step 2, the complexity of Algorithm A is O(t). Since running Algorithm A to a 3–cactus networks Gt ∈ (t) can be performed in a reverse order of building Gt as described in Definition 1, it is possible to arrange the iterations in Step 2 during the running of Algorithm A so that when Algorithm A terminates, only the initial vertex of Gt is left.
Example 1. As examples, it is inspected that η(G0) = 1. Let G1 = (u0, u1, u2) be a triangle. Then G1 has three subtrees avoiding u0, namely, {u1}, {u2} and the complete graph on {u1, u2}, in G1 that avoids the vertex u0, and six subtrees containing u0, induced by the vertex subset {u0} or by the edge subsets, {u0u1}, {u0u2}, {u0u1, u0u2}, {u0u1, u1u2}, {u0u2, u1u2}. It follows that η(G1) = 3 + 6 = 9. On the other hand, using Algorithm A, with each of u0, u1, u2 assigned the initial weight (1, 0), by (1), we have a3 = 6 and b3 = 3. By Step 3 of Algorithm A, we also have η(G1) = 9.
Example 2. Let H be the 3–cactus network generated by 6 iterations, as depicted in Figure 3. Using Algorithm A to H, the steps of calculating the number of subtrees of H are shown in Figure 3, which shows η(H) = 21, 096 + 378 = 21, 474.
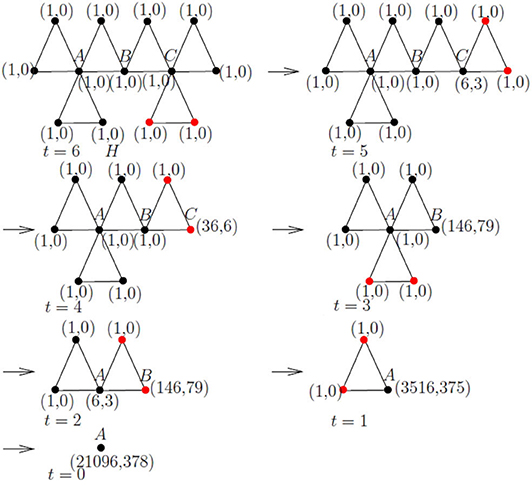
Figure 3. An example of calculating the number of subtrees by Algorithm A, where two red vertices are deleted at each step.
Theorem 1 proves the correctness of Algorithm A.
Theorem 1. Let Gt be a 3–cactus network generated by t steps with vertex set V = {u0, u1, v1, u2, v2, …, ut, vt}. Let (a, b) denote the weight of vertex u0. Each of the following holds when Algorithm A stops.
(i) The value of a, denoted by ηu0(Gt), is the number of subtrees containing vertex u0 in Gt.
(ii) The value of b, denoted by η(Gt − u0), is the number of subtrees that do notcontain vertex u0 in Gt.
(iii) The value of a + b, denoted by η(Gt), is the number of subtrees in Gt.
Proof: We argue by induction on t. If t = 1, then G1 is a triangle. By Algorithm A, we have that a = 6 and b = 3, and by inspection, η(G1) = 9. Thus, the result holds for t = 1. Suppose that k ≥ 2 and the result holds for all values of t < k.
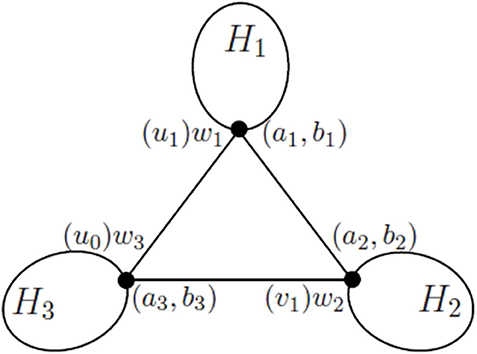
The structural of Gt when t = k ≥ 2 is depicted in Figure 4, and we shall use Figure 4 and its notation to illustrate our arguments. Thus, H1, H2 and H3 are the three vertex disjoint subgraphs of Gt such that H1 contains exactly one vertex u1 in the initial 3-cycle G1 = (u0, u1, v1), H2 contains exactly one vertex v1 in G1 = (u0, u1, v1) and H3 contains exactly one vertex u0 in G1 = (u0, u1, v1), as described in Definition 1.
Relabel the vertices u1, v1, and u0 as w1, w2, and w3, when each of them is considered as a vertex in H1, H2, and H3, respectively. In the rest of the proof of this theorem, we keep in mind that u1 = w1, v1 = w2, and u0 = w3.
As G1 = (u0, u1, v1) is an initial 3-cycle of Gt, we can view wi as the initial vertex of the 3–cactus network Hi. For each i ∈ {1, 2, 3}, since each Hi is a 3–cactus network generated by at most t−1 iterations, by applying Algorithm A to Hi ending at the initial vertex wi of Hi, we obtain the weights (a1, b1), (a2, b2), (a3, b3) of the vertices w1, w2, and w3, respectively. By the induction hypothesis, we have, for i ∈ {1, 2, 3}, both (A) and (B) of the following.
At this stage of Algorithm A, the graph to be computed is G1 = (u0, u1, v1) with the weights assigned to u0, u1, v1 being (a3, b3), (a1, b1), and (a2, b2), respectively. Running Algorithm A at the last iteration, we delete the vertices u1 and v1, and reset the weight (a, b) to the vertex u0 by (1),
Let denote the collection of subtrees of Gt. Define
and for i ∈ {1, 2}, define
Thus is a partition. By (A) and (B) in (2), , , and . As the edge u0u1 lies in every tree in , we have . Likewise, and . Since every tree in contains exactly two edges in G1 and there are three pairs of such edges in G1, we have . By definition and (3),
With a similar argument and using , we have
It follows that
This shows that when Algorithm A terminates, it outputs the values as stated in Theorem 1 (i), (ii), and (iii), and justifies the correctness of Algorithm A. □
4. Upper and Lower Bounds of the Number of Subtrees in a 3–Cactus Network
The following lemma [8] will be used in our proof.
Lemma 1 ([8]). Let G be a connected network with n (n ≥ 3) vertices and let G1 and G2 be two subnetworks of G such that G = G1 ∪ G2, V(G1) ∩ V(G2) = {v} and E(G1) ∩ E(G2) = ∅. Then
Theorem 2. For an integer t, is the unique 3–cactus network with the maximum number of subtrees in (t).
Proof: We prove the theorem by induction on t, and observe that the theorem holds when t ∈ {1, 2}. Let k ≥ 3 be an integer and assume that the result is true for t < k. We consider that case when t = k.
Let G′ be a 3–cactus network with k triangles, and let (u, v, w) be a pendant triangle such that and . By Observation 1(iii), u is a cut vertex. Let and .
By the induction hypothesis, , where the equality holds if and only if . If , then , where P2 is the path with 2 vertices. If , then (k − 1)P2 must be a proper subnetwork of , which implies . Since and , it follows from (4) that , where the equality holds if and only if , which completes the proof. □
The next lemma presents some observations which follow from Algorithm A.
Lemma 2. Let Gt ∈ (t) be a 3–cactus network with a pendant triangle (u, v, w) such that dGt(w) = dGt(v) = 2, and let Gt−1 = Gt − {w, v}. Then
(i) η(Gt) = 5ηu(Gt−1) + η(Gt−1) + 3;
(ii) ηw(Gt) = 4ηu(Gt−1) + 2. □
Lemma 3. Let t ≥ 3 be an integer and G ∈ (t) be a Class II 3–cactus network. Then there exists a Class I 3–cactus network G′ in (t) satisfying η(G′) < η(G).
Proof: Let G ∈ (t) be a Class II 3–cactus network. By Observation 1(iv), G contains two pendant triangles (u0, u1, u2) and (u0, u, w) such that dG(u0) ≥ 6 and dG(u1) = dG(u2) = dG(u) = dG(w) = 2, as depicted in Figure 5A. Let H be the graph depicted in Figure 5. Denote by a0 (b0, respectively) the number of subtrees containing u0 (not containing u0) in H. By Algorithm A, when deleting the vertices u1 and u2 from G, the weight of vertex u0, denoted by (au0, bu0), can be reset as follows: au0 = 6a0 and bu0 = b0 + 3. Then in the step of deleting the vertices u0 and w from G, the weight of vertex u is given by ηu(G) = 4au0 + 2, η(G − u) = 2au0 + bu0 + 1. Thus, we have η(G) = 36a0 + b0 + 6.
Let G′ denote the graph depicted in Figure 5B, which is obtained from H by identifying vertex u0 of H and a vertex of degree 2 in . By Algorithm A, when deleting the vertices u0 and u2 from G′, the weight of vertex u1, denoted by (au1, bu1), is obtained as au1 = 4a0 + 2, bu1 = 2a0 + b0 + 1. Then in the step of deleting the vertices u1 and w from G′, the weight of vertex u is given by , . Thus, we have . Algebraic computation yields that , and so the lemma is proved. □
Theorem 3. For an integer t, is the unique 3–cactus network with the minimum number of subtrees in (t).
Proof: By Lemma 3, within the family (t), for every 3–cactus network G in Class II, there is always a 3–cactus network G′ in Class I containing fewer subtrees. Thus, we only need to show that is the unique 3–cactus network with the minimum number of subtrees, among all the networks of (t) in Class I.
We prove the conclusion by induction on t. Let Gt ∈ (t) be a 3–cactus network with a pendant triangle (u, v, w) such that dGt(u) = 4 and dGt(w) = dGt(v) = 2. We will prove the following results: (i) is the unique 3–cactus network with the minimum number of subtrees in (t); (ii) ηw(Gt) attains the minimum value if and only if .
The results hold for t = 1 and 2. Suppose that k ≥ 3 and the results are true for t < k, we consider the case when t = k. Let Gk−1 = Gk − {w, v}. Since dGk−1(u) = 2, by Lemma 2 and the induction hypothesis, we have that
and
where the equalities hold if and only if . □
With Algorithm A, we can compute the numbers of subtrees of and , respectively. Let u0 be the center of and v0 be a vertex of degree 2 in a pendant triangle of . From Algorithm A, it follows that
and
By algebraic manipulations, we obtain that
and
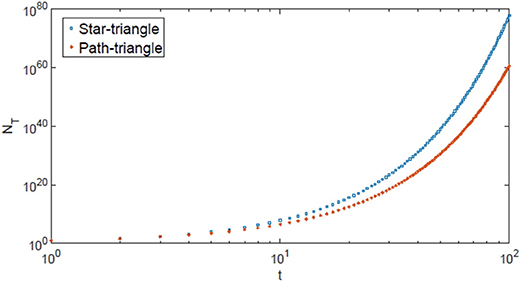
By Theorems 2 and 3, and represent the upper and lower bounds of the number of subtrees in a 3–cactus network with t triangles, respectively. As shown in (5) and (6), the numbers of subtrees in and grow exponentially as the number of triangles increases, as seen in Figure 6, where the curves of values of and vs. t are plotted.
5. The Entropy of Subtrees of Koch Networks
The entropy of spanning trees has been well-studied, as seen in Lyons et al. [21] and Zhang et al. [22, 23], among others. The entropy of subtrees can be similarly defined.
Definition 2. Let G be a network with N(G) vertices. The entropy of subtrees of G is defined as follows:
Let T be a tree with n vertices. Székely and Wang [2] and Yan and Yeh[3] obtained the results of the number of subtrees in a tree as follows: , where Pn and K1,n−1 are the path and star with n vertices, respectively. So, we have
and
From Equations (5) and (6), we can calculate the entropies of subtrees of and , respectively, as follows:
and
Therefore, for a tree T with n vertices and a 3–cactus network Gt with t triangles, we have
Now we calculate the entropy of subtrees of Koch networks. The following definition and notation will be used in this section.
Let α(x) and β(x) be two infinities when x is close to infinity. If , we say that α(x) and β(x) are equivalent infinities, and write α(x) ~ β(x) (x → ∞).
For Koch networks, another construction is given as follows. The network Gm, g is obtained from Gm,i (i = 0, 1, 2, …, g − 1) and the initial triangle by adding m copies of Gm,i to each of the three hub vertices of the initial triangle, as shown in Figure 7.
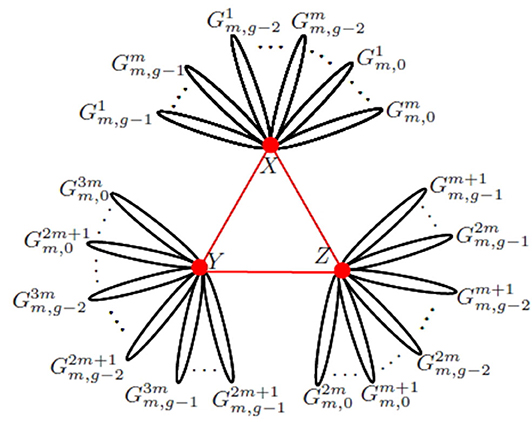
Figure 7. Another construction of Koch networks. The network after g iterations, Gm,g, consists of 3m copies of Gm,i labeled by .
According to the construction, Gm,g has the form illustrated in Figure 8, where Hg is the subnetwork of Gm,g obtained from m copies of Gm,i (i = 0, 1, 2, …, g − 1) by identifying mg hub vertices X in m copies of Gm,i (i = 0, 1, 2, …, g − 1). Then ηX(Hg) and η(Hg − X) are given by
By Algorithm A to the initial triangle (X, Y, Z), we get that
and initial conditions are ηX(Gm,0) = 6 and η(Gm,0 − X) = 3. So, we arrive at
From Equation (7), we obtain
According to the above theoretical analysis, we give a linear algorithm for counting the number of subtrees in a Koch network, as follows.
Algorithm B: Initial condition: Let Gm,g be a Koch network generated by g iterations and X, Y and Z be three hub vertices in Gm,g. Let η(Gm,g) denote the number of subtrees of Gm,g.
Step 1. Take k = 1, a = 6, b = 3, x = 1 and y = 0.
Step 2. Suppose that, at iteration k, the number of subtrees containing X in Hk and the number of subtrees not containing X in Hk are denoted by x and y, respectively. One gets the values x and y as
Step 3. Suppose that a and b denote the number of subtrees containing X in Gm,k and the number of subtrees not containing X in Gm,k, respectively. We get a and b by
Step 4. If k = g, then stop, output η(Gm,g) = a + b. Otherwise, k: = k + 1, go to Step 2.
It is not difficult to see that the complexity of the above algorithm is O(g). In order to calculate the entropy of subtrees of Koch networks, we need the following lemma:
Lemma 4. Let Gm,g be a Koch network generated by g iterations. Then
Proof: From Equation (10), we have the following recurrence relations:
It is easy to obtain . Note that .
It follows that
Since η(H1 − X) = 3m, we have
From Equations (11) and (12), we get that . From Equation (9), it is easy to see that
From Equations (11) and (13), we conclude that
The proof is thus complete. □
From Lemma 4, we can calculate the entropy of subtrees of Koch networks, as
Next, we can compare the entropy of subtrees of Koch networks with those of and . Observe that and Thus, the following inequality holds.
The entropy of subtrees of Koch networks reflects the fact that although the number of subtrees of Koch networks grows exponentially, the growth rate is lower than that of the triangle–star and higher than that of the triangle–path. This result suggests that if the vertex failure probability p satisfies p → 0, the edge failure probability q satisfies q → 1, and p and 1 − q are equivalent infinitesimals, then Koch networks are less reliable than the triangle–star, and more reliable than the triangle–path. Noticing that E(Gm,g) can be considered as a function of the variable m, it is easy to see that the entropy of subtrees of Koch networks tends to the maximum entropy of subtrees of all 3–cactus networks as m tends to infinity.
6. Conclusions
In this paper, we have given the definition of the entropy of subtrees, which is used to compare the average number of subtrees for networks of different sizes. We have established a linear algorithm for counting the number of subtrees in any 3–cactus network, and characterized the 3–cactus networks with upper and lower bounds of the entropy of subtrees among all 3–cactus networks with t triangles. In order to avoid exponential computation, we have also proposed a linear algorithm for calculating the number of subtrees in Koch networks. Finally, we have determined the entropy of subtrees of Koch networks which tends to the maximum entropy of subtrees of all 3–cactus networks as m tends to infinity.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
LD, HZ, and H-JL contributed the conception and design of the study. LD organized the literature, wrote the simulation programs, and performed the design of figures. LD and HZ wrote the first draft of the manuscript. All authors contributed to the manuscript revision, read, and approved the submitted version.
Funding
This work was supported by National Science Foundation of China (Grant No. 11661069), the Program for Changjiang Scholars and Innovative Research Team in Universities (Grant No. IRT-15R40), the Key Laboratory of Qinghai Province (Grant No. 2013-Z-Y17), the Research Fund for the Chunhui Program of Ministry of Education of China, the Nature Science Foundation from Qinghai Province (Grant No. 2018-ZJ-718), and the Research Foundation from Qinghai Normal University (Grant No. 2018zr010).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors were very grateful to the referees and the editor for their valuable comments and suggestions, which significantly improved the presentation of this manuscript.
References
1. Zhao HX. Research on subgraph polynomials and reliability of networks (Ph.D. thesis), School of Computer, Northwestern Polytechnical University, Xi'an, China (2004).
2. Székely LA, Wang H. On subtrees of trees. Adv Appl Math. (2005) 34:138–55. doi: 10.1016/j.aam.2004.07.002
3. Yan WG, Yeh Y-N. Enumeration of subtrees of trees. Theoret Comput Sci. (2006) 369:256–68. doi: 10.1016/j.tcs.2006.09.002
4. Kirk R, Wang H. Largest number of subtrees of trees with a given maximum degree. SIAM J Discrete Math. (2008) 22:985–95. doi: 10.1137/070687736
5. Zhang XM, Zhang XD. The minimal number of subtrees with a given degree sequence. Graphs Comb. (2015) 31:309–18. doi: 10.1007/s00373-013-1383-z
6. Zhang XM, Zhang XD, Gray D, Wang H. Trees with the most subtrees-an algorithmic approach. J Comb. (2012) 3:207–23. doi: 10.4310/JOC.2012.v3.n2.a5
7. Zhang XM, Zhang XD, Gray D, Wang H. The number of subtrees of trees with given degree sequence. J Graph Theory. (2013) 73:280–95. doi: 10.1002/jgt.21674
8. Xiao YZ, Zhao HX, Liu Z, Mao YP. Trees with large numbers of subtrees. Int J Comput Math. (2017) 94:372–85. doi: 10.1080/00207160.2015.1109640
9. Yang Y, Liu HB, Wang H, Fu HS. Subtrees of spiro and polyphenyl hexagonal chains. Appl Math Comput. (2015) 268:547–60. doi: 10.1016/j.amc.2015.06.094
10. Yang Y, Liu HB, Wang H, Deng AS, Magnant C. On algorithms for enumerating subtrees of hexagonal and phenylene chains. Comput J. (2017) 60:690–710. doi: 10.1093/comjnl/bxw091
11. Axenovich M, Osang G. Unavoidable subtrees. Discrete Math. (2013) 313:924–30. doi: 10.1016/j.disc.2013.01.015
12. Christou M, Crochemore M, Flouri T, Iliopoulos CS, Janoušek J, Melichar B, et al. Computing all subtree repeats in ordered trees. Inform Process Lett. (2012) 112:958–62. doi: 10.1016/j.ipl.2012.09.001
13. Li S, Wang S. Further analysis on the total number of subtrees of trees. Electron J Comb. (2012) 19:P48. doi: 10.37236/2186
14. Martin DM, Thatte BD. The maximum agreement subtree problem. Discrete Appl Math. (2013) 161:1805–17. doi: 10.1016/j.dam.2013.02.037
15. Székely LA, Wang H. Extremal values of ratios: distance problems vs. subtree problems in trees II. Discrete Math. (2014) 322:36–47. doi: 10.1016/j.disc.2013.12.027
16. Vince A, Wang H. The average order of a subtree of a tree. J Combin Theory B. (2010) 100:161–70. doi: 10.1016/j.jctb.2009.05.006
17. Wang H. Some results on trees (Ph.D. thesis), Department of Mathematics, University of South Carolina, Columbia, United States (2005).
18. Zhang ZZ, Gao SY, Chen LC, Zhou SG, Zhang HJ, Guan JH. Mapping Koch curves into scale-free small-world networks. J Phys A Math Theor. (2010) 43:395101. doi: 10.1088/1751-8113/43/39/395101
19. Bondy JA, Murty USR. Graph Theory With Applications. New York, NY; North-Holland: The Macmillan Press Ltd. (1976).
20. Wu B, Zhang ZZ, Chen GR. Properties and applications of Laplacian spectra for Koch networks. J Phys A Math Theor. (2012) 45:025102. doi: 10.1088/1751-8113/45/2/025102
21. Lyons R, Peled R, Schramm O. Growth of the number of spanning trees of the Erdős-Rényi giant component. Combin Probab Comput. (2008) 17:711–26. doi: 10.1017/S0963548308009188
22. Zhang ZZ, Liu HX, Wu B, Zou T. Spanning trees in a fractal scale-free lattice. Phys Rev E. (2011) 83:016116. doi: 10.1103/PhysRevE.83.016116
Keywords: cactus networks, Koch networks, the number of subtrees, entropy of subtrees, reliability
Citation: Dong L, Zhao H and Lai H-J (2020) Entropy and Enumeration of Subtrees in a Cactus Network. Front. Phys. 8:575648. doi: 10.3389/fphy.2020.575648
Received: 23 June 2020; Accepted: 24 August 2020;
Published: 08 October 2020.
Edited by:
Yang-Hui He, City University of London, United KingdomReviewed by:
Praveen Agarwal, Anand International College of Engineering, IndiaSimon Chiossi, Fluminense Federal University, Brazil
Copyright © 2020 Dong, Zhao and Lai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Haixing Zhao, aC54LnpoYW9AMTYzLmNvbQ==
 Lixin Dong
Lixin Dong Haixing Zhao1*
Haixing Zhao1*