- 1Strathclyde Institute of Pharmacy and Biomedical Sciences, University of Strathclyde, Glasgow, United Kingdom
- 2Key Laboratory of Ultra-fast Photoelectric Diagnostics Technology, Xi'an Institute of Optics and Precision Mechanics, Xi'an, China
- 3University of Chinese Academy of Sciences, Beijing, China
- 4Department of Physics, Scottish Universities Physics Alliance, University of Strathclyde, Glasgow, United Kingdom
Intensity- and amplitude-weighted average lifetimes, denoted as τI and τA hereafter, are useful indicators for revealing Förster resonance energy transfer (FRET) or fluorescence quenching behaviors. In this work, we discussed the differences between τI and τA and presented several model-free lifetime determination algorithms (LDA), including the center-of-mass, phasor, and integral equation methods for fast τI and τA estimations. For model-based LDAs, we discussed the model-mismatch problems, and the results suggest that a bi-exponential model can well approximate a signal following a multi-exponential model. Depending on the application requirements, suggestions about the LDAs to be used are given. The instrument responses of the imaging systems were included in the analysis. We explained why only using the τI model for FRET analysis can be misleading; both τI and τA models should be considered. We also proposed using τA/τI as a new indicator on two-photon fluorescence lifetime images, and the results show that τA/τI is an intuitive tool for visualizing multi-exponential decays.
1. Introduction
Fluorescence lifetime imaging (FLIM) is a crucial technique for assessing microenvironments of fluorescent molecules [1, 2], such as pH [3], Ca2+ [4, 5], O2 [6], viscosity [7], or temperature [8]. Combining with Förster Resonance Energy Transfer (FRET) techniques, FLIM can be a powerful “quantum ruler” to measure protein conformations and interactions [9–12]. Compared with fluorescence intensity imaging, FLIM is independent of the signal intensity and fluorophore concentrations, making FLIM a powerful quantitative imaging technique for applications in life sciences [13], medical diagnosis [14–16], drug developments [17–19], and flow diagnosis [20–22]. FLIM techniques can build on time-correlated single-photon counting (TCSPC) [23–25], time-gating [26–28], or streak cameras [29]; they record time-resolved fluorescence intensity profiles to extract lifetimes with a lifetime determination algorithm (LDA) [1]. There is a rapid growth of real-time applications that fast analysis is sought after [12, 30]. Traditional LDAs usually use the least square method (LSM) or maximum likelihood estimation (MLE) [31] to analyze decay models chosen by users, and model-fitting analysis follows a reduced chi-squared criterion [1]. In reality, however, it is difficult to know the exact decay model as fluorescent molecules in biological systems can demonstrate complex multi-exponential decay profiles. For instance, a mixture of fluorophores, a multi-tryptophan protein, single fluorophores in varied environments, and single-tryptophan proteins in multiple conformational states [1] can show multi-exponential decays as
where A represents the amplitude, qi and τi (i = 1, …, p) denote the amplitude fractions and lifetimes, respectively, and p is the number of lifetime components. There are time-domain or frequency-domain [32–35] FLIM systems to measure a fluorescence decay. In this work, we focus on time-domain approaches.
Suppose the instrument response function (IRF) of the measurement system is irf(t), the task performed by FLIM analysis tools is to extract f(t) from the measured decay h(t), as
The problems with traditional LSM or MLE are two-fold. (1) It is challenging to categorize a fluorescence emission into a specific exponential model described by Equation (1) in complex biological processes. An arbitrary choice of p in Equation (1) simply based on reduced chi-squared tests [36] would lead to totally different interpretations. As the fitting routine is not mathematically unique; a measured decay could be fitted equally well with a bi-exponential or a tri-exponential model. (2) To ensure the accuracy, it usually needs a high photon count (long acquisition time) when p ≥ 2 [37]. Instead of completely extracting qi and τi (i = 1, …, p), which is doubtful as mentioned above and time-consuming, in many applications, it is often useful to determine only the average lifetime which can be expressed in two forms [1]: the intensity-weighted average lifetime
and the amplitude-weighted average lifetime
The question about which average lifetime we should use according to the applications has been investigated in [38]. For instance, they suggested:
(a) τA can estimate the energy transfer efficiency in FRET [39],
where E is the energy transfer efficiency, IDA and ID are the fluorescence intensities of the donor in the presence and absence of energy transfer, respectively, and τDA, A and τD, A are τA of the donor in the presence and absence of energy transfer, respectively. E can further estimate the donor-acceptor distance.
(b) τA can also assess dynamic quenching behaviors, described by the Stern-Volmer equation [40],
where I0 and I1 are fluorescence intensities, τ0, A and τ1, A are τA of the fluorophore in the absence and presence of the quencher, respectively, KD is the Stern-Volmer quenching constant, and [Q] is the concentration of the quencher. Additionally, the average radiative rate constant can be expressed as, kr = QE/τ1, A, where QE is the quantum yield.
(c) τI can be used to estimate the average collisional constant kq from the Stern-Volmer constant KD.
Average lifetimes can either be calculated by extracting the lifetime components using model-based LDAs and then using Equations (3) and (4). Or they can be directly obtained with model-free LDAs, such as hardware-friendly center-of-mass methods (CMM) [41–44], the phasor method (Phasor) [45–47], the rapid lifetime determination method (RLD) [30, 48–51], or the integral extraction method (IEM) [52, 53], without assuming any decay model.
In this work, we theoretically investigated two types of average lifetimes evaluated by model-free LDAs, examined the performances of τA and τI estimations using different LDAs, and suggested the choices of LDAs in terms of accuracy, precision, and estimation speeds according to the applications. We also described a multi-exponential decay visualization tool using the ratio τA/τI. Experimental results demonstrate the performance of τA/τI in comparison with Phasor.
2. Theory
In this section, we derived the average lifetimes determined by the model-free methods, CMM, Phasor, and IEM and described the general work flow of average lifetime estimations with the model-free and model-based LDAs.
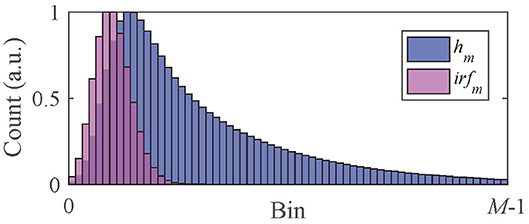
As Equation (2), the measured signal h(t) is the convolution of f(t) with irf(t). Here we focus on the signal hm and irfm obtained from a TCSPC system, as shown in Figure 1,
where hm is the photon count collected in Bin m at tm = (m + 1/2)Δt, M is the number of bins, and Δt is the time resolution.
(a) CMM
The average lifetime evaluated with CMM is
which is equal to τI. The derivation of Equation (8) is shown in the Appendix.
(b) Phasor
The average lifetime evaluated with Phasor is
where ω = 2π/T, T = MΔt is the measurement window, and g and s are the phasor components expressed as
where
τP is a weighted average lifetime whose weights are . If τi ≪ T, then the weights are approximately equal to qiτi, i.e., τP is close to τI.
(c) IEM
For IEM, the underlying exponential decay should be extracted by a model-free deconvolution method. With the estimated exponential decay , the average lifetime with IEM is
where Sm = [1/3, 4/3, 2/3, 4/3, 1/3] are the coefficients for numerical integration based on Simpson's rule. τIEM is actually an estimator for τA.
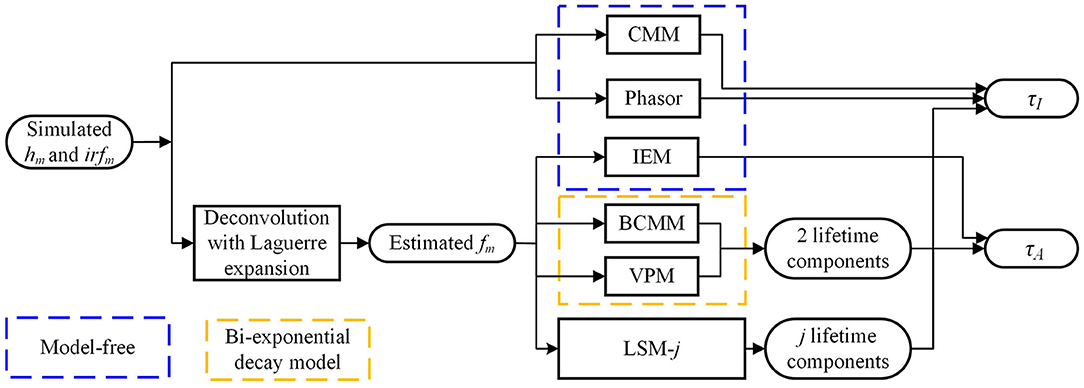
Figure 2 summarizes the flow diagram for τI and τA estimations with different algorithms used in this study. The simulated signals hm and irfm are directly sent into CMM and Phasor blocks to estimate τI. The estimated fm (from hm and irfm with the Laguerre expansion deconvolution method with L = 16 and α = 0.912 [54, 55]) is sent to IEM to estimate τA and sent to the bi-decay center-of-mass method (BCMM; j = 2) [56], the variable projection method (VPM; j = 2) [57], or LSM with a j-exponential model (denoted as LSM-j), to estimate τI and τA. CMM and Phasor are fast as no deconvolution routine is needed, whereas IEM, BCMM, VPM, and LSM are direct or iterative estimation approaches once fm is extracted. Artificial neural network assisted analysis tools [58, 59] can be included in this diagram, but they are out of the scope of this work.
3. Results
3.1. Simulations
In reality, it is difficult to characterize a real fluorescence profile with a suitable exponential model described in Equation (1). To demonstrate how model-free analysis can be beneficial, we examined two scenarios. Case A: we used exponential decay signals with p = 1 ~ 4 to assess the influence of the model mismatch between the signal and the algorithm on τI and τA estimations. This study is to investigate the scenario when users select a j-exponential model to analyze a p-exponential decay (p can be different from j). Case B: we generated synthetic bi-exponential (p = 2) decay signals to assess the performances of τI and τA estimations with the model-free and model-based LDAs.
The performances of lifetime estimations can be assessed in two aspects: (1) the accuracy and the precision [60], where n = I or A for the intensity- or the amplitude-weighted lifetimes, τn and are actual and estimated values, is the standard deviation of , and Ntot is the total photon count. The lower the F, the higher the precision (F = 1 for the ideal case).
3.1.1. Case A: Model Mismatch
Ideally, a bi-exponential signal should be analyzed by a bi-exponential model. For instance, BCMM, VPM, and LSM-2 are used for bi-exponential decay models, and LSM-j for j-exponential models, j > 2. However, in realistic biological processes, it is difficult to know precisely how many lifetime components a decay profile contains. In traditional FLIM analysis tools, users usually need to select an exponential model to fit measured decays and use the reduced chi-squared to evaluate the goodness-of-fit. If the reduced chi-squared is not satisfactory, then a different exponential model is chosen. This process continues until the reduced chi-squared is acceptable. Often different exponential models can produce similar reduced chi-squared values, and the question is which fitting we should use? It is quite common that a j-exponential model might analyze a signal containing p lifetime components and j ≠ p. We would like to know if p is unknown to the user, whether using a different analysis model (j ≠ p) would lead to a different biological story.
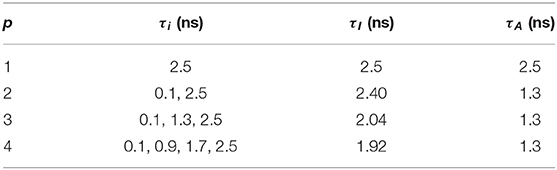
We generated exponential decay signals hm (m = 0,…, M-1) to test the LDAs for τI and τA estimations. hm can be artificially generated with , where p = [1, 2, 3, 4], qi = 1/p, and the IRF is approximated with a Poisson distribution with λ = 500 ps, FWHM ≃ 300 ps, and M = 256. The measurement window T = 10 ns, and the total photon count Ntot = 103. τi, τI, and τA for each p are summarized in Table 1.
The performances of τI and τA estimations with the simulated exponential decays are shown in Figures 3A–D for BI, FI, BA, and FA, respectively. For model-free LDAs, BI and BA are below 10% and are independent of p. For LSM-1, when p = 1, BI, and BA are zero, whereas when p > 1, BI and BA increase especially for p = 2. For model-based LDAs where j > 1, BCMM, VPM, and LSM-j have similar performances even for p ≠ j, seemingly suggesting that a bi-exponential model can well approximate a signal following an arbitrary p-exponential model. We generated 100 signals with τi and qi chosen randomly in the ranges of 0.1 ~ 2.5 ns and 0.1 ~ 0.9, respectively, for each p. BCMM, VPM, and LSM-2 were used to fit the signals with bi-exponential decays. The goodness-of-fit is judged by the reduced chi-squared , where fm and fc, m are actual and fitted signals of Bin m. The box plots of χ2 for BCMM, VPM, and LSM-2 are shown in Figures 3E–G, respectively. The χ2 values are insensitive to p for the three LDAs so that we conclude that a bi-exponential decay is suitable to approximate an arbitrary p-exponential decay (p ≤ 4).
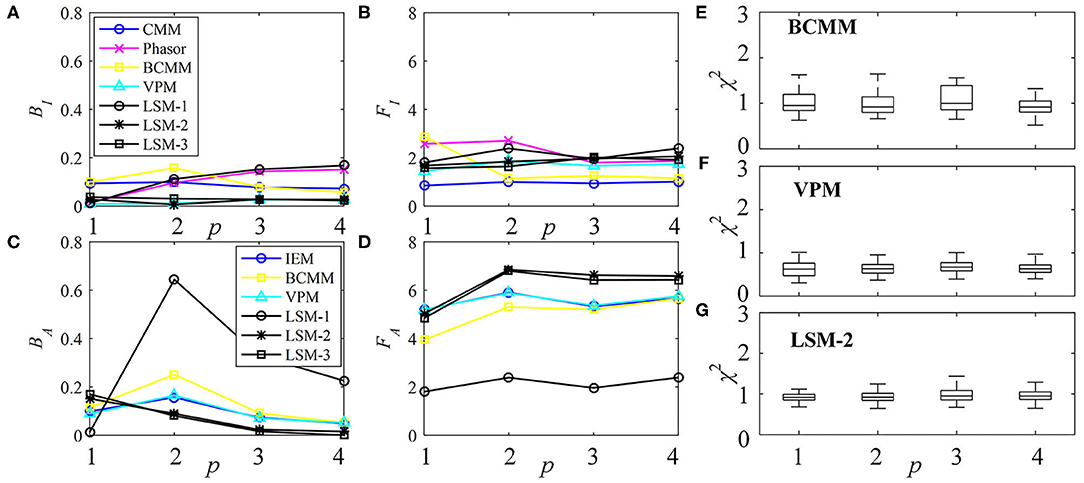
Figure 3. Performances of τI and τA estimations with exponential decay signals using different algorithms, (A) BI, (B) FI, (C) BA, and (D) FA. (E–G) Box plots of χ2 for BCMM, VPM, and LSM-2.
Therefore, if the decay model of the signal is inaccessible, model-free and model-based LDAs, BCMM, VPM, and LSM-2 are enough for τI and τA estimations.
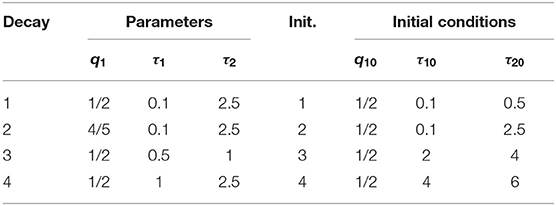
In practice, users can choose an optimization algorithm and set initial conditions to analyze FLIM images when LSM-2 is used. We would like to know how they can affect τI and τA estimations. Four bi-exponential decays, Decays 1 ~ 4, with different parameters (q1, τ1, τ2) were analyzed using LSM-2 with different initial conditions (q10, τ10, τ20), denoted as Init. 1 ~ 4 listed in Table 2 with Ntot = 103. When either of the estimated τ1 and τ2 is larger than T (10 ns), we say that the estimation fails. The probabilities of producing a failed trial, P(τ1 or τ2 > 10) and producing biased τI and τA with BI and BA > 0.3, i.e., P(Bn > 0.3), n = I or A, are shown in Figure 4. Figures 4A–F are the LSM-2 results with the unconstrained and constrained trust-region-reflective (TRR) algorithms, respectively. The constraints are 0 < q1 < 1 and 0 < τ1, τ2 < 10 ns. Figures 4G–I are the LSM-2 results using the Levenberg-Marquardt (LM) algorithm. For the unconstrained TRR, the performances are relatively sensitive to initial conditions. P(τ1 or τ2 > 10) for Init. 4 is quite significant which results in large P(Bn > 0.3), n = I or A, for all four decays. Although Init. 3 leads to a low P for Decays 2 ~ 3, P(BA > 0.3) for Decay 1 rises to 0.7. Thus, if the initial conditions are not chosen properly, the quality of τI and τA images cannot be guaranteed. The constrained TRR and LM are insensitive to initial conditions. Although the LM has failed trials, they barely affect P(Bn > 0.3), n = I or A. Therefore, to ensure accurate τI and τA estimations, the constrained TRR and LM are recommended for LSM-2.
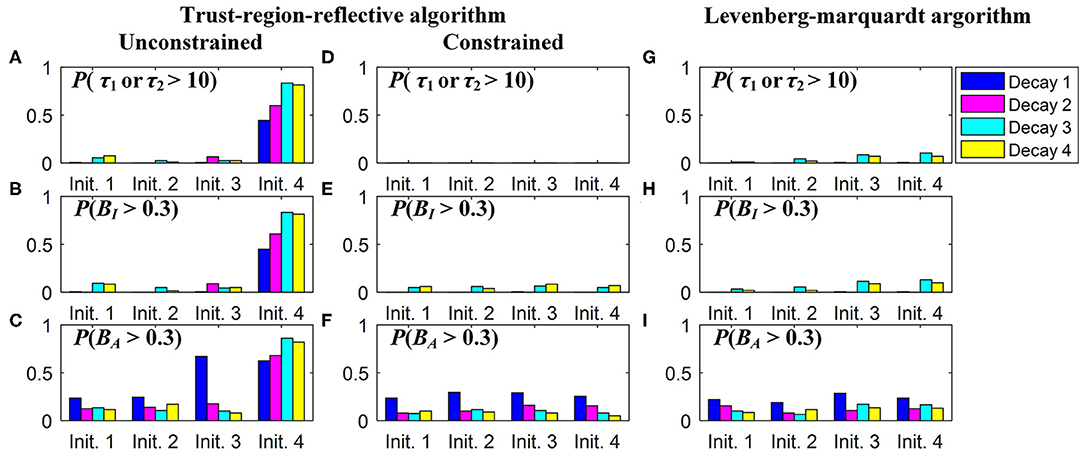
Figure 4. (A,D,G) P(τ1 or τ2 > 10), (B,E,H) P(BI > 0.3), and (C,F,I) P(BA > 0.3), for estimations of Decays 1 ~ 4 with Init. 1 ~ 4 using (A–C) the unconstrained TRR, (D–F) the constrained TRR, and (G–I) the LM algorithms.
3.1.2. Case B: Performances of Average Lifetime Estimations
As mentioned above, it might be challenging to use a proper exponential model to describe realistic biological processes; a bi-exponential model might well approximate them. Here we will use a bi-exponential model to explain why model-free LDAs have the benefits of higher photon efficiency and faster analysis than model-based LDAs for τI and τA estimations.
hm can be artificially generated with the same IRF used in Case A and f(t) = A[q1exp(−t/τ1) + (1 − q1)exp(−t/τ2)], where τ1 < τ2 and q1 is the amplitude fraction of τ1. Figure 5A shows the signal and IRF. In FRET and dynamic quenching applications, the fluorescence lifetime of the donor fluorophore is in general decreasing, and we assume τ2 = 2.5 ns and τ1 varying from 0.1 to 2.5 ns to emulate FRET or quenching. The theoretical τI, τA, and τP with q1 = 0.5 are shown in Figure 5B. τP has a negative bias from τI. With T/τ2 increasing, τP approaches τI. Figure 5B that two different (τ1, τ2) sets can deliver the same τI, for instance, (0.32, 2.5) ns and (2.1, 2.5) ns have the same τI of 2.3 ns.
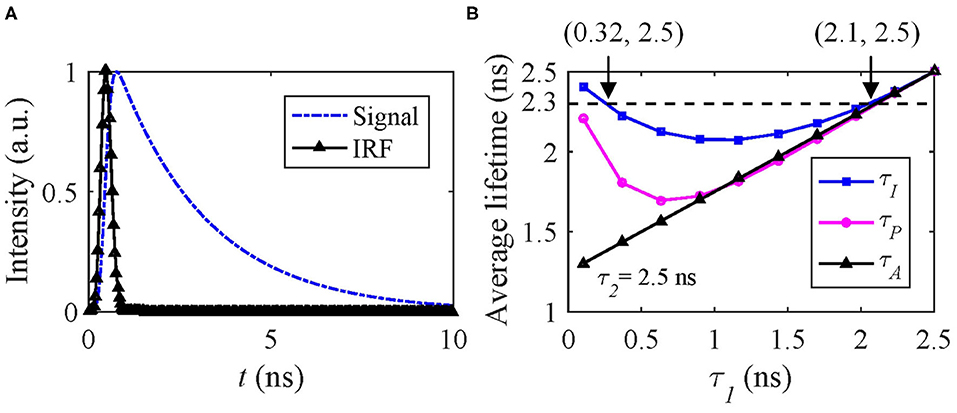
Figure 5. (A) Simulated signal (blue) and IRF (black), (B) theoretical τI (blue), τA (black), and τP (magenta) average lifetimes with q1 = 0.5.
Therefore, only estimating τI can be misleading. Figure 5B also shows that the dynamic range of τI is only 2.5–2.23 = 0.27 ns and within which the above problem persists. Whereas τA does not have this problem for this case. We conducted Monte Carlo simulations to estimate τI and τA with the simulated signals, including Poisson noise under different conditions q1 = 0.2, 0.5, and 0.8.
The performances of τI and τA estimations with bi-exponential decay signals are shown in Figures 6A–D for BI, FI, BA, and FA, respectively. For , BI, CMM, and BI, BCMM are roughly 10 and 8%, respectively determined by T/τ2. The larger T/τ2 is, the smaller BI becomes (with FI, CMM and FI, BCMM being closer to 1). Phasor has a lower accuracy when q1 becomes larger and τ1 smaller, and it is less precise than CMM. VPM and LSM-2 both have a smaller BI = 3% but higher FI (1.5 ~ 5) than CMM and BCMM. For , BA is 7% except for τ1 = 0.1 ns, and FA is around 5 for the four LDAs. Figures 6C,D show that if only τA is needed, there is no need to resort to slower model-based LDAs.
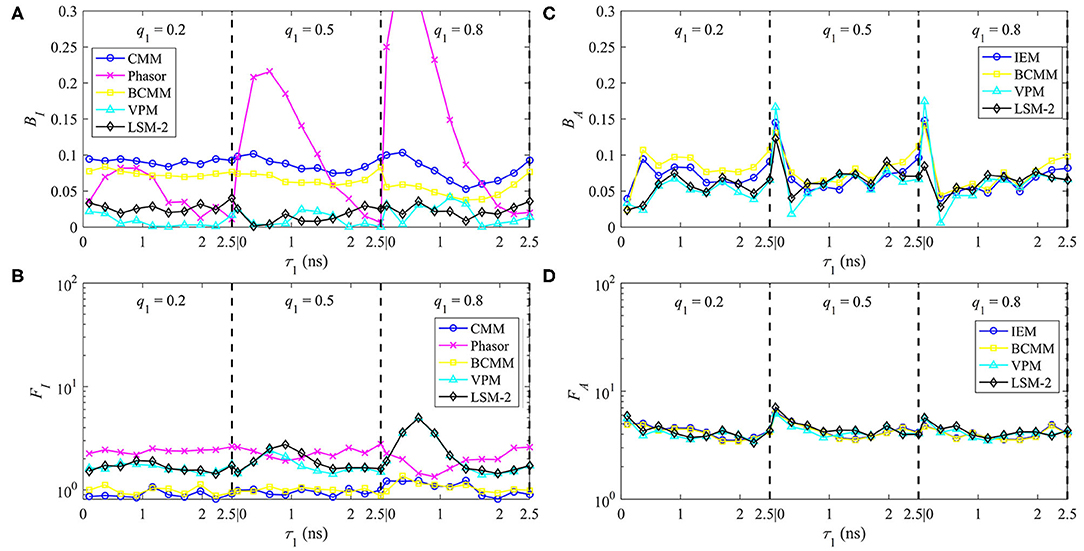
Figure 6. The performances of τI and τA estimations with bi-exponential decay signals with τ1 = 0.1 ~ 2.5 ns, τ2 = 2.5 ns, q1 = 0.2, 0.5, 0.8, (A) BI, (B) FI and (C) BA, (D) FA.
For τI estimations, LSM-2 and VPM are preferred when high accuracy is required. Still, they are slower and have lower photon efficiency than CMM and BCMM which means the photon count should be higher to have similar precision, for instance, a relative standard deviation of 5% can be reached with Ntot = 3,600 for LSM-2 and Ntot = 500 for CMM and BCMM. When the accuracy of CMM or BCMM (10% @ T/τ2 = 4) is acceptable, CMM or BCMM should be employed for their high photon efficiency and estimation speeds. CMM is faster than BCMM as it can work without deconvolution. For τA estimations, since the performances of IEM, BCMM, VPM, LSM-2 are similar, IEM can be the right candidate for fast analysis. Notice that the τA method is less photon efficient than the τI method as FA is higher than FI.
3.2. Experimental Results
tSA201 cells, which are a transformed human kidney cell line, were co-transfected with hP2Y12-eCFP and hP2Y1-eYFP receptors. After 48 h of transfection, the cells on the coverslips were washed once gently with PBS followed by fixation with ice-cold methanol for 10 min at room temperature. After being washed three times with PBS, they were mounted on to glass microscope slides with Mowiol. The microscope slides were then stored in the dark at room temperature overnight to allow the coverslips to dry, then stored at 4°C for later use.
Cells were imaged on LSM510 (Carl Zeiss) equipped with a TCSPC module (SPC-830, Becker & Hickl GmbH), to determine the fluorescence lifetime and consequently the amount of FRET. The donor is CFP with the excitation wavelength range of 350 ~ 500 nm and the emission wavelength range of 450 ~ 600 nm. The acceptor is YFP. The sample is scanned pixel by pixel by a femtosecond Ti:Sapphire laser (Chameleon, Coherent) with an average output laser power of 3.8 W at 800 nm, as a two-photon excitation source to reduce cellular damage. The laser power is controlled with two polarizers. The repetition rate is 80 MHz with illuminating duration <200 fs. The emitted fluorescence signal from the donor is collected through a 63 × water-immersion objective lens (N.A. = 1.0), a 480 ~ 520 nm bandpass filter, and transferred into a photomultiplier tube (PMT) detector. The FLIM scanning was performed in a dark room containing the microscope. A set of experimental data (256 × 256 pixels, M = 256, T = 10 ns) was collected over an exposure period of up to 15 min. The IRF is obtained from the measurement of dried urea [(NH2)2CO] [61].
3.2.1. Average Lifetime Images With LSM, CMM, and IEM
Figures 7A,C show the τI and τA images of the data evaluated by LSM-2 with an execution time of 410 s. The lifetime images were evaluated on Matlab R2016a, 64-bit with the Intel(R) Celeron(R) CPU (2950M @ 2 GHz) with 20923 pixels above an intensity threshold. Figures 7B,D show the τI and τA images evaluated by CMM and IEM with execution times of 0.25 and 92.3 s, respectively. IEM can be further accelerated to 0.6 s per image with histogram classification methods (we will report the details soon), as shown in Figure 7E. Although Fast-IEM causes a small bias in some pixels, the mean square error is acceptable with 0.005 ns2. The color bar represents lifetimes and the pixel brightness represents photon counts. The Figures 7F,G are histograms of τI and τA, respectively. Although the histogram of τI with CMM deviates slightly from the one with LSM-2, CMM is 1,800-fold faster than LSM-2. If T/τi > 4, the bias of τI with CMM would become smaller. The τA images are almost the same with IEM and LSM-2, whereas IEM and Fast-IEM are much faster than LSM-2.
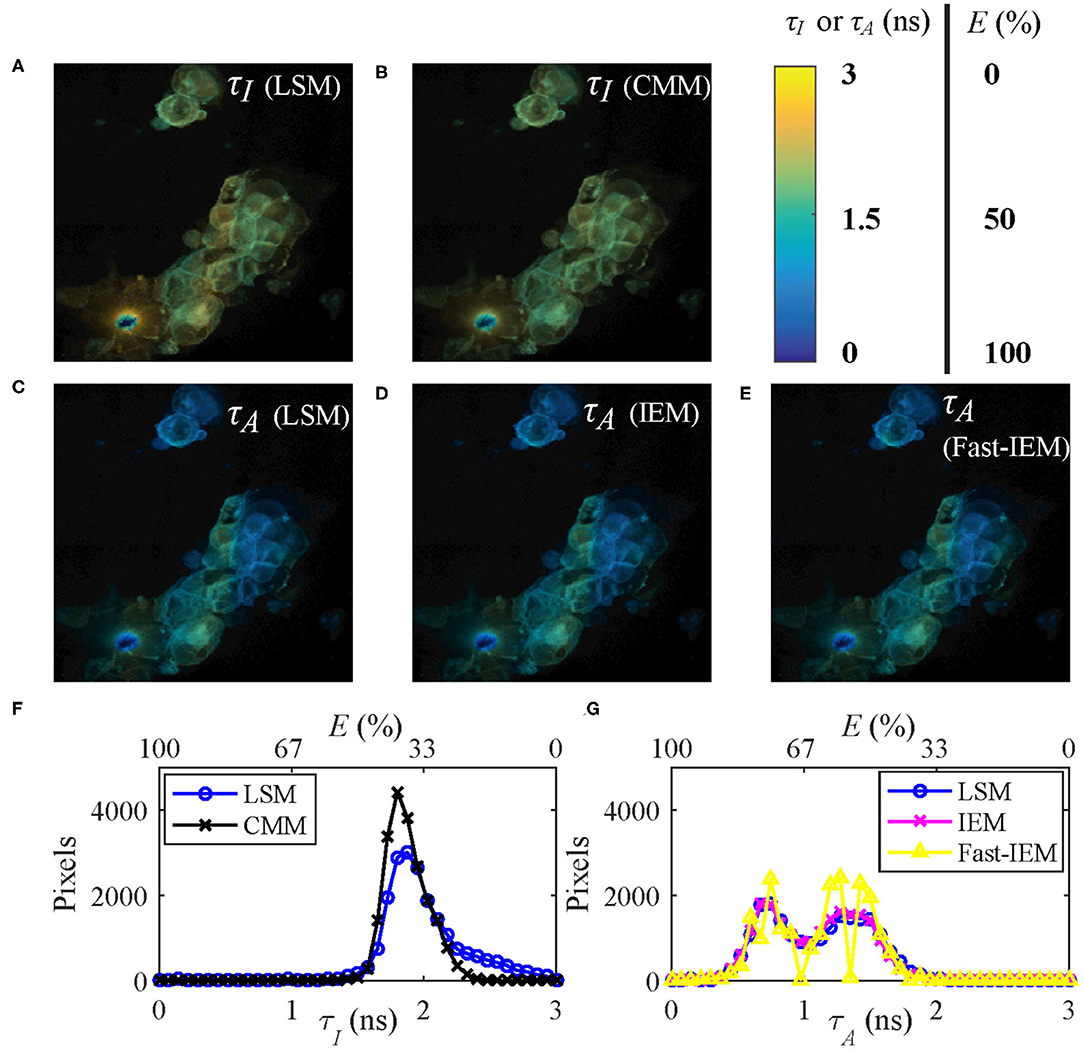
Figure 7. (A,C) τI and τA images evaluated with LSM-2, (B,D) τI and τA images evaluated with CMM and IEM, respectively. (E) τA image with Fast-IEM. (F) Histograms of τI with LSM-2 (blue) and CMM (black). (G) Histograms of τA with LSM-2 (blue), IEM (magenta), and Fast-IEM (yellow). The color bar represents lifetimes and the pixel brightness represents photon counts. (A–E) Can also represent FRET efficiency (E) images evaluated with the corresponding lifetime images with the color bar representing the range of E, 0 ~ 100%. (F,G) Can also be used to show the histograms of E with the upper x label.
Since the FRET efficiency E has a linear relationship with the average lifetimes as shown in Equation (5), Figures 7A–E can also be used to represent E images with the color bar in the range of 0 ~ 100%. As we mentioned in Introduction, it is straightforward to obtain E images from τA images, so that Figures 7C–E are proper E images. If τI images are misused for E, the results would be different, as shown in Figures 7A,B, leading to a different biological story.
3.2.2. Visualization of Multi-Exponential Decays With τA/τI
τI and τA can not only access the essential parameters in FRET and dynamic quenching processes but also indicate the positions where multi-exponential decays occur. As mentioned previously, a fluorescence signal can be approximated by a bi-exponential decay, so that the ratio of τI and τA can be expressed as
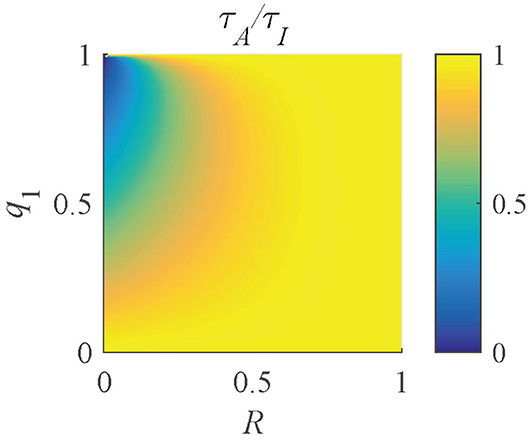
where R = τ1/τ2. The distribution of τA/τI (Figure 8) shows that when R ≃ 1 or q1 ≃ 0 or 1, τA/τI ≃ 1. With a decrease of R or an increase of q1, τA/τI decreases. Therefore, the ranges of q1 and R of a pixel can be determined by τA/τI.
To present the multi-exponential decay visualization performance of τA/τI, the τI and τA images evaluated by LSM-2, Figures 9A,B, were used to generate the τA/τI image as shown in Figure 9C. The histograms of τI and τA and the phasor plot are shown in Figures 9D,E. Figure 9F shows the possible range of q1 and R of the selected pixels in Figure 9C. Figures 9C,F share the same color bar. Figure 9D shows that τA has a broader lifetime dynamic range than τI, which is consistent with the theoretical lines shown in Figure 5B. The τA histogram shows two clusters with different peaks, whereas the τI histogram only indicates a single merged group, meaning that there is no way to differentiate these two clusters. It is why using τI to analyze samples with a strong FRET can be misleading.
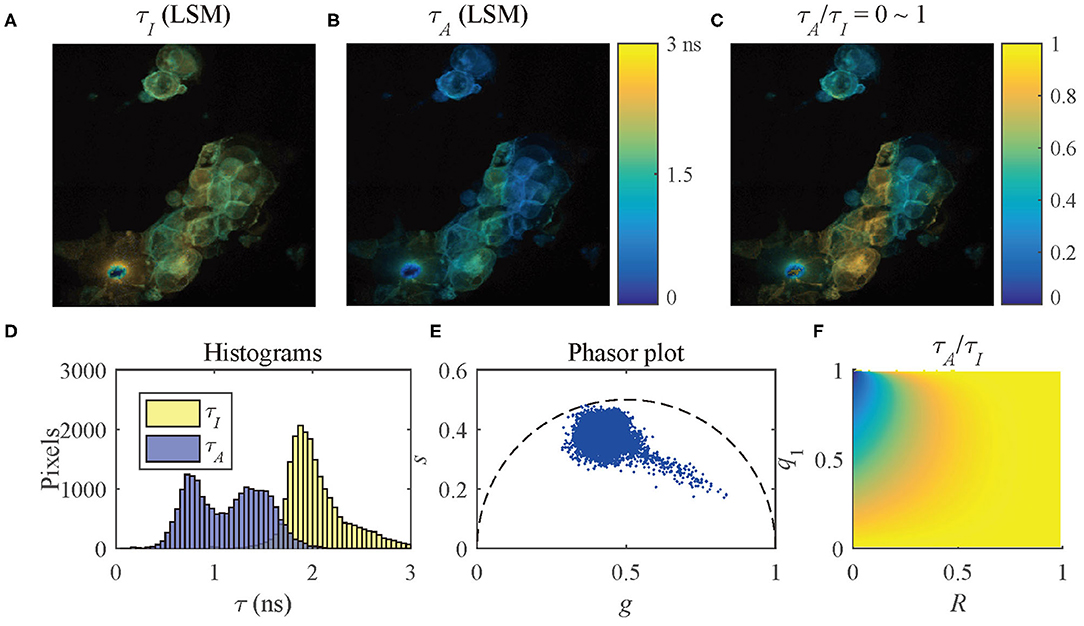
Figure 9. (A) τI-intensity image, (B) τA-intensity image evaluated by LSM-2, (C) τA/τI ratio image, (D) histograms of τI (yellow) and τA (blue), (E) phasor plot, and (F) distribution of τA/τI of the selected pixels in (C).
The results of the selected pixels within different τA/τI ranges are shown in Figure 10, τA/τI = 0.2 ~ 0.5, and Figure 11, τA/τI = 0.5 ~ 1. For the pixels with τA/τI = 0.2 ~ 0.5, the histograms clearly show that τA is much smaller than τI, which means the difference between τ1 and τ2 is significant. Figure 10F shows that the ranges of q1 and R are approximately 0.5 ~ 1 and 0 ~ 0.2, respectively. For the pixels with τA/τI = 0.5 ~ 1, τA is closer to τI, meaning the pixels have decays close to mono-exponential. Separating the average lifetime images with τA/τI is easier than phasor plots because τA/τI is one dimensional and phasors are two dimensional. Furthermore, τA/τI can show the q1 and R ranges more intuitively than phasor plots. τA/τI can be a useful tool to visualize the properties of the fluorescence decays within a lifetime image.
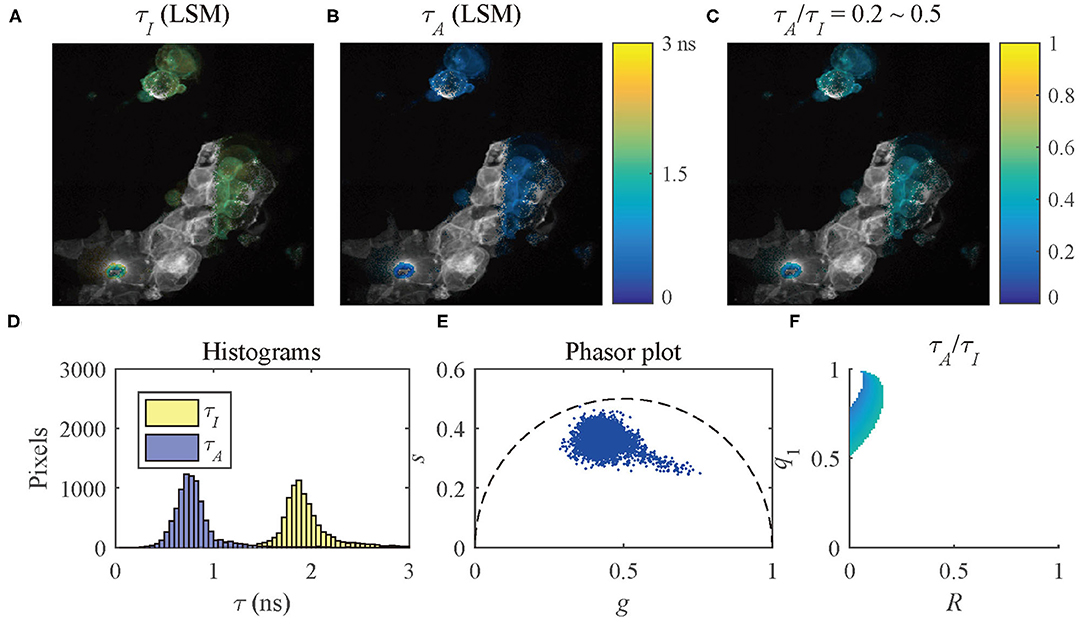
Figure 10. (A) τI-intensity image, (B) τA-intensity image evaluated by LSM-2, (C) τA/τI ratio image, (D) histograms of τI (yellow) and τA (blue), (E) phasor plot, and (F) distribution of τA/τI of the selected pixels in (C) with τA/τI = 0.2 ~ 0.5.
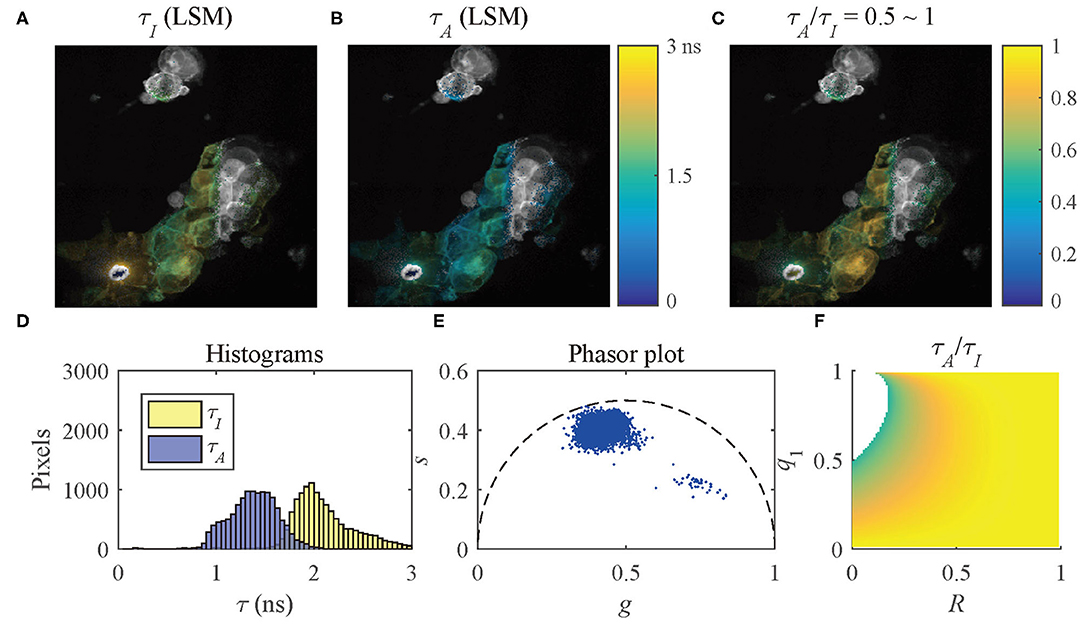
Figure 11. (A) τI-intensity image, (B) τA-intensity image evaluated by LSM-2, (C) τA/τI ratio image, (D) histograms of τI (yellow) and τA (blue), (E) phasor plot, and (F) distribution of τA/τI of the selected pixels in (C) with τA/τI = 0.5 ~ 1.
4. Discussion
In realistic samples, fluorescence signals always follow multi-exponential decay models. However, extracting lifetime components with a traditional fitting method is a time-consuming process. For some applications that require calculating FRET efficiency and accessing dynamic quenching behaviors, average lifetimes are satisfactory. Model-free lifetime determination algorithms can be used to evaluate average lifetimes directly, for instance, CMM and Phasor for intensity-weighted average lifetimes τI and IEM for amplitude-weighted average lifetimes τA. Discussions of the influence of the model mismatch between the real signal and the model-based LDAs on τI and τA estimations suggest that a bi-exponential model can well-approximate a signal following a multiple-exponential model. The results of the Monte-Carlo simulations suggest that VPM and LSM based on a bi-exponential model can be used for applications requiring high accuracy. The constrained TRR and LM algorithms with proper initial conditions are supported for LSM to guarantee accuracy. In contrast, CMM and IEM are recommended for applications requiring high estimation speeds. We also explained why τI models can be misleading, and τI and τA models should be considered. Experimental data were used to compare the performances of LSM-2, CMM, and IEM for evaluating τI and τA images. Similar τI and τA images were generated, whereas CMM and IEM are much faster than LSM-2. The data were further analyzed with τA/τI, which is capable of indicating the possible ranges of the amplitude proportion of the short lifetime and the ratio of the short and long lifetimes. We believe τA/τI is a useful and intuitive tool for visualizing multi-exponential decays in a lifetime image.
Data Availability Statement
FLIM image raw data and the instrument response are available at https://doi.org/10.15129/062e9e11-9d7f-49e5-a332-2b10d695bdcd.
Author Contributions
YL conducted theoretical and experimental analysis and developed analysis tools. MS and MC conceived FRET experiments and prepared samples. SN and YC contributed to FRET-FLIM experiments. JT contributed to tool developments. DL initiated the research concept and supervised the project. All authors wrote and revised the paper.
Funding
We would like to acknowledge support from Medical Research Scotland, China Scholarship Council, and Engineering and Physical Sciences Research Council (EP/M506643/1).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Lakowicz JR. Principles of Fluorescence Spectroscopy. New York, NY: Springer (2006). doi: 10.1007/978-0-387-46312-4
2. Berezin MY, Achilefu S. Fluorescence lifetime measurements and biological imaging. Chem Rev. (2010) 110:2641–84. doi: 10.1021/cr900343z
3. Ning Y, Cheng S, Wang JX, Liu YW, Feng W, Li F, et al. Fluorescence lifetime imaging of upper gastrointestinal pH in vivo with a lanthanide based near-infrared τ probe. Chem Sci. (2019) 10:4227–35. doi: 10.1039/C9SC00220K
4. Agronskaia AV, Tertoolen L, Gerritsen HC. Fast fluorescence lifetime imaging of calcium in living cells. J Biomed Opt. (2004) 9:1230–7. doi: 10.1117/1.1806472
5. Zheng K, Jensen TP, Rusakov DA. Monitoring intracellular nanomolar calcium using fluorescence lifetime imaging. Nat Protoc. (2018) 13:581–97. doi: 10.1038/nprot.2017.154
6. Hosny NA, Lee DA, Knight MM. Single photon counting fluorescence lifetime detection of pericellular oxygen concentrations. J Biomed Opt. (2012) 17:016007. doi: 10.1117/1.JBO.17.1.016007
7. Peng X, Yang Z, Wang J, Fan J, He Y, Song F, et al. Fluorescence ratiometry and fluorescence lifetime imaging: using a single molecular sensor for dual mode imaging of cellular viscosity. J Am Chem Soc. (2011) 133:6626–35. doi: 10.1021/ja1104014
8. Okabe K, Inada N, Gota C, Harada Y, Funatsu T, Uchiyama S. Intracellular temperature mapping with a fluorescent polymeric thermometer and fluorescence lifetime imaging microscopy. Nat Commun. (2012) 3:705. doi: 10.1038/ncomms1714
9. Fruhwirth GO, Fernandes LP, Weitsman G, Patel G, Kelleher M, Lawler K, et al. How förster resonance energy transfer imaging improves the understanding of protein interaction networks in cancer biology. ChemPhysChem. (2011) 12:442–61. doi: 10.1002/cphc.201000866
10. Marcu L. Fluorescence lifetime techniques in medical applications. Ann Biomed Eng. (2012) 40:304–31. doi: 10.1007/s10439-011-0495-y
11. Nobis M, McGhee EJ, Morton JP, Schwarz JP, Karim SA, Quinn J, et al. Intravital FLIM-FRET imaging reveals Dasatinib-induced spatial control of Src in pancreatic cancer. Cancer Res. (2013) 73:4674–86. doi: 10.1158/0008-5472.CAN-12-4545
12. Levitt JA, Poland SP, Krstajic N, Pfisterer K, Erdogan A, Barber PR, et al. Quantitative real-time imaging of intracellular FRET biosensor dynamics using rapid multi-beam confocal FLIM. Sci Rep. (2020) 10:5146. doi: 10.1038/s41598-020-61478-1
13. Becker W. Fluorescence lifetime imaging-applications and instrumental principles. In: Bradshaw RA, Stahl PD, editors. Encyclopedia of Cell Biology. Vol. 2. Waltham, MA: Elsevier. (2016). p. 107–20. doi: 10.1016/B978-0-12-394447-4.20095-3
14. Coda S, Thompson AJ, Kennedy GT, Roche KL, Ayaru L, Bansi DS, et al. Fluorescence lifetime spectroscopy of tissue autofluorescence in normal and diseased colon measured ex vivo using a fiber-optic probe. Biomed Opt Express. (2014) 5:515. doi: 10.1364/BOE.5.000515
15. Canals J, Franch N, Alonso O, Vilá A, Diéguez A. A point-of-care device for molecular diagnosis based on CMOS SPAD detectors with integrated microfluidics. Sensors. (2019) 19:445. doi: 10.3390/s19030445
16. Alonso O, Franch N, Canals J, Arias-Alpízar K, de la Serna E, Baldrich E, et al. An internet of things-based intensity and time-resolved fluorescence reader for point-of-care testing. Biosens Bioelectron. (2020) 154:112074. doi: 10.1016/j.bios.2020.112074
17. Heger Z, Kominkova M, Cernei N, Krejcova L, Kopel P, Zitka O, et al. Fluorescence resonance energy transfer between green fluorescent protein and doxorubicin enabled by DNA nanotechnology. Electrophoresis. (2014) 35:3290–301. doi: 10.1002/elps.201400166
18. Karpf S, Riche CT, Di Carlo D, Goel A, Zeiger WA, Suresh A, et al. Spectro-temporal encoded multiphoton microscopy and fluorescence lifetime imaging at kilohertz frame-rates. Nat Commun. (2020) 11:2062. doi: 10.1038/s41467-020-15618-w
19. Hirmiz N, Tsikouras A, Osterlund EJ, Richards M, Andrews DW, Fang Q. Highly multiplexed confocal fluorescence lifetime microscope designed for screening applications. IEEE J Select Top Quant Electron. (2020) 27:1–9. doi: 10.1109/JSTQE.2020.2997834
20. Ehn A, Johansson O, Arvidsson A, Aldén M, Bood J. Single-laser shot fluorescence lifetime imaging on the nanosecond timescale using a Dual Image and Modeling Evaluation algorithm. Opt Exp. (2012) 20:3043. doi: 10.1364/OE.20.003043
21. Jonsson M, Ehn A, Christensen M, Aldén M, Bood J. Simultaneous one-dimensional fluorescence lifetime measurements of OH and CO in premixed flames. Appl Phys B. (2014) 115:35–43. doi: 10.1007/s00340-013-5570-7
22. Ehn A, Zhu J, Li X, Kiefer J. Advanced laser-based techniques for gas-phase diagnostics in combustion and aerospace engineering. Appl Spectrosc. (2017) 71:341–66. doi: 10.1177/0003702817690161
23. Becker W. Advanced Time-Correlated Single Photon Counting Techniques. Heidelberg: Springer (2005). doi: 10.1007/3-540-28882-1
24. Rinnenthal JL, Börnchen C, Radbruch H, Andresen V, Mossakowski A, Siffrin V, et al. Parallelized TCSPC for dynamic intravital fluorescence lifetime imaging: quantifying neuronal dysfunction in neuroinflammation. PLoS ONE. (2013) 8:e60100. doi: 10.1371/journal.pone.0060100
25. Erdogan AT, Finlayson N, Williams GS, Williams E, Henderson RK. Video rate spectral fluorescence lifetime imaging with a 512 x 16 SPAD line sensor. In: Goda K, Tsia KK, editors. High-Speed Biomedical Imaging and Spectroscopy IV. San Francisco, CA: SPIE (2019). p. 22. doi: 10.1117/12.2509607
26. Cole MJ, Siegel J, Webb SED, Jones R, Dowling K, Dayel MJ, et al. Time-domain whole-field fluorescence lifetime imaging with optical sectioning. J Microsc. (2001) 203:246–57. doi: 10.1046/j.1365-2818.2001.00894.x
27. Grant DM, McGinty J, McGhee EJ, Bunney TD, Owen DM, Talbot CB, et al. High speed optically sectioned fluorescence lifetime imaging permits study of live cell signaling events. Opt Exp. (2007) 15:15656. doi: 10.1364/OE.15.015656
28. Gu L, Hall DJ, Qin Z, Anglin E, Joo J, Mooney DJ, et al. In vivo time-gated fluorescence imaging with biodegradable luminescent porous silicon nanoparticles. Nat Commun. (2013) 4:2326. doi: 10.1038/ncomms3326
29. Camborde L, Jauneau A, Briére C, Deslandes L, Dumas B, Gaulin E. Detection of nucleic acid-protein interactions in plant leaves using fluorescence lifetime imaging microscopy. Nat Protoc. (2017) 12:1933–50. doi: 10.1038/nprot.2017.076
30. Li DDU, Ameer-Beg S, Arlt J, Tyndall D, Walker R, Matthews DR, et al. Time-Domain fluorescence lifetime imaging techniques suitable for solid-state imaging sensor arrays. Sensors. (2012) 12:5650–69. doi: 10.3390/s120505650
31. Bajzer Ž, Prendergast FG. [10] Maximum likelihood analysis of fluorescence data. Methods Enzymol. (1992) 210:200–37. doi: 10.1016/0076-6879(92)10012-3
32. Verveer PJ, Hanley QS. Chapter 2: Frequency domain FLIM theory, instrumentation, and analysis. In: Gadella TWJ, editor. Laboratory Techniques in Biochemistry and Molecular Biology. New York, NY: Elesvier B.V. (2009). p. 59–94. doi: 10.1016/S0075-7535(08)00002-8
33. Zhao Q, Schelen B, Schouten R, van den Oever R, Leenen R, van Kuijk H, et al. Modulated electron-multiplied fluorescence lifetime imaging microscope: all-solid-state camera for fluorescence lifetime imaging. J Biomed Opt. (2012) 17:126020. doi: 10.1117/1.JBO.17.12.126020
34. Howard SS, Straub A, Horton NG, Kobat D, Xu C. Frequency-multiplexed in vivo multiphoton phosphorescence lifetime microscopy. Nat Photon. (2013) 7:33–7. doi: 10.1038/nphoton.2012.307
35. Serafino MJ, Applegate BE, Jo JA. Direct frequency domain fluorescence lifetime imaging using field programmable gate arrays for real time processing. Rev Sci Instrum. (2020) 91:033708. doi: 10.1063/1.5127297
37. Fišerová E, Kubala M. Mean fluorescence lifetime and its error. J Luminesc. (2012) 132:2059–64. doi: 10.1016/j.jlumin.2012.03.038
38. Sillen A, Engelborghs Y. The correct use of “average” fluorescence parameters. Photochem Photobiol. (1998) 67:475–486. doi: 10.1111/j.1751-1097.1998.tb09082.x
40. Gehlen MH. The centenary of the Stern-Volmer equation of fluorescence quenching: from the single line plot to the SV quenching map. J Photochem Photobiol C. (2020) 42:100338. doi: 10.1016/j.jphotochemrev.2019.100338
41. Li DDU, Arlt J, Tyndall D, Walker R, Richardson J, Stoppa D, et al. Video-rate fluorescence lifetime imaging camera with CMOS single-photon avalanche diode arrays and high-speed imaging algorithm. J Biomed Opt. (2011) 16:096012. doi: 10.1117/1.3625288
42. Padilla-Parra S, Auduge N, Coppey-Moisan M, Tramier M. Non fitting based FRET-FLIM analysis approaches applied to quantify protein-protein interactions in live cells. Biophys Rev. (2011) 3:63–70. doi: 10.1007/s12551-011-0047-6
43. Won Y, Moon S, Yang W, Kim D, Han WT, Kim DY. High-speed confocal fluorescence lifetime imaging microscopy (FLIM) with the analog mean delay (AMD) method. Opt Exp. (2011) 19:3396. doi: 10.1364/OE.19.003396
44. Hwang W, Kim D, Lee S, Won YJ, Moon S, Kim DY. Analysis of biexponential decay signals in the analog mean-delay fluorescence lifetime measurement method. Opt Commun. (2019) 443:136–43. doi: 10.1016/j.optcom.2019.02.059
45. Digman MA, Caiolfa VR, Zamai M, Gratton E. The phasor approach to fluorescence lifetime imaging analysis. Biophys J. (2008) 94:L14–6. doi: 10.1529/biophysj.107.120154
46. Stringari C, Cinquin A, Cinquin O, Digman MA, Donovan PJ, Gratton E. Phasor approach to fluorescence lifetime microscopy distinguishes different metabolic states of germ cells in a live tissue. Proc Natl Acad Sci USA. (2011) 108:13582–7. doi: 10.1073/pnas.1108161108
47. Ranjit S, Malacrida L, Jameson DM, Gratton E. Fit-free analysis of fluorescence lifetime imaging data using the phasor approach. Nat Protoc. (2018) 13:1979–2004. doi: 10.1038/s41596-018-0026-5
48. Ballew RM, Demas JN. An error analysis of the rapid lifetime determination method for the evaluation of single exponential decays. Analyt Chem. (1989) 61:30–3. doi: 10.1021/ac00176a007
49. Elangovan M, Day RN, Periasamy A. Nanosecond fluorescence resonance energy transfer-fluorescence lifetime imaging microscopy to localize the protein interactions in a single living cell. J Microsc. (2002) 205:3–14. doi: 10.1046/j.0022-2720.2001.00984.x
50. Moore C, Chan SP, Demas JN, DeGraff BA. Comparison of methods for rapid evaluation of lifetimes of exponential decays. Appl Spectrosc. (2004) 58:603–7. doi: 10.1366/000370204774103444
51. Elson DS, Munro I, Requejo-Isidro J, McGinty J, Dunsby C, Galletly N, et al. Real-time time-domain fluorescence lifetime imaging including single-shot acquisition with a segmented optical image intensifier. New J Phys. (2004) 6:180. doi: 10.1088/1367-2630/6/1/180
52. Li DDU, Bonnist E, Renshaw D, Henderson R. On-chip, time-correlated, fluorescence lifetime extraction algorithms and error analysis. J Opt Soc Am A. (2008) 25:1190. doi: 10.1364/JOSAA.25.001190
53. Li DDU, Arlt J, Richardson J, Walker R, Buts A, Stoppa D, et al. Real-time fluorescence lifetime imaging system with a 32 × 32 0.13μm CMOS low dark-count single-photon avalanche diode array. Opt Exp. (2010) 18:10257. doi: 10.1364/OE.18.010257
54. Liu J, Sun Y, Qi J, Marcu L. A novel method for fast and robust estimation of fluorescence decay dynamics using constrained least-squares deconvolution with Laguerre expansion. Phys Med Biol. (2012) 57:843–65. doi: 10.1088/0031-9155/57/4/843
55. Zhang Y, Chen Y, Li DDU. Optimizing Laguerre expansion based deconvolution methods for analysing bi-exponential fluorescence lifetime images. Opt Exp. (2016) 24:13894. doi: 10.1364/OE.24.013894
56. Li DDU, Yu H, Chen Y. Fast bi-exponential fluorescence lifetime imaging analysis methods. Opt Lett. (2015) 40:336–9. doi: 10.1364/OL.40.000336
57. Zhang Y, Cuyt A, Lee W, Lo Bianco G, Wu G, Chen Y, et al. Towards unsupervised fluorescence lifetime imaging using low dimensional variable projection. Opt Exp. (2016) 24:26777. doi: 10.1364/OE.24.026777
58. Wu G, Nowotny T, Zhang Y, Yu HQ, Li DDU. Artificial neural network approaches for fluorescence lifetime imaging techniques. Opt Lett. (2016) 41:2561. doi: 10.1364/OL.41.002561
59. Smith JT, Yao R, Sinsuebphon N, Rudkouskaya A, Un N, Mazurkiewicz J, et al. Fast fit-free analysis of fluorescence lifetime imaging via deep learning. Proc Natl Acad Sci USA. (2019) 116:24019–30. doi: 10.1073/pnas.1912707116
60. Draaijer A, Sanders R, Gerritsen HC. Fluorescence lifetime imaging, a new tool in confocal microscopy. In: Pawley JB, editor. Handbook of Biological Confocal Microscopy. Boston, MA: Springer US (1995). p. 491–505. doi: 10.1007/978-1-4757-5348-6_31
61. Sapermsap N, Li DDU, Al-Hemedawi R, Li Y, Yu J, Birch DJ, et al. A rapid analysis platform for investigating the cellular locations of bacteria using two-photon fluorescence lifetime imaging microscopy. Methods Appl Fluoresc. (2020) 8:034001. doi: 10.1088/2050-6120/ab854e
Appendix
Derivation of τCMM. Take the integration of t·h(t) and h(t),
Dividing Equation (1) by Equation (2) gives
Then,
Keywords: fluorescence lifetime imaging, lifetime determination algorithm, average lifetimes, multi-exponential decays, lifetime image visualization, FRET—fluorescence resonance energy transfer
Citation: Li Y, Natakorn S, Chen Y, Safar M, Cunningham M, Tian J and Li DD-U (2020) Investigations on Average Fluorescence Lifetimes for Visualizing Multi-Exponential Decays. Front. Phys. 8:576862. doi: 10.3389/fphy.2020.576862
Received: 27 July 2020; Accepted: 09 September 2020;
Published: 16 October 2020.
Edited by:
Klaus Suhling, King's College London, United KingdomReviewed by:
Nirmal Mazumder, Manipal Academy of Higher Education, IndiaIlia L. Rasskazov, University of Rochester, United States
Copyright © 2020 Li, Natakorn, Chen, Safar, Cunningham, Tian and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David Day-Uei Li, ZGF2aWQubGlAc3RyYXRoLmFjLnVr
 Yahui Li
Yahui Li Sapermsap Natakorn4
Sapermsap Natakorn4 Yu Chen
Yu Chen Margaret Cunningham
Margaret Cunningham David Day-Uei Li
David Day-Uei Li