Pattern Formation and Tropical Geometry

1. Pattern Formation and Cellular Automata

Animals show beautiful skin and wing patterns. Explaining how these come about has been a longstanding puzzle. In line with the Darwinian paradigm, an evolutionary biologist may suggest that formations of patterns on the skin of animals are visual traces of certain biological mechanisms that help survival in terms of natural selection.

In his seminal book, however, Thomson [1] argues that the geometry of patterns may be mainly dictated by chemical forces, albeit it is known that patterns may benefit their owners in certain cases. In his famous paper on morphogenesis [2], Turing speculated on the mechanism behind pattern formation on the skin of animals and proposed the famous reaction diffusion system, which consists of an inhibitor and an activator with different diffusion rates. Historically, this was the first explicit model of pattern formation, though it is purely theoretical.

An important example of self-oscillating patterns in the real world was discovered soon after, see the Belousov-Zhabotinsky reaction [3, 4]. Both the Turing model and the Belousov-Zhabotinsky reaction produce beautiful spatiotemporal patterns with quasi-ordered strips and spots, see a popular concise exposition of both topics in Ball [5]. A recent discussion about parallels in emerging complexities and patterns in biological systems and physical glass-like models can be found in Wolf et al. [6].

A possibility to obtain all sorts of patterns starting from local interactions suggests trying relatively simple models to explore patterns by pure or computer mathematics. Assuming that on a big scale all coarse grained functions are smooth and continuous, one may use differential equations in the study of patterns; see comprehensive reviews [7, 8]. But, appealing to the discrete nature of pattern formation, we shift our attention to cellular automata.

Historically, cellular automata were introduced to “abstract the logical structure of life” in 1948 by J. von Neumann and S. Ulam [9, 10]. Since then, cellular automata were used with great success to analyze complexity [11], pattern formation [12], self-organized criticality [13], and segregation [14]. Recent examples of using cellular automata for pattern prediction in biology include marine angelfish [15], seashells [16], and lizard skin [17]; see also a survey [18].

In this article we focus on so-called sandpile models, and firstly, discuss in section 2 how the patterns in that model were obtained in experimental computer physics, and secondly, we survey the main ideas permitting to study these patterns with mathematical rigor: discrete harmonic analysis (section 3), tropical geometry (section 4), toppling function (section 5), and the most technical part of the proofs, the lower bound (section 6). We mention open problems and new research directions when appropriate.

2. Pattern Formation in Sandpiles

2.1. Definitions

A sandpile model, which we consider here, consists of the standard integer lattice grid inside a compact convex domain Ω ⊂ ℝ², i.e., the graph Γ = Ω ∩ ℤ².

A state of a sandpile model is a function φ(i, j), representing the number of grains of sand at the vertex (i, j) ∈ Γ. A state, thus, is an integer-valued function φ : Γ → ℤ_≥0.

A vertex (i, j) is unstable if there are four or more grains of sand at (i, j), i.e., φ(i, j) ≥ 4. The evolution proceeds as follows: any unstable vertex (i, j) topples by sending one grain of sand to each of its four neighbors (i+1, j+1), (i+1, j−1), (i−1, j+1), (i−1, j−1). The sand, falling outside Ω, disappears from the system. Vertices outside of Ω (formally they do not even belong to Γ) and stable vertices are never toppled. Equivalently, one may think that all the lattice points outside of Ω are sinks; sand, falling to sinks, disappears. Given an initial state φ, the state φ° denotes the stable state reached after all possible topplings have been performed. It is a classical fact that φ° does not depend on the order of topplings [19, 20].

2.2. Line-Shaped Patterns in the Literature

Line-shaped patterns [which can also go under different names: solitons, linear defects, and (p, q)-webs] can be found in the pictures in Liu et al. [21] and Ostojic [22], but the main subject of the latter article was quadratic patches, recently explained in Pegden and Smart [23, 24] and Levine at al. [25, 26] using Apollonian circle packings.

Let us put three grains in all the vertices of the intersection between the standard grid ℤ² and a planar domain Ω. Let us choose several vertices and add one more grain to each of them. An example of the relaxation of such a state for Ω being a square is shown in Figure 1. We sequentially drop grains to blue points, performing a relaxation after each dropping (thus we have one blue point on the first pictures and four blue points on the fourth picture, where blue points indicate the positions of additional grains). One may easily guess a graph with straight edges along non-white parts of the pictures. With each new blue point such a graph changes, but its edges always pass through the blue points. In Figure 2 we added grains to all blue points simultaneously and took snapshots of the subsequent relaxation (since the order of topplings does not influence the final picture, we might add grains sequentially).

FIGURE 1

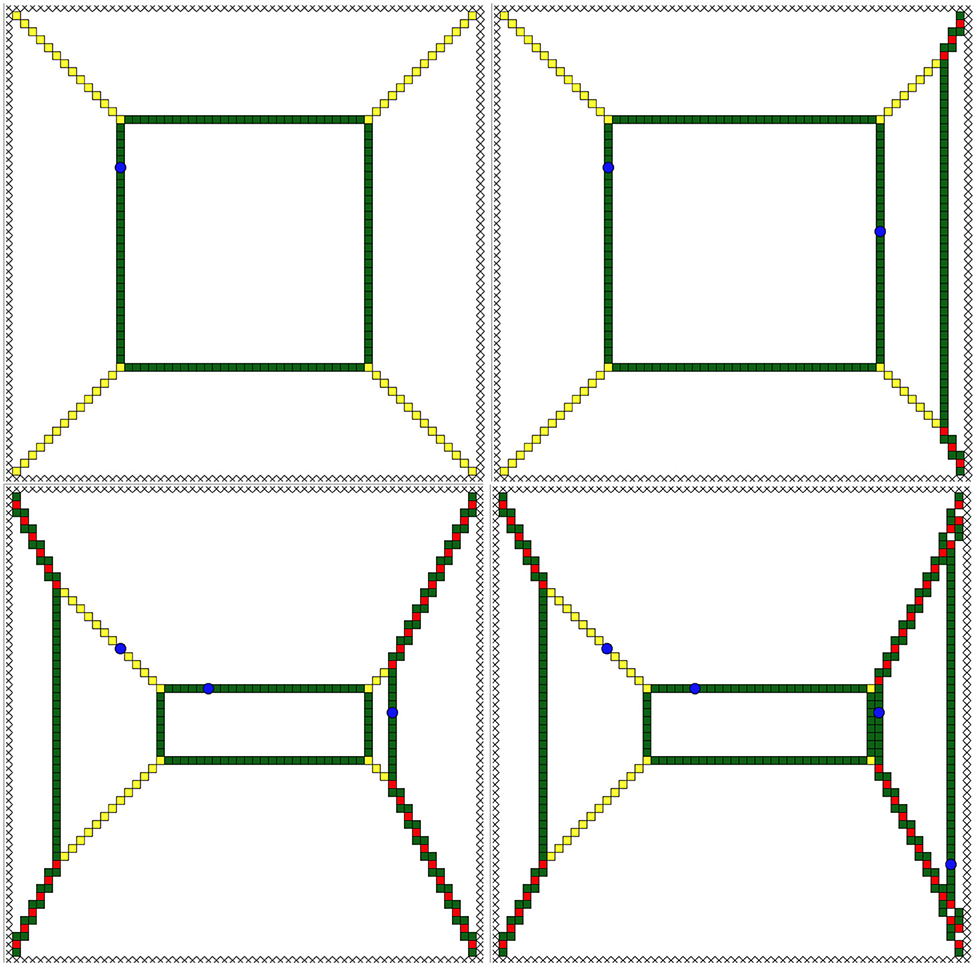
Figure 1. Ω is a square [0, 100] × [0, 100], we put 3 grains at every vertex of the lattice inside Ω and drop 1 additional grain to each blue point (sequentially). The result of the relaxation after one additional grain is on the top-left picture. Then we added a grain of sand to the second blue point and performed a relaxation, the result of which is the top-right picture. The third picture is the bottom left one, and the last one is the bottom right one. White is three grains, green is two, yellow is one, and red is zero. Crosses mark the sinks in the model.

FIGURE 2

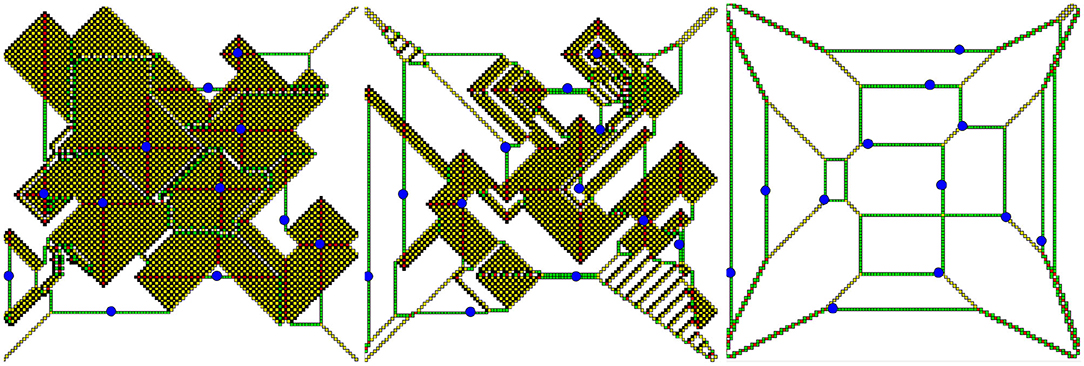
Figure 2. Ω is a square [0, 100] × [0, 100], and we put 3 grains at every vertex of the lattice inside Ω and drop 1 additional grain to each blue point. On the left we see the initial phase of the relaxation. The central picture shows an intermediate phase. On the right we see the final result.

Line-shaped patterns, clearly recognizable in Figures 1, 2 along straight edges of the imaginable graph, explicitly came in the sight of researchers in Dhar et al. [27] and Dhar and Sadhu [28] with an emphasis on a proportional growth phenomenon, and later, in Caracciolo et al. [29] (see also [30, 31]). These papers performed the analysis from the point of view of theoretical physics and explained the pictures based on experimental evidence.

The use of tropical geometry was predicted in Sadhu and Dhar [32] and later implemented with rather involved mathematical proofs in a series of articles [33–35]. A certain limit of the sandpile model gives a continuous limiting piece-wise linear model that also exhibits power-law behavior [36]; the statistical properties of the latter model can be found in Kalinin and Prieto [37]. Line-shaped patterns may be viewed as spacetime diagrams of two incoming particles that join to form one particle. It turns out that we can associate the “energy of the particle” with each world line such that total energy is conserved in these collisions. As it was recently shown (experimentally), quadratic patches may be thought of as a limit of many line-shaped patterns coming together during a relaxation [38].

2.3. Our Main Problem: Small Perturbation of the Maximal Stable State

Let us formalize the observations in Figure 1 in the following way. Let Ω be a non-degenerate compact domain with non-empty interior and P be a finite non-empty subset of Ω. For each N ∈ ℕ consider a set ${\Gamma }_N=\Omega \cap \frac{1}{N}{\mathbb{Z}}^2$, i.e., the intersection of Ω with the lattice of mesh $\frac{1}{N}$. Define the state ${\phi }_N={(3+\sum _{p\in P}{\delta }_p)}^{°}$ on Γ_N, i.e., we put three grains everywhere on Γ_N and dropped one additional grain to each of the points p ∈ P or to a near vertex in Γ_N if p ∉ Γ_N, and then we performed a relaxation. Define the deviation set

$C_N=\{v\in {\Gamma }_N|{\phi }_N(v)<3\}\subset \Omega .$

Experimental evidence suggests that when N grows, the sets C_N ⊂ Ω converge to a thin balanced graph (see Figure 1).

Theorem 1. announced in [33] and proven in [33–35] The sequence of sets C_N ⊂ Ω converges (in the Hausdorff sense) to a set ${\tilde{C}}_{\Omega ,P}.$ The set ${\tilde{C}}_{\Omega ,P}$ is a planar graph passing through the points P. Each edge of ${\tilde{C}}_{\Omega ,P}$ is a straight segment with a rational slope.

At least in this setting, we have proven that the limiting/asymptotic patterns exist, though there is no close description of the shape and exact amount of grains for the pattern in the direction (p, q) ∈ ℤ².

More intricate instances of the line-shaped patterns, namely, in the identity element of the sandpile group of Ω, await an explanation. Recall that the recurrent states of a sandpile model on a given graph form an Abelian group, the sandpile group of a graph [19, 39]. In Figure 3, the identity of the sandpile group for a cylinder consists of linear-shaped patterns. In Figure 4, we see similar patterns (along with quadratic patches) on the identity of the sandpile group for a non-convex domain. It has not yet been mathematically proven that the sandpile identity of such graphs indeed contains these linear patterns. A remarkably simple pattern for the identity on a circular base was found by Melchionna [40] [see Figures 7, 10 in [40]], the sandpile identity on ellipses of certain type consists of a unique pattern, up to “linear defects.”

FIGURE 3

Figure 3. The identity of the sandpile group on a skewed cylinder is presented, that is, we took the standard lattice in the rectangle [0, 200] × [0, 12] and identified each point (x, 0) with (x + 5, 12) for x ∈ [0, 195]. Let sinks be the vertices with less than four neighbors. The picture presents the identity of the sandpile group of this graph. White is three, green is two, red is one, and blue is zero. If we would take a flat cylinder, i.e., we would identify (x, 0) with (x, 12), then, in the picture for the identity of the sandpile group, we would have 3 everywhere except several green vertical lines, i.e., columns with two grains.

FIGURE 4

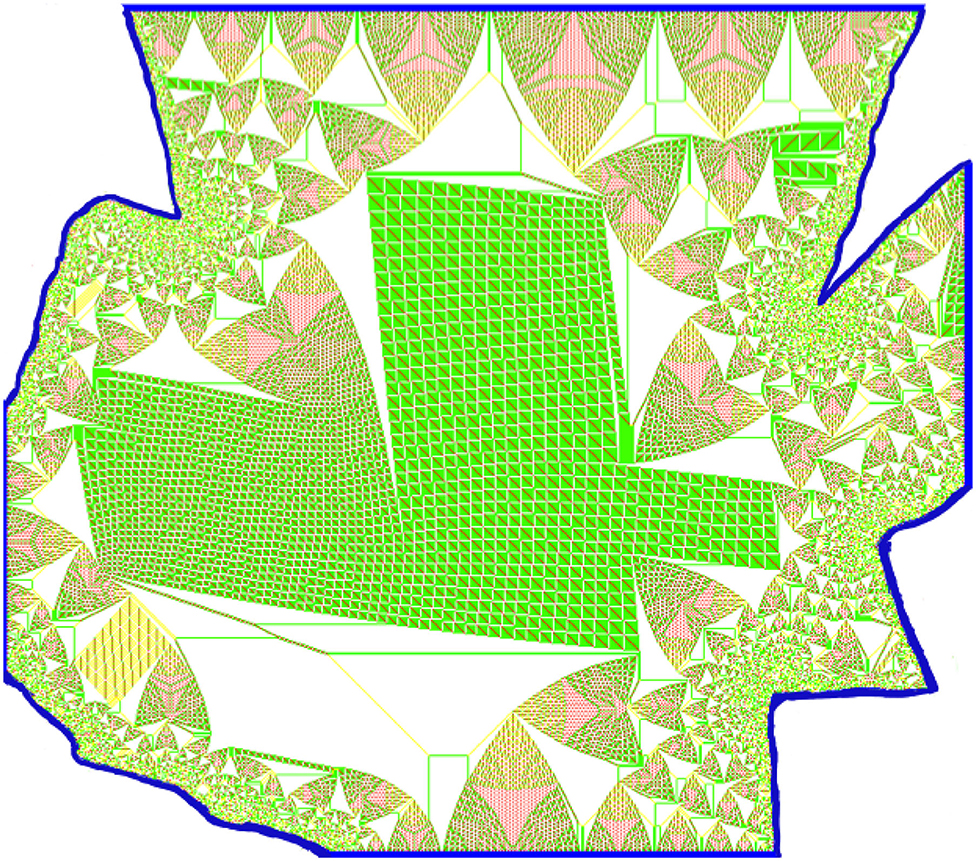
Figure 4. The blue points mark the sinks. The identity of the remaining part of the lattice is presented. Note the presence of the linear patterns, the same as in the previous pictures. Colors are the same as in Figure 1.

In the further text we briefly explain the main ideas behind the proof of Theorem 2. All the details of the actual proofs, exact notation, omitted conditions, etc., can be found in Kalinin and Shkolnikov [33–35]. We believe that our tools are worth generalizing for other situations and can be used to prove the aforementioned appearance of linear patterns in different setups.

3. Discrete Harmonic Analysis

The laplacian ΔF of a function F : ℤ² → ℤ is defined as

$\begin{array}{l}(\Delta F)(i,j)=-4F(i,j)+F(i+1,j)+F(i-1,j)+F(i,j+1)\\ +F(i,j-1).\end{array}$

A function F : Γ → ℤ is harmonic (resp., superharmonic) if ΔF = 0 (resp., ΔF ≤ 0) at every point of Γ ⊂ ℤ² where ΔF is defined. Recall the Liouville theorem: a non-negative harmonic function on ℤ² must be a constant (for several proofs see Theorem 9.24 in [41]).

Assume that Γ is an intersection of a big convex subset Ω ⊂ ℝ² with ℤ². Fix an arbitrary linear function L : ℤ² → ℤ. The following lemmata are close in spirit to Buhovsky et al. [42] where an improvement of the Liouville theorem is presented.

Lemma 1. A positive integer-valued harmonic function F which is less than L on a large enough subdomain Γ′ of Γ, is linear itself on a (smaller, but still large) subdomain Γ″ of Γ′, i.e., there exists Γ″ ⊂ Γ′ such that

$F(x,y){|}_{{\Gamma }^{″}}=ix+jy+a_{ij},\text{where }i,j,a_{ij}\in \mathbb{Z}.$

Lemma 2. Fix a constant c > 0. Consider a positive integer-valued superharmonic function F such that the sum of its laplacian at points in Γ′ ⊂ Γ linearly depends on the diameter of Γ′ with an a priori bound c, i.e.,

${\displaystyle \sum _{v\in {\Gamma }^{\prime }}}\Delta F(v)<c·diam({\Gamma }^{\prime }).$

Then, if F is less than L and the domain is large enough then F is linear itself on a large subdomain Γ″ ⊂ Γ′.

In other words, given an upper estimate of a natural-valued function F by a linear function L, we may deduce that F is linear on a large subdomain provided F is harmonic or almost harmonic. Precise formulations can be found in Kalinin and Shkolnikov [34]. The two main ideas used in the proofs are as follows.

• The green function (harmonic at all points except one) on the plane grows as the logarithm.

• For a positive discrete harmonic function F on a ball of radius R with the center O, the discrete derivative of F at O (i.e., F(O) − F(O′) for a neighbor O′ of O) is at most the maximum of F on the ball, divided by R. If F has only integer values, then |F(O) − F(O′)| <1 implies that F(O) = F(O′).

We conjecture that the line-shaped patterns show up in the relaxation of a perturbation of the maximal stable state in the sandpile model on a certain graph, if there is a notion of a linear function on such a graph and both lemmata above hold. To perform a “scaling” one needs a graph that is self-similar on different scales, such as ℤ². A natural candidate is a Cayley graph of a group.

Recall that given a group G and a set S of its generators, one may construct the so-called Cayley graph of G, whose vertices are elements of G and two vertices u, v ∈ G are connected by an edge if u⁻¹v or v⁻¹u belongs to S. If G = ℤ², S = {(1, 0), (0, 1)}, then the Cayley graph is the standard grid ℤ² with all vertices of valency four. If G = ℤ², S = {(1, 0), (0, 1), (1, 1)} then the Cayley graph is ℤ² and each vertex (i, j) is connected by edges to (i ± 1, j), (i, j ± 1), (i + 1, j + 1), (i − 1, j − 1).

On a Cayley graph, the generators of the group play the role of coordinates [modulo relations, as (1, 0) + (0, 1) = (1, 1) in the example above] so the notion of a linear function can be easily extended. The discrete harmonic function theory is quite developed for several classes of groups [43–46].

Question. Do Lemmata 1,2 hold for the harmonic and superharmonic functions on Cayley graphs of amenable groups? If yes, then, under an appropriately chosen scaling procedure, one should be able to prove convergence of the deviation sets of the relaxations of a slightly perturbed maximal stable states (on a big bounded polygonal-shaped part of the Cayley graph) to the corner locus of a piecewise linear function on the scaling limit of these polygonal shaped parts of the Cayley graphs. The first thing to prove is that the toppling function has a piecewise linear estimate from above.

The Cayley graphs of abelian groups are composed of ℤ^k and cylinders as in Figure 3. The simplest non-abelian group, which is not much different from ℤ³, is the Heisenberg group.

Question. Are there any patterns in the sandpile for the Cayley graph of the Heisenberg group H?

$H=\{H_{a,b,c}|a,b,c\in \mathbb{Z}\}\text{ where }{H}_{a,b,c}=\left(\begin{array}{ccc}1& a& b\\ 0& 1& c\\ 0& 0& 1\end{array}\right).$

Two generators H_1,0,0, H_0,1,0 of the group commute; the Cayley graph of H therefore looks like a collection of standard lattices ℤ² with additional edges corresponding to the third generator H_0,0,1. Consider the intersection of this Cayley graph with a large cube, e.g., let Γ = {H_a,b,c|0 ≤ a,b,c ≤ 100}. Then, all vertices v ∈ Γ have a valency of six, since they are connected to v · H_±1,0,0, v · H_0,±1,0, v · H_0,0,±1, and all the vertices of ℤ³ outside of Γ are treated as sinks.

Consider a maximal stable state (i.e., 5 grains at every vertex) and add one grain to several vertices. One expects that the relaxation of such a state on Γ should be not a very complicated “extension” of a relaxation of a perturbation of the maximal stable sandpile on domains in ℤ².

4. Tropical Curves

A tropical polynomial is a piecewise linear function f : ℝ² → ℝ of the form

$f(x,y)=min\{ix+jy+a_{ij}|(i,j)\in A\},$

where A is a finite subset of ℤ² and a_ij ∈ ℝ are coefficients. Each term ix + jy + a_ij is called a monomial and should be thought of $log(t^{a_{ij}}{x}^i{y}^j)$, f should be thought of the limit of a certain logarithmic rescaling of

$f_t(x,y)={\displaystyle \sum _{(i,j)\in A}}{t}^{a_{ij}}{x}^i{y}^j.$

To each tropical polynomial f there is a corresponding tropical curve C(f), which, by definition, is the corner locus of f, i.e., the set of points (x, y) where f is not smooth. An equivalent definition follows.

Definition 3. C(f) = {(x, y) ∈ ℝ|the minimum among ix + jy + a_ij is attainedat least twice}.

More on algebra-geometric aspects of tropical curves can be found in Brugallé et al. [47], Itenberg and Mikhalkin [48], and Maclagan and Sturmfels [49] along with recent applications in symplectic topology [50–53]. In this set-up, tropical curves should be thought of Riemann surfaces, and each vertex A of a tropical curve corresponds to a small surface S_A with the boundary, the valency of A is equal to the number of the boundary components of S_A, and each edge AB of the tropical curve corresponds to a very long thin cylinder connecting small surfaces S_A and S_B. Unfortunately, we found no connection between tropical curves in sandpiles and tropical curves in algebraic or symplectic geometry.

4.1. Tropical Series

Pick a convex compact set Ω ⊂ ℝ² with non-empty interior. Let P be a finite subset of Ω.

Definition 4. Kalinin and Shkolnikov [35] an Ω-tropical series is a piecewise linear function in Ω given by the following:

$\begin{array}{ll}F(x,y)={\displaystyle \underset{(i,j)\in {A}}{inf}}(a_{ij}+ix+jy),& (1)\end{array}$

where the set ${A}$ is not necessarily finite and F|_∂Ω = 0. See an example in Figure 5.

FIGURE 5

Figure 5. An Ω-tropical series and the corresponding Ω-tropical curve.

Consider the family ${{F}}_P$ of Ω-tropical series that are not smooth at every point of P.

Note that all functions in ${{F}}_P$ are concave and thus superharmonic. Let F_P be the pointwise minimum of functions in ${{F}}_P$. In Kalinin and Shkolnikov [35] it is proven that this pointwise minimum exists (that is easy) and belongs to ${{F}}_P$ (a bit more involved, because it may be not continuous or not a tropical series).

For each $F\in {{F}}_P$ we may consider the set

$C(F)=\{(x,y)\in \Omega |(\Delta F)(x,y)\ne 0\}.$

It is easy to see that C(F) is the corner locus of the function F, i.e., exactly those points where F is not linear but changes its slope. The set C(F) is called the Ω-tropical curve defined by F, and C(F) is a planar graph with straight edges of rational directions, the sum of directions of outgoing edges is zero for every vertex, and this is called the balancing condition.

Theorem 2. (elaboration) The sequence of sets C_N ⊂ Ω converges (in the Hausdorff sense) to the Ω-tropical curve C(F_P).

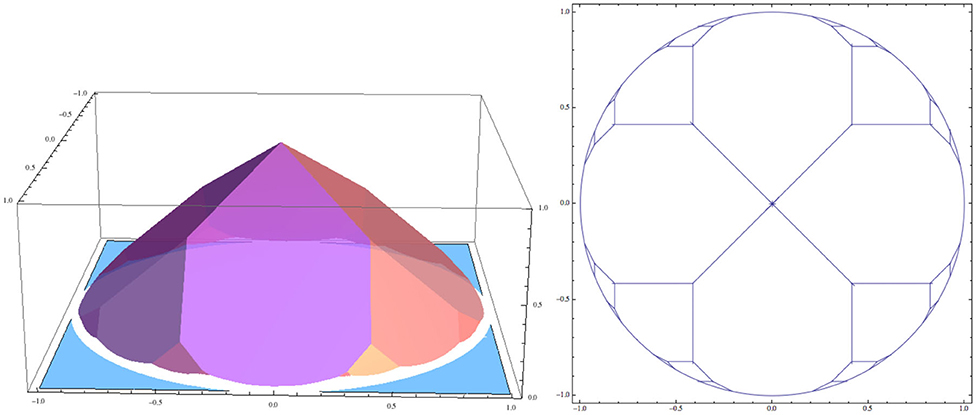
Let Ω be a disk {x² + y² ≤ 1}. An example of an Ω-tropical series is $min\left\{ix+jy+a_{ij}|(i,j)\in {\mathbb{Z}}^2\right\}$ with $\left|a_{ij}\right|=\sqrt{i^2+j^2}$ is presented on the left in Figure 5, and its corresponding Ω-tropical curve, which is an infinitely branching tree, is presented on the right. See details in Kalinin and Shkolnikov [54].

Question. The sum of the values of the above Ω-tropical series for a circle (or other plane curve) gives interesting formulae in number theory [54] which are related to Mordell-Tornheim and Witten zeta functions [55, 56]. These formulae take as input the coefficients of the equations of the tangent lines to a given plane curve, and they are thus easy to compute and may provoke interesting questions in the experimental computer mathematics. However, no analogs of these formulae for three dimensional bodies are known.

5. Toppling Function

To understand the appearance of tropical geometry in sandpiles, consider the toppling function H(v) defined for every v in Γ_N as follows: given an initial state φ on Γ and its relaxation φ°, the value H(v) equals the number of times that the vertex v toppled in the process taking φ to φ°.

The toppling function is clearly non-negative on Γ and vanishes at the boundary of Γ. The Laplacian ΔH of H completely determines the final state φ° by the formula [22]:

$\begin{array}{ll}{\phi }^{\circ }(v)=\phi (v)+\Delta H(v).& (2)\end{array}$

It can be shown by induction that the toppling function H satisfies the Least Action Principle [57, 58]: if φ(v) + ΔF(v) ≤ 3 is stable, then F(v) ≥ H(v). Ostojic noticed that H(i, j) is a piecewise quadratic function if we drop a lot of sand in the origin of the otherwise empty plane [22].

5.1. Piecewise Linearity of the Toppling Function in Our Main Problem

Consider a state φ_P, which consists of three grains of sand at every vertex, except at a finite family of points P = {p₁, …, p_r} where we have four grains of sand:

$\begin{array}{ll}\phi :=\langle 3\rangle +{\delta }_{p_1}+\cdots +{\delta }_{p_r}=\langle 3\rangle +{\delta }_P.& (3)\end{array}$

The state φ° and the evolution of the relaxation can be described by means of tropical geometry. This was discovered in Caracciolo et al. [29]. The crucial (experimental) observation is that the toppling function H of the state φ is almost harmonic everywhere since φ° = φ almost everywhere (see Figure 1). Even better, in this case the toppling function H is piecewise linear on the most part of Ω and the line-shaped patterns belong to a finite neighborhood of the corner locus of H (in the next section we give a more detailed statement). It is easy to observe but tricky to prove.

We provide an upper bound H_u and a lower bound H_l for H, which are close to H. These tight bounds force the set

$\{v\in \Gamma |\phi (v)+\Delta H_u(v)\ne 3\}$

to belong to a small neighborhood of the set

$\{v\in \Gamma |\phi (v)+\Delta H(v)\ne 3\}.$

The upper bound H_u is a piece-wise linear function, φ is equal to 3 everywhere except a small set P of points, the laplacian of a function is zero on the domains of its linearity. The set ΔH_u(v) ≠ 0 (the corner locus of a piece-wise linear function) is thus close to the set ΔH ≠ 0, the deviation locus of φ°. This concludes the proof of the theorem.

5.2. Upper Bound for the Toppling Function

Denote by H(φ_N) the toppling function of the state φ_N = 〈3〉 + ∑δ_pi on Γ_N. Abusing notation we will write $H(x,y)=\frac{1}{N}H({\phi }_N)(x,y):\Omega \to ℝ$ for the rescaled toppling function without specifying N. Consider the pointwise minimal function F_P in ${{F}}_P$. Then F_P ≥ H(φ_N) by the Least Action Principle (since ΔF_P ≤ 0, ΔF_P(p_i) < 0 for each i). Thus, F_P ≥ H.

Corollary. The total defect $\sum _{v\in {\Gamma }_N}(3-{\phi }^{°}(v))$ grows linearly in N.

Indeed, the total defect is equal to the amount of the sand fallen outside of the system, which, in turn, is equal to the sum of H(φ_N) near the boundary, which can be estimated as $N·{\int }_{\partial {\Omega }_{1/N}}N{F}_P$, i.e., N times the integral of F_P over the 1/N-neighborhood of the boundary of Ω.

In order to study the dependence of the deviation set {φ ° ≠3} on Ω and P (positions of points where we added grains), one may study F_P because it determines the tropical curve. The dependence of F_P on P is in no sense continuous: when P passes through degenerate configurations (e.g., several points on a vertical line), F_P and the corresponding tropical curve drastically change. Similar phenomenon appears when we keep P fixed and change Ω: no meaningful results about stability of the resulting picture are known.

6. Lower Bound. Wave Operators

Let φ be a sandpile state on a graph Γ. Given a fixed vertex p ∈ Γ, we define the wave operator W_p acting on a sandpile state φ as the following:

$W_p(\phi ):={(T_p(\phi +{\delta }_p)-{\delta }_p)}^{\circ },$

where T_p is the operator that topples once the state φ at p if it is possible ([59–61]) (see Figure 6). In a computer simulation, the application of this operator looks like one wave of topplings spreading from p, while each vertex topples at most once.

FIGURE 6

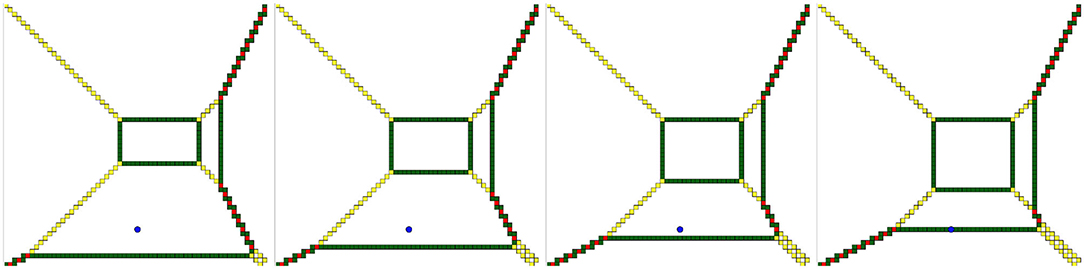
Figure 6. For a given sandpile state we apply several times the wave operator at the blue point p. One can see that the line-shaped pattern around p point creeps toward p until it belongs to one on them. Recall that white cells contain 3 grains, so the deviation set is the green, yellow, and red cells, which belong to a small neighborhood of a certain tropical curve. Let us present this tropical curve as a corner locus of a pointwise minimum of several linear functions (cf. Figure 5), i.e., as an Ω-tropical series F. The planar graph is then the projection of edges of a three-dimensional polytope (the graph of F). Then the action of the wave operator corresponds to shifting one of the faces of this polytope, i.e., increasing by one the constant coefficient of the linear function, defining this face. On the level of planar graphs, we take the linear function in F (see Equation 1), which is the minimal at p, and increase its constant coefficient until p belongs to the corner locus of the new piecewise linear function.

The first important property of W_p is that, for the initial state φ: = 〈3〉 + δ_P, we can achieve the final state φ° by successive applications of the operator W_p1 ° ⋯ ° W_pr a large but finite number of times (we write ∞ in spite of the notation):

${\phi }^{\circ }={(W_{p_1}\cdots W_{p_r})}^{\infty }\phi +{\delta }_P.$

This is not a deep theorem but a rather useful description of a relaxation. We thus decompose the total relaxation φ ↦ φ° into layers of controlled avalanching

$\phi \to W_{p_1}^{k_1}\phi ={\phi }_1\to W_{p_2}^{k_2}{\phi }_1\to \dots$

These layers, in turn, can be described by means of tropical geometry. We only need to prove that the linear-shaped patterns, visible in the pictures, move toward the point where we apply a wave operator.

6.1. Construction of Solitons

For each direction (p, q) ∈ ℤ², gcd(p, q) = 1 we construct a function F_{p, q} whose laplacian coincides with the linear pattern in the direction (p, q). To do that, consider a function

$\tilde{F}:{\mathbb{Z}}^2\to \mathbb{Z},\tilde{F}(x,y)=min(0,qx-py).$

Note that the corner locus l (the set of points in ℝ² where min(0, qx − py) is not smooth) of $\tilde{F}$ is a line of direction (p, q). Next, consider all the integer-valued superharmonic functions on ℤ², which coincide with $\tilde{F}$ outside of a finite neighborhood of l. A non-trivial fact is that there exists a pointwise minimum F_p,q among this family of functions [34].

The idea of the proof is as follows: instead of taking the pointwise minimum at once, we first prove that we can achieve it by “smoothings,” namely, by a sequence of steps $\tilde{F}=F_0\to F_1\to F_2\to \dots$; in each step F_k → F_k+1 we subtract the characteristic function of a certain set in a finite neighborhood of l (thus, a kind of inverse operator to the wave operator) and 0 ≤ F_k − F_k+1 ≤ 1. Then, since $\tilde{F}$ is periodic, we may factor the plane by the action of the vector (p, q) and reduce the problem to a cylinder.

Then we use lemmata about superharmonic functions: if it would be possible to perform smoothings an infinite number of times, then Lemma 1 would imply that F_k is linear with integer slope in a compact neighborhood of l, hence there exists a linear function with integer slope which is less than $\tilde{F}$ only on a finite neighborhood of the corner locus. This function would be periodic with respect to the shift on (p, q) and would therefore be like k(qx − py)+c (since gcd(p, q) = 1), but any such function (with an integer k) is less than $\tilde{F}$ outside of a finite neighborhood of l, which is a contradiction. Then we cannot perform smoothings an infinite number of times, and thus there is a pointwise minimum in the aforementioned family.

Once proved that the pointwise minimum exists, we may define solitons.

Definition 4. A soliton [a linear-shaped pattern in the direction (p, q)] is φ_pq = 〈3〉 + ΔF_p,q.

Then, from the Least Action principle and the minimality of F_p,q it easily follows that sending a wave from one side of the deviation set of φ_pq translates it [i.e., for certain p′, q′ we have $W_x{\phi }_{pq}(i,j)={\phi }_{pq}(i+p^{\prime },j+q^{\prime })$ for all (i, j)], otherwise not changing. This is why we call them solitons.

The same can be done for three solitons of direction (p₁, q₁), (p₂, q₂), (p₃, q₃), meeting at a point, provided that ∑p_i = ∑q_i = 0 and the triangle (p₁, q₁), (p₂, q₂), (p₃, q₃) does not contain lattice points except vertices. The ideas of the proof are the same, we use Lemma 2 and the final step is that if a linear function px + qy is less than min(p₁y − q₁x, p₂y − q₂x, p₃y − q₃x) only in a compact neighborhood of the apex of the latter function, then (p, q) ∈ ℤ² must belong to the triangle (p₁, −q₁), (p₂, −q₂), (p₃, −q₃), which is a contradiction.

We summarize the results as follows: there are certain functions f_p,q,… (“at infinity” being described by piecewise functions, i.e., tropical functions), pointwise minimal in special families of superharmonic functions, such that 〈3〉 + Δf_{p, q, …} models solitons, and three or four solitons coming to a point.

The crucial property of the wave operator W_p is that its action on a state φ = 〈3〉 + Δf_p,q,… has an interpretation in terms of tropical geometry; see the next section.

6.2. Tropical Wave Operators and the Lower Bound

Whenever, “at infinity” f is a piecewise linear function with integral slopes that, in a neighborhood of p, is expressed as a_i0j0 + i₀x + j₀y, then

$W_p(\langle 3\rangle +\Delta f)=\langle 3\rangle +\Delta W(f),$

where W(f), another piece-wise linear “at infinity” function, has the same coefficients a_ij as f, except one, namely $a_{i_0{j}_0}^{\prime }=a_{i_0{j}_0}+1$. This is to emulate the fact that the support of the wave (the set of vertices that toppled during the wave) is exactly the part of the plane where a_i0j0 + i₀x + j₀y is the leading part of f.

Consider an Ω-tropical series f. We will write $G_p:=W_p^{\infty }$ to denote the operator that “applies W_p to 〈3〉 + Δf until p lies in the corner locus of f”; i.e., G_p increases the coefficient a_ij, corresponding to a neighborhood of p, by lifting the plane lying above p in the graph of f by integral steps until p belongs to the corner locus of G_pf. Thus, G_p has the effect of pushing the tropical curve closer toward p until it contains p (see Figure 6).

From the properties of the wave operators, it follows immediately that (recall that F_P is the upper bound):

$F_P={(G_{p_1}\cdots G_{p_r})}^{\infty }0,$

where 0 is the function which is identically zero on Ω.

Now we are ready to provide a lower bound in the main theorem.

Note that the upper bound can be obtained by (possibly infinite) series of applying tropical wave operators (which are nothing else but repetitive increasing of coefficients on linear parts in a piecewise linear function). Then, by the properties of the solitons, this can be emulated in the sandpile model, where wave operators are performed on the sandpile level, and instead of piecewise linear functions we have pictures as in Figure 6.

In other words, we choose an approximation of F_P by a finite composition G_p1G_p2…  of tropical wave operators, and we then choose an N big enough before starting from a state on Γ_N with a tropical series and a collection of solitons, representing the corresponding Ω-tropical curve. Then we perform the sandpile wave operators W_p1W_p2…  as prescribed by tropical wave operators (see Figure 6). Since N is big enough we have full control on the picture and know that the solitons move exactly as edges of the tropical curve on the tropical pictures. By the nature of the construction, this will give us a lower bound for the relaxation of φ (constructed by the wave decomposition), which is close to the upper bound (given by an Ω-tropical series) with any prescribed accuracy. The deviation set of ${\phi }_N^{°}$ consequently converges to the Ω-tropical curve defined by F_P.

7. Discussion

We surveyed several mathematical tools which have been used for a concrete problem of sandpiles on a part of ℤ². These tools may be generalized in several directions. One may consider sandpiles on other graphs, e.g., parts of the Cayley graphs for amenable groups. Also, one can take a part of hyperbolic tessellation [62] or other tiling of the plane [63] and ask similar questions about patterns and rescaling procedures.

It seems that the only tool to describe explicitly the picture for the sandpile identity is to compute the toppling function with high precision and controlled error. Above, we explained that the “smoothing” procedure allows us to show that there exists a pointwise minimal function in certain classes of superharmonic functions, and certain localization techniques (tropical geometry) could then be applied based of the properties of harmonic or almost harmonic functions on big domains with an explicit linear upper bound.

Tropical series for planar domains are connected to certain zeta functions. It would be nice to (at least, experimentally) compute series, similar to Kalinin and Shkolnikov [54], for higher dimensions with a good precision and guess what kind of numbers (e.g., polynomials in π if we start with a round sphere) will be obtained.

It would be interesting to find another decomposition of a relaxation into waves of higher magnitude, i.e., such a decomposition will allow us to control the change of not only linear-shaped pattern but the quadratic patches too.

Similar to Sadhu and Dhar [32] it would be nice to run the same research, and in particular, to establish continuity properties for the toppling functions of sandpiles on Cayley graphs and see whether one can get a kind of balancing conditions out of that.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

NK was supported in part by Young Russian Mathematics award. Support from the Basic Research Program of the National Research University Higher School of Economics was gratefully acknowledged.

References

1. Thompson DW. On Growth and Form. Cambridge: Cambridge University Press (1942).

Google Scholar

2. Turing AM. The chemical basis of morphogenesis. Philos Trans R Soc Lond B Biol Sci. (1952) 237:37–72. doi: 10.1098/rstb.1952.0012

CrossRef Full Text | Google Scholar

3. Belousov BP. Periodicheski deistvuyushchaya reaktsia i ee mekhanism [Periodically acting reaction and its mechanism]. In: Sbornik Referatov po Radiotsionnoi Meditsine, 1958 [Collection of Abstracts on Radiation Medicine, 1958]. Moscow: Medgiz (1959). p. 145–7.

Google Scholar

4. Kiprijanov KS. Chaos and beauty in a beaker: the early history of the Belousov-Zhabotinsky reaction. Ann Phys. (2016) 528:233–7. doi: 10.1002/andp.201600025

CrossRef Full Text | Google Scholar

5. Ball P. Forging patterns and making waves from biology to geology: a commentary on Turing (1952) ‘the chemical basis of morphogenesis'. Philos Trans R Soc B Biol Sci. (2015) 370:20140218. doi: 10.1098/rstb.2014.0218

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Wolf YI, Katsnelson MI, Koonin EV. Physical foundations of biological complexity. Proc Natl Acad Sci USA. (2018) 115:E8678–87. doi: 10.1073/pnas.1807890115

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Cross MC, Hohenberg PC. Pattern formation outside of equilibrium. Rev Mod Phys. (1993) 65:851. doi: 10.1103/RevModPhys.65.851

CrossRef Full Text | Google Scholar

8. Koch A, Meinhardt H. Biological pattern formation: from basic mechanisms to complex structures. Rev Mod Phys. (1994) 66:1481. doi: 10.1103/RevModPhys.66.1481

CrossRef Full Text | Google Scholar

9. Von Neumann J. The general and logical theory of automata. In: Jeffress LA, editor. Cerebral Mechanisms in Behavior; The Hixon Symposium. Wiley (1951). p. 1–41.

Google Scholar

10. Ulam S. Random processes and transformations. In: Proceedings of the International Congress on Mathematics. Cambridge: Citeseer (1952). p. 264–75.

Google Scholar

11. Wolfram S. Cellular automata as models of complexity. Nature. (1984) 311:419–24. doi: 10.1038/311419a0

CrossRef Full Text | Google Scholar

12. Ermentrout GB, Edelstein-Keshet L. Cellular automata approaches to biological modeling. J Theor Biol. (1993) 160:97–133. doi: 10.1006/jtbi.1993.1007

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Bak P, Tang C, Wiesenfeld K. Self-organized criticality. Phys Rev A. (1988) 38:364. doi: 10.1103/PhysRevA.38.364

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Schelling TC. Micromotives and Macrobehavior. WW Norton & Company (2006). p. 252.

Google Scholar

15. Kondo S, Asai R. A reaction–diffusion wave on the skin of the marine angelfish pomacanthus. Nature. (1995) 376:765–8. doi: 10.1038/376765a0

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Fowler DR, Meinhardt H, Prusinkiewicz P. Modeling seashells. ACM SIGGRAPH Comput Graph. (1992) 26:379–87. doi: 10.1145/142920.134096

CrossRef Full Text | Google Scholar

17. Manukyan L, Montandon SA, Fofonjka A, Smirnov S, Milinkovitch MC. A living mesoscopic cellular automaton made of skin scales. Nature. (2017) 544:173–9. doi: 10.1038/nature22031

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Rietkerk M, Van de Koppel J. Regular pattern formation in real ecosystems. Trends Ecol Evol. (2008) 23:169–75. doi: 10.1016/j.tree.2007.10.013

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Dhar D. Self-organized critical state of sandpile automaton models. Phys Rev Lett. (1990) 64:1613–6. doi: 10.1103/PhysRevLett.64.1613

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Dhar D. Theoretical studies of self-organized criticality. Phys A. (2006) 369:29–70. doi: 10.1016/j.physa.2006.04.004

CrossRef Full Text | Google Scholar

21. Liu S, Kaplan T, Gray L. Geometry and dynamics of deterministic sand piles. Phys Rev A. (1990) 42:3207. doi: 10.1103/PhysRevA.42.3207

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Ostojic S. Patterns formed by addition of grains to only one site of an abelian sandpile. Phys A. (2003) 318:187–99. doi: 10.1016/S0378-4371(02)01426-7

CrossRef Full Text | Google Scholar

23. Pegden W, Smart CK. Convergence of the Abelian sandpile. Duke Math J. (2013) 162:627–42. doi: 10.1215/00127094-2079677

CrossRef Full Text | Google Scholar

24. Pegden W, Smart CK. Stability of patterns in the abelian sandpile. Ann Henri Poinc. (2020) 21:1383–99. doi: 10.1007/s00023-020-00898-1

CrossRef Full Text | Google Scholar

25. Levine L, Pegden W, Smart CK. Apollonian structure in the Abelian sandpile. Geom Funct Anal. (2016) 26:306–36. doi: 10.1007/s00039-016-0358-7

CrossRef Full Text | Google Scholar

26. Levine L, Pegden W, Smart CK. The Apollonian structure of integer superharmonic matrices. Ann Math. (2017) 186:1–67. doi: 10.4007/annals.2017.186.1.1

CrossRef Full Text | Google Scholar

27. Dhar D, Sadhu T, Chandra S. Pattern formation in growing sandpiles. Europhys Lett. (2009) 85:48002. doi: 10.1209/0295-5075/85/48002

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Dhar D, Sadhu T. A sandpile model for proportionate growth. J Stat Mech Theory Exp. (2013) 2013:P11006. doi: 10.1088/1742-5468/2013/11/P11006

CrossRef Full Text | Google Scholar

29. Caracciolo S, Paoletti G, Sportiello A. Conservation laws for strings in the abelian sandpile model. Europhys Lett. (2010) 90:60003. doi: 10.1209/0295-5075/90/60003

CrossRef Full Text | Google Scholar

30. Caracciolo S, Paoletti G, Sportiello A. Deterministic abelian sandpile and square-triangle tilings. In: Combinatorial Methods in Topology and Algebra. Cham: Springer International Publishing (2015). p. 127–36. doi: 10.1007/978-3-319-20155-9_23

CrossRef Full Text | Google Scholar

31. Paoletti G. Deterministic Abelian sandpile models and patterns (Springer Theses), Springer, Cham, Switzerland (2014).

Google Scholar

32. Sadhu T, Dhar D. Pattern formation in fast-growing sandpiles. Phys Rev E. (2012) 85:021107. doi: 10.1103/PhysRevE.85.021107

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Kalinin N, Shkolnikov M. Tropical curves in sandpiles. Comptes Rendus Math. (2016) 354:125–30. doi: 10.1016/j.crma.2015.11.003

CrossRef Full Text | Google Scholar

34. Kalinin N, Shkolnikov M. Sandpile solitons via smoothing of superharmonic functions. (2017) arXiv[Preprint].arXiv:1711.04285. doi: 10.1007/s00220-020-03828-8

CrossRef Full Text | Google Scholar

35. Kalinin N, Shkolnikov M. Introduction to tropical series and wave dynamic on them. Discrete Contin Dyn Syst A. (2018) 38:2843–65. doi: 10.3934/dcds.2018120

CrossRef Full Text | Google Scholar

36. Kalinin N, Guzmán-Sáenz A, Prieto Y, Shkolnikov M, Kalinina V, Lupercio E. Self-organized criticality and pattern emergence through the lens of tropical geometry. Proc Natl Acad Sci USA. (2018) 115:E8135–42. doi: 10.1073/pnas.1805847115

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Kalinin N, Prieto Y. Statistics for tropical sandpile model. (2015) arXiv[Preprint].arXiv:1906.02802.

Google Scholar

38. Lang M, Shkolnikov M. Harmonic dynamics of the abelian sandpile. Proc Natl Acad Sci USA. (2019) 116:2821–30. doi: 10.1073/pnas.1812015116

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Creutz M. Abelian sandpiles. Comput Phys. (1991) 5:198–203. doi: 10.1063/1.168408

CrossRef Full Text | Google Scholar

40. Melchionna A. The sandpile identity element on an ellipse. (2020) arXiv[Prerpint].arXiv:2007.0579.

Google Scholar

41. Lyons R, Peres Y. Probability on Trees and Networks, Vol. 42. Cambridge: Cambridge University Press (2017).

Google Scholar

42. Buhovsky L, Logunov A, Malinnikova E, Sodin M. A discrete harmonic function bounded on a large portion of z² is constant. (2017) arXiv[Preprint].arXiv:1712.07902.

Google Scholar

43. Hua B, Jost J, Li-Jost X. Polynomial growth harmonic functions on finitely generated abelian groups. Ann Glob Anal Geom. (2013) 44:417–32. doi: 10.1007/s10455-013-9374-0

CrossRef Full Text | Google Scholar

44. Meyerovitch T, Perl I, Tointon M, Yadin A. Polynomials and harmonic functions on discrete groups. Trans Am Math Soc. (2017) 369:2205–29. doi: 10.1090/tran/7050

CrossRef Full Text | Google Scholar

45. Meyerovitch T, Yadin A. Harmonic functions of linear growth on solvable groups. Israel J Math. (2016) 216:149–80. doi: 10.1007/s11856-016-1406-6

CrossRef Full Text | Google Scholar

46. Benjamini I, Duminil-Copin H, Kozma G, Yadin A. Minimal growth harmonic functions on lamplighter groups. (2016) arXiv[Preprint].arXiv:1607.00753.

Google Scholar

47. Brugallé E, Itenberg I, Mikhalkin G, Shaw K. Brief introduction to tropical geometry. In: Proceedings of the Gökova Geometry-Topology Conference (GGT), Gökova (2015). p. 1–75.

Google Scholar

48. Itenberg I, Mikhalkin G. Geometry in the tropical limit. Math Semesterb. (2012) 59:57–73. doi: 10.1007/s00591-011-0097-7

CrossRef Full Text | Google Scholar

49. Maclagan D, Sturmfels B. Introduction to Tropical Geometry, Graduate Studies in Mathematics, Vol. 161. Providence, RI: American Mathematical Society (2015).

Google Scholar

50. Matessi D. Lagrangian pairs of pants. Int Math Res Notices. (2018) rnz126. doi: 10.1093/imrn/rnz126

CrossRef Full Text | Google Scholar

51. Sheridan N, Smith I. Lagrangian cobordism and tropical curves. (2018) arXiv.[Preprint].arXiv:1805.07924.

Google Scholar

52. Mikhalkin G. Examples of tropical-to-Lagrangian correspondence. Eur J Math. (2018) 5:1033–66. doi: 10.1007/s40879-019-00319-6

CrossRef Full Text | Google Scholar

53. Hicks J. Tropical lagrangians and homological mirror symmetry. (2019) arXiv[Preprint].arXiv:1904.06005.

Google Scholar

54. Kalinin N, Shkolnikov M. Tropical formulae for summation over a part of SL(2;ℤ). Eur J Math. (2019) 5:909–28. doi: 10.1007/s40879-018-0218-0

CrossRef Full Text | Google Scholar

55. Matsumoto K. On analytic continuation of various multiple zeta-functions. In: Surveys in Number Theory: Papers from the Millennial Conference on Number Theory. AK Peters; CRC Press (2002). p. 169.

Google Scholar

56. Romik D. On the number of n-dimensional representations of Su(3), the Bernoulli numbers, and the Witten zeta function. (2015) arXiv[Preprint].arXiv:1503.03776.

Google Scholar

57. Fey A, Levine L, Peres Y. Growth rates and explosions in sandpiles. J Stat Phys. (2010) 138:143–59. doi: 10.1007/s10955-009-9899-6

CrossRef Full Text | Google Scholar

58. Sadhu T, Dhar D. The effect of noise on patterns formed by growing sandpiles. J Stat Mech Theory Exp. (2011) 2011:P03001. doi: 10.1088/1742-5468/2011/03/P03001

CrossRef Full Text | Google Scholar

59. Ivashkevich EV, Ktitarev DV, Priezzhev VB. Waves of topplings in an Abelian sandpile. Phys A. (1994) 209:347–60. doi: 10.1016/0378-4371(94)90188-0

CrossRef Full Text | Google Scholar

60. Dhar D, Manna S. Inverse avalanches in the Abelian sandpile model. Phys Rev E. (1994) 49:2684. doi: 10.1103/PhysRevE.49.2684

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Ktitarev D, Lübeck S, Grassberger P, Priezzhev V. Scaling of waves in the Bak-Tang-Wiesenfeld sandpile model. Phys Rev E. (2000) 61:81. doi: 10.1103/PhysRevE.61.81

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Kalinin N, Shkolnikov M. Sandpiles on the heptagonal tiling. J Knot Theory Ramif . (2016) 25:1642005. doi: 10.1142/S0218216516420050

CrossRef Full Text | Google Scholar

63. Fersula J, Noûs C, Perrot K. Sandpile toppling on penrose tilings: identity and isotropic dynamics. (2020) arXiv[Preprint].arXiv:2006.06254.

Google Scholar