Network Coherence in a Family of Book Graphs

1. Introduction

With the discovery of deterministic small-world [1] and scale-free [2] networks, deterministically growing network models have gained increasing attention because they can provide exact results for topology and dynamics. As a special type of deterministic networks, fractal networks constructed by fractal structures, such as Koch fractals [3], Sierpinski fractals [4], and Vicsek fractals [5], have been widely studied. Presently the main issues that require consideration in fractal networks include random walks [6–9], consensus dynamics [10, 11] and percolation [12]. It is proved that fractal networks are good candidate network models for verifying the results of random graphs.

Calculating the Laplacian spectrum of a network plays an important role in the study of network characteristics. For example, the Kirchhoff index and global mean first-passage time of a network are related to the sum of reciprocals of non-zero eigenvalues [13–15]. The synchronizability [16] of a network refers to the ratio of the second smallest eigenvalue to the largest eigenvalue of the Laplacian matrix. In addition, the effective graph resistance is connected with the Laplacian spectrum [17]. Recently, network coherence [10] was introduced to characterize the extent of consensus of coupled agents under the noisy circumstance and was determined by the Laplacian spectrum in an H₂ norm. This concept of the network coherence helps to study the relationship between the Laplacian eigenvalues and network consistency. Great progress has been made for some special networks such as Vicsek fractals [10], tree-like networks [11], Sierpiński graphs [18] and weighted networks [19]. Many works have been devoted to studying the network coherence. Hong et al. studied the role of Laplacian energy on the coherence in a family of tree-like networks with controlled initial states [20]. Patterson and Bamieh investigated the leader-follower coherence and proposed optimal algorithms to select the leaders [21]. Later, Sun et al. proposed a leader centrality to identify more influential spreaders using the optimal coherence [22].

It is known that the topology of a graph dominates the Laplacian eigenvalues [23]. Thus, calculating the Laplacian eigenvalues is a technical challenge and it is theoretical and practical interest to find new ways to calculate them. In this paper, a family of book graphs is chosen as our network models. The topological indices, e.g., randic index, sum connectivity index, geometric-arithmetic index, fourth atom-bond connectivity index, and edge labeling, have been analytically obtained [24, 25]. However, the dynamics of the book graphs remains less understood, in spite of the facts that studying the dynamical processes leads to a better understanding of how the underlying systems work.

The rest of this paper is organized as follows. Book graphs and network coherence are presented in section 2. Section 3 gives detailed calculations of network coherence. Conclusions are given in section 4.

2. Model Presentation and Network Coherence

2.1. Book Graphs

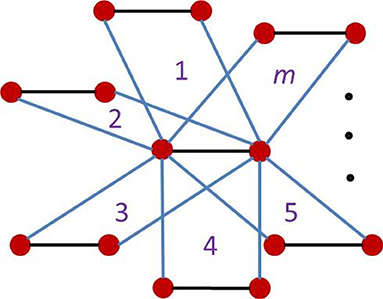
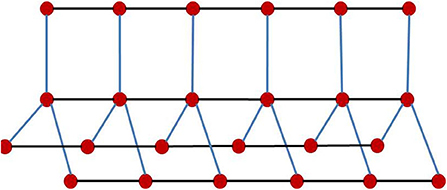
Book graphs B_m are defined as the graph Cartesian product [26], i.e., B_m = S_m+1□P₂, where S_m(m ≥ 1) is a star graph and P₂ is the path graph on two nodes, see Figure 1. The stacked book graphs B_m,n of order (m, n) are B_m,n = S_m+1□P_n, where P_n(n ≥ 2) is the path graph on n nodes, see Figure 2.

FIGURE 1

Figure 1. Book graphs B_m.

FIGURE 2

Figure 2. Stacked book graphs B_m,n with m = 3, n = 6.

2.2. Network Coherence

The network coherence was introduced to characterize the steady-state variance of the deviation from consensus. The relationship [10] between network coherence and Laplacian eigenvalues was established. The consensus dynamics with the additive noise are given by

$\begin{array}{l}\stackrel{\bullet }{x_i}(t)=-{\displaystyle \sum _{j\in {\Omega }_i}}{L}_{ij}{x}_j(t)+{\eta }_i(t),\end{array}$

where x_i(t) is the state of node i and subject to the stochastic noise η_i(t). L is the Laplacian matrix. Ω_i is the neighboring node set of node i, and η_i(t) is a delta-correlated Gaussian noise.

Then, the first-order network coherence is defined as the mean, steady-state variance of the deviation from the average of all node values, i.e.,

$\begin{array}{l}H:=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\displaystyle \underset{t\to \infty }{lim}}\text{var}\left\{x_i(t)-\frac{1}{N}{\displaystyle \sum _{j=1}^N}{x}_j(t)\right\},\end{array}$

where var is the expectation of the squared deviation of a random variable from its mean.

Let 0 = λ₁ < λ₂ ≤ … ≤ λ_N be the Laplacian eigenvalues. The network coherence is given by

$\begin{array}{ll}H=\frac{1}{2N}{\displaystyle \sum _{i=2}^N}\frac{1}{{\lambda }_i}.& (1)\end{array}$

When the network has a smaller variance, it has a higher network coherence, meaning that it is more robust to the noise.

3. Calculations of Network Coherence

In this section, we present the detailed calculations of the sum of reciprocals of the Laplacian eigenvalues and obtain exact expressions of network coherence. According to the structure of B_m,n, its Laplacian matrix reads as

$\begin{array}{l}{L}_{m,n}=\left(\begin{array}{cccccc}{L}_m+I_{m+1}& -I_{m+1}& 0& \cdots & 0& 0\\ -I_{m+1}& L_m+2I_{m+1}& -I_{m+1}& \cdots & 0& 0\\ 0& -I_{m+1}& L_m+2I_{m+1}& \cdots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & L_m+2I_{m+1}& -I_{m+1}\\ 0& 0& 0& \cdots & -I_{m+1}& L_m+I_{m+1}\end{array}\right),\end{array}$

where L_m is the Laplacian matrix of a star graph S_m, that is,

$L_m=\left(\begin{array}{cccc}m& -1& \cdots & -1\\ -1& 1& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮\\ -1& 0& \cdots & 1\end{array}\right).$

Then, we need to solve the characteristic equation L_m,nx = λx, which is given by

$\begin{array}{ll}\begin{array}{cccc}& (L_m+I_{m+1})x_1-I_{m+1}{x}_2& =& \lambda x_1,\\ -I_{m+1}{x}_1& +(L_m+2I_{m+1})x_2-I_{m+1}{x}_3& =& \lambda x_2,\\ & ⋮& ⋮& ⋮\\ & -I_{m+1}{x}_{n-1}+(L_m+I_{m+1})x_n& =& \lambda x_n,\end{array}& (2)\end{array}$

where $x={(x_1^{\text{T}},x_2^{\text{T}},\dots ,x_n^{\text{T}})}^{\text{T}}$ and the dimension of x_i(1 ≤ i ≤ n) is m + 1.

Suppose L_mx_i = λ_jx_i, i = 1, 2, …, n, where λ_j(j = 1, 2, …, m + 1) are the eigenvalues of L_m. Then, Equation (2) becomes

$\begin{array}{ll}\begin{array}{ccc}\left({\lambda }_j+1\right)x_1-x_2& =& \lambda x_1,\\ -x_1+\left({\lambda }_j+2\right)x_2-x_3& =& \lambda x_2,\\ ⋮⋮⋮& & \\ -x_{n-1}+({\lambda }_j+1)x_n& =& \lambda x_n.\end{array}& (3)\end{array}$

We then rewrite Equation (3) as

$\begin{array}{l}\left(R_n^j(\lambda )-{\lambda }_j\right)x_1=0,n\ge 2,\end{array}$

where

$\begin{array}{l}{R}_n^j(\lambda )=\lambda -1-\frac{1}{\lambda -({\lambda }_j+2)-\frac{1}{\lambda -({\lambda }_j+2)-\frac{1}{\cdots \lambda -({\lambda }_j+2)-\frac{1}{\lambda -({\lambda }_j+1)}}}}.\end{array}$

Further, we have

$\begin{array}{ll}{R}_n^j(\lambda )={\lambda }_j,j=1,2,\dots ,m+1.& (4)\end{array}$

We rewrite $R_n^j(\lambda )$ in a recursive form as

$\begin{array}{l}\{\begin{array}{l}{R}_n^j(\lambda )=\lambda -1-\frac{1}{R_{n-1}^j(\lambda )-\left({\lambda }_j+1\right)},\\ R_2^j(\lambda )=\lambda -1-\frac{1}{\lambda -({\lambda }_j+1)}=\frac{{\lambda }^2-(2+{\lambda }_j)\lambda +{\lambda }_j}{\lambda -({\lambda }_j+1)}.\end{array}\end{array}$

From Equation (4), each eigenvalue λ_j produces to n eigenvalues and B_m,n has n(m + 1) eigenvalues, denoted by ${\Lambda }_n=\left\{{\lambda }_i^n|1\le i\le n(m+1)\right\}={\Lambda }_n^1\cup {\Lambda }_n^2\dots \cup {\Lambda }_n^{m+1}$. For convenient calculations, we denote the smallest eigenvalues ${\lambda }_1^n=0$. In the following subsections, we divide λ_j into two cases: λ_j ≠ 0 and λ_j = 0 to obtain the network coherence.

3.1. When λ_j ≠ 0, j = 2, …, m + 1

Let $R_n^j(\lambda )=T_n^j(\lambda )/P_n^j(\lambda )$, where $T_n^j(\lambda )$ and $P_n^j(\lambda )$ are two polynomials satisfying $\text{gcd}\left[T_n^j(\lambda ),P_n^j(\lambda )\right]=1$, the term gcd is the greatest common divisor. Then, we obtain the following recursive relationships as

$\begin{array}{l}{T}_n^j(\lambda )=[T_{n-1}^j(\lambda )-\left({\lambda }_j+1\right)P_{n-1}^j(\lambda )]\lambda -T_{n-1}^j(\lambda )+{\lambda }_j{P}_{n-1}^j(\lambda ),\\ P_n^j(\lambda )=T_{n-1}^j(\lambda )-\left({\lambda }_j+1\right)P_{n-1}^j(\lambda ),& (5)\end{array}$

where the initial conditions are

$\begin{array}{l}{T}_2^j(\lambda )={\lambda }^2-(2+{\lambda }_j)\lambda +{\lambda }_j,\\ P_2^j(\lambda )=\lambda -({\lambda }_j+1).\end{array}$

From Equation (5), we have

$\begin{array}{ll}\{\begin{array}{l}{t}_n^j(0)=-t_{n-1}^j(0)+{\lambda }_j{p}_{n-1}^j(0),\\ p_n^j(0)=t_{n-1}^j(0)-\left({\lambda }_j+1\right)p_{n-1}^j(0).\end{array}& (6)\end{array}$

where $t_n^j(0)$ and $p_n^j(0)$ are the constant terms of $T_n^j(\lambda )$ and $P_n^j(\lambda )$.

It follows from Equation (6) that

$\begin{array}{ll}{p}_n^j(0)+\left({\lambda }_j+2\right)p_{n-1}^j(0)+p_{n-2}^j(0)=0.& (7)\end{array}$

Solving Equation (7) with initial conditions of $p_2^j(0)=-({\lambda }_j+1)$ and $p_3^j(0)={\lambda }_j^2+3{\lambda }_j+1$ yields

$\begin{array}{ll}{p}_n^j(0)=c_1^j{(r_1^j)}^g+c_2^j{(r_2^j)}^g,& (8)\end{array}$

where $r_1^j$ and $r_2^j$ are the roots of the characteristic equation ${\lambda }^2+({\lambda }_j+2)\lambda +1=0$. The constants $r_1^j,r_2^j,c_1^j$ and $c_2^j$ are

$\begin{array}{l}\{\begin{array}{l}{r}_1^j=\frac{-({\lambda }_j+2)+\sqrt{{\lambda }_j({\lambda }_j+4)}}{2},\\ r_2^j=\frac{-({\lambda }_j+2)-\sqrt{{\lambda }_j({\lambda }_j+4)}}{2},\\ c_1^j=\frac{1}{{(r_1^j)}^2-1}{\displaystyle \left[{({\lambda }_j)}^2+3{\lambda }_j+1+({\lambda }_j+1)r_2^j\right]},\\ c_2^j=\frac{1}{{(r_2^j)}^2-1}\left[{({\lambda }_j)}^2+3{\lambda }_j+1+({\lambda }_j+1)r_1^j\right].\end{array}\end{array}$

Substituting Equation (8) into Equation (6) yields

$\begin{array}{l}{t}_n^j(0)=-\left[c_1^j{(r_1^j)}^{n-2}\left(1+r_1^j\right)+c_2^j{(r_2^j)}^{n-2}\left(1+r_2^j\right)\right].\end{array}$

Next, we need to calculate the first-order terms $t_n^j(1),p_n^j(1)$ of $T_n^j(\lambda )$ and $P_n^j(\lambda )$. Using the relationship between $T_n^j(\lambda )$ and $P_n^j(\lambda )$ of Equation (5) gives

$\begin{array}{l}{t}_n^j(1)=t_{n-1}^j(0)-\left({\lambda }_j+1\right)p_{n-1}^j(0)-t_{n-1}^j(1)+{\lambda }_j{p}_{n-1}^j(1),\\ p_n^j(1)=t_{n-1}^j(1)-\left({\lambda }_j+1\right)p_{n-1}^j(1),\end{array}$

where the initial values are $t_2^j(1)=-({\lambda }_j+2),p_2^j(1)=1,p_3^j(1)=-(2{\lambda }_j+3)$. Then, we obtain

$\begin{array}{l}{t}_n^j(1)=\{e_j{(r_1^j)}^2+\left[n{g}_j+\left({\lambda }_j+1\right)e_j\right]r_1^j\\ +(n-1)\left({\lambda }_j+1\right)g_j\}{(r_1^j)}^{n-2}\\ +\{f_j{(r_2^j)}^2+\left[n{h}_j+\left({\lambda }_j+1\right)f_j\right]r_2^j\\ +(n-1)\left({\lambda }_j+1\right)h_j\}{(r_2^j)}^{n-2},\\ p_n^j(1)=e_j{(r_1^j)}^{n-1}+f_j{(r_2^j)}^{n-1}+(n-1)\left[g_j{(r_1^j)}^{n-2}+h_j{(r_2^j)}^{n-2}\right],\end{array}$

where

$\begin{array}{l}\{\begin{array}{l}{g}_j=-\frac{c_1^j\left[({\lambda }_j+2)r_1^j+1\right]}{2{(r_1^j)}^2+({\lambda }_j+2)r_1^j},\\ h_j=-\frac{c_2^j\left[({\lambda }_j+2)r_2^j+1\right]}{2{(r_2^j)}^2+({\lambda }_j+2)r_2^j},\\ e_j=\frac{[1-(g_j+h_j)]r_2^j+2(g_j{r}_1^j+h_j{r}_2^j)+(2{\lambda }_j+3)}{1-{(r_1^j)}^2},\\ f_j=\frac{[1-(g_j+h_j)]r_1^j+2(g_j{r}_1^j+h_j{r}_2^j)+(2{\lambda }_j+3)}{1-{(r_2^j)}^2}.\end{array}\end{array}$

We introduce a new polynomial as

$\begin{array}{l}{D}_n^j(\lambda )=T_n^j(\lambda )-{\lambda }_j{P}_n^j(\lambda ),\\ =\left(\lambda -{\lambda }_{(j-1)n+1}^n\right)\left(\lambda -{\lambda }_{(j-1)n+2}^n\right)\dots \left(\lambda -{\lambda }_{jn}^n\right).& (9)\end{array}$

Using the Vieta's formula [26, 27] for $D_n^j(\lambda )=0$, we obtain its constant and first-order terms, denoted by $d_n^j(0),d_n^j(1)$, that is,

$\begin{array}{ll}\{\begin{array}{l}{d}_n^j(0)=t_n^j(0)-{\lambda }_j{p}_n^j(0)\\ =-c_1^j{(r_1^j)}^{n-2}\left[1+\left(1+{\lambda }_j\right)r_1^j\right]\\ -c_2^j{(r_2^j)}^{n-2}\left[1+\left(1+{\lambda }_j\right)r_2^j\right],\\ d_n^j(1)=t_n^j(1)-{\lambda }_j{p}_g^j(1)\\ ={(r_1^j)}^{n-2}\left[e_j{(r_1^j)}^2+\left(n{g}_j+e_j\right)r_1^j+(n-1)g_j\right]\\ +{(r_2^j)}^{n-2}\left[f_j{(r_2^j)}^2+\left(n{h}_j+f_j\right)r_2^j+(n-1)h_j\right].\end{array}& (10)\end{array}$

3.2. When λ_j = 0

When λ_j = 0, $R_n^1(\lambda )=0$ has only one root ${\lambda }_1^n=0$. To obtain all the non-zero roots of $R_n^j(\lambda )=0$, we introduce a new polynomial, i.e.,

$\begin{array}{l}{Z}_n^1(\lambda )=\frac{1}{\lambda }{R}_n^1(\lambda ).\end{array}$

Further,

$\begin{array}{l}{T}_n^1(\lambda )=(\lambda -1)T_{n-1}^1(\lambda )-P_{n-1}^1(\lambda ),\\ P_n^1(\lambda )=\lambda T_{n-1}^1(\lambda )-P_{n-1}^1(\lambda ),\end{array}$

where the initial conditions are $T_2^1(\lambda )=\lambda -2,P_2^1(\lambda )=\lambda -1$. In the same way, we obtain the following coefficients, which are given by

$\begin{array}{l}\{\begin{array}{l}{t}_n^1(0)={(-1)}^{n-1}n,\\ t_n^1(1)={(-1)}^{n-2}·\frac{n(n^2-1)}{6},\end{array}\end{array}$

$\begin{array}{l}\{\begin{array}{l}{p}_n^1(0)={(-1)}^{n-2},\\ p_n^1(1)={(-1)}^{n-2}·\frac{n(n-1)}{2},\end{array}\end{array}$

It follows from Equation (9) that

$\begin{array}{ll}\{\begin{array}{lll}{d}_n^1(0)\hfill & =\hfill & {(-1)}^{n-1}{\lambda }_2^n{\lambda }_3^n\dots {\lambda }_n^n,\hfill \\ \hfill & =\hfill & {(-1)}^{n-1}n,\hfill \\ d_n^1(1)\hfill & =\hfill & {(-1)}^{n-2}[{\lambda }_3^n{\lambda }_4^n\dots {\lambda }_n^n+{\lambda }_2^n{\lambda }_4^n\dots {\lambda }_n^n+\dots \hfill \\ \hfill & +\hfill & {\lambda }_2^n{\lambda }_3^n\dots {\lambda }_{n-1}^n],\hfill \\ \hfill & =\hfill & {(-1)}^{n-2}·\frac{n(n^2-1)}{6}.\hfill \end{array}& (11)\end{array}$

3.3. Exact Solution of Network Coherence for B_m,n

We introduce a polynomial D_n(λ) to obtain the exact solution of the network coherence, i.e.,

$D_n(\lambda )={\displaystyle \prod _{j=1}^{m+1}}{D}_n^j(\lambda )={\displaystyle \prod _{i=2}^{n(m+1)}}(\lambda -{\lambda }_i^n).$

According to Equations (10) and (11), the constant and first-order terms of D_n(λ) are

$\begin{array}{l}{d}_n(0)={\displaystyle \prod _{j=1}^{m+1}}{d}_n^j(0),\\ d_n(1)={\displaystyle \underset{m+1}{{\displaystyle \underbrace{d_n^1(1)d_n^2(0)\dots d_n^{m+1}(0)}}}}\\ +{\displaystyle \underset{m+1}{{\displaystyle \underbrace{d_n^1(0)d_n^2(1)\dots d_n^{m+1}(0)}}}}+\dots +{\displaystyle \underset{m+1}{{\displaystyle \underbrace{d_n^1(0)d_n^2(0)\dots d_n^{m+1}(1)}}}}.\end{array}$

Based on the Vieta's theorem [26, 27], the network coherence reads as

$H=\frac{1}{2N}{\displaystyle \sum _{i=2}^N}\frac{1}{{\lambda }_i}=-\frac{1}{2N}\frac{d_n(1)}{d_n(0)}.$

When m = 3, the Laplacian matrix L_m has four eigenvalues, that is, λ₁ = 0, λ₂ = λ₃ = 1, λ₄ = 4. Using the above-mentioned calculations, we obtain the analytical expression of network coherence, i.e.,

$\begin{array}{l}{H}_{(n)}=\frac{1}{8n}\{\frac{n^2-1}{6}\\ -20\frac{[{\alpha }_1+g_2(n{r}_1^2+n-1)]{(r_1^2)}^{n-2}+[{\alpha }_2+h_2(n{r}_2^2+n-1)]{(r_2^2)}^{n-2}}{{\beta }_1{(r_1^2)}^{n-2}+{\beta }_2{(r_2^2)}^{n-2}}\\ -2\frac{[{\theta }_1+g_4(n{r}_1^4+n-1)]{(r_1^4)}^{n-2}+[{\theta }_2+h_4(n{r}_2^4+n-1)]{(r_2^4)}^{n-2}}{{\eta }_1{(r_1^4)}^{n-2}+{\eta }_2{(r_2^4)}^{n-2}}\},& (12)\end{array}$

where ${\alpha }_1=-\frac{5-2\sqrt{5}}{25}$, ${\alpha }_2=-\frac{5+2\sqrt{5}}{25}$, ${\beta }_1=15-7\sqrt{5}$,${\beta }_2=15+7\sqrt{5}$, ${\theta }_1=-\frac{10-7\sqrt{2}}{32}$, ${\theta }_2=-\frac{10+7\sqrt{2}}{32}$, ${\eta }_1=24-17\sqrt{2}$, ${\eta }_2=24+17\sqrt{2}$, $g_2=-\frac{(5-\sqrt{5})(3r_1^2+1))}{10r_1^2(2r_1^2+3)}$, $h_2=-\frac{(5+\sqrt{5})(3r_2^2+1))}{10r_2^2(2r_2^2+3)}$, $g_4=-\frac{(2-\sqrt{2})(6r_1^4+1))}{8r_1^4(r_1^4+3)}$, $h_4=-\frac{(2+\sqrt{2})(6r_2^4+1))}{8r_2^4(r_2^4+3)}$, $r_1^2=\frac{-3+\sqrt{5}}{2}$, $r_2^2=\frac{-3-\sqrt{5}}{2}$, $r_1^4=-3+2\sqrt{2}$, $r_2^4=-3-2\sqrt{2}$.

3.4. Exact Solution of Network Coherence for B_m

To investigate the effect of the parameters m on the network coherence, we propose another method to obtain the solution regarding the parameters m. When n = 2, the Laplacian matrix is

$\begin{array}{l}{L}_{m,2}=\left(\begin{array}{cc}{L}_m& -I_{m+1}\\ -I_{m+1}& L_m\end{array}\right).\end{array}$

Then, the characteristic polynomial P(λ) of L_{m, 2} is

$\begin{array}{l}\begin{array}{l}P(\lambda )={\displaystyle \left|\begin{array}{cc}\hfill L_m-\lambda I_{m+1}\hfill & \hfill -I_{m+1}\hfill \\ \hfill -I_{m+1}\hfill & \hfill L_m-\lambda I_{m+1}\hfill \end{array}\right|}\\ ={\displaystyle \left|\begin{array}{c}{L}_m-(\lambda +1)I\end{array}\right|}·{\displaystyle \left|\begin{array}{c}{L}_m-(\lambda -1)I\end{array}\right|}\\ =\lambda (\lambda -2)(\lambda -m-1)(\lambda -m-3){(\lambda -1)}^{m-1}{(\lambda -3)}^{m-1}.\end{array}\end{array}$

The roots of this polynomial P(λ) are as follows,

$\left\{0,2,m+1,m+3,{\displaystyle \underset{m-1}{{\displaystyle \underbrace{1,\dots ,1}}}},{\displaystyle \underset{m-1}{{\displaystyle \underbrace{3,\dots ,3}}}}\right\}.$

By the definition (1), we finally obtain the network coherence with regard to the parameters m, which is given by

$\begin{array}{ll}{H}_{(m)}=\frac{1}{4m+4}\left[\frac{1}{2}+\frac{1}{m+1}+\frac{1}{m+3}+\frac{4(m-1)}{3}\right].& (13)\end{array}$

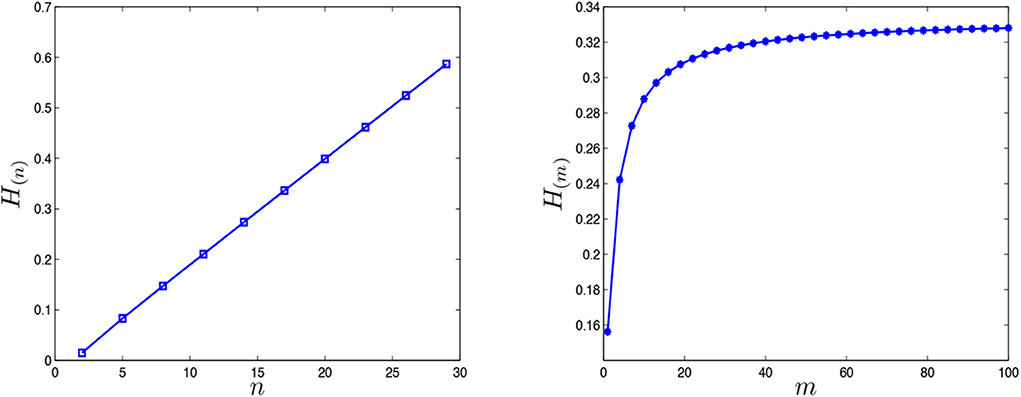
From the expressions (12) and (13), we plot the relationships between network coherence and the parameters m and n, see Figure 3. It shows that the values of network coherence linearly increase with n, while the network coherence will achieve a steady constant state for a large m, i.e., $H_{(m)}\to \frac{1}{3}$, meaning that the consensus displays worse with increasing values of n. In a word, the number of nodes n in the path graph has more influence than the number of nodes m in the star graph.

FIGURE 3

Figure 3. Network coherence regarding the parameters n and m.

4. Conclusions

In this paper, we have studied the consensus problems in noisy book graphs. Using the graph's constructions, we have obtained the recursive relationships for the Laplacian matrix and Laplacian eigenvalues and proposed a method to derive exact expressions of the sum of reciprocals of these eigenvalues. We then have presented exact solutions of network coherence with regard to graph parameters and investigated their effects on the coherence. It is shown that the larger size of star graphs results in better consensus, while the larger size of path graphs leads to worse consensus. The obtained results showed that the structure difference produces distinct performance on the coherence. Our method for the book graphs could be applied to study their random walks and Kirchhoff index.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

JC, YL, and WS contributed to the conception and design of the study. JC and YL performed the analytical and numerical results. JC and WS wrote the manuscript. All authors contributed to the manuscript revision, read, and approved the submitted version. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Zhejiang Provincial Natural Science Foundation of China (No. LY20F030007).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Comellas F, Ozon J, Peters JG. Deterministic small-world communication networks. Inf Process Lett. (2000) 76:83–90. doi: 10.1016/S0020-0190(00)00118-6

CrossRef Full Text | Google Scholar

2. Barabási AL, Ravasz E, Vicsek T. Deterministic scale-free networks. Phys A. (2001) 299:559–64. doi: 10.1016/S0378-4371(01)00369-7

CrossRef Full Text | Google Scholar

3. Dai MF, Li XY, Xi LF. Random walks on non-homogenous weighted Koch networks. Chaos. (2013) 23:033106. doi: 10.1063/1.4810927

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wang SJ, Yu ZY, Xi LF. Average geodesic distance of Sierpinski gasket and Sierpinski networks. Fractals. (2017) 25:1750044. doi: 10.1142/S0218348X1750044X

CrossRef Full Text | Google Scholar

5. Zhang ZZ, Wu B, Zhang HJ, Zhou SG, Guan JH, Wang ZG. Determining global mean-first-passage time of random walks on Vicsek fractals using eigenvalues of Laplacian matrices. Phys Rev E. (2010) 81:031118. doi: 10.1103/PhysRevE.81.031118

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Condamin S, Bénichou O, Tejedor V, Voituriez R, Klafter J. First-passage times in complex scale-invariant media. Nature. (2007) 450: 77–80. doi: 10.1038/nature06201

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Wu ZK, Hou BY, Zhang HJ, Jin F. Scaling of average weighted shortest path and average receiving time on weighted expanded Koch networks. Int J Mod Phys B. (2014) 28:1450111. doi: 10.1142/S0217979214501112

CrossRef Full Text | Google Scholar

8. Peng JH, Agliari E, Zhang ZZ. Exact calculations of first-passage properties on the pseudofractal scale-free web. Chaos. (2015) 25:073118. doi: 10.1063/1.4927085

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Peng JH, Agliari E. Exact results for the first-passage properties in a class of fractal networks. Chaos. (2019) 29:023105. doi: 10.1063/1.5080481

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Patterson S, Bamieh B. Consensus and coherence in fractal networks. IEEE Trans Control Netw Syst. (2014) 1:338–48. doi: 10.1109/TCNS.2014.2357552

CrossRef Full Text | Google Scholar

11. Sun WG, Ding QY, Zhang JY, Chen FY. Coherence in a family of tree networks with an application of Laplacian spectrum. Chaos. (2014) 24:043112. doi: 10.1063/1.4897568

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Balankin AS, Martinez-Cruz MA, Susarrey-Huerta O, Adame LD. Percolation on infinitely ramified fractal networks. Phys Lett A. (2018) 382:12–9. doi: 10.1016/j.physleta.2017.10.035

CrossRef Full Text | Google Scholar

13. Klein DJ and Randić M. Resistance distance. J Math Chem. (1993) 13:81–95. doi: 10.1007/BF01164627

CrossRef Full Text | Google Scholar

14. Bonchev D, Balaban AT, Liu X, Klein DJ. Molecular cyclicity and centricity of polycyclic graphs. I. Cyclicity based on resistance distances or reciprocal distances. Int J Quant Chem. (1994) 50:1–20. doi: 10.1002/qua.560500102

CrossRef Full Text | Google Scholar

15. Wang XQ, Dai MF, Chen YF, Zong Y, Sun Y, Su WY. Determining entire mean first-passage time for Cayley networks. Int J Mod Phys C. (2018) 29:1850009. doi: 10.1142/S0129183118500092

CrossRef Full Text | Google Scholar

16. Duan ZS, Chen GR, Huang L. Complex network synchronizability: analysis and control. Phys Rev E. (2007) 76:056103. doi: 10.1103/PhysRevE.76.056103

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Ellens W, Spieksma FM, Van Mieghem P, Jamakovic A, Kooij RE. Effective graph resistance. Linear Algebra Appl. (2011) 435:2491–506. doi: 10.1016/j.laa.2011.02.024

CrossRef Full Text | Google Scholar

18. Qi Y, Zhang ZZ, Yi Y, Li H. Consensus in self-similar hierarchical graphs and Sierpiński graphs: Convergence speed, delay robustness, and coherence. IEEE Trans Cybern. (2019) 49:592–603. doi: 10.1109/TCYB.2017.2781714

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Dai MF, He JJ, Zong Y, Ju TT, Sun Y, Su WY. Coherence analysis of a class of weighted networks. Chaos. (2018) 28:043110. doi: 10.1063/1.4997059

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hong MD, Sun WG, Liu SY, Xuan TF. Coherence analysis and Laplacian energy of recursive trees with controlled initial states. Front Inform Technol Elect Eng. (2020) 21:931–8. doi: 10.1631/FITEE.1900133

CrossRef Full Text | Google Scholar

21. Patterson S, Bamieh B. Leader selection for optimal network coherence. In: Proceedings of the 49th IEEE Conference on Decision and Control. Atlanta, GA (2010). p. 2692–7. doi: 10.1109/CDC.2010.5718151

CrossRef Full Text | Google Scholar

22. Sun WG, Sun MT, Guan JB, Jia Q. Robustness of coherence in noisy scale-free network and applications to identification of influential spreaders. IEEE Trans Circuits Syst II. (2020) 67:1274–8. doi: 10.1109/TCSII.2019.2929139

CrossRef Full Text | Google Scholar

23. Grone R, Merris R, Sunder VS. The Laplacian spectrum of a graph. SIAM J Matrix Anal Appl. (1990) 11:218–38. doi: 10.1137/0611016

CrossRef Full Text | Google Scholar

24. Khalid R, Idrees N, Saif MJ. Topological characterization of book graph and stacked book graph. Comput Mater Con. (2019) 60:41–54. doi: 10.32604/cmc.2019.06554

CrossRef Full Text | Google Scholar

25. Daoud SN, Elsawy AN. Edge even graceful labelling of some book graphs. J Taibah Univ Sci. (2018) 12: 315–30. doi: 10.1080/16583655.2018.1469292

CrossRef Full Text | Google Scholar

26. Beineke LW, Wilson RJ, Cameron PJ. Topics in Algebraic Graph Theory. New York, NY: Cambridge University Press (2004).

Google Scholar

27. Comellas F, Miralles A. Mean first-passage time for random walks on generalized deterministic recursive trees. Phys Rev E. (2010) 81:061103. doi: 10.1103/PhysRevE.81.061103

PubMed Abstract | CrossRef Full Text | Google Scholar