On a Statistical Mechanics Approach to Some Problems of the Social Sciences

1. Introduction

The work of Max Weber [1] in the social and economic sciences is often considered at the origin of the modern approaches toward the understanding of how and why some types of social behavior occur. On that work a profound concept made its first appearance. Weber aims at distinguishing a common social behavior, i.e., a behavior shared by many people regardless of the mutual relation among them, from what he calls social action, which instead is a behavior taking place exactly because of the relation among individuals. In this second case an isolated individual would behave in a totally different way than in the presence of others, while in the first case such presence does not affect his choices and actions. It is impossible to explain the concept by a better example than the one chosen by the author: Social action is not identical with the similar actions of many persons. Thus, if at the beginning of a shower a number of people on the street put up their umbrellas at the same time, this would not ordinarily be a case of action mutually oriented to that of each other, but rather of all reacting in the same way to the like need of protection from the rain [1]. While the work of Max Weber has shaped ever since the development of sociology and economy it was not until recently that the same ideas reemerged as crucial concepts within the hard science approaches to some problems of those disciplines. In the last couple of decades in fact, the enormous advantages of data collection and data analysis favored the development of a quantitative theory that allowed not only the rational interpretation of the phenomenological outcomes but led also, sometimes, to a genuine predictive ability with remarkable precision [2].

There are therefore two paradigmatic behaviors or, in other words, two modes of action. We will refer to the first, the one where the role of others is not influent, as common action or independent behavior while to the second, led by the presence of others, as social action or interacting behavior. The two have profoundly different quantitative and qualitative features.

In the independent case the measured quantities, like the average values of some social choice, are smooth function of the natural parameters. By this we mean that a small change in those parameters leads to a small change in the observed quantity. Those quantities are locally well-approximated by linear functions. The fluctuations from the average values are typically sensibly smaller than the size of the quantities themselves. This feature implies an efficient prediction ability from the available observed data. In the interacting case instead smoothness is not guaranteed as there is the presence of tipping points where a small variation of the parameters leads to a sudden shift in the observed quantity. Fluctuations are often much larger than in the previous case and make predictions highly unreliable in the absence of a well-established theory that has quantitatively classified the phenomena.

The first appearance of a successful approach to deal quantitatively with social systems is due to the work of Daniel McFadden who was awarded the Nobel Prize in Economics in the year 2000. His contribution, called Discrete Choice Theory, is an example of a predictive theory, in the sense of the hard sciences, within the social and economic phenomena [2]. The purpose of the discrete choice theory is to describe, understand and predict people behavior and was presented as an econometric technique to infer people preferences based on empirical data. In discrete choice theory the individual is assumed to make choices that maximize its own benefit. The “benefit” is described by an utility function, not necessarily rational, whose parameters are derived from data collected in polls. The theory moreover includes an assumption on the fluctuations from the individual benefit described by the logistic probability distribution. The case study at the origin of its success was the work that McFadden made to predict the use of the Bay Area Rapid Transit (BART) system, a public transportation system serving the San Francisco Bay Area in California. The construction of such system was of course subject to the approval of public authority and subordinated to the social usefulness that depends on how many people use the trains. The prediction made by McFadden turned out to be correct with a remarkable precision for the social sciences, i.e., an error smaller than 2 percent. The method gained immediately a more than justified credit and is still used worldwide for similar predictions on commuting habits and job allocations. Nevertheless when it was tested on different types of problems the precision of the predictions could oscillate from unsatisfactory to totally wrong. The main issues, as it was understood from 1995 [3], is that some type of choices are intrinsically dependent on the choices of others. This happens, for instance, when the choice to be made is of complex nature or when the information is not enough to reach a rational conclusion, or again when we feel pressured or reassured by social consensus. The formalism introduced by Brock and Durlauf [4] is directly imported from an exactly solvable classical Statistical Mechanics model (Curie-Weiss [5, 6]) in the Hamiltonian formulation and, in the socio-economic sciences, provides a conceptual generalization of the McFadden ideas when the hypothesis of independent agents is not suitable. The one-dimensional nature of their proposal, i.e., the fact it doesn't allow a layering of the social groups like in the original discrete choice theory, was addressed and solved few years later in [7, 8]. The physics approach to the social sciences is of course much more general than the one presented here. The reader is invited to see [9] for a broad overview and [10] for a perspective on the challenges ahead.

The present work summarizes two case studies where all these ideas have been tested. The first is about the study of the immigration phenomena on both their social and economic features [11–13]. The second is on the study of health screening campaigns done for prevention purposes [14].

2. Immigration

In this section we analyse two data sets relative to the immigration phenomena that have involved Italy and Spain. Our investigation concentrates on some classical sociological quantifiers of integration. Those are the fraction of temporary and permanent job contracts assigned to immigrants, the fraction of marriages with spouses of mixed origin (native and immigrant), and the fraction of newborns with parents of mixed origin.

The quantifiers we study are defined as

$\begin{array}{ll}{J}_p=\frac{\#ofpermanentcontractstoimmigrants}{\#ofpermanentcontracts},& (1)\end{array}$

$\begin{array}{ll}{J}_t=\frac{\#oftemporarycontractstoimmigrants}{\#oftemporarycontracts},& (2)\end{array}$

$\begin{array}{ll}{M}_m=\frac{\#ofmixedmarriages}{\#ofmarriages},& (3)\end{array}$

$\begin{array}{ll}{B}_m=\frac{\#ofnewbornswithmixedparents}{\#ofnewborns}.& (4)\end{array}$

They can be expressed as a function of the density of immigrants γ, i.e., the ratio between the number of immigrants N_imm and the whole population N = N_imm+N_nat, where N_nat is the number of natives

$\gamma =\frac{N_{imm}}{N_{imm}+N_{nat}}\in \left[0,1\right].$

Within this work we are interested in the average values of the quantifiers, at the national scale.

The possibility to extract useful information from our analysis stems from the fact that the size of the social interaction in the phenomena we study is tuned by the fraction of immigrants γ. In fact, the number of possible cross-links among native and immigrants is:

$N_{imm}{N}_{nat}=\Gamma (\gamma )N^2=\gamma (1-\gamma )N^2,$

where it is evident that

$\Gamma (\gamma )=\gamma (1-\gamma )$

acts as a natural parameter to study the system. Observing the community at different Γ allows us to study how the integration quantifiers behave as a function of it and overcomes the difficulty of measuring the cost function by introducing an artificial unit in its definition.

We use immigration data from Spain on the time interval 1999 to 2010 (the period in which Spain received most of its immigrant population) and from Italy in the time interval from 2001 to 2011. Spanish data on labor contracts come from Spain's Continuous Sample of Employment Histories. Sampling is conducted on a quarterly basis and we have about 3,600 data from 2005 to 2010. Data on marriages and births are drawn from the local offices of Vital Records and Statistics across Spain. We have data for each quarter of year from 1999 to 2008 for a whole amount of about 27,000 entries but coming from municipalities whose population is larger than 10,000 due to data protection restrictions (only 735 municipalities out of about 8,000 in Spain, but 85% of Spanish immigrants reside in these municipalities) [11, 12].

Italian data (that are on marriages and newborns) are collected by the Italian National Statistical Institute for each of the 8,100 municipalities from 2001 to 2011 and they are census data. The data set contains over 1,100,000 data, yearly describing the total population, the number of immigrants, the number of marriages and newborns originating from different types of couples (either mixed or not). The entire Italian's data set includes all municipalities from tiny villages to big cities [13]. Not using neither obtaining personal local information but only average ones, our method fully complies with the requirements of privacy and confidentiality.

The data we examined have, as smallest geographical unit, the municipality from the spatial point of view and the quarter for the time point of view. For each space time point we collected the immigration density. The data on employment contracts contain information about temporary or indefinite nature as well as the validity interval. Residential data reveal municipality and place of birth. Data on marriages detail the time validity,the nationality, the place of birth, the municipality of residence, for both spouses. Following customary definition used by social scientists we consider a marriage as mixed when a Spanish (or Italian)-born person, i.e., a native, marries a person that was born abroad. On a similar fashion, data on births contain information about the place of birth, nationality, municipality of residence, among other things, of all the newborn parents. Analogously, we consider all newborns with one native and one foreign born parent to be newborns with parents of mixed origin, briefly called mixed newborns.

The first step in setting the functional dependence of the quantifiers on Γ is the statistical approach with the time series of the parameters involved. Starting from the raw data, we consider the average values of each quantifier defined in (1)–(4), and from now on shortly denoted by Q, and of the cross-link density Γ in the two database as a function of the quarters t. The result is shown in Figure 1A. While the two labor quantifiers exhibit a complex behavior over time, the newborns with mixed parents display a regular linear increase over time. The mixed marriages behave like the newborns, but with an added seasonal periodicity. The two lower panels of Figure 1A show how Γ, that tunes the total number of available cross-link couplings among immigrants and natives, increases over time in the two databases. This also indicates that the density of immigration γ has a similar behavior (increasing over time). Using those functions Γ(t) and inverting them in t(Γ), we can plot each quantifier Q(t) in terms of Γ, thereby obtaining Q(t(Γ)) represented in the four panels of Figure 1B. Apart from an unclear functional dependence on the newborns, all of the other quantifiers display irregular behavior and escape a functional law. This means that there are spurious external effects that affect the time fluctuations used to obtain these graphs and when those effects are not present (as in the newborns case), the marginalization over time and the inversion procedure weaken the result as well. The conclusion is that the time series approach is not the suitable method for obtaining the functional dependence we are looking for, since it loses relevant information and propagates spurious external effects.

FIGURE 1

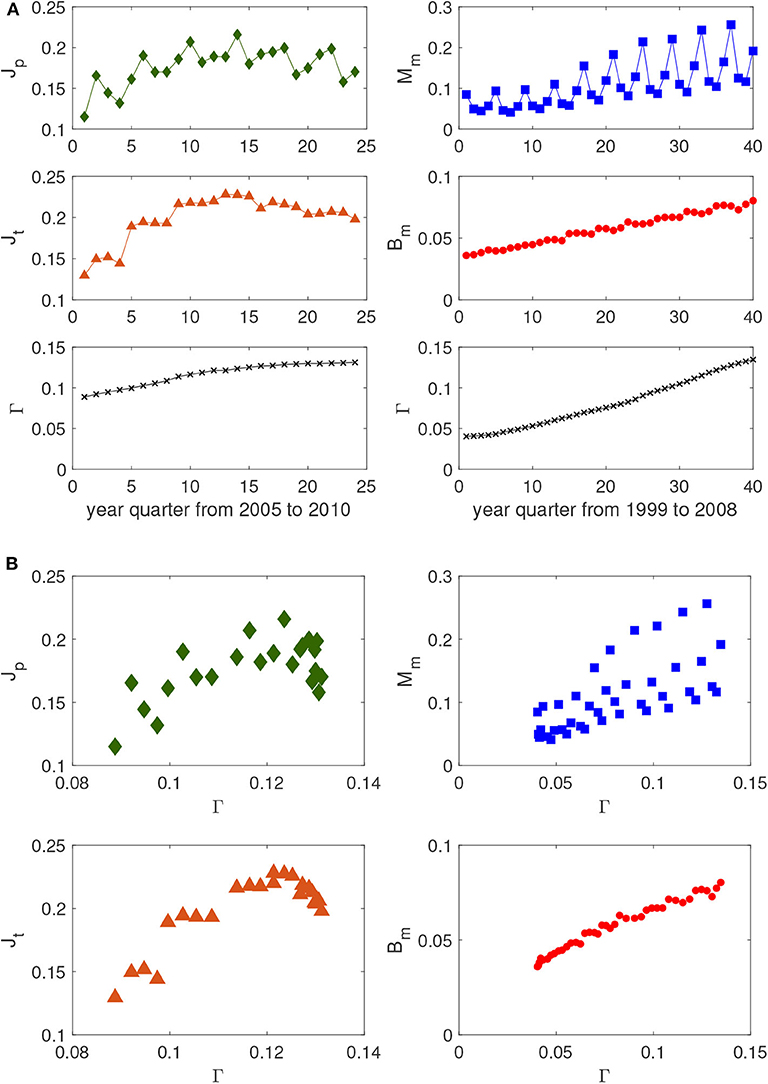
Figure 1. (A) Time series representing the quantifiers Q (permanent jobs J_p, temporary jobs J_t, mixed marriages M_m, newborns from mixed parents B_m) and the proportion Γ of the possible cross-links among natives and immigrants vs. year quarters t in the two databases. Each point in the plot is the average value of Q in the quarter t. (B) Quantifiers Q vs. Γ obtained from time series of (A), i.e., Q(t(Γ)), where t(Γ) is the inverse of Γ(t) [two lower panels of (A)].

To take advantage of all the information ad to extract from the databases the functional dependence of the quantifiers in terms of Γ we merge into a unique set the data entries in each database, regardless of their coordinates in space and time, and we order them by increasing values of Γ. We then proceed by grouping the data into bins over Γ in which the averages at the national scale can be evaluated. In Figure 2 we show the outcome of the average criteria and coarse graining procedure. For the job market quantifiers (permanent and temporary jobs given to immigrants) we have that the best fitting curve is linear in Γ.

$\begin{array}{ll}Q=c_f\gamma (1-\gamma )=c_f\Gamma (\gamma ),& (5)\end{array}$

The smooth, linear dependence on the parameter Γ is a strong indication that the underlying mathematical model is of McFadden type. From the social choice point of view it turns out that the likelihood of giving a job to an immigrant is independent of the fact that another job has been given to an immigrant or not. We can say that giving a job to an immigrant is a common action and not a social action.

FIGURE 2

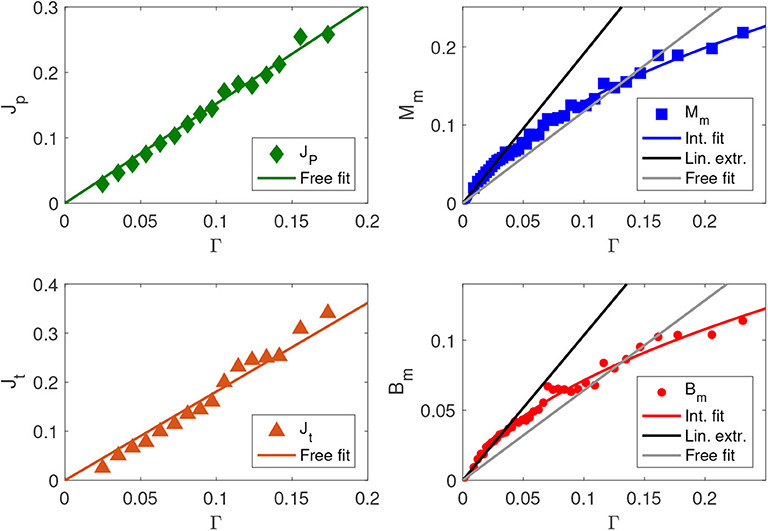
Figure 2. Dots are average quantities against Γ. Left upper: the fraction of permanent labor contracts given to immigrants on the total of labor contracts J_p (green rhombs), together with the best linear fit (free fit) aΓ (a = 1.52 ± 0.05, goodness of fit R² = 0.985). Left lower: fraction of temporary contracts given to immigrants J_t (orange triangles), together with the best linear fit (free fit) aΓ (a = 1.81 ± 0.09, goodness of fit R² = 0.963). Right upper: fraction of mixed marriages M_m (blue squares), together with the best square root fit (blue curve) $c\sqrt{\Gamma }$ (c = 0.53 ± 0.02, goodness of fit R² = 0.992), the best linear free fit (gray line) aΓ (a = 1.18 ± 0.07, goodness of fit R² = 0.855) and the best linear extrapolation fit (black line) bΓ (b = 1.92 ± 0.07, for 0 < Γ ≤ 0.035, goodness of fit R² = 0.964). Right lower: fraction of newborns with mixed parents B_m (red dots), with the best square root fit (red curve) $c\sqrt{\Gamma }$ (c = 0.28 ± 0.01, goodness of fit R² = 0.984), the best linear free fit (gray line) aΓ (a = 0.64 ± 0.05, goodness of fit R² = 0.789) and the best linear extrapolation fit (black line) bΓ (b = 1.04 ± 0.05, for 0 < Γ ≤ 0.04, goodness of fit R² = 0.922).

As far as mixed marriages and newborns are concerned (right panels of Figure 2), the data show an very high growth at small values of Γ, that are largely underestimated by the theory without interaction (free theory). That is followed by a crossover, where once it is passed, the free theory overestimates the quantity (the error is up to 30%). This observation strongly suggests that the theory without interaction, which proved to be in excellent agreement with the data about the labor market, is failing to properly capture the phenomenon in this context. From the right panels of the Figure 2, a different type of curve provides an optimal fit, which is the square root of the main quantity γ(1−γ) i.e.,

$\begin{array}{ll}Q=c_I\sqrt{\gamma (1-\gamma )}=c_I\sqrt{\Gamma (\gamma )},& (6)\end{array}$

for a suitable proportionality constant c_I. It is known that the square-root curve $\sqrt{\Gamma -{\Gamma }_c}$ is the distinctive feature of the mean-field monomer-dimer interacting model of statistical mechanics describing the imitative behavior of particles in dichotomic states. Within this context a monomer-dimer configuration is a set of couples assigned among vertices. By requiring that configurations with two dimers covering the same vertex are not allowed (hard-core interaction in Physics), the condition of monogamy is imposed. From the mathematical point of view the model is described in the Appendix where the relevant feature is the possibility to obtain the two regimes, according to the fact that the interaction is relevant or not. The emerging two functional dependencies are the linear one when interaction is absent and the square root one when it is present.

Also for the italian data, we performed the same average and binning procedure as for the spanish case. Figure 3 displays the output averages vs. Γ. The emerging behaviors are well fitted by two different laws: square root for the quantifiers on small municipalities (below 10,000 inhabitants) and linear on large ones (above 10,000 inhabitants). The partition of both marriages and newborns datasets, was proposed since an analysis performed over a unified dataset happened to be unsatisfactory. It displayed in fact a high dependence on the binning parameter settings revealing the typical presence of data mixture of interacting and non-interacting type. The implemented threshold of 10,000 inhabitants has been obtained as a result of an optimization test (the coefficients of determination of the data fitting in the two regimes—small and large cities—were maximal).

FIGURE 3

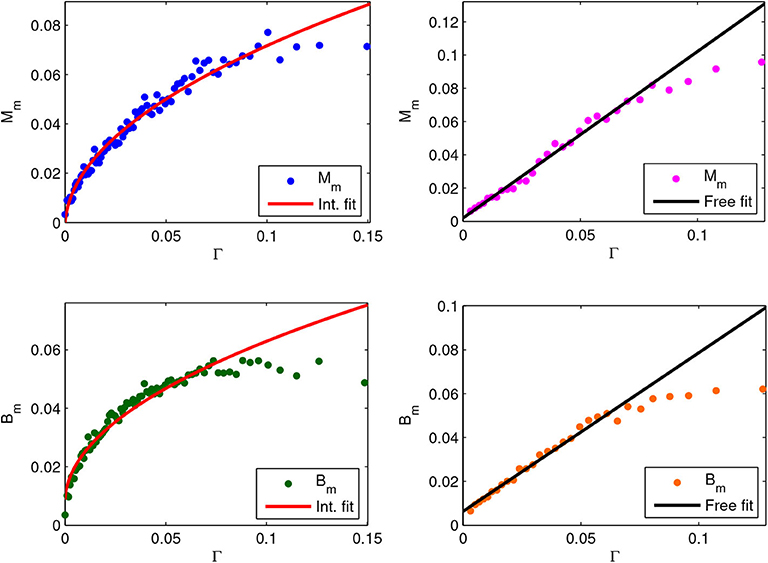
Figure 3. Dots are average quantities for the mixed marriages and mixed newborns quantifiers against Γ. Left upper: quantifier M_m (blue dots), fraction of mixed marriages occurred in municipalities with less than 10,000 inhabitants, with the best square root fit (red curve) $a\sqrt{\Gamma }+b$ (a = 0.233 ± 0.009, b = –0.002 ± 0.002, with a goodness of fit R² = 0.97 computed for Γ <0.13). Right upper: quantifier M_m (magenta dots), fraction of mixed marriages occurred in municipalities with more than 10,000 inhabitants, with the best linear fit (black curve) aΓ+b (a = 1.00 ± 0.05, b = 0.002 ± 0.002, with a goodness of fit R² = 0.98 computed for Γ <0.08). Left lower: quantifier B_m (green dots), fraction of newborns with mixed parents, born in municipalities with less than 10,000 inhabitants, with the best square root fit (red curve) $a\sqrt{\Gamma }+b$ (a = 0.174 ± 0.008, b = 0.008 ± 0.002, with a goodness of fit R² = 0.96 computed for Γ <0.10). Right lower: quantifier B_m (orange dots), fraction of newborns with mixed parents, born in municipalities with more than 10,000 inhabitants, with the best linear fit (black curve) aΓ+b (a = 0.78 ± 0.04, b = 0.005 ± 0.001, with a goodness of fit R² = 0.99 computed for Γ <0.07).

The statistical physics approach suggests an interpretation for these results. We know, in fact, that the linear behavior emerges, in strong ties conditions, from collective effects when the network is sparse and unpercolated. The links are rare and the connected groups are made of only few units (the social behavior is similar to a group of independent individuals). On the other side, the square root law emerges when the social network of strong personal ties is fully connected where the cases of isolated individuals or small groups inside the communities are rare or completely absent.

Our results on the italian data provide a quantitative confirmation of the classical sociological theories of alienation and anomie about the social behavior on large cities, where social connections are seldom and ineffective, in comparison to villages where they are strong [15].

In particular if the social network is extremely sparse (see the left panel of Figure 4 for an example of a sparse and unpercolated graph), with links that are so rare that do not allow the whole group to connect and percolate, we expect a social behavior similar to a group of independent individuals. Conversely, if the network is globally well connected (see the right panel of Figure 4 for an example of a percolated graph), with rare cases of isolated individuals or small groups, we expect a genuine social action effect to emerge.

FIGURE 4

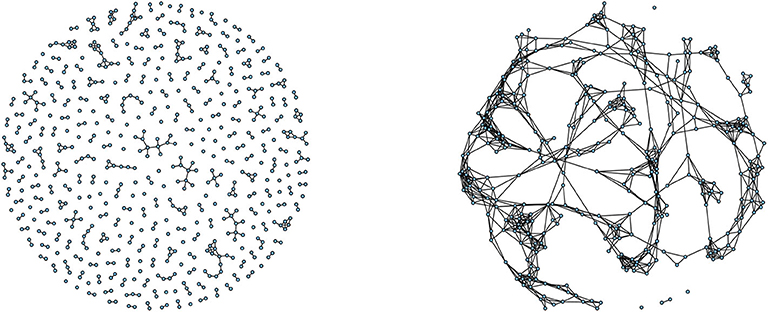
Figure 4. (Left) Sparse unpercolated graph. An example of a local view of a sparse unpercolated graph. Individuals are either isolated or, seldomly, connected with few others. The number of connected components in the graph grows proportionally to the graph's size. Our findings indicate that the average local trust network in large Italian cities is of this type. (Right) Percolated graph. An example of a local view of a percolated graph. Individuals are connected with several others. The graph, a part for few individuals, is completely connected. The number of connected components grows much slower than the graph size. Our findings indicate that the average local trust network in small Italian cities is of this type.

3. Screening

In this section we study how the population responds to an invitation to participate to a screening test for health prevention purposes. As a case study, we consider adhesion data to the Pap test (Papanicolaou smear test), which is a screening control used to prevent cervical cancer. The data are collected by Italian National Health System in a campaign conducted in the district of Parma in Northern Italy, on an average annual population of 120,000 women, from 2004 to 2012. The campaign calls for all women between the ages of 25 and 64 (target population) to be invited to take the test every 3 years.

The underlying mathematical model is used with an inference method (inverse problem [16, 17]) to compute the model parameters with the help of the maximum likelihood procedure which uses the measure of the mean values and the fluctuations of the attendance fractions. In the typical screening program each woman is invited typically once every 2–5 years: for this reason correlations between single individuals cannot be successfully measured. The huge dimension of the data set allows instead for a precise estimate of the correlations between groups and it is well-suited for testing the role of peer-to-peer effect and for seeing if it can be used to enhance participation.

To measure the network effects from adhesion data, we extract the yes/no answers in our data set: this generates an appropriate division of the women involved in the campaign. Although the final decision depends on both the individual attitude and the peer-to-peer mechanisms and it differs from woman to woman, the analysis of empirical data on the screening campaign has allowed us to detect some similar features, in particular among women of the same generation. The available attributes emerging from the data show that age is the main characteristic that influences women's participation. Figure 5 represents the attendance rate to the first invitation as a function of the woman age averaged over the whole time period, bringing out in an evident way the presence of three age sets: from 25 to 39, from 40 to 51, and from 52 to 64. In each set it is possible to recognize a linear growth rate (apart from small oscillations) but at different speed. It is interesting to note that the two age class separators, 39 and 52, coincide with two significant age thresholds in women life statistics: the first is the age at which 90% of women with children had their first child and the second is the average age of menopause in Italy (data from ISTAT 2011). It is therefore not surprising that these thresholds can be associated to important changes in the women's social behavior and attitude toward the screening campaign. In accordance with this finding, we consider three groups: Y = {women from 25 to 39 years old}, M = {women from 40 to 51 years old} and A = {women from 52 to 64 years old} and we use a three-species mean-field model to describe their decisions to attend the Pap test.

FIGURE 5

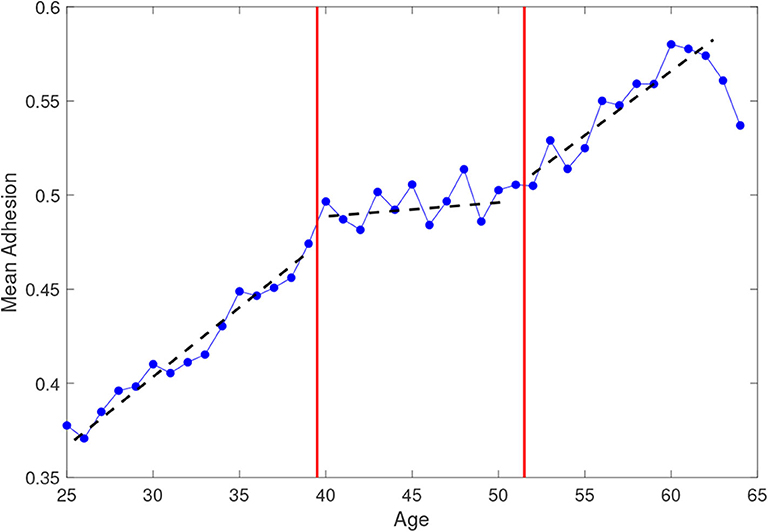
Figure 5. Mean adhesion to the screening program on first invitation, averaged over the whole time period 2004–2012, as a function of age of the target population.

The three population model

$\begin{array}{ll}\{\begin{array}{c}{m}_1=tanh(w_{11}{m}_1+\sqrt{\frac{{\alpha }_2}{{\alpha }_1}}{w}_{12}{m}_2+\sqrt{\frac{{\alpha }_3}{{\alpha }_1}}{w}_{13}{m}_3+b_1)\\ m_2=tanh(\sqrt{\frac{{\alpha }_1}{{\alpha }_2}}{w}_{12}{m}_1+w_{22}{m}_2+\sqrt{\frac{{\alpha }_3}{{\alpha }_2}}{w}_{23}{m}_3+b_2)\\ m_3=tanh(\sqrt{\frac{{\alpha }_1}{{\alpha }_3}}{w}_{13}{m}_1+\sqrt{\frac{{\alpha }_2}{{\alpha }_3}}{w}_{23}{m}_2+w_{33}{m}_3+b_3).\end{array}& (7)\end{array}$

depends on 9 free parameters: six imitation coefficients w_ℓs and three biases b_s to be determined by the inverse problem approach. The measured α's, that is the fraction of the population in each group, are α₁ = 0.412, α₁ = 0.321, α₃ = 0.267 and the mean adhesion/opinion m_ℓ in the group ℓ is 43% for group Y, 51% for group M and 58% for group A (see the Appendix for a description of the mathematical model).

once estimated the average value and the correlations of the women's average choice in the age groups from the data, the inverse problem procedure [14] gives

$\begin{array}{ll}\text{w}=\left(\begin{array}{ccc}0.9169& 0.0325& -0.0124\\ 0.0325& 0.9276& 0.0350\\ -0.0124& 0.0350& 0.9854\end{array}\right)\text{b}=\left(\begin{array}{c}-0.0120\\ 0.0020\\ 0.0004\end{array}\right)& (8)\end{array}$

for the interaction strengths and the bias.

These numerical results show that the personal motivation to attend the test increases with age. The coherence of behavior within each group is quantitatively highlighted by the high values of the self interactions w_ℓℓ. The off-diagonal terms of the matrix w, all of the same order of magnitude, show the existence of a pivotal group, the middle age women, well connected to both the younger and the adult women, as expected for generational proximity. The pivotal role of the group M will be proposed to build an effective strategy of participation increase. In fact, the screening campaign, following the EU recommendations, should cover 95−98% of the target population and reach an attendance of 60% or higher to be successful.

The standard system to encourage the participation to screening campaign consists in increasing the individual availability, i.e., increasing the personal propensities b_s. Actions of this type can be the invitation with a letter, the suggestion by the general practitioner and also the advertising on media. Acting on these parameters has a cost that is proportional to the number of people. Therefore, the unit cost per person can be reasonably parametrized by

$\begin{array}{ll}C={\alpha }_1\Delta b_1+{\alpha }_2\Delta b_2+{\alpha }_3\Delta b_3& (9)\end{array}$

where α_ℓ, ℓ = 1, 2, 3 is the relative size of each group on N = N₁+N₂+N₃ and Δb_s is the variation of the s-th parameter.

To study the return on investment we proceed by comparing the forecasts provided by tuning the parameters of the model. In Figures 6, 7 the results of the forecasting strategies are reported using a schematic representation: each ball is a woman group with the radius of the ball proportional to the adhesion percentage, the thickness of the arrows connecting the balls measure quantitatively the values of the interaction parameters w_ij between the groups (couple of outer-pointing arrows for w_ij > 0 and couple of inner-pointing arrows for w_ij < 0) and the length of the light blue arrows, that represent the bias b_s, s = 1, 2, 3 indicates the intensity of the fields (up-pointing arrow for b_s > 0 and down-pointing arrow for b_s < 0).

FIGURE 6

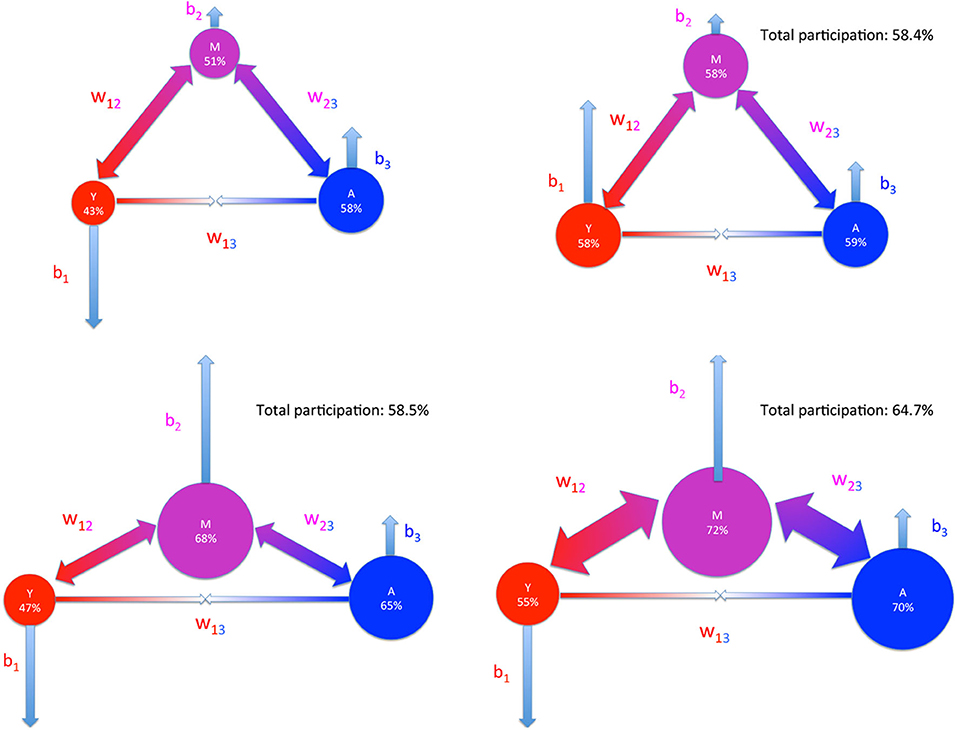
Figure 6. Adhesion forecast under a fixed unit cost of 0.01. Sketch of participation percentage p₁, p₂, p₃ of the three age groups. The radius of the ball is proportional to the adhesion percentage, the thickness of the arrows connecting the balls measures quantitatively the values of the interaction parameters w_ij between the groups (couple of outer-pointing arrows for w_ij > 0 and couple of inner-pointing arrows for w_ij < 0) and the length of the light blue arrows, that represent the parameters b_s, s = 1, 2, 3, indicates the intensity of the bias (up-pointing arrow for b_s > 0 and down-pointing arrow for b_s < 0). Young women are represented in red, middle-age women in magenta and adult women in blue. Left upper: starting point of the three strategies of participation increase under fixed unit cost. Right upper: First strategy. The whole cost is invested on the individual incentive b₁ of the less responders (the young women). Left lower: Second strategy. The cost is invested on the individual incentive b₂ toward the individuals of the pivoting group (middle-age women). Right lower: Third strategy. The cost is invested on the individual incentive b₂ toward the pivoting group together with an increase of a factor 2 of the interaction strength related to the same group M with higher influence, namely w₁₂ and w₂₃.

FIGURE 7

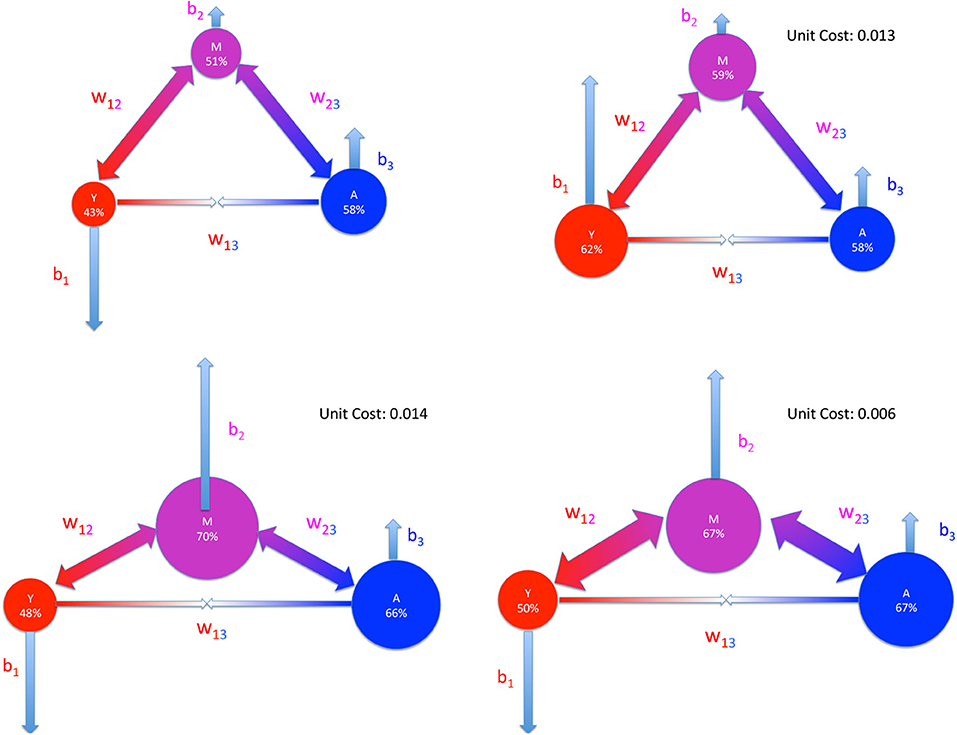
Figure 7. Same representation scheme, same meaning of symbols and same strategies of Figure 6 studied to reach a global 60% participation.

Figure 6 shows what are the effects, under the same unit cost of 0.01, of increasing the individual incentive b₁ of the less responders, the young women (right upper panel), of acting on the middle age group by individual incentives b₂ (left lower panel) and of a third strategy where we couple the same action on b₂ with an increased intensity of the two parameters w₁₂ and w₂₃, by a factor 2 (right lower panel). The common starting point of all strategies of participation increase is represented in the left upper panel of Figure 6. The first and second strategies show quantitatively the dragging effect of the boosted group on the other two allowing the achievement of a global participation percentage of 58%. The third panel shows not only an increase in participation of the targeted group but it reveals also an homogeneous significant increase of the other two groups leading to a substantial global result (65%) that crosses the bound of the 60% as recommended by the EU guidelines.

Finally, in Figure 7 we represent the cost for the strategies illustrated previously that we propose here in order to reach an overall participation of 60%. The first strategy, that consists in providing incentives only to the non-responders (group Y), turns out to have a unit cost of 0.013. The second strategy, where the incentives are toward the group M, comes with a unit cost of 0.014, while the third strategy, that couples incentives on M with an increase of interactions, has a cost 0.006. This clearly shows that the strategy with increase of interactions provides a saving of resources of more than 50% with respect to the other two. The policy maker can thus decide how to invest those savings, either by covering the cost of the increased interactions or to further improve the participation.

All the considered strategies showed that acting only on the less-responders yields poor results on the overall attendance. Better performances are obtained targeting the pivotal middle age group and increasing the strength of their interaction with the other groups.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Weber M. Economy and Society: An Outline of Interpretative Sociology. Berkeley, CA: California University Press (1978). p. 23.

Google Scholar

2. McFadden D. Economic choices. Am Econ Rev. (2001) 91:351–78. doi: 10.1257/aer.91.3.351

CrossRef Full Text | Google Scholar

3. Brock W, Durlauf S. Discrete Choice with Social Interactions I: Theory. Cambridge, MA: NBER Working Paper No.5291 (1995).

Google Scholar

4. Brock W, Durlauf S. Discrete choice with social interactions. Cambridge: Rev Econ Stud. (2001) 68:235–60. doi: 10.1111/1467-937X.00168

CrossRef Full Text | Google Scholar

5. Curie P. Propriété ferromagnétique des corps a diverse temperatures. Ann Chim Phys. (1895) 5:289–405.

Google Scholar

6. Weiss P. L' hypothése du champ moléculaire e la propriété ferromagnétique. J Phys. (1907) 6:661–89.

Google Scholar

7. Contucci P, Ghirlanda S. Modeling society with statistical mechanics: an application to cultural contact and immigration. Qual Quant. (2007) 41:569–78. doi: 10.1007/s11135-007-9071-9

CrossRef Full Text | Google Scholar

8. Gallo I, Contucci P. Bipartite mean-field spin systems. Existence and solution. Math Phys Electron J. (2008) 14:1–22.

Google Scholar

9. Perc M. The social physics collective. Sci Rep. (2019) 9:16549. doi: 10.1038/s41598-019-53300-4

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Capraro V, Perc M. Grand challenges in social physics: in pursuit of moral behavior. Front Phys. (2018) 6:107. doi: 10.3389/fphy.2018.00107

CrossRef Full Text | Google Scholar

11. Barra A, Contucci P, Sandell R, Vernia C. An analysis of a large dataset on immigrant integration in Spain. The statistical mechanics perspective on social action. Sci Rep. (2014) 4:4174. doi: 10.1038/srep04174

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Agliari E, Barra A, Contucci P, Sandell R, Vernia C. A stochastic approach for quantifying immigrant integration: the Spanish test case. New J Phys. (2014) 16:103034. doi: 10.1088/1367-2630/16/10/103034

CrossRef Full Text | Google Scholar

13. Agliari E, Barra A, Contucci P, Pizzoferrato A, Vernia C. Social interaction effects on immigrant integration. Palgrave Commun. (2018) 4:55. doi: 10.1057/s41599-018-0097-5

CrossRef Full Text | Google Scholar

14. Burioni R, Contucci P, Fedele M, Vernia C, Vezzani A. Enhancing participation to health screening campaigns by group interactions. Sci Rep. (2015) 5:9904. doi: 10.1038/srep09904

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Durkheim E. Le Suicide: Etude de Sociologie. Paris: Flix Alcan (1897). p. 462.

Google Scholar

16. Fedele M, Vernia C, Contucci P. Inverse problem robustness for multi-species mean field spin models. J Phys A Math Theor. (2013) 46:065001. doi: 10.1088/1751-8113/46/6/065001

CrossRef Full Text | Google Scholar

17. Fedele M, Vernia C. Inverse problem for multispecies ferromagnetic-like mean-field models in phase space with many states. Phys Rev E. (2017) 96:042135. doi: 10.1103/PhysRevE.96.042135

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Alberici D, Contucci P, Mingione E. The exact solution of a mean-field monomer-dimer model with attractive potential. Europhys Lett. (2014) 106:10001. doi: 10.1209/0295-5075/106/10001

CrossRef Full Text | Google Scholar

19. Alberici D, Contucci P, Mingione E. A mean-field monomer-dimer model with attractive interaction: exact solution and rigorous results. J Math Phys. (2014) 55:063301. doi: 10.1063/1.4881725

CrossRef Full Text | Google Scholar

20. Durlauf SN. How can statistical mechanics contribute to social science? Proc Natl Acad Sci USA. (1999) 96:10582–8.

PubMed Abstract | Google Scholar

Appendix

The mathematical model that describes the immigration setting depends on two parameters: h that measures how likely is for an individual to stay single (or without a job) and J, a positive parameter, that measures how the individual choice to marry or stay single (to accept a job or not) is influenced by the choice of her/his peers in the acquaintance neighborhood. The larger J, the higher the imitation among peers on this particular choice. The probability measure defining the model can be parametrized, for an assigned matching configuration D, as

$p(D)=\frac{e^{hM(D)+JI(D)}}{\sum _{D\in {D}{e}^{hM(D)+JI(D)}}}$

where M(D) is the number of monomers and I(D) the number of neighboring sites occupied by the same type of particles, either both monomers or both dimers. Its solution provides the following consistency equation for the dimer density d:

$\begin{array}{ll}d=g((2d-1)J+h)& (\mathrm{A1})\end{array}$

where $g(\xi )=\frac{1}{2}\left(\sqrt{e^{4\xi }+4e^{2\xi }}-e^{2\xi }\right)$ [18, 19]. Eq. (A1) is the analog of the consistency equation of the Curie-Weiss model for ferromagnets where the role of the function g is played by the hyperbolic tangent. In particular, it has been shown [18, 19] that for small values of J (i.e., smaller than a critical value J_c > 0) the functional behavior of d is smooth in the parameter space (J; h) and behaves essentially like the case J = 0, thus reproducing the empirical growth of the labor market quantifiers. For large values of J instead (i.e., J ≥ J_c) a singular behavior appears and is described by a critical exponent 1/2 that leads to the square root scaling, in agreement with the empirical growth of the quantifier M_m and B_m. Its relevance in social sciences has been clearly advocated by Durlauf [20].

The mathematical model that describes the screening setting can be thought of as an extension of the Curie-Weiss model to systems composed of many interacting groups that interact with each other and with an external influence (or bias). We can consider n disjoint groups P₁, P₂, …, P_n of size N_ℓ, into which the N individuals are grouped and we denote by α_ℓ = N_ℓ/N the relative group size. We suppose that the external influence b_i takes n distinct values depending on the group the individual i belongs to.

We can say heuristically that this model favors the agreement of people's choices m_s(σ) with some external influence b_s varying from group to group and also the agreement between groups ℓ and s of people who have positive interaction coefficient w_ℓs, while favors the disagreement when w_ℓs is negative. (The parameters w_ℓs tune the interaction between an individual of the group P_ℓ and one of the group P_s).

We define the mean opinion (or magnetization in statistical mechanics language) of a group P_ℓ as:

$\begin{array}{ll}{m}_{\ell }=\frac{1}{N_{\ell }}{\displaystyle \sum _{i\in P_{\ell }}}{\sigma }_i& (\mathrm{A2})\end{array}$

It has been shown [12] that the model is described by the system of mean-field equations

$\begin{array}{ll}\{\begin{array}{l}{m}_1=tanh(\sum _{s=1}^n\sqrt{\frac{{\alpha }_s}{{\alpha }_1}}{w}_{1s}{m}_s+b_1)\\ m_2=tanh(\sum _{s=1}^n\sqrt{\frac{{\alpha }_s}{{\alpha }_2}}{w}_{2s}{m}_s+b_2)\\ ⋮\\ m_n=tanh(\sum _{s=1}^n\sqrt{\frac{{\alpha }_s}{{\alpha }_n}}{w}_{ns}{m}_s+b_n),\end{array}& (\mathrm{A3})\end{array}$

or, in other words, that the equilibrium state of the model is described by the Equations (A3). The case studied in this paper corresponds to N = 3. Using this model it is possible to provide not only a new perspective to approach the problem of improving participation in screening campaigns but also a minimal model prototype for making useful prediction. In general, the choice of each person to participate in the screening campaign is related both to their individual attitude to the invitation [represented by the parameters b_s in Eq. (A3)] and to peer-to-peer effects, arising from the interaction with other individuals involved in the campaign [parameters w_ℓs in Eq. (A3)].