- Department of Chemical Engineering, Faculty of Technology and Metallurgy, University of Belgrade, Belgrade, Serbia
Various types of mechanical waves, such as propagative waves and standing waves, are observed during 2D collective cell migration. Propagative waves are generated during monolayer free expansion, whereas standing waves are generated during swirling motion of a confluent monolayer. Significant attempts have been made to describe the main characteristics of mechanical waves obtained within various experimental systems. However, much less attention is paid to correlate the viscoelasticity with the generated oscillatory instabilities. Mechanical waves have recognized during flow of various viscoelastic systems under low Reynolds number and called “the elastic turbulence.” In addition to Reynolds number, Weissenberg number is needed for characterizing the elastic turbulence. The viscoelastic resistive force generated during collective cell migration caused by a residual stress accumulation is capable of inducing apparent inertial effects by balancing with other forces such as the surface tension force, the traction force, and the resultant force responsible for cell migration. The resultant force represents a product of various biochemical processes such as cell signaling and gene expression. The force balance induces (1) forward flow and backward flow in the direction of cell migration as characteristics of the propagative waves and (2) inflow and outflow perpendicular to the direction of migration as characteristics of the standing waves. The apparent inertial effects are essential for appearing the elastic turbulence and represent the characteristic of (1) the backward flow during the monolayer free expansion and (2) the inflow during the cell swirling motion within a confluent monolayer.
Introduction
Collective cell migration within a monolayer induces spontaneous generation of mechanical waves [1–5]. A more comprehensive account of oscillatory patterns generation is essential for a wide range of biological processes such as morphogenesis, wound healing, regeneration, and cancer invasion [6–9]. Specifically, in this review, we concentrate on mechanical oscillations, a term we use to identify all periodical fluctuations of mechanical parameters, such as cell velocity, the resulting strain, substrate tractions, and stresses. These oscillations can be divided into two major categories: (1) standing waves generated in a confined environment [3, 5, 10–12] and (2) propagative waves generated during monolayer free expansion that travel through the system [2, 5, 13]. The standing waves represent a characteristic of local cell rearrangement, which leads to swirling motion [3]. Propagative waves have been observed during wound healing [2]. This monolayer expansion induces fluctuations of cell packing density [13]. Tlili et al. [13] reported that the frequency of velocity weaves depends only on cell packing density at the moving forward. Both types of waves induce a periodical softening and stiffening of multicellular domains [2, 3, 5]. It is necessary to correlate cell packing density with cell strains and residual stress accumulation.
Oscillator, wave-like motion of multicellular systems has been related to long-time effective inertia [3, 11]. The effective inertia is induced by generated cellular stress during long-time rearrangement. Notbohm et al. [3] considered a cell stress generation as a product of a chemical coupling where cellular stress results in increased contractility, which has a feedback impact to the effective inertia. The effective inertia, together with cellular elasticity, supports the oscillatory waves of motion [3]. Serra-Picamal et al. [2] assumed a biphasic stress response of single cells as a product of cytoskeletal reinforcement and fluidization. They also neglected long-time inertial effects. Banerjee et al. [14] coupled local strain with contractility and impose a turnover time for contractile elements, resulting in effective inertia and viscoelasticity based on the formulated continuum model. They did not take into consideration stress relaxation and residual stress accumulation caused by collective cell migration. Murray et al. [15] related cell packing density with cell stress. They also neglected inertial effects. Various approaches have been applied. Notbohm et al. [3] proposed a continuum model formulated in terms of a few coarse-grained fields such as traction and velocity, measured directly in the experiments. Murray et al. [15] proposed a continuum model presented as a system of equations capable for describing interrelation between variables such as (1) cell packing density, (2) matrix density, and (3) matrix viscoelasticity. Serra-Picamal et al. [2] and Deforet et al. [11] formulated stochastic particle-based simulations. Serra-Picamal et al. [2] balanced active propulsion force with cell elastic force and cell–matrix friction force. Deforet et al. [11] accounted for the force of inertia and balanced it with friction, intercellular adhesions, and active propulsion.
Significant attempts have been made to describe the main characteristics of mechanical waves by considering various types of experimental systems. The main characteristics of standing waves are (1) the radial velocity and cell tractions are uncorrelated; (2) radial stress component σcrr and the corresponding strain rate are uncorrelated; (3) radial stress component is simultaneously tensional and compressional; and (4) time derivative of the stress component is in a phase with the corresponding strain rate [3]. The main characteristics of propagative waves are that (1) normal stress component σcxx and corresponding strain rate are in phase quadrature, (2) normal stress component is always tensional, and (3) velocity and cell tractions are uncorrelated [2]. Even though the most studied model is Madin-Darbvy canine kidney cells (MDCK), other types have been employed, and despite the intrinsic variability between them, all reports seem to agree on the typical times and space scale: mechanical oscillations happen with a periodicity of ~0.5–1 mm and ~3–6 h [2, 3, 5]. The effective velocity of transmission of mechanical signals, whether traveling or standing waves, is 0.2–1 μm/min [2, 3]. These cooperative motions are driven by active cellular forces, but the physical nature of these forces and how they generate elastic waves remain poorly understood. However, it is well-known that generation of waves and their transfer strongly depends on the state of cell–cell junctions and contractility [2, 3, 16, 17]. Most of the works on generation of mechanical waves within cell monolayers have been carried out on fibroblasts, which develop weaker cell–cell adhesions [5]. The knowledge obtained on these cell types is difficult to transfer on epithelial cells, which develop strong cell–cell junctions. However, various confluent multicellular systems under in vivo conditions are capable of generating the cell swirling motion and on that base mechanical waves, which have been experimentally confirmed [18, 19]. Additional experimental work is necessary to correlate the state of cell–cell adhesion contacts and the characteristics of mechanical waves. Until now, little is reported about influence of the monolayer viscoelasticity on propagation of mechanical waves. Tambe et al. [1], Serra-Picamal et al. [2], and Notbohm et al. [3] treated a monolayer as homogeneous, isotropic, and elastic. On that basis, they neglected inertial effects during collective cell migration. Viscoelastic relaxation is expected to result in long-time-scale stress accumulation and consequently give rise to oscillations through the effective inertia. The stress accumulation can induce local stiffening and on that basis perturb established cell migrated pattern. In general, inertial effects have been discussed in the context of turbulence and quantified by dimensionless Reynolds number (where v is the velocity, L is the characteristic length, ρ is the density, and η is the viscosity). The turbulence of Newtonian liquids is induced at large Re number, i.e., high velocity and low viscosity. However, viscoelastic systems have a few properties that distinguish them from Newtonian fluids [20, 21]. The stress field in viscoelastic systems is not uniquely defined by the current rate of strain, but rather depends on the flow history, with characteristic relaxation times for stress and strain-rate [20]. To the contrary of the turbulence generated within the Newtonian liquids, the so-called “elastic turbulence” appears during flow of viscoelastic liquids such as solutions of flexible long-chain polymers under low Reynolds number Re → 0, i.e., low velocity and high viscosity [22, 23]. The elastic turbulence represents a consequence of the system viscoelastic nature and is quantified by Weissenberg number (τR is the stress relaxation time). For the case of polymer solutions, this elastic turbulence is accompanied by stretching of polymer chains resulting in significant system stiffening. The system stiffening is caused by residual stress accumulation, which leads to sharp growth of the flow resistance. Groisman and Steinberg [23] proposed the dimensionless elastic parameter for characterization of the elastic turbulence rather than Re number. Steinberg [24] pointed out that the elastic turbulence of polymer solutions represents the characteristic of large Wi> 1 and vanishingly small Re≪1 number. Larson et al. [25] physically described the elastic parameter X as the ratio between the stress relaxation time τR and the viscous diffusion time tv, i.e., (where ). Groisman and Steinberg [26] considered Couette-Taylor (CT) flow of viscoelastic polymer solutions and pointed out that the flow can become unstable when the stress relaxation time is large enough. They considered the oscillatory instabilities generation in highly elastic polymeric liquids. The rheological response of these systems corresponds to the case when the centrifugal force is totally suppressed by the elastic hoop stress. At those conditions, the flow instabilities in the form of swirls appear as a consequence of this hoop stress. Swirling flow induces inflow and outflow in radial direction driven by action of centrifugal force against elastic force [22]. This important result points out that apparent inertial effects are caused by the system simultaneous stiffening and softening occurring when Re → 0 which lead to inflow and outflow. The inflow for vr< 0 (where vr is the radial velocity component) corresponds to the compression and the outflow for vr> 0 corresponds to extension. Multicellular systems are much complex than polymer solutions, but their viscoelastic nature significantly influences cell rearrangement and should not be neglected [8, 9]. Flow instabilities generated during collective cell migration show similar rheological properties as ones recognized for other viscoelastic systems. However, cellular systems have not been considered in the context of the elastic turbulence yet. Murray et al. [15], Serra-Picamal et al. [2], Tambe et al. [1], and Notbohm et al. [3] neglected inertial effects during collective migration of cell monolayers. This assumption has been supported by low Re number flow. However, apparent inertial effects could represent a consequence of inflow during cell swirling motion and backward flow during monolayer expansion caused by residual stress accumulation. The aim of this work is to relate viscoelastic nature of cell monolayer during collective cell migration with generated standing and propagative mechanical waves. Consequently, it is necessary to (1) postulate viscoelastic constitutive model for cell monolayer and extracellular matrix; (2) describe cell packing density change, matrix density change, and their interrelation (needed for the description of volume force balance); and (3) formulate the volume force balance that drives cell rearrangement by accounting for two time scales, i.e., a time scale of minutes (for the stress relaxation) and time scale of hours (for collective cell migration, strain change, and residual stress accumulation).
Viscoelasticity of Cell Monolayer Caused by Collective Cell Migration: The Dimensionless Criteria
Flow of viscoelastic systems should be characterized by two dimensionless numbers: (1) Reynolds number Re and Weissenberg number Wi as well as (2) their ratio X [23]. The oscillatory instabilities in the flow, the so-called elastic turbulence, represent the characteristic of large Wi> 1 and vanishingly small Re → 0 number [24]. The underlying mechanism of this oscillatory phenomenon is related to the coupling of the collective cell migration with the viscoelastic force, which resists the movement. The viscoelastic force arises as a consequence of the residual stress accumulation. While stress relaxation time corresponds to a time scale of minutes, the residual stress accumulation corresponds to a time scale of hours [8, 9, 27]. The parameters Re and Wi can be estimated based on experimental data from the literature such as (1) the cell velocity [2]; (2) the characteristic length L = vxΔτ (where Δτ is the period of oscillation equal to Δτ ≈ 4 − 6 h, [2]); (3) the density of cells could be close to the density of water, i.e., ; (4) the viscosity of epithelium η = 4.4 × 105 Pas [27]; (5) the stress relaxation time τR = 3 − 14 min [24]; and (6) the characteristic time of residual stress accumulation corresponds to the period of mechanical oscillations Δτ [2, 3]. Instead of Wi, we formulated the effective value of the Weissenberg number, which accounts for the characteristic time for the residual stress accumulation equal to . Corresponding dimensionless numbers are , Wi eff~ 0.3, while X ~1014. Groisman and Steinberg [23] distinguished critical experimental conditions for the appearance of oscillatory instabilities during flow of polyacrylamide in viscous sugar syrup as a consequence of stress relaxation. They pointed out that critical parameters are Re = 0.3 and Wi = 3.5. Generation of oscillatory instabilities in 2D collective cell migration has been experimentally confirmed [2, 3]. For deeply understanding of this complex phenomenon, it is necessary to consider the viscoelasticity of multicellular systems.
Cell Long-Time Rearrangement During Collective Cell Migration: Modeling Consideration
Cell long-time rearrangement caused by collective cell migration should be discussed based on formulated interrelations between various variables such as (1) cell velocity as a function of matrix viscoelasticity , cell viscoelasticity , and cell surface tension γst and (2) cell packing density n as a function of cell velocity, matrix density ρ, and matrix viscoelasticity (where is the cell stress, is the cell strain, is the matrix stress, and is the matrix strain). The interrelations between various variables are shown in Figure 1.
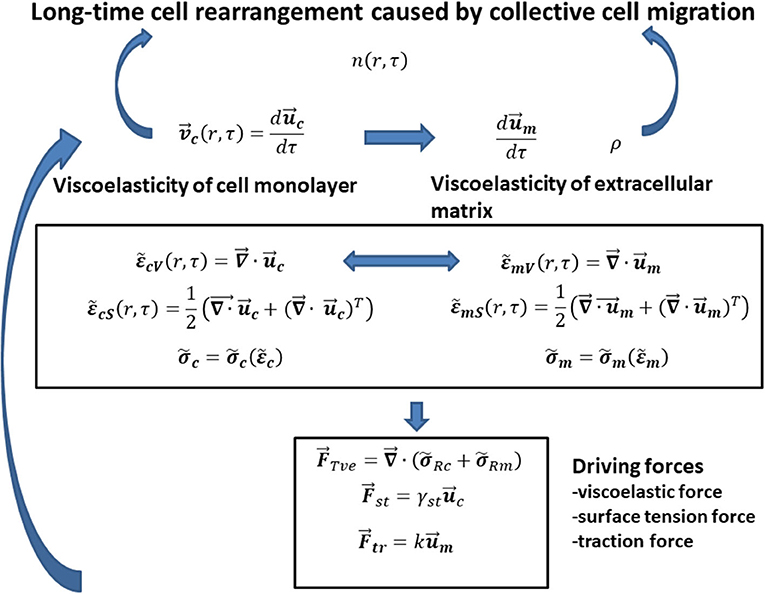
Figure 1. The schematic representation of interrelations between main model parameters that influence the generation of mechanical waves during (1) monolayer free expansion and (2) cell swirling motion within a confluent monolayer.
Consequently, the modeling consideration accounts for the following steps: (1) the expression of cell velocity as the rate of change the cell displacement field, i.e., (where is the cell displacement field) [8, 9]; (2) the formulation of local cell shear and volumetric strains and , respectively, as a function of the cell displacement field [8, 9]; (3) the introduction of a constitutive viscoelastic model for cells (where is the cell stress and is the cell strain) [28, 29]; (4) the formulation of the rate of change the matrix displacement field as a function of [29, 30], (5) the formulation of local matrix shear and volumetric strains , , respectively, as a function of the matrix displacement field [29, 30]; (6) the discussion of the rheological behaviors of various matrix applied as a substrate for 2D collective cell migration (where is the matrix stress and is the matrix strain) [2, 3, 30]; (7) the formulation of changing the cell packing density n (r, τ) as function of various fluxes, such as cell convective flux, conductive flux, durotaxis flux, haptotaxis flux, and galvanotaxis flux [15]; (8) the expression of matrix density change as a function of matrix convective flux [15]; (9) the formulation of forces that influences cell long-time rearrangement such as the viscoelastic force, the traction force, and the surface tension force based on modified model proposed by Murray et al. [15]; and (10) the formulation of the interrelation between the cell velocity and the forces that influences generation of propagative waves and standing wave based on the corresponding momentum balance. Discussion of cell long-time rearrangement in the context of the elastic turbulence proposed by Groisman and Steinberg [23] is the main goal of this paper.
Viscoelasticity of Multicellular Systems
Viscoelasticity of multicellular systems caused by collective cell migration has been considered on two time scales [8, 9]. The stress relaxation happens at a short-time scale t, whereas the long time scale τ is important for tracking the strain change and the residual stress accumulation as shown in Figures 2A,B for (A), a monolayer free expansion inspired by Serra-Picamal et al. [2], and (B), swirling motion of a confluent monolayer inspired by Notbohm et al. [3].
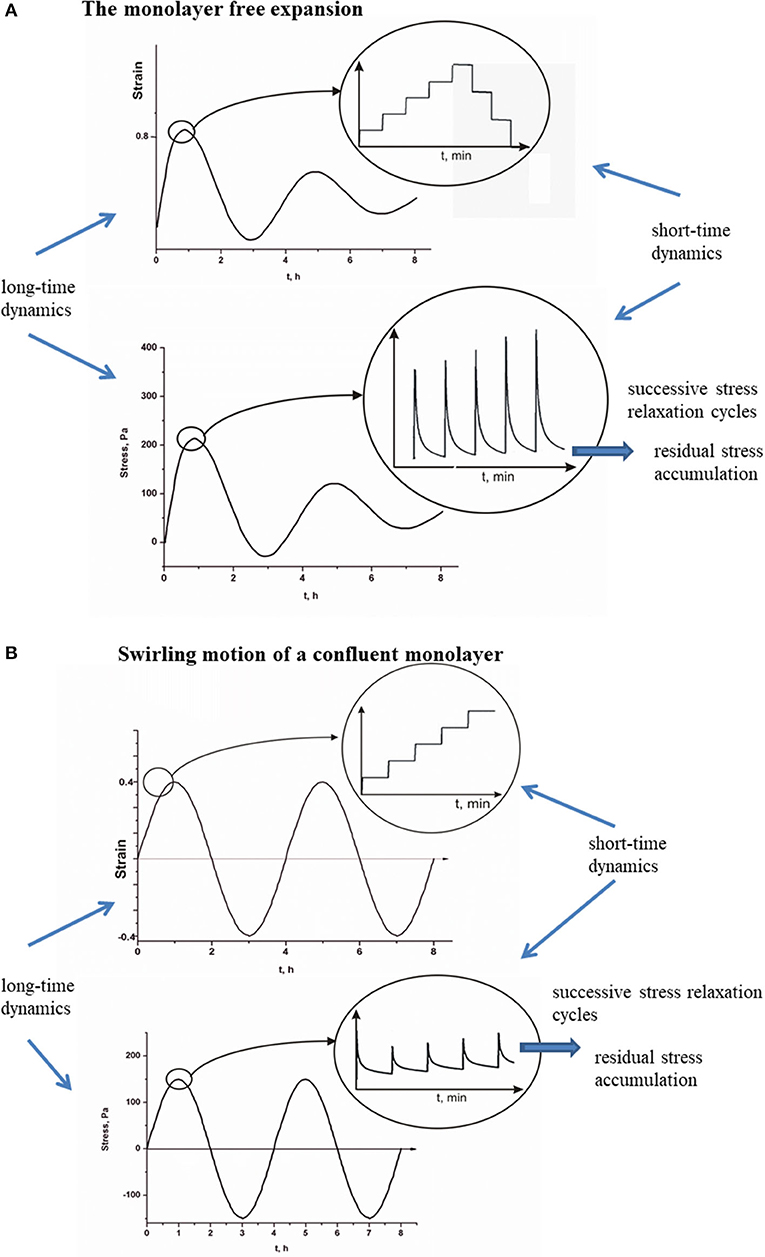
Figure 2. (A,B) Short-time relaxation cycles of cell stress and long-time residual stress accumulation for propagative and standing waves.
Stress relaxation is primarily induced by adaptation of adhesion contacts and cell shapes [16, 31], which occur at time scale of minutes. However, the local change of strain caused by collective cell migration is slower and occurs at time scale of hours. This long time scale corresponds to collective cell migration, which accounts for cumulative effects of various biochemical processes such as cell signaling and gene expression [6, 32].
Cell velocity can be expressed as follows:
where is the cell displacement field. The cell local velocity is influenced by various forces such as the viscoelastic force, the traction force, and the surface tension force. Detailed description of the forces and formulation of the force balance is necessary for understanding the mechanical waves. Corresponding cell local volumetric and shear strains depend on and can be expressed as follows [8, 9]:
where is the identity tensor, is the cell volumetric strain, and is the cell shear strain. Strains induce generation of stress within a cell monolayer. Collective cell migration induces inhomogeneous distribution of stress [9]. Tambe et al. [1] considered long-time residual stress distribution within collective migrated epithelial cell monolayers. Consequently, stress relaxation phenomena have not been reconstructed from their data. Maximum stress accumulation corresponds to 100–150 Pa [1]. However, Marmottant et al. [27] considered stress relaxation of cellular aggregate under constant strain (i.e., the aggregate shape) condition caused by the aggregate uniaxial compression between parallel plates. The stress decreases exponentially with the relaxation time equal to 3–14 min up to equilibrium value. Stress relaxes from ~27 Pa to the residual stress value equal to ~17 Pa during 25 min [27]. This time period corresponds to a short-time cycle. On the other hand, the strain is constant during the short-time cycle and changes from one stress cycle to another. Maximum average strain rate in x-direction during monolayer free expansion is [2], while the corresponding period of oscillation is 4–6 h [2, 3].
Stress relaxation ability under constant strain condition represents the characteristic of the viscoelastic solid rather than viscoelastic liquid. The Maxwell model suitable for viscoelastic liquid describes stress relaxation under constant strain rate [20]. However, in the case we considered, the strain change was much slower than the stress relaxation [8, 9]. Accordingly, stress relaxes under constant strain per short-time cycle. Cell stress at a supracellular level accounts for cumulative effects of cell–cell and cell–matrix interactions [17, 33]. Cell–cell interactions influence generation of active forces as a product of the contractility of actomyosin cytoskeleton and cell's protrusions in the polarization direction. Passive forces accounts for deformation of cells during their migration. Cumulative effects of cell–cell and cell–matrix frictions influence energy dissipation obtained at a long time scale. The cell stress accounts for normal stress and shear stress contributions [9]. Normal and shear stresses consist of elastic and viscous parts and can be expressed as follows: for volumetric stress and for shear stress (where and are elastic contributions, while and are viscous contributions, respectively), similarly as was formulated by Murray et al. [15] for viscoelastic systems. The simplest constitutive model for a viscoelastic solid capable to describe stress relaxation is the Zener model [28]. The Zener model is expressed as follows:
where , , Gc is the elastic modulus, and η is the viscosity. The relaxation of stress under constant strain condition is as follows:
where t is the short-time scale, τ is the long time scale, is the initial value of the stress for single short-time relaxation cycle, and the stress relaxation time is . The residual stress is equal to
Notbohm et al. [3] considered 2D cell swirling motion within a confluent monolayer by monitoring long-time change of stress radial component σcrrR. They pointed out that the long-time change of residual stress correlated well with the long-time strain change during the time period of 24 h. This result indicates that the Zener model could be suitable for describing the viscoelasticity of cell monolayers because it accounts for experimentally obtained correlations between and and describes the stress relaxation. The residual stress accumulation represents the consequence of generated strain and its long-time change [9, 34]. This cause–consequence relation is expressed by the constitutive model (Equations 1–5). The residual stress accumulation induces local stiffening of the monolayer, which is responsible for generation of flow instabilities. Pajic-Lijakovic and Milivojevic [8, 9, 34] pointed out that the residual stress accumulation can suppress cell migration by decreasing cell velocity and local strain. On that basis, this stress accumulation is a main cause of the generation of apparent inertial effects, which results in the elastic turbulence. For deeper insight into the influence of cell viscoelasticity on the cell velocity in the form of apparent inertial effects, it is necessary to formulate a force balance for (1) monolayer free expansion and (2) cell swirling motion within a confluent monolayer. Besides the viscoelasticity of cells, the viscoelasticity of a supracellular matrix significantly influences cell long-time rearrangement in the context of durotaxes, haptotaxis, and galvanotaxes [15].
Viscoelasticity of an Extracellular Matrix
Various hydrogel matrices have been used as a substrate for cell migration. The rheological behavior of hydrogels frequently corresponds to a poroviscoelasticity [35]. The matrix stress relaxation phenomena caused by cell tractions include (1) the hydrogel viscoelastic relaxation and (2) poroelastic relaxation caused by solvent diffusion. Polyacrylamide gel coated by collagen has been a widely used matrix for 2D cellular systems [1–3]. Hydrogels of natural origins are basement membrane–based gel preparations; some examples include fibrin gel, collagen gel, alginate gel, chitosan gel, and Matrigel [15, 30, 35, 36]. Matrigel is a commercially available basement membrane based gel. These cell–matrix systems are suitable for considering collective cell migration in 2D and 3D. Chaudhuri et al. [37] considered the influence of Ca-alginate viscoelasticity on cell spreading. Chaudhuri et al. [37] and Pajic-Lijakovic et al. [30] proposed the Burgers model for describing the viscoelasticity of Ca-alginate hydrogel. Various hydrogel matrices have been treated as elastic [1–3], while the others have been treated as a viscoelastic [26, 36]. Murray et al. [15] proposed the Kelvin-Voigt model for describing the viscoelasticity of fibrous extracellular matrices. Pajic-Lijakovic et al. [29] described the long-time change of the matrix displacement field by cell action as follows:
where Fm is the free energy function that accounts for cell–matrix mechanical and electrostatic interactions, and is the cell displacement field. The first term of the right-hand side of Equation (6) accounts for the rheological response of a matrix caused by its structural changes, whereas the second one represents the driving force for the matrix displacement field fluctuations. The corresponding matrix volumetric and shear strains are equal to
where is the matrix volumetric strain and is the matrix shear strain. Corresponding matrix stress-strain constitutive model depends on the choice of the matrix and the type of cells (where is the matrix stress). Cell traction force depends on the matrix displacement field and was expressed as (where k is an elastic constant) [15]. Pajic-Lijakovic et al. [30] considered residual stress accumulation within Ca-alginate hydrogel matrix without cells. It is useful in order to estimate cell–matrix interactions. They pointed out that the increase in the residual stress within the Ca-alginate matrix was significant (~7 kPa) after 10 repeated cycles, even under a low externally induced compression strain of 2% per cycle.
Cell migration speed, cell packing density, and correlation of cell migration depend on cell–matrix mechanical and electrostatic interactions, which influence the state of cell–matrix adhesion contacts and on that basis the state of single cells. Viscoelasticity of matrix influences accumulated stress within a monolayer and on that basis the correlation of cell migration [38]. Intensive cell stress accumulation can perturb and even suppress cell migration. This cause–consequence relation was to be discussed based on (1) the rate of change the cell packing density [15] and (2) the force balance formulated by modified the model proposed by Murray et al. [15]. The cell speed has been correlated with the matrix stiffness. The speed of migrating cells is lower at softer matrices due to weak traction and cell slipping [39]. However, high matrix stiffness leads to a decrease in the migration speed caused by cell–matrix adhesion strengthening. Thus, medium matrix stiffness is suitable for cell migration. The relation between matrix stiffness and cell spreading can be expressed in the form of durotaxis flux [15] as follows:
where kd represents a measure of cell–matrix mechanical interactions, which influence the matrix displacement field and the state of cell–matrix adhesion contacts, n (r, τ) is the packing density of cells, and Gsm is the elastic shear modulus of a matrix. Besides of the matrix viscoelasticity, the matrix density is also influenced by cell–matrix interaction. Long-time change of the matrix density has the feedback impact on the packing density of cells as well. The phenomenon can be expressed in the form of haptotaxis flux [15] as follows:
where kh is the measure of cell–matrix interactions which influences the matrix density ρ. Change of the matrix density ρ caused by cell tractions has been described by Murray et al. [15] in the form of matrix convective flux as:
where is the matrix displacement field change expressed by Equation (6). Cell tractions induce water outflow from the hydrogel by changing its density as well as the rheological behavior. Polyelectrolyte nature of matrix influences cell–matrix electrostatic interactions as well as the state of cell–matrix adhesion contacts. The good example is Ca-alginate hydrogel matrix [30]. Electrostatic interchain and intrachain interactions caused by cell tractions influence the residual stress accumulation within a matrix , which has the feedback impact to the matrix local stiffness. The phenomenon can be expressed in the form of galvanotaxis flux [15] as follows:
where kg is the measure of cell–matrix electrostatic interactions, and ϕe is the local electrostatic potential.
Long-Time Change of Cell Packing Density
Cell packing density change is a product of cell–cell and cell–matrix interactions. It is self-regulated property due to the contact inhibition during collective cell migration and force-induced cell repolarization [17, 39]. Several processes have been accounted for such behaviors as follows: (1) contact inhibition of locomotion (CIL), (2) contact following of locomotion, and (3) contact enhancement of locomotion [17]. Cell packing density change during collective cell migration is expressed as follows [15]:
where is the flux of cells equal to , such that is the convective flux, is cell velocity (Equation 1), is the conductive flux, Deff is the effective diffusion coefficient, and , are haptotaxis, durotaxis, plitotaxis, galvanotaxis, and chemotaxis fluxes such that ϕ ≡ ρ is the matrix density for the haptotaxis, ϕ ≡ ϕe is the electrostatic potential for the galvanotaxis, ϕ ≡ c is the concentration of nutrients for the chemotaxis, ϕ ≡ Gsm is the local shear modulus of a matrix for the durotaxis, ϕ ≡ Gsc is the local shear modulus of cells for plitotaxis, whereas ki is the model parameter that accounts for various types of interactions such as mechanical, electrostatic, or chemical. Conductive flux accounts for cell response to a local variation of cell density. Haptotaxis, durotaxis, and galvanotaxis fluxes account for cell–matrix mechanical and electrostatic interactions. The tractions exerted by cells on the matrix generate gradients in (1) the matrix density and correspondingly the haptotaxis flux, (2) the electrostatic potential and the galvanotaxis flux, and (3) the matrix stiffness and the durotaxis flux [15]. Chemotaxis flux accounts for cell response to a concentration of nutrients [15]. Plitotaxis flux represents the consequence of cell–cell mechanical interactions, which leads to the establishing of gradients in cell shear modulus. Cell mitosis is neglected at this time scale. Rieu et al. [40] reported that diffusion coefficient for collectively migrated endodermal cells is , whereas for ectodermal cells the diffusion coefficient is . If the conductive mechanism is dominant, the model Equation (12) becomes the second Fick's law. In this case, the solution for the density is oscillatory in space. If the convective mechanism is dominant, the oscillatory change of the cell packing density can be induced only by oscillatory change of the cell velocity. At this step of consideration, it is necessary to determine which mechanism is dominant convective or conductive during 2D cell migration. To do so, we postulated following condition:
1. if , the conductive mechanism is dominant, and
2. if , the convective mechanism is dominant.
where tC is the period of long-time oscillations equal to tC ≈ 4 − 6 h [2, 3], and Lmax is the maximum velocity correlation length. As the cell packing density increases and cells become more dense and slow down their movement, the correlation length first increases to ~10-cell lengths or Lmax ~ 150 μm and later decreases [41, 42]. The result of this simple calculation points out that the convective mechanism dominantly influences the cell packing density change, while the conductive mechanism can be neglected. This finding indicates that oscillatory changes of cell packing density come primarily from the oscillatory change of cell velocity.
Cell long-time rearrangement is described by interrelation between the following variables such as (1) the displacement of cells (Equation 1) and corresponding cell volumetric and shear strains, (2) the displacement of matrix (Equation 6) and corresponding matrix volumetric and shear strains, (3) the cell packing density n (Equation 12), and (4) the matrix density ρ (Equation 10). Displacement fields of cells and matrix induce generation of strains. The strains lead to generation of the corresponding stresses based on the proposed constitutive models for cells and for a matrix. Oscillatory change of one variable induces oscillatory changes of the others. For deeper understanding of this oscillatory dynamic, it is necessary to formulate the force balance for (1) monolayer expansion and (2) cell swirling motion within a confluent monolayer.
The Force Balance
The force balance is responsible for oscillatory patterning the cell long-time rearrangement. Murray et al. [15] formulated the momentum balance by neglecting inertia effects as . They supported this assumption by pointing out the fact that the corresponding Re number is low. The force balance proposed by Murray et al. [15] should be expanded by accounting for the additional surface tension force which significantly influences the monolayer free expansion [43]. The surface tension has been recognized as one of the key parameters, which influences cell aggregate rounding after uniaxial compression [27]. The aggregate rounding occurs via collective cell migration [27]. The resulted force balance can be expressed as follows:
where is the cell traction force, k is an elastic constant [15], is the surface tension force, γst is the surface tension, is the cell displacement field, is the viscoelastic force per unit volume equal to , is the cell residual stress (Equation 5), and is the matrix residual stress. Consequently, the viscoelastic force accounts for cell and matrix contributions. The is the resistive force directed always opposite to the direction of migration. The surface tension force always acts in order to decrease a surface and on that basis to decrease a surface free energy. When cells undergo the forward flow during monolayer expansion, both forces and act in the direction opposite of migration in order to resist this movement. However, when cells undergo the backward flow driven by the surface tension force , the viscoelastic force acts in the direction opposite of backward flow. The traction force acts in the direction of cell migration and influences the rate of cell expansion depending on the rheological behavior of a matrix [3, 15, 30]. The force balance is established and perturbed many times during collective cell migration. These perturbations are primarily induced by accumulation of the residual stress within a multicellular system [8, 9] and by cell adaptation under stress conditions [16]. In order to completely understand this complex dynamic of cell long-time rearrangement, it is necessary to distinguish (1) equilibrium regimens for which and (2) perturbed regimens for which in various experimental conditions. Every perturbation induces change of cell velocity and corresponding strain rates and , and on that basis provokes the cell rheological response, which can lead to a local softening or stiffening of monolayer parts. Local stiffening represents a consequence of the cell residual stress accumulation [9]. Consequently, the momentum balance can be expressed in the form of inertial wave equation:
where is the material derivative [44]. The left-hand side of Equation (14) corresponds to the resultant force. Inertial waves, i.e., inertial oscillations, are a type of mechanical waves. The perturbations of the force balance, caused by cell viscoelasticity, represent the main cause for generation of (1) propagative waves during monolayer free expansion and (2) standing waves during collective cell migration within a confluent monolayer. Consequently, various types of perturbations were to be elaborated in more details.
Propagative Waves Generation in a Freely Expanded Monolayer: Modeling Consideration
The free expansion of a cell monolayer has been considered in 2D by using Cartesian coordinates such that (where vx and vy are the velocity components) [2]. The corresponding momentum balance can be expressed as follows:
For x-direction:
For y-direction:
The monolayer expansion occurs in two opposite directions, i.e., x ∈ (0, L(τ)) and x ∈ (0, − L(τ)). The main characteristic of propagative waves is that (1) normal stress component σcxx and corresponding strain rate are in phase quadrature; (2) normal stress component is always tensional; and (3) velocity and cell tractions are uncorrelated [2, 5]. These periodic extensions of multicellular domains lead to alternate softening and stiffening of cell monolayer. The periodic change of the rheological behavior is connected to the forward flow and backward flow, which is experimentally confirmed by Serra-Picamal et al. [2]. These forward flow and backward flow were shown schematically in Figure 3.
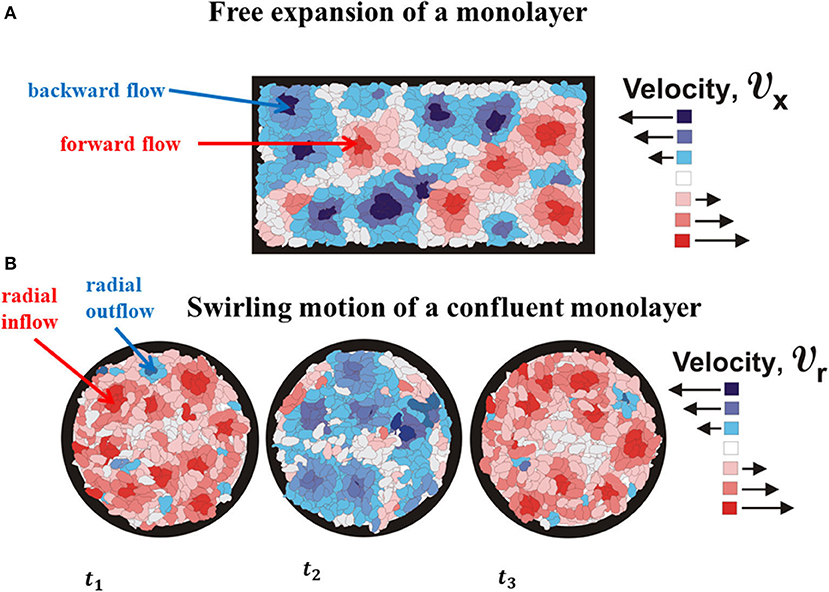
Figure 3. The schematic presentation of (A) cell forward and backward flows as the characteristics of propagative waves and (B) cell outflow and inflow as the characteristics of standing waves.
Serra-Picamal et al. [2] considered a free expansion of Madin-Darbvy canine kidney type II cells on polyacrylamide gels. Cellular domains that undergo forward flow can be divided into two regimens: (1) initial, unlimited cell migration, which corresponds to the condition that cell velocity increases with x, i.e., ; and (2) final limited cell migration, which corresponds to the condition that cell velocity decreases with x, i.e., (where is the volumetric strain rate in x-direction equal to and vcx is the x-component of cell velocity) [2]. Maximum velocity for the forward flow is [2]. The characteristic of the domains with maximum cell velocity is the intensive normal and shear residual stresses accumulation up to ~ 400 Pa [2]. Cellular domains that undergo backward flow are unstable primarily due to collisions with surrounding cell domains, which undergo the forward flow. These collisions additionally reduce the cell velocity within surrounding domains under forward flow. The lifetime of domains under backward flow is shorter than the period of oscillations due to (1) domain collisions and (2) rapid decrease in the surface tension force, which drives the backward flow. The phenomenon will be explained in detail in a few steps.
The initial unlimited forward flow of cellular domains leads to their extension. When the extension becomes significant, it induces (1) an increase in the resistive force caused by accumulation of the residual stress, which leads to the monolayer local stiffening; and (2) an increase in the surface tension force . Both forces act to suppress the cell forward flow (Figure 4A).
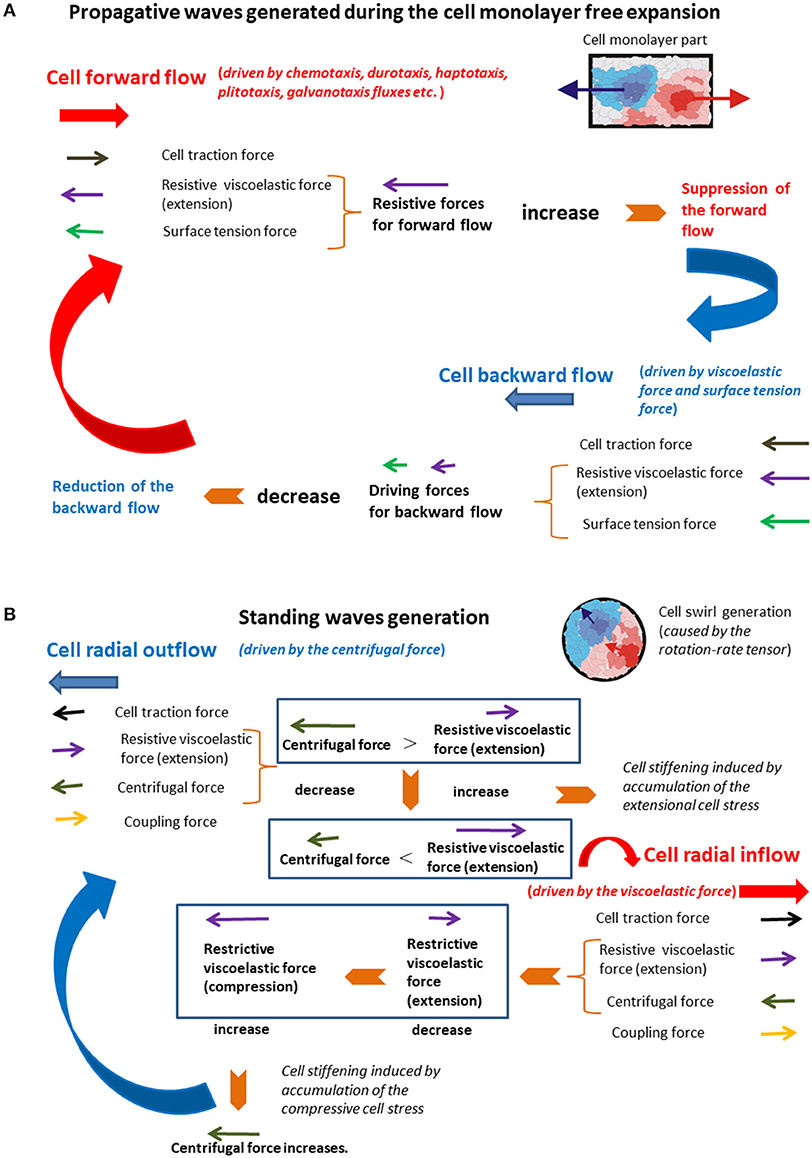
Figure 4. (A,B) The schematic presentation of the force balance for the generation of (A) propagative waves and (B) standing waves.
This state corresponds to the limited forward flow. Cell domains that correspond to the unlimited forward flow conditions are softer than those related to the limited forward flow conditions due to an accumulation of the cell residual stress. The local stiffening of the monolayer, which corresponds to the limited forward flow regime, is induced by the extension of adhesion contacts and force-induced repolarization (FIR) [17]. When the cell velocity tends to zero and the surface tension force becomes large enough, they induce onset of the backward flow by decreasing the displacement (thus reducing the surface tension force itself), which leads to rapid reduction of the backward flow. Collision of backward flow domains with surrounding domains under forward flow additionally suppresses the backward flow. This backward flow leads to the monolayer local softening and decreases in both forces and , which establishes the unlimited forward flow again. The action of the viscoelastic force to forward flow and backward flow is not symmetric and induce delay effects. The action of viscoelastic force and the surface tension force in order to suppress the forward flow and generate the backward flow are responsible for periodical extension of the monolayer in the form of propagative waves. Stiffer domains, which correspond to the limited forward flow regimen, form some kind of supracellular network within a monolayer. This supracellular network has a main role in keeping cellular integrity during the monolayer free expansion. The supracellular network formation is experimentally confirmed by Serra-Picamal et al. [2]. After consideration of the standing waves generation, the comparative analysis of the main characteristics of both types of waves was to be performed from the standpoint of single cells.
Standing Waves Generation in Confluent Cell Monolayers
Collective cell migration within a confluent monolayer leads to cell swirling motion [3]. The prerequisite of cell swirl appearing is the reduction of cell polarity alignment (LA) and strong CIL as reported by Lin et al. [45]. Weak LA and strong CIL can be established under confluent environment. Collective cell migration induces a gradient of velocity field during shear flow. The gradient of the velocity field can be decomposed into its symmetric and antisymmetric parts [where is the symmetric shear-rate tensor equal to and is the antisymmetric rotation-rate tensor equal to ]. The tensor is responsible for the cell swirling motion if the conditions of weak LA and strong CIL are satisfied [45]. Cell swirling motion within a confluent monolayer has been considered in 2D by using cylindrical coordinates, i.e., (where vcr is the radial component and vcθ is the azimuthal component of velocity) [3]. A circular cell motion induces the generation of internal centrifugal force equal to responsible for radial extension of the swirl parts and local radial outflow such that vcr > 0. The centrifugal force decreases with an increase in r. Consequently, the action of the centrifugal force is more intensive in the swirl core region in comparison with the peripheral region. The viscoelastic force is the resistive force and acts against centrifugal force in order to suppress cell migration. The traction force acts in the direction of cell migration and influences the rate of cell spreading depending on the rheological behavior of a matrix [3, 15, 30]. The surface tension force can be neglected during collective cell migration within a confluent monolayer.
The corresponding momentum balance can be expressed as follows:
For r-direction:
For θ-direction:
where the internal centrifugal is equal to , and the force that accounts for coupling between radial elongation (or compression) with azimuthal shear flow is expressed as . The coupling force FCL acts to reinforce the radial flow [22].
The standing waves represent a characteristic of local cell rearrangement, which leads to swirling motion. The main characteristics of standing waves are (1) the radial velocity and cell tractions are uncorrelated, (2) normal stress component σcrr and the corresponding strain rate are uncorrelated, (3) normal stress component is simultaneously tensional and compressional, and (4) time derivative of the stress component is in phase with the corresponding strain rate component [3]. Coordinated motion of close-packed cell monolayer with confining border leads to local swirling. Critical diameter of swirls is ~ 250 μm, above which global rotation is substituted by smaller vortices and transient coordinated flow. This value of the critical diameter is expected if we have in mind that the velocity correlation length is ~ 150 μm [5].
Notbohm et al. [3] considered confluent migration of Madin-Darbvy canine kidney type II cells on polyacrylamide gels. They reported that radial component of velocity vcr simultaneously changes a direction every ~ 4to6 h. The velocity vcr is approximately constant within domains Δr ~ 30to40 μm during the time period Δτ ~ 1to2 h and fluctuates in the same direction within a time period of ~ 4to6 h [3]. The corresponding local strain rate is during the time period Δτ ~ 1to2 h. If the , it means that the corresponding strain component is εcrr ≈ const. The maximum radial velocity is equal to , while the maximum normal residual stress is ~ 300 Pa for extension and ~ − 300 Pa for compression. The swirling motion of the viscoelastic multicellular system induces generation of the standing waves. This type of waves will be considered in the context of cell inflow and outflow within a swirl (Figure 3). Presence of inflow and outflow during a cell swirling motion is recognized experimentally by Notbohm et al. [3]. These inflow and outflow are shown schematically in Figure 4B.
Radial extension of swirl parts (the cell outflow for vcr > 0 and during Δτ, [3]) caused by the action of the centrifugal force induces intensive coupling between radial elongation flow and azimuthal shear flow and an increase in the viscoelastic force , which leads to the local system stiffening. The system stiffening leads to a decrease in the cell velocity component vcθ, as well as a decrease in the centrifugal force, which causes the cell radial inflow and consequently the local compression of swirl parts. The inflow is characterized by the radial component of velocity such that vcr < 0 and during Δτ [3]. The inflow induces change of the viscoelastic force direction from extension to compression, which results in the increase in the centrifugal force. Consequently, the viscoelastic (elongation) force resists the outflow, while the viscoelastic (compressive) force resists the inflow. The increase in the centrifugal force leads to the system outflow again characterized by the radial component of velocity vcr > 0. The centrifugal force is larger in the swirl core region in comparison with the peripheral region. Consequently, the inflow and outflow events are more intensive in the core region as was experimentally observed by Notbohm et al. [3]. The action of the viscoelastic force to the inflow and outflow is not symmetric and induces delay effects [22]. These delay effects can induce time shift between inflow and outflow. This time shift induces perturbations of inflow–outflow dynamic, which leads to altered extension and compression of the swirl parts. These long-time cycles correspond to standing waves. Differences between these two types of mechanical waves were to be discussed from the standpoint of single cells.
Results and Discussion
The aim of this theoretical consideration is to emphasize the role of viscoelasticity in provoking apparent inertial effects and generating the oscillatory mechanical instabilities in the form of standing waves and propagative waves within multicellular systems caused by collective cell migration. The propagative waves are generated during monolayer expansion, while the standing waves are generated during the cell swirling motion within a confluent monolayer. These flow instabilities represent a characteristic of the elastic turbulence that occurs under low Re number. The phenomenon has been experimentally confirmed during flow of various viscoelastic systems such as polymer liquids [23, 25], and it has been recognized in experiments of 2D collective cell migration but has not been explained properly yet [1–3]. The elastic turbulence is induced primarily by viscoelastic force, which acts against a movement of the system constituents. The system viscoelastic response under migration is a product of the energy storage and energy dissipation caused by its structural ordering. The structural ordering accounts for orientation and deformation of the system constituents in the direction of flow, which can induce significant accumulation of residual stress and the system stiffening. The system stiffening changes the characteristic of flow, which has the feedback impact to its rheological behavior. This cause–consequence cycle can be understood in the form of apparent inertial effects, which leads to generation of mechanical waves [22].
Multicellular systems are much complex than polymer liquids, but their viscoelastic nature significantly influences characteristics of collective cell migration [8, 9]. In this case, the system structural ordering accounts for cumulative effects of various interrelated processes at cellular and supracellular levels. Processes at cellular level are cell activation, polarization, signaling, and changes the state of cell–cell and cell–matrix adhesion contacts [16, 20, 32, 46]. Processes at the supracellular level account for cumulative effects of processes at the cellular level. These are polarity alignment, polarity-flow alignment, contact regulation of locomotion, and FIR [17, 33, 47].
Generation of mechanical waves caused by collective cell migration accounts for cause–consequence relations between (1) cell packing density n (r, τ) change (Equation 12) as the result of cell–cell and cell–matrix interactions described by convective, conductive, haptotaxis, durotaxis, galvanotaxis, plitotaxis, and chemotaxis fluxes; (2) matrix density ρ(r, τ) change (Equation 10) as the result of cell–matrix interactions described by convective flux caused by cell tractions; (3) force balance equation (Equation 14), which relates cell velocity with viscoelasticity of multicellular system; viscoelasticity of a matrix; cell surface tension; cell tractions; cell packing density; and matrix density.
A long-time cell rearrangement during monolayer expansion is accomplished by local forward flow and backward flow. The forward flow is divided into two regimens unlimited forward flow and limited forward flow. The limitations come from the action of the viscoelastic force against migration. The forward flow induces an accumulation of the extensional residual stress and an increase in the resistive viscoelastic force, which leads to the stiffening of monolayer parts and suppresses cell migration. The forward flow also induces an increase in cell displacement field and on that basis an increase in the surface tension force. Once the forward flow is suppressed, the surface tension force induces the backward flow, which leads to (1) a decrease in the surface tension force itself and (2) the softening of the monolayer part. The backward flow decreases rapidly because of (1) a decrease in the surface tension force and (2) collisions with surrounding domains under forward flow. This softening results in a decrease in the viscoelastic force. Lower values of the viscoelastic force as well as the surface tension force induce forward flow of the monolayer again. Those long-time cycles repeat many times in the form of the propagative waves [2].
A long-time cell rearrangement during the cell swirling motion (within a confluent monolayer) should be considered in the context of cell radial inflow and outflow. The confluence induces reduction of cell polarity alignment, which is essential for appearing cell swirls [45]. The inflow and outflow are induced by action of the centrifugal force against the viscoelastic force. The centrifugal force leads to radial extension of swirl parts, which results in the cell outflow. This radial extension causes an increase in the viscoelastic force, which leads to the system local stiffening. The viscoelastic force suppresses cell migration by increasing the residual stress accumulation, which results in a decrease in the centrifugal force. The consequence of the centrifugal force decrease is the radial cell inflow, which leads to the softening of swirl parts. This softening causes a decrease in the viscoelastic force and consequently the increase in the centrifugal force responsible for the cell outflow again. Those long-time cycles repeat many times in the form of the standing waves [3].
Both types of waves represent a consequence of apparent inertial effects. The apparent inertial effects are related to the periodic generation of (1) the backward flow during monolayer expansion and (2) the inflow during a cell swirling motion. The maximum velocity for (1) inflow and outflow is , and (2) forward flow and backward flow is . The maximum extensional stress accumulated during (1) forward flow is ~ 300 Pa and (2) outflow is ~ 400 Pa. It would be interesting to calculate maximum extensional stress necessary to break cell–cell adherens junction (AJs). AJs are cadherin–catenin complexes linked to actin filaments. Cadherins are transmembrane glycoproteins containing an extracellular domain that mediates cell–cell adhesion via homophilic or heterophilic interactions and an intracellular domain that controls signaling cascades involved in a variety of cellular processes, including polarity, gene expression, etc. [7]. E-cadherin bond breakage requires the force of ~ 200 nN, while the maximum area of single AJ is ~ 100 μm2 [48]. It corresponds to the extensional stress equal to ~ 2 kPa. This result means that forward flow and backward flow and inflow and outflow are not capable to perturb the integrity of multicellular system.
The main difference between propagative waves generated during monolayer expansion and standing waves generated during cell swirling motion within a confluent monolayer is related to oscillatory stress change. Generated propagative waves induce damped oscillatory change of the extensional residual stress, whereas the compressive stress is not generated based on the experimental data by Serra-Picamal et al. [2] (Figure 2A). To the contrary with the propagative waves, the generation of standing waves induces altered extension and compression [3] (Figure 2B). Corresponding stress oscillations were not damped during time period of 24 h. This difference can be discussed in the context of two cellular processes: (1) contact regulation of locomotion (CRL) and (2) FIR. The CRL depends strongly on the cell–cell collision angle [15, 36]. While the forward flow and backward flow act parallel to the direction of migration, the inflow and outflow act perpendicular to the direction of migration. The forward flow and backward flow intensify cell head-to-tail interactions and induce periodic cell repolarization in the direction of flow by keeping the strong of AJs [39]. Reinforced AJs are capable to resist strain and reduce residual stress accumulation [49]. Consequently, the backward flow induces a decrease in the extensional stress rather than to create cell compression. The inflow and outflow intensify cell side-to-side interactions, which can induce cell depolarization and weakening of AJs [16]. Consequently, the inflow can lead to the accumulation of compressive residual stress.
Model developed can be applied to describe generation of mechanical waves within 3D multicellular systems. Standing waves as a characteristic of the cell swirling motion (1) can be generated during migration of strongly connected cell clusters through dense environment made by cells in passive (resting) state during a tissue development [9] and (2) have been observed during migration of the internal cell group within a Neural crest supracell caused by contractions of an actin cable [18, 19]. Propagative waves could be generated during collective cell migration of stratified epithelium under in vivo conditions [18].
The rheological behavior of a matrix influences cell–cell and cell–matrix interactions and through the viscoelastic force influences the rate of cell spreading, as well as characteristics of generated mechanical waves.
Conclusion
Oscillatory instabilities in the form of mechanical waves are generated during collective cell migration such as propagative waves and standing waves. The propagative waves are generated during monolayer free expansion, whereas standing waves are generated during cell swirling motion of a confluent monolayer. Significant attempts have been made to describe the main characteristics of mechanic waves. The main characteristics of standing waves are (1) the radial velocity and cell tractions are uncorrelated; (2) radial stress component σcrr and the corresponding strain rate are uncorrelated; (3) radial stress component is simultaneously tensional and compressional; and (4) time derivative of the stress component is in a phase with the corresponding strain rate. The main characteristic of propagative waves is that (1) normal stress component σcxx and corresponding strain rate are in phase quadrature; (2) normal stress component is always tensional; and (3) velocity and cell tractions are uncorrelated. However, a little is reported about the influence of the monolayer viscoelasticity on generation of mechanical waves. Mechanical waves have recognized during flow of various viscoelastic systems under low Re number. The phenomenon is called the elastic turbulence. The elastic turbulence has been quantified by the ratio between two dimensionless parameters such Weissenberg number and Reynolds number. These oscillatory flow instabilities have also been monitored experimentally during 2D collective cell migration.
Propagative waves represent the consequence of cell forward flow and cell backward flow during monolayer expansion driven by interrelation between forces such as the viscoelastic force, the traction force, and the surface tension force. These forces influence the rate of change of momentum and lead to periodic extensions in the direction of flow. Standing waves represent the consequence of cell radial inflow and outflow during swirling motion driven by the interrelation between the centrifugal force, the viscoelastic force, and the traction force, while the influence of the surface tension force can be neglected. This force balance leads to the periodic extension and compression in the direction perpendicular to flow. The apparent inertial effects represent the characteristic of (1) the backward flow during monolayer free expansion and (2) the inflow during the cell swirling motion within a confluent monolayer.
Additional experiments are necessary in order to determine a long-time constitutive model for 2D multicellular systems caused by collective cell migration and correlate the migrating patterns with the residual stress distribution and the rate of its change. Cell long-time rearrangement can be controlled by matrix viscoelasticity. This theoretical consideration could help in deeper understanding of various biological processes by which an organism develops its shape and heals wounds in the context of the mechanism underpinning the epithelial expansion.
Author Contributions
IP-L: conceptualization, methodology, and writing—original draft preparation. MM: illustrations and writing—review and editing. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the Ministry of Education, Science and Technological Development of the Republic of Serbia (Contract No. 451-03-68/2020-14/200135).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Authors would like to thank Dr. Giovanni Cappello for useful discussion which inspired this work.
References
1. Tambe DT, Croutelle U, Trepat X, Park CY, Kim JH, Millet E, et al. Monolayer stress microscopy: limitations, artifacts, and accuracy of recovered intercellular stresses. PLoS ONE. (2013) 8:e551721-13. doi: 10.1371/journal.pone.0055172
2. Serra-Picamal X, Conte V, Vincent R, Anon E, Tambe DT, Bazellieres E, et al. Mechanical waves during tissue expansion. Nat Phys. (2012) 8:628–34. doi: 10.1038/nphys2355
3. Notbohm J, Banerjee S, Utuje KJC, Gweon B, Jang H, Park Y, et al. Cellular contraction and polarization drive collective cellular motion. Biophys J. (2016) 110:2729–38. doi: 10.1016/j.bpj.2016.05.019
4. Peyret G, Mueller R, Alessandro J, Begnaud S, Marcq P, Me‘ge RM, et al. Sustained oscillations of epithelial cell sheets. Biophys J. (2019) 117:464–78. doi: 10.1016/j.bpj.2019.06.013
5. Petrolli V, Boudou T, Balland M, Cappello G. Oscillations in collective cell migration. In: Pajic-Lijakovic I, Barriga E, editors. Viscoelasticity Collective Cell Migration. Elsevier (2020). Available online at: https://www.elsevier.com/books/viscoelasticity-and-collective-cell-migration/pajic-lijakovic/978-0-12-820310-1
6. Blanchard GB, Fletcher AG, Schumacher LJ. The devil is in the mesoscale: mechanical and behavioural heterogeneity in collective cell movement. Sem Cell Dev Biol. (2019) 93:46–54. doi: 10.1016/j.semcdb.2018.06.003
7. Barriga EH, Mayor R. Adjustable viscoelasticity allows for efficient collective cell migration. Sem Cell Dev Biol. (2019) 93:55–68. doi: 10.1016/j.semcdb.2018.05.027
8. Pajic-Lijakovic I, Milivojevic M. Long-time viscoelasticity of multicellular surfaces caused by collective cell migration – multi-scale modeling considerations. Sem Cell Dev Biol. (2019) 93:87–96. doi: 10.1016/j.semcdb.2018.08.002
9. Pajic-Lijakovic I, Milivojevic M. Collective cell migration and residual stress accumulation: rheological consideration. J Biomech. (2020) 108:109898. doi: 10.1016/j.jbiomech.2020.109898
10. Doxzen K, Vedula SRK, Leong MC, Hirata H, Gov NS, Kabla AJ, et al. Guidance of collective migration by substrate geometry. Integr Biol. (2013) 5:1026–35. doi: 10.1039/c3ib40054a
11. Deforet M, Hakim V, Yevick H, Duclos G, Silberzan P. Emergence of collective modes and tri-dimensional structures from epithelial confinement. Nat Comm. (2014) 5:3747. doi: 10.1038/ncomms4747
12. Kocgozlu L, Saw TB, Le AP, Yow I, Shagirov M, Wong E, et al. Epithelial cell packing induces distinct modes of cell extrusions. Curr Biol. (2016) 26:2942–50. doi: 10.1016/j.cub.2016.08.057
13. Tlili S, Gauquelin E, Li B, Cardoso O, Ladoux B, Delanoë-Ayari H, et al. Collective cell migration without proliferation: density determines cell velocity and wave velocity. R Soc Open Sci. (2018) 5:172421. doi: 10.1098/rsos.172421
14. Banerjee S, Utuje KJC, Marchetti MC. Propagating stress waves during epithelial expansion. Phys Rev Lett. (2015) 114:228101. doi: 10.1103/PhysRevLett.114.228101
15. Murray JD, Maini PK, Tranquillo RT. Mechanochemical models for generating biological pattern and form in development. Phys Rep. (1988) 171:59–84. doi: 10.1016/0370-1573(88)90003-8
16. Iyer KV, Gomez RP, Paijmans J, Julicher F, Eaton S. Epithelial viscoelasticity is regulated by mechanosensitive e-cadherin turnover. Curr Biol. (2019) 29:578–91.e5. doi: 10.1016/j.cub.2019.01.021
17. Alert R, Trepat X. Physical models of collective cell migration. Annu Rev Condens Matter Phys. (2020) 11:77–101. doi: 10.1146/annurev-conmatphys-031218-013516
18. Shellard A, Mayor R. Supracellular migration – beyond collective cell migration. J Cell Sci. (2019) 132:jcs226142. doi: 10.1242/jcs.226142
19. Shellard A, Mayor R. Rules of collective migration: from the wildebeest to the neural crest. Phil Trans R Soc B. (2020) 375:20190387. doi: 10.1098/rstb.2019.0387
20. Pajic-Lijakovic I, Milivojevic M. Viscoelasticity of multicellular surfaces. J Biomech. (2017) 60:1–8. doi: 10.1016/j.jbiomech.2017.06.035
21. Pajic-Lijakovic I. The basic concept of viscoelasticity. In: Pajic-Lijakovic I, Barriga E, editors. Viscoelasticity Collective Cell Migration. Elsevier (2020). Available online at: https://www.elsevier.com/books/viscoelasticity-and-collective-cell-migration/pajic-lijakovic/978-0-12-820310-1
22. Groisman A, Steinberg V. Mechanism of elastic instability in Couette flow of polymer solutions. Exp Phys Fluids. (1998) 10:2451–63. doi: 10.1063/1.869764
23. Groisman A, Steinberg V. Elastic turbulence in a polymer solution flow. Nature. (2000) 405:53–5. doi: 10.1038/35011019
24. Steinberg V. Scaling relations in elastic turbulence. Phys Rev Lett. (2019) 123:234501. doi: 10.1103/PhysRevLett.123.234501
25. Larson RG. Flow-induced mixing, demixing, and phase transitions in polymeric fluids. Rheol Acta. (1992) 31:497–520. doi: 10.1007/BF00367006
26. Groisman A, Steinberg V. Couette-taylor flow in a dilute polymer solution. Phys Rev Lett. (1996) 77:1480–3. doi: 10.1103/PhysRevLett.77.1480
27. Marmottant P, Mgharbel A, Kafer J, Audren B, Rieu JP, Vial JC, et al. The role of fluctuations and stress on the effective viscosity of cell aggregates. Proc Natl Acad Sci USA. (2009) 106:17271–5. doi: 10.1073/pnas.0902085106
28. Pajic-Lijakovic I, Milivojevic M. Jamming state transition and collective cell migration. J Biol Eng. (2019) 13:73. doi: 10.1186/s13036-019-0201-4
29. Pajic-Lijakovic I, Levic S, Nedovic V, Bugarski B. Biointerface dynamics-multi scale modeling considerations. Col Surf B Biointerf. (2015) 132:236–45. doi: 10.1016/j.colsurfb.2015.05.013
30. Pajic-Lijakovic I, Milivojevic M, Levic S, Trifkovic K, Stevanovic-Dajic Z, Radosevic R, et al. Matrix resistance stress: a key parameter for immobilized cell growth regulation. Proc Biochem. (2017) 52:30–43. doi: 10.1016/j.procbio.2016.10.017
31. Friedl P, Alexander S. Cancer invasion and the microenvironment: plasticity and reciprocity. Cell. (2011) 147:992–1009. doi: 10.1016/j.cell.2011.11.016
32. Petrungaro G, Morelli L, Uriu K. Information flow in the presence of cell mixing and signaling delays during embryonic development. Sem Cell Dev Biol. (2019) 93:26–35. doi: 10.1016/j.semcdb.2018.09.008
33. Koride S, Loza AJ, Sun SX. Epithelial vertex models with active biochemical regulation of contractility can explain organized collective cell motility. APL Bioeng. (2018) 2:031906. doi: 10.1063/1.5023410
34. Pajic-Lijakovic I, Milivojevic M. Viscoelasticity of multicellular systems caused by collective cell migration: dynamics at the biointerface. Europ Biophys J. (2020) 49:253–265. doi: 10.1007/s00249-020-01431-2
35. Kane KIW, Moreno EL, Lehr CM, Hachi S, Dannert R, Sanctuary R, et al. Determination of the rheological properties of Matrigel for optimum seeding conditions in microfluidic cell cultures. AIP Advances. (2018) 8:125332. doi: 10.1063/1.5067382
36. Chaudhuri O, Gu L, Darnell M, Klumpers D, Bencherif SA, Weaver JC, et al. Substrate stress regulates cell spreading. Nat Commun. (2015) 6:6364. doi: 10.1038/ncomms7365
37. Zhao X, Huebsch N, Mooney DJ, Suo Z. Stress-relaxation behaviour in gels with ionic and covalent crosslinks. J App Phys. (2010) 107:063509 1–5. doi: 10.1063/1.3343265
38. Murrell M, Kamm R, Matsudaira P. Substrate viscosity enhances correlation in epithelial sheet movement. Biophys J. (2011) 101:297–306. doi: 10.1016/j.bpj.2011.05.048
39. Pathak A, Kumar S. Independent regulation of tumor cell migration by matrix stiffness and confinement. Proc Natl Acad Sci USA. (2012) 109:10334–9. doi: 10.1073/pnas.1118073109
40. Rieu JP, Upadhyaya A, Glazier JA, Ouchi NB, Sawada Y. Diffusion and deformations of single hydra cells in cellular aggregates. Biophys J. (2000) 79:1903–14. doi: 10.1016/S0006-3495(00)76440-X
41. Petitjean L, Reffay M, Grasland-Mongrain E, Poujade M, Ladoux B, Buguin A, et al. Velocity fields in a collectively migrating epithelium. Biophys J. (2010) 98:1790–800. doi: 10.1016/j.bpj.2010.01.030
42. Puliafito A, Hufnagel L, Neveu P, Streichan S, Sigal A, Fygenson DK, et al. Collective and single cell behavior in epithelial contact inhibition. Proc Natl Acad Sci USA. (2012) 109:739–44. doi: 10.1073/pnas.1007809109
43. Zhao T, Zhang Y, Wei Q, Shi X, Zhao P, Chen LQ, et al. Active cell-matrix coupling regulates cellular force landscapes of cohesive epithelial monolayers. NPJ Comp Mat. (2018) 10:1–6. doi: 10.1038/s41524-018-0069-8
44. Bird RB, Stewart WE, Lightfoot EN. Transport Phenomena. New York, NY: John Wiley & Sons INC (1960).
45. Lin SZ, Ye S, Xu GK, Li B, Feng XQ. Dynamic migration modes of collective cells. Biophys J. (2018) 115:1826–35. doi: 10.1016/j.bpj.2018.09.010
46. Zemel A, Rehfeldt F, Brown ACX, Disher DE, Safran SA. Optimal matrix rigidity for stress fiber polarization in stem cells. Nat Phys. (2010) 6:468–73. doi: 10.1038/nphys1613
47. George M, Bullo F, Campàs O. Connecting individual to collective cell migration. Sci Rep. (2017) 7:9720. doi: 10.1038/s41598-017-10069-8
48. Pinheiro D, Bellaiche Y. Mechanical force-driven adherens junction remodeling and epithelial dynamics. Dev Cell. (2018) 47:3–19. doi: 10.1016/j.devcel.2018.09.014
Keywords: multi scale nature of viscoelasticity of multicellular system, collective cell migration, apparent inertia effects, the elastic turbulence, rheological behavior of extracellular matrix
Citation: Pajic-Lijakovic I and Milivojevic M (2020) Mechanical Oscillations in 2D Collective Cell Migration: The Elastic Turbulence. Front. Phys. 8:585681. doi: 10.3389/fphy.2020.585681
Received: 21 July 2020; Accepted: 14 September 2020;
Published: 06 November 2020.
Edited by:
Aljaz Godec, Max Planck Institute for Biophysical Chemistry, GermanyCopyright © 2020 Pajic-Lijakovic and Milivojevic. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ivana Pajic-Lijakovic, aXZhQHRtZi5iZy5hYy5ycw==
 Ivana Pajic-Lijakovic
Ivana Pajic-Lijakovic Milan Milivojevic
Milan Milivojevic