- Department of Industrial Engineering, Università degli Studi di Napoli “Federico II”, Napoli, Italy
A careful inspection of the cumulative curve of confirmed COVID-19 infections in Italy and in other hard-hit countries reveals three distinct phases: i) an initial exponential growth (unconstrained phase), ii) an algebraic, power-law growth (containment phase), and iii) a relatively slow decay. We propose a parsimonious compartment model based on a time-dependent rate of depletion of the susceptible population that captures all such phases for a plausible range of model parameters. The results suggest an intimate interplay between the growth behavior, the timing and implementation of containment strategies, and the subsequent saturation of the outbreak.
1. Introduction
The coronavirus disease 2019 (COVID-19) is an infectious respiratory illness caused by the newly discovered virus strain SARS-CoV-2 [1–3]. The on-going COVID-19 outbreak started in Wuhan (Hubei, China) in late December 2019 and spread quickly to all Chinese provinces and to several countries, prompting the World Health Organization (WHO) to declare a pandemic on March 11, 2020 [4]. The high human-to-human transmission rate and clinical severity of the infection have raised enormous concern on an international scale, with governments worldwide taking drastic and unprecedented measures to contain the disease spread. Despite the efforts, 34,804,348 people have been infected world-wide, and 1,030,738 have died as of October 4, 2020 [5].
The global emergency has issued a massive call-to-arms for researchers from several disciplines. Among the various fields of study, epidemic modeling is of utmost importance to inform policy makers about the required sanitary system capacity, to guide the design of containment strategies, and to assess their effectiveness in real time [6]. Humongous efforts are currently on-going to develop accurate mathematical models of the disease spread, ranging from top-down (i.e., static curve fitting) approaches [7, 8] to dynamic compartment models of various degree of complexity [9, 10]. The latter class is especially appealing, as it allows a rather straightforward incorporation and testing of physics-based hypotheses. Nonetheless, the modeling process is hindered by several factors, including incomplete knowledge of the disease, as well as the challenging incorporation of containment strategies and unreported cases [11]. Retrospective analysis of data from countries that have already overcome a turning point in the COVID-19 epidemic is highly valuable to inspire and calibrate novel mathematical models with predictive capabilities.
In this paper, we aimed to derive a physics-based dynamic compartment model able to adhere as much as possible to the qualitative and quantitative nature of the observed data. To this purpose we take Italy, one of the early hard-hit countries that has overcome a first epidemic wave, as a primary modeling source. We start by preliminarily analyzing the epidemic data in Section 2, drawing important qualitative observations about the scaling laws of the growth and decay of the outbreak. Guided by these, in Section 3 we propose a compartment model that incorporates key epidemiological features of the disease and is able to reproduce the observed trends. In Section 4 we report and discuss the results of the proposed model, and compare them to official data from Italy. Concluding remarks are given in Section 5.
2. Data Analysis of the COVID-19 Outbreak in Italy
The outbreak in Italy started on February 21, 2020, when a local cluster of COVID-19 cases was identified in Codogno (Lodi). The Italian government immediately ordered lockdown for 11 hard-hit Northern-Italy municipalities; however, the rapid and seemingly uncontrolled growth of infections in the following days led to increasingly tight regulations on the entire national territory, including closure of schools (March 4) and, shortly after, quarantine (March 9). The measures proved to be effective and, following the decline of the number of confirmed cases, the containment measures were gradually released since May 4. As of early July, the epidemic was mostly under control, with a reproductive number
It is instructive to preliminarily analyze the cumulative curve of laboratory-confirmed infections
Figure 1A shows a logarithmic plot of confirmed COVID-19 cases in Italy in a restricted time interval (from February 22 to April 30), while Figure 1B reports new daily cases in a linear plot for the same time range. Three distinct phases can be inferred from static data analysis:
(1) an initial exponential growth, which is typical of unconstrained outbreaks, with best-fit exponent
(2) a phase of algebraic growth, starting approximately on March 6 and ending on March 18. The power-law scaling
as shown in the inset of Figure 1A. The plot shows a distinct plateau within the mentioned time window with
(3) a relatively slow decay. The decay phase is deliberately assumed to start from the turning point of the epidemic, that occurred on March 23, after roughly 5 days of “transition” from the previous algebraic phase. The slow decay is evident from Figure 1B, which shows a markedly asymmetric bell-shaped curve with respect to the turning point.
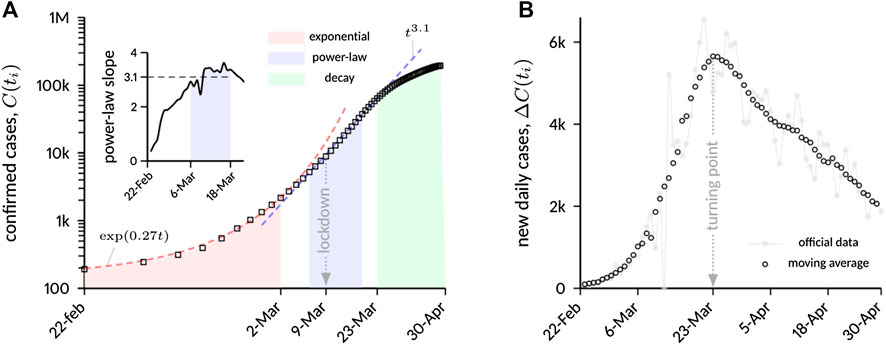
FIGURE 1. (A) Cumulative number of laboratory-confirmed COVID-19 infections in Italy. A moving average with a time window of 7 days was applied to the data to filter weekly fluctuations in case reporting. After an initial exponential growth, on March 6 the increase starts to follow a scaling law
Evidence of algebraic growth has been observed and described elsewhere for other countries, including China [14] as well as other European countries [15], with exponents generally ranging from 2 to 4. From a fundamental perspective, this behavior has been attributed to structural changes in the topology of the population network that supports the epidemic spreading. Several authors [15, 16] have resorted to the small-world hypothesis [17] to justify the algebraic growth. More in general, spatial networks where short links are favored over long-range connections have been shown to produce power-law exponents in close similarity with the observed COVID-19 dynamics [18]. Similarly, the asymmetric decay has been put into some (empirical) connection with the simultaneous presence of a persistent phase of algebraic growth, in contrast with other countries where the epidemic has been characterized by a rather symmetric rise-and-fall behavior [19]. In this regard, graphs with a power-law degree distribution are known to produce outbreaks characterized by a polynomial growth followed by an exponential decay [20]. A functional form of this type was successfully used to fit COVID-19 data from over 100 countries [21], supporting the evidence that the nature of the underlying network is key to the infectious dynamics, and that growth and decay of the epidemic are indeed intimately connected. Network effects and their relationship with COVID-19 epidemic trends are further discussed in Ref. 22.
The reported observations have important consequences on traditional modeling approaches. From the perspective of classical population growth models, standard logistic models appear to be inappropriate, as they provide symmetric S-shaped curves for the cumulative number of infections; in contrast, the generalized Richard’s model (GRM) has been shown to provide a rather accurate description of the epidemic in Chinese provinces [8]. While the GRM can provide sub-exponential growth and asymmetric decline [23], it is known to lack clear epidemiological significance [24]. Compartment models are richer in terms of physics and allow addition of several degrees of freedom. The basic version of the celebrated Susceptible–Infectious–Removed (SIR) framework [25] can be easily transformed, under mild assumptions, into a logistic model [26], therefore suffering from the same above-mentioned limitations. Several refined SIR-like approaches have been proposed, particularly aiming at quantifying undetected cases [27] and at modeling the effect of containment policies [14, 28]. These have been modeled in most cases by means of a piecewise constant transmission rate (or, alternatively, by changing the local reproduction number) [29], or possibly by incorporating the effects of individual reaction [30].
Reconciling algebraic growth with mean-field models is not straightforward. Recently Ref. 21, observed that a general solution of the type
We conjecture that the three phases reported above are inherently coupled by endogenous epidemic processes, and thus they can be accurately modeled into a unique framework that relies exclusively on physics-based assumptions and policy-driven changes of the model parameters. Inspired by M&B, we aim to propose a compartment model that is able to: 1) capture the power-law growth; 2) generate an asymmetric decay; 3) incorporate unreported cases.
3. Proposed Compartment Model
We propose a compact compartment model of SEIQR-type (Susceptible–Exposed–Infectious–Quarantined–Removed), whose schematic is shown in Figure 2. Although many more compartments can be added to increase the level of detail and supposedly the realism of the model, we rather opted for a parsimonious framework, while focusing primarily on the reproduction of the observed scaling laws. We note explicitly that the inclusion of the Q-compartment is highly warranted for countries characterized by strong government interventions, since identified infectious individuals are typically quarantined and therefore they are no longer able to spread the disease. On the contrary, the necessity of taking the incubation period into account via the E-class is currently debated, mainly due to incomplete understanding of the relationship between incubation and latency periods for SARS-CoV-2 infection. However, a certain time lag between infection and infectiousness (in either clinical or subclinical cases) has often been observed [2, 31]; therefore, we chose to include the exposed class with an average incubation period
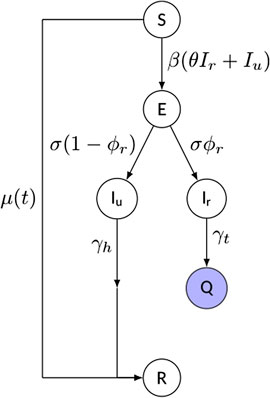
FIGURE 2. Schematic of the model and of its parameters (see text for details). The “quarantined” variable
Additional key features of the model include:
• a time-dependent rate of depletion of the susceptible population,
where
• an explicit distinction between reported and unreported cases. The infectious class has been split into reported (Ir) and unreported (Iu) individuals, modulated by a reporting rate
Note that, for the sake of simplicity, we do not explicitly model the subsequent recovery/death of quarantined individuals, nor we distinguish between hospitalized and home-isolated patients; however, information in this regard can be inferred a-posterior once the temporal dynamics of
In summary, the temporal dynamics of the compartments is governed by the following system of ordinary differential equations:
where
and
The model defined by Eq. 3 has eight free parameters; some of them can be set a-priori based on epidemiological, clinical or policy-related evidence. The incubation time
4. Results and Discussion
Numerical simulations of the outbreak in Italy were obtained upon integration of Eq. 3 for the time range from February 24 to June 30, 2020. Table 1 summarizes the values of the entire set of model parameters, including those assigned a-priori and the ones inferred from the data. After several preliminary tests aimed to circumvent overfitting issues, we chose to optimize the parameter space containing

TABLE 1. Optimal values of the estimated model parameters for the simulation of the outbreak in Italy.
Main results are shown in Figure 3. Figure 3A reports the temporal evolution of
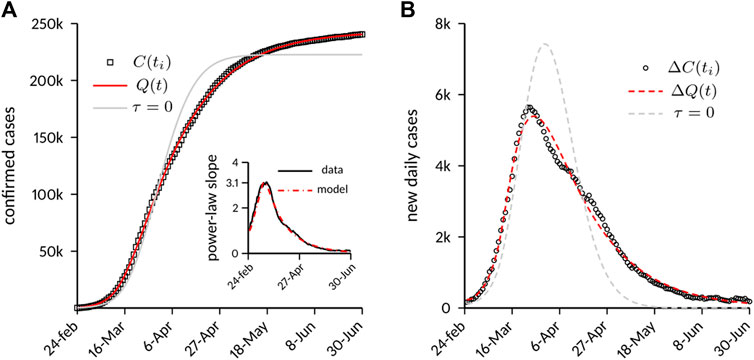
FIGURE 3. Case numbers in Italy compared to model predictions. (A) Cumulative number of laboratory-confirmed infections. The model predictions are shown both with the full model and with a variant obtained by setting
Of note, the model was able to capture the decay phase of the epidemic correctly without any further change of the parameters. This circumstance suggests a strong link between the decay dynamics and the timing and implementation of the containment strategies. It is conjectured that an incomplete depletion of the susceptible population during the lockdown (provided by the exponential decay of
We also tested a variant of the model that more closely resembles the original M&B approach, with a constant depletion rate of the susceptible population
In light of the above mentioned results and observations, it is instructive to directly quantify the effects of
showing that τ is explicitly responsible for the incomplete removal. Although it is possible, in principle, to derive a closed-form expression for
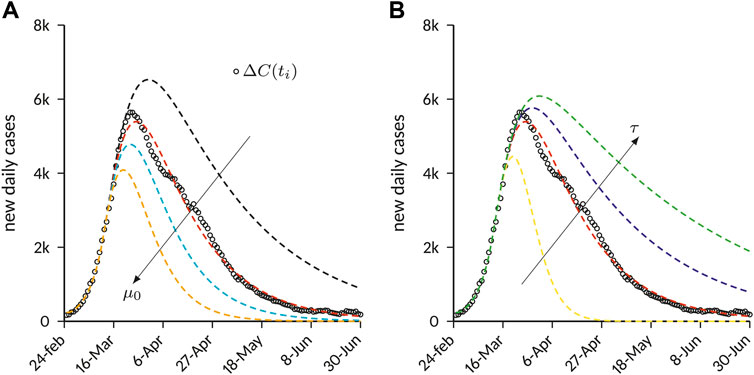
FIGURE 4. Effects of containment on the number of new daily cases predicted by the SEIQR compartment model. The results are obtained with the parameters provided in Table 1, and by varying the parameters
With regards to the functional form of the time-varying depletion rate
In such case, assuming that in a certain time interval
where
The role of subclinical infected with regards to the spread of the disease is one of the most debated epidemiological and biomedical issues in the context of the COVID-19 outbreak [37]. Accurate studies in small-scale, “laboratory-like” contexts with blanket testing showed that a substantial fraction of SARS-CoV-2-positive individuals can display very mild symptoms or even remain completely asymptomatic throughout the course of the infection, while having a viral load comparable to that of symptomatic patients [38–40]. Here we found a very good fit for values of the reporting rate in the range
It is worth to remark, in general, that we were able to generate outbreaks in good agreement with official data for a certain range and combination of the model parameters. While we did not quantify sensitivity, nor we carried out specifical statistical analyses of the confidence interval of such parameters, we chose the set of values that yielded the best accordance with the observed scaling laws (exponential growth rate, peak power-law slope, decay dynamics) and a reasonable value for the basic reproduction number. For the best-fit reported in Table 1, we get
5. Concluding Remarks
In this study, we started from the preliminary observation that in countries such as Italy, the cumulative number of infections displays an initial exponential amplification, followed by a power-law growth and a markedly asymmetric saturation behavior. We conjecture that these three phases are intimately connected and can be described by the interplay between the contagion process and the behavioral changes/containment policies acting on the population over comparable time scales.
Based on this hypothesis, and inspired by previous work by Ref. 14, we proposed a SEIQR-type compartment model with the following salient features: i) a compartment for unreported (asymptomatic) infected, that are supposed to play a major role in the spread of the disease; ii) a time-dependent rate of depletion of the susceptible population, which allows for a non-zero asymptotic residual of susceptible individuals.
The model was able to accurately reproduce the entire epidemic course in Italy, including quantitative agreement with exponential growth and power-law slope, for a plausible range of the model free parameters, with only one steep change of the parameters driven by the introduction of strict containment strategies. This circumstance suggests that the timing and implementation of containment policies (as quantified by model parameters
The proposed modeling framework could be profitably used to gain insights and predictions on the so-called “second wave” of the epidemic, which (as of early October 2020) appears to be hitting Italy and other countries. To this purpose, the model could be modified by 1) introducing a release rate of protected individuals (from compartment R to S), that reflects the relaxation of containment measures as well as the gradually diminished perception of the pandemic; 2) accounting for a different testing policy: while only symptomatic individuals were tested during the first wave of the epidemic, the introduction of contact tracing and screening procedures has certainly contributed to increase the reporting rate
This study presents a number of simplifications and limitations that, however, do not affect the main conclusions. Among others, the number of confirmed infections is influenced by the number of tests performed each day, an aspect that was only weakly incorporated into the model via the (constant) fraction of reported cases
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
FC designed the study, conducted the data analysis, developed the mathematical model, interpreted the data and wrote the article.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author is indebted to Valerio Carandente, Marco Cozzo, Vincenzo Di Savino and Andrea Piccolo for insightful discussions.
References
1. Zhu N, Zhang D, Wang W, Li X, Yang B, Song J, et al. A novel coronavirus from patients with pneumonia in China, 2019. N Engl J Med (2020). 382:727–33. doi:10.1056/NEJMoa2001017
2. Li Q, Guan X, Wu P, Wang X, Zhou L, Tong Y, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N Engl J Med (2020). 382:1199–207. doi:10.1056/NEJMoa2001316
3. Wu F, Zhao S, Yu B, Chen Y-M, Wang W, Song Z-G, et al. A new coronavirus associated with human respiratory disease in China. Nature (2020). 579:265–9. doi:10.1038/s41586-020-2008-3
5.World Health Organization. Coronavirus disease 2019 (COVID-19) weekly epidemiological update—5 october 2020 (2020). https://www.who.int/publications/m/item/weekly-epidemiological-update---5-october-2020.
6. Adam D. Special report: the simulations driving the world's response to COVID-19. Nature (2020). 580:316–8. doi:10.1038/d41586-020-01003-6
7. Shen CY. Logistic growth modelling of COVID-19 proliferation in China and its international implications. Int J Infect Dis (2020). 96:582–9. doi:10.1016/j.ijid.2020.04.085.
8. Wu K, Darcet D, Wang Q, Sornette D. Generalized logistic growth modeling of the COVID-19 outbreak in 29 provinces in China and in the rest of the world (2020). arXiv preprint arXiv:2003.05681.
9. Prem K, Liu Y, Russell TW, Kucharski AJ, Eggo RM, Davies N, et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: a modelling study. Lancet Public Health (2020). 5:e261–70. doi:10.1016/S2468-2667(20)30073-6
10. Jit A, Russell T, Diamond C, Liu Y, Edmunds J, Funk S, et al. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect Dis (2020). 20:P553–8. doi:10.1016/S1473-3099(20)30144-4
11. Jewell NP, Lewnard JA, Jewell BL. Predictive mathematical models of the COVID-19 pandemic. J Am Med Assoc (2020). 323:1893–4. doi:10.1001/jama.2020.6585
12. Ministero della Salute (2020). COVID‐19 weekly monitoring reportAvailable from: http://www.salute.gov.it/nuovocoronavirus (Accessed July 6, 2020).
13. Dong E, Du H, Gardner L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect Dis (2020). 20:533–4. doi:10.1016/S1473-3099(20)30120-1
14. Maier BF, Brockmann D. Effective containment explains subexponential growth in recent confirmed COVID-19 cases in China. Science (2020). 368:742–6. doi:10.1126/science.abb4557
15. Manchein C, Brugnago EL, da Silva RM, Mendes CFO, Beims MW. Strong correlations between power-law growth of COVID-19 in four continents and the inefficiency of soft quarantine strategies. Chaos (2020). 30:041102. doi:10.1063/5.0009454
17. Watts DJ, Strogatz SH. Collective dynamics of 'small-world' networks. Nature (1998). 393:440–2. doi:10.1038/30918
18. Medo M. Contact network models matching the dynamics of the COVID-19 spreading (2020). arXiv preprint ArXiv:2003.13160.
19. Singer HM. The COVID-19 pandemic: growth patterns, power law scaling, and saturation. Phys Biol (2020). 17(5):055001. doi:10.1088/1478-3975/ab9bf5
20. Vazquez A. Polynomial growth in branching processes with diverging reproductive number. Phys Rev Lett (2006). 96:038702. doi:10.1103/physrevlett.96.038702
21. Bodova K, Kollar R. Emerging algebraic growth trends in SARS-CoV-2 pandemic data. Phys Biol (2020). 20:42. doi:10.1088/1478-3975/abb6db
22. Thurner S, Klimek P, Hanel R. A network-based explanation of why most COVID-19 infection curves are linear. Proc Natl Acad Sci USA (2020). 117:22684–9. doi:10.1073/pnas.2010398117
23. Chu KH. Fitting the Gompertz equation to asymmetric breakthrough curves. J Environ Chem Eng (2020). 8:103713. doi:10.1016/j.jece.2020.103713
24. Li J, Lou Y. Characteristics of an epidemic outbreak with a large initial infection size. J Biol Dynam (2016). 10:366–78. doi:10.1080/17513758.2016.1205223
25. Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc Roy Soc Lond (1927). 115:700–21. doi:10.1098/rspa.1927.0118
26. Postnikov EB. Estimation of COVID-19 dynamics “on a back-of-envelope”: does the simplest SIR model provide quantitative parameters and predictions? Chaos Solit Fractals (2020). 135:109841. doi:10.1016/j.chaos.2020.109841
27. Li R, Pei S, Chen B, Song Y, Zhang T, Yang W, et al. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science (2020). 368:489–93. doi:10.1126/science.abb3221
28. Hellewell J, Abbott S, Gimma A, Bosse NI, Jarvis CI, Russell TW, et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Global Health (2020). 8:e488–96. doi:10.1016/S2214-109X(20)30074-7
29. Munday G, Blanchini F, Bruno R, Colaneri P, Di Filippo A, Di Matteo A, et al. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat Med (2020). 26:855–60. doi:10.1038/s41591-020-0883-7
30. Lin Q, Zhao S, Gao D, Lou Y, Yang S, Musa SS, et al. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int J Infect Dis (2020). 93:211–6. doi:10.1016/j.ijid.2020.02.058
31. Lauer SA, Grantz KH, Bi Q, Jones FK, Zheng Q, Meredith HR, et al. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann Intern Med (2020). 172:577–82. doi:10.7326/M20-0504
32. Deng W, Bao L, Liu J, Xiao C, Liu J, Xue J, et al. Primary exposure to SARS-CoV-2 protects against reinfection in rhesus macaques. Science (2020). 369:818–23. doi:10.1126/science.abc5343
33. Lv P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci (2002). 180:29–48. doi:10.1016/S0025-5564(02)00108-6
34. Sun G-Q, Wang S-F, Li M-T, Li L, Zhang J, Zhang W, et al. Transmission dynamics of COVID-19 in Wuhan, China: effects of lockdown and medical resources. Nonlinear Dynam (2020). 16:1–13. doi:10.1007/s11071-020-05770-9
35. Li M-T, Sun G-Q, Zhang J, Zhao Y, Pei X, Li L, et al. Analysis of COVID-19 transmission in Shanxi Province with discrete time imported cases. Math Biosci Eng (2020). 17:3710–20. doi:10.3934/mbe.2020208
36. Li Y, Yao L, Wei T, Tian F, Jin D-Y, Chen L, et al. Presumed asymptomatic carrier transmission of COVID-19. J Am Med Assoc (2020). 323:1406–7. doi:10.1001/jama.2020.2565
37. Wang M, Yokoe DS, Havlir DV. Asymptomatic transmission, the Achilles’ heel of current strategies to control COVID-19. N Engl J Med (2020). 382:2158–60. doi:10.1056/NEJMe2009758
38. Lavezzo E, Franchin E, Ciavarella C, Cuomo-Dannenburg G, Barzon L, Del Vecchio C, et al. Suppression of a SARS-CoV-2 outbreak in the Italian municipality of Vo′. Nature (2020). 584, 425–9. doi:10.1038/s41586-020-2488-1
39. Mizumoto K, Kagaya K, Zarebski A, Chowell G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship. Euro Surveill (2020). 25:2000180. doi:10.2807/1560-7917.ES.2020.25.10.2000180
40. Russell TW, Hellewell J, Jarvis CI, van Zandvoort K, Abbott S, Ratnayake R, et al. Estimating the infection and case fatality ratio for coronavirus disease (COVID-19) using age-adjusted data from the outbreak on the Diamond Princess cruise ship, February 2020. Euro Surveill (2020). 25:200256. doi:10.2807/1560-7917.ES.2020.25.12.2000256
41. Flasche M, Bertuzzo E, Mari L, Miccoli S, Carraro L, Casagrandi R, et al. Spread and dynamics of the COVID-19 epidemic in Italy: effects of emergency containment measures. Proc Natl Acad Sci USA (2020). 117:10484–91. doi:10.1073/pnas.2004978117
42. Rinaldo Y, Eggo RM, Kucharski AJ. Secondary attack rate and superspreading events for SARS-CoV-2. Lancet (2020). 395:e47. doi:10.1016/s0140-6736(20)30462-1
Keywords: COVID-19, power-law growth, compartment model, containment strategies, unreported cases
Citation: Capuano F (2020) Modeling Growth, Containment and Decay of the COVID-19 Epidemic in Italy. Front. Phys. 8:586180. doi: 10.3389/fphy.2020.586180
Received: 22 July 2020; Accepted: 30 October 2020;
Published: 30 November 2020.
Edited by:
Zhen Wang, Hong Kong Baptist University, Hong KongReviewed by:
Matúš Medo, University of Electronic Science and Technology of China, ChinaGui-Quan Sun, North University of China, China
Copyright © 2020 Capuano. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francesco Capuano, ZnJhbmNlc2NvLmNhcHVhbm9AdW5pbmEuaXQ=
 Francesco Capuano
Francesco Capuano