- Skolkovo Institute of Science and Technology, Moscow, Russia
Tensor network algorithms seek to minimize correlations to compress the classical data representing quantum states. Tensor network algorithms and similar tools—called tensor network methods—form the backbone of modern numerical methods used to simulate many-body physics and have a further range of applications in machine learning. Finding and contracting tensor network states is a computational task, which may be accelerated by quantum computing. We present a quantum algorithm that returns a classical description of a rank-r tensor network state satisfying an area law and approximating an eigenvector given black-box access to a unitary matrix. Our work creates a bridge between several contemporary approaches, including tensor networks, the variational quantum eigensolver (VQE), quantum approximate optimization algorithm (QAOA), and quantum computation.
1 Introduction
Tensor network methods provide the contemporary state of the art in the classical simulation of quantum systems. A range of numerical and analytical tools have now emerged, including tensor network algorithms, to simulate quantum systems classically; these algorithms are based in part on powerful insights related to the area law [1–9]. The area law places bounds on quantum entanglement that a many-body system can generate, which translates directly to the amount of memory required to store a given quantum state; see, e.g., [8].
The leading classical methods to simulate random circuits for quantum computational supremacy demonstration are also based on tensor network contractions. Additionally, classical machine learning has been merged with matrix product states and other tensor network methods [10–14]. How might quantum computing accelerate tensor network algorithms?
Although tensor network tools have traditionally been developed to simulate quantum systems classically, we propose a quantum algorithm to approximate an eigenvector of a unitary matrix with bounded rank tensor network states. The algorithm works given only black-box access to a unitary matrix. In general, tensor network contraction can simulate any quantum computation.
We focus on 1D chains of tensors (matrix product states) due to some associated analytical simplifications; indeed, matrix product states can be approximated classically which offers an attractive gold standard to compare the quantum algorithm against. The general framework we develop applies equally well to 2D and, e.g., sparse networks (projected entangled pair states, etc.). However, an early merger between these topics is better situated to focus on 1D.
Even in 1D, tensor networks offer certain insights into quantum algorithms. For example, the maximal degree of entanglement can often be bounded in the description of the tensor network state itself. In other words, the bond dimension (the dimension of the wires) in the tensor network acts to bound the maximal entanglement. Merging quantum computation with ideas from tensor networks provides new tools to quantify the entanglement that a given quantum circuit can generate [15, 16].
For the sake of simplicity, we work in the black-box setting and assume access to a provided unitary Q. The black-box setting does not consider the implementation of Q. Prima facie, this appears to be a limitation; in practice, however, the restriction can easily be lifted. For example, in QAOA, the problem Hamiltonian can be applied for varying times, offering a natural extension of the oracle idea by giving Q a simple time dependence [17].
In Discussion, we drop the black-box access restriction and cast the steps needed to perform a meaningful near-term demonstration of our algorithm on a quantum computer, providing a low-rank approximation to eigenvectors of the quantum computers free- (or effective) Hamiltonian. The presented algorithm falls into the class of variational quantum algorithms [18–25]. It returns a classical description, in the form of a tensor network, of an eigenvector of an operator found through an iterative classical-to-quantum optimization process.
We present a general framework to determine tensor networks using quantum processors. We focus on 1D, which enables several results related to the maximum amounts of entanglement required to demonstrate these methods. This analysis is followed by a discussion focused on applications of these techniques and what might be required for a meaningful near-term experimental demonstration.
2 Methods
The algorithm we propose solves the following problem: given black-box access to a unitary Q, find any eigenvector of Q.
We work in the standard mathematical setting of quantum computing. We define n qubits arranged on a line and fix the standard canonical (computational) basis. We consider the commutative Hermitian subalgebra generated by the n-projectors:
where the subscript i denotes the corresponding ith qubit acted on by
Rank is the maximum Schmidt number (the nonzero singular values) across any of the
An ebit is the amount of entanglement contained in a maximally entangled two-qubit (Bell) state. A quantum state with q ebits of entanglement (quantified by any entanglement measure) has the same amount of entanglement (in that measure) as q Bell states. If a task requires l ebits, it can be done with l or more Bell states, but not with fewer. Maximally entangled states in
have
We parameterize a circuit family generating matrix product states with θ, a real vector with entries in
and
both of yet to be specied rank.
We will construct an objective function (Eq. 6) to minimize and hence to recover our approximate eigenvector. The choice of this function provides a desirable degree of freedom to further tailor the algorithm to the particular quantum processor at hand. We choose
and call
the log-likelihood function of the n-point correlator
The minimization of Eq. 6 corresponds to maximizing the probability of measuring each qubit in
Algorithm 1: Find successive tensor network approximations of an eigenvector of Q.
Choose the maximum number of ebits
Choose the maximum number of optimization iterations
for
Construct the ansatz
Set
for
Evaluate
Evaluate
Update
end for
Store
end for
return
The algorithm begins with rank-1 qubit states as
Minimization of the objective function Eq. 6 returns
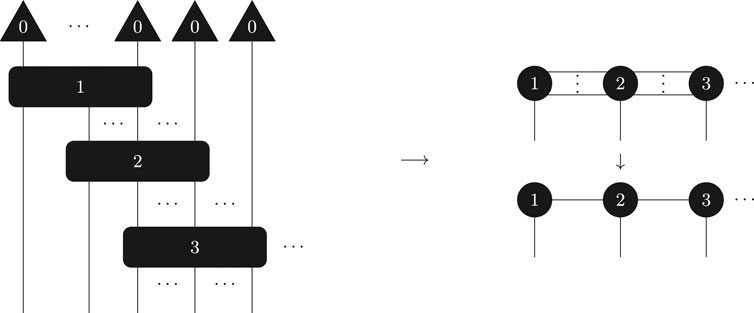
FIGURE 1. Example of a tensor network as a quantum circuit: (left) quantum circuit realization of a matrix product state with open boundary conditions; (right) using standard graphical rewrite rules—or by manipulating equations—one readily recovers the familiar matrix product state depiction as a “train of tensors.”
3 Results
The algorithm works given only oracle access to a unitary Q. The spectrum of Q is necessarily contained on the complex unit circle and so we note immediately that
with equality of the left-hand side if and only if
Importantly, the maximization over θ on the right-hand side of Eq. 9 corresponds to the minimization of the log-likelihood Eq. 6. We will then parameterize
which is valid for
Indeed, increasing the rank of the matrix product state approximation can improve the eigenvector approximation. Yet, it should be noted that ground state eigenvectors of physical systems are in many cases known to be well approximated with low-rank matrix product states [1–9]. This depends on the further properties of Q and is a subject of intensive study in numerical methods, further motivating the quantum algorithm we present here. We will develop our algorithm agnostic to Q, leaving a more specific near-term demonstration (in which Q is implemented); e.g., we will express any
In Eq. 11, the rank-r of the representation is embedded into the realization of the A’s. Quantum mechanics allows the deterministic generation of a class of isometries, where an isometry U that is also an endomorphism on a particular space is called unitary.
Matrix product states (Eq. 11) are not isometries, though correlation functions are readily calculated from them. Furthermore, matrix product states can be deterministically generated by the uniform quantum circuit given in Figure 1. Other isometric structures of interest include trees and the so-called Multiscale Entanglement Renormalization Ansatz (MERA) networks [3, 26–28].
Consider then a rank-r approximation to an eigenvector of Q. The blocks in Figure 1 represent unitary maps. These circuits act on at most
CNOT gates, where the method in [29] requires
Instead of preparing
where
where T orders the sequence by time and superscript k indexes the kth operator
We then consider vertical partitions of a quantum circuit with the n qubits positioned horizontally on a line. For an m-depth quantum circuit (where m is presumably bounded above by a low-order polynomial in n), the maximum number of two-qubit gates crossed in a vertical partition is never more than m. The maximum number of ebits generated by a fully entangling two-qubit CNOT gate is never more than a single ebit. We then consider the
ebits of entanglement. This immediately puts a lower bound of
In Figure 2, we demonstrate our algorithm for finding an eigenstate of randomly generated 5-qubit unitary matrices. For minimizing the function Eq. 6, we used the Broyden-Fletcher-Goldfarb-Shanno (BFGS) minimization method [30]. For each k ebit MPS, we place the k-layered hardware-efficient ansatz as the operators in blocks [21].
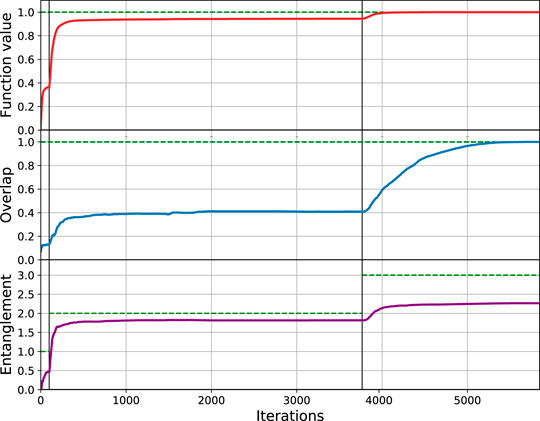
FIGURE 2. Algorithm demonstration on randomly generated 6-qubit unitaries Q: the value of Eq. 9(upper), overlap between the variational state and the closest eigenstate of Q(middle), and the von Neumann entropy of the subsystem of the first three qubits (lower). The vertical solid lines indicate the iteration numbers after which k, the number of ebits that the MPS ansatz can support, increases by 1. The plot is obtained by averaging over 10 randomly generated unitaries Q.
4 Discussion
We now turn to the realization of Q and sketch a possible demonstration for a near-term device. Polynomial-time simulation of Hamiltonian evolution is well known to be BQP-hard. This provides an avenue for Q to represent a problem of significant computational interest, as simulating quantum evolution and quantum factoring are in BQP. We aim to bootstrap properties of the quantum processor as much as possible to reduce resources for a realization; see, for example, [21].
Let
we can minimize the overall eigenvectors, which is NP-hard. Hence, finding even rank-1 states can be NP-hard. This provides a connection between our method and QAOA [31]. Similarly, we can also use this external minimization to connect our method to VQE [20]. However, our method provides a certificate that, on proper termination, the system is indeed in such a desired eigenstate.
When
is in turn QMA-hard. For example, pairing our procedure with an additional procedure (quantum phase estimation) to minimize Q, the overall eigenvectors would hence provide rank-k variational states and hence our methods provide a research direction which incorporates tensor network methods in works such as, e.g., [19–21]. It should however be noted that phase estimation adds significant experimental difficultly compared with the algorithm presented here and the algorithm is closer to VQE (with evident differences as listed above and in the main text).
For a near-term demonstration, we envision Q to be realized by bootstrapping the underlying physics of the system realizing Q, e.g., using the hardware-efficient ansatz [21]. For instance, one can realize Q as a modification of the systems free Hamiltonian using effective Hamiltonian methods (modulating local gates). This greatly reduces practical requirements on Q.
The interaction graph of the Hamiltonian generating Q can be used to define a PEPS tensor network (as it will have the same structure as the layout of the chip, it will no longer have the contractable properties of matrix product states, and yet is still of interest) [4]. The algorithm works otherwise unchanged, but the circuit acts on this interaction graph (instead of a line) to create a corresponding tensor network state (a quantum circuit in the form of, e.g., the variational ansatz). Tailored free evolution of the system Hamiltonian generates Q. Our algorithm returns a tensor network approximation of an eigenstate of Q.
The first interesting demonstrations of the quantum algorithm we have presented should realize rank-k tensor networks (matrix product state), and the corresponding tensor network can be realized with a few hundred gates for a system with a few hundred qubits.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found: GitHub, https://git.io/JkjvV.
Author Contributions
All authors conceived and developed the theory and design of this study and verified the methods. AK developed and deployed the code to collect numerical data. All authors contributed to interpreting the results and writing the manuscript.
Acknowledgements
AK and JB acknowledge support from agreement No. 014/20, Leading Research Center on Quantum Computing. AU acknowledges RFBR project No. 19-31-90159 for financial support. This manuscript has been released as a preprint as arXiv:1804.02398 (32).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Biamonte J. Charged string tensor networks. Proc Natl Acad Sci USA (2017) 114(10):2447. doi:10.1073/pnas.1700736114
2. Orús R. A practical introduction to tensor networks: matrix product states and projected entangled pair states. Ann Phys (2014) 349:117–58. doi:10.1016/j.aop.2014.06.013
3. Vidal G. Entanglement renormalization: an introduction. In: Carr LD., editor. Understanding quantum phase transitions. Boca Raton, United States: Taylor and Francis (2010) p. 756.
4. Verstraete F, Murg V, Cirac JI. Matrix product states, projected entangled pair states, and variational renormalization group methods for quantum spin systems. Adv Phys (2008) 57:143–224. doi:10.1080/14789940801912366
5. Cirac JI, Verstraete F. Renormalization and tensor product states in spin chains and lattices. J Phys Math Theor (2009) 42(50):504004. doi:10.1088/1751-8113/42/50/504004
6. Schollwöck U. The density-matrix renormalization group in the age of matrix product states. Ann Phys (2011) 326:96–192. doi:10.1016/j.aop.2010.09.012
7. Orús R. Advances on tensor network theory: symmetries, fermions, entanglement, and holography. Eur Phys J B (2014) 87:280. doi:10.1140/epjb/e2014-50502-9
9. Evenbly G, Vidal G. Tensor network states and geometry. J Stat Phys (2011) 145:891–918. doi:10.1007/s10955-011-0237-4
10. Cichocki A, Lee N, Oseledets I, Phan A-H, Zhao Q, Danilo P, et al. Tensor networks for dimensionality reduction and large-scale optimization: Part 1 low-rank tensor decompositions. Found Trends Machine Learn (2016) 9(4–5):249–429. doi:10.1561/2200000059
11. Cichocki A, Phan A-H, Zhao Q, Lee N, Oseledets I, Sugiyama M, et al. Tensor networks for dimensionality reduction and large-scale optimization: Part 2 applications and future perspectives. Found Trends Machine Learn (2017) 9(6):431–673. doi:10.1561/2200000067
12. Clark SR. Unifying neural-network quantum states and correlator product states via tensor networks. J Phys Math Theor (2018) 51(13):135301. doi:10.1088/1751-8121/aaaaf2
13. Huggins W, Patil P, Mitchell B, Whaley KB, Miles Stoudenmire E. Towards quantum machine learning with tensor networks. Quant Sci Technol (2019) 4(2):024001. doi:10.1088/2058-9565/aaea94
14. Ding L, Ran S-J, Wittek P, Cheng P, García RB, Su G, et al. Machine learning by unitary tensor network of hierarchical tree structure. New J Phys (2017) 21:073059. doi:10.1088/1367-2630/ab31ef
15. Biamonte JD, Morales MES, Koh DE. Entanglement scaling in quantum advantage benchmarks. Phys Rev (2020) 101(1):012349. doi:10.1103/PhysRevA.101.012349
16. Biamonte J, Bergholm V, Lanzagorta M. Tensor network methods for invariant theory. J Phys A Math Gener (2013) 46:475301. doi:10.1088/1751-8113/46/47/475301
17. Morales MES, Tlyachev T, Jacob B. Variational learning of grovers quantum search algorithm. Phys Rev (2018) 98(6):062333. doi:10.1103/PhysRevA.98.062333
18. Yung MH, Casanova J, Mezzacapo A, McClean J, Lamata L, Aspuru-Guzik A, et al. From transistor to trapped-ion computers for quantum chemistry. Sci Rep (2014) 4:3589. doi:10.1038/srep03589
19. McClean J, Romero J, Ryan B, Aspuru-Guzik A. The theory of variational hybrid quantum-classical algorithms. New J Phys (2016) 18:023023. doi:10.1088/1367-2630/18/2/023023
20. Peruzzo A, McClean J, Shadbolt P, Yung MH, Zhou XQ, Love PJ, et al. A variational eigenvalue solver on a photonic quantum processor. Nat Commun (2014) 5:4213. doi:10.1038/ncomms5213
21. Kandala A, Mezzacapo A, Temme K, Takita M, Brink M, Chow JM, et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature (2017) 549:242–6. doi:10.1038/nature23879
22. Jacob B. Universal variational quantum computation. Preprint repository name [Preprint] (2019) Available from: arXiv:1903.04500 (Accessed March 11, 2019).
23. Xia R, Kais S. Quantum machine learning for electronic structure calculations. Nat Commun (2018) 9(1):4195. doi:10.1038/s41467-018-06598-z
24. Grant E, Benedetti M, Cao S, Hallam A, Lockhart J, Stojevic V, et al. Hierarchical quantum classifiers. Npj Quant Inform (2018) 4:65. doi:10.1038/s41534-018-0116-9
25. Akshay V, Philathong H, Morales MES, Biamonte JD. Reachability deficits in quantum approximate optimization. Phys Rev Lett (2020) 124(9):090504. doi:10.1103/PhysRevLett.124.090504
26. Entanglement GV. Entanglement renormalization. Phys Rev Lett (2007) 99(22):220405. doi:10.1103/PhysRevLett.99.220405
27. Giovannetti V, Montangero S, Fazio R. Quantum Multiscale entanglement renormalization ansatz channels. Phys Rev Lett (2008) 101(18):180503. doi:10.1103/PhysRevLett.101.180503
28. Vidal G. Class of quantum many-body states that can be efficiently simulated. Phys Rev Lett (2008) 101(11):110501. doi:10.1103/PhysRevLett.101.110501
29. Möttönen M, Vartiainen JJ, Bergholm V, Salomaa MM. Quantum circuits for general multiqubit gates. Phys Rev Lett (2004) 93(13):130502. doi:10.1103/PhysRevLett.93.130502
31. Farhi E, Goldstone J, Gutmann S. A quantum approximate optimization algorithm. Preprint repository name [Preprint] (2014) Available from: arXiv:1411.4028 (Accessed November 14, 2014).
32. Jacob B, Kardashin A, Uvarov A. Quantum machine learning tensor network states. Preprint repository name [Preprint] (2018) Available from: arXiv:1804.02398 (Accessed April 06, 2014).
Keywords: quantum computing, quantum algorithms and circuits, tensor network algorithms, ground state, properties, machine learning, quantum information
Citation: Kardashin A, Uvarov A and Biamonte J (2021) Quantum Machine Learning Tensor Network States. Front. Phys. 8:586374. doi: 10.3389/fphy.2020.586374
Received: 23 July 2020; Accepted: 08 December 2020;
Published: 01 March 2021.
Edited by:
Sabre Kais, Purdue University, United StatesReviewed by:
Peter McMahon, Cornell University, United StatesKathleen Hamilton, Oak Ridge National Laboratory (DOE), United States
Copyright © 2021 Kardashin, Uvarov and Biamonte. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrey Kardashin, YW5kcmV5LmthcmRhc2hpbkBza29sdGVjaC5ydQ==
 Andrey Kardashin
Andrey Kardashin Alexey Uvarov
Alexey Uvarov Jacob Biamonte
Jacob Biamonte