Quantum Machine Learning Tensor Network States

Tensor network algorithms seek to minimize correlations to compress the classical data representing quantum states. Tensor network algorithms and similar tools—called tensor network methods—form the backbone of modern numerical methods used to simulate many-body physics and have a further range of applications in machine learning. Finding and contracting tensor network states is a computational task, which may be accelerated by quantum computing. We present a quantum algorithm that returns a classical description of a rank-r tensor network state satisfying an area law and approximating an eigenvector given black-box access to a unitary matrix. Our work creates a bridge between several contemporary approaches, including tensor networks, the variational quantum eigensolver (VQE), quantum approximate optimization algorithm (QAOA), and quantum computation.

1 Introduction

Tensor network methods provide the contemporary state of the art in the classical simulation of quantum systems. A range of numerical and analytical tools have now emerged, including tensor network algorithms, to simulate quantum systems classically; these algorithms are based in part on powerful insights related to the area law [1–9]. The area law places bounds on quantum entanglement that a many-body system can generate, which translates directly to the amount of memory required to store a given quantum state; see, e.g., [8].

The leading classical methods to simulate random circuits for quantum computational supremacy demonstration are also based on tensor network contractions. Additionally, classical machine learning has been merged with matrix product states and other tensor network methods [10–14]. How might quantum computing accelerate tensor network algorithms?

Although tensor network tools have traditionally been developed to simulate quantum systems classically, we propose a quantum algorithm to approximate an eigenvector of a unitary matrix with bounded rank tensor network states. The algorithm works given only black-box access to a unitary matrix. In general, tensor network contraction can simulate any quantum computation.

We focus on 1D chains of tensors (matrix product states) due to some associated analytical simplifications; indeed, matrix product states can be approximated classically which offers an attractive gold standard to compare the quantum algorithm against. The general framework we develop applies equally well to 2D and, e.g., sparse networks (projected entangled pair states, etc.). However, an early merger between these topics is better situated to focus on 1D.

Even in 1D, tensor networks offer certain insights into quantum algorithms. For example, the maximal degree of entanglement can often be bounded in the description of the tensor network state itself. In other words, the bond dimension (the dimension of the wires) in the tensor network acts to bound the maximal entanglement. Merging quantum computation with ideas from tensor networks provides new tools to quantify the entanglement that a given quantum circuit can generate [15, 16].

For the sake of simplicity, we work in the black-box setting and assume access to a provided unitary Q. The black-box setting does not consider the implementation of Q. Prima facie, this appears to be a limitation; in practice, however, the restriction can easily be lifted. For example, in QAOA, the problem Hamiltonian can be applied for varying times, offering a natural extension of the oracle idea by giving Q a simple time dependence [17].

In Discussion, we drop the black-box access restriction and cast the steps needed to perform a meaningful near-term demonstration of our algorithm on a quantum computer, providing a low-rank approximation to eigenvectors of the quantum computers free- (or effective) Hamiltonian. The presented algorithm falls into the class of variational quantum algorithms [18–25]. It returns a classical description, in the form of a tensor network, of an eigenvector of an operator found through an iterative classical-to-quantum optimization process.

We present a general framework to determine tensor networks using quantum processors. We focus on 1D, which enables several results related to the maximum amounts of entanglement required to demonstrate these methods. This analysis is followed by a discussion focused on applications of these techniques and what might be required for a meaningful near-term experimental demonstration.

2 Methods

The algorithm we propose solves the following problem: given black-box access to a unitary Q, find any eigenvector of Q.

We work in the standard mathematical setting of quantum computing. We define n qubits arranged on a line and fix the standard canonical (computational) basis. We consider the commutative Hermitian subalgebra generated by the n-projectors:

$P_i=|0\rangle \langle 0{|}_i,(1)$

where the subscript i denotes the corresponding ith qubit acted on by $P_i$, with the remainder of the state space acting on trivially. These form our observables.

Rank is the maximum Schmidt number (the nonzero singular values) across any of the $n-1$ stepwise partitions of the qubits on a line. Rank provides an upper bound on the bipartite entanglement that a quantum state can support; as will be seen, a rank-r state has at most $k={\text{log}}_2\left(r\right)$ ebits of entanglement. The quantum algorithm we present works by finding a sequence of maximally k ebit approximations, where the k’th approximation can be used to seed the $\left(k+1\right)$’th approximation.

An ebit is the amount of entanglement contained in a maximally entangled two-qubit (Bell) state. A quantum state with q ebits of entanglement (quantified by any entanglement measure) has the same amount of entanglement (in that measure) as q Bell states. If a task requires l ebits, it can be done with l or more Bell states, but not with fewer. Maximally entangled states in

${\mathrm{ℂ}}^d\otimes {\mathrm{ℂ}}^d(2)$

have ${\text{log}}_2\left(d\right)$ ebits of entanglement. The question is then to upper bound the maximum amount of entanglement a given quantum computation can generate, providing a coarse-graining to classify quantum algorithms in terms of both the circuit depth and the maximum ebits possible. For low-depth circuits, these arguments are surprisingly relevant.

We parameterize a circuit family generating matrix product states with θ, a real vector with entries in $\left[\mathrm{0,2}\pi \right)$. We consider action on the initial rank-1 state $|0\rangle =|0{\rangle }^{\otimes n}$ and define two states

$|\psi \left(\theta \right)\rangle =U^{†}\left(\theta \right)QU\left(\theta \right)|0\rangle (3)$

and

$|\tilde{\psi }\left(\theta \right)\rangle =U\left(\theta \right)|0\rangle ,(4)$

both of yet to be specied rank.

We will construct an objective function (Eq. 6) to minimize and hence to recover our approximate eigenvector. The choice of this function provides a desirable degree of freedom to further tailor the algorithm to the particular quantum processor at hand. We choose

$p_i\left(\theta \right)=\langle \psi \left(\theta \right)\left|P_i\right|\psi \left(\theta \right)\rangle (5)$

and call

$\mathrm{ℒ}\left(\theta \right)={\displaystyle \sum }_{i=1}^n\text{ln}{p}_i\left(\theta \right)(6)$

the log-likelihood function of the n-point correlator

${\displaystyle \prod }_{i=1}^n{p}_i\left(\theta \right).(7)$

The minimization of Eq. 6 corresponds to maximizing the probability of measuring each qubit in $|0\rangle$. This minimization can be done using a variety of optimization and machine learning algorithms. The following summarizes the steps of the algorithm.

Algorithm 1: Find successive tensor network approximations of an eigenvector of Q.

Choose the maximum number of ebits $k_{\text{max}}$

Choose the maximum number of optimization iterations $n_{\text{it}}$

for$k\leftarrow 1$ to $k_{\text{max}}$do

Construct the ansatz $U_k$ corresponding to a k ebit MPS

Set ${\mathit{\theta }}_k$ randomly

for$j\leftarrow 1$ to $n_{\text{it}}$do

Evaluate $\mathit{p}\left({\mathit{\theta }}_k\right)$

Evaluate $\mathrm{ℒ}\left(\mathit{p}\right)$

Update ${\mathit{\theta }}_k$ using a classical optimizer

end for

Store ${\mathrm{ℒ}}_k=\mathrm{ℒ}\left(\mathit{p}\right)$

end for

return${\left\{{\mathit{\theta }}_k\right\}}_{k=1}^{k_{\text{max}}},{\left\{{\mathrm{ℒ}}_k\right\}}_{k=1}^{k_{\text{max}}}$

The algorithm begins with rank-1 qubit states as

$|\tilde{\psi }\left(\theta \right)\rangle =\stackrel{n}{\underset{i=1}{\otimes }}\left(\text{cos}{\theta }_1^i|0\rangle +e^{-ı{\theta }_2^i}\text{sin}{\theta }_1^i|1\rangle \right).(8)$

Minimization of the objective function Eq. 6 returns $2n$ real numbers describing a local matrix product state. Approximations of higher rank are made by utilizing the quantum circuit structure given in Figure 1.

FIGURE 1

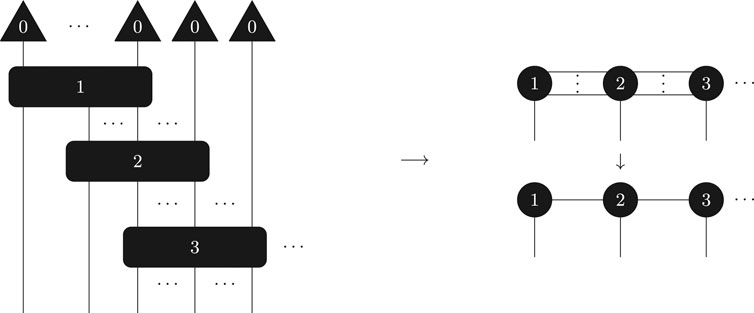
FIGURE 1. Example of a tensor network as a quantum circuit: (left) quantum circuit realization of a matrix product state with open boundary conditions; (right) using standard graphical rewrite rules—or by manipulating equations—one readily recovers the familiar matrix product state depiction as a “train of tensors.”

3 Results

The algorithm works given only oracle access to a unitary Q. The spectrum of Q is necessarily contained on the complex unit circle and so we note immediately that

$1=\underset{\varphi }{\text{max}}{\left|\langle \varphi \left|Q\right|\varphi \rangle \right|}^2\ge \underset{\theta }{\text{max}}{\left|\langle 0|\psi \left(\theta \right)\rangle \right|}^2(9)$

$=\underset{\theta }{\text{max}}{\left|\langle \tilde{\psi }\left(\theta \right)\left|Q\right|\tilde{\psi }\left(\theta \right)\rangle \right|}^2$

with equality of the left-hand side if and only if $|\varphi \rangle$ is an eigenvector of Q. One advantage of the presented method is that it terminates when the measurement reaches a given value. This implies that the system is in an eigenstate. Such a certificate is not directly established using other variational quantum algorithms.

Importantly, the maximization over θ on the right-hand side of Eq. 9 corresponds to the minimization of the log-likelihood Eq. 6. We will then parameterize $\tilde{\psi }\left({\theta }_k\right)$, where k denotes a k ebit matrix product state of interest. Learning this matrix product state recovers an approximation to an eigenvector of Q. With a further promise on Q that all eigenvectors have a rank-p matrix product state representation, we conclude that $r<p$ implies a fundamental error in our approximation. We consider then that the r’th singular value of the state takes the value ε. It then follows that the one-norm error scales with $O\left(\epsilon \right)$ and the two-norm error scales only with $O\left({\epsilon }^2\right)$. In general, we arrive at the monotonic sequence ordered by the following relation:

$1\ge \underset{{\theta }_{k+1}}{\text{max}}{\left|\langle \tilde{\psi }\left({\theta }_{k+1}\right)\left|Q\right|\tilde{\psi }\left({\theta }_{k+1}\right)\rangle \right|}^2(10)$

$\ge \underset{{\theta }_k}{\text{max}}|\langle \tilde{\psi }\left({\theta }_k\right)\left|Q\right|\tilde{\psi }\left({\theta }_k\right)\rangle {|}^2$

which is valid for $k=1$ to $\lfloor n/2\rfloor$ (minimum to maximum possible number of ebits).

Indeed, increasing the rank of the matrix product state approximation can improve the eigenvector approximation. Yet, it should be noted that ground state eigenvectors of physical systems are in many cases known to be well approximated with low-rank matrix product states [1–9]. This depends on the further properties of Q and is a subject of intensive study in numerical methods, further motivating the quantum algorithm we present here. We will develop our algorithm agnostic to Q, leaving a more specific near-term demonstration (in which Q is implemented); e.g., we will express any $|\tilde{\psi }\left(\theta \right)\rangle$ as a matrix product state as

$\left|\tilde{\psi }\left(\theta \right)\rangle ={\displaystyle \sum }_{q,s,\dots ,n}{A}_q^{\left[{\theta }_q\right]}{A}_s^{\left[{\theta }_s\right]}\cdots A_n^{\left[{\theta }_n\right]}\right|q,s,\dots ,n\rangle .(11)$

In Eq. 11, the rank-r of the representation is embedded into the realization of the A’s. Quantum mechanics allows the deterministic generation of a class of isometries, where an isometry U that is also an endomorphism on a particular space is called unitary.

Matrix product states (Eq. 11) are not isometries, though correlation functions are readily calculated from them. Furthermore, matrix product states can be deterministically generated by the uniform quantum circuit given in Figure 1. Other isometric structures of interest include trees and the so-called Multiscale Entanglement Renormalization Ansatz (MERA) networks [3, 26–28].

Consider then a rank-r approximation to an eigenvector of Q. The blocks in Figure 1 represent unitary maps. These circuits act on at most ${\lceil \text{log}}_2\left(r\right)\rceil$ qubits. Hence, each of these blocks has at most $r^2$ real degrees of freedom in $\left[\mathrm{0,2}\pi \right)$. The general realization of these blocks using the typical basis of CNOT gates and arbitrary local unitaries can be done by a range of methods; see, e.g., [29]. A commonly used theoretical lower bound requires

$\frac{1}{4}\left(r^2-3{\text{log}}_{2}r-1\right)(12)$

CNOT gates, where the method in [29] requires $r^2$ local qubit gates and did not reach this theoretical lower bound of CNOT gates. The total number of single qubits and CNOT gates nevertheless scales as $O\left(r^2\right)$ for each block, where the number of blocks is bounded by n. Hence, the implementation complexity scales as $O\left(l\cdot n\cdot r^2\right)$, where the optimization routine terminates after l steps (perhaps in a local minimum).

Instead of preparing $|\tilde{\psi }\left(\mathit{\theta }\right)\rangle$ by a quantum circuit with $\mathit{\theta }\in {\left(\mathrm{0,2}\pi \right]}^{\times l}$ tunable parameters as

$\left|\tilde{\psi }\left(\mathit{\theta }\right)\rangle ={\displaystyle \prod }_l{U}_l\right|0{\rangle }^{\otimes n}(13)$

where $U_l$ is adjusted by ${\theta }_l$, one might adopt an alternative (heuristic) circuit realization performed by adjusting controllable Hamiltonian parameters realizing each block, subject again to the minimization of Eq. 6. With such an approach, one will prepare $|\tilde{\psi }\left(\mathit{\theta }\right)\rangle$ by tuning accessible time-dependent parameters ${\theta }_k\left(t\right)$ corresponding to Hermitian $A^k$ as

$\left|\tilde{\psi }\rangle =\mathcal{T}\left\{e^{-ı{{\displaystyle \sum }}^{\text{}}{\theta }_k\left(t\right)A^k}\right\}\right|0{\rangle }^{\otimes n},(14)$

where T orders the sequence by time and superscript k indexes the kth operator $A^k$. Provided these sequences are localized appropriately, the matrix product structure still remains.

We then consider vertical partitions of a quantum circuit with the n qubits positioned horizontally on a line. For an m-depth quantum circuit (where m is presumably bounded above by a low-order polynomial in n), the maximum number of two-qubit gates crossed in a vertical partition is never more than m. The maximum number of ebits generated by a fully entangling two-qubit CNOT gate is never more than a single ebit. We then consider the $\left(n-1\right)$ partitions of the qubits, the maximum partition with represent to ebits is into two (ideally) equal halves, which is never more than $\lceil n/2\rceil$. We then arrive at the general result that an m-depth quantum circuit on n qubits never applies more than

$\text{min}\left\{\lceil n/2\rceil ,m\right\}(15)$

ebits of entanglement. This immediately puts a lower bound of $\sim n/2$ on the two-qubit gate depth for Q to potentially drive a system into a state supporting the maximum possible ebits of entanglement.

In Figure 2, we demonstrate our algorithm for finding an eigenstate of randomly generated 5-qubit unitary matrices. For minimizing the function Eq. 6, we used the Broyden-Fletcher-Goldfarb-Shanno (BFGS) minimization method [30]. For each k ebit MPS, we place the k-layered hardware-efficient ansatz as the operators in blocks [21].

FIGURE 2

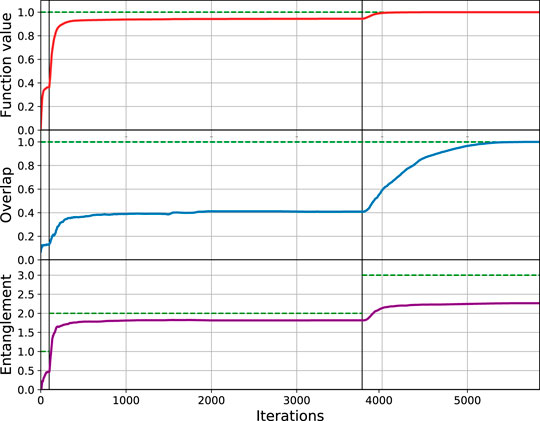
FIGURE 2. Algorithm demonstration on randomly generated 6-qubit unitaries Q: the value of Eq. 9(upper), overlap between the variational state and the closest eigenstate of Q(middle), and the von Neumann entropy of the subsystem of the first three qubits (lower). The vertical solid lines indicate the iteration numbers after which k, the number of ebits that the MPS ansatz can support, increases by 1. The plot is obtained by averaging over 10 randomly generated unitaries Q.

4 Discussion

We now turn to the realization of Q and sketch a possible demonstration for a near-term device. Polynomial-time simulation of Hamiltonian evolution is well known to be BQP-hard. This provides an avenue for Q to represent a problem of significant computational interest, as simulating quantum evolution and quantum factoring are in BQP. We aim to bootstrap properties of the quantum processor as much as possible to reduce resources for a realization; see, for example, [21].

Let $Q\left(t\right)$ be the one-parameter unitary group generated by $\mathrm{\mathscr{H}}$, where $\mathrm{\mathscr{H}}$ represents a 3-SAT instance. Given access to an oracle computing

$\langle \tilde{\psi }\left({\theta }_1\right)\left|\mathrm{\mathscr{H}}\right|\tilde{\psi }\left({\theta }_1\right)\rangle ,(16)$

we can minimize the overall eigenvectors, which is NP-hard. Hence, finding even rank-1 states can be NP-hard. This provides a connection between our method and QAOA [31]. Similarly, we can also use this external minimization to connect our method to VQE [20]. However, our method provides a certificate that, on proper termination, the system is indeed in such a desired eigenstate.

When $\mathrm{\mathscr{H}}$ is a general quantum Hamiltonian, minimization of

$\langle \tilde{\psi }\left({\theta }_k\right)\left|\mathrm{\mathscr{H}}\right|\tilde{\psi }\left({\theta }_k\right)\rangle (17)$

is in turn QMA-hard. For example, pairing our procedure with an additional procedure (quantum phase estimation) to minimize Q, the overall eigenvectors would hence provide rank-k variational states and hence our methods provide a research direction which incorporates tensor network methods in works such as, e.g., [19–21]. It should however be noted that phase estimation adds significant experimental difficultly compared with the algorithm presented here and the algorithm is closer to VQE (with evident differences as listed above and in the main text).

For a near-term demonstration, we envision Q to be realized by bootstrapping the underlying physics of the system realizing Q, e.g., using the hardware-efficient ansatz [21]. For instance, one can realize Q as a modification of the systems free Hamiltonian using effective Hamiltonian methods (modulating local gates). This greatly reduces practical requirements on Q.

The interaction graph of the Hamiltonian generating Q can be used to define a PEPS tensor network (as it will have the same structure as the layout of the chip, it will no longer have the contractable properties of matrix product states, and yet is still of interest) [4]. The algorithm works otherwise unchanged, but the circuit acts on this interaction graph (instead of a line) to create a corresponding tensor network state (a quantum circuit in the form of, e.g., the variational ansatz). Tailored free evolution of the system Hamiltonian generates Q. Our algorithm returns a tensor network approximation of an eigenstate of Q.

The first interesting demonstrations of the quantum algorithm we have presented should realize rank-k tensor networks (matrix product state), and the corresponding tensor network can be realized with a few hundred gates for a system with a few hundred qubits.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found: GitHub, https://git.io/JkjvV.

Author Contributions

All authors conceived and developed the theory and design of this study and verified the methods. AK developed and deployed the code to collect numerical data. All authors contributed to interpreting the results and writing the manuscript.

Acknowledgements

AK and JB acknowledge support from agreement No. 014/20, Leading Research Center on Quantum Computing. AU acknowledges RFBR project No. 19-31-90159 for financial support. This manuscript has been released as a preprint as arXiv:1804.02398 (32).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Biamonte J. Charged string tensor networks. Proc Natl Acad Sci USA (2017) 114(10):2447. doi:10.1073/pnas.1700736114

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Orús R. A practical introduction to tensor networks: matrix product states and projected entangled pair states. Ann Phys (2014) 349:117–58. doi:10.1016/j.aop.2014.06.013

CrossRef Full Text | Google Scholar

3. Vidal G. Entanglement renormalization: an introduction. In: Carr LD., editor. Understanding quantum phase transitions. Boca Raton, United States: Taylor and Francis (2010) p. 756.

CrossRef Full Text | Google Scholar

4. Verstraete F, Murg V, Cirac JI. Matrix product states, projected entangled pair states, and variational renormalization group methods for quantum spin systems. Adv Phys (2008) 57:143–224. doi:10.1080/14789940801912366

CrossRef Full Text | Google Scholar

5. Cirac JI, Verstraete F. Renormalization and tensor product states in spin chains and lattices. J Phys Math Theor (2009) 42(50):504004. doi:10.1088/1751-8113/42/50/504004

CrossRef Full Text | Google Scholar

6. Schollwöck U. The density-matrix renormalization group in the age of matrix product states. Ann Phys (2011) 326:96–192. doi:10.1016/j.aop.2010.09.012

CrossRef Full Text | Google Scholar

7. Orús R. Advances on tensor network theory: symmetries, fermions, entanglement, and holography. Eur Phys J B (2014) 87:280. doi:10.1140/epjb/e2014-50502-9

CrossRef Full Text | Google Scholar

8. Eisert J. Entanglement and tensor network states. Model Simulat (2013) 3:520.

CrossRef Full Text | Google Scholar

9. Evenbly G, Vidal G. Tensor network states and geometry. J Stat Phys (2011) 145:891–918. doi:10.1007/s10955-011-0237-4

CrossRef Full Text | Google Scholar

10. Cichocki A, Lee N, Oseledets I, Phan A-H, Zhao Q, Danilo P, et al. Tensor networks for dimensionality reduction and large-scale optimization: Part 1 low-rank tensor decompositions. Found Trends Machine Learn (2016) 9(4–5):249–429. doi:10.1561/2200000059

CrossRef Full Text | Google Scholar

11. Cichocki A, Phan A-H, Zhao Q, Lee N, Oseledets I, Sugiyama M, et al. Tensor networks for dimensionality reduction and large-scale optimization: Part 2 applications and future perspectives. Found Trends Machine Learn (2017) 9(6):431–673. doi:10.1561/2200000067

CrossRef Full Text | Google Scholar

12. Clark SR. Unifying neural-network quantum states and correlator product states via tensor networks. J Phys Math Theor (2018) 51(13):135301. doi:10.1088/1751-8121/aaaaf2

CrossRef Full Text | Google Scholar

13. Huggins W, Patil P, Mitchell B, Whaley KB, Miles Stoudenmire E. Towards quantum machine learning with tensor networks. Quant Sci Technol (2019) 4(2):024001. doi:10.1088/2058-9565/aaea94

CrossRef Full Text | Google Scholar

14. Ding L, Ran S-J, Wittek P, Cheng P, García RB, Su G, et al. Machine learning by unitary tensor network of hierarchical tree structure. New J Phys (2017) 21:073059. doi:10.1088/1367-2630/ab31ef

CrossRef Full Text | Google Scholar

15. Biamonte JD, Morales MES, Koh DE. Entanglement scaling in quantum advantage benchmarks. Phys Rev (2020) 101(1):012349. doi:10.1103/PhysRevA.101.012349

CrossRef Full Text | Google Scholar

16. Biamonte J, Bergholm V, Lanzagorta M. Tensor network methods for invariant theory. J Phys A Math Gener (2013) 46:475301. doi:10.1088/1751-8113/46/47/475301

CrossRef Full Text | Google Scholar

17. Morales MES, Tlyachev T, Jacob B. Variational learning of grovers quantum search algorithm. Phys Rev (2018) 98(6):062333. doi:10.1103/PhysRevA.98.062333

CrossRef Full Text | Google Scholar

18. Yung MH, Casanova J, Mezzacapo A, McClean J, Lamata L, Aspuru-Guzik A, et al. From transistor to trapped-ion computers for quantum chemistry. Sci Rep (2014) 4:3589. doi:10.1038/srep03589

PubMed Abstract | CrossRef Full Text | Google Scholar

19. McClean J, Romero J, Ryan B, Aspuru-Guzik A. The theory of variational hybrid quantum-classical algorithms. New J Phys (2016) 18:023023. doi:10.1088/1367-2630/18/2/023023

CrossRef Full Text | Google Scholar

20. Peruzzo A, McClean J, Shadbolt P, Yung MH, Zhou XQ, Love PJ, et al. A variational eigenvalue solver on a photonic quantum processor. Nat Commun (2014) 5:4213. doi:10.1038/ncomms5213

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kandala A, Mezzacapo A, Temme K, Takita M, Brink M, Chow JM, et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature (2017) 549:242–6. doi:10.1038/nature23879

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Jacob B. Universal variational quantum computation. Preprint repository name [Preprint] (2019) Available from: arXiv:1903.04500 (Accessed March 11, 2019).

CrossRef Full Text | Google Scholar

23. Xia R, Kais S. Quantum machine learning for electronic structure calculations. Nat Commun (2018) 9(1):4195. doi:10.1038/s41467-018-06598-z

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Grant E, Benedetti M, Cao S, Hallam A, Lockhart J, Stojevic V, et al. Hierarchical quantum classifiers. Npj Quant Inform (2018) 4:65. doi:10.1038/s41534-018-0116-9

CrossRef Full Text | Google Scholar

25. Akshay V, Philathong H, Morales MES, Biamonte JD. Reachability deficits in quantum approximate optimization. Phys Rev Lett (2020) 124(9):090504. doi:10.1103/PhysRevLett.124.090504

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Entanglement GV. Entanglement renormalization. Phys Rev Lett (2007) 99(22):220405. doi:10.1103/PhysRevLett.99.220405

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Giovannetti V, Montangero S, Fazio R. Quantum Multiscale entanglement renormalization ansatz channels. Phys Rev Lett (2008) 101(18):180503. doi:10.1103/PhysRevLett.101.180503

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Vidal G. Class of quantum many-body states that can be efficiently simulated. Phys Rev Lett (2008) 101(11):110501. doi:10.1103/PhysRevLett.101.110501

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Möttönen M, Vartiainen JJ, Bergholm V, Salomaa MM. Quantum circuits for general multiqubit gates. Phys Rev Lett (2004) 93(13):130502. doi:10.1103/PhysRevLett.93.130502

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Nocedal J, Wright SJ. Numerical optimization. New York, NY: Springer (2006) p. 597.

CrossRef Full Text | Google Scholar

31. Farhi E, Goldstone J, Gutmann S. A quantum approximate optimization algorithm. Preprint repository name [Preprint] (2014) Available from: arXiv:1411.4028 (Accessed November 14, 2014).

CrossRef Full Text | Google Scholar

32. Jacob B, Kardashin A, Uvarov A. Quantum machine learning tensor network states. Preprint repository name [Preprint] (2018) Available from: arXiv:1804.02398 (Accessed April 06, 2014).

CrossRef Full Text | Google Scholar