- 1IMADA & CP3-Origins, University of Southern Denmark, Odense, Denmark
- 2CP3-Origins and D-IAS, University of Southern Denmark, Odense, Denmark
- 3Dipartimento di Fisica, E. Pancini, University di Napoli, Federico II and INFN sezione di Napoli Complesso Universitario di Monte S, Napoli, Italy
We generalise the epidemic Renormalization Group framework while connecting it to a SIR model with time-dependent coefficients. We then confront the model with COVID-19 in Denmark, Germany, Italy and France and show that the approach works rather well in reproducing the data. We also show that a better understanding of the time dependence of the recovery rate would require extending the model to take into account the number of deaths whenever these are over 15% of the cumulative number of infected cases.
1 Introduction
Epidemic dynamics is often described in terms of a simple model introduced long time ago in [1]. Here, the affected population is described in terms of compartmentalised sub-populations that have different roles in the dynamics. Then, differential equations are designed to describe the time evolution of the various compartments. The sub-populations can be chosen to represent (S)usceptible, (I)nfected and (R)ecovered individuals (SIR model), obeying the following differential equations:
with the conservation law
The system depends on three parameters, namely γ, ε and N. Due to the conservation law (2), only two equations are independent, so that one can drop the equation for S.
The cumulative number of infected,
We can therefore re-write the two independent SIR equations as
Empirical modifications of the basic SIR model exist and range from including new sub-populations to generalise the coefficients γ, ε to be time-dependent in order to better reproduce the observed data (see Refs. [2–5] for recent examples).
Recently the epidemic Renormalization Group approach (eRG) to pandemics, inspired by particle physics methodologies, was put forward in [6]. The approach builds on scale transformations and invariances as introduced by Wilson in [7, 8], applied in this case to the evolution of social systems. The method has been further explored in [9], where it was demonstrated the eRG effectiveness when describing how the pandemic spreads across different regions of the world. This allowed to successfully simulate the onset of the second wave pandemic in Europe [10]. The eRG framework provided useful also to determine the impact and level of social distancing when combined with mining the Google and Apple mobility data [11]. We refer the reader to the review in [12] for a clear and comparative discussion of several approaches used in order to model the COVID-19 pandemic.
The goal of the present work is to further extend the eRG framework to properly take into account the number of recovered cases so that a better understanding of the reproduction number can also be achieved. We will start, first, by providing a map between the original eRG model and certain modified SIR models, establishing in this way and for the first time an exact connection between two powerful approaches to pandemics. We will finally test the framework via COVID-19 data.
1.1 Reviewing the Epidemic Renormalization Group
In the epidemic Renormalization group (eRG) approach [6], rather than the number of cases, it is convenient to discuss its logarithm, which is a more slowly varying function
where
More specifically, as the Renormalization group equations in high energy physics are expressed in terms of derivatives with respect to the energy μ, it is natural to identify the time as
It has been shown in [6] that α captures the essential information about the infected population within a sufficiently isolated region of the world. The pandemic beta function can be parametrised as
whose solution, for
The dynamics encoded in Eq. (1.8) is that of a system that flows from an UV fixed point at
1.2 Connecting Epidemic Renormalization Group With SIR While Extending It
To start connecting with compartmental models we rewrite Eq. (1.8) as
whose solution, with the initial condition
In the original eRG framework the number of recovered individuals were not explicitly taken into account. This is, however, straightforward to implement by introducing an equation for
where the parameters are
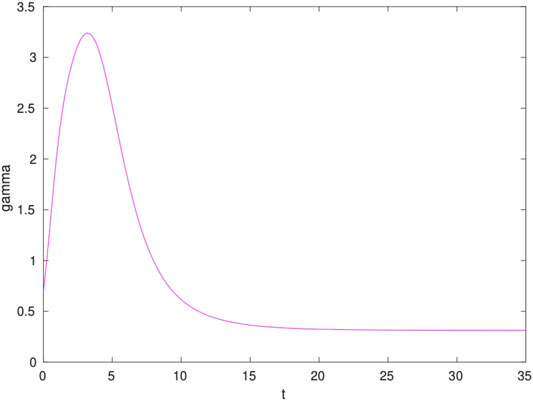
As we shall see this is a welcome feature. To better appreciate the mapping we show in Figure 1 the time-dependent γ parameter for a hypothetical case with
The result is a smooth function that peaks at short times and then plateaus to a fraction of
In terms of
1.3 Reproduction Number
An important quantity for pandemics is the reproduction number related to the expected average number of infected cases due to one case. In the time-dependent generalised SIR model it is identified as:
To extract
The result holds for γ and ε generic functions of time. Here we also generalise the time-dependence of ε to be:
The choice above has been empirically devised to best describe the data within the current approach. As it is clear from its form this function has a dip at
As we shall see the shape allows for a substantial increase of
2 Testing the Framework
As a timely application we consider the COVID-19 pandemic. Here the factor
The values for the numerator and denominator for different regions of the world can be obtained from several sources such as the World Health Organization (WHO) and Worldometers.
As testbed scenarios we consider four benchmark cases, namely Denmark, Germany, France and Italy. These countries adopted different degrees of containment measures. We find convenient to bin the data in weeks to smooth out daily fluctuations. We associate an error to both newly infected and newly recovered given by the square root of their values.
Procedurally we first fit the function
For each country we show the data and the model results by grouping together five graphs in a single figure. The different panels represent
In general we find good agreement between the data and the model with the exception of the increase in the number of infected cases occurring in the last weeks for some of the countries. Those are non-smooth events resulting from an abrupt change in the social distancing measures or from new and previously un-accounted disease hotspots. As such those events cannot be predicted by smooth models.
2.1 Denmark
The data and the model results for Denmark are shown in Figure 2. For the time-dependence of
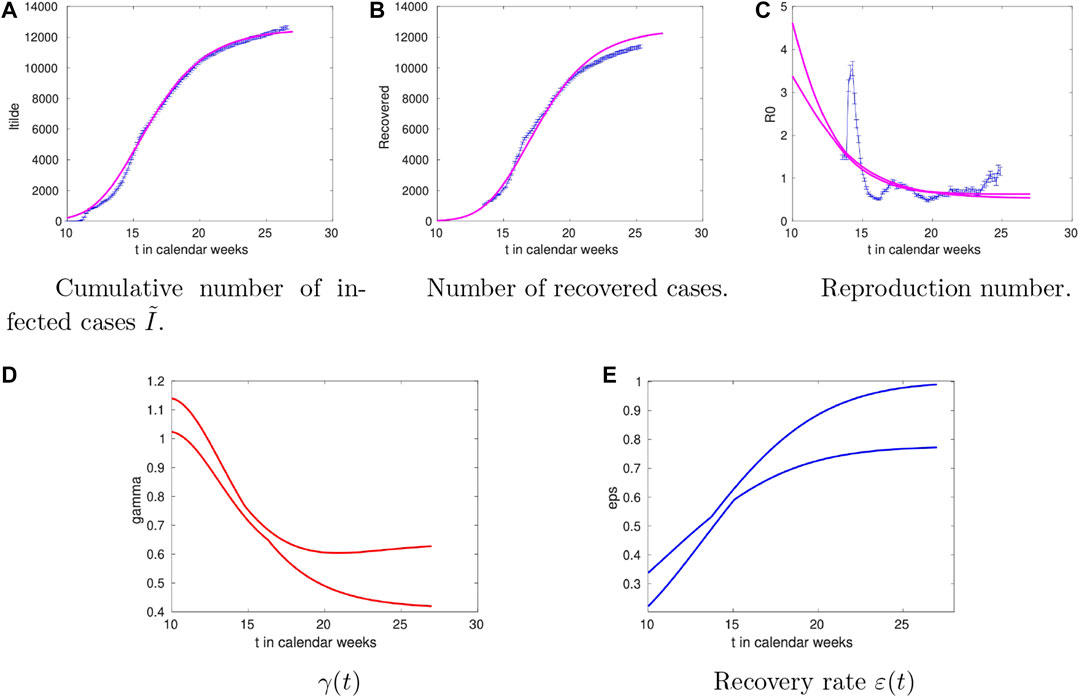
FIGURE 2. Time dependence of
2.2 Germany
For Germany the analysis is summarised in Figure 3. The overall trends are similar to the Danish case including the temporal trend of the recovery rate
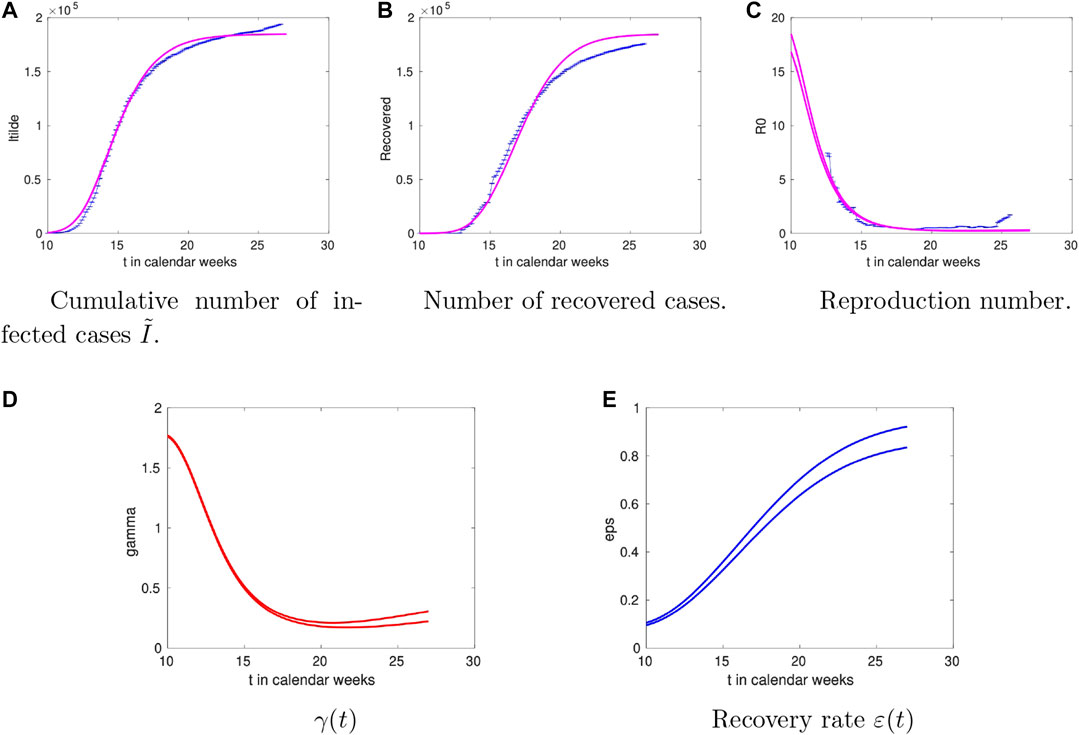
FIGURE 3. Time dependence of
2.3 Italy
The analysis for Italy is shown in Figure 4. We observe rather large values of
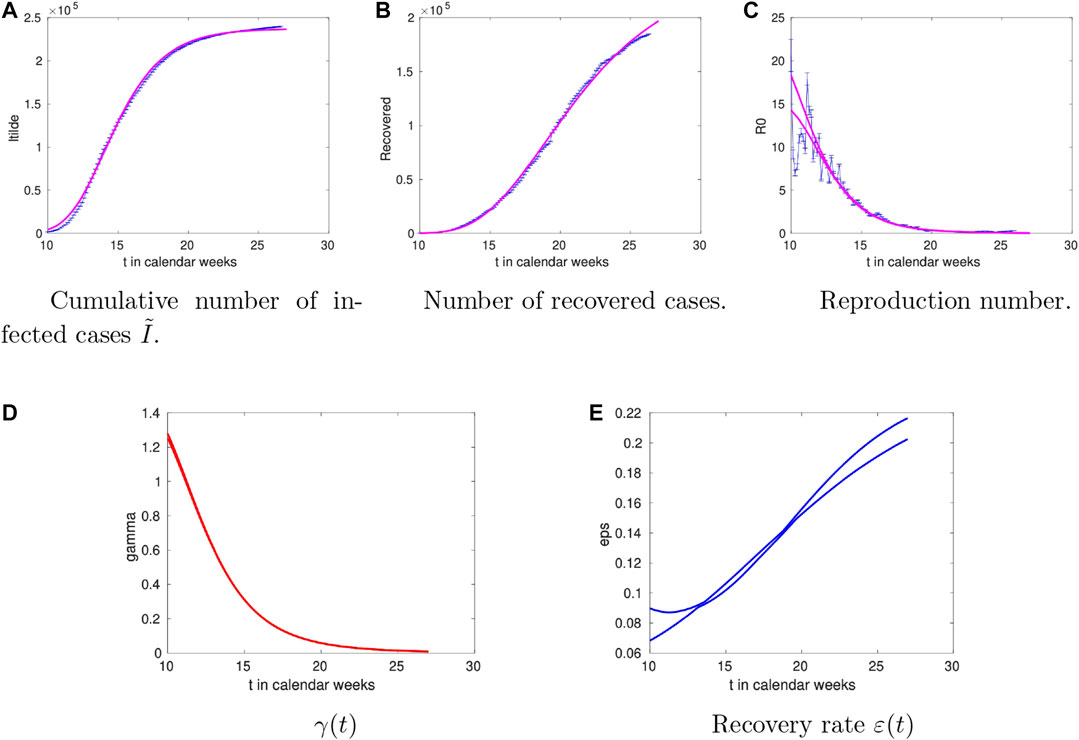
FIGURE 4. Time dependence of
2.4 France
The results for the French case can be found in Figure 5 with the overall picture similar to the Italian one. The striking difference compared to the other countries is that the recovery rate decreases at late times. Given that the deaths in France amount to about 20% of the total infected, such difference indicates that a more complete model (including the deaths compartment) is needed.
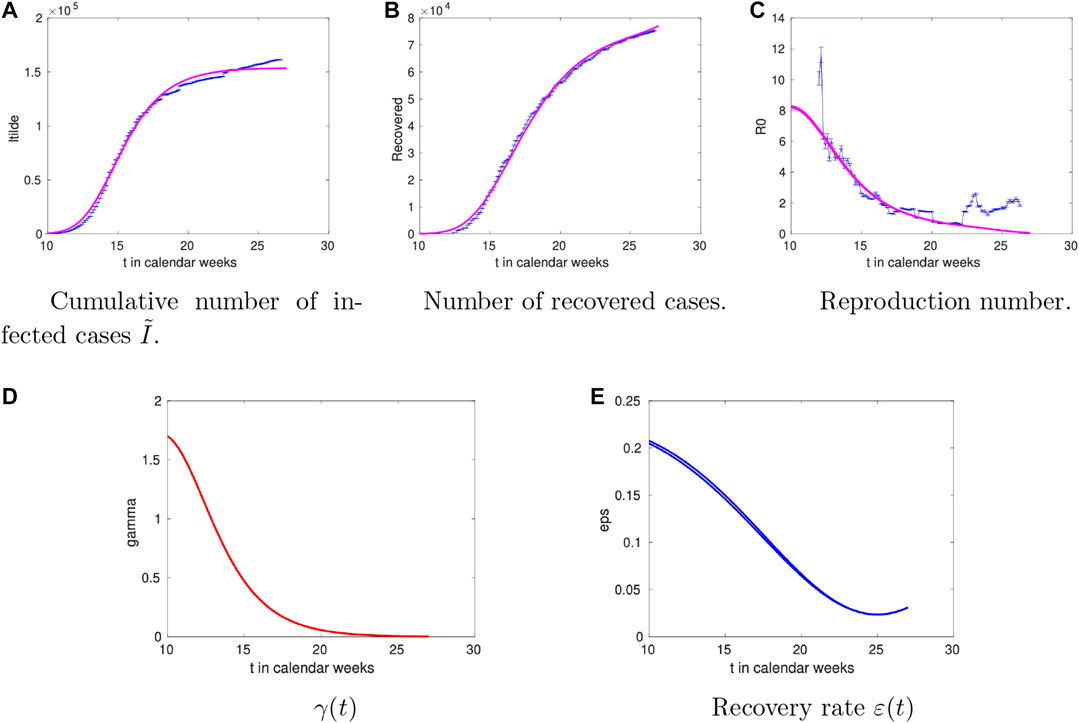
FIGURE 5. Time dependence of
3 Conclusions and Outlook
We generalised the epidemic Renormalization Group framework to take into account the recovered cases and to be able to determine the time dependence of the reproduction number. At the same time we show that the eRG framework can be embedded into a SIR model with time-dependent coefficients. Interestingly the resulting infection rate
We then move to confront the model to actual data by considering the spread of COVID-19 in the following countries: Denmark, Germany, Italy and France. We show that the overall approach works rather well in reproducing the data. Nevertheless the interpretation for the recovery rate is natural for Denmark and Germany while it requires to add the deaths compartment for Italy and France. The reason being that for the first two countries the number of deaths is below 5% of the number of infected cases while it is above 15% for France and Italy1. We therefore expect that this compartment will be relevant to include for countries with similar number of deaths. The extension of the eRG to include also the death compartment is a natural next step. Upon introducing thD-compartment, the system of differential equations in 1.1 (and similarly for Eq. 1.12) extends to
with
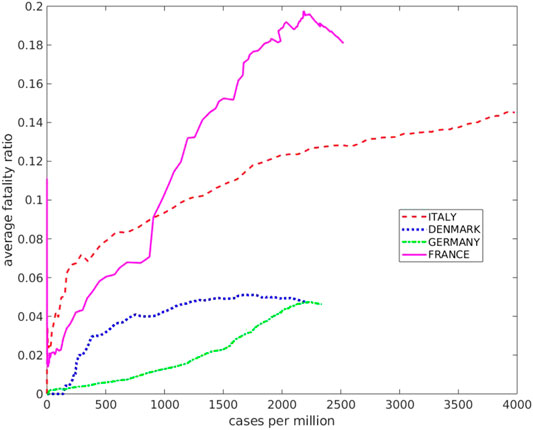
FIGURE 6. The average fatality ratio as a function of the cumulative number of infected per million inhabitants for the countries discussed here.
Here the running average fatality ratio (cumulative number of deaths over cumulative number of infected) is displayed, as a function of the number of infected per million inhabitants, for the countries considered here.
We are now investigating different parameterizations of these curves, however, since our main focus here is to establish an exact connection between two well known frameworks describing social dynamics (the renormalization group and compartmental models) we have restricted our attention to the simplest compartmental model, i.e., the SIR model. To our knowledge such an exact matching could not be found in previous literature. Another interesting approach could be to include the death compartment in the recovered one as put forward in [13].
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://www.who.int/csr/sars/country/en/ World Health Organization (WHO) and https://www.worldometers.info/coronavirus/Worldometers.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer KT declared a past co-authorship with one of the authors FS to the handling editor.
References
1. Kermack WO, McKendrick AG, A contribution to the mathematical theory of epidemics, Proc R Soc A (1927) 115(772):700–21. doi:10.1007/BF02464423
2. Zheng M, Zhao M, Min B, Liu Z. Synchronized and mixed outbreaks of coupled recurrent epidemics. Sci Rep (2017) 7:2424. doi:10.1038/s41598-017-02661-9
3. Zheng M, Wang C, Zhou J, Guan S, Zou Y, et al. Non-periodic outbreaks of recurrent epidemics and its network modelling. Sci Rep (2015) 5:16010. doi:10.1038/srep16010
4. Li R, Pei S, Chen B, Song Y, Zhang T, Yang W, et al. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science (2020) 368(6490):489–93. doi:10.1126/science.abb3221
5. Zhang X, Ma R, Wang L, Predicting turning point, duration and attack rate of COVID-19 outbreaks in major Western countries. Chaos Solit Fractals (2020) 140:110130. doi:10.1016/j.chaos.2020.109829
6. Della Morte M, Orlando D, Sannino F, Renormalization group approach to pandemics: the COVID-19 case. Front Physiol (2020) 8:144. doi:10.3389/fphy.2020.00144
7. Wilson K, Renormalization group and critical phenomena. I. Renormalization group and the Kadanoff scaling picture. Phys Rev B (1971) 4:3174–83. doi:10.1103/PhysRevB.4.3174
8. Wilson K, Renormalization group and critical phenomena. II. Phase-space cell analysis of critical behavior. Phys Rev B (1971) 4:3184–205. doi:10.1103/PhysRevB.4.3184
9. Cacciapaglia G, Sannino F, (2005) [arXiv:2005.04956 [physics.soc-ph]]. Accepted for publication in Nature Scientific Reports.
12. Smit AJ, Fitchett JM, Engelbrecht FA, Scholes RJ, Dzhivhuho G, Sweijd NA, Winter is coming: a southern hemisphere perspective of the environmental drivers of SARS-CoV-2 and the potential seasonality of COVID-19, Int J Environ Res Publ Health (2020) 17:5634. doi:10.3390/ijerph17165634
Keywords: Compartmental models, epidemic renormalisation group, pandemic, pandemic (COVID-19), COVID-19
Citation: Della Morte M and Sannino F (2021) Renormalization Group Approach to Pandemics as a Time-Dependent SIR Model. Front. Phys. 8:591876. doi: 10.3389/fphy.2020.591876
Received: 05 August 2020; Accepted: 13 November 2020;
Published: 15 January 2021.
Edited by:
Matjaž Perc, University of Maribor, SloveniaReviewed by:
Muhua Zheng, East China Normal University, ChinaKimmo Tuominen, University of Helsinki, Finland
Antonio Scala, Institute of Complex Systems, National Research Council (CNR), Italy
Copyright © 2021 Della Morte and Sannino. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francesco Sannino, c2Fubmlub0BjcDMuc2R1LmRr
 Michele Della Morte
Michele Della Morte Francesco Sannino
Francesco Sannino