Peregrine Solitons on a Periodic Background in the Vector Cubic-Quintic Nonlinear Schrödinger Equation

We present exact explicit Peregrine soliton solutions based on a periodic-wave background caused by the interference in the vector cubic-quintic nonlinear Schrödinger equation involving the self-steepening effect. It is shown that such periodic Peregrine soliton solutions can be expressed as a linear superposition of two fundamental Peregrine solitons of different continuous-wave backgrounds. Because of the self-steepening effect, some interesting Peregrine soliton dynamics such as ultrastrong amplitude enhancement and rogue wave coexistence are still present when they are built on a periodic background. We numerically confirm the stability of these analytical solutions against non-integrable perturbations, i.e., when the coefficient relation that enables the integrability of the vector model is slightly lifted. We also demonstrate the interaction of two Peregrine solitons on the same periodic background under some specific parameter conditions. We expect that these results may shed more light on our understanding of the realistic rogue wave behaviors occurring in either the fiber-optic telecommunication links or the crossing seas.

1 Introduction

Originally, rogue waves refer to the surface gravity waves occurring in the open ocean whose wave heights are at least twice as high as the significant wave height of the surrounding waves [1]. Under extreme conditions, they soar like a wall of water that can dwarf even the largest of modern ships, and then disappear into the sea as if all this does not happen [2, 3]. As these massive waves usually possess a devastating power and behave unpredictably, they are hard to observe and study. Historically, the first scientific observation that proved the existence of rogue waves was made at the Draupner oil platform in the North Sea on January 1, 1995, hence named “New Year Wave” afterward [4]. Since then, rogue waves became an active multidisciplinary area of research, ranging from hydrodynamics to optics and photonics [5–8].

Despite the extensive studies, there is still a lot of debate over the physical mechanisms behind rogue waves [9, 10]. While the linear theory based on the superposition of random waves or the inhomogeneity has prevailed for some time [11, 12], the nonlinear viewpoint gains increasing popularity, as in a stricter sense only the superposition process of nonlinear waves could bring about extreme waves higher than the sum of the wave heights involved [13]. Actually, the most accepted mechanisms—integrable turbulence [14, 15] and modulation instability (MI) [16, 17] are of nonlinear nature, by which irregular extreme wave events could be created. This is easily understood within the MI framework, where the periodic perturbations on a continuous-wave (cw) background tend to undergo exponential growth initially, and then evolve into a multiplicity of waves, from which rogue waves may arise [18–20]. Therefore, using nonlinear Schrödinger (NLS) equation or other relevant equations to model realistic rogue waves is not only possible but also fascinating, as done in the current rogue wave investigations [21–23].

Mathematically, one can associate rogue waves to the rational solutions of the integrable nonlinear wave equation, which are localized on both time and space [18]. A typical example is the Peregrine soliton, which is a fundamental rational solution of the celebrated NLS equation [24]. This type of soliton solution exhibits a single doubly-localized peak on a finite background, with its peak position and constant phase all undetermined, hence matching well the fleeting and transient wave characteristics of rogue waves as witnessed in real world. For this reason, the Peregrine soliton was thought of as a promising prototype of rogue wave events seen in nature [25]. Its importance and universality have been confirmed by a succession of well-designed experiments, with physical settings spanning from the water-wave tanks [26] to optical fibers [21, 27], and from the deep ocean [28] to plasmas [29]. Moreover, in a multicomponent (or vector) nonlinear system, some variants of Peregrine solitons such as dark Peregrine solitons [30] and anomalous Peregrine solitons [31, , 32] have come to light, opening new perspectives on the versatility of Peregrine solitons as an essential prototype in rogue wave science. Here, in a broad sense, we still term the fundamental rogue waves in a multicomponent system Peregrine solitons or Peregrine solitary waves, provided that they inherit the basic wave features of the Peregrine soliton in the original NLS equation [33, 34].

Recently, there has also been an intense research on the so-called periodic Peregrine soliton, by which we mean a Peregrine soliton formed on a periodic background [35–41]. Normally, when a multicomponent nonlinear system is confronted, it may occur to us that an interference would occur when two or more monochromatic waves of different frequencies are simultaneously present in the same region. The appearance of interference fringes, which was ever instrumental in establishing the wave nature of light in the history, is a direct evidence of such interference effects. As interference effects are inherent to the vector nonlinear system consisting of continuous waves, it is therefore reasonable for us to inspect the possibility of the existence of Peregrine solitons on a periodic background caused by interference.

In this paper, we present an in-depth study of the formation of Peregrine solitons on a periodic background, within the framework of the vector cubic-quintic NLS (CQ-NLS) equation, which is a two-component version of the scalar NLS-type Gerdjikov–Ivanov equation [42]. As will be shown, this model has included the necessary ingredients such as group-velocity dispersion (GVD), Kerr nonlinearity, quintic nonlinearity, and self-steepening, which could provide more accurate descriptions for realistic rogue waves met in complex systems, as compared to the simple Manakov model [43, 44] and to the vector Gerdjikov–Ivanov equation [45]. We will show that in this vector nonlinear system, a periodic background could form as a result of an interference between two continuous waves. Further, we present explicitly the general Peregrine soliton solutions built on such a periodic background, which were not reported previously, to the best of our knowledge. The robustness of these analytical solutions against non-integrable perturbations has been numerically confirmed, by lifting the integrality condition of the above vector CQ-NLS model. With these exact solutions, the dynamics of the coexisting and anomalous Peregrine solitons, as well as their interactions, of course occurring on a periodic background, are exhibited. The underlying mechanisms responsible for the generation of such periodic Peregrine solitons are also discussed.

2 Theoretical Framework

In the context of fiber optics, we write the vector CQ-NLS equation as

$\text{i}{u}_{1z}+\frac{1}{2}{u}_{1tt}+\sigma u_1\left(|u_1{|}^2+|u_2{|}^2\right)+{\gamma }^2{u}_1{\left(|u_1{|}^2+|u_2{|}^2\right)}^2-\text{i}\gamma u_1\left(u_1{u}_{1t}^{\text{*}}+u_2{u}_{2t}^{\text{*}}\right)=0,(1)$

$\text{i}{u}_{2z}+\frac{1}{2}{u}_{2tt}+\sigma u_2\left(|u_1{|}^2+|u_2{|}^2\right)+{\gamma }^2{u}_2{\left(|u_1{|}^2+|u_2{|}^2\right)}^2-\text{i}\gamma u_2\left(u_1{u}_{1t}^{\text{*}}+u_2{u}_{2t}^{\text{*}}\right)=0,(2)$

where $u_{\mathrm{1,2}}\left(z,t\right)$ are the normalized complex envelopes of two optical components, and z and t are the distance and retarded time, respectively. Subscripts z and t stand for partial derivatives. While the constant coefficient 1/2 points to the GVD effect and the coefficient σ to the self-phase modulation, γ accounts for the pulse self-steepening effect [46], and ${\gamma }^2$ relates to the quintic nonlinearity, which was often found in highly nonlinear materials such as chalcogenide fibers [47]. Here, in terms of the anomalous and normal dispersion cases, the parameter σ can be normalized to 1 and $-1$, respectively, which have an otherwise interpretation of self-focusing and self-defocusing in the context of beam optics, when the independent variable t is interpreted as the transversal spatial coordinate [48]. Besides, the combination of cubic and quintic nonlinearity is a conventional consideration in the design of mode-locked fiber lasers [49] or in stabilizing the soliton propagation in nonlinear media [50]. With the above ingredients included, this vector model represents an important generalization of the Manakov system [43, 44], although the former involves a specific relation between the coefficients for quintic nonlinearity and self-steepening terms. Therefore, from a mathematical perspective, it can provide a more accurate description of the propagation of ultrashort optical pulses in highly nonlinear birefringent fibers. The physical relevance of this integrable model can be seen by inspecting the stability of its solutions against non-integrable perturbations, i.e., when the above mentioned specific relation is lifted. We should point out that, to weigh the nonlinearity factors that affect the rogue wave dynamics, we have excluded the higher-order dispersion terms from Eqs 1 and 2, which usually appear when pulses are driven in the few-cycle regime [47] or in the microstructure fiber [51].

Obviously, the above vector system could be reproduced from the compatibility condition, ${\mathbf{R}}_{tz}={\mathbf{R}}_{zt}$ (which can read ${\mathbf{U}}_z-{\mathbf{V}}_t+\mathbf{UV}-\mathbf{VU}=0$), of the following $3\times 3$ linear eigenvalue problem:

${\mathbf{R}}_t=\mathbf{UR},{\mathbf{R}}_z=\mathbf{VR},(3)$

where $\mathbf{R}={[r,s,w]}^{\mathsf{T}}$ is the eigenfunction (T means a matrix transpose, and r, s, and w are functions of the variables z, t, and the complex spectral parameter λ), and

$\begin{array}{c}\mathbf{U}=-\frac{\text{i}\left(\lambda -\sigma \right){\sigma }_3}{2\gamma }+\sqrt{\lambda }\mathbf{Q}-\text{i}\gamma {\sigma }_3{\mathbf{Q}}^2,\\ \mathbf{V}=-\frac{\text{i}{\left(\lambda -\sigma \right)}^2{\sigma }_3}{4{\gamma }^2}+\frac{\sqrt{\lambda }}{2}\left(\frac{\lambda -\sigma }{\gamma }\mathbf{Q}-\text{i}\sqrt{\lambda }{\sigma }_3{\mathbf{Q}}^2+\text{i}{\sigma }_3{\mathbf{Q}}_t\right)\\ +\frac{\text{i}{\gamma }^2{\sigma }_3}{2}{\mathbf{Q}}^4-\frac{\gamma }{2}\left({\mathbf{QQ}}_t-{\mathbf{Q}}_t\mathbf{Q}\right),\end{array}$

with ${\sigma }_3=\text{diag}\left(1,-1,-1\right)$ being the diagonal matrix, and

$\mathbf{Q}=\left(\begin{array}{ccc}0& u_1& u_2\\ -u_1^{\text{*}}& 0& 0\\ -u_2^{\text{*}}& 0& 0\end{array}\right).$

We should point out that the Lax pair Eq. 3 takes the same form as used in the scalar CQ-NLS equation [42], except that the Q is now defined by a $3\times 3$ matrix. The subsequent Darboux dressing operation is straightforward. In simple terms, let first $u_{\mathrm{1,2}}$ be the seeding solutions and substitute them into the Lax pair Eq. 3 to yield the eigenfunction R. Then, in terms of R at given spectral parameter, a dress operator D can be properly constructed, by which R will be dressed into ${\mathbf{R}}^{\prime }$ (i.e., ${\mathbf{R}}^{\prime }$= DR). It requires that ${\mathbf{R}}^{\prime }$ must satisfy the Lax pair Eq. 3 of the same form, but with a new pair of potentials $u_1^{\prime }$ and $u_2^{\prime }$ in U and V. Lastly, the Darboux transformation formulas that relate the new solutions $u_{\mathrm{1,2}}^{\prime }$ to the seeding solutions $u_{\mathrm{1,2}}$ can be found. As concerns this standard procedure, one can refer to Refs. 52–56 for more details. Intended for rogue wave states only, a generalized or nonrecursive Darboux transformation method can be developed, which can give the nth-order rogue wave solutions without any iteration operation [42, 57, 58, 59].

For our present purposes, we are merely concerned with the fundamental rogue wave solutions, which evolve directly from the MI of continuous wave fields. It is easily shown that the initial plane-wave solutions $u_{j0}$$\left(j=\mathrm{1,2}\right)$ of the vector CQ-NLS equation, defined by the amplitudes $a_j$, wavenumbers $k_j$, frequencies ${\omega }_j$, and initial constant phases ${\varphi }_j$, all of which are real, can be expressed as

$u_{j0}=a_j\exp \left[\mathrm{i}\left(k_{j}z+{\omega }_{j}t+{\varphi }_j\right)\right],(4)$

under the dispersion relations:

$k_j=A\left(\sigma +{\gamma }^{2}A\right)-\gamma \left({\omega }_1{a}_1^2+{\omega }_2{a}_2^2\right)-\frac{{\omega }_j^2}{2}.$

Here and in what follows, we define $A=a_1^2+a_2^2$ for the sake of brevity. Also, we will assume below the initial constant phases ${\varphi }_j$ to be zero, without loss of generality. Then, with the help of the Darboux transformation technique outlined above [42, 58, 59] followed by tedious algebraic manipulations, we obtain the exact fundamental rogue wave solutions on a periodic background, expressed by

$u_1=\frac{\sqrt{2}}{2}\left(U{u}_{10}+V{u}_{20}\right),u_2=\frac{\sqrt{2}}{2}\left(U{u}_{10}-V{u}_{20}\right),(5)$

where $u_{10}$ and $u_{20}$ are initial plane-wave solutions denoted by Eq. 4, and U(z,t) and $V\left(z,t\right)$ are the complex rational polynomials given by

$U=1-\frac{2\text{i}\alpha [{\nu }^{2}z-\left(A\gamma +\mu +{\omega }_1\right)\theta ]+\eta \left(A{\gamma }^2-\gamma {\omega }_1+\sigma \right)}{[{(A\gamma +\mu +{\omega }_1)}^2+{\nu }^2](M+\text{i}N)},(6)$

$V=1-\frac{2\text{i}\alpha [{\nu }^{2}z-\left(A\gamma +\mu +{\omega }_2\right)\theta ]+\eta \left(A{\gamma }^2-\gamma {\omega }_2+\sigma \right)}{[{(A\gamma +\mu +{\omega }_2)}^2+{\nu }^2](M+\text{i}N)},(7)$

with

$\theta =t+\left(A\gamma +\mu \right)z,(8)$

$\eta =2A{\gamma }^2+\mu \gamma +\sigma ,\alpha ={\nu }^2{\gamma }^2+{\eta }^2,(9)$

$M=\alpha \left({\theta }^2+{\nu }^2{z}^2\right)+\frac{{\eta }^2}{4{\nu }^2},N=\gamma \left({\nu }^2\gamma z-\eta \theta \right).(10)$

The parameters μ and ν in Eqs 6–10 are the real and imaginary parts of the root χ $\left(=\mu +\text{i}\nu \right)$ of the algebraic equation:

$1+\frac{a_1^2\left(A{\gamma }^2-\gamma {\omega }_1+\sigma \right)}{{\left(A\gamma +\chi +{\omega }_1\right)}^2}+\frac{a_2^2\left(A{\gamma }^2-\gamma {\omega }_2+\sigma \right)}{{\left(A\gamma +\chi +{\omega }_2\right)}^2}=0.(11)$

We would like to emphasize that our solutions given by Eq. 5 entail the most general closed form for a pair of Peregrine rogue waves on a periodic background, and their existence relies on the algebraic condition given by Eq. 11. Generally, the real-coefficient quartic Eq. 11 admits two different pairs of complex roots and hence the solutions (Eq. 5) may exhibit two different Peregrine soliton structures for the same set of initial parameters. Moreover, in our solutions, the rational polynomials U and V have been well separated by real and imaginary parts, and their peaks have been translated to locate on the origin so that their peak-to-background ratios read $\left|f_U\right|$ and $\left|f_V\right|$, respectively, where

$f_U\equiv U\left(\mathrm{0,0}\right)=1-\frac{4\left(A{\gamma }^2-\gamma {\omega }_1+\sigma \right){\nu }^2}{\eta [{(A\gamma +\mu +{\omega }_1)}^2+{\nu }^2]},(12)$

$f_V\equiv V\left(\mathrm{0,0}\right)=1-\frac{4\left(A{\gamma }^2-\gamma {\omega }_2+\sigma \right){\nu }^2}{\eta [{(A\gamma +\mu +{\omega }_2)}^2+{\nu }^2]}.(13)$

Once the real parameters μ and ν are known from Eq. 11, the intriguing rogue wave dynamics on a periodic background, defined by Eq. 5, could be uncovered. As a matter of fact, the conventional rogue wave dynamics on a cw background, which are known as $u_1=U{u}_{10}$ and $u_2=V{u}_{20}$, can be understood as well, and one can refer to [59] for more information.

Let us now consider the special case where the quartic Eq. 11 admits two pairs of equal complex roots. In this situation, one can find that, when the plane-wave parameters satisfy

$A{\left(2A{\gamma }^2-\kappa \gamma +2\sigma \right)}^2-\left(9A{\gamma }^2-4\kappa \gamma +8\sigma \right){\delta }^2=0,(14)$

$B=\frac{A\delta \gamma }{2A{\gamma }^2-\kappa \gamma +2\sigma },(15)$

where $\kappa ={\omega }_1+{\omega }_2$, $\delta ={\omega }_1-{\omega }_2$, and $B=a_1^2-a_2^2$ (the same below, for the sake of brevity), the real and imaginary parts of the root χ would take the following simple form

$\mu =-A\gamma -\frac{\kappa }{2},\nu =\frac{\sqrt{3}}{2}\delta .(16)$

Substituting Eq. 16 into Eqs 6 and 7 yields (noting now that $\alpha =\frac{3}{4}{\delta }^2{\gamma }^2+{\eta }^2$)

$U=1-\frac{\text{i}\left(\frac{3}{2}\delta z-\theta \right)\delta \alpha +\eta \left(\eta -\frac{1}{2}\delta \gamma \right)}{{\delta }^2\alpha \left(\frac{3}{4}{\delta }^2{z}^2+{\theta }^2\right)+\frac{1}{3}{\eta }^2-\text{i}{\delta }^2\gamma \left(\eta \theta -\frac{3}{4}{\delta }^2\gamma z\right)},(17)$

$V=1-\frac{\text{i}\left(\frac{3}{2}\delta z+\theta \right)\delta \alpha +\eta \left(\eta +\frac{1}{2}\delta \gamma \right)}{{\delta }^2\alpha \left(\frac{3}{4}{\delta }^2{z}^2+{\theta }^2\right)+\frac{1}{3}{\eta }^2-\text{i}{\delta }^2\gamma \left(\eta \theta -\frac{3}{4}{\delta }^2\gamma z\right)},(18)$

which result in the special type of deterministic Peregrine rogue wave solutions denoted by Eq. 5, for any given set of parameters that meets Eqs 14 and 15. As there is only one pair of ($\mu ,\nu$) value given by Eq. 16, no rogue wave coexistence [23] would occur any more in this special case.

Further, we find that when the parameter conditions given by Eqs 14 and 15 are satisfied, there would exist a pair of two-Peregrine-soliton states that can describe the interaction between two Peregrine rogue waves on the periodic background. After some algebra, we can express this special kind of two-Peregrine-soliton solutions by the same Eq. 5, but let the complex rational polynomials U and V be denoted by

$U=1-\frac{3\sqrt{3}\delta \gamma R{S}^{\text{*}}\beta {\varphi }^{\text{*}}}{\gamma \left(\left|\beta {|}^2\right|R{|}^2+{\lambda }_0{a}_1^2|S{|}^2+{\lambda }_0{a}_2^2|W{|}^2\right)},(19)$

$V=1+\frac{3\sqrt{3}\delta \gamma R{W}^{\text{*}}\beta \varphi }{\gamma \left(\left|\beta {|}^2\right|R{|}^2+{\lambda }_0{a}_1^2|S{|}^2+{\lambda }_0{a}_2^2|W{|}^2\right)},(20)$

where

$R={\gamma }_1+{\gamma }_2\xi +{\gamma }_3\left(\frac{3{\xi }^2}{2}-\frac{\text{i}\sqrt{3}\xi }{\delta }-\frac{\text{i}3z}{2}\right),(21)$

$S=R+\frac{\gamma a_2^2-\delta \varphi }{\delta \left(\delta +\gamma B\right)}[{\gamma }_2+{\gamma }_3\left(3\xi +\frac{\text{i}\sqrt{3}}{\delta \varphi }\right)],(22)$

$W=R+\frac{\gamma a_1^2+\delta {\varphi }^{\text{*}}}{\delta \left(\delta +\gamma B\right)}[{\gamma }_2+{\gamma }_3\left(3\xi +\frac{\text{i}\sqrt{3}}{\delta {\varphi }^{\text{*}}}\right)],(23)$

with $\xi =\frac{\sqrt{3}}{2}\delta z-\text{i}\left(t-\kappa z/2\right)$, $\varphi =\frac{1}{2}-\frac{\text{i}\sqrt{3}}{2}$, ${\lambda }_0=\sigma -\frac{\gamma \kappa }{2}+\frac{\text{i}3\sqrt{3}}{2}\delta \gamma$, $\beta =\frac{\sqrt{3}}{2}\gamma A+\frac{\text{i}}{2}\left(\gamma B-2\delta \right)$, and ${\gamma }_1,{\gamma }_2$ and ${\gamma }_3\left(\ne 0\right)$ being three arbitrary complex constants (not confused with the system parameter γ). It should be noted that, as ${\gamma }_3=0$, the above polynomials U and V can reduce to Eqs 17 and 18, and then the two-soliton dynamics would disappear.

3 Intriguing Rogue Wave Dynamics on a Periodic Background

For given initial parameters, our analytical solutions Eqs 5–7 may exhibit intriguing rogue wave characteristics, including periodic background hallmark, rogue wave coexistence, anomalous peak amplitude, and applicability for both normal and anomalous dispersions. In the following, we proceed to uncover these interesting features as well as their underlying generation mechanisms.

First of all, it is obvious that the periodic Peregrine soliton solutions of the vector CQ-NLS equation can be generally expressed as a linear superposition of two fundamental Peregrine solitons of different cw backgrounds, provided that the continuous waves involve a nonvanishing frequency difference. In fact, as one might check, when the frequency difference meets $\delta ={\omega }_1-{\omega }_2=0$, the two field components $u_1$ and $u_2$ would take the form of conventional Peregrine solitons, with a three-fold peak amplitude but without any periodicity on the amplitude of the background, as seen in Figures 1A,B, where the Peregrine solitons defined by Eq. 5 are demonstrated in the anomalous dispersion regime ($\sigma =1$), with the initial parameters ${\omega }_1={\omega }_2=3/2$, $\gamma =1$, $a_1=\sqrt{3/2}$, and $a_2=\sqrt{1/2}$. However, once $\delta \ne 0$, the background fields that support the rogue waves would feature the periodic or amplitude-modulated waves defined by

$\left|u_1^{\text{bg}}\right|=\sqrt{\frac{A}{2}+a_1{a}_2\text{cos}\left[\delta \left(t-z\kappa /2\right)\right]},(24)$

$\left|u_2^{\text{bg}}\right|=\sqrt{\frac{A}{2}-a_1{a}_2\text{cos}\left[\delta \left(t-z\kappa /2\right)\right]}.(25)$

It follows easily that the characteristic periodicity results from the interference effects of two plane waves (see the second terms in the radicals), and that the background waves will be modulated at a temporal beat frequency equal to δ, with their patterns moving at a transversal velocity equal to $v=t/z=\kappa /2$. Figures 1C–F show two pairs of Peregrine solitons formed on such periodic backgrounds, using otherwise identical initial parameters as in Figures 1A,B except ${\omega }_2=-3/2$, which means $\delta \ne 0$ and $\kappa =0$. These two pairs of periodic Peregrine solitons are caused by two different $\left(\mu ,\nu \right)$ values (see caption) that are obtained by substituting the same set of initial parameters into the quartic Eq. 11. This means that on the same periodic background would occur the pair of Peregrine soliton states shown in Figures 1C,D or the other pair shown in Figures 1E,F, or both pairs simultaneously. This is what we meant the rogue wave coexistence first proposed for multi-component long-wave–short-wave resonance [23].

FIGURE 1

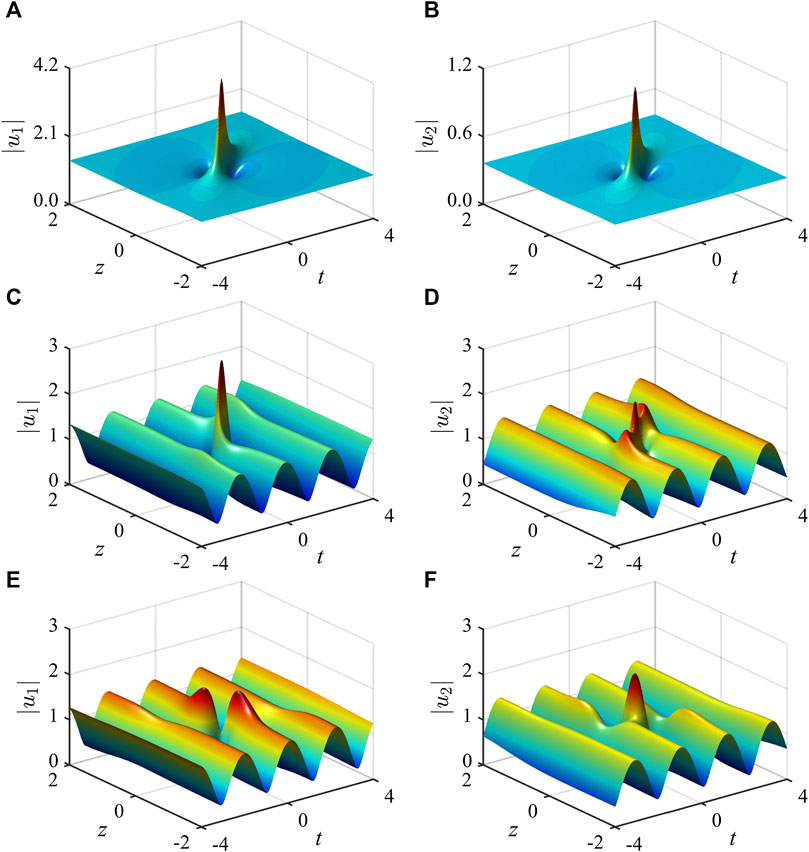
FIGURE 1. Peregrine soliton states formed on (A),(B) the cw backgrounds when $\delta =0$ and (C)–(F) the periodic-wave backgrounds when $\delta \ne 0$, in the anomalous dispersion regime ($\sigma =1$), under the same parameters $a_1=\sqrt{3/2}$, $a_2=\sqrt{1/2}$, and $\gamma =1$. The other parameters are specified by (A),(B): ${\omega }_1={\omega }_2=3/2$, $\mu =-7/2$, $\nu =\sqrt{3}$; (C),(D): ${\omega }_1=3/2$, ${\omega }_2=-3/2$, $\mu =-2-\frac{3}{4}\sqrt{2\sqrt{3}}$, $\nu =\frac{3}{4}\sqrt{2\sqrt{3}}$; and (E),(F): ${\omega }_1=3/2$, ${\omega }_2=-3/2$, $\mu =-2+\frac{3}{4}\sqrt{2\sqrt{3}}$, $\nu =\frac{3}{4}\sqrt{2\sqrt{3}}$.

Further, we find that the Peregrine solitons formed will possess the following enhancement factors, relative to the average amplitude, $\sqrt{A/2}$, of the periodic background:

$f_{u_1}=\frac{\left|u_1\left(\mathrm{0,0}\right)\right|}{\sqrt{A/2}}=\frac{|f_U{a}_1+f_V{a}_2|}{\sqrt{A}},(26)$

$f_{u_2}=\frac{\left|u_2\left(\mathrm{0,0}\right)\right|}{\sqrt{A/2}}=\frac{|f_U{a}_1-f_V{a}_2|}{\sqrt{A}},(27)$

where $f_{U,V}$ are defined by Eqs 12 and 13. According to the above definitions, one can find that the Peregrine solitons shown in Figures 1C–F are actually enhanced in the center position up to 2.91 [Figure 1C], 1.80 [Figure 1D], 0.89 [Figure 1E], and 2.18 [Figure 1F] times as high as the average height of the periodic backgrounds, respectively. These enhancement values are all below 3 and do not seem to be different from what we observed in Manakov systems [43, 44].

However, there is more to our story intended for the vector CQ-NLS system, which involves the self-steepening effect denoted by the parameter γ. It is found that due to the presence of the self-steepening effect, the enhancement factors of periodic Peregrine solitons, defined by Eqs 26 and 27, can also be larger than 3, when an appropriate set of initial parameters is selected [32]. To show this, we demonstrate in Figures 2A,B the periodic Peregrine solitons in the same anomalous dispersion regime, but using another set of initial parameters $\gamma =1$, $a_1=\sqrt{7/6}$, $a_2=\sqrt{5/6}$, ${\omega }_1=1/2$, and ${\omega }_2=-1/2$, which, according to Eq. 11, can give rise to $\mu =-2$ and $\nu =\sqrt{96+3\sqrt{805}}/6$. It is seen that one Peregrine soliton component shown in Figure 2A has an enhancement value of around 3.9, while the other one shown in Figure 2B has a much smaller value, 0.56 or so. For comparison, we also provide in Figures 2C,D the surface plots of the rational polynomials $\left|U\right|$ and $\left|V\right|$ obtained under the same parameter condition, which correspond to the conventional bright-bright Peregrine soliton solutions of the vector CQ-NLS equation, each involving the peak-to-background ratios $\left|f_U\right|\approx 2.18$ and $\left|f_V\right|\approx 3.45$, respectively. It is hence obvious that the ultrastrong peak shown in Figure 2A results from the constructive interference of such bright-bright Peregrine soliton components, while the peak in Figure 2B may almost disappear due to the destructive interference, as implied in Eqs 26 and 27.

FIGURE 2

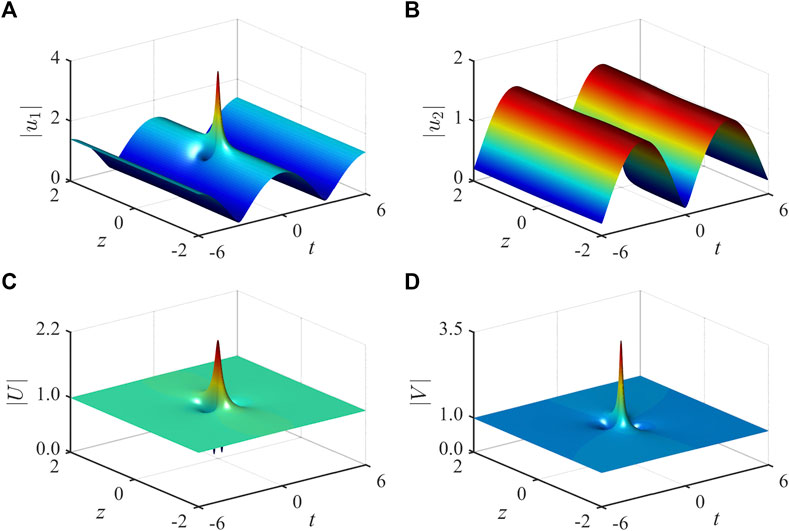
FIGURE 2. Peregrine soliton states on a periodic background, with (A) an anomalous amplitude enhancement on the $u_1$ field component, and (B) a heavy falling-off on the $u_2$ field component, formed in the anomalous dispersion regime $\left(\sigma =1\right)$. The initial parameters are specified by $\gamma =1$, $a_1=\sqrt{7/6}$, $a_2=\sqrt{5/6}$, ${\omega }_1=1/2$, ${\omega }_2=-1/2$, $\mu =-2$, and $\nu =\frac{1}{6}\sqrt{96+3\sqrt{805}}$. For comparison, the surface plots of the rational polynomials $\left|U\right|$ and $\left|V\right|$ are shown in (C) and (D), respectively.

Of most concern is the case of the combination of negative cubic nonlinearity and positive quintic nonlinearity in our vector model, which admits the existence of periodic Peregrine solitons as well. One may recall that such a competing nonlinearity can often be used to support the formation of stable dissipative solitons in mode-locked fiber lasers [49] or to stabilize the soliton propagation in nonlinear media [50]. A study of MI of the background fields reveals that such a competing nonlinearity, which actually means $\sigma =-1$ (i.e., normal dispersion in the context of fiber optics), may favor the generation of Peregrine solitons, with larger transient wave-packet size, as compared to the anomalous dispersion case discussed above [59]. Figure 3 shows the formation of periodic Peregrine solitons in the normal dispersion regime, which is a linear superposition of the given U and V distributions shown in Figures 3A,B. For simplicity, we used a special set of initial parameters that meets Eqs 14 and 15 and thus used Eqs 17 and 18 for U and V in Eq. 5. Clearly, using this set of parameters, we can obtain $\left|f_U\right|=4$ and $\left|f_V\right|=0$, as indicated in Figures 3A,B. Hence, both periodic Peregrine soliton components shown in Figures 3C,E would involve an enhancement value 1.63 in the center position, despite that they have a different amplitude distribution, as indicated by the contour plots in Figures 3D,F. As compared with Figure 1, the periodic Peregrine solitons shown in Figure 3 exhibit a larger spatiotemporal dimension and thus a larger transient wave-packet size.

FIGURE 3

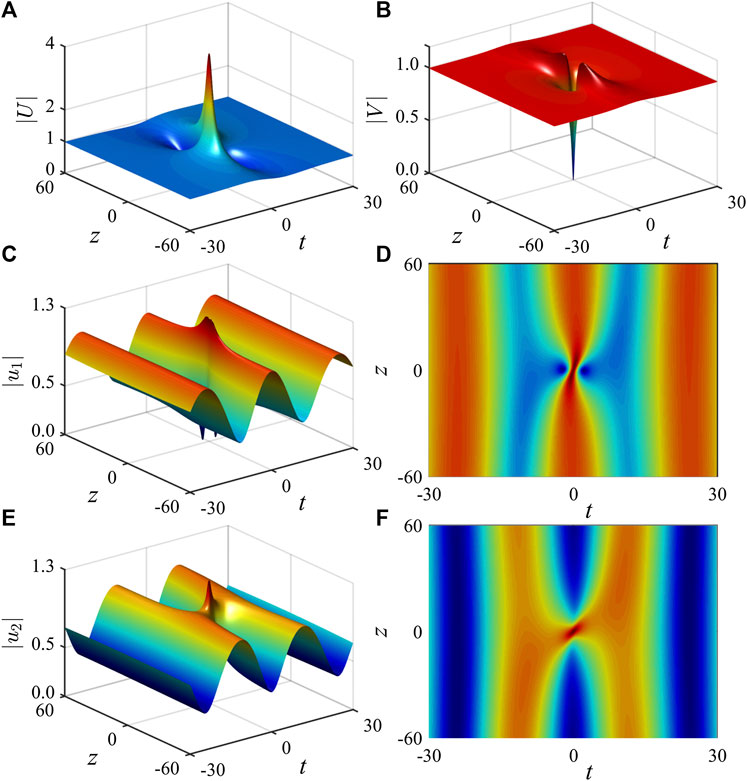
FIGURE 3. Peregrine solitons on a periodic background formed in the normal dispersion regime ($\sigma =-1$), defined by the solutions Eqs 5, 17, and 18, under the parameters $\gamma =1$, $a_1=4/9$, $a_2=4\sqrt{5}/9,{\omega }_1=-10/81$, ${\omega }_2=10/81$, $\mu =-32/27$, and $\nu =-10\sqrt{3}/81$. While (A) and (B) display the surface plots for $\left|U\right|$ and $\left|V\right|$, (C) and (E) show the surface plots of Peregrine solitons for the $u_1$ and $u_2$ fields, respectively, with their corresponding contour plots given in (D) and (F).

Now a natural question arises as to whether these periodic-background Peregrine soliton solutions are robust against numerical noises or even against strong “non-integrable” perturbations by which we mean that the specific relation between the coefficients for quintic nonlinearity and self-steepening terms can be lifted. To answer this question, we perform extensive numerical simulations with respect to our analytical solutions (Eq. 5), using an efficient code based on the exponential time differencing Crank–Nicolson (ETDCN) scheme with Padé approximation [60, 61]. Here we present merely two sets of numerical results, for a typical set of system parameters $\sigma =1$, $\gamma =1/4$, $a_1=8/9$, $a_2=4\sqrt{5}/9$, ${\omega }_1=-40/81$, and ${\omega }_2=40/81$, which would lead to $\mu =-4/9$ and $\nu =-40\sqrt{3}/81$. First, for the purpose of comparison, we integrated the original integrable CQ-NLS Eqs 1 and 2 numerically, with the analytical solutions at $z=-4$ as initial conditions. Simulation results are shown in Figures 4A,B. It is clear that our numerical code gave precisely the whole solution profiles as predicted by the analytical solutions (Eq. 5) till $z=4$, despite the intrinsic numerical noises. Second, we violate the integrability of the governed model by solely changing the coefficient $\text{i}\gamma$ of the self-steepening term to $\text{i}\gamma \left(1+10\text{\%}\right)$ in the model, and simulate again the Peregrine soliton solutions under otherwise identical parameter conditions, with results given in Figures 4C,D. It is clearly seen that the whole Peregrine soliton profiles on a periodic background can still be well maintained till $z=2$ (see the region before the white dashed line), almost the same as shown in Figures 4A,B, implying that our analytical solutions (Eq. 5) are still robust against such strong non-integrable perturbations. After $z=2$, due to the onset of MI, there would appear complex wave structures, which tend to interfere with the trailing edge of Peregrine soliton profiles. The above simulations also confirm, to an extent, the physical relevance of our analytical solutions obtained with the coupled CQ-NLS Eqs 1 and 2, although the model involves a special parameter relation between the quintic nonlinearity and the self-steepening terms in order to enable integrability.

FIGURE 4

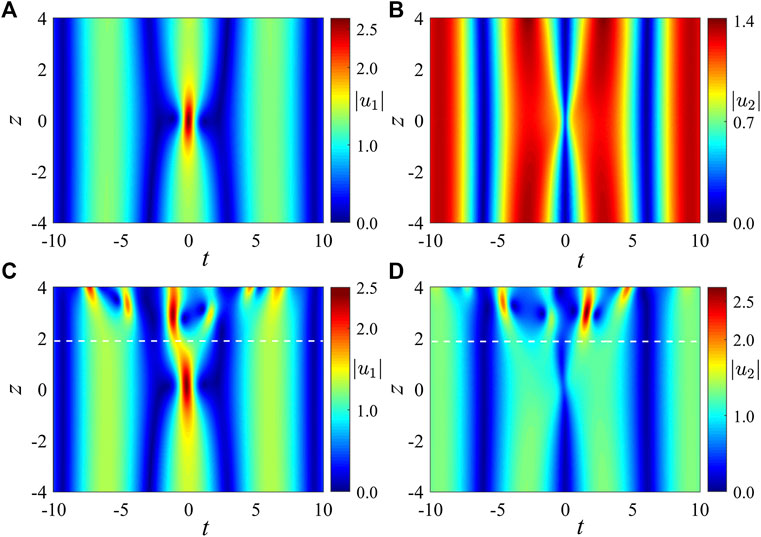
FIGURE 4. Typical simulations of the periodic Peregrine soliton solutions (Eq. 5) for given parameters $\sigma =1$, $\gamma =1/4$, $a_1=8/9$, $a_2=4\sqrt{5}/9$, ${\omega }_1=-40/81$, ${\omega }_2=40/81$, $\mu =-4/9$, and $\nu =-40\sqrt{3}/81$, under (A),(B) the original integrable CQ-NLS Eqs 1 and 2, and (C),(D) the same CQ-NLS model but with the coefficient $\text{i}\gamma$ of the self-steepening term being changed to $\text{i}\gamma \left(1+10\text{\%}\right)$, respectively.

Finally, we would like to point out that our solution form defined by Eq. 5 is universal and can be applied to the higher-order rogue wave hierarchy built on a periodic background, only when $U{u}_{10}$ and $V{u}_{20}$ are the corresponding conventional higher-order solutions of the underlying vector model. Here for our current purpose, we provide the periodic two-Peregrine-soliton solutions defined by Eqs 5, 19, and 20, which describe the interaction between two Peregrine soliton constituents, for any set of initial parameters that meets Eqs 14 and 15. Typical results are demonstrated in Figure 5, where we used the same system parameters as in Figure 3, and three extra parameters ${\gamma }_1=60$, ${\gamma }_2=8\text{i}$, and ${\gamma }_3=1$. It is shown that on a periodic background, there appear two well-separated Peregrine soliton states on each field component; one may behave like a spike, while the other is weaker in peak amplitude. Of course, there would occur other complex patterns on the periodic background, when the free parameters ${\gamma }_s$ (s=1,2,3) are changed. However, it is due to the inclusion of these extra parameters that our general solutions presented above can be used to model the multivariant rogue wave events met in practical conditions.

FIGURE 5

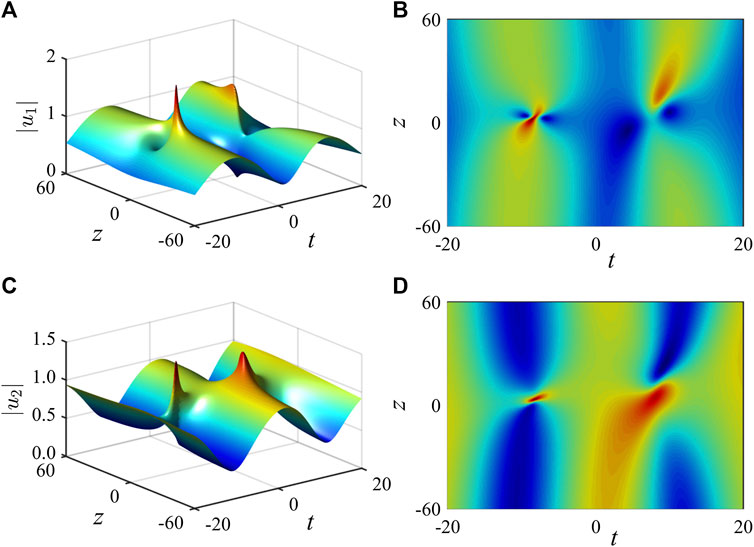
FIGURE 5. Interaction of two Peregrine solitons on a periodic background, under the same initial parameters as in Figure 3. The three extra parameters in Eqs 19 and 20 are given by ${\gamma }_1=60$, ${\gamma }_2=8\text{i}$, and ${\gamma }_3=1$.

4 Conclusion

In conclusion, we presented exact Peregrine soliton solutions built on a periodic background caused by the interference in the vector CQ-NLS equation involving self-steepening. It is revealed that such periodic Peregrine soliton solutions are indeed a linear superposition of two fundamental Peregrine solitons of different cw backgrounds, provided that the continuous waves possess a nonvanishing frequency difference. With these exact solutions, we demonstrated the coexistence of Peregrine solitons on the same periodic background, under certain parameter conditions. Further, the ultrastrong amplitude enhancement was proved to occur on the periodic background as well, due to the presence of the self-steepening effect. We numerically confirm the stability of these analytical solutions against significant non-integrable perturbations. We also showed the interaction of two Peregrine solitons on the periodic background, which are still a linear superposition of those on the cw background. Basically, such simple superposition rule can be applied to the higher-order rogue wave hierarchy on a periodic background. As one might expect, these findings may shed more light on our understanding of the realistic rogue wave behaviors occurring in either the fiber-optic telecommunication links [7] or the crossing seas [9].

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding authors.

Author Contributions

YY, LB, and WW performed the derivations and plotted the figures. SC, FB, and DM proposed the theoretical framework, performed simulations, and wrote and revised the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grants No. 11474051 and No. 11974075) and by the Scientific Research Foundation of Graduate School of Southeast University (Grant No. YBPY1872).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Dysthe K, Krogstad HE, Müller P. Oceanic Rogue waves. Annu Rev Fluid Mech (2008). 40:287–310. doi:10.1146/annurev.fluid.40.111406.102203.

CrossRef Full Text | Google Scholar

2. Adcock TAA, Taylor PH, Draper S. Nonlinear dynamics of wave-groups in random seas: unexpected walls of water in the open ocean. Proc R Soc A (2015). 471:20150660. doi:10.1098/rspa.2015.0660.

CrossRef Full Text | Google Scholar

3. Akhmediev N, Ankiewicz A, Taki M. Waves that appear from nowhere and disappear without a trace. Phys Lett (2009). 373:675–8. doi:10.1016/j.physleta.2008.12.036

CrossRef Full Text | Google Scholar

4. Kharif C, Pelinovsky E, Slunyaev A. Rogue waves in the ocean Berlin, Germany: Springer (2009). 216 p.

Google Scholar

5. Solli DR, Ropers C, Koonath P, Jalali B. Optical rogue waves. Nature (2007). 450:1054–7. doi:10.1038/nature06402.

CrossRef Full Text | Pubmed | Google Scholar

6. Shats M, Punzmann H, Xia H. Capillary rogue waves Phys Rev Lett (2010). 104:104503. doi:10.1103/PhysRevLett.104.104503.

CrossRef Full Text | Pubmed | Google Scholar

7. Wabnitz S. Nonlinear guided wave optics: a testbed for extreme waves Bristol, UK: IOP Publishing (2017). 387 p.

Google Scholar

8. Malomed BA, Mihalache D. Nonlinear waves in optical and matter-wave media: a topical survey of recent theoretical and experimental results. Rom J Phys (2019). 64:106.

Google Scholar

9. Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi FT. Rogue waves and their generating mechanisms in different physical contexts. Phys Rep (2013). 528:47–89. doi:10.1016/j.physrep.2013.03.001.

CrossRef Full Text | Google Scholar

10. Pisarchik AN, Jaimes-Reátegui R, Sevilla-Escoboza R, Huerta-Cuellar G, Taki M. Rogue waves in a multistable system. Phys Rev Lett (2011). 107:274101. doi:10.1103/PhysRevLett.107.274101.

CrossRef Full Text | Pubmed | Google Scholar

11. Vergeles S, Turitsyn SK. Optical rogue waves in telecommunication data streams. Phys Rev A (2011). 83:061801. doi:10.1103/PhysRevA.83.061801.

CrossRef Full Text | Google Scholar

12. Arecchi FT, Bortolozzo U, Montina A, Residori S. Granularity and inhomogeneity are the joint generators of optical rogue waves. Phys Rev Lett (2011). 106:153901. doi:10.1103/PhysRevLett.106.153901.

CrossRef Full Text | Pubmed | Google Scholar

13. Dudley JM, Dias F, Erkintalo M, Genty G. Instabilities, breathers and rogue waves in optics. Nat Photon (2014). 8:755–64. doi:10.1038/NPHOTON.2014.220.

CrossRef Full Text | Google Scholar

14. Walczak P, Randoux S, Suret P. Optical rogue waves in integrable turbulence. Phys Rev Lett (2015). 114:143903. doi:10.1103/PhysRevLett.114.143903.

CrossRef Full Text | Pubmed | Google Scholar

15. Soto-Crespo JM, Devine N, Akhmediev N. Integrable turbulence and rogue waves: breathers or solitons? Phys Rev Lett (2016). 116:103901. doi:10.1103/PhysRevLett.116.103901.

CrossRef Full Text | Pubmed | Google Scholar

16. Onorato M, Osborne AR, Serio M. Modulational instability in crossing sea states: a possible mechanism for the formation of freak waves. Phys Rev Lett (2006). 96:014503. doi:10.1103/PhysRevLett.96.014503.

CrossRef Full Text | Pubmed | Google Scholar

17. Baronio F, Conforti M, Degasperis A, Lombardo S, Onorato M, Wabnitz S. Vector rogue waves and baseband modulation instability in the defocusing regime. Phys Rev Lett (2014). 113:034101. doi:10.1103/PhysRevLett.113.034101.

CrossRef Full Text | Pubmed | Google Scholar

18. Chen S, Baronio F, Soto-Crespo JM, Grelu P, Mihalache D. Versatile rogue waves in scalar, vector, and multidimensional nonlinear systems. J Phys Math Theor (2017). 50:463001. doi:10.1088/1751-8121/aa8f00.

CrossRef Full Text | Google Scholar

19. Grinevich PG, Santini PM. The exact rogue wave recurrence in the NLS periodic setting via matched asymptotic expansions, for 1 and 2 unstable modes. Phys Lett A (2018). 382:973–9. doi:10.1016/j.physleta.2018.02.014.

CrossRef Full Text | Google Scholar

20. Grinevich PG, Santini PM. The finite-gap method and the periodic NLS Cauchy problem of anomalous waves for a finite number of unstable modes. Russ Math Surv (2019). 74:211–63. doi:10.1070/RM9863.

CrossRef Full Text | Google Scholar

21. Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, et al. . The Peregrine soliton in nonlinear fibre optics. Nat Phys (2010). 6:790–5. doi:10.1038/NPHYS1740.

CrossRef Full Text | Google Scholar

22. Chen S, Baronio F, Soto-Crespo JM, Liu Y, Grelu P. Chirped Peregrine solitons in a class of cubic-quintic nonlinear Schrödinger equations. Phys Rev E (2016). 93:062202. doi:10.1103/PhysRevE.93.062202.

CrossRef Full Text | Pubmed | Google Scholar

23. Chen S, Soto-Crespo JM, Grelu P. Coexisting rogue waves within the (2+1)-component long-wave-short-wave resonance. Phys Rev E (2014). 90:033203. doi:10.1103/PhysRevE.90.033203.

CrossRef Full Text | Google Scholar

24. Peregrine DH, Water waves, nonlinear Schrödinger equations and their solutions. J Aust Math Soc Ser B Appl Math (1983). 25:16–43. doi:10.1017/S0334270000003891.

CrossRef Full Text | Google Scholar

25. Shrira VI, Geogjaev VV. What makes the Peregrine soliton so special as a prototype of freak waves? J Eng Math (2010). 67:11–22. doi:10.1007/s10665-009-9347-2.

CrossRef Full Text | Google Scholar

26. Chabchoub A, Hoffmann NP, Akhmediev N. Rogue wave observation in a water wave tank. Phys Rev Lett (2011). 106:204502. doi:10.1103/PhysRevLett.106.204502.

CrossRef Full Text | Pubmed | Google Scholar

27. Tikan A, Billet C, El G, Tovbis A, Bertola M, Sylvestre T, et al. . Universality of the peregrine soliton in the focusing dynamics of the cubic nonlinear schrödinger equation. Phys Rev Lett (2017). 119:033901. doi:10.1103/PhysRevLett.119.033901.

CrossRef Full Text | Pubmed | Google Scholar

28. Dudley JM, Genty G, Mussot A, Chabchoub A, Dias F. Rogue waves and analogies in optics and oceanography. Nat Rev Phys (2019). 1:675–89. doi:10.1038/s42254-019-0100-0.

CrossRef Full Text | Google Scholar

29. Bailung H, Sharma SK, Nakamura Y. Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys Rev Lett (2011). 107:255005. doi:10.1103/PhysRevLett.107.255005.

CrossRef Full Text | Pubmed | Google Scholar

30. Frisquet B, Kibler B, Morin P, Baronio F, Conforti M, Millot G, et al. . Optical dark rogue wave. Sci Rep (2016). 6:20785. doi:10.1038/srep20785.

CrossRef Full Text | Pubmed | Google Scholar

31. Chen S, Ye Y, Soto-Crespo JM, Grelu P, Baronio F. Peregrine solitons beyond the threefold limit and their two-soliton interactions. Phys Rev Lett (2018). 121:104101. doi:10.1103/PhysRevLett.121.104101.

CrossRef Full Text | Pubmed | Google Scholar

32. Chen S, Pan C, Grelu P, Baronio F, Akhmediev N. Fundamental Peregrine solitons of ultrastrong amplitude enhancement through self-steepening in vector nonlinear systems. Phys Rev Lett (2020). 124:113901. doi:10.1103/PhysRevLett.124.113901.

CrossRef Full Text | Pubmed | Google Scholar

33. Baronio F. Akhmediev breathers and Peregrine solitary waves in a quadratic medium. Opt Lett (2017). 42:1756–9. doi:10.1364/OL.42.001756.

CrossRef Full Text | Pubmed | Google Scholar

34. Baronio F, Chen S, Mihalache D. Two-color walking Peregrine solitary waves. Opt Lett (2017). 42:3514–7. doi:10.1364/OL.42.003514.

CrossRef Full Text | Pubmed | Google Scholar

35. Liu W, Zhang Y, He J. Rogue wave on a periodic background for Kaup–Newell equation. Rom Rep Phys (2018). 70:106.

CrossRef Full Text | Google Scholar

36. Andral U, Kibler B, Dudley JM, Finot C. Akhmediev breather signatures from dispersive propagation of a periodically phase-modulated continuous wave. Wave Motion (2020). 95:102545. doi:10.1016/j.wavemoti.2020.102545.

CrossRef Full Text | Google Scholar

37. Zhao L-C, Duan L, Gao P, Yang Z-Y, Vector rogue waves on a double-plane wave background. Europhys Lett (2019). 125:40003. doi:10.1209/0295-5075/125/40003.

CrossRef Full Text | Google Scholar

38. Rao J, He J, Mihalache D, Cheng Y. PT-symmetric nonlocal Davey-Stewartson I equation: general lump-soliton solutions on a background of periodic line waves. Appl Math Lett (2020). 104:106246. doi:10.1016/j.aml.2020.106246.

CrossRef Full Text | Google Scholar

39. Chen J, Pelinovsky DE, Rogue periodic waves of the focusing nonlinear Schrödinger equation. Proc R Soc A (2018). 474:20170814. doi:10.1098/rspa.2017.0814.

CrossRef Full Text | PubmedGoogle Scholar

40. Chen J, Pelinovsky DE, White RE. Rogue waves on the double-periodic background in the focusing nonlinear Schrödinger equation. Phys Rev E (2019). 100:052219. doi:10.1103/PhysRevE.100.052219.

CrossRef Full Text | Google Scholar

41. Xu G, Chabchoub A, Pelinovsky DE, Kibler B. Observation of modulation instability and rogue breathers on stationary periodic waves. Phys Rev Res (2020). 2:033528. doi:10.1103/PhysRevResearch.2.033528.

CrossRef Full Text | Google Scholar

42. Chen S, Zhou Y, Bu L, Baronio F, Soto-Crespo JM, Mihalache D. Super chirped rogue waves in optical fibers. Optic Express (2019). 27:11370–84. doi:10.1364/OE.27.011370.

CrossRef Full Text | Pubmed | Google Scholar

43. Baronio F, Degasperis A, Conforti M, Wabnitz S. Solutions of the vector nonlinear schrödinger equations: evidence for deterministic Rogue waves. Phys Rev Lett (2012). 109:044102. doi:10.1103/PhysRevLett.109.044102.

CrossRef Full Text | Pubmed | Google Scholar

44. Chen S, Mihalache D. Vector rogue waves in the Manakov system: diversity and compossibility. J Phys Math Theor (2015). 48:215202. doi:10.1088/1751-8113/48/21/215202.

CrossRef Full Text | Google Scholar

45. Zhang Y, Cheng Y, He J. Riemann-Hilbert method and N-soliton for two-component Gerdjikov-Ivanov equation. J Nonlinear Math Phys (2017). 24:210–23. doi:10.1080/14029251.2017.1313475.

CrossRef Full Text | Google Scholar

46. Kodama Y, Hasegawa A. Nonlinear pulse propagation in a monomode dielectric guide. IEEE J Quant Electron (1987). 23:510–24. doi:10.1109/JQE.1987.1073392.

CrossRef Full Text | Google Scholar

47. Agrawal GP. Nonlinear fiber optics 4th ed. San Diego, CA: Academic (2007). 529 p

Google Scholar

48. Kivshar YS, Agrawal GP. Optical solitons: from fibers to photonic crystals San Diego, CA: Academic (2003). 557 p.

Google Scholar

49. Grelu P. Nonlinear optical cavity dynamics: from microresonators to fiber lasers Weinheim, Germany: Wiley VCH (2016). 785 p.

Google Scholar

50. Mihalache D, Mazilu D, Crasovan L-C, Towers I, Buryak AV, Malomed BA, et al. Stable spinning optical solitons in three dimensions. Phys Rev Lett (2002). 88:073902. doi:10.1103/PhysRevLett.88.073902.

CrossRef Full Text | Pubmed | Google Scholar

51. Dudley JM, Genty G, Coen S. Supercontinuum generation in photonic crystal fiber. Rev Mod Phys (2006). 78:1135–84. doi:10.1103/RevModPhys.78.1135.

CrossRef Full Text | Google Scholar

52. Chen S, Song L-Y. Rogue waves in coupled Hirota systems. Phys Rev E (2013). 87:032910. doi:10.1103/PhysRevE.87.032910.

CrossRef Full Text | Google Scholar

53. Degasperis A, Lombardo S. Rational solitons of wave resonant-interaction models. Phys Rev E (2013). 88:052914. doi:10.1103/PhysRevE.88.052914.

CrossRef Full Text | Google Scholar

54. Degasperis A, Lombardo S. Multicomponent integrable wave equations: I. Darboux-dressing transformation. J Phys Math Theor (2007). 40:961–77. doi:10.1088/1751-8113/40/5/007.

CrossRef Full Text | Google Scholar

55. Degasperis A, Lombardo S. Multicomponent integrable wave equations: II. soliton solutions. J Phys Math Theor (2009). 42:385206. doi:10.1088/1751-8113/42/38/385206.

CrossRef Full Text | Google Scholar

56. Degasperis A, Lombardo S, Sommacal M. Rogue wave type solutions and spectra of coupled nonlinear schrödinger equations. Fluids (2019). 4:57. doi:10.3390/fluids4010057.

CrossRef Full Text | Google Scholar

57. Guo B, Ling L, Liu QP. Nonlinear Schrödinger equation: generalized Darboux transformation and rogue wave solutions. Phys Rev E (2012). 85:026607. doi:10.1103/PhysRevE.85.026607.

CrossRef Full Text | Google Scholar

58. Ye Y, Zhou Y, Chen S, Baronio F, Grelu P. General rogue wave solutions of the coupled Fokas-Lenells equations and non-recursive Darboux transformation. Proc R Soc A (2019). 475:20180806. doi:10.1098/rspa.2018.0806.

CrossRef Full Text | Pubmed | Google Scholar

59. Ye Y, Liu J, Bu L, Pan C, Chen S, Mihalache D. Rogue waves and modulation instability in an extended Manakov system. Nonlinear Dyn (2020). doi:10.1007/s11071-020-06029-z.

60. Kleefeld B, Khaliq AQM, Wade BA. An ETD Crank-Nicolson method for reaction-diffusion systems. Numer Methods Part Differ Equ (2012). 28:1309–35. doi:10.1002/num.20682.

CrossRef Full Text | Google Scholar

61. Chen S, Ye Y, Baronio F, Liu Y, Cai X-M, Grelu P. Optical Peregrine rogue waves of self-induced transparency in a resonant erbium-doped fiber. Optic Express (2017). 25:29687–98. doi:10.1364/OE.25.029687.

CrossRef Full Text | Pubmed | Google Scholar