Abstract
In this article, an model of COVID-19 epidemic on networks is established and analyzed. Following the method of the next-generation matrix, we derive the basic reproduction number R0, and it shows that the asymptomatic infector plays an important role in disease spreading. We analytically show that the disease-free equilibrium is asymptotically stable if moreover, the effects of various quarantine strategies are investigated and compared by numerical simulations. The results obtained are informative for us to further understand the asymptomatic infector in COVID-19 propagation and get some effective strategies to control the disease.
1 Introduction
Coronaviruses are a group of enveloped viruses with a positive-sense, single-stranded RNA and viral particles resembling a crown from which the name derives. They belong to the order of Nidovirales, family of Coronaviridae, and subfamily of Orthocoronavirinae. A recent coronavirus outbreak has started since December 2019. So far, the new virus has infected more than 25 million people and killed at least 842,000 of them [1–3].
In order to better study the spread and control of infectious diseases, several classical mathematical models have been discussed to understand the transmission mechanism and dynamics of the disease, such as the SI model, SIR model, SEIR model, and SEIRS model [4, 5]. Different factors are considered in different models, and the purpose of these models is finding the transmission mechanism and dynamics of the diseases for controlling the diseases. This process needs a contact between them. It is found that the best pattern of contact is contact in the networks [6–11], and study epidemic model on networks has been a hot field in mathematical biology [6–20,35].
To find the transmission mechanism, we have to know who is the infector [27]. An infector is an individual who carries the virus and can export the virus. Sometimes, an individual with the infected state may not show any symptoms of disease, and the state can be defined as asymptomatically infected. An individual with the infected state who shows symptoms of disease can be defined as symptomatically infected. Exposed state and asymptomatically infected state are more dangerous than symptomatically infected state. When a susceptible individual contacts a symptomatic one, he(she) will usually do something possible to prevent the disease spreading.
In the disease spreading process, a symptomatic infector will be restricted by individual behavior or public behavior, but a symptomatic one has a higher efficiency than an asymptomatic one. A class of works studied the role of symptomatic infectors and asymptomatic infectors in diseases infections, such as dengue virus [21, 22], malaria [23], and Norovirus [24–27]. The results of these works all show that the asymptomatic cases cannot be neglected. Recently, several mathematic models within asymptomatic infection have been studied, such as model [21], CI model [28], model [29], and model [30]. But mathematical models within asymptomatic infection on networks are still relatively rare. When the COVID-19 pandemic begin to outbreak, quarantining certain individuals may be the most efficient way to stop the outbreak of disease, but the choice of which is an important step in the control process, and thus we also discuss the effect of different quarantine strategies.
In this article, we consider an epidemic model on scale-free networks to study the spread of COVID-19. Further, we consider the effect of the asymptomatic state changing into the symptomatic state. By studying the dynamics of the model, we try to find what role the three infectors, E, A, and I, play in disease spreading, especially for the asymptomatic infectors, E and A. Next, in Section 2, we establish an COVID-19 model on network. In Section 3, we study the dynamics of the model. In Section 4, we study and compare the effects of various control strategies, and carry out numerical simulations to illustrate the theoretical results in Section 5. Finally, conclusions and some discussions are given in Section 6.
2 The Model
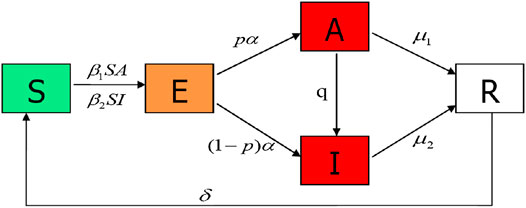
In the spread process, each node has five states: susceptible (S); exposed (E); asymptomatically infected (A), those who are infectious but have no symptoms; symptomatically infected (I), those who are infectious but have symptoms; and removed (R). The disease transmission flow is depicted in Figure 1. A susceptible individual can be infected by contact at rate if there are infected individuals with A in its neighbors, or be infected by contact at rate if there are symptomatically infected individuals I. The exposed individual will become A and I with rate and , and A will become I individual at rate q. The infected A and I will become a recovered individual at rate and due to treatment, respectively. A recovered individual will become S at rate δ. All parameters are nonnegative.
FIGURE 1
In this article, we consider an epidemic model on scale-free networks as follows:
Following [6], describes the average degree and describes the degree distribution; the probability is a link pointing to an exposed individual, asymptomatic infected individual, and symptomatic infected individual. Here, is a constant that stands for the number of nodes with degree k. Then, and . We have
For the practice, the initial condition for model (2.1) satisfies the following:
3 Dynamical Behaviors of the Model
In this section, we study the stability of disease-free equilibrium of model (2.1). First, we derive the basic reproduction number of the model.
3.1 Equilibria and Basic Reproduction Number
Lemma 3.1.Lemma 3.1. Suppose that is a solution of model (2.1) satisfying initial conditions of Eq. (2.4), thenis a positive invariant for model (2.1).The proof of this lemma is similar to that in [31]. We ignore it here. The stability analysis and numerical simulations are investigated in the positive invariant .It is easy to find that model (2.1) has a disease-free equilibrium , it is the only susceptible state. , where , . Following the method of the next-generation matrix [32], the basic reproduction number can be calculated by . Here, F is the matrix of the rate of generation of new infections, and V is the matrix of the rate of transfer of individuals out of the two compartments. F is given byandIn addition, , whereandso, , and the basic reproduction number R0 can be obtained:Let be the Jacobian matrix of the middle three equations of model (2.1), then and : λ is an eigenvalue of , , . [34]
Remark 3.1.Let , , then , if , this result is corresponding to the result in [27].
Remark 3.2.If we do not consider the asymptomatic infected state, that is , , , then , which is corresponding to the result in [6, 33].
Lemma 3.2.If and only if , there is a unique endemic equilibrium .
Proof.We consider the right side of the model (2.1) to be equal to zero. Then, we obtainFollowing the above equation, using , we can findAccording to the condition , we can getSubstituting , , and of Eq.(3.2) and Eq.(3.3) into θ, we can obtain , whereand , , . It is easy to find that has a trivial solution with no condition, and model (2.1) has a disease-free equilibrium. In addition,Thus, has a nontrivial solution if and only if , that is if and only if , there is a unique endemic equilibrium.
3.2 Stability of Disease-free and Endemic Equilibrium
If , of model (2.1) is locally asymptotically stable; if , is unstable, and there is a unique endemic equilibrium , and is locally asymptotically stable.
Proof.From the results of Lemma 3.1, Lemma 3.2, and the basic reproduction number, we only need to prove the case of . We consider the following model:The Jacobian matrix of model (3.4) at disease-free equilibrium is given bywithThe characteristic equation of the disease-free equilibrium iswherewhen , , andThen, we obtain , and the characteristic equation can be written aswhere the eigenvalues of J are all negative except zero eigenvalue when .
4 Quarantine Strategies
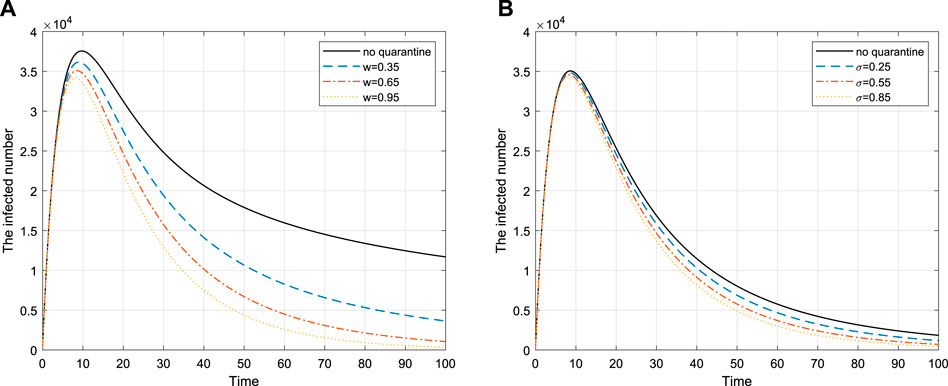
Quarantine is helpful in controlling diseases. In this section, we will discuss three different quarantine strategies for COVID-19 disease model on networks.
4.1 Proportional Quarantine
In this case, for fixed spreading rates and , let is the density of quarantine nodes in the network. At the mean-field level, the presence of proportional quarantine will effectively reduce the spreading rate. Thus, we can approximately use to substitute and use to substitute ; thus, the system (2.1) becomes
Using the same method in Section 3, we obtain a self-consistency equation as follows:
By arguments similar to those in Section 3, the epidemic threshold is determined by the following inequality:therefore, it can be shown thatthat is,
Note that in (4.3), when , that is, if no quarantine were done, then ; when , , that is, the quarantine scheme is effective; while as , , that is, in the case of a full quarantine, it would be impossible for the epidemic to spread in the network.
4.2 Targeted Quarantine
While proportional quarantine schemes are effective, there may be more efficient schemes due to the heterogeneous nature of scale-free networks. We introduce an upper threshold κ such that all nodes with connectivity are immunized, that is, we define the quarantine rate bywhere and , where is the average quarantine rate. The epidemic dynamics model isThis leads to
Therefore, the epidemic threshold
Note that where is the covariance of and . There may be κ (usually big enough) where , but for appropriately small κ, and have the same signs except for some k where and/or is zero; Therefore for appropriate κ. Then,
If we set , then,which means the targeted quarantine scheme is more efficient than the uniform quarantine scheme for the same average quarantine rate.
4.3 High-Risk Quarantine
If a neighbor of a susceptible individual is infected, vaccinating this susceptible individual is called high-risk immunity [37]. We introduce the parameter σ, that is, the probability that a node is quarantined per unit time, and , which denotes the probability that any given node is the neighbor of some specific nodes. The epidemic dynamics model isThis leads toAnd the epidemic threshold
This means that the implementation of high-risk quarantine is effective, and the longer the period of , the more effective it is.
5 Numerical Simulations
In this section, we present numerical simulations of model (2.1), (4.1) and (4.6) to illustrate the results in Section 3 and 4. Without loss of generality, we consider the dynamical process on scale-free networks with and , , . The average infected number is . The parameters of the model are estimated by MCMC using the number of cases in Wuhan (http://wjw.wuhan.gov.cn/ztzl_28/fk/yqtb/).
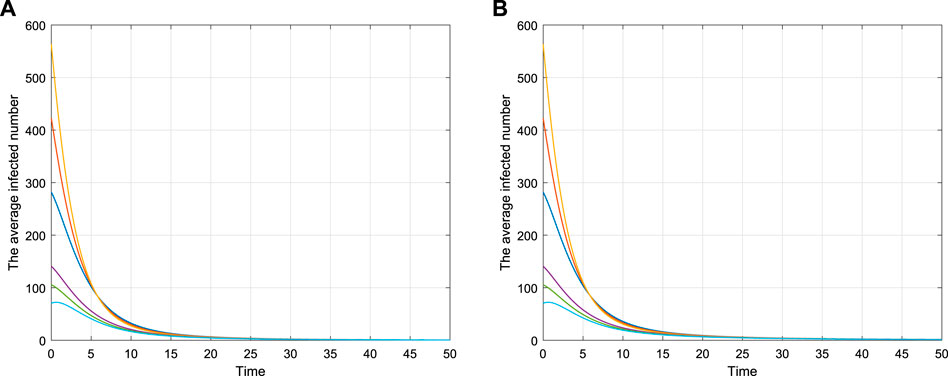
Figure 2 shows the asymptotical stability of model (2.1) with different values, and the parameter values are shown in Table 1. Figures 2A,B show the time series of the average infected number I(t) with different initial values, which is in accord with the asymptotical stability of the disease-free equilibrium.
FIGURE 2
TABLE 1
| Figure 2 | β1 | β2 | δ | α | p | q | μ1 | μ2 | R0 |
|---|---|---|---|---|---|---|---|---|---|
| A | 0.08 | 0.08 | 0.4 | 0.4 | 0.5 | 0.5 | 0.2 | 0.4 | 0.8193 1 |
| B | 0.0905 | 0.10003 | 0.4 | 0.4 | 0.5 | 0.5 | 0.2 | 0.4 | 1 |
Parameters of Figure 2
TABLE 2
Parameters of Figure 4
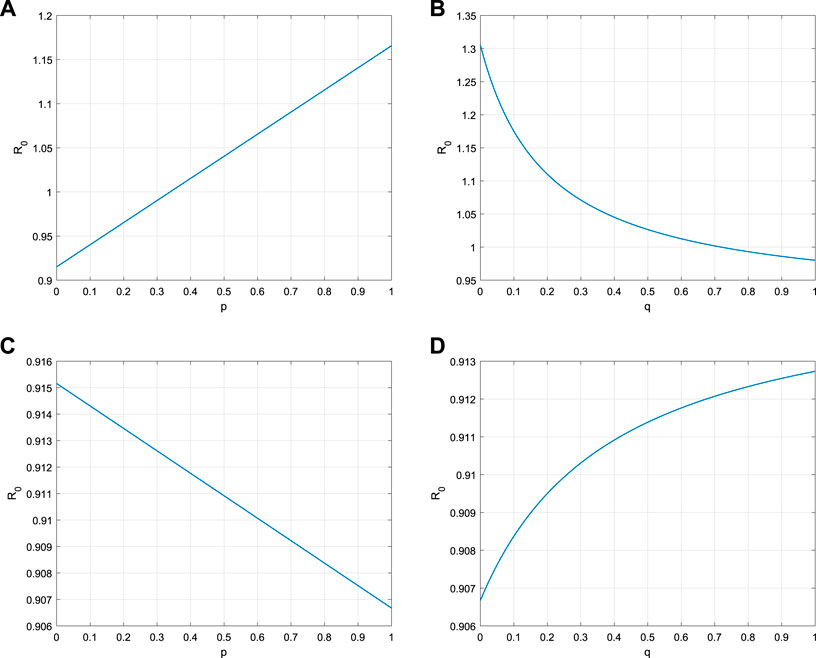
The sensitivity analysis of the basic reproduction number R0 can be performed by model parameters. It is easy to obtain that
Equation (5.1) shows is linearly positively correlated with and ; is negatively correlated with and ; the correlation between and p or q is determined by As can be seen from Figure 3 that the monotonicity of R0 increases or decreases with respect to p and q, respectively. In Figure 4, the parameters of the model are estimated by MCMC using the number of cases in Wuhan and the parameter values are shown in Table 2. Figure 4 shows the change of total infection density with time under different ω and σ. It can be seen that with the increase of ω and σ, the total infection density is becoming lower as ω and σ increase.
FIGURE 3
FIGURE 4
6 Conclusion and Discussion
In this article, we have generalized a traditional homogeneous epidemic model with asymptomatic infectors to a network case to study the spread of COVID-19. As one can see, homogeneous epidemic models can be considered as a special case of network epidemic models, and network epidemic models are more realistic and refined description of disease propagation in population. Considering two cases of infected state (show symptoms and show no symptoms), we investigated an model of COVID-19 on scale-free networks to approach the disease progress and calculated the basic reproduction number R0. By theoretical analysis, we obtained the asymptotical stability of the equilibria: if , is asymptotically stable. Then, we analyzed the different quarantine strategies in the model. At last, numerical simulations illustrated the theoretical analysis. The results show that the asymptomatic infectors may infect health individuals as well as symptomatic infectors.
The SEAIRS model is an extension of the SEAIRS model, and it is a case of the model. The model, model, and model differ in terms of pathological mechanisms. It is difficult to say which one is better than others except introducing a special disease. Within models, formally, either the model or model can be a special case of the model. The parameters and denoted in the model are constant. In fact, many infectious diseases show seasonal phenomenon, such as measles, chickenpox, and mumps [36], and each individual has a periodic order; the parameters above should have some periodic property.
At the same time, we have also discussed proportional, targeted quarantine and high-risk quarantine schemes for network models. The result of Leung et al. [27] by illustration is suitable for Norovirus and measles. Different from their work, the formulaic result seems to be unsuitable for any kind of disease, for none of the parameters in the model is assigned to a specific value. In fact, for different disease, the parameters in the model may present special values. COVID-19 is now spreading faster abroad. Susceptible people will also be infected by asymptomatic patients. If not controlled, the epidemic will spread more widely and the number of infected people will be more difficult to control. The epidemic situation in China was obviously well controlled after the implementation of the strategy of lockdown, and other quarantine strategies. Therefore, the model and quarantine strategy in this article can also be applied to other countries. And, we hope that the results will be helpful to study and control the spread of COVID-19 disease.
Funding
Research Project Supported by Fund for Shanxi 1331KIRT and the outstanding youth fund of North University of China.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
ML and YS designed the study, and WL and ML carried out the analysis and contributed to writing the article. XF and YS performed numerical simulations.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1.
Report on novel coronavirus pneumonia epidemic in real time. (2020) https://voice.baidu.com/act/newpneumonia/newpneumonia/.
2.
TangBWangXLiQBragazziNLTangSYXiaoYNet alEstimation of the transmission risk of the 2019-nCoV and its implication for public health interventions. J Comput Math (2020) 9:462. 10.3390/jcm9020462
3.
TangBBragazziNLLiQTangSXiaoYWuJ. An updated estimation of the risk of transmission of the novel coronavirus (2019-nCov). Infect Dis Model (2020) 5:248–55. 10.1016/j.idm.2020.02.001
4.
HethcoteHW. Three basic epidemiological models. Appl Math Ecol (1989) 355:119–44.
5.
LiMYMuldowneyJSvan den DriesscheP. Global stability of SEIRS models in epidemiology. Can Appl Math Q (1999) 7:409–25.
6.
Pastor-SatorrasRVespignaniA. Epidemic spreading in scale-free networks. Phys Rev Lett (2001) 86:3200–3. 10.1103/PhysRevLett.86.3200
7.
ButtsCT. Revisiting the foundations of network analysis. Science (2009) 325(5939):414–6. 10.1126/science.1171022
8.
NewmanM. Networks: an introduction. New York, NY, USA: Oxford University Press (2010).
9.
VespignaniA. Predicting the behavior of techno-social systems. Science (2009) 325(5939):425–8. 10.1126/science.1171990
10.
VespignaniA. Modeling dynamical processes in complex socio-technical systems. Nat Phys (2012) 8:32–9. 10.1038/nphys2160
11.
Pastor-SatorrasRCastellanoCVan MieghemPVespignaniA. Epidemic processes in complex networks. Rev Mod Phys (2015) 87:925–79. 10.1017/cbo9780511791383.010
12.
WangBHanYTanakaG. Interplay between epidemic spread and information propagation on metapopulation networks. J Theor Biol (2017) 420:18–25. 10.1016/j.jtbi.2017.02.020
13.
LiuGLiuZJinZ. Dynamics analysis of epidemic and information spreading in overlay networks. J Theor Biol (2018) 444:28–37. 10.1016/j.jtbi.2018.02.010
14.
ZhangXShanCJinZZhuH. Complex dynamics of epidemic models on adaptive networks. J Differ Equ (2019) 266(1):803–32. 10.1016/j.jde.2018.07.054
15.
MassadEMaSChenMStruchinerCStollenwerkNMaraA. Scale-free network of a dengue epidemic. Appl Math Comput (2008) 195:376–81. 10.1016/j.amc.2007.04.102
16.
MishraBKPandeySK. Dynamic model of worms with vertical transmission in computer network. Appl Math Comput (2011) 217:8438–46. 10.1016/j.amc.2011.03.041
17.
ZhangJPJinZ. The analysis of an epidemic model on networks. Appl Math Comput (2011) 217:7053–64. 10.1007/978-3-662-47824-0_3
18.
NianFYaoS. The epidemic spreading on the multi-relationships network. Appl Math Comput (2018) 339:866–73. 10.1016/j.amc.2018.07.030
19.
WangZSGuoQTSunSWXiaCY. The impact of awareness diffusion on SIR-like epidemics in multiplex networks. Appl Math Comput (2019) 349:134–47. 10.1016/j.chaos.2019.109425
20.
WangZSXiaCYChenZQChenGR. Epidemic propagation with positive and negative preventive information in multiplex networks. IEEE Trans Cybern (2020) 10.1109/TCYB.2019.2960605
21.
GrunnillM. An exploration of the role of asymptomatic infections in the epidemiology of dengue viruses through susceptible, asymptomatic, infected and recovered (SAIR) models. J Theor Biol (2018) 439:195–204. 10.1016/j.jtbi.2017.12.009
22.
MishraAGakkharS. Modeling of Dengue with impact of asymptomatic infection and ADE factor. Differ Equ Dyn Syst (2018) 19:1–17. 10.1007/s12591-018-0436-4
23.
BerettaECapassoVGaraoDG. A mathematical model for malaria transmission with asymptomatic carriers and two age groups in the human population. Math Biosci (2018) 300:87–101. 10.1016/j.mbs.2018.03.024
24.
GallimoreCICubittDdu PlessisNGrayJJ. Asymptomatic and symptomatic excretion of noroviruses during a hospital outbreak of gastroenteritis. J Clin Microbiol (2004) 42:2271–4. 10.1128/jcm.42.5.2271-2274.2004
25.
GarcíaCDuPontHLLongKZSantosJIKoG. Asymptomatic norovirus infection in Mexican children. J Clin Microbiol (2006) 44:2997–3000. 10.1128/JCM.00065-06
26.
BucardoFNordgrenJCarlssonBKindbergEPaniaguaMMöllbyRet alSvenssonL. Asymptomatic norovirus infections in Nicaraguan children and its association with viral properties and histo-blood group antigens. Pediatr Infect Dis J (2010) 29:934–9. 10.1097/INF.0b013e3181ed9f2f
27.
LeungKYTrapmanPBrittonT. Who is the infector? Epidemic models with symptomatic and asymptomatic cases. Math Biosci (2018) 301:190–8. 10.1016/j.mbs.2018.04.002
28.
ChisholmRHCampbellPTWuYTongSYCMcVernonJGeardNImplications of asymptomatic carriers for infectious disease transmission and control. R Soc Open Sci (2018) 5:172341. 10.1098/rsos.172341
29.
De la SenMAlonso-QuesadaSIbeasANistalR. On an SEIADR epidemic model with vaccination, treatment and dead-infectious copses removal controls. Math Comput Simul (2019) 163:47–79. 10.3390/ijerph16152689
30.
MaYLiuMHouQZhaoJ. Modelling seasonal HFMD with the recessive infection in Shandong, China. Math Biosci Eng (2013) 10:1159–71. 10.3934/mbe.2013.10.1159
31.
CaoJWangYAlofiAMazrooeiAAElaiwA. Global stability of an epidemic model with carrier state in heterogeneous networks. IMA J Appl Math (2015) 80:1025. 10.1093/imamat/hxu040
32.
van den DriesschePWatmoughJ. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci (2002) 180:29–48. 10.1016/s0025-5564(02)00108-6
33.
LiuJZhangT. Epidemic spreading of an SEIRS model in scale-free networks. Commun Nonlinear Sci Numer Simulat (2011) 16:3375–84. 10.1063/1.5001176
34.
ZhaoXQJingZJ. Global asymptotic behavior in some cooperative systems of functional differential equations. Can Appl Math Q (1996) 4:421–44.
35.
BarthélemyMBarratAPastor-SatorrasRVespignaniA. Velocity and hierarchical spread of epidemic outbreaks in scale-free networks. Phys Rev Lett (2004) 92:178701. 10.1103/PhysRevLett.92.178701
36.
YorkeJALondonWP. Recurrent outbreaks of measles, chickenpox and mumps. II. Systematic differences in contact rates and stochastic effects. Am J Epidemiol (1973) 98:469–82. 10.1093/oxfordjournals.aje.a121575
37.
NianFWangX. Efficient immunization strategies on complex networks. J Theor Biol (2010) 264:77–83. 10.1016/j.jtbi.2010.01.007
Summary
Keywords
COVID-19 epidemic, networks, asymptomatic, the basic reproduction number, quarantine
Citation
Li W, Fu X, Sun Y and Liu M (2021) Dynamical Analysis of a Mathematical Model of COVID-19 Spreading on Networks. Front. Phys. 8:601459. doi: 10.3389/fphy.2020.601459
Received
01 September 2020
Accepted
25 November 2020
Published
18 January 2021
Volume
8 - 2020
Edited by
Chengyi Xia, Tianjin University of Technology, China
Reviewed by
Chuansheng Shen, Anqing Normal University, China
Weigang Sun, Hangzhou Dianzi University, China
Updates
Copyright
© 2021 Li, Fu, Sun and Liu.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Maoxing Liu, liumaoxing@126.com
This article was submitted to Social Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.